Reconciling conflicting cross-border data sources for updating national accounts: The cross-entropy econometrics approach

3.1Cross-border traffic as NIIP

Technically, we deal with an ill-posed inverse problem [21] when the number of observed data points is lower than the number of unknown mapping noisy points11 to be estimated. Using simplified words, a direct problem is one for which we know the causes (parameters, unknowns), and we are asked to compute the effects (data, observation), having in mind that the same causes lead to the same effects. In the case of an inverse problem, we are given the effect and asked to reconstitute the true random cause [14] among different possible ones, suggesting that the problem may be undetermined. When there is no uniqueness or stability of solutions due to, for example, a noisy observed effect, we are dealing with an ill-posed inverse problem. Among the areas where inverse problems elicited substantial interest in the past [19] are medical imaging, radar and underwater acoustics (determining the shape of an obstacle), petroleum engineering. The ubiquity of ill-posed inverse problems in real life goes beyond the natural sciences and includes manmade systems, the complexity of which may explain, for example, the lack of consensus in phenomena in the social sciences.22 Nonetheless, explicit ill-posed inverse problem application in the social sciences is much more recent.

For almost a century, mathematical and statistical tools devoted to the generalized ill-posed inverse problem recovery system have been proposed in diverse fields of science aimed at, among other things, model parameter recovery. Besides the well-known Tikhonov regularization theory [21], the Gibbs-Shannon-Jaynes [13] maximum (minimum) entropy principle and its recent extensions [22, 2] remain the most used techniques for solving this class of problem.

Let us now consider the case of the Polish-German cross-border traffic case and propose an explicit model. While the German road sensors produce high frequency data (BD) on the traffic by type of vehicle, Poland statistics provides quarterly, low frequency weighted survey series on vehicles by country of origin without specifying the type of vehicle. Obviously, both types of data may represent different data generating systems. Then, combining them could lead to statistical inconsistencies, and overcoming this usually requires additional, simplifying hypotheses. Suggesting that data produced by road sensors display BD characteristics deserves a clarification. In fact, as noted in, e.g. Sivarajah [20], the lack of a clear definition of BD may impact the analytical technique to be applied to produce the information sought. In spite of recent progress, the concept of BD remains evasive (e.g., [11]) since its characterization as data volume is relative and varies due to underlying factors, such as the type of data and time involved. In this paper, we follow Laney [17] and consider that Volume, Variety, and Velocity (or the Three V’s) are the three basic dimensions of the challenges in data management. As such, we consider the first data source described above as a BD source while we do not consider the second source of quarterly data from survey techniques a BD source. For reasons of space, the table containing the original values has not been fully presented in this article.33 Tables 2 and 3 represent its prototype and mimic the same structure. Not reported numerical values in Table 2 constitute priors in the model presented below. Comparing the two above sources of data, the totals of vehicles from the survey sampling for the first quarter are available for each country (25 countries plus others) in the last column (Sk⁣⋅) with a global total of 563,475. Likewise, available information in the last row (D⋅l) from road sensors concerns totals by type of vehicle (4 types) with a global total of 759,330. While measurement precision of road sensors is known to be very high, survey output may inherently suffer from limited human capacities and/or environmental conditions. Hence, on the basis of these mutually conflicting sources of data, we had to reconcile them through an optimisation framework and produce balanced, statistically reliable information about the type of vehicle and the country of its origin. Therefore, Table 2 illustrates an ill-conditioned data matrix with (K-1) (L-1) degrees of freedom, suggesting 75 unknown parameters to be estimated on the basis of the available 26 (countries) and 4 (types of vehicles) quantities of column and row totals, respectively. Furthermore, since this limited information is known with uncertainty, clearly, we have an ill-posed inverse problem to solve.

We notice a significant difference between column and row totals with ⌊S1⁣⋅+…+…⁢SK⁣⋅+ε⌋/[D⋅1+…+D⋅L+e]=563475759330×100≅75% in the Polish case analysed. In the model presented below, we consider this high level of discrepancy to be due to systematic and random errors. Equation (2) below formalizes this fact by the presence of a multiplicative scaling factor Ck⁣⋅. In fact, since each data source concerns the same quarter, both totals are expected to be equal. Next, one can consider that neither the sampling survey nor the electronic vehicle detection measurement systems are accurate, thus suggesting random errors e (from road detector) and ε (from survey sampling). This is illustrated in the Eqs (2) and (3). It follows that joint values inside Table 2[ak⁢l] are unknown. Since we are dealing with a contingency table, we know – with uncertainty – the different conditional probability vectors related to Sk⁣⋅ and D⋅l.

Among very large joint probabilistic configurations related to matrix [ak⁢l] able to map the conditional structures Sk⁣⋅ and D⋅l while ensuring their total balance (Eq. (4)), we need to find the optimal mapping proposed by the NCEE model.

3.2NCEE: The canonical model-based estimator

Through this section, we present and comment on just the main blocks of the NCEE model so as to enable readers to interpret the outputs shown in the next section. NCEE generalises the traditional Shannon-Kullback-Leibler-Jaynes-Golan (Shannon, July & October 1948) [16, 15, 13] based cross-entropy econometrics to PL-related non-ergodic systems, thus suggesting nonlinear complex phenomena. What is important to underscore is that certain types of series keep displaying PL even when aggregated at low frequency (e.g., year scale). Final distribution will result from two independent forces in action: PL and Gaussian C-Limit Theorem (Gabaix, Winter, 2016). Readers interested in more details about the NCEE empirical implementation for similar purposes are referred to, e.g. Bwanakare [4] or Eurostat [10]. The model is formulated as follows:

s.t.:

where: Yk⁣⋅: expected total quantity of vehicles by country, Hk⁣⋅: expected quantity of vehicles by type, Dk⁣⋅: means each total by row (observed values by country k) including unknown random error e⋅l, Sk⁣⋅: observed total – by column l – of crossings by vehicle type l, including unknown random error εk⁣⋅, pk⁢l: joint probabilities related to the structure of vehicle crossings by country k and vehicle type l, r⋅l⁢j: probabilities on column total errors defined on the outcome support space j∈ (2…J), μk⋅s: probabilities on row total errors defined on the outcome support space s∈ (2…S), Ck⁣⋅: a random scaling factor with respect to the two sources of data, q: Tsallis parameter indicating the complexity of the analysed system with respect to the Gaussian system (ergodic system) for which q equals unity, ⋅: variable related on the column and row totals, according to context.

Above, Hq(p//p0,r//r0,μ//μ0) is nonlinear (Eq. (3.2)) and measures the entropy Hq in the model. Relative entropies of the three independent terms (the three posteriors p, r, μ and the corresponding priors p0, r0, μ0, respectively) are then summed up. These are real positives summing up to unity under the given restrictions (Eqs (5) to (7)). In this criterion Eq. (3.2), an unknown posterior p and a priori po matrices are confronted so as to measure entropy reduction resulting from exclusive new content of data information explained by the econometric model (Eqs (2) to (7)) in the form of (first) moments. For instance, Yk⁣⋅ in Eq. (2) stands for the expected value, given Sk, Ck and the random error in the context of an entropic system including the criterion Eq. (3.2). From initial, conflicting data, we have computed the matrix of priors a𝑜𝑘𝑙 as follows:

where symbols in this relation are presented in Table 2. In other terms, by dividing the above particular a𝑜𝑘𝑙 by the corresponding D⋅l total, we get the joint prior probabilities matrix p𝑜𝑘𝑙.

When any unknown parameter values are not all constrained between 0 and 1, this suggests the necessity for reparametrization. As a general case, let us suppose that such parameters are bk⁢l, where some of them are higher than unity. Taking each bk⁢l(k=1…K,l=1…L) as a discrete, random variable with compact support [13] and possible outcomes; one can estimate it with

where p𝑘𝑙𝑚 is the probability of outcome v𝑘𝑙𝑚, and the probabilities must be non-negative and sum up to one. Outcomes v𝑘𝑙𝑚 of the random parameters bk⁢l are defined on a support space 2<m<M where m may vary between 2 and ∞. This reasoning has been applied for computing the above total errors εk⁣⋅ and e⋅l with respective probabilities r and μ.

The minimum cross-entropy principle is a strong hypothesis. Moreover, NCEE can be cast, like Shannon-based cross-entropy (e.g., [13]), into the Bayesian efficient information processing rule. Thus, though priors may be relatively weak, the maximum entropy principle will quickly tend to lead the system towards the global optimum, thereby generating posteriors closer to the optimal solution [13].

Since we are dealing with cross-entropy model formulation, given the prior information (explained through po) and the moments (new data in the form of an econometric model) describing the properties of the system (Eqs (2) to (7)), we are asked to find out, of all possible probability distributions (the posterior p), the one closest to po. One should note that when po is fully consistent with moments, then p=po and the uniform distribution will result with pk⁢l=1/k (for all l), thus suggesting non-informative proposed new facts embodied within the econometric model. This leads to the basic solution of maximum entropymaximum entropy. Thus, the consistence of new facts (in the present case the econometric model) with the unknown true probabilistic structure of the system does matter.

The cross-entropy principle represents a certain form of the generalization of maximum entropymaximum entropy. The above q-generalized Kullback-Leibler Eq. (3.2) has the same basic information measure properties as the standard Kullback-Leibler entropy and can be used for the same purpose [22]. In empirical applications, the value of the q-Tsallis should vary inside an interval from unity to 5/3, which corresponds to cases of finite variance for phenomena dwelling within the Gaussian basin of attraction. The higher the q-Tsallis parameter value, the more complex the system with respect to Gaussian distribution. In particular, when the q-Tsallis parameter converges to unity, outputs derived from NCEE and the Gaussian-related Shannon entropy also converge. Hence, NCEE generalizes traditional Shannon entropy. This explains the choice of NCEE for solving the problem presented in this paper.

As far as the model statistical inference is concerned, information properties and the above formulation of NCEE show that the model inference information indexes should fulfil the basic Fisher-Rao-Cramer information index properties, among them, continuity, symmetry, maximum, and additivity.

4.1Data sources

The data sources are three sample surveys and road sensors (BD). Data concerning border traffic and the expenditure of residents and non-residents (foreigners) at the Polish-German border and in its vicinity are from the following sample surveys: (a) survey of border traffic; (b) survey questionnaire of trips and expenditure of foreigners in the vicinity of the border; (c) survey of residents in households.

Data concerning border traffic at the Polish-German border are from the sample survey of border traffic. The border traffic survey covers persons and vehicles crossing the Polish border with the countries of the European Union at selected road border crossings. The number of vehicles crossing the border, the country of vehicle registration, and the number of persons travelling in these vehicles are registered. It is conducted on a sample of about 1.14% of the total number of vehicles crossing the borders.

An additional source of data comes from road sensors which are managed by the German Federal Highway Research Institute (Bundesanstalt für Straßenwesen). Data contain hourly information on type and number of road, test dates, traffic direction, and vehicle type. The automatic measurement is carried out using accurate measuring devices installed on motorways and federal roads, which record data throughout the year with an overall accuracy of more than 99%.

Another important data source is a sample survey of trips and expenditure of foreigners in the vicinity of the border. Due to the lack of the survey frame, this survey is conducted on an “elusive” population.44 This is a questionnaire survey conducted in the vicinity of selected border crossings using the direct interview method. Individuals are surveyed by means of a systematic sampling. The survey is conducted on 7 selected days. It is conducted on a sample of about 0.1% of the total number of foreigners coming to Poland in a given quarter. The survey covers expenditure incurred by non-residents on the purchase of goods and services, purpose and duration of stay, frequency of crossing the border, etc.

Data concerning trips and expenditure of residents come from the sample household survey. This survey covers expenditure incurred by residents on the purchase of goods and services, purpose and duration of stay, frequency of crossing the border, etc. Households for the survey are selected at random from a census sampling frame by two-step sampling with stratification on the first step (strata were defined by sub-regions and size classes of towns). It is conducted on a sample of about 0.14% of the total number of households in Poland. The questionnaire survey is carried out in quarter periods. The results are used by the Polish National Bank for the BoP, as well as by Poland Statistics and the Ministry of Sport and Tourism for tourism statistics.

On the basis of the sample survey of border traffic (movement of vehicles and persons) the volume of border traffic of residents and non-residents is estimated in quarterly periods at the Polish-German border. Then, weights are determined for particular border crossings, proportionally to the volume of traffic at each of them. In the next step the sample survey of trips and expenditure of foreigners is used. Each questionnaire of this survey is given its own weight, depending on the border crossing in the vicinity of which it was collected. In this way, a generalised number of trips of foreigners arriving to Poland and expenditure they incurred are obtained.

Data concerning border traffic at the Polish-German border are from the following surveys: sample survey of border traffic and data from road sensors, which record data throughout the year with an overall accuracy of more than 99%.

4.2Outputs and comments

The outputs reported in Table 3 of such an inverse ill-posed problem have been computed using the GAMS code (General Algebraic Modelling System). Thanks to the model (Eqs (3.2)–(7)), we estimated unknown posterior quantities Yk⁣⋅=Ck⁣⋅ from Table 2, related to which type of vehicle and from which country, crossed the main German-Polish border during the first quarter of 2015. The use of the traditional Shannon entropy related econometric model led to similar outputs to those in Table 3, which suggests the Gaussian structure of the data used. It is worth emphasizing that these outputs conform to the empirical expectations of subject specialists. Interestingly enough, such detailed information reflecting the new knowledge about type of vehicle by country of origin is crucial to get higher precision about the cross-border tourist movement. This information will be used in the next section for national accounts updating.

In his work [5], the author proposed a non-negative information index I⁢(p,p0) as a measure of non-extensive cross-entropy model accuracy. This index is a continuous function of prior and data (the model) values within the interval from zero to unity. When this information index I⁢(p,p0)=0, this indicates that information content from data and prior values are fully consistent, suggesting that no new information is provided through the data (the model). Thus, the higher its value, the higher the reliability of estimated model parameters. As already mentioned, adding a new piece of consistent information in the form of a model constraint will increase its parameter precision and lead to a higher information index value. The value of that index is 0.72 in the present model. This means that information contained within the proposed model has improved the quality of the initial parameters (related to Table 2) up to 72% with respect to the unknown benchmark model. This could be the one which will improve this index to 100%, suggesting that we retrieve the true, unknown values of the posterior probability matrix p or likewise, the true model parameters. Finally, let us underscore, as shown in their work [13], that the superiority of the generalized cross-entropy technique over other estimating approaches is its property to effectively discount incorrect prior information if it does not agree with the sample. In this case, the problem solution will shift towards the one resulting from the maximum entropy principle.

4.3Impact on the balance of payments

The BoP on the current account, which covers, among other things, transactions in services, includes items related to expenses of non-residents during a visit to a given country and residents of that country during a visit abroad. Note that revenue from non-residents’ trips accounts for 10.7% of revenues on the current account as a whole in 28 European Union countries.

The Polish-German border is the main European transport corridor between west and east with the largest traffic in Poland. We choose for the analysis the border crossing in Jędrzychowice, one of the 27 border crossings with Germany, where border traffic constitutes approximately 20% of border traffic for the entire Polish-German border.

Figure 1.

Assessment of expenditure of Poles and foreigners crossing the Polish-German border based on combined sources in Q1 2015.

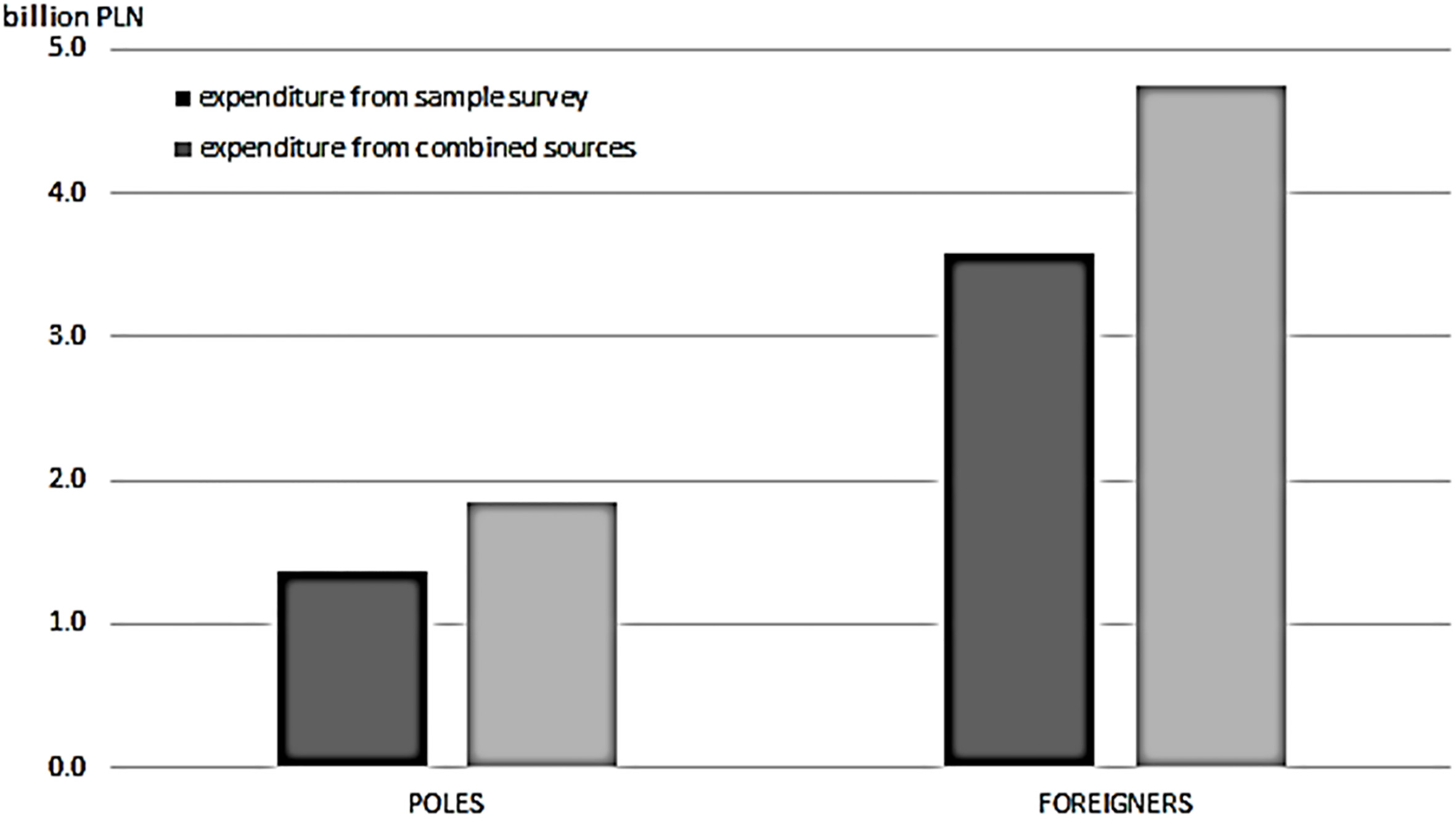
Figure 1 shows the difference between expenditure of Poles and foreigners at the Polish-German border based exclusively on the sample surveys and on combined information sources (sample surveys plus data from road sensors).

For further analysis, a correction regarding the scale of crossings at the Jędrzychowice point for both Poles (an increase of 49.3%) and foreigners (an increase of 40.4%) was adopted and applied in appropriate proportions to the change of border traffic at the whole Polish-German border. This type of calculation could be made because the structure of vehicle crossing at the Polish-German border is similar at key crossing points.

Next, let us briefly describe how the above crossing volumes are related to expenditures by foreigners and by Poles. In the case of foreigner expenditures, the sample survey of trips and expenditure of foreigners is used. Each questionnaire of this survey is given its own weight, depending on the border crossing in the vicinity of which it was collected. In this way, a generalised number of trips of foreigners crossing the Polish-German borders and expenditures they incurred are obtained (PLN 502/foreigner).

In the case of residents, the number of trips and the volume of expenditure are estimated on the basis of the sample survey of residents in households and the sample survey of border traffic. The sample survey of residents in households uses a questionnaire, which contains information about the name of the border crossing, among other things. Based on this information, the questionnaire is assigned an appropriate weight, which is calculated based on the sample survey of border traffic. Therefore, the average expenditure of residents for a given border crossing is calculated on the basis of collected household questionnaires. In this way, the total number of trips made by residents going abroad and the expenditure they incurred in connection with these trips are obtained (PLN 304/resident).

Thus, taking into account the updated outputs summarised in Table 2 or in Table 4, we observe a difference of almost 35% in the case of expenses made by Poles. This difference is almost 33% in the case of foreigners. It is worth noting that the balance of expenses made by foreigners and Poles crossing the Polish-German border constitutes nearly 50% of this balance for the whole country. Considering these facts, it should be assumed that a change in the research methodology has brought a difference in the estimation of the BoP in the first quarter of 2015 for the Polish-German border of about 31% while in the case of the whole country of over 14%.