An estimating parameter of nonparametric regression model based on smoothing techniques
Abstract
This paper studies the estimating parameter of a nonparametric regression model that consists of the function of independent variables and observation of dependent variables. The smoothing spline, penalized spline, and B-spline methods in a class of smoothing techniques are considered for estimating the unknown parameter on nonparametric regression model. These methods use a smoothing parameter to control the smoothing performance on data set by using a cross-validation method. We also compare these methods by fitting a nonparametric regression model on simulation data and real data. The nonlinear model is a simulation data which is generated in two different models in terms of mathematical function based on statistical distribution. According to the results, the smoothing spline, the penalized spline, and the B-spline methods have a good performance to fit nonlinear data by considering the hypothesis testing of biased estimator. However the penalized spline method shows the minimum mean square errors on two models. As real data, we use the data from a light detection and ranging (LIDAR) experiment that contained the range distance travelled before the light as an independent variable and the logarithm of the ratio of received light from two laser sources as a dependent variable. From the mean square errors of fitting data, the penalized spline again shows the minimum values.
1.Introduction
In statistical modelling, regression analysis is a statistical process for estimating parameters of the relationships between dependent and independent variables in terms of a regression function. However, regression analysis requires an assumption of the underlying regression function to be met. If an inappropriate assumption is used, it is possible to produce misleading results. To overcome this problem, the nonparametric regression is a choice to analyze data when the data are not meeting the assumption of regression analysis. The nonparametric regression is an alternative way for looking at scatter diagram smoothing to depict the relationship between dependent and independent variables. The single independent variable is called scatterplot smoothing it can be used to enhance the visual appearance to help our eyes pick out the trend in the plot.
The smoothing technique is a part of a method to estimate unknown parameters (trend or smoothing estimators) of nonparametric regression models. There are many popular smoothing techniques such as the smoothing spline [1, 2], the penalized spline [3], and the B-spline [4]. The estimating parameters of these methods depend on the smoothing parameter which is controlled the trade-off between fidelity to the data and roughness of function. Smoothing Spline (SS) is a technique that estimates the natural polynomial spline by minimizing the penalized sum of squares based on a smoothing parameter. The penalized Spline (PS) smoother is approximated by minimizing the truncated power function on a low rank thin-plate spline depended on the smoothing parameter. The concept of the B-spline is similar to the smoothing spline and penalized spline. This requires the piecewise constant B-spline that can be obtained from truncated counterparts by differencing the B-spline function.
In this paper, we consider the nonparametric regression model in Section 2, and use the smoothing spline, penalized spline, and B-spline methods to estimate the unknown parameter of nonparametric regression model in Section 3. In Sections 4 and 5, we show the estimation of these methods for simulation data and real data. The conclusion is presented in Section 6.
2.The nonparametric regression model
The nonparametric regression model consists of the cubic spline of piecewise polynomials function based on a function of independent variables (
(1)
The error process is assumed to follow the normal distribution with mean zero and variance one.
3.Method of smoothing techniques
The following smoothing techniques show the process to estimate parameters based on nonparametric regression model.
3.1Smoothing spline method
Wahba [1] defined the natural polynomial spline
The natural measure associated with the function
(2)
where
Consider the simple nonparametric regression model, to estimate
(3)
where
The natural cubic spline is given the value and second derivatives at each knots
Let
The condition of natural cubic spline depends on two matrices
where
Matrix
The matrix
(4)
The roughness penalty will satisfy
(5)
To illustrate, it can be written in matrix form introduced by [2] as residual sum of squares (RSS)
(6)
where
The roughness penalty term
(7)
It therefore follows that Eq. (7) has a unique minimum, other smoothing spline estimator is obtained by
then
(8)
In this paper, we also select the smoothing parameter using the method of generalized cross-validation (GCV) suggested by Wahba [5] and Craven and Wahba [6]. In practice, this step can be implemented by using the function of smooth.spline in the software R.
3.2Penalized spline method
Eubank [7, 8] introduced the regression spline that the local neighbourhoods are specified by a group of locations:
(9)
in the range of interval
A regression spline can be constructed using the
(10)
where
(11)
where
The penalized spline is a method to estimate a unknown smooth function using the truncated power function [9], and the penalized spline can be expressed as
(12)
where
In this case, we focus
(13)
where
This class of penalized spline smoothers
(14)
where
and
3.3B-spline method
B-splines are very interesting as a basic function for univariate independent variable of nonparametric regression function. De Boor [10] gave an algorithm to compute B-spline of lower degree on piece wise polynomials function.
The
(15)
where basis of order
The nonparametric regression model can written in form of B-splines as
(16)
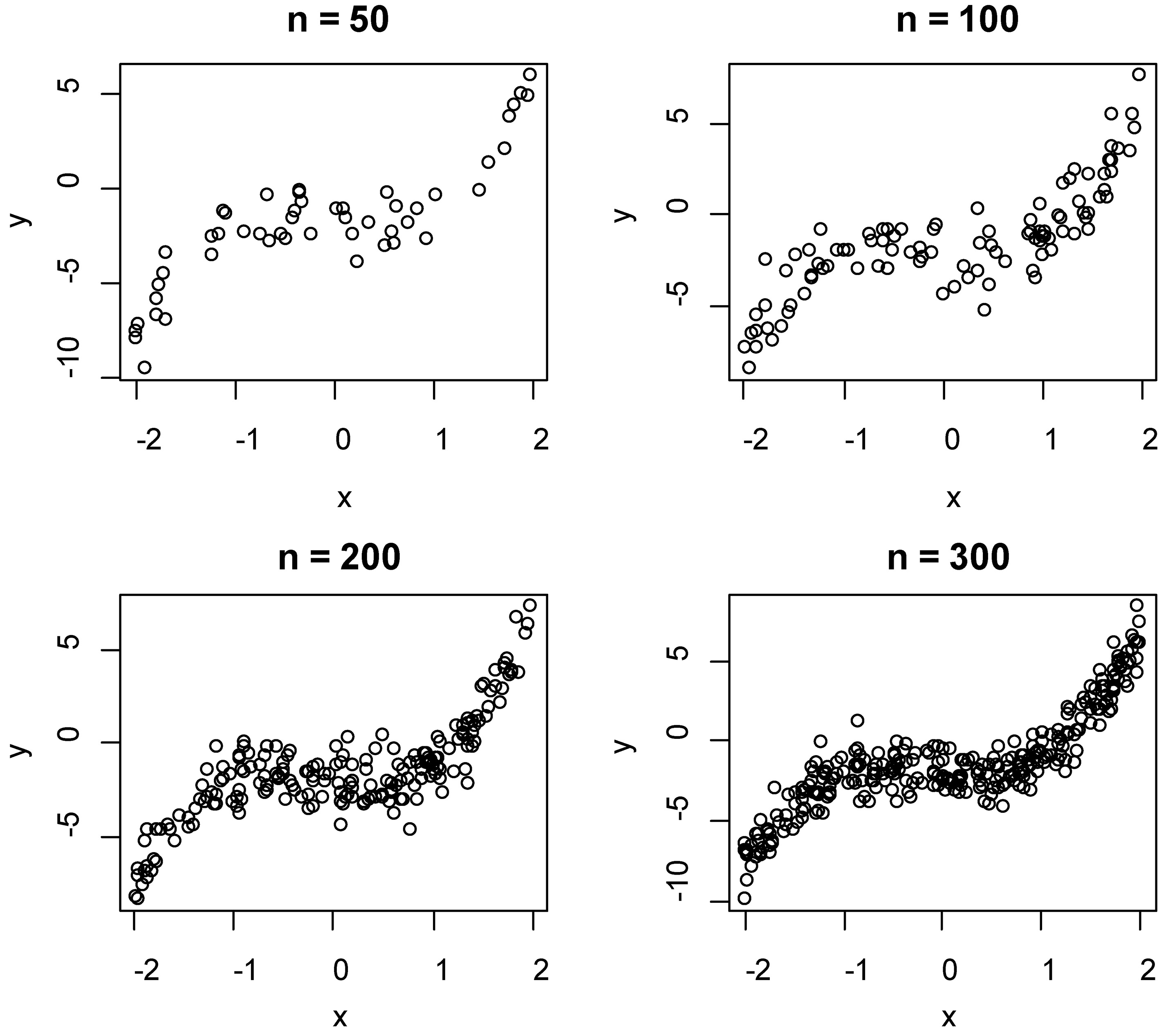
Figure 1.
The scatter plot of dependent and independent variables on model 1.
In matrix form, B-splines can be written in form a linear model
The B-splines estimators are approximated by least square problems as
The B-spline and penalties are studied by Eilers and Marx [4] that advocate the use of the equally spaced knots, instead of the order statistics of the independent variable. The B-spline coefficients can be estimated as
(17)
where
The fitting cubic B-splines are
Figure 2.
The scatter plot of dependent and independent variables on model 2.

Table 1
The summary statistics of simulation studies with model 1 based on smoothing spline (SS), penalized spline (PS), and B-spline (BS)
| Sample sizes | Methods | Mean | S.D. | LCI | UCI | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SS | 3344 | 6. | 5444 | 9095 | 0. | 2405 | 1428 | 0. | 2537 | ||||
| PS | 3484 | 6. | 7454 | 9411 | 0. | 2442 | 1552 | 0. | 2468 | ||||
| BS | 0. | 3666 | 6. | 6935 | 2214 | 0. | 9548 | 1. | 2249 | 0. | 2212 | ||
| SS | 0. | 0719 | 4. | 2680 | 3031 | 0. | 4469 | 0. | 3767 | 0. | 7065 | ||
| PS | 0. | 0837 | 4. | 2029 | 2855 | 0. | 4530 | 0. | 4454 | 0. | 6562 | ||
| BS | 0895 | 4. | 2152 | 4599 | 0. | 2807 | 4751 | 0. | 6349 | ||||
| SS | 0954 | 2. | 8932 | 3504 | 0. | 1595 | 7353 | 0. | 4625 | ||||
| PS | 0921 | 2. | 9123 | 3480 | 0. | 1637 | 7072 | 0. | 4798 | ||||
| BS | 0. | 0149 | 3. | 2685 | 2299 | 0. | 2598 | 0. | 1200 | 0. | 9045 | ||
| SS | 1574 | 4. | 2673 | 5347 | 0. | 2197 | 8201 | 0. | 4125 | ||||
| PS | 1441 | 4. | 1982 | 5130 | 0. | 2247 | 7676 | 0. | 4431 | ||||
| BS | 0. | 1475 | 1. | 8514 | 2786 | 0. | 5738 | 0. | 6802 | 0. | 4966 | ||
Table 2
The summary statistics of simulation studies with model 2 based on smoothing spline (SS), penalized spline (PS), and B-spline (BS)
| Sample sizes | Methods | Mean | S.D. | LCI | UCI | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SS | 0037 | 24. | 2710 | 1363 | 2. | 1288 | 0034 | 0. | 9972 | ||||
| PS | 2582 | 23. | 8736 | 3559 | 1. | 9893 | 2419 | 0. | 8089 | ||||
| BS | 3230 | 27. | 1906 | 7121 | 2. | 0660 | 2656 | 0. | 7906 | ||||
| SS | 3966 | 15. | 8261 | 7871 | 0. | 9939 | 5603 | 0. | 5755 | ||||
| PS | 2489 | 16. | 4557 | 6947 | 1. | 1969 | 3382 | 0. | 7353 | ||||
| BS | 0. | 5461 | 16. | 2381 | 8806 | 1. | 9729 | 0. | 7520 | 0. | 4524 | ||
| SS | 3704 | 8. | 1031 | 0838 | 0. | 3430 | 0201 | 0. | 3082 | ||||
| PS | 3447 | 7. | 8716 | 0363 | 0. | 3468 | 9792 | 0. | 3279 | ||||
| BS | 0. | 4035 | 8. | 5116 | 3443 | 1. | 1514 | 1. | 0602 | 0. | 2896 | ||
| SS | 0. | 0411 | 7. | 3081 | 6055 | 0. | 6878 | 0. | 1250 | 0. | 9005 | ||
| PS | 0. | 0408 | 7. | 0664 | 5800 | 0. | 6617 | 0. | 1291 | 0. | 8973 | ||
| BS | 0. | 0344 | 7. | 2205 | 5999 | 0. | 6688 | 0. | 1066 | 0. | 9151 | ||
4.Simulation study
The nonlinear data of this study is simulated in two models for estimating the performance of smoothing techniques based on independent variables which are considered in the class of uniform distribution. These models in the process of construction a curve on mathematical function, that show the best fit to a series of data points. Figures 1 and 2 show the scatter plot of
Model 1
Model 2
The next step, the estimates of
The data are generated and repeated for fitting the model 500 times. A
Figure 3.
Histogram of bias for fitting data of smoothing spline method with model 1.
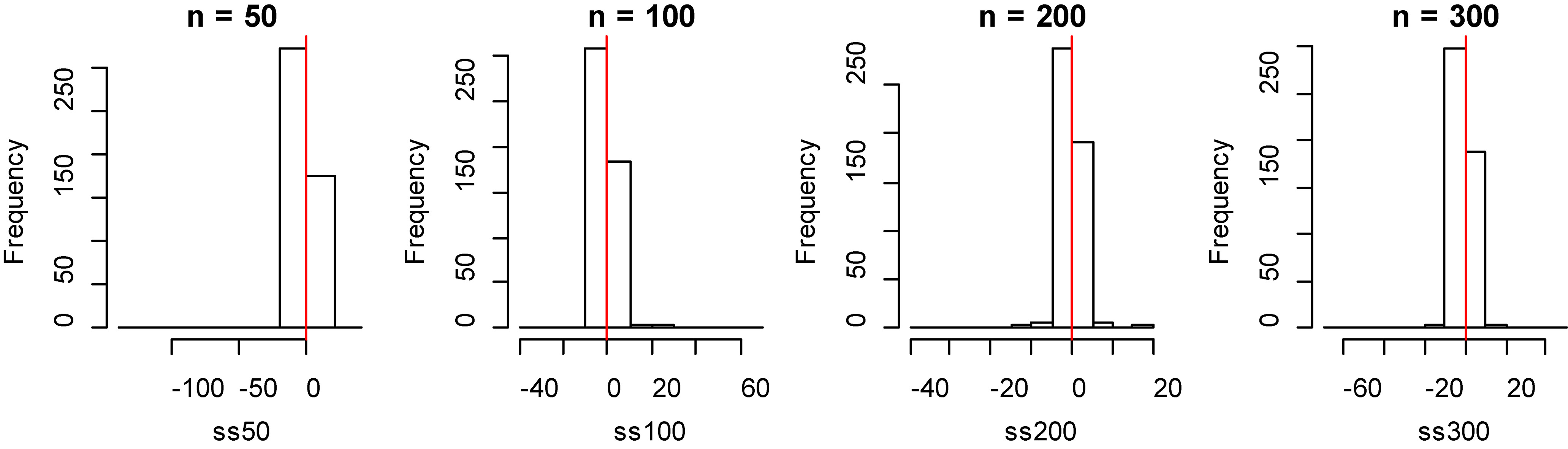
Figure 4.
Histogram of bias for fitting data of penalized spline method with model 1.
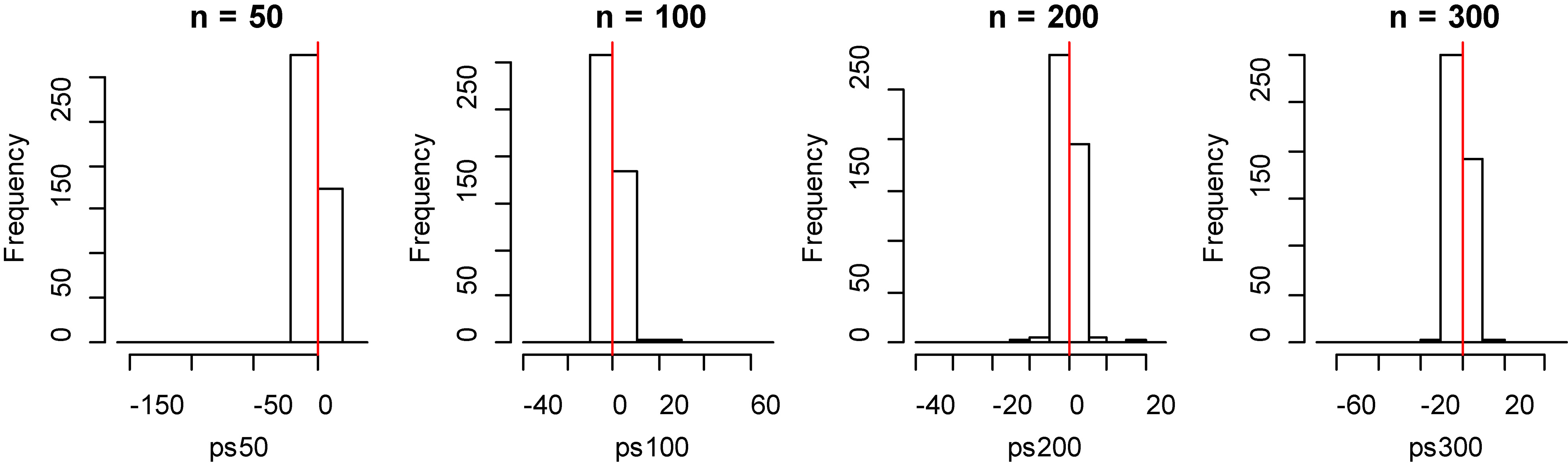
Figure 5.
Histogram of bias for fitting data of B-spline method with model 1.
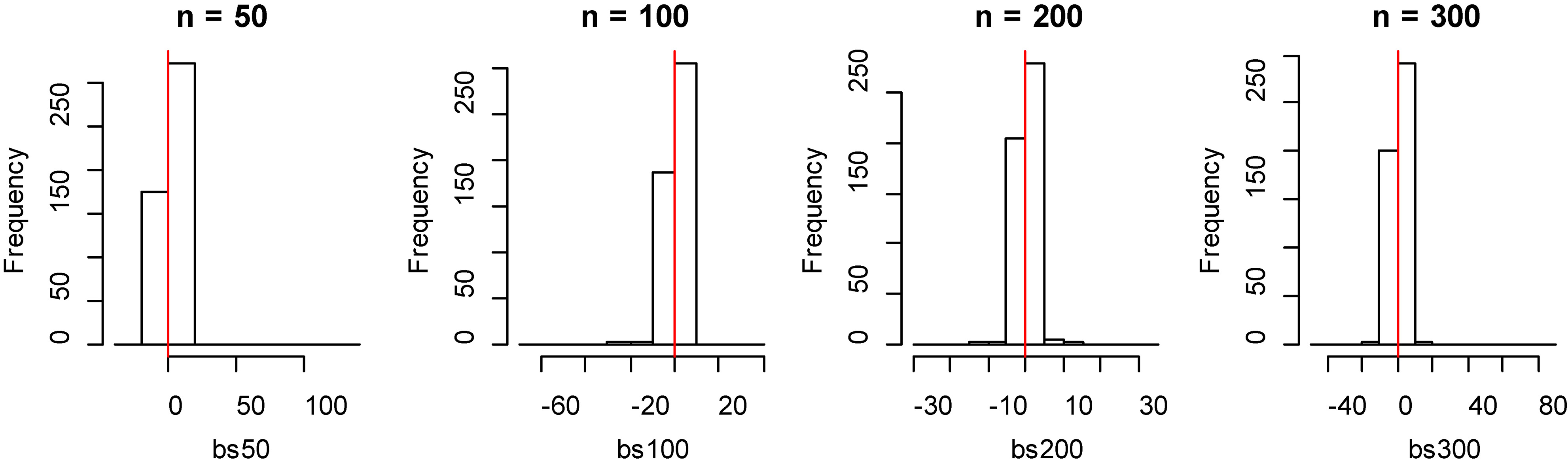
Figure 6.
Histogram of bias for fitting data of smoothing spline method with model 2.
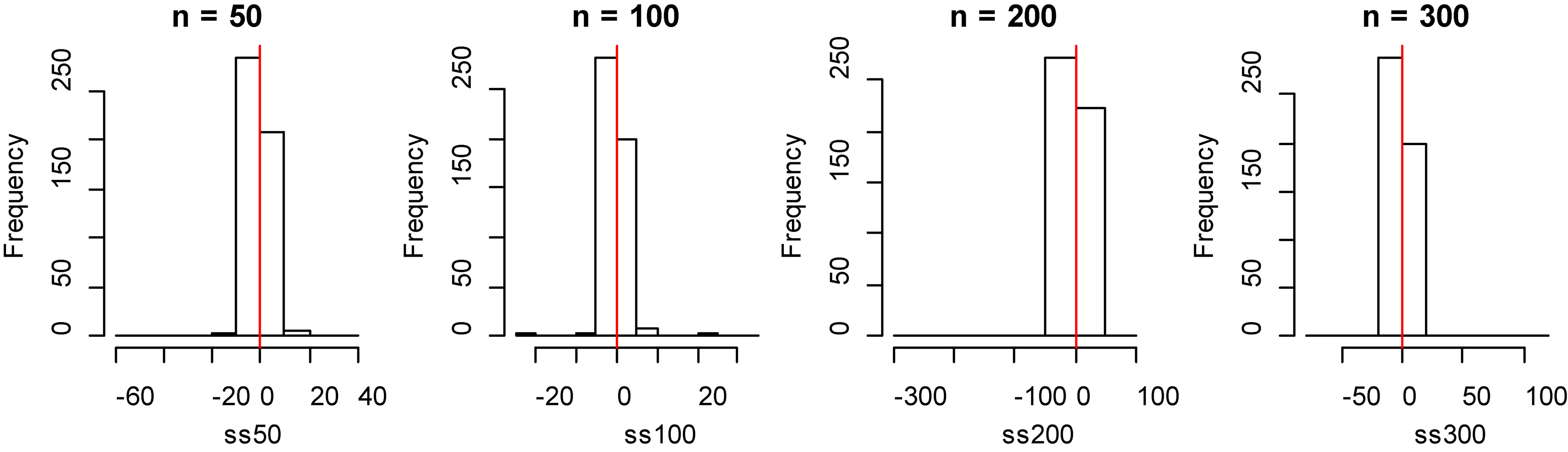
Figure 7.
Histogram of bias for fitting data of penalized spline method with model 2.
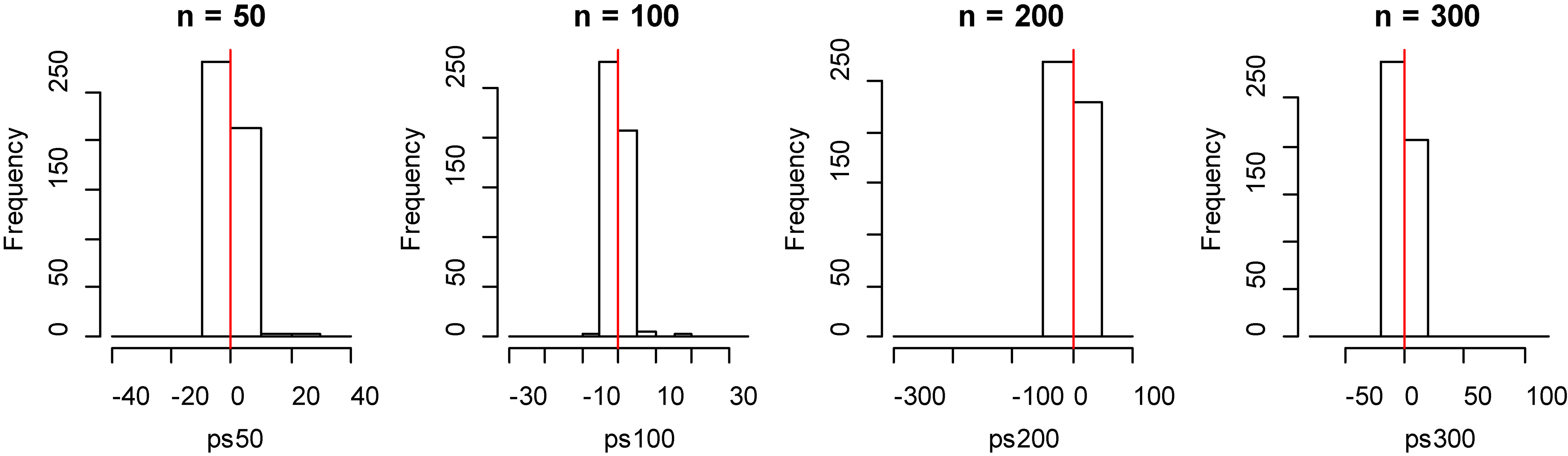
Figure 8.
Histogram of bias for fitting data of B-spline method with model 2.
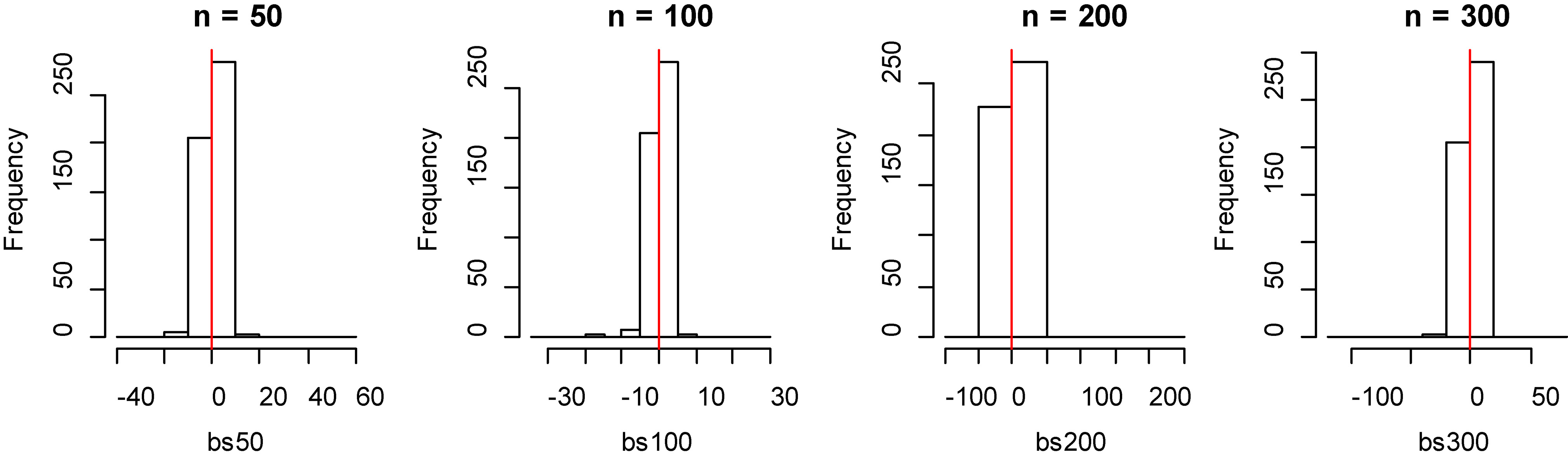
From Tables 1 and 2, by observing the
Table 3
The average MSE of simulation studies with 3 models based on smoothing spline (SS), penalized spline (PS), and B-spline (BS)
| Sample sizes | Methods | Model 1 | Model2 |
|---|---|---|---|
| SS | 0.8225 | 0.8348 | |
| PS | 0.7712 | 0.7846 | |
| BS | 0.9174 | 0.9364 | |
| SS | 0.9087 | 0.9029 | |
| PS | 0.8810 | 0.8719 | |
| BS | 0.9632 | 0.9508 | |
| SS | 0.9528 | 0.9521 | |
| PS | 0.9387 | 0.9439 | |
| BS | 0.9784 | 0.9840 | |
| SS | 0.9666 | 0.9648 | |
| PS | 0.9640 | 0.9615 | |
| BS | 0.9899 | 0.9877 |
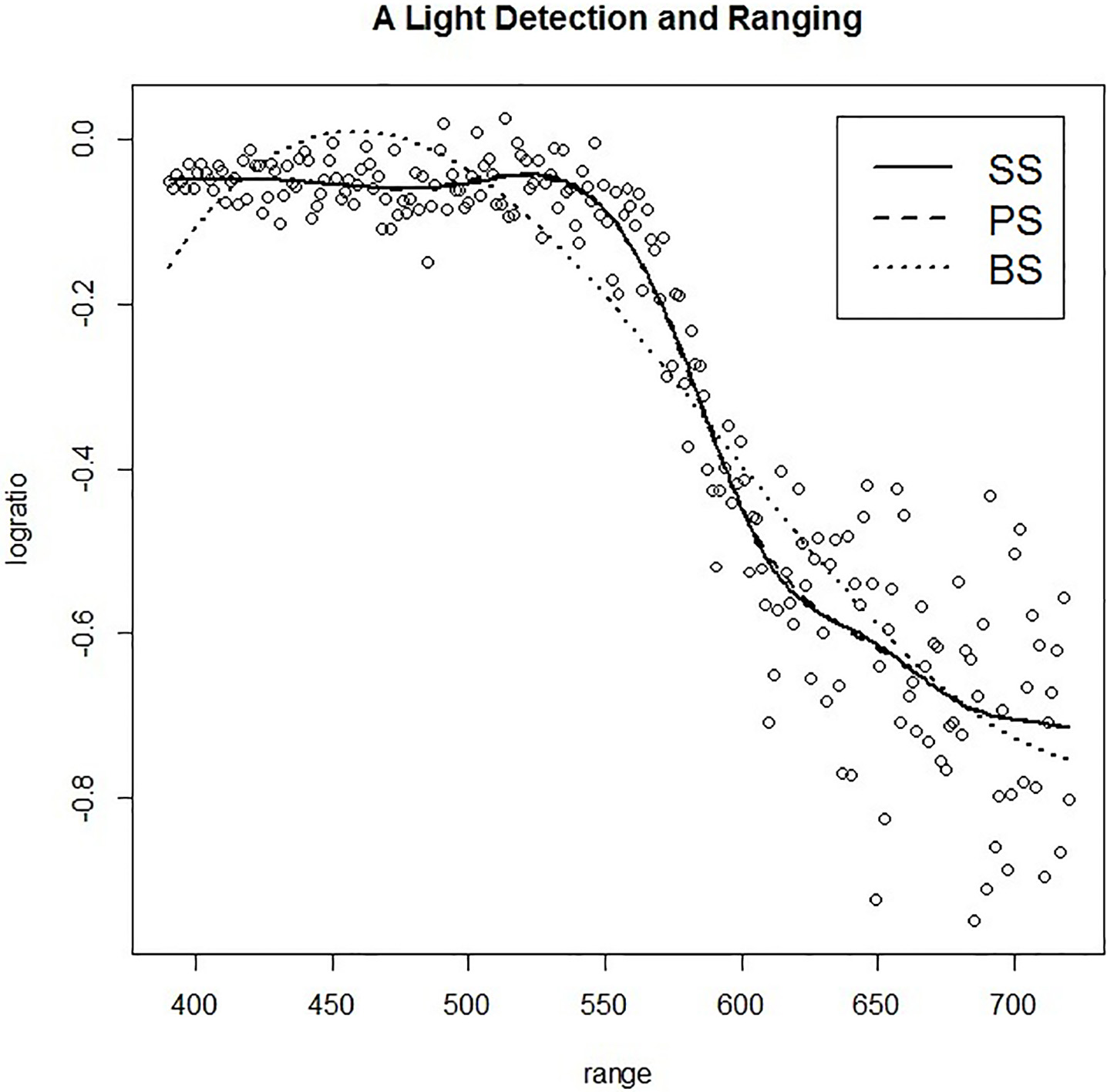
Figure 9.
The plot of LIDAR data frame and model fitting of SS, PS, and BS methods.
5.Application of real data
In this section, we consider the application of smoothing method based on SS, PS, and BS methods that we developed in the previous section. As the real data, we use the data frame which consists of 221 observations from a light detection and ranging (LIDAR) experiment. This data frame contains the range distance travelled before the light is reflected back to its source and logarithm of the ratio of received light from two laser sources as shown in the plot in Fig. 9.
After fitting the model, the estimating values play on a plot of light detection of ranging. It can be seen that the SS and PS interpolate in mass data more than the BS method that followed the MSE values such as SS
6.Conclusion
In this section, we used the smoothing techniques of SS, PS, and BS methods based on nonparametric regression models. Through a Monte Carlo simulation study, we evaluated the smoothing estimator of SS, PS, and BS methods. For hypothesis testing based on the
Acknowledgments
This work was supported by Faculty of Science Fund, King Mongkut’s Institute of Technology Ladkrabang, Bangkok, Thailand.
References
[1] | Wahba G. Spline Models for Observational Data, SIAM: Philadelphia; (1990) . |
[2] | Green PJ, Silverman BW. Nonparametric Regression and Generalized Linear Models: A Roughness Penalty Approach, Chapman and Hall: London; (1994) . |
[3] | Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression, Cambridge University Press: New Your; (2003) . |
[4] | Eilers PHC, Marx BD. Flexible Smoothing with B-splies and Penalties, Statistical Science 11: (2) ((1996) ), 89–102. |
[5] | Wahba G. A survey of some smoothing problems and the method of generalized cross-validation for solving them, In Proceeding of the Conference on the Application of Statistic, (1976) , pp. 507–523. |
[6] | Craven P, Wahba G. Smoothing noisy data with spline functions: estimating the correct degree of smoothing by the method of generalized cross-validation, Numerische Mathematik 31: ((1979) ), 377–403. |
[7] | Eubank RL. Spline Smoothing and Nonparametric Regression, Marcel Dekker: New York; (1988) . |
[8] | Eubank RL. Nonparametric Regression and Spline Smoothing, Marcel Dekker: New York; (1999) . |
[9] | Ruppert D, Carroll RJ. Spatial-adaptive penalties for spline fitting Australian and New Zealand Journal of Statistics 42: ((2000) ), 205–224. |
[10] | De Boor C. A Practical Guide to Splines, Springer: Berlin; (1978) . |




