DegreEmbed: Incorporating entity embedding into logic rule learning for knowledge graph reasoning
Abstract
Knowledge graphs (KGs), as structured representations of real world facts, are intelligent databases incorporating human knowledge that can help machine imitate the way of human problem solving. However, KGs are usually huge and there are inevitably missing facts in KGs, thus undermining applications such as question answering and recommender systems that are based on knowledge graph reasoning. Link prediction for knowledge graphs is the task aiming to complete missing facts by reasoning based on the existing knowledge. Two main streams of research are widely studied: one learns low-dimensional embeddings for entities and relations that can explore latent patterns, and the other gains good interpretability by mining logical rules. Unfortunately, the heterogeneity of modern KGs that involve entities and relations of various types is not well considered in the previous studies. In this paper, we propose DegreEmbed, a model that combines embedding-based learning and logic rule mining for inferring on KGs. Specifically, we study the problem of predicting missing links in heterogeneous KGs from the perspective of the degree of nodes. Experimentally, we demonstrate that our DegreEmbed model outperforms the state-of-the-art methods on real world datasets and the rules mined by our model are of high quality and interpretability.
1.Introduction
Recent years have witnessed the growing attraction of knowledge graphs in a variety of applications, such as dialogue systems [19,23], search engines [40] and domain-specific softwares [22,30]. Capable of incorporating large-scale human knowledge, KGs provide graph-structured representation of data that can be comprehended and examined by humans. Knowledge in KGs is stored in triple form
Predicting missing triples based on the existing facts is usually called link prediction as a subtask of knowledge graph completion (KGC) [14], and numerous models have been developed for solving such problems. One prominent direction in this line of research is representation learning methods that learn distributed embedding vectors for entities and relations, such as TransE [4] and ComplEx [34]. In this work, they are referred to as embedding-based methods. This kind of models are capable of capturing latent knowledge through low-dimensional vectors, e.g. we can classify male and female entities in a family KG by clustering their points at the semantic space. In spite of achieving high performance, these models suffer from non-transparency and can poorly be understood by humans, which is a common issue for most deep learning models. In addition, most embedding-based methods work in a transductive setting, where they require the entities in training and test data to overlap, hindering the way to generalize in some real-world situations.
Fig. 1.
An example of KG containing heterogeneous entities and relations: paper, person and institution. Entities in different colors mark their type. The existing links in the KG are presented as solid black lines, the missing one as dashed lines in red and the proper rule for inferring the link as blue lines.
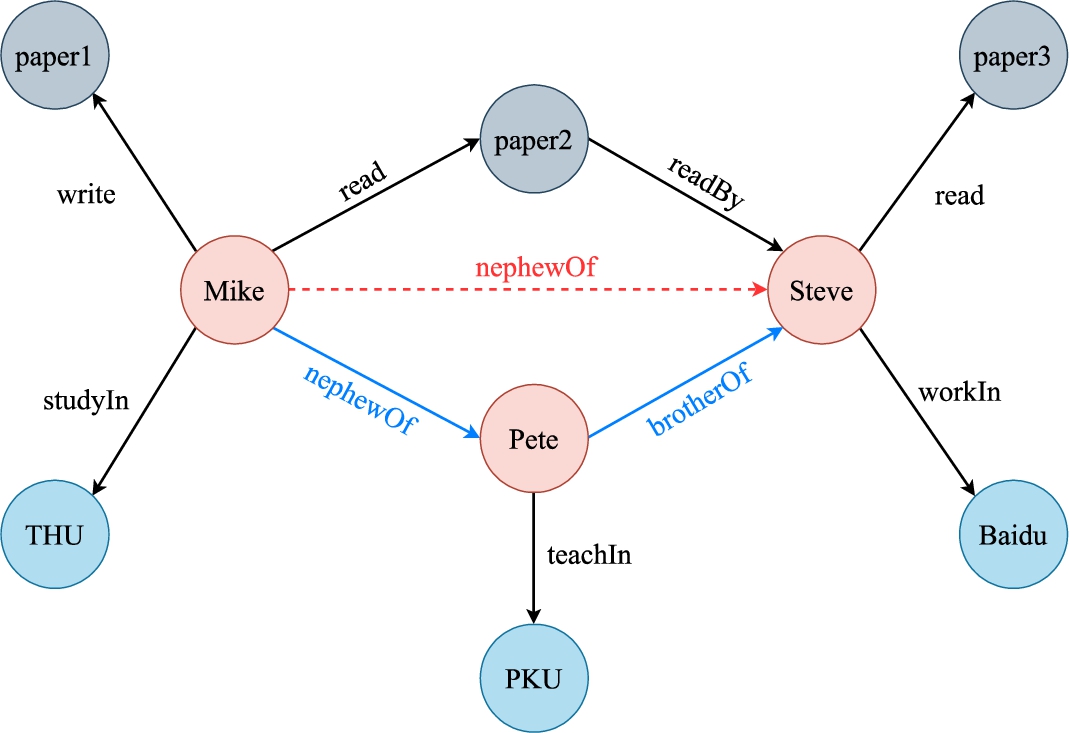
Another popular approach is rule mining that discovers logical rules through mining co-occurrences of frequent patterns in KGs [5,11]. This paper studies the problem of learning first-order logical Horn clauses for knowledge graph reasoning (KGR). As illustrated in Fig. 1, there is a missing link (i.e. nephewOf) between the subject Mike and the object Steve, but we can complete the fact through a logic rule nephewOf(Mike, Pete) ∧ brotherOf(Pete, Steve) ⇒ nephewOf(Mike, Steve), meaning that if Mike is the nephew of Pete and Steve has a brother Pete, then we can infer that Mike is the nephew of Steve. Reasoning on KGs through Horn clauses has been previously studied in the area of Inductive Logic Programming [24]. One representative method, Neural LP [42], is the first fully differentiable neural system that successfully combines learning discrete rule structures as well as confidence scores in continuous space. Although learning logical rules equips a model with strong interpretability and the ability to generalize to similar tasks [28,45], these methods often focus only on the relations of which the rules are made up, while the intrinsic properties of the involved entities are not considered. For example, in the KG shown in Fig. 1, it is definitely wrong to infer by a rule containing a female-type relation path like sisterOf starting from Mike, because Mike is the nephew of Pete, which indirectly tells us he is a male. This sort of deficiency is more severe in heterogeneous KGs where there are entities and relations of different types mixing up. In these KGs, there might be multiple rules of no use, becoming inevitable noises for reasoning tasks. For instance, the rule read(Mike, paper2) ∧ readBy(paper2, Steve) ⇒ nephewOf(Mike, Steve) is obviously wrong in logic, which might decrease the performance and interpretability of ILP models.
In this paper, in order to bridge the gap between the two lines of research mentioned above, we propose DegreEmbed, a model of logic rule learning that integrates the inner attributes of entities by embedding nodes in the graph from the perspective of their degrees. DegreEmbed is not only interpretable to humans, but also able to mine relational properties of entities. We also evaluate our model on several knowledge graph datasets, and show that we are able to learn more accurately, and meanwhile, gain strong interpretability of mined rules.
Our main contributions are summarized below:
– We propose an original model based on logic rule learning to predict missing links in heterogeneous KGs. Specifically, a new technique for encoding entities, called degree embedding, is designed to capture hidden features through the relation type of edges incident to a node.
– Comparative experiments on knowledge graph completion task with five benchmark datasets prove that our DegreEmbed model outperforms baseline models. Besides, under the evaluation of a metric called Saturation, we show that our method is capable of mining meaningful logic rules from knowledge graphs.
– Visualizing learned entity embeddings, we demonstrate that clear features of entities can be obtained by our model, thus benefitting the prediction in heterogeneous settings. Moreover, we prove the necessity of each component of our model using ablation study.
This paper is structured as follows. We briefly introduce our related work and review preliminary definitions of knowledge graphs respectively in Section 2 and Section 3. Section 4 introduces our proposed DegreEmbed model based on logic rule learning for link prediction in heterogeneous KGs. We present the experimental results in Section 5 and conclude our work by pointing out the future direction.
2.Related work
Our work is first related to previous efforts on relational data mining, based on which, a large body of deep rule induction models have been developed for link prediction. Since our approach achieves a combination of logic rule learning and knowledge graph embedding, we conclude related work in this topic as well.
Relational data mining. The problem of learning relational rules has been traditionally addressed in the field of inductive logic programming (ILP) [24]. These methods often view the task of completing a missing triple as a query
Neural logic programming. In recent years, models borrowing the idea of logic rule learning in a deep manner have emerged as successful approaches for link prediction task. Extending the idea of TensorLog that tackles the problem of rule-based logic reasoning through sparse matrix multiplication, Neural LP [42] is the first end-to-end differentiable approach to simultaneously learn continuous parameters and discrete structure of rules. Some recent methods [29,38,43] have improved the framework done by Neural LP [42] in different manners. DRUM [29] introduces tensor approximation for optimization and reformulate Neural LP to support rules of varied lengths. Neural-Num-LP [38] extends Neural LP to learn numerical relations like age and weight with dynamic programming and cumulative sum operation. NLIL [43] proposes a multi-hop reasoning framework for general ILP problem through a divide-and-conquer strategy as well as decomposing the search space into three subspaces. However, the existing methods ignore the effects caused by entities of different types while reasoning over a specific relational path, thus witness a more obvious failure where heterogeneous entities and relations are involved in the KGs.
Representation learning. Capturing their semantic information by learning low-dimensional embeddings of entities and relations, also known as knowledge graph embedding, is a vital research issue in KGC, and we term those models as embedding-based models. Newly proposed methods, including RotatE [32], ConvE [9] and TuckER [2], predict missing links by learning embedding vectors from various perspectives of the problem. Specifically, the work of RotatE [32] focuses on inferring patterns such as symmetry and inversion, where they proposed a rotational model that rotates the relation from the subject to the object in the complex space as
We also notice that there are methods trying to establish a connection between learning logical rules and learning embedding vectors [37,44], where they augment the dataset by exploring new triplets from the existing ones in the KG using pre-defined logical rules to deal with the sparsity problem, which differs from our goal to consider entities of various types for learning in heterogeneous KGs.
3.Preliminaries
In this section, we introduce background concepts of logic rule learning for knowledge graph reasoning as well as the definition of topological structure of KGs.
3.1.Knowledge graph reasoning
Knowledge graph can be modeled as a collection of factual triples
Logic rule reasoning. We perform reasoning on KGs by learning a confidence score
The link prediction task here is considered to contain a variety of queries, each of which is composed of a query body
During inference, given an entity h, the unified score of the answer t can be computed by adding up the confidence scores of all rule paths that infer
3.2.Graph structure
Definition 1
Definition 1(Directed Labeled Multigraph).
A directed labeled multigraph G is a tuple
Because of its graph structure, a knowledge graph can be regarded as a directed labeled multigraph [31]. In this paper, “graph” is used to refer to “directed labeled multigraph” for the sake of simplicity.
Formally, in a graph
But in this paper, we use “degree” to represent the edges incident to a specific node v for conciseness.
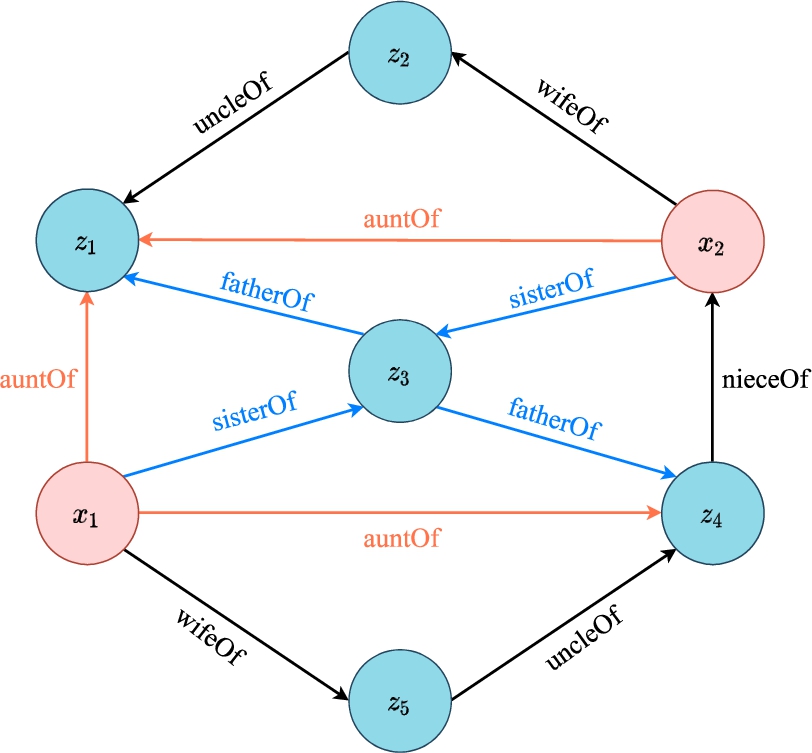
Fig. 2.
A KG example of family members and the relations between them.
Definition 2
Definition 2(Heterogeneous Graph [39]).
A graph
As shown in Fig. 2, nodes of different types are marked in different colors, and edges are categorized by their relational labels.
4.Methodology
Capable of simultaneously learning representations and logical rules, Neural LP [42] is the first differentiable neural system for knowledge graph reasoning that combines structure learning and parameter learning. Our work follows the work of Neural LP and extensive studies based on it to consider the problem of reasoning in heterogeneous KGs, from the view of mining intrinsic properties of the entities in KGs.
4.1.Neural LP for logic reasoning
4.1.1.TensorLog
The work of TensorLog [6,7] successfully simulates the reasoning process using first-order logic rules by performing sparse matrix multiplication, based on which, Neural LP [42] proposed a fully differentiable reasoning system. In the following, we will first introduce the TensorLog operator. In a KG involving a set of entities
For example, every KG entity

And the rule

By setting
4.1.2.Neural LP
Neural LP [42] inherits the idea of TensorLog. Given a query
The operators above are used to learn for query q by calculating the weighted sum of all possible patterns:
To summarize, we update the score function in Eq. (5) by finding an appropriate α in
Whereas the searching space of learnable parameters is exponentially large, i.e.
To perform training and prediction over the Neural LP framework, we should first construct a KG from a large subset of all triplets. Then we remove the edge
4.2.Our DegreEmbed model
In this section, we propose our DegreEmbed model based on Neural LP [42] as a combination of models relying on knowledge graph embedding and ILP models where the potential properties of individual entities are considered through a technique we call degree embedding. We discover that the attributes of nodes in a KG can make a difference via observation on their degrees. In Fig. 1, we notice that Mike is a male because he is a nephew of someone, hence it is incorrect indeed to reason by a rule containing a female-type relation starting from Mike. Also, the in-degree (i.e. studyIn) of entity THU proves its identity as a university. Besides, as illustrated in Section 4.1.1, all knowledge of a KG is stored in the relational matrices, which is our aim to reconstruct for harboring type information of entities. For a query
Fig. 3.
An illustration of computing the DegreEmbed operators for the KG shown in Fig. 2. Superscripts (+) and (−) of the labels of degree embedding vectors denote their in and out direction. All DegreEmbed operators are initialized to zero matrices.
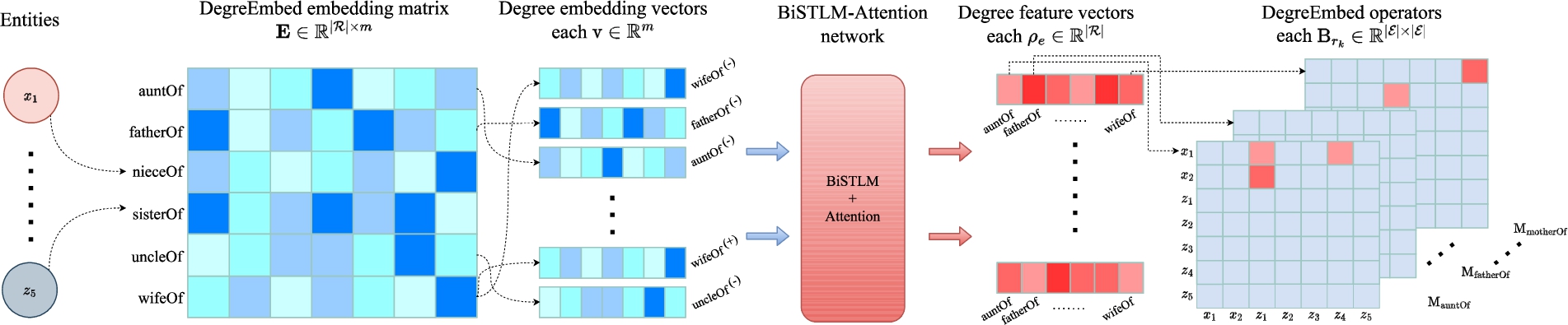
For any entity
To compute the attention value on each relation imposed by entity e, we have
Finally, the confidence scores are learned over the bidirectional LSTM followed by the attention using Eqs (13) and (14) for the temporal dependency among several consecutive steps. The input in Eq. (13) is query embedding from another lookup table. For
4.3.Optimization of the model
Loss construction. In general, this task of link prediction is treated as a classification of entities to build the loss. For each query
Low-rank approximation. It can be shown that the final confidences obtained by expanding
More concretely, we update Eqs (13) and (14), as is shown in Eqs (17) and (18), by deploying number of T BiLSTMs of the same network structure, each of which can extract features from various dimensions.
5.Experiment
In this section, we report the evaluation results of our model on a knowledge graph completion task, where we compare the effectiveness of our model against the state-of-the-art learning systems for link prediction. Meanwhile, as DegreEmbed takes advantage in the interpretability in contrast to embedding-based methods, we also examine the rules mined by DegreEmbed with the help of the indicator saturation, which assesses the quality of rules from the corresponding topological structure of a KG. We show that the top-scored rules mined by our method coincide with those of high saturation scores, which in turn reflect the interpretability of our model. To this end, we use ablation study to show how different components of our model contribute to its performance.
The knowledge graph completion task we use is a canonical one as described in [42]. When training the model, the query and head are part of incomplete triplets for training, and the goal is to find the most possible entity as the answer tail. For example, if nephewOf(Mike, Steve) is missing from the knowledge graph, our goal is to learn rules for reasoning over the existing KG and retrieve Steve when presented with the query nephewOf(Mike, ?).
5.1.Experiment setting
5.1.1.Datasets
To evaluate our method for learning logic rules in heterogeneous KGs, we select the following datasets for knowledge graph completion task:
– FB15K-237 [33], a more challenging version of FB15K [4] based on Freebase [3], a growing knowledge graph of general facts.
– WN18 [9], a subset of knowledge graph WordNet [20,21] constructed for a widely used dictionary.
– Medical Language System (UMLS) [16], from biomedicine, where the entities are biomedical concepts (e.g. organism, virus) and the relations consist of affects and analyzes, etc.
– Kinship [16], containing kinship relationships among members of a Central Australian native tribe.
– Family [16], containing individuals from multiple families that are biologically related.
Statistics about each dataset used in our experiments are presented in Table 1. All datasets are randomly split into 4 files: facts, train, valid and test, and the ratio is 6:2:1:1. The facts file contains a relatively large proportion of the triplets for constructing the KG. The train file is composed of query examples
Table 1
Statistics of datasets
| Dataset | # Relation | # Entity | # Triplets | # Facts | # Train | # Validation | # Test |
| FB15K-237 | 237 | 14541 | 310116 | 204087 | 68028 | 17535 | 20466 |
| WN18 | 18 | 40943 | 151442 | 106088 | 35353 | 5000 | 5000 |
| Family | 12 | 3007 | 28356 | 17615 | 5868 | 2038 | 2835 |
| Kinship | 25 | 104 | 10686 | 6375 | 2112 | 1099 | 1100 |
| UMLS | 46 | 135 | 6529 | 4006 | 3009 | 569 | 633 |
5.1.2.Evaluation metrics
During training on the task of knowledge graph completion, for each triplet
When evaluating the interpretability of rules, we choose a set of indicators called macro, micro and comprehensive saturations that measure the probability of a rule pattern occurring in a certain relational subgraph
Definition 3
Definition 3(Macro Reasoning Saturation).
Given a query
We can compute the macro reasoning saturation
Definition 4
Definition 4(Micro Reasoning Saturation).
Given the maximum length L of a rule pattern, we define the micro reasoning saturation of pattern
The equation to compute
Then, we average
In Eqs (19) and (21),
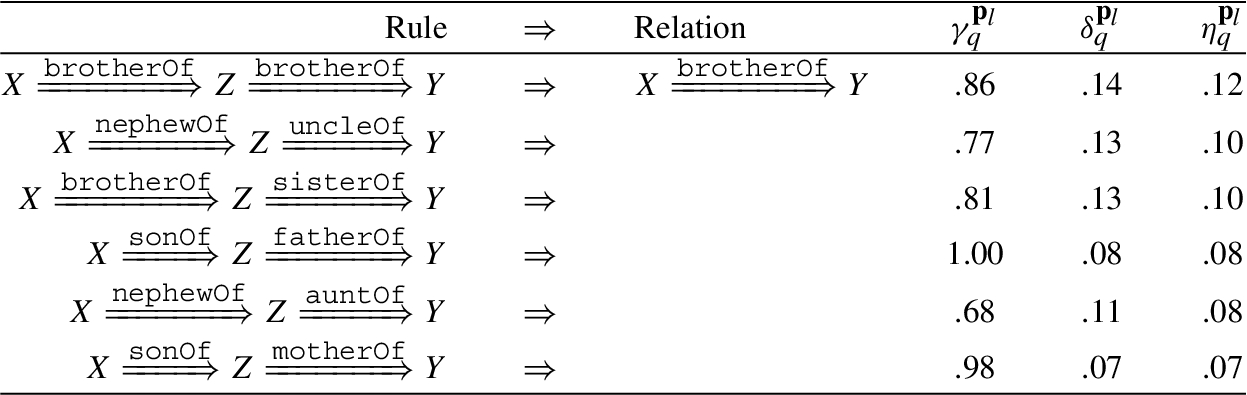
We can take the relation
Table 2
Saturations of the Family dataset.
We show a small subset of saturations computed from Family dataset in Table 2 for joint evaluation with logical rules mined by our model. More results can be obtained in App. C.
5.1.3.Comparison of algorithms
In experiment, the performance of our model is compared with that of the following algorithms:
– Rule learning algorithms. Since our model is based on neural logic programming, we choose Neural LP and a Neural LP-based method DRUM [29]. We also consider a probabilistic model called RNNLogic [27].
– Embedding-based algorithms. We choose several embedding-based algorithms for comparison of the expressive power of our model, including TransE [4], DistMult [41], ComplEx [34], TuckER [2] and RotatE [32].
The implementations of the above models we use are available at the links listed in App. A.
5.1.4.Model configuration
Our model is implemented using PyTorch [26] and the code will be publicly available. We use the same hyperparameter setting during evaluation on all datasets. The query and entity embedding have the dimension 128 and are both randomly initialized. The hidden state dimension of BiLSTM(s) for entity and degree embedding are also 128. As for optimization algorithm, we use mini-batch ADAM [15] with the batch size 128 and the learning rate initially set to 0.001. We also observe that the whole model tends to be more trainable if we use the normalization skill.
Note that Neural LP [42], DRUM [29] and our method all conform to a similar reasoning framework. Hence, to reach a fair comparison, we ensure the same hyperparameter configuration during experiments on these models, where the maximum rule length L is 2 and the rank T is 3 for DRUM and DegreEmbed, because Neural LP is not developed using the low-rank approximation method.
5.2.Results on KGC task
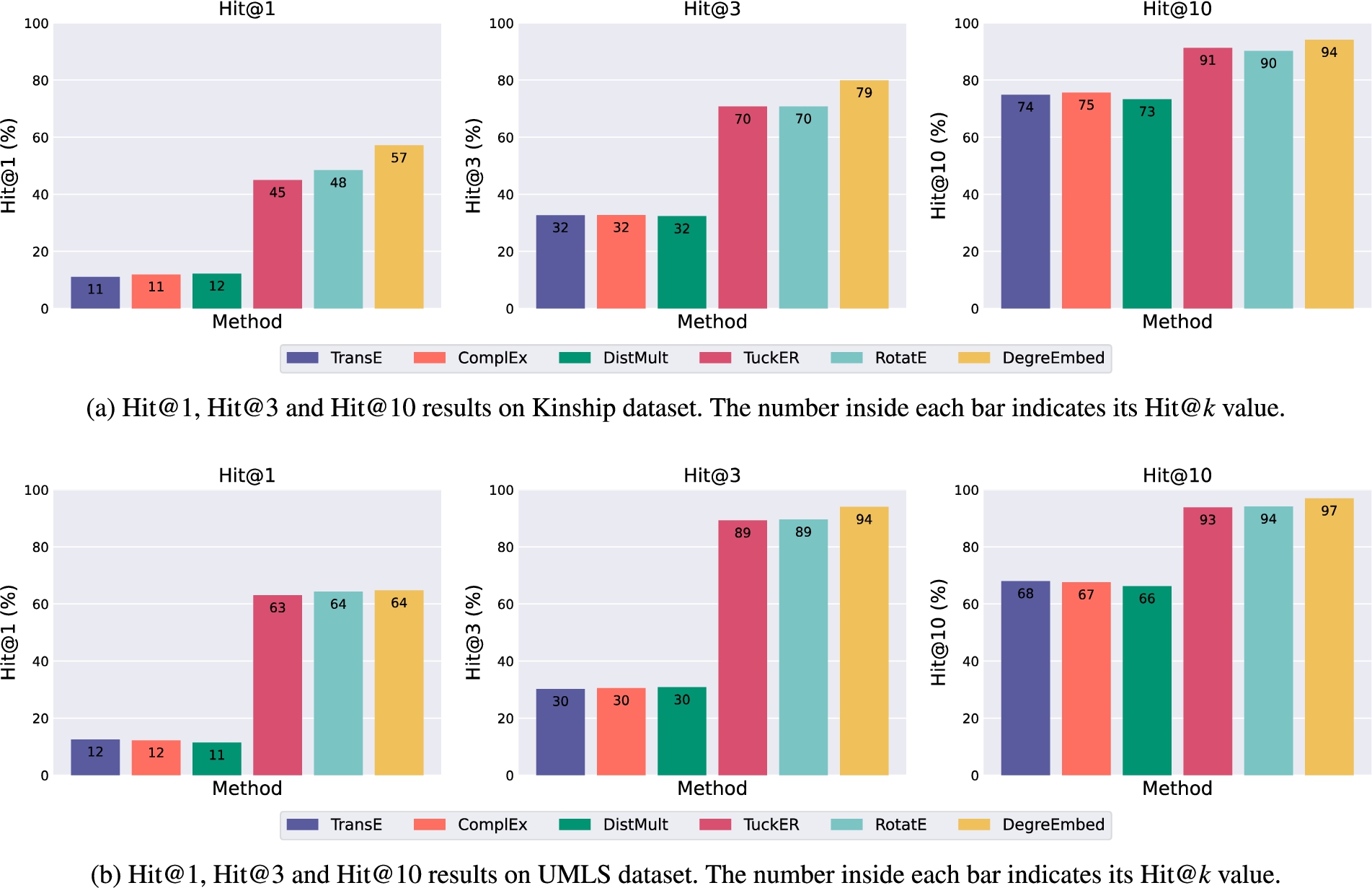
We compare our DegreEmbed to several baseline models on the KGC benchmark datasets as stated in the Section 5.1.1 and Section 5.1.3. Our results on the selected benchmark datasets are summarized in Table 3 and App. B.
Table 3
Knowledge graph completion performance comparison. Hit@k (H@k) is in %
| Family | Kinship | UMLS | ||||||||||
| MRR | H@1 | H@3 | H@10 | MRR | H@1 | H@3 | H@10 | MRR | H@1 | H@3 | H@10 | |
| TransE | .34 | 7 | 53 | 86 | .26 | 1 | 42 | 76 | .57 | 28 | 84 | 96 |
| DistMult | .58 | 39 | 71 | 91 | .51 | 36 | 57 | 87 | .73 | 63 | 81 | 90 |
| ComplEx | .83 | 72 | 94 | 98 | .61 | 44 | 71 | 92 | .79 | 69 | 87 | 95 |
| TuckER | .43 | 28 | 52 | 72 | .60 | 46 | 70 | 86 | .73 | 63 | 81 | 91 |
| RotatE | .90 | 85 | 95 | 99 | .65 | 50 | 76 | 93 | .73 | 64 | 82 | 94 |
| RNNLogic | .93 | 91 | 95 | 99 | .64 | 50 | 73 | 93 | .75 | 63 | 83 | 92 |
| Neural LP | .91 | 86 | 95 | 99 | .62 | 48 | 69 | 91 | .75 | 62 | 86 | 92 |
| DRUM | .94 | 90 | 98 | 99 | .58 | 43 | 67 | 90 | .80 | 66 | 94 | 97 |
| DegreEmbed | .95 | 91 | 99 | 100 | .70 | 57 | 79 | 94 | .80 | 65 | 94 | 98 |
We notice that except that ComplEx [34] produces the best result among all methods on UMLS under the evaluation of Hit@1, all models are outperformed by DegreEmbed with a clear margin in Table 3, especially on the dataset Kinship where we can see about 10% improvement on some metrics. As expected, incorporating entity embedding enhances the expressive power of DegreEmbed and thus benefits to reasoning on heterogeneous KGs.
In Table 7, our model achieves state-of-the-art performance on WN18. It is intriguing that embedding-based methods provide better predictions on FB15K-237 dataset, with rule based methods, including RNNLogic, Neural LP, DRUM and ours, left behind. As pointed in [9], there are inverse relations from the training data present in the test data in FB15K, which is called the problem of test set leakage, resulting in the variant FB15K-237 where inverse relations are removed. No wonder that methods depending on logic rule learning fails on this dataset. Future work on more effective embedding representation of a node and its neighbor edges is likely to significantly advance the performance of link prediction models based on logic rules.
Notably, DegreEmbed not only is capable of producing state-of-the-art results on KGC task thanks to the degree embedding of entities, but also maintains the advantage of logic rule learning that enables our model to be interpretable to humans, which is of vital significance in current research of intelligent systems. We will show the experiment results on the interpretability of our DegreEmbed model later.
5.3.Interpretability of our model
To demonstrate the interpretability of our method, we first report the logical rules mined by our model and compare them with those by DRUM [29]. Then we visualize the embedding vectors learned through the proposed technique degree embedding to prove its expressive power.
5.3.1.Quality of mined rules
Apart from reaching state-of-the-art performance on KGC task which is largely thanks to the mechanism of entity embedding, our DegreEmbed, as a knowledge graph reasoning model based on logic rule mining, is of excellent interpretability as well. Our work follows the Neural LP [42] framework, which successfully combines structure learning and parameter learning to generate rules along with confidence scores.
In this section, we report evaluation results on explanations of our model where some of the rules learned by DegreEmbed and DRUM are shown. As for evaluation metrics, we use the indicator saturations to objectively assess the quality of mined rules in a computable manner. We conduct two separate KGC experiments for generating the logical rules where the only difference is whether the inverted queries are learned. For better visualization purposes, experiments are done on the Family dataset, while other datasets such as UMLS produce similar results.
We sort the rules by their normalized confidence scores, which are computed by dividing by the maximum confidence of rules for each relation, and show top rules mined by our DegreEmbed and DRUM without augmented queries respectively in Table 4 and Table 5. Saturations of rules according to specific relations are shown in Table 2. For more results of saturations, learned rules w.r.t. both pure and augmented queries, please refer to the Appendix.
Table 4
Top rules without reverse queries mined by DegreEmbed on the Family dataset

Table 5
Top rules without reverse queries mined by DRUM on the Family dataset
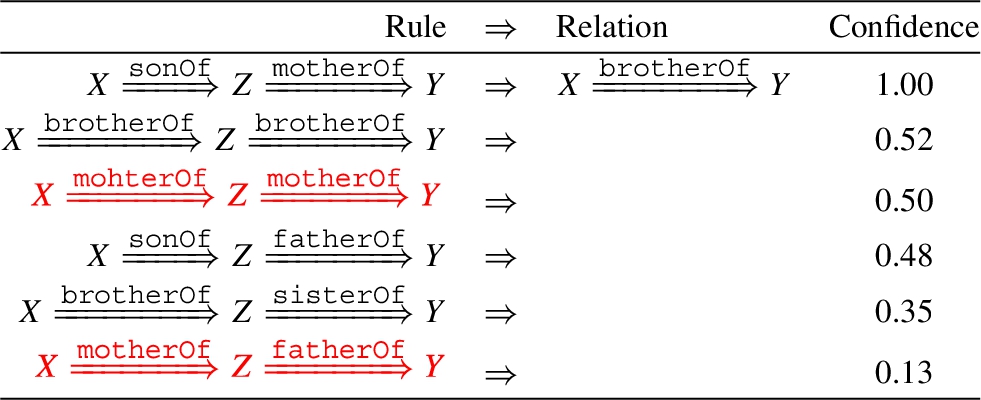
By referring to the results given by computing saturations, we can see the rules mined by our model solidly agree with the ones with high saturation level. Meanwhile, our model obviously gets rid of the noises rendered by the heterogeneousness of the dataset through blending entity attributes (e.g. gender of entities) into rule learning. The rules mined for predicting the relation brotherOf, such as brotherOf ∧ sisterOf and brotherOf ∧ brotherOf, all show up with a male-type relation at the first hop. However, there are logically incorrect rules mined by DRUM which are highlighted by red in Table 5. We think this is mainly because DRUM does not take entity attributes in to account. In this case, our DegreEmbed model is capable of learning meaningful rules, which indeed proves the interpretability of our model.
Fig. 4.
A t-SNE plot of the entity embedding of our trained model on Family dataset. Node colors denote their classes (i.e. degree feature vectors).

5.3.2.Learned entity embeddings
To explain the learned degree embedding, we visualize the embeddings vectors of some entities from the Family dataset. We use t-SNE [36] to project the embeddings to two-dimensional space and plot them in Fig. 4. In order to obtain the entity embeddings, we first train our DegreEmbed model on Family with the same hyperparameter settings mentioned in Section 5.1.4, and store the entire entity embedding matrix given by Eq. (10). Then, we classify the entities according to their degree feature vector proposed in Section 4.2 and choose top ten most populated clusters marked with various colors to plot in Fig. 4.
Note that, we use a logarithmic scale for the embedding plot to get better visualization results. In fact, the representation of entities exhibits localized clustering in the projected 2D space, which verifies the capability of our model to encode latent features of entities in heterogeneous KGs through their degrees.
5.4.Ablation study
Fig. 5.
Model performance on Family with the original entity embeddings replaced by pre-trained ones from embedding-based methods. Hit@k is in %. The number inside each bar indicates its Hit@k value.
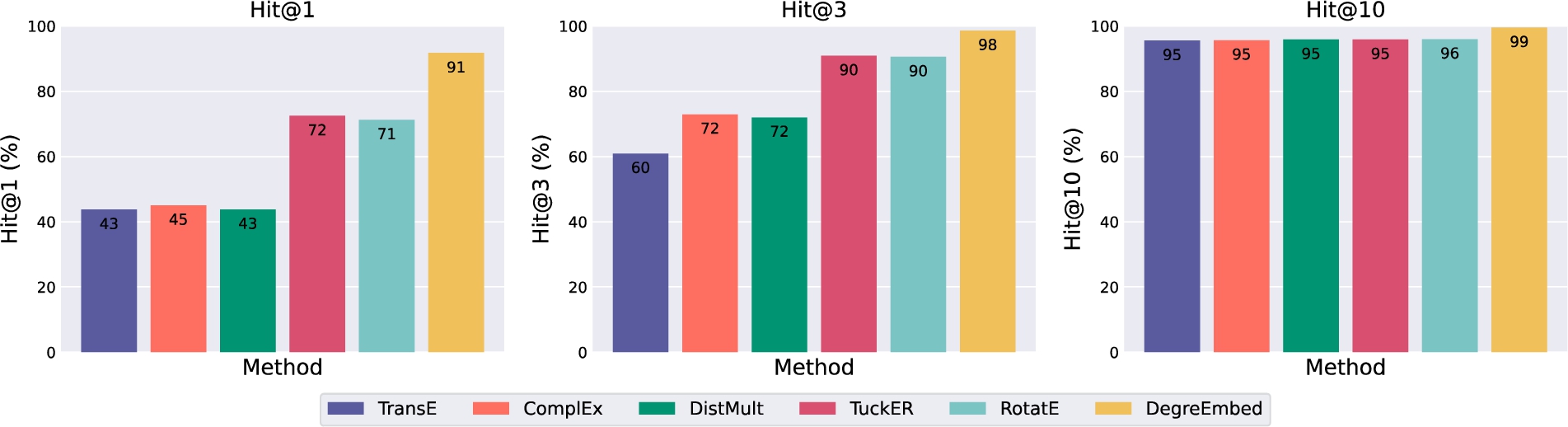
Fig. 6.
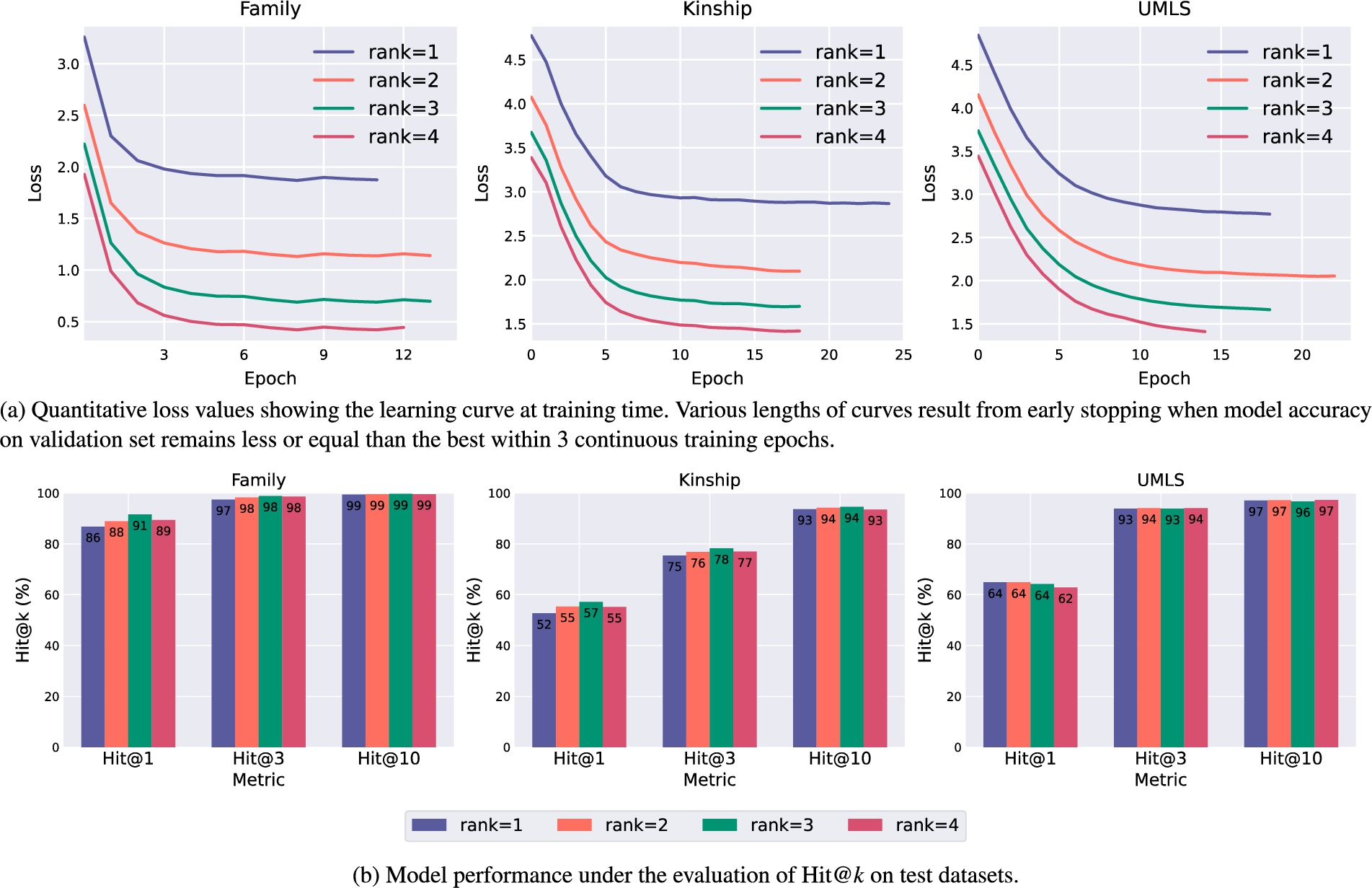
Comparison among DegreEmbed variants with different ranks on three benchmark datasets.
To study the necessity of each component of our method, we gradually change the configuration of each component and observe how the model performance varies.
Degree embedding. In this work, degree embedding is proposed as a new technique of entity embedding for incorporating heterogeneous information in KGs. We successively replace this component with learned entity embeddings from five pre-trained embedding-based models listed in Section 5.1.3 on three datasets. We measure the Hit@1, Hit@3 and Hit@10 metrics and show the results on Family in Fig. 5. Results on another two datasets are placed in the Appendix. In summary, the original model using degree embedding to encode entities produces the best results among all variants. We hypothesis that this is due to the fact that many inner attributes of entities are lost in the embeddings of those variants while DegreEmbed can learn to utilize these features implicitly.
Low-rank approximation. Tensor approximation of rank T enables our model to learn latent features from various dimensions, as show Eqs (17) and (18). We conduct experiments on three datasets and show how model behavior differs with rank ranging from 1 to 4 in Fig. 6. Training curves in Fig. 6(a) imply that model may converge faster with lower training loss as rank goes up. However, Fig. 6(b) demonstrates that higher rank does not necessarily bring better test results. We conjecture that this is because the amount of learnable features of distinct dimensions varies from dataset to dataset, where the choice of rank matters a lot. An intriguing insight can be obtained by combining Fig. 6(a) and Fig. 6(b): training loss degrades as model rank increases while it barely contributes to results on test sets, which provides a view of over-fitting.
6.Conclusions
In this paper, a logic rule learning model called DegreEmbed has been proposed for reasoning more effectively in heterogeneous knowledge graphs, where there exist entities and relations of different types. Based on mining logic rules, DegreEmbed simultaneously leverages latent knowledge of entities by learning embedding vectors for them, where the degrees of the entities are closely observed. Experiment results show that our model benefits from the advantages of both embedding-based methods and rule learning systems, as one can see DegreEmbed outperforms the state-of-the-art models with a clear margin, and it produces high-quality rules with great interpretability. In the future, we would like to optimize the way of entity embedding to increase the expressive power of logic rule learning models for knowledge graph reasoning.
Acknowledgements
The work of this paper is supported by the “National Key R&D Program of China” (2020YFB2009502), “the Fundamental Research Funds for the Central Universities” (Grant No. HIT.NSRIF.2020098).
Appendices
Appendix A.
Appendix A.Algorithm URLs
Table 6
Available links to the models used in this work
| Algorithm | Link |
| TransE, DistMult and ComplEx | https://github.com/Accenture/AmpliGraph |
| TuckER | https://github.com/ibalazevic/TuckER |
| RotatE | https://github.com/liyirui-git/KnowledgeGraphEmbedding_RotatE |
| RNNLogic | https://github.com/DeepGraphLearning/RNNLogic |
| Neural LP | https://github.com/fanyangxyz/Neural-LP |
| DRUM | https://github.com/alisadeghian/DRUM |
| DegreEmbed (ours) | https://github.com/lirt1231/DegreEmbed |
Appendix B.
Appendix B.Results on FB15K-237 and WN18
Table 7
Knowledge graph completion results on FB15K-237 and WN18. Hit@k is in %
| FB15K-237 | WN18 | |||||||
| MRR | Hit@1 | Hit@3 | Hit@10 | MRR | Hit@1 | Hit@3 | Hit@10 | |
| TransE | .15 | 5 | 19 | 25 | .36 | 4 | 63 | 81 |
| DistMult | .25 | 17 | 28 | 42 | .71 | 56 | 83 | 93 |
| ComplEx | .26 | 17 | 29 | 44 | .90 | 88 | 92 | 94 |
| TuckER | .36 | 27 | 39 | 46 | .94 | 93 | 94 | 95 |
| RotatE | .34 | 24 | 38 | 53 | .95 | 94 | 95 | 96 |
| RNNLogic | .29 | 21 | 31 | 43 | .94 | 93 | 94 | 96 |
| Neural LP | .25 | 19 | 27 | 37 | .94 | 93 | 94 | 95 |
| DRUM | .25 | 19 | 28 | 38 | .54 | 49 | 54 | 66 |
| DegreEmbed | .25 | 19 | 27 | 38 | .95 | 94 | 95 | 97 |
Appendix C.
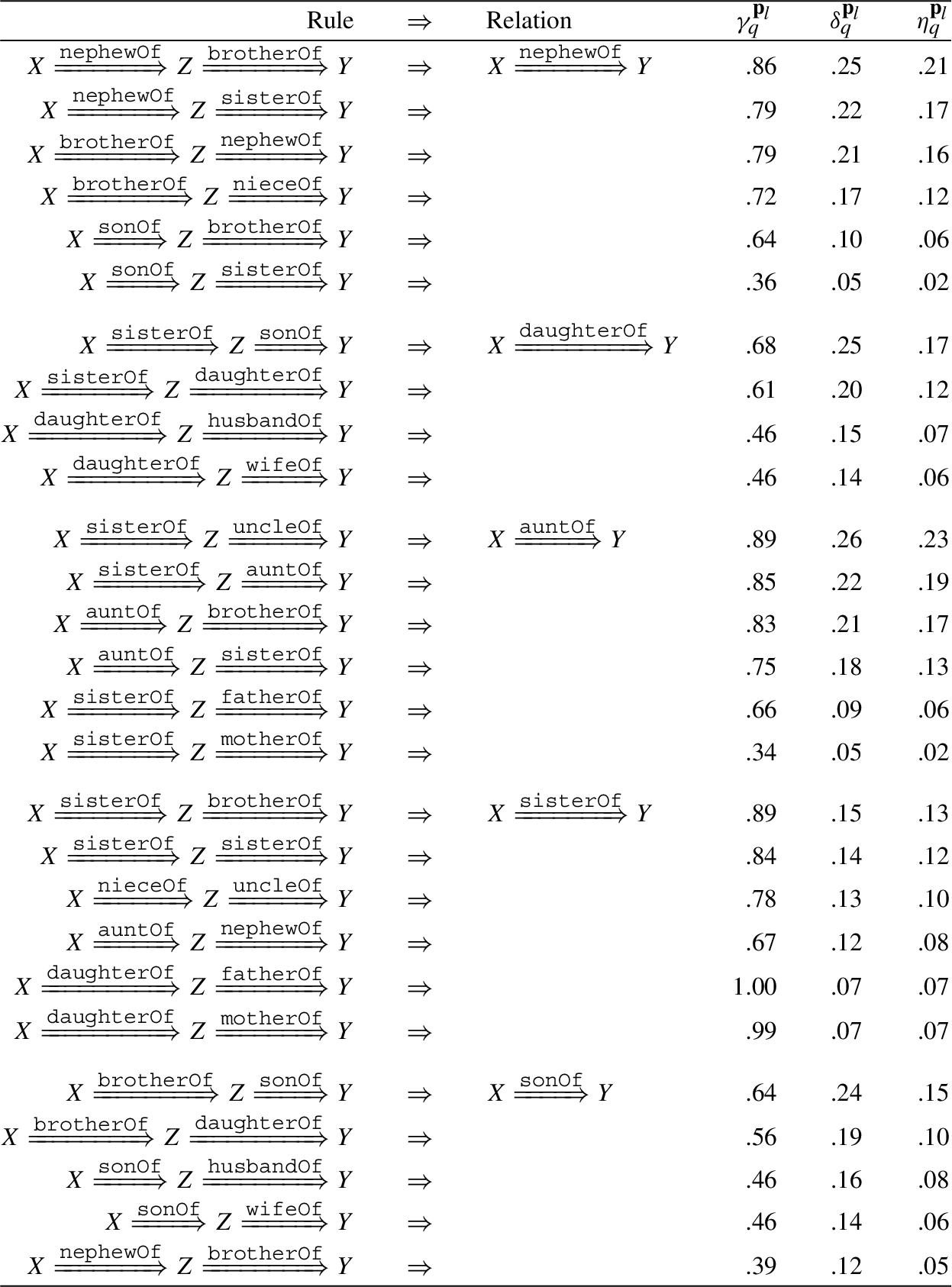
Appendix C.Extension to Table 2: More saturations of Family
Table 8
Saturations of the Family dataset.
Appendix D.
Appendix D.Extension to Table 4: Top rules obtained by our model
Table 9
Top rules without reverse queries mined by DegreEmbed on the Family dataset

Table 10
Top rules with reverse queries mined by DegreEmbed on the Family dataset

Appendix E.
Appendix E.Ablation results
Fig. 7.
Model performance on Kinship and UMLS with the original entity embeddings replaced by pre-trained ones from embedding-based methods. Hit@k is in %.
References
[1] | S. Auer, C. Bizer, G. Kobilarov, J. Lehmann, R. Cyganiak and Z. Ives, DBpedia: A nucleus for a web of open data, in: The Semantic Web, Springer, (2007) , pp. 722–735. doi:10.1007/978-3-540-76298-0_52. |
[2] | I. Balažević, C. Allen and T.M. Hospedales, Tucker: Tensor factorization for knowledge graph completion, 2019, arXiv preprint arXiv:1901.09590. |
[3] | K. Bollacker, C. Evans, P. Paritosh, T. Sturge and J. Taylor, Freebase: A collaboratively created graph database for structuring human knowledge, in: Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, (2008) , pp. 1247–1250. doi:10.1145/1376616.1376746. |
[4] | A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston and O. Yakhnenko, Translating embeddings for modeling multi-relational data, Advances in neural information processing systems 26: ((2013) ). |
[5] | Y. Chen, S. Goldberg, D.Z. Wang and S.S. Johri, Ontological pathfinding, in: Proceedings of the 2016 International Conference on Management of Data, (2016) , pp. 835–846. doi:10.1145/2882903.2882954. |
[6] | W.W. Cohen, TensorLog: A differentiable deductive database, 2016, arXiv preprint arXiv:1605.06523. |
[7] | W.W. Cohen, F. Yang and K.R. Mazaitis, TensorLog: Deep learning meets probabilistic databases, Journal of Artificial Intelligence Research 1: ((2018) ), 1–15. |
[8] | R. Das, A. Neelakantan, D. Belanger and A. McCallum, Chains of reasoning over entities, relations, and text using recurrent neural networks, 2016, arXiv preprint arXiv:1607.01426. |
[9] | T. Dettmers, P. Minervini, P. Stenetorp and S. Riedel, Convolutional 2D knowledge graph embeddings, in: Thirty-Second AAAI Conference on Artificial Intelligence, (2018) . |
[10] | X. Dong, E. Gabrilovich, G. Heitz, W. Horn, N. Lao, K. Murphy, T. Strohmann, S. Sun and W. Zhang, Knowledge vault: A web-scale approach to probabilistic knowledge fusion, in: Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, (2014) , pp. 601–610. doi:10.1145/2623330.2623623. |
[11] | L. Galárraga, C. Teflioudi, K. Hose and F.M. Suchanek, Fast rule mining in ontological knowledge bases with AMIE+, The VLDB Journal 24: (6) ((2015) ), 707–730. |
[12] | K. Guu, J. Miller and P. Liang, Traversing knowledge graphs in vector space, 2015, arXiv preprint arXiv:1506.01094. |
[13] | S. Hochreiter and J. Schmidhuber, Long short-term memory, Neural computation 9: (8) ((1997) ), 1735–1780. doi:10.1162/neco.1997.9.8.1735. |
[14] | S. Ji, S. Pan, E. Cambria, P. Marttinen and S.Y. Philip, A survey on knowledge graphs: Representation, acquisition, and applications, IEEE Transactions on Neural Networks and Learning Systems ((2021) ). |
[15] | D.P. Kingma and J. Ba, Adam: A method for stochastic optimization, 2014, arXiv preprint arXiv:1412.6980. |
[16] | S. Kok and P. Domingos, Statistical predicate invention, in: Proceedings of the 24th International Conference on Machine Learning, (2007) , pp. 433–440. doi:10.1145/1273496.1273551. |
[17] | D. Krompaß, S. Baier and V. Tresp, Type-constrained representation learning in knowledge graphs, in: International Semantic Web Conference, Springer, (2015) , pp. 640–655. |
[18] | N. Lao and W.W. Cohen, Relational retrieval using a combination of path-constrained random walks, Machine learning 81: (1) ((2010) ), 53–67. doi:10.1007/s10994-010-5205-8. |
[19] | Z. Liu, Z.-Y. Niu, H. Wu and H. Wang, Knowledge aware conversation generation with explainable reasoning over augmented graphs, 2019, arXiv preprint arXiv:1903.10245. |
[20] | G.A. Miller, WordNet: A lexical database for English, Communications of the ACM 38: (11) ((1995) ), 39–41. doi:10.1145/219717.219748. |
[21] | G.A. Miller, WordNet: An Electronic Lexical Database, MIT Press, (1998) . |
[22] | S.K. Mohamed, V. Nováček and A. Nounu, Discovering protein drug targets using knowledge graph embeddings, Bioinformatics 36: (2) ((2020) ), 603–610. doi:10.1093/bioinformatics/btz600. |
[23] | S. Moon, P. Shah, A. Kumar and R. Subba, OpenDialKG: Explainable conversational reasoning with attention-based walks over knowledge graphs, in: Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, (2019) , pp. 845–854. doi:10.18653/v1/P19-1081. |
[24] | S. Muggleton and L. De Raedt, Inductive logic programming: Theory and methods, The Journal of Logic Programming 19: ((1994) ), 629–679. doi:10.1016/0743-1066(94)90035-3. |
[25] | A. Neelakantan, B. Roth and A. McCallum, Compositional vector space models for knowledge base completion, 2015, arXiv preprint arXiv:1504.06662. |
[26] | A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga et al., PyTorch: An imperative style, high-performance deep learning library, Advances in neural information processing systems 32: ((2019) ), 8026–8037. |
[27] | M. Qu, J. Chen, L.-P. Xhonneux, Y. Bengio and J. Tang, RNNLogic: Learning logic rules for reasoning on knowledge graphs, 2020, arXiv preprint arXiv:2010.04029. |
[28] | M. Qu and J. Tang, Probabilistic logic neural networks for reasoning, 2019, arXiv preprint arXiv:1906.08495. |
[29] | A. Sadeghian, M. Armandpour, P. Ding and D.Z. Wang, Drum: End-to-end differentiable rule mining on knowledge graphs, 2019, arXiv preprint arXiv:1911.00055. |
[30] | R.T. Sousa, S. Silva and C. Pesquita, Evolving knowledge graph similarity for supervised learning in complex biomedical domains, BMC Bioinformatics 21: (1) ((2020) ), 1–19. doi:10.1186/s12859-019-3325-0. |
[31] | F.N. Stokman and P.H. de Vries, Structuring knowledge in a graph, in: Human-Computer Interaction, Springer, (1988) , pp. 186–206. doi:10.1007/978-3-642-73402-1_12. |
[32] | Z. Sun, Z.-H. Deng, J.-Y. Nie and J. Tang, Rotate: Knowledge graph embedding by relational rotation in complex space, 2019, arXiv preprint arXiv:1902.10197. |
[33] | K. Toutanova and D. Chen, Observed versus latent features for knowledge base and text inference, in: Proceedings of the 3rd Workshop on Continuous Vector Space Models and Their Compositionality, (2015) , pp. 57–66. doi:10.18653/v1/W15-4007. |
[34] | T. Trouillon, J. Welbl, S. Riedel, É. Gaussier and G. Bouchard, Complex embeddings for simple link prediction, in: International Conference on Machine Learning, PMLR, (2016) , pp. 2071–2080. |
[35] | L.R. Tucker, Some mathematical notes on three-mode factor analysis, Psychometrika 31: (3) ((1966) ), 279–311. doi:10.1007/BF02289464. |
[36] | L. Van der Maaten and G. Hinton, Visualizing data using t-SNE, Journal of machine learning research 9: (11) ((2008) ). |
[37] | P. Wang, D. Dou, F. Wu, N. de Silva and L. Jin, Logic rules powered knowledge graph embedding, 2019, arXiv:1903.03772 [cs]. |
[38] | P.-W. Wang, D. Stepanova, C. Domokos and J.Z. Kolter, Differentiable learning of numerical rules in knowledge graphs, in: International Conference on Learning Representations, (2019) . |
[39] | X. Wang, H. Ji, C. Shi, B. Wang, Y. Ye, P. Cui and P.S. Yu, Heterogeneous graph attention network, in: The World Wide Web Conference, WWW’19, Association for Computing Machinery, New York, NY, USA, (2019) , pp. 2022–2032. ISBN 9781450366748. doi:10.1145/3308558.3313562. |
[40] | C. Xiong, R. Power and J. Callan, Explicit semantic ranking for academic search via knowledge graph embedding, in: Proceedings of the 26th International Conference on World Wide Web, (2017) , pp. 1271–1279. doi:10.1145/3038912.3052558. |
[41] | B. Yang, W.-t. Yih, X. He, J. Gao and L. Deng, Embedding entities and relations for learning and inference in knowledge bases, 2014, arXiv preprint arXiv:1412.6575. |
[42] | F. Yang, Z. Yang and W.W. Cohen, Differentiable learning of logical rules for knowledge base reasoning, 2017, arXiv preprint arXiv:1702.08367. |
[43] | Y. Yang and L. Song, Learn to explain efficiently via neural logic inductive learning, 2019, arXiv preprint arXiv:1910.02481. |
[44] | W. Zhang, B. Paudel, L. Wang, J. Chen, H. Zhu, W. Zhang, A. Bernstein and H. Chen, Iteratively learning embeddings and rules for knowledge graph reasoning, in: The World Wide Web Conference, (2019) , pp. 2366–2377. doi:10.1145/3308558.3313612. |
[45] | Y. Zhang, X. Chen, Y. Yang, A. Ramamurthy, B. Li, Y. Qi and L. Song, Efficient probabilistic logic reasoning with graph neural networks, 2020, arXiv preprint arXiv:2001.11850. |




