Neural axiom network for knowledge graph reasoning
Abstract
Knowledge graph reasoning (KGR) aims to infer new knowledge or detect noises, which is essential for improving the quality of knowledge graphs. Recently, various KGR techniques, such as symbolic- and embedding-based methods, have been proposed and shown strong reasoning ability. Symbolic-based reasoning methods infer missing triples according to predefined rules or ontologies. Although rules and axioms have proven effective, it is difficult to obtain them. Embedding-based reasoning methods represent entities and relations as vectors, and complete KGs via vector computation. However, they mainly rely on structural information and ignore implicit axiom information not predefined in KGs but can be reflected in data. That is, each correct triple is also a logically consistent triple and satisfies all axioms. In this paper, we propose a novel NeuRal Axiom Network (NeuRAN) framework that combines explicit structural and implicit axiom information without introducing additional ontologies. Specifically, the framework consists of a KG embedding module that preserves the semantics of triples and five axiom modules that encode five kinds of implicit axioms. These axioms correspond to five typical object property expression axioms defined in OWL2, including ObjectPropertyDomain, ObjectPropertyRange, DisjointObjectProperties, IrreflexiveObjectProperty and AsymmetricObjectProperty. The KG embedding module and axiom modules compute the scores that the triple conforms to the semantics and the corresponding axioms, respectively. Compared with KG embedding models and CKRL, our method achieves comparable performance on noise detection and triple classification and achieves significant performance on link prediction. Compared with TransE and TransH, our method improves the link prediction performance on the Hits@1 metric by 22.0% and 20.8% on WN18RR-10% dataset, respectively.
1.Introduction
Knowledge Graphs (KGs) are multi-relational directed graphs with entities and relations as nodes and edges. Typically, knowledge graphs contain a large number of triples in the form of (subject entity, relation, object entity), abbreviated as
Symbolic-based methods [5,10,11,40] use predefined logic rules or ontologies for KG reasoning and can achieve good performance. For example, suppose the axiom DisjointObjectProperties(:hasParent :hasSpouse) that indicates the relations hasSpouse and hasParent are disjoint has already defined, then it is impossible for the two triples (Linda, hasSpouse, Bruce) and (Linda, hasParent, Bruce) to be correct at the same time. The reason is that a person’s spouse can not be the parent of this person. Although such methods are more reliable and human-interpretable, they require rich ontologies that are usually missing or incomplete in KGs. Moreover, it is tedious to define and maintain axioms manually. Thus we explore how to encode implicit axioms with only triples for KG reasoning in this paper.
Embedding-based methods, such as translation-based methods [2,20,36], semantic-based methods [33,39] and neural network methods [6,25,26], embed entities and relations into low-dimensional vector space. They use vector computation to complete knowledge graphs, which is scalable and efficient. However, despite the success of embedding models, they mainly focus on structural information and neglect implicit axiom information. Take the implicit domain/range axiom as an example. For the correct triple (Linda, hasSpouse, Bruce), we can infer that it satisfies domain/range axiom without the type of the subject entity Linda and the object entity Bruce, and domain/range of the relation hasSpouse.
In this paper, we propose a neural axiom network framework NeuRAN for KG reasoning. This framework encodes explicit structural information through a knowledge graph embedding model and implicit axiom information through neural networks. The main idea is that although ontology information is not explicitly defined in the given KG, any correct triple satisfies all axioms. Thus, the score to measure the plausibility of each triple is composed of a score from structural information and five axiom scores from axiom information. Here we consider five different axioms corresponding to five typical object property expression axioms selected from OWL2 ontology language,11 including ObjectPropertyDomain, ObjectPropertyRange, DisjointObjectProperties, IrreflexiveObjectProperty and AsymmetricObjectProperty. As domain and range axioms are related to type compatibility, we distinguish the type and semantic embeddings. Each entity has a type embedding and a semantic embedding. Each relation has two type embeddings (i.e., subject and object entity types excepted by the relation) and a semantic embedding. We encode the inherent structure of triples via an embedding module to learn semantic embeddings of entities and relations. In this paper, TransE and TransH are taken as examples of knowledge graph embedding modules to show the validity of our method. Any KGE model can be the KGE module. We introduce five axiom modules to encode axioms implicit in triples. The design of the axiom modules depends on the conditions that the axioms satisfy, as listed in Table 1. Specifically, for a triple
Table 1
Five types of object property expression axioms selected from OWL2 ontology language. OP is the short for ObjectProperty. OPE denotes Object Property Expression, and x, y, z are entity variables.
| Object Property Axioms | Condition | Examples |
| OPDomain(OPE CE) | Domain(hasWife, Man) | |
| OPRange(OPE CE) | Range(hasWife, Woman) | |
| Disjoint(hasParent, hasSpouse) | ||
| IrreflexiveOP(OPE) | Irreflexive(parentOf) | |
| AsymmetricOP(OPE) | Asymmetric(hasChild) |
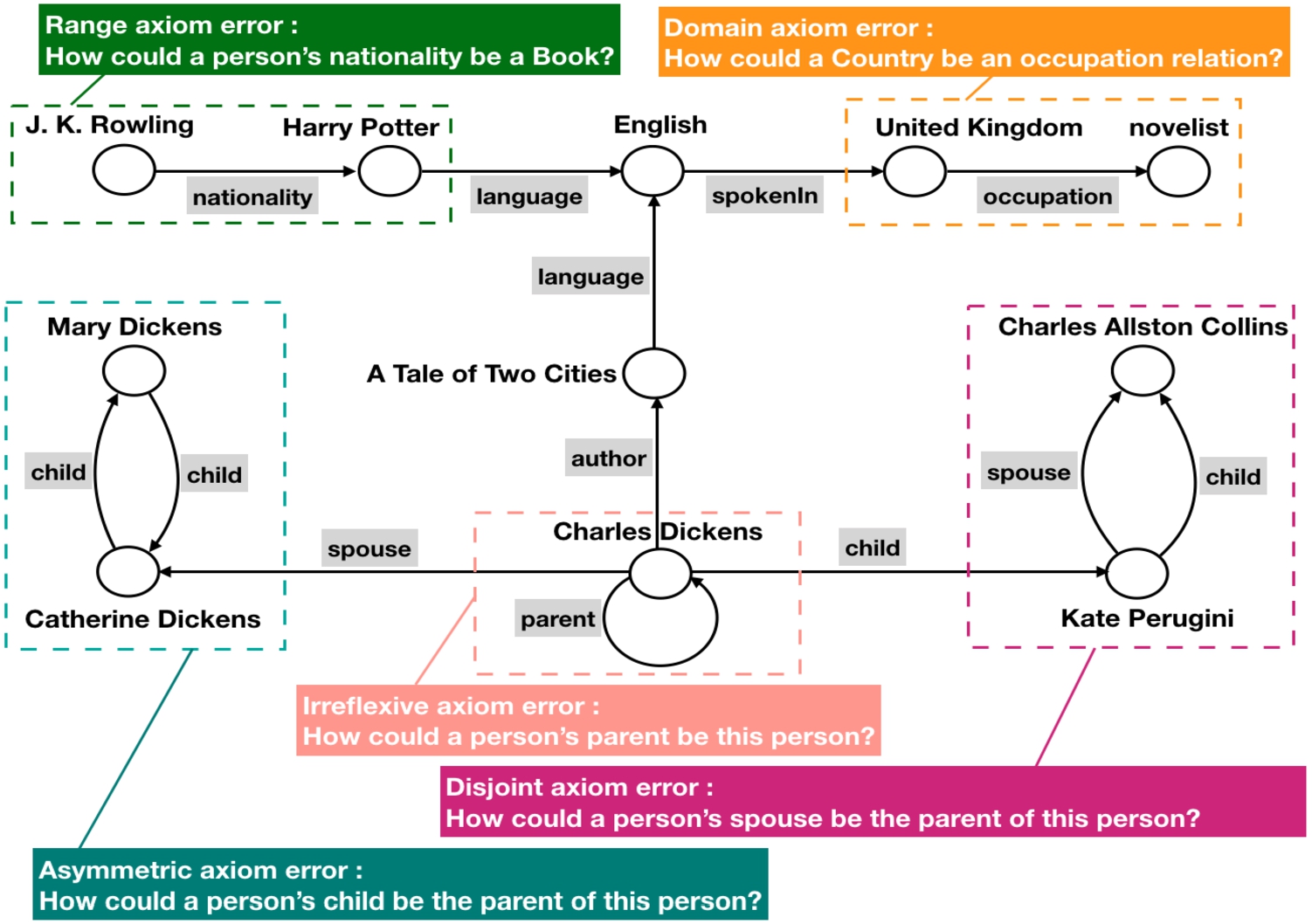
Fig. 1.
In the hypothetical knowledge graph, there may exist erroneous triples. The reason for these errors is that the triples do not conform to the axioms considered in this paper, including domain, range, disjoint, irreflexive and asymmetric axioms.
In summary, our main contributions are as follows:
– We raise the problem of neural axiom learning, in which axiom information is not given but can be reflected by and learned from existing triples in KGs.
– We propose a framework NeuRAN that uses a knowledge graph embedding module and five axiom modules to encode explicit structural and implicit axiom information, respectively.
– We evaluate NeuRAN on datasets with different ratios of noise. The experimental results demonstrate the effectiveness of our method on knowledge graph reasoning.
2.Related work
We discuss the following three lines of research work closely relevant to this paper, including symbolic-based reasoning, embedding-based reasoning and hybrid reasoning.
2.1.Symbolic-based reasoning
Symbolic-based reasoning methods aim at inferring new knowledge or detecting noises with the help of rules or ontologies and show good reasoning ability. For example, inductive logic programing (ILP) has been used to mine logical rules and use the rules to learn a good predictor. However, it has limitations on the open-world assumption of KGs. AMIE [11] and AMIE+ [10] make up for this shortcoming by introducing an altered confidence metric based on the partial completeness assumption. With the rules generated with AMIE+, [14] proposes to discover inverse and symmetric axioms by applying the predefined reasoning rules. Due to the incompleteness of rules and axioms, and the time-consuming process of annotating them, existing methods using ontologies for reasoning are usually accompanied by the enrichment of ontology information. For example, the work [9] presents a set of inductive methods based on statistical inductive learning, consisting of correlation computing and association rule mining to enrich ontologies with disjointness axioms. It evaluates the validity of association rule mining by computing the precision and recall scores. Then [22] proposes an improvement of association rule mining for learning disjointness axioms and applies the learned axioms to inconsistency detection. In addition to disjoint axioms, enriching DBpedia ontology with domain and range restrictions and class disjointness axioms is also discussed [31]. The enhanced ontologies are further used for error detection.
2.2.Embedding-based reasoning
Knowledge graph embedding methods embed entities and relations of a KG into a continuous vector space to preserve the structure information of the KG. There are three categories of embedding models: translational distance, semantic matching and neural network models. Translational distance models learn embeddings by translating a subject entity to an object entity through a relation. For example, TransE [2] represents entities and relations in the same vector space and assumes (
2.3.Hybrid reasoning
There is also a line of work concerning hybrid methods for KG reasoning, such as the combination of symbolic- and embedding-based reasoning, and the combination of symbolic and statistical reasoning. For the former methods, TransC [21] learns the SubClassOf axiom between types by encoding each type as a sphere and each entity as a vector. Besides, SetE [42] computes the two axioms SubClassOf and SubPropertyOf in subsumption by employing linear programming methods on embeddings, focusing on domain, range or subClassOf axioms. Recently, IterE [41] iteratively learns embeddings and rules, and considers seven object property expression axioms for rule learning. It combines rule learning and embedding learning to improve the quality of sparse entity embeddings by injecting new triples about sparse entities according to the scores of the axioms. As for the latter, the statistic-based methods, such as SDType and SDValidate [28], exploit statistical distributions of types and relations. SDType deduces missing type information based on the statistical distribution of types in the subject or object position of the relation. While SDValidate measures the deviation between actual types of the subject/object entity and the apriori probabilities given by the distribution. Furthermore, [4] first exploits a combination of entailment vectors, entailment weights, and a consistency vector to encode knowledge as embeddings in ontology streams to deal with concept drifts. It takes the concepts as input. The difference is that we design the axiom modules with the help of the definition of axioms.
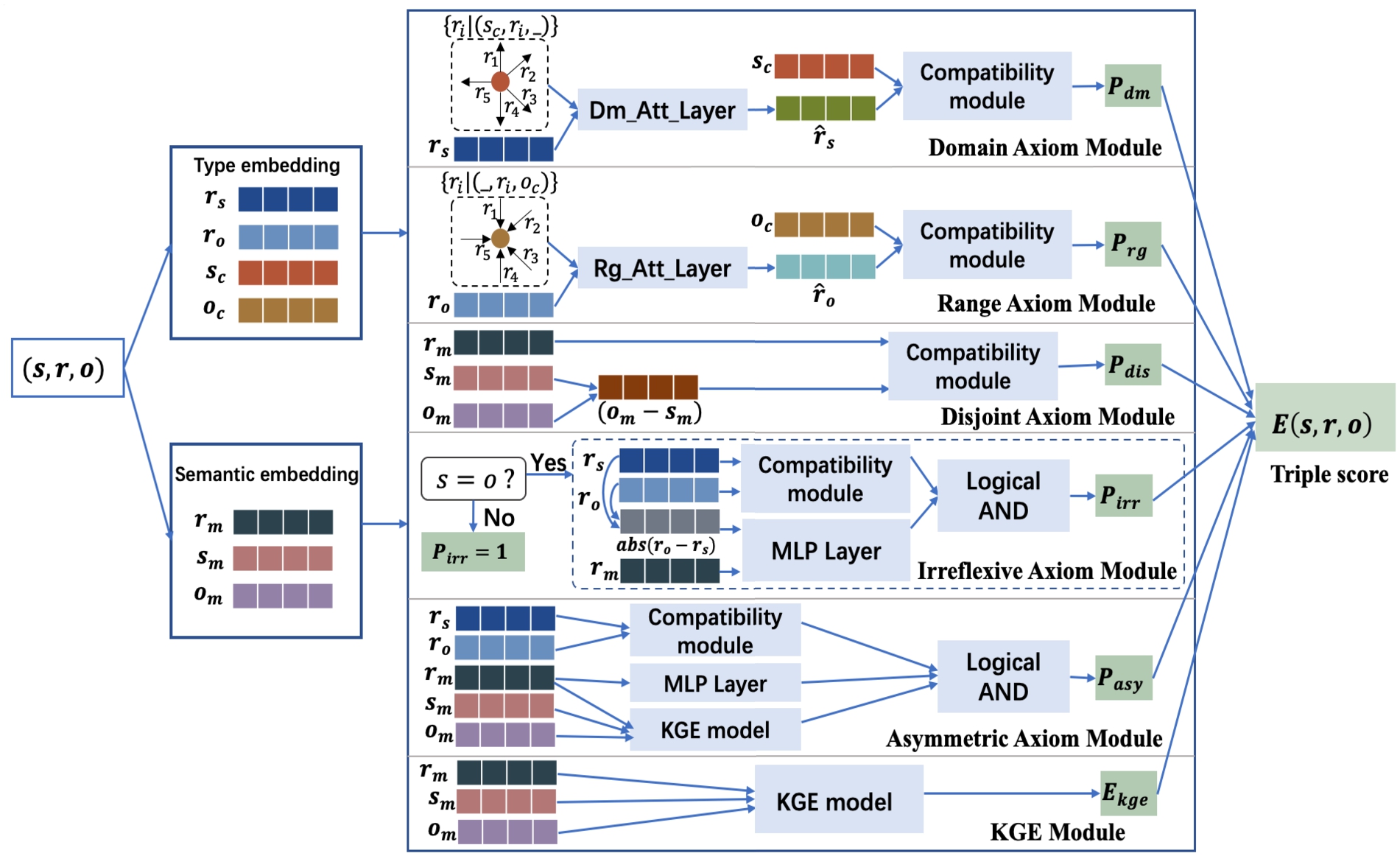
Fig. 2.
The key idea of our framework. For the input triple
3.Method
We begin this section by briefly describing some notations. We denote a knowledge graph as
Then, we introduce the neural axiom network NeuRAN which combines a knowledge graph embedding module and five axiom modules (Section 3.1). Afterward, we introduce the KGE module that encodes explicit structural information (Section 3.2) and the five axiom modules that aim to encode five kinds of implicit axiom information (Section 3.3).
3.1.Neural axiom network
We present our neural axiom network NeuRAN in Fig. 2, where the overall score of each triple is composed of a semantic score from the KGE module and five axiom scores from five axiom modules (i.e., domain, range, disjoint, irreflexive and asymmetric axiom modules). The score of each axiom module indicates the probability that the axiom holds. The assumption is that the probability values of these axioms intensify or mitigate the probability of the existence of a triple. Thus, the score of the triple
Following the conventional training strategy of previous models, we train NeuRAN based on the local-closed world assumption. In this case, the observed triples in KGs are regarded as positive triples, while the unobserved ones are regarded as negative triples. We utilize a margin-based ranking loss on pair-wise score functions (i.e.,
It is worth mentioning that, we attempt to introduce type embeddings in the design of the model. Considering domain/range axioms are associated with type compatibility, and type information is not provided, we distinguish type embeddings from semantic embeddings. Following the type-sensitive models TypeDM and TypeComplex [15], each entity is represented as two vectors (a type embedding and a semantic embedding), and each relation is represented as three vectors (two type embeddings and a semantic embedding). Take the triple
3.2.KG embedding module
The knowledge graph embedding module of the framework concerns the learning of a function
3.2.1.TransE
TransE is the simplest translation-based model, which interprets relations as translating operations between subject and object entities. Given a triple
3.2.2.TransH
TransH extends TransE by translating on hyperplanes, which models the relation
3.3.Five axiom modules
In addition to focusing on structural information, we consider the inherent implicit axioms in triples. Although axioms are not pre-given, it is intuitive that a correct triple is also a logically consistent triple. Any correct triple satisfies all the five axioms, including domain, range, disjoint, irreflexive, and asymmetric axioms. For example, in the case of missing domain and range of the relation nationality and types of the entities J. K. Rowling and United Kingdom, we can infer the triple (J. K. Rowling, nationality, United Kingdom) satisfies domain and range axioms by its correctness.
The design of the axiom modules relies on the definition of these axioms. To be specific, for domain/range axioms, we use the type embedding of the subject/object entity expected by the relation
3.3.1.Domain axiom module
Domain axiom module focuses on type compatibility between the subject entity type expected by the relation r and the type of the subject entity s. TypeDM uses the function
3.3.2.Range axiom module
Range axiom module focuses on type compatibility between the object entity type expected by the relation r and the type of the object entity o. Similarly, TypeDM uses
3.3.3.Disjoint axiom module
Disjoint axiom module focuses on the compatibility of the semantic embeddings of two relations with the same subject and object entities. For example, given the correct triple (John, spouse, Mary), and other two triples (John, friend, Mary) and (John, child, Mary), the disjoint axiom module computes probability scores of the two relation pairs including (spouse, friend), and (spouse, child). Then we can infer (John, friend, Mary) is a correct triple, and (John, child, Mary) is an incorrect triple. The reason is that the disjoint probability score of spouse and friend is high as they can exist between two persons simultaneously. In contrast, the score of spouse and child is low as a person’s spouse can not be that person’s child. In other words, spouse and child are defined to be semantically disjoint. Following the condition of disjoint axiom, we have to traverse the whole knowledge graph to find all the relations with s being the subject entity and o being the object entity. The relation set is
3.3.4.Irreflexive axiom module
Irreflexive axiom module considers two aspects of judgment. One is the property of the relation (i.e., whether r is irreflexive), and the other is whether the subject and object entity are equal (i.e., whether s and o are the same entity). In OWL2, a relation is irreflexive means that no entity can be related to itself by such a relation. Thus, only the two conditions the relation r is irreflexive and
Due to the judgment of
3.3.5.Asymmetric axiom module
Asymmetric axiom module considers two aspects of judgment as well, which are the property of the relation (i.e., whether r is asymmetric) and the existence of the symmetric triple of the given triple (i.e., whether
In this axiom, we begin with determining the property of the relation by focusing on the semantic embedding
4.Experiments
We evaluate our proposed method NeuRAN on three main knowledge graph reasoning tasks: noise detection, link prediction, and triple classification. Our code is available at https://github.com/JuanLi1621/NeuRAN.
4.1.Experimental settings
Datasets. In this paper, we use two popular benchmark datasets: FB15K237 [32] and WN18RR [6] to evaluate NeuRAN. They are constructed from FB15K and WN18 by removing inverse relations to solve test leakage. FB15K is a relatively dense subset extracted from the collaborative knowledge graph Freebase [1], which consists of billions of real-world facts. WN18 is a subset of WordNet [24] that describes relations between words.
Error Imputation. Since KGs are constructed in an automated or semi-automated way, noises can not be avoided. However, existing knowledge graph reasoning methods assume that triples in KGs are positive triples. Thus there are no pre-given noisy triples in FB15K237 and WN18RR. In order to verify our method, we generate new datasets with different noise rates based on the two datasets to simulate the real noisy knowledge graphs. Before generating noises, for each dataset with training, validation and test sets, we generate negative triples for the validation and test sets. The positive and negative triples in the validation set are used to find the optimum thresholds for each relation. To evaluate the performance of NeuRAN on triple classification, the positive and negative triples in the test set are classified as positive or negative triples based on both the triple scores and the thresholds. Here, we directly use the negative triples generated in OpenKE.22 Then, we randomly sample positive triples from the training set with different noise rates and generate the same number of negative triples as the sampled triples. Specifically, we corrupt either the subject or object entity of a triple with equal probability and ensure the generated negative triples do not exist in the KG. The generated negative triples are regarded as noises. All three tasks are evaluated on these simulated noisy datasets. For each dataset, we construct three noisy datasets with the ratio of negative triples to be 10%, 20%, and 40% of the positive triples. The generated negative triples (noises) with different ratios listed in Table 3 will be added to the training set as part of the training triples and labeled as positive triples. For example, for the datasets FB15K237-10%, FB15K237-20% and FB15K237-40%, the number of triples in the training set is 299326 (272115 + 27211), 326538 (272115 + 54423) and 380961 (272115 + 108846), respectively. The number of positive triples in the validation and test sets is 17535 and 20466, which is the same as FB15K237. Besides, the number of negative triples in the validation and test sets is the same as the number of positive triples. All the three noisy datasets share the same entities and relations with the original dataset. The detailed statistics of the two datasets and the generated noisy datasets are shown in Table 2 and 3.
Table 2
Statistics of FB15K237 and WN18RR
| Dataset | #Ent | #Rel | #Train | #Valid | #Test |
| FB15K237 | 14541 | 237 | 272115 | 17535 | 20466 |
| WN18RR | 40943 | 11 | 86835 | 3034 | 3134 |
Table 3
Statistics of negative triples generated from FB15K237 and WN18RR
| Datasets | FB15K237-10% | FB15K237-20% | FB15K237-40% |
| #Neg triple | 27211 | 54423 | 108846 |
| Datasets | WN18RR-10% | WN18RR-20% | WN18RR-40% |
| #Neg triple | 8683 | 17367 | 34734 |
Baselines. We choose TransE or TransH as the knowledge graph embedding module and compare our methods (i.e., NeuRAN(TransE), NeuRAN(TransH)) with them. Results of TransE and TransH are produced by running OpenKE [12]. We also consider CKRL(TransE) and CKRL(TransH) as baselines, which introduce path information for knowledge graph reasoning in noisy KGs. Results of CKRL(TransE) and CKRL(TransH) are reproduced by us. In the following tasks, the results of TransE, TransH, CKRL(TransE) and CKRL(TransH) are all obtained in this way.
Training Details. We use SGD [7] or Adam [18] to optimize the model for different tasks on different datasets. We select the learning rate from {0.01, 0.1, 0.5, 1}, the margin among {2,4,6,8,10}, the batch size from {100, 500}, dimension of the type from {20, 50, 100, 200}, dimension of the semantic from {50, 100, 200, 300}, the combination weight of the axiom scores λ from {0.01, 0.05, 0.1, 0.5, 1}. The number of training epochs is set as 1000.
4.2.Noise detection
To verify the capability of our method on noise detection task, we follow the setting of KG noise detection proposed in [38]. It aims to detect possible noises in noisy KGs according to the scores of triples and can be viewed as triple classification task on the training set.
Evaluation Protocol. First of all, we compute the score of the triple
Table 4
Noise detection results on noisy datasets with different ratios based on FB15K237 and WN18RR. The numbers are auc values
| FB15K237-10% | FB15K237-20% | FB15K237-40% | WN18RR-10% | WN18RR-20% | WN18RR-40% | |
| TransE | 0.9805 | 0.9799 | 0.9801 | 0.9370 | 0.9305 | 0.9018 |
| CKRL(TransE) | 0.9809 | 0.9804 | 0.9653 | 0.9337 | 0.9255 | 0.8971 |
| NeuRAN(TransE) | 0.9807 | 0.9807 | 0.9802 | 0.9403 | 0.9337 | 0.9141 |
| TransH | 0.9763 | 0.9746 | 0.9758 | 0.9331 | 0.9169 | 0.8614 |
| CKRL(TransH) | 0.9683 | 0.9697 | 0.9663 | 0.9279 | 0.9091 | 0.8527 |
| NeuRAN(TransH) | 0.9781 | 0.9783 | 0.9796 | 0.9340 | 0.9239 | 0.8780 |
Result Analysis. Evaluation results on noisy datasets generated based on FB15K237 and WN18RR can be found in Table 4. We observe that: (1) Regardless of whether the embedding module is TransE or TransH, our models achieve comparable performance or slightly outperform TransE, CKRL(TransE), TransH, and CKRL(TransH) on the two datasets WN18RR and FB15K237 with different noise rates (i.e., WN18RR-10%, WN18RR-20%, WN18RR-40%, FB15K237-10%, FB15K237-20%, and FB15K237-40%). (2) When the complex relations are well encoded, for example, in TransH. Our model with axiom information performs better than path information on noise detection on WN18RR- and FB15K237-based datasets. (3) With the increase of noises, the ability of baselines and our models to detect noises decreases on WN18RR-based datasets. However, it may increase on FB15K237-based datasets, which indicates that the more relations and triples in noisy datasets, the more valid information may be introduced, even though these triples may be noises.
We can thus conclude that implicit axiom information is helpful for noise detection and is better reflected on datasets with a large number of relations and triples.
4.3.Triple classification
Triple classification aims to judge whether a triple in the test set is correct or not, according to triple scores calculated by the energy function
Evaluation Protocol. As the test sets of the datasets used for triple classification only have correct triples, we generate negative triples by randomly corrupting the subject or object entity of correct triples. For the validation and test sets, the number of negative triples is the same as the number of positive triples. Thus there are labeled positive and negative triples in the two sets. For example, for WN18RR-based datasets, the number of triples is 6068 in the validation set and 6268 in the test set. As for triple classification, we learn a relation-specific threshold
Table 5
Triple classification results on WN18RR, WN18RR-10%, WN18RR-20% and WN18RR-40%. “ACC”, “P” and “R” are the abbreviation of “accuracy”, “precision” and “recall”, respectively
| Methods | WN18RR-10% | WN18RR-20% | WN18RR-40% | ||||||
| ACC | P | R | ACC | P | R | ACC | P | R | |
| TransE | 0.8764 | 0.9232 | 0.8210 | 0.8575 | 0.8889 | 0.8172 | 0.8355 | 0.9046 | 0.7502 |
| CKRL(TransE) | 0.8759 | 0.9201 | 0.8232 | 0.8574 | 0.8994 | 0.8047 | 0.8350 | 0.9127 | 0.7409 |
| NeuRAN(TransE) | 0.8856 | 0.9281 | 0.8360 | 0.8703 | 0.9100 | 0.8197 | 0.8598 | 0.9328 | 0.7754 |
| TransH | 0.8618 | 0.9216 | 0.7910 | 0.8444 | 0.9039 | 0.7709 | 0.8146 | 0.8772 | 0.7317 |
| CKRL(TransH) | 0.8556 | 0.9233 | 0.7757 | 0.8403 | 0.8829 | 0.7846 | 0.8116 | 0.8629 | 0.7409 |
| NeuRAN(TransH) | 0.8687 | 0.9300 | 0.7974 | 0.8598 | 0.9040 | 0.8050 | 0.8323 | 0.8802 | 0.7693 |
Table 6
Triple classification results for FB15K237-10%, FB15K237-20% and FB15K237-40%. “ACC”, “P” and “R” are the abbreviation of “accuracy”, “precision” and “recall”, respectively
| Methods | FB15K237-10% | FB15K237-20% | FB15K237-40% | ||||||
| ACC | P | R | ACC | P | R | ACC | P | R | |
| TransE | 0.7758 | 0.7743 | 0.7786 | 0.7605 | 0.7353 | 0.8140 | 0.7422 | 0.7269 | 0.7759 |
| CKRL(TransE) | 0.7767 | 0.7728 | 0.7839 | 0.7579 | 0.7407 | 0.7936 | 0.7420 | 0.7314 | 0.7651 |
| NeuRAN(TransE) | 0.7810 | 0.7846 | 0.7749 | 0.7656 | 0.7711 | 0.7554 | 0.7484 | 0.7497 | 0.7459 |
| TransH | 0.7978 | 0.8023 | 0.7904 | 0.7831 | 0.7816 | 0.7857 | 0.7623 | 0.7754 | 0.7387 |
| CKRL(TransH) | 0.7835 | 0.7922 | 0.7686 | 0.7660 | 0.7669 | 0.7642 | 0.7473 | 0.7528 | 0.7365 |
| NeuRAN(TransH) | 0.7882 | 0.8080 | 0.7561 | 0.7784 | 0.7891 | 0.7600 | 0.7617 | 0.7796 | 0.7299 |
Result Analysis. Table 5 and 6 show the detailed evaluation results of triple classification. From the two tables, we can observe that: (1) Regarding the three metrics, our method outperforms baselines on the WN18RR-based datasets and achieves the best results. It confirms that learning knowledge representations with axiom information can help triple classification. (2) On the FB15K237-based dataset, the results are comparable with baselines. The improvements on WN18RR-10%, WN18RR-20% and WN18RR-40% are more evident than on FB15K237-10%, FB15K237-20% and FB15K237-40%. It demonstrates that implicit axiom information is more effective on a dataset with a smaller number of relations and triples. (3) Compared with TransE, TransH, CKRL(TransE) and CKRL(TransH), the higher the noise rate, the smaller the decrease in the accuracy metric of our method on WN18RR-10%, WN18RR-20% and WN18RR-40%. It indicates that on noisy datasets, triple classification results of NeuRAN can be more robust than baselines on small datasets.
From the triple classification results, we can conclude that the combination of implicit axiom and structural information reflected by existing triples in knowledge graphs works better than using only structural information on datasets with a small number of relations and triples. In comparison, path information is more helpful when the number of relations and triples is large.
4.4.Link prediction
To show that axiom information could improve the embedding learning of entities and relations and further help complete knowledge graphs, we conduct link prediction to evaluate the performance of knowledge graph completion. This task aims to predict the missing entity when given one entity and one relation of a triple, including subject entity prediction
Evaluation Protocol. For each test triple, suppose the subject entity prediction
Result Analysis. Link prediction results are shown in Table 7 and 8. We analyze the results as follows: (1) The link prediction results of our method are improved compared with baselines on WN18RR-10%, WN18RR-20% and WN18RR-40% datasets, as well as on FB15K237-10%, FB15K237-20% and FB15K237-40%. It confirms that the learned knowledge graph embeddings’ quality is better and could help complete KGs. Besides, it indicates axiom information can be more useful than path information on noisy datasets. (2) On WN18RR-10%, WN18RR-20% and WN18RR-40% datasets, our method achieves the best performance on all metrics. The improvements are significant on all metrics, especially on Hits@1. It demonstrates that axiom information is of great help in improving the predictive ability of a missing triple when the dataset has fewer relations and triples. (3) On FB15K237-10%, FB15K237-20% and FB15K237-40%, although the improvements of the results are less prominent compared with WN18RR-based datasets, the results are better than baselines. It reaffirms that our method can improve link prediction, and the more relations and triples, the more information and noises brought by axiom information. Therefore, the advantages of implicit axiom information would not be as significant as in small-scale datasets.
Table 7
Link prediction results on FB15K237-10%, FB15K237-20% and FB15K237-40%
| FB15K237-10% | FB15K237-20% | FB15K237-40% | |||||||
| MRR | Hit@ | MRR | Hit@ | MRR | Hit@ | ||||
| 3 | 1 | 3 | 1 | 3 | 1 | ||||
| TransE | 0.258 | 0.299 | 0.159 | 0.240 | 0.279 | 0.144 | 0.230 | 0.270 | 0.137 |
| CKRL(TransE) | 0.252 | 0.294 | 0.150 | 0.236 | 0.278 | 0.136 | 0.225 | 0.268 | 0.129 |
| NeuRAN(TransE) | 0.284 | 0.313 | 0.199 | 0.269 | 0.292 | 0.189 | 0.251 | 0.273 | 0.176 |
| TransH | 0.241 | 0.296 | 0.125 | 0.213 | 0.270 | 0.094 | 0.193 | 0.248 | 0.078 |
| CKRL(TransH) | 0.194 | 0.254 | 0.070 | 0.172 | 0.229 | 0.050 | 0.156 | 0.209 | 0.041 |
| NeuRAN(TransH) | 0.288 | 0.317 | 0.203 | 0.270 | 0.293 | 0.189 | 0.249 | 0.272 | 0.173 |
Table 8
Link prediction results on WN18RR-10%, WN18RR-20% and WN18RR-40%
| WN18RR-10% | WN18RR-20% | WN18RR-40% | |||||||
| MRR | Hit@ | MRR | Hit@ | MRR | Hit@ | ||||
| 3 | 1 | 3 | 1 | 3 | 1 | ||||
| TransE | 0.211 | 0.351 | 0.036 | 0.206 | 0.349 | 0.031 | 0.193 | 0.334 | 0.027 |
| CKRL(TransE) | 0.215 | 0.349 | 0.044 | 0.205 | 0.340 | 0.034 | 0.154 | 0.233 | 0.024 |
| NeuRAN(TransE) | 0.342 | 0.393 | 0.256 | 0.334 | 0.392 | 0.247 | 0.320 | 0.377 | 0.236 |
| TransH | 0.218 | 0.360 | 0.043 | 0.208 | 0.352 | 0.038 | 0.191 | 0.327 | 0.032 |
| CKRL(TransH) | 0.206 | 0.339 | 0.038 | 0.199 | 0.334 | 0.034 | 0.176 | 0.309 | 0.019 |
| NeuRAN(TransH) | 0.330 | 0.380 | 0.251 | 0.328 | 0.378 | 0.250 | 0.314 | 0.371 | 0.232 |
Thus we can conclude that implicit axiom information encoded by neural axiom networks helps to improve the quality of learned embeddings of entities and relations and link prediction results. Moreover, such information is more effective on datasets with relatively few relations and triples.
4.5.Ablation study
We conduct ablation studies on link prediction to assess the effectiveness of NeuRAN. As our model is composed of a knowledge graph embedding module and five neural axiom modules, we add each axiom module to the knowledge graph embedding module to investigate the contributions of the axiom module. Specifically, we use the score function and loss function defined in equation (1) and (2) to train our model. TransE is taken as the knowledge graph embedding module. For evaluation, we set the score function as
Table 9
Ablation study of link prediction results on WN18RR-10% and FB15K237-10%. KGE is TransE
| WN18RR-10% | FB15K237-10% | |||||
| MRR | Hit@ | MRR | Hit@ | |||
| 3 | 1 | 3 | 1 | |||
| KGE | 0.2103 | 0.3468 | 0.0333 | 0.2267 | 0.2851 | 0.1067 |
| KGE + DM | 0.2108 | 0.3476 | 0.0337 | 0.2267 | 0.2848 | 0.1067 |
| KGE + RG | 0.2134 | 0.3500 | 0.0370 | 0.2268 | 0.2853 | 0.1069 |
| KGE + DIS | 0.2203 | 0.3529 | 0.0490 | 0.2723 | 0.3069 | 0.1795 |
| KGE + IRRE | 0.3407 | 0.3925 | 0.2554 | 0.2746 | 0.3030 | 0.1864 |
| KGE + ASYM | 0.2108 | 0.3472 | 0.0341 | 0.2267 | 0.2851 | 0.1067 |
| KGE + ALL | 0.3417 | 0.3926 | 0.2562 | 0.2838 | 0.3128 | 0.1987 |
From Table 9, we can observe that adding these five axioms can improve link prediction results on WN18RR-10%. The disjoint and irreflexive modules work better than other modules. Notably, the irreflexive axiom module has substantially improved on MRR and Hits@1 metrics. As the number of relations is small and most relations are asymmetric on WN18RR%, using the attention mechanism to aggregate relation representations or adding the asymmetric module has a small gain. For the results on the FB15K237-10% dataset with more relations, the improvement of the disjoint module increases compared to on WN18RR%. Although the domain, range and asymmetric modules are not as efficient as the other modules, we consider them for a comprehensive exploration.
5.Conclusion
In this paper, we propose a novel neural axiom network model which aims to do reasoning on noisy knowledge graphs. We consider encoding not only structural information but also axiom information of triples. Specifically, we propose a knowledge graph embedding module for preserving the structure and five different axiom modules for calculating probability scores that satisfy the corresponding axioms. We evaluate our method on KG noise detection, triple classification and link prediction. Experiments show that axiom information can benefit these tasks.
In the future, we will attempt to explore more implicit or explicit information in triples to enhance the performance of knowledge graph reasoning. Furthermore, we will improve our method to apply it for inconsistency reasoning, as axiom information may be able to provide explanations for inconsistent triples.
Notes
Acknowledgements
This work was supported by Zhejiang Provincial Natural Science Foundation of China (No. LQ23F0200 17) and Yongjiang Talent Introduction Programme.
References
[1] | K.D. Bollacker, C. Evans, P. Paritosh, T. Sturge and J. Taylor, Freebase: A collaboratively created graph database for structuring human knowledge, in: SIGMOD Conference, ACM, (2008) , pp. 1247–1250. |
[2] | A. Bordes, N. Usunier, A. García-Durán, J. Weston and O. Yakhnenko, Translating embeddings for modeling multi-relational data, in: NIPS, (2013) , pp. 2787–2795. |
[3] | A. Bordes, J. Weston and N. Usunier, Open question answering with weakly supervised embedding models, in: ECML/PKDD (1), Lecture Notes in Computer Science, Vol. 8724: , Springer, (2014) , pp. 165–180. |
[4] | J. Chen, F. Lécué, J.Z. Pan, S. Deng and H. Chen, Knowledge graph embeddings for dealing with concept drift in machine learning, J. Web Semant. 67: ((2021) ), 100625. doi:10.1016/j.websem.2020.100625. |
[5] | W.W. Cohen, TensorLog: A differentiable deductive database, CoRR abs/1605.06523, 2016. |
[6] | T. Dettmers, P. Minervini, P. Stenetorp and S. Riedel, Convolutional 2D knowledge graph embeddings, in: AAAI, AAAI Press, (2018) , pp. 1811–1818. |
[7] | J.C. Duchi, E. Hazan and Y. Singer, Adaptive subgradient methods for online learning and stochastic optimization, J. Mach. Learn. Res. 12: ((2011) ), 2121–2159. |
[8] | T. Ebisu and R. Ichise, TorusE: Knowledge graph embedding on a Lie group, in: AAAI, AAAI Press, (2018) , pp. 1819–1826. |
[9] | D. Fleischhacker and J. Völker, Inductive learning of disjointness axioms, in: OTM Conferences (2), Lecture Notes in Computer Science, Vol. 7045: , Springer, (2011) , pp. 680–697. |
[10] | L. Galárraga, C. Teflioudi, K. Hose and F.M. Suchanek, Fast rule mining in ontological knowledge bases with AMIE+, VLDB J. 24: (6) ((2015) ), 707–730. |
[11] | L.A. Galárraga, C. Teflioudi, K. Hose and F.M. Suchanek, AMIE: Association rule mining under incomplete evidence in ontological knowledge bases, in: WWW, International World Wide Web Conferences Steering Committee / ACM, (2013) , pp. 413–422. |
[12] | X. Han, S. Cao, X. Lv, Y. Lin, Z. Liu, M. Sun and J. Li, OpenKE: An open toolkit for knowledge embedding, in: EMNLP (Demonstration), Association for Computational Linguistics, (2018) , pp. 139–144. |
[13] | J. Hoffart, F.M. Suchanek, K. Berberich and G. Weikum, YAGO2: A spatially and temporally enhanced knowledge base from Wikipedia, Artif. Intell. 194: ((2013) ), 28–61. doi:10.1016/j.artint.2012.06.001. |
[14] | R. Irny and P.S. Kumar, Mining inverse and symmetric axioms in linked data, in: JIST, Lecture Notes in Computer Science, Vol. 10675: , Springer, (2017) , pp. 215–231. |
[15] | P. Jain, P. Kumar, Mausam and S. Chakrabarti, Type-sensitive knowledge base inference without explicit type supervision, in: ACL (2), Association for Computational Linguistics, (2018) , pp. 75–80. |
[16] | G. Ji, S. He, L. Xu, K. Liu and J. Zhao, Knowledge graph embedding via dynamic mapping matrix, in: ACL (1), The Association for Computer Linguistics, (2015) , pp. 687–696. |
[17] | S. Jia, Y. Xiang, X. Chen, K. Wang and S. E, Triple trustworthiness measurement for knowledge graph, in: WWW, ACM, (2019) , pp. 2865–2871. |
[18] | D.P. Kingma and J. Ba, Adam: A method for stochastic optimization, in: ICLR (Poster), (2015) . |
[19] | J. Lehmann, R. Isele, M. Jakob, A. Jentzsch, D. Kontokostas, P.N. Mendes, S. Hellmann, M. Morsey, P. van Kleef, S. Auer and C. Bizer, DBpedia – a large-scale, multilingual knowledge base extracted from Wikipedia, Semantic Web 6: (2) ((2015) ), 167–195. doi:10.3233/SW-140134. |
[20] | Y. Lin, Z. Liu, M. Sun, Y. Liu and X. Zhu, Learning entity and relation embeddings for knowledge graph completion, in: AAAI, AAAI Press, (2015) , pp. 2181–2187. |
[21] | X. Lv, L. Hou, J. Li and Z. Liu, Differentiating concepts and instances for knowledge graph embedding, in: EMNLP, Association for Computational Linguistics, (2018) , pp. 1971–1979. |
[22] | Y. Ma, H. Gao, T. Wu and G. Qi, Learning disjointness axioms with association rule mining and its application to inconsistency detection of linked data, in: CSWS, Communications in Computer and Information Science, Vol. 480: , Springer, (2014) , pp. 29–41. |
[23] | A. Melo and H. Paulheim, Automatic detection of relation assertion errors and induction of relation constraints, Semantic Web 11: (5) ((2020) ), 801–830. doi:10.3233/SW-200369. |
[24] | G.A. Miller, WordNet: A lexical database for English, Commun. ACM 38: (11) ((1995) ), 39–41. doi:10.1145/219717.219748. |
[25] | D.Q. Nguyen, T.D. Nguyen, D.Q. Nguyen and D.Q. Phung, A novel embedding model for knowledge base completion based on convolutional neural network, in: NAACL-HLT (2), Association for Computational Linguistics, (2018) , pp. 327–333. |
[26] | D.Q. Nguyen, T. Vu, T.D. Nguyen, D.Q. Nguyen and D.Q. Phung, A capsule network-based embedding model for knowledge graph completion and search personalization, in: NAACL-HLT (1), Association for Computational Linguistics, (2019) , pp. 2180–2189. |
[27] | M. Nickel, L. Rosasco and T.A. Poggio, Holographic embeddings of knowledge graphs, in: AAAI, AAAI Press, (2016) , pp. 1955–1961. |
[28] | H. Paulheim and C. Bizer, Improving the quality of linked data using statistical distributions, Int. J. Semantic Web Inf. Syst. 10: (2) ((2014) ), 63–86. doi:10.4018/ijswis.2014040104. |
[29] | Z. Sun, Z. Deng, J. Nie and J. Tang, RotatE: Knowledge graph embedding by relational rotation in complex space, in: ICLR (Poster), OpenReview.net, (2019) . |
[30] | T.P. Tanon, D. Vrandecic, S. Schaffert, T. Steiner and L. Pintscher, From freebase to Wikidata: The great migration, in: WWW, ACM, (2016) , pp. 1419–1428. |
[31] | G. Töpper, M. Knuth and H. Sack, DBpedia ontology enrichment for inconsistency detection, in: I-SEMANTICS, ACM, (2012) , pp. 33–40. |
[32] | K. Toutanova and D. Chen, Observed versus latent features for knowledge base and text inference, in: Proceedings of the 3rd Workshop on Continuous Vector Space Models and Their Compositionality, (2015) , pp. 57–66. doi:10.18653/v1/W15-4007. |
[33] | T. Trouillon, J. Welbl, S. Riedel, É. Gaussier and G. Bouchard, Complex embeddings for simple link prediction, in: ICML, JMLR Workshop and Conference Proceedings, Vol. 48: , JMLR.org, (2016) , pp. 2071–2080. |
[34] | Q. Wang, Z. Mao, B. Wang and L. Guo, Knowledge graph embedding: A survey of approaches and applications, IEEE Trans. Knowl. Data Eng. 29: (12) ((2017) ), 2724–2743. doi:10.1109/TKDE.2017.2754499. |
[35] | X. Wang, X. He, Y. Cao, M. Liu and T. Chua, KGAT: Knowledge graph attention network for recommendation, in: KDD, ACM, (2019) , pp. 950–958. |
[36] | Z. Wang, J. Zhang, J. Feng and Z. Chen, Knowledge graph embedding by translating on hyperplanes, in: AAAI, AAAI Press, (2014) , pp. 1112–1119. |
[37] | R. West, E. Gabrilovich, K. Murphy, S. Sun, R. Gupta and D. Lin, Knowledge base completion via search-based question answering, in: WWW, ACM, (2014) , pp. 515–526. |
[38] | R. Xie, Z. Liu, F. Lin and L. Lin, Does William Shakespeare REALLY write Hamlet? Knowledge representation learning with confidence, in: AAAI, AAAI Press, (2018) , pp. 4954–4961. |
[39] | B. Yang, W. Yih, X. He, J. Gao and L. Deng, Embedding entities and relations for learning and inference in knowledge bases, in: ICLR (Poster), (2015) . |
[40] | F. Yang, Z. Yang and W.W. Cohen, Differentiable learning of logical rules for knowledge base reasoning, in: NIPS, (2017) , pp. 2319–2328. |
[41] | W. Zhang, B. Paudel, L. Wang, J. Chen, H. Zhu, W. Zhang, A. Bernstein and H. Chen, Iteratively learning embeddings and rules for knowledge graph reasoning, in: WWW, ACM, (2019) , pp. 2366–2377. |
[42] | L. Zhao, X. Zhang, K. Wang, Z. Feng and Z. Wang, Learning ontology axioms over knowledge graphs via representation learning, in: ISWC Satellites, CEUR Workshop Proceedings, Vol. 2456: , CEUR-WS.org, (2019) , pp. 57–60. |




