An unsupervised data-driven method to discover equivalent relations in large Linked Datasets
Abstract
This article addresses a number of limitations of state-of-the-art methods of Ontology Alignment: 1) they primarily address concepts and entities while relations are less well-studied; 2) many build on the assumption of the ‘well-formedness’ of ontologies which is unnecessarily true in the domain of Linked Open Data; 3) few have looked at schema heterogeneity from a single source, which is also a common issue particularly in very large Linked Dataset created automatically from heterogeneous resources, or integrated from multiple datasets. We propose a domain- and language-independent and completely unsupervised method to align equivalent relations across schemata based on their shared instances. We introduce a novel similarity measure able to cope with unbalanced population of schema elements, an unsupervised technique to automatically decide similarity threshold to assert equivalence for a pair of relations, and an unsupervised clustering process to discover groups of equivalent relations across different schemata. Although the method is designed for aligning relations within a single dataset, it can also be adapted for cross-dataset alignment where sameAs links between datasets have been established. Using three gold standards created based on DBpedia, we obtain encouraging results from a thorough evaluation involving four baseline similarity measures and over 15 comparative models based on variants of the proposed method. The proposed method makes significant improvement over baseline models in terms of F1 measure (mostly between 7% and 40%), and it always scores the highest precision and is also among the top performers in terms of recall. We also make public the datasets used in this work, which we believe make the largest collection of gold standards for evaluating relation alignment in the LOD context.
1.Introduction
The Web of Data is currently seeing remarkable growth under the Linked Open Data (LOD) community effort. The LOD cloud currently contains over 9,000 datasets and more than 85 billion triples.11 It is becoming a gigantic, constantly growing and extremely valuable knowledge source useful to many applications [16,30]. Following the rapid growth of the Web of Data is the increasingly pressing issue of heterogeneity, the phenomenon that multiple vocabularies exist to describe overlapping or even the same domains, and the same objects are labeled with different identifiers. The former is usually referred to schema-level heterogeneity and the latter as data or instance-level heterogeneity. It is widely recognized that currently LOD datasets are characterized by dense links at data-level but very sparse links at schema-level [15,24,38]. This may hamper the usability of data over large scale and reduces interoperability between Semantic Web applications built on LOD datasets. This work explores this issue and particularly studies linking relations across different schemata in the LOD domain, a problem that is currently under-represented in the literature.
Research in the area of Ontology Alignment [13,39] has contributed to a plethora of methods towards solving heterogeneity on the Semantic Web. A lot of these [7,9,21,25,27,29,34–36,41] are archived under the Ontology Alignment Evaluation Initiative (OAEI) [10]. However, we identify several limitations of the existing work. First, it has been criticized that most methods are tailored to cope with nicely structured and well defined ontologies [17], which are different from LOD ontologies characterized by noise and incompleteness [15,17,37,38,46,51]. Many features used by such methods may not be present in LOD ontologies.
Second, we notice that aligning heterogeneous relations is not yet well-addressed, especially in the LOD context. Recent research has found that this problem is considered to be harder than, e.g., aligning classes or concepts [6,15,18]. Relation names are more diverse than concept names [6], and the synonymy and polysemy problems are also more typical [6,15]. This makes aligning relations in the LOD domain more challenging. Structural information of relations is particularly lacking [15,51], and the inconsistency between the intended meaning of schemata and their usage in data is more wide-spread [15,17,18]. Further, some emerging data linking problems such as linkkey discovery [2,45] can also benefit from the solutions of this problem since some methods depend on sets of mapped relations from different schemata.
Third, while it makes a lot of sense to study cross-dataset heterogeneity, solving heterogeneity from within a single dataset is also becoming increasingly important. Recent years have seen a rising trend of using (semi-)automatic Information Extraction techniques to create very large knowledge bases from semi- or un-structured text input [5,14,28] as they significantly reduces the tremendous human cost involved in traditional ontology engineering process. Due to polysemy in natural language, the extracted schemata are often heterogeneous. For example, in DBpedia,22 more than five relations are used to describe the name of a University, such as dbpp33:uname, dbpp:name and foaf44:name. In the ReVerb [14] database containing millions of facts extracted from natural language documents from the Web, the relation ‘contain vitamin’ has more than five expressions. The problem worsens when such datasets are exposed on the LOD cloud, as data publishes attempting to link to such datasets may struggle to conform to a universal schema. As a realistic scenario, the DBpedia mappings portal55 is a community effort dedicated to solving heterogeneity within the DBpedia dataset itself.
Last, a common limitation to nearly all existing methods is the need for setting a cutoff threshold of computed similarity scores in order to assert correspondences. It is known that the performance of different methods are very sensitive to thresholds [6,19,29,35,44], while finding optimal thresholds requires tuning on expensive training data; unfortunately, the thresholds are often context-dependent and requires re-tuning for different tasks [22,40].
To address these issues, we introduce a completely unsupervised method for discovering equivalent relations for specific concepts, using only data-level evidence without any schema-level information. The method has three components: (1) a similarity measure that computes pair-wise similarity between relations, designed to cope with the unbalanced (and particularly sparse) population of schemata in LOD datasets; (2) an unsupervised method of detecting cutoff thresholds based on patterns discovered in the data; (3) and an unsupervised clustering process that groups mutually equivalent relations, potentially discovering relation alignments among multiple schemata. The principle of the method is studying the shared instances between two relations. This makes it particularly suitable for matching relations across multiple ontologies annotating the same dataset, or for contributing matching ontologies when sameAs links between different datasets have been established.
For a thorough evaluation, we use a number of datasets collected in a controlled manner, including one based on the practical problem faced by the DBpedia mapping portal. We create a large number of comparative models to assess the proposed method along the following dimensions: its similarity measure, capability of coping with dataset featuring unbalanced usage of schemata, automatic threshold detection, and clustering. We report encouraging results from these experiments. The proposed method successfully discovers equivalent relations across multiple schemata, and the similarity measure is shown to significantly outperform all baselines in terms of F1 (maximum improvement of 0.47, or 47%). It also handles unbalanced populations of schema elements and shows stability against several alternative models. Meanwhile, the automatic threshold detection method is shown to be very competitive – it even outperforms the supervised models on one dataset in terms of F1.
In the remainder of this paper, Section 2 discusses related work; Section 3 introduces the method; Section 4 describes a series of designed experiments and 5 discusses results, followed by conclusion in Section 6.
2.Related work
2.1.Terminology and scope
An alignment between a pair of ontologies is a set of correspondences between entities across the ontologies [13,39]. Ontology entities are usually: classes defining the concepts within the ontology; individuals denoting the instances of these classes; literals representing concrete data values; datatypes defining the types that these values can have; and properties comprising the definitions of possible associations between individuals, called object properties, or between one individual and a literal, called datatype properties [25]. Properties connect other entities to form statements, which are called triples each consisting of a subject, a predicate (i.e., a property) and an object.66 A correspondence asserts that certain relation holds between two ontological entities, and the most frequently studied relations are equivalence and subsumption. Ontology alignment is often discussed at ‘schema’ or ‘instance’ level, where the former usually addresses alignment for classes and properties, the latter addresses alignment for individuals. This work belongs to the domain of schema level alignment.
As we shall discuss, in the LOD domain, data are not necessarily described by formal ontologies, but sometimes vocabularies that are simple renderings of relational databases [38]. Therefore in the following, wherever possible, we will use the more general term schema or vocabulary instead of ontology, and relation and concept instead of property and class. When we use the terms class or property we mean strictly in the formal ontology terms unless otherwise stated.
A fundamental operation in ontology alignment is matching pairs of individual entities. Such methods are often called ‘matchers’ and are usually divided into three categories depending on the type of data they work on [13,39]. Terminological matchers work on textual strings such as URIs, labels, comments and descriptions defined for different entities within an ontology. The family of string similarity measures has been widely employed for this purpose [6]. Structural matchers make use of the hierarchy and relations defined between ontological entities. They are closely related to measures of semantic similarity, or relatedness in more general sense [49]. Extensional matchers exploit data that constitute the actual population of an ontology or schema in the general sense, and therefore, are often referred to as instance- or data-based methods. For a concept, ‘instances’ or ‘populated data’ are individuals in formal ontology terms; for a relation, these can depend on specific matchers, but are typically defined based on triples containing the relation. Matchers compute a degree of similarity between entities in certain numerical range, and use cutoff thresholds to assert correspondences.
In the following, we begin by a brief overview of the literature on the general topic of ontology alignment, then focus our discussion of related work on two dimensions that characterize this work: in the context of LOD, and aligning relations.
2.2.Ontology alignment in general
A large number of ontology alignment methods have been archived under the OAEI, which maintains a number of well-known public datasets and hosts annual evaluations. Work under this paradigm has been well-summarized in [13,39]. A predominant pattern shared by these work [7,9,19,21,25,27,29,34–36,41] is the strong preference of terminological and structural matchers to extensional methods [39]. Many of these show that ontology alignment can benefit from the use of background knowledge sources such as WordNet and Wikipedia [9,19,25,27,34,35]. There is also a trend of using a combination of different matchers, since it is argued that the suitability of a matcher is dependent on different scenarios and therefore combining several matchers could improve alignment quality [36].
These methods are not suitable for our task for a number of reasons. First, most methods are designed to align concepts and individuals, while adaptation to relations is not straightforward. Second, terminological and structural matchers require well-formed ontologies, which are not necessarily available in the context of LOD. As we shall discuss in the next sections, tougher challenges arise in the LOD domain and in the problem of aligning heterogeneous relations.
2.3.Ontology alignment in the LOD domain
Among the three categories of matchers, extensional matchers are particularly favoured due to certain characteristics of Linked Data.
First and foremost, vocabulary definitions are often highly inconsistent and incomplete [17]. Textual features such as labels and comments for concepts and relations that are used by terminological matchers are non-existent in some large ontologies. In particular, many vocabularies generated from (semi-)automatically created large datasets are based on simple renderings of relational databases and are unlikely to contain such information. For instance, Fu et al. [15] showed that the DBpedia ontology contained little linguistic information about relations except their names.
Even when such information is available, the meaning of schemata may be dependent on their actual usage pattern in the data [17,37,51] (e.g., foaf:Person may represent researchers in a scientific publication dataset, but artists in a music dataset). This means that strong similarity measured at terminological or structural level does not always imply strict equivalence. This problem is found to be particularly prominent in the LOD domain [17,37,46]. Empirically, Jain et al. [23] and Cruz et al. [7] showed that the top-performing systems in ‘classic’ ontology alignment settings such as the OAEI do not have clear advantage over others in the LOD domain.
Second, the Linked Data environment is characterized by large volumes of data and the availability of many interconnected information sources [17,37,38,44]. Thus extensional matchers can be better suited for the problem of ontology alignment in the LOD domain as they provide valuable insights into the contents and meaning of schema entities from the way they are used in data [37,46].
The majority of state-of-the-art in the LOD domain employed extensional matchers. Nikolov et al. [37] proposed to recursively compute concept mappings and entity mappings based on each other. Concept mappings are firstly created based on the overlap of their individuals; such mappings are later used to support mapping individuals in LOD ontologies. The intuition is that mappings between entities at both levels influence each other. Similar idea was explored by Suchanek et al. [44], who built a holistic model starting with initializing probabilities of correspondences based on instance (for both concepts and relations) overlap, then iteratively re-compute probabilities until convergence. However, equivalence between relations is not addressed.
Parundekar et al. [38] discussed aligning ontologies that are defined at different levels of granularity, which is common in the LOD domain. As a concrete example, they mapped the only class in the GeoNames77 ontology – geonames:Feature – with a well defined one, such as the DBpedia ontology, by using the notion of ‘restriction class’. A restriction class is defined by combining value-restricted-properties, such as (rdfs88:type=Feature, featureCode=gn99:A.PCLI). This effectively defines more fine-grained concepts that can then be aligned with other ontologies. A similar matcher as Nikolov et al. [37] is used. Slabbekoorn et al. [43] explored a similar problem: matching a domain-specific ontology to a general purpose ontology. It is unclear if these approaches can be applied to relation matching or not.
Jain et al. [24] proposed BLOOMS+, the idea of which is to build representations of concepts as sub-trees from Wikipedia category hierarchy, then determine equivalence between concepts based on the overlap in their representations. Both structural and extensional matcher are used and combined. Cruz et al. [8] created a customization of the AgreementMaker system [9] to address ontology alignment in the LOD context, and achieved better average precision but worse recall than BLOOMS+. Gruetze et al. [17] and Duan et al. [12] also used extensional matchers in the LOD context but focusing on improving computation efficiency of the algorithms.
2.4.Matching relations
Compared to concepts, aligning relations is generally considered to be harder [6,15,18]. The challenges concerning the LOD domain can become more noticeable when dealing with relations. In terms of linguistic features, relation names can be more diverse than concept names, this is because they frequently involve verbs that can appear in a wider variety of forms than nouns, and contain more functional words such as articles and prepositions [6]. The synonymy and polysemy problems are common. Verbs in relation names are more generic than nouns in concept names and therefore, they generally have more synonyms [6,15].
Same relation names are found to bear different meanings in different contexts [18]. For example, in the DBpedia dataset ‘before’ is used to describe relationship between consecutive space missions, or Roman emperors such as Nero and Claudius. If a user creates a query using such relations without enough additional constraints, the result may contain irrelevant records since the user might be only interested in particular aspects of these polysemous relations [15]. Indeed, Gruetze et al. [17] suggested definitions of relations should be ignored when they are studied in the LOD domain due to such issues.
In terms of structural features, Zhao et al. [51] showed that relations may not have domain or range defined in the LOD domain. Moreover, we carried out a test on the ‘well-formed’ ontologies released by the OAEI-2013 website, and found that among 21 downloadable1010 ontologies 7 defined relation hierarchy and the average depth is only 3. Fu et al. [15] also showed hierarchical relations between DBpedia properties were very rare.
For these reasons, terminological and structural matchers can be seriously hampered if applied to matching relations, particularly in the LOD domain. Indeed, Cheatham et al. [6] compared a wide selection of string similarity measures in several tasks and showed their performance on matching relations to be inferior to matching concepts. Thus in line with Nikolov et al. [37] and Duan et al. [12], we argue in favour of extensional matchers.
We notice that only a few related work specifically focused on matching relations based on data-level evidence. Fu et al. [15] studied mapping relations in the DBpedia dataset. The method uses three types of features: data level, terminological, and structural. Similarity is computed using three types of matchers corresponding to the features. An extensional matcher similar to the Jaccard function compares the overlap in the subject sets of two relations, balanced by the overlap in their object sets. Zhao et al. [50,51] first created triple sets each corresponding to a specific subject that is an individual, such as dbr1111:Berlin. Then initial groups of equivalent relations are identified for each specific subject: if, within the triple set containing the subject, two lexically different relations have identical objects, they are considered equivalent. The initial groups are then pruned by a large collection of terminological and structural matchers, applied to relation names and objects to discover fuzzy matches. Zhao et al. [52] used nine WordNet-based similarity measures to align properties from different ontologies. They firstly use NLP tools to extract terms from properties, then compute similarity between the groups of terms from the pair of properties. These similarity measures make use of the terminological and structural features of the WordNet lexical graph.
Many extensional matchers used for matching concepts could be adapted to matching relations. One popular strategy is to compare the size of the overlap in the instances of two relations against the size of their total combined, such as the Jaccard measure and Dice coefficient [12,15,17,22]. However, in the LOD domain, usage of vocabularies can be extremely unbalanced due to the collaborative nature of LOD. Data publishers have limited knowledge about available vocabularies to describe their data, and in worst cases they simply do not bother [46]. As a result, concepts and relations defined from different vocabularies bearing the same meaning can have different population sizes. In such cases, the above strategy is unlikely to succeed [37].
Another potential issue is that current work assumes relation equivalence to be ‘global’, while it has been suggested that, interpretation of relations should be context-dependent, and argued that equivalence should be studied at concept-specific context because essentially relations are defined specifically with respect to concepts [15,18]. Global equivalence cannot deal with the polysemy issue such as the previously illustrated example of ‘before’ bearing different meanings in different contexts. Further, to our knowledge, there is currently no public dataset specifically for aligning relations in the LOD domain, and current methods [15,50,51] have been evaluated on smaller datasets than those used in this study.
2.5.The cutoff thresholds in matchers
To date, nearly all existing matchers require a cutoff threshold to assert correspondence between entities. The performance of a matcher can be very sensitive to thresholds and finding an optimal point is often necessary to warrant the effectiveness of a matcher [6,19,29,35,44]. Such thresholds are typically decided based on some annotated data (e.g., [18,29,41]), or even arbitrarily in certain cases. In the first case, expensive effort must be spent on annotation and training. In both cases, the thresholds are often context-dependent and requires re-tuning for different tasks [22,40,41]. For example, Seddiqui et al. [41] showed that for the same matcher, previously reported thresholds in related work may not perform satisfactorily on new tasks. For extensional matchers, finding best thresholds can be difficult since they too strongly depend on the collection of data [12,22].
One study that reduces the need of supervision in learning thresholds is based on active learning by Shi et al. [42]. The system automatically learns similarity thresholds by repeatedly asking feedback from a user. However, this method still requires certain supervision. Another approach adopted in Duan et al. [12] and Fu et al. [15] is to sort the matching results in a descending order of the similarity score, and pick only the top-k results. This suffers from the same problem as cutoff thresholds since the value of k can be different in different contexts (e.g., in Duan et al. this varied from 1 to 86 in the ground truth). To the best of our knowledge, our work is the first that automatically detects thresholds without using annotated training data.
2.6.Remark
To conclude, the characteristics of relations found in the schemata from the LOD domain, i.e., incomplete (or lack of) definitions, inconsistency between intended meaning of schemata and their usage in data, and very large amount of data instances, advocate for a renewed inspection of existing ontology alignment methods. We believe that the solution rests on extensional methods that provide insights into the meaning of relations based on data, and unsupervised methods that alleviate the need for threshold tuning.
Towards these directions we developed a prototype [47] specifically to study aligning equivalent relations in the LOD domain. We proposed a different extensional matcher designed to reduce the impact of the unbalanced populations, and a rule-based clustering that employs a series of cutoff thresholds to assert equivalence between relation pairs and discover groups of equivalent relations specific to individual concepts. The method showed very promising results in terms of precision, and was later used in constructing knowledge patterns based on data [3,48]. The work described in this article is built on our prototype but extends it in several dimensions: (1) a revised and extended extensional matcher; (2) a method of automatic threshold detection without need of training data; (3) an unsupervised machine learning clustering approach to discover groups of equivalent relations; (4) augmented and re-annotated datasets that we make available to public; (5) extensive and thorough evaluation against a large set of comparative models, together with an in-depth analysis of the task of aligning relations in the LOD domain.
We focus on equivalence only because firstly, it is considered the major issue in ontology alignment and studied by the majority of related work; secondly, hierarchical structures for relations are very rare, especially in the LOD domain.
3.Methodology
3.1.Task formalization
Our domain- and language-independent method for aligning heterogeneous relations belongs to the category of extensional matchers, and only uses instances of relations as its evidence to predict equivalence. In the following, we write
Table 1
Notations used in this paper and their meaning
| <x, r, y> | <dbr:Sydney_Opera_House, dbo*:openningDate, ‘1973’>, <dbr:Royal_Opera_House, dbo:openningDate, ‘1732’>, <dbr:Sydney_Opera_House, dbpp:yearsactive, ‘1973’> |
| dbo:openningDate | |
| dbpp:yearsactive | |
| (dbr:Sydney_Opera_House, ‘1973’), (dbr:Royal_Opera_House, ‘1732’) | |
| dbr:Sydney_Opera_House, dbr:Royal_Opera_House | |
| ‘1973’,‘1732’ |
We start by taking as input a URI representing a specific concept C and a set of triples
Our task can be formalized as: given the set of triples
3.2.Measure of similarity
The goal of the measure is to assess the degree of similarity between a pair of relations within a concept-specific context, as illustrated in Fig. 1. The measure consists of three components, the first two of which are previously introduced in our prototype [47].1212
Fig. 1.
The similarity measure computes a numerical score for pairs of relations.
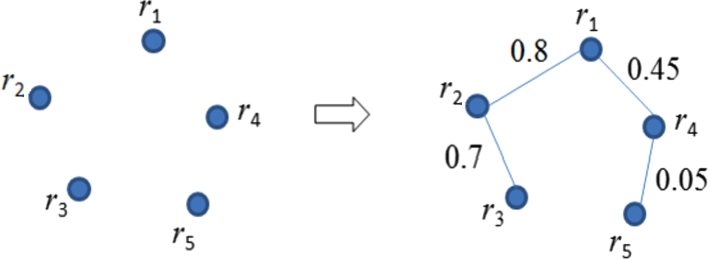
Fig. 2.
Illustration of triple agreement.
3.2.1.Triple agreement
Triple agreement evaluates the degree of shared argument pairs of two relations in triples. Equation (1) firstly computes the overlap (intersection) of argument pairs between two relations.
Then the triple agreement is a function that returns a value between 0 and 1.0:
The intuition of triple agreement is that if two relations
3.2.2.Subject agreement
Subject agreement provides a complementary view by looking at the degree to which two relations share the same subjects. The motivation of having
Fig. 3.
Illustration of subject agreement.
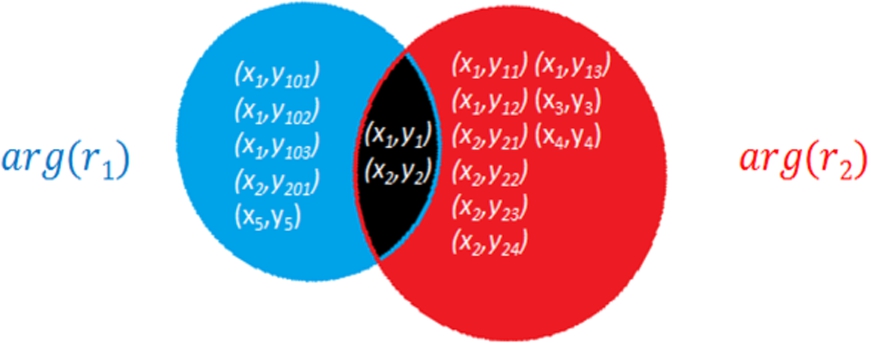
Subject agreement captures this situation by hypothesizing that two relations are likely to be equivalent if (α) a large number of subjects are shared between them and (β) a large number of such subjects also have shared objects.
Equation (5) evaluates the degree to which two relations share subjects based on the intersection and the union of the subjects of two relations. Equation (6) counts the number of shared subjects that have at least one overlapping object. The higher the β, the more the two relations ‘agree’ in terms of their shared subjects
3.2.3.Knowledge confidence modifier
Fig. 4.
The logistic function modelling knowledge confidence.
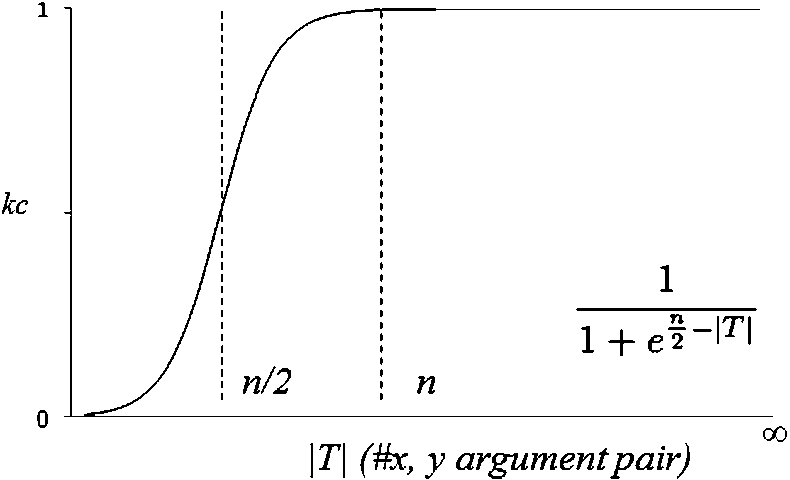
Although
It could be argued that other learning curves (e.g., exponential) could be used as alternative; or we could use simple heuristics instead (e.g., discard any relations that have fewer than n argument pairs). However, we believe that the logistic model better fits the problem since the exponential model usually implies rapid convergence, which is hardly the case in many real learning situations; while the simplistic threshold based model may harm recall. We show empirical comparison in Section 5.
Next we revise
Both equations return a value between 0 and 1.0. Finally, the similarity between
3.3.Determining thresholds
After computing similarity scores for relation pairs of a specific concept, we need to interpret the scores and be able to determine the minimum score that justifies equivalence between two relations (Fig. 5). This is also known as a part of the mapping selection problem. As discussed before, one typically derives a threshold from training data or makes an arbitrary decision. The solutions are non-generalizable and the supervised method also requires expensive annotations.
Fig. 5.
Deciding a threshold beyond which pairs of relations are considered to be truely equivalent.

We use an unsupervised method that determines thresholds automatically based on observed patterns in data. We hypothesize that a concept may have only a handful of equivalent relation pairs whose similarity scores should be significantly higher than the non-equivalent noisy ones that also have non-zero similarity. The latter can happen due to imperfections in data such as schema misuse or merely by chance. For example, Fig. 6 shows the scores (e) of 101 pairs of relations of the DBpedia concept
Fig. 6.
The long-tailed pattern in similarity scores between relations computed using e. t could be the boundary threshold.
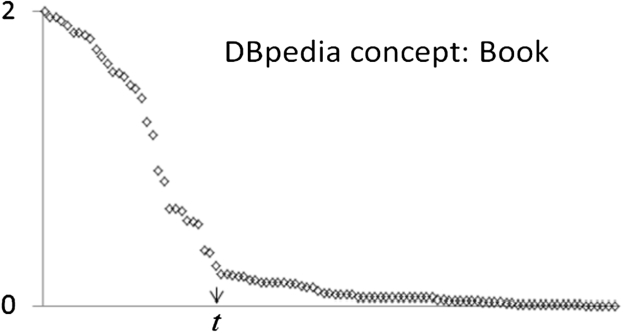
We do this based on the principle of maximizing the difference of similarity scores between the groups. While a wide range of data classification and clustering methods can be applied for this purpose, here we use an unsupervised method – Jenks natural breaks [26]. Jenks natural breaks determines the best arrangement of data values into different classes. It seeks to reduce within-class variance while maximizing between-class variance. Given a set of data points and i the expected number of groups in the data, the algorithm starts by splitting the data into arbitrary i groups, followed by an iterative process aimed at optimizing the ‘goodness-of-variance-fit’ based on two figures: the sum of squared deviations between classes, and the sum of squared deviations from the array mean. At the end of each iteration, a new splitting is created based on the two figures and the process is repeated until the sum of the within class deviations reaches a minimal value. The resulting optimal classification is called Jenks natural breaks. Essentially, Jenks natural breaks is k-means [32] applied to univariate data.
Empirically, given the set of relation pairs for a concept C we apply Jenks natural breaks to the similarity scores with
Although it is not necessary to compute a threshold of similarity (denoted as t) under this method, this can be done by simply selecting the maximum similarity score in the larger group1414 as similarity scores of all equivalent pairs in the smaller group should be greater than this value. We will use this method to derive our threshold later in experiments when compared against other methods.
3.4.Clustering
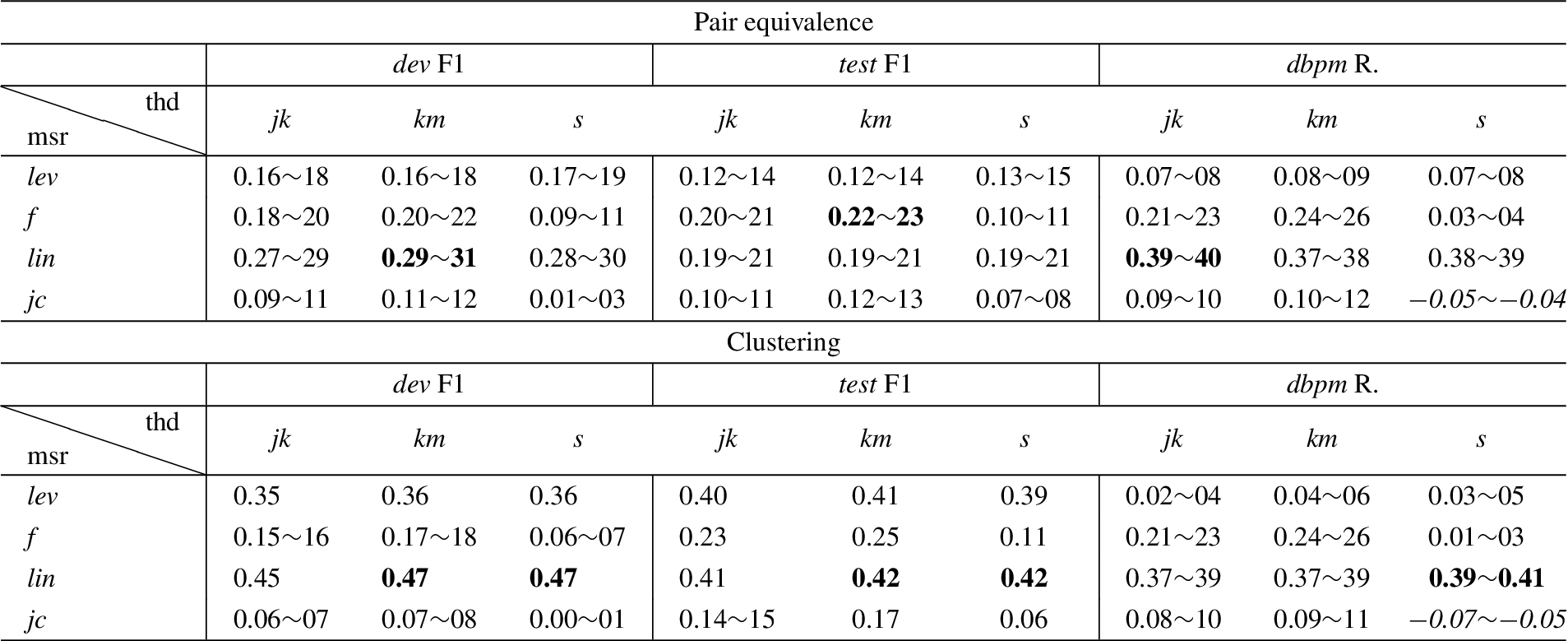
So far, Sections 3.2 and 3.3 described our method to answer the first question set out in the beginning of this section, i.e., predicting relation equivalence. The proposed method studies each relation pair independently from other pairs. This may not be sufficient for discovering equivalent relations due to two reasons. First, two relations may be equivalent even though no supporting data are present. For example, in Fig. 7 we can assume
Fig. 7.
Clustering discovers transitive equivalence and invalidates weak links.
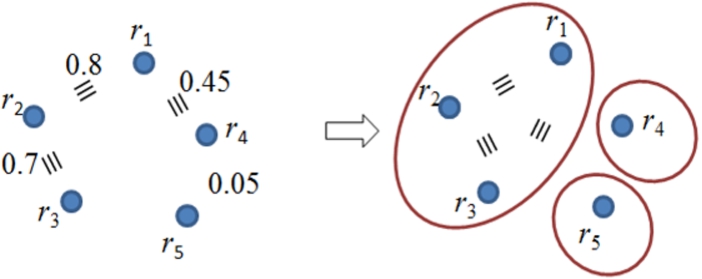
To address such issues we cluster mutually equivalent relations for a concept. Essentially clustering brings in additional context to decide pair-wise equivalence, which allows us to (1) discover equivalence that may be missed by the proposed similarity measure and the threshold detection method, and (2) discard equivalence assertion the similarity of which appears relatively weak to join a cluster. Potentially, this also allows creating alignments between multiple schemata at the same time. Given the set of equivalent relation pairs discovered before,
At the end of this process, we obtain groups of relations that are mutually equivalent in the context of a specific concept C, such as that shown in the right part of Fig. 7.
4.Experiment settings
We design a series of experiments to thoroughly evaluate our method in terms of the two goals described at the beginning of Section 3, i.e., its capability of predicting equivalence of two relations of a concept (pair equivalence) and clustering mutually equivalent relations (clustering) for a concept. Different settings are created along three dimensions by selecting from several choices of (1) similarity measures, (2) threshold detection methods and (3) different knowledge confidence models
4.1.Measures of similarity
We compare the proposed measure of similarity against four baselines. Our criteria for the baseline measures are: (1) to cover different types of matchers; (2) to focus on methods that have been practically shown effective in the LOD context, and where possible, particularly for aligning relations; (3) to include some best performing methods for this particular task.
The first is a string similarity measure, the Levenshtein distance (lev) that proves to be one of the best performing terminological matcher for aligning both relations and classes [6]. Specifically, we measure the string similarity (or distance) between the URIs of two relations, but we remove namespaces from relation URIs before applying the measure. As a result, dbpp:name and foaf:name will be both normalized to name and thus receiving the maximum similarity score.
The second is a semantic similarity measure by Lin (lin) [31], which uses both WordNet’s hierarchy and word distributional statistics as features to assess similarity of two words. Thus two lexically different words (e.g., ‘cat’ and ‘dog’) can also be similar. Since URIs often contain strings that are concatenation of multiple words (e.g., ‘birthPlace’), we use simple heuristics to split them into multiple words when necessary (e.g., ‘birth place’). Note that this method is also used by Zhao et al. [52] for aligning relations.
The third is the extensional matcher proposed by Fu et al. [15] (fu) to address particularly the problem of aligning relations in DBpedia:
The fourth baseline is the ‘corrected’ Jaccard function proposed by Isaac et al. [22]. The original Jaccard function has been used in a number of studies concerning mapping concepts across ontologies [12,22,40]. Isaac et al. [22] showed that it is one of the best performing measures in their experiment, however, they also pointed out that one of the issue with Jaccard is its inability to consider the absolute sizes of two compared sets. As an example, Jaccard does not distinguish the cases of
4.2.Methods of detecting thresholds
We compare three different methods of threshold detection. The first is Jenks Natural Breaks (jk) that is used in the proposed method, discussed in Section 3.3. For the second method we use the k-means clustering algorithm (km) for unsupervised threshold detection. As discussed before, the two methods are very similar, with the main distinction being that
Next, we also use a supervised method (denoted by s) to derive a uniform threshold for all concepts based on annotated data. To do so, suppose we have a set of m concepts and for each concept, we create pairs of relations found in data and ask humans to annotate each pair (to be detailed in Section 4.5) as equivalent or not. Then given a similarity measure, we use it to score each pair and rank pairs by scores. A good measure is expected to rank equivalent pairs higher than inequivalent ones. Next, we calculate accuracy at each rank taking into account the number of equivalent v.s. inequivalent pairs by that rank, and it is expected that maximum accuracy can be reached at one particular rank. We record the similarity score at this rank, and use it as the optimal threshold for that concept. Due to the difference in concept-specific data, we expect to obtain different optimal thresholds for each of the m concepts in the training data. However, in reality, the thresholds for new data will be unknown a priori. Therefore we use the average of all thresholds derived from the training data concepts as an approximation and use it for testing.
4.3.Knowledge confidence models kc
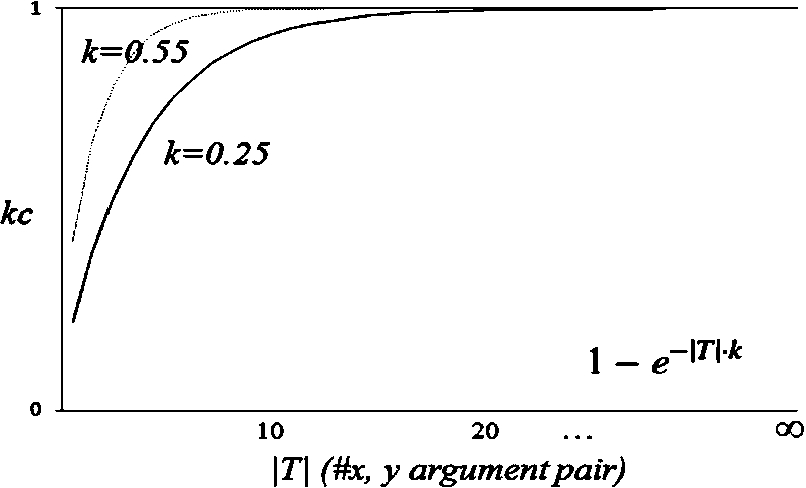
We compare the proposed logistic model (lgt) of
The second is an exponential model, denoted by exp and shown in Fig. 8. We model such a curve using an exponential function shown in Eq. (16), where k is a scalar that controls the speed of convergence and
Fig. 8.
The exponential function modelling knowledge confidence.
For each model we need to define a parameter. For
We apply the same principle to the
Additionally, we also compare against a variant of the proposed similarity measure without
4.4.Creation of settings
By taking different choices from the three dimensions above, we create different models for experimentation. We will denote each setting in the form of
Fig. 9.
Different settings based on the choices of three dimensions. kc is a variable whose value could be lgt (Eq. (9)), exp (Eq. (16)), or

The Metrics we use for evaluating pair accuracy are the standard Precision, Recall and F1; and the metrics for evaluating clustering are the standard purity, inverse-purity and F1 [1].
4.5.Dataset preparation
4.5.1.DBpedia
Although a number of benchmarking datasets are published under the OAEI, as discussed before, they are not suitable for our task since they do not represent the particular characteristics in the LOD domain and the number of aligned relations is also very small – less than 2‰ (56) of mappings found in their gold standard datasets are equivalent relations.1616 Therefore, we study the problem of heterogeneous relations on DBpedia, the largest LOD dataset serving as a hub for connecting multiple sources in the LOD domain. DBpedia is also a representative example of relation heterogeneity [15,18]. Multiple vocabularies are used in the dataset, including RDFS, Dublin Core,1717 WGS84 Geo,1818 FOAF, SKOS,1919 the DBpedia ontology, original Wikipedia templates and so on. The DBpedia ontology version 3.9 covers 529 concepts and 2,333 different relations.2020 Heterogeneity is mostly found between the DBpedia ontology and other vocabularies, especially the original Wikipedia templates, due to the enormous amount of relations in both vocabularies. A Wikipedia template usually defines a concept and its properties.2121 When populated, they become infoboxes, which are processed to extract triples that form the backbone of the DBpedia dataset. Currently, data described by relations in the DBpedia ontology and the original Wikipedia template properties co-exist and account for a very large population in the DBpedia dataset.
The disparity between the different vocabularies in DBpedia is a pressing issue that has attracted particular effort, which is known as the DBpedia mappings portal. The goal of the portal is to invite collaborative effort to create mappings between certain structured content on Wikipedia to the manually curated DBpedia ontology. One task is mapping Wikipedia templates to concepts in the DBpedia ontology, and then mapping properties in the templates to relations of mapped concepts. It is known that manually creating such mappings requires significant work, and as a result, as by September 2015, less than 65% of mappings between Wikipedia template properties and relations in the DBpedia ontology are complete.2222 Hence the community can significantly benefit from an automatic mapping system.
4.5.2.Datasets
We collected three datasets for experiments. The first dataset (dbpm) is created based on the mappings published on the DBpedia mappings portal. We processed the DBpedia mappings Webpages as by 30 Sep 2013 and created a dataset containing 203 DBpedia concepts. Each concept has a page that defines the mapping from a Wikipedia template to a DBpedia concept, and lists a number of mapping pairs from template properties to the relations of the corresponding concept in the DBpedia ontology. We extracted a total of 5388 mappings and use them as gold standard. However, there are three issues with this dataset. First, the community portal focuses on mapping the DBpedia ontology with the original Wikipedia templates. Therefore, mappings between the DBpedia ontology and other vocabularies are rare. Second, the dataset is largely incomplete. Therefore, we only use this dataset for evaluating recall. Third, it has been noticed that the mappings created are not always strictly ‘equivalence’. Some infrequent mappings such as ‘broader-than’ have also been included.
For these reasons, we manually created the second and the third datasets based on 40 DBpedia (DBpedia ontology version 3.8) and YAGO2323 concepts. The choices of such concepts are based on the QALD1 question answering dataset2424 for Linked Data. For each concept, we query the DBpedia SPARQL endpoint using the following query template to retrieve all triples related to the concept.2525
SELECT * WHERE {
?s a <[Concept_URI]> .
?s ?p ?o .
}
Next, we build a set P containing unordered pairs of predicates from these triples and consider them as candidate relation pairs for the concept. We also use a stop list of relation URIs to filter meaningless relations that usually describe Wikipedia meta-level information, e.g., dbpp:wikiPageID, dbpp:wikiPageUsesTemplate. Each of the measures listed in Section 4.1 is then applied to compute similarity of the pairs in this set and may produce either a zero or non-zero score. We then create a set
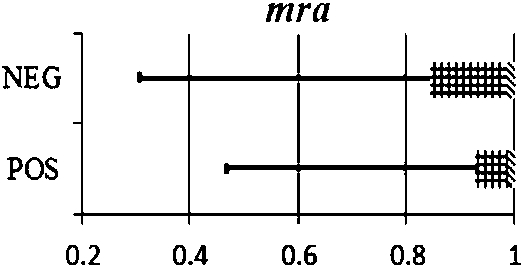
The data is annotated by four computer scientists and then randomly split into a development set (dev) containing 10 concepts and a test set (test) containing 30 concepts. The dev set is used for analyzing the patterns in the data, developing components of the method, and learning cutoff thresholds by the supervised experimental settings; the test set is used for evaluation. All datasets and associated resources used in this study are publicly available.2626 The statistics of the three datasets are shown in Table 2. Figure 10 shows the ranges of the percentage of true positives in the dev and test datasets. To our knowledge, this is by far the largest annotated dataset for evaluating relation alignment in the LOD domain.
Table 2
Dataset statistics
| Dev | Test | dbpm | |
| Concepts | 10 | 30 | 203 |
| Relation pairs (P.) | 2316 | 6657 | 5388 |
| True positive P. | 473 | 868 | – |
| P. with incomprehensible relations (I.R.) | 316 | 549 | – |
| % of triples with I.R. | 0.2% | 0.2% | – |
| Schemata in datasets | dbo, dbpp, rdfs, skos, dc, geo, foaf | ||
4.5.3.Difficulty of the task
Annotating relation equivalence is a non-trivial task. The process took three weeks, where one week was spent on creating guidelines. Annotators queried DBpedia for triples containing the relation to assist their interpretation. However, a notable number of relations are still incomprehensible. As Table 2 shows, this accounts for about 8 to 14% of data. Such relations have peculiar names (e.g., dbpp:v, dbpp:trW of dbo:University) and ambiguous names (e.g., dbpp:law, dbpp:bio of dbo:University). They are undocumented and have little usage in data, which makes them difficult to interpret. Pairs containing such relations cannot be annotated and are ignored in evaluation. On average, it takes 0.5 to 1 hour to annotate one concept. We measured inter-annotator-agreement using a sample dataset based on the method by Hripcsak et al. [20], and the average IAA is 0.8 while the lowest bound is 0.68 and the highest is 0.87.
Moreover, there is also a high degree of inconsistent usage of relations. A typical example is dbo:railway Platforms of dbo:Station. It is used to represent the number of platforms in a station, but also the types of platforms in a station. These findings are in line with Fu et al. [15].
Table 2 and Fig. 10 both show that the dataset is overwhelmed by negative examples (i.e., true negatives). On average, less than 25% of non-zero similarity pairs are true positives and in extreme cases this drops to less than 6% (e.g., 20 out of 370 relation pairs of yago:EuropeanCountries are true positive). These findings suggest that finding equivalent relations on Linked Data is indeed a challenging task.
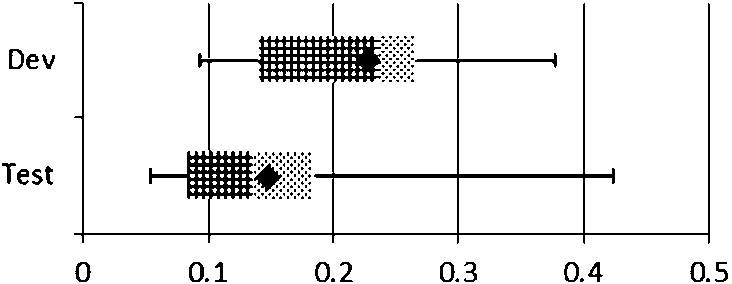
Fig. 10.
% of true positives in
4.6.Running experiment
Each setting (see Section 4.4) to be evaluated starts with one concept at a time to query the DBpedia SPARQL endpoint to obtain triples related to the concept (see the query template before). Querying DBpedia is the major bottleneck throughout the process and therefore, we cache query results and re-use them for different settings. Next, candidate relation pairs are generated from the triples and (1) their similarity is computed using the measure of each setting; then (2) relations are clustered based on pair-wise similarity, to generate clusters of mutually equivalent relations for the concept.
The output from (1) is then evaluated against the three gold standard datasets described above. Only true positive pairs are considered as the larger amount of true negatives may bias results. To evaluate clustering, we derived gold standard clusters using the three pair-equivalence gold standards by assuming equivalence transitivity, i.e., if
We ran experiments on a multi-core laptop computer with an allocated 2 GB of memory. However, the system is not programmed to utilize parallel computing as the actual computation (i.e., excluding querying DBpedia) is fast. When caching is used, on average it takes 40 seconds to process a concept, which has an average of 264 pairs of relations.
5.Results and discussion
We firstly show the learned thresholds based on the
Table 3
Optimal thresholds t for each baseline similarity measures derived from the
| lev | jc | fu | lin | |
| t | 0.43 | 0.07 | 0.1 | 0.65 |
| min | 0.06 | 0.01 | 0.14 | |
| max | 0.77 | 0.17 | 0.31 | 1.0 |
Table 4
Optimal thresholds (t) for different variants of the proposed similarity measure derived from the
| t | min | max | |
| lgt, | 0.24 | 0.06 | 0.62 |
| lgt, | 0.22 | 0.05 | 0.62 |
| lgt, | 0.2 | 0.06 | 0.39 |
| exp, | 0.32 | 0.06 | 0.62 |
| exp, | 0.31 | 0.06 | 0.62 |
| exp, | 0.33 | 0.11 | 0.62 |
| 0.29 | 0.06 | 0.62 | |
| 0.28 | 0.07 | 0.59 | |
| 0.28 | 0.07 | 0.59 |
5.1.Performance of the proposed method
In Table 5 we show the results of our proposed method on the three datasets with varying n in the
Table 5
Results of the proposed method on all datasets. R – Recall
| n of | 10 | 15 | 20 |
| Pair equivalence | |||
| dev, F1 | 0.67 | 0.66 | 0.65 |
| test, F1 | 0.61 | 0.60 | 0.59 |
| dbpm, R | 0.68 | 0.66 | 0.66 |
| Clustering | |||
| dev, F1 | 0.74 | 0.74 | 0.74 |
| test, F1 | 0.70 | 0.70 | 0.70 |
| dbpm, R | 0.72 | 0.70 | 0.70 |
Fig. 11.
Performance ranges on a per-concept basis for
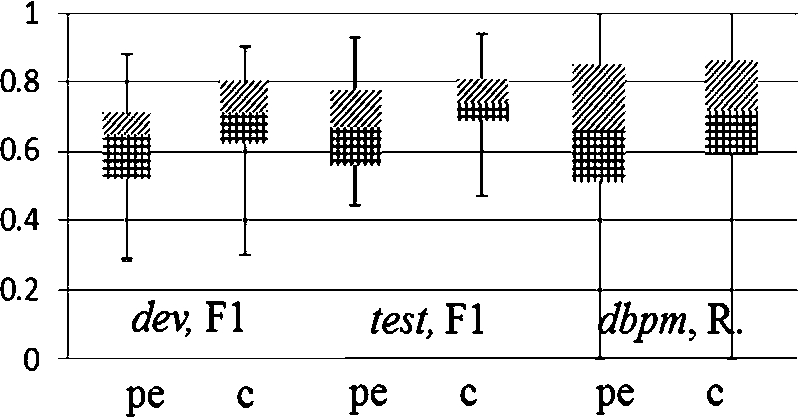
Table 6
Examples clusters of equivalent relations
| Concept | Example cluster |
| dbo:Actor | dbpp:birthPlace, dbo:birthPlace, dbpp:placeOfBirth |
| dbo:Book | dbpp:name, foaf:name, dbpp:titleOrig, rdfs:label |
| dbo:Company | dbpp:website, foaf:website, dbpp:homepage, dbpp:url |
On average, our method obtains 0.65∼0.67 F1 in predicting pair equivalence on the
Table 7
Relative prevalence of error types
| Error Type | Prevalence % |
| False Positives | |
| Semantically similar | 52.4 |
| Low variability | 29.1 |
| Entailment | 14.6 |
| Arguable gold standard | 3.88 |
| False Negatives | |
| Object representation | 25.1 |
| Different datatype | 24.7 |
| Noisy relation | 19.4 |
| Different lexicalisations | 11.7 |
| Sparsity | 10.5 |
| Limitation of method | 5.67 |
| Arguable gold standard | 2.83 |
Figure 11 shows that the performance of our method can vary depending on specific concepts. To understand the errors, we randomly sampled 100 false positive and 100 false negative examples from the
5.1.1.False positives
The first main source of errors are due to high degree of semantic similarity: e.g., dbpp:residence and dbpp:birthPlace of dbo:TennisPlayer are highly semantically similar but non-equivalent. The second type of errors is due to low variability in the objects of a relation: semantically dissimilar relations can have the same datatype and have many overlapping values by coincidence. The overlap is caused by some relations having a limited range of object values, which is especially typical for relations with boolean datatype because they only have two possible values. The third type of errors is entailment, e.g., for dbo:EuropeanCountries, dbpp:officialLanguage entails dbo:language because official languages of a country are a subset of languages spoken in a country. These could be considered as cases of subsumption, which accounts for less than 15%. Finally, some of the errors are arguably due to imperfect gold standard, as analysers sometimes disagree with the annotations (see Table 8).
Table 8
The equivalent relations for dbo:Monument discovered by the proposed method are false positives according to the gold standard
| dbo:synonym | dbp:otherName | 6 |
| rdfs:label | foaf:name | 10 |
| rdfs:label | dbp:name | 10 |
| rdfs:comment | dbo:abstract | 41 |
| dbp:material | dbo:material | 10 |
| dbp:city | dbo:city | 5 |
5.1.2.False negatives
The first type of common errors is due to representation of objects. For instance, for dbo:American FootballPlayer, dbo:team are associated with mostly resource URIs (e.g., ‘dbr:Detroit_Lions’) while dbpp: teams are mostly associated with lexicalization of literal objects (e.g., ‘* Detroit Lions’) that are typically names of the resources. The second type is due to different datatypes, e.g., for dbo:Building, dbpp:startDate typically have literal objects indicating years, while dbo:buildingStartDate usually has precisely literal date values as objects. Thirdly, the lexicalization of objects can be different. An example for this category is dbpp:dialCode and dbo:areaCode of dbo:Settlement, the objects of the two relations are represented in three different ways, e.g. ‘0044’, ‘+44’, ‘44’. Many false negatives are due to sparsity: e.g., dbpp:oEnd and dbo:originalEndPoint of dbo:Canal have in total only 2 triples. There are also noisy relations, whose lexicalization appears to be inconsistent with how it is used. Usually the lexicalization is ambiguous, such as the dbo:railwayPlatforms example discussed before. Some errors are simply due to the limitation of our method, i.e., our method still fails to identify equivalence even if sufficient, quality data are available, possibly due to inappropriate automatic threshold selection. And further, arguable gold standard also exist (e.g., dbpp:champions and dbo:teams of dbo:SoccerLeague are mapped to each other in the
We then also manually inspected some worst performing concepts in the dbpm dataset, and noticed that some of them are due to extremely small gold standard. For example, dbo:SportsTeamMember and dbo:Monument have only 3 true positives each in their gold standard and as a result, our method scored 0 in recall. However, we believe that these gold standards are largely incomplete. For example, we consider most equivalent relation pairs proposed by our method as shown in Table 8 to be correct.
Some of the error types mentioned above could be rectified with by modifying the proposed method in certain ways. String similarity measures may help errors due to representation of objects and different lexicalization of objects. Regular expressions could be used to parse values in order to match data at semantic level, e.g., for dates, weights, and lengths. These could be useful to solve errors due to different datatypes. Other error groups are much harder to prevent: even annotators often struggled to distinguish between semantically similar and equivalent relations or to understand what a relation is supposed to mean.
5.2.Performance against baselines
Next, Table 9 shows the improvement of the proposed method over different models that use a baseline similarity measure. Since the performance of the method depends on the parameter n in the similarity measure, we show the ranges between minimum and maximum improvement due to the choice of n.
It is clear from Table 9 that the proposed method significantly outperforms most baseline models, either supervised or unsupervised. Exceptions are noted against
Fig. 12.
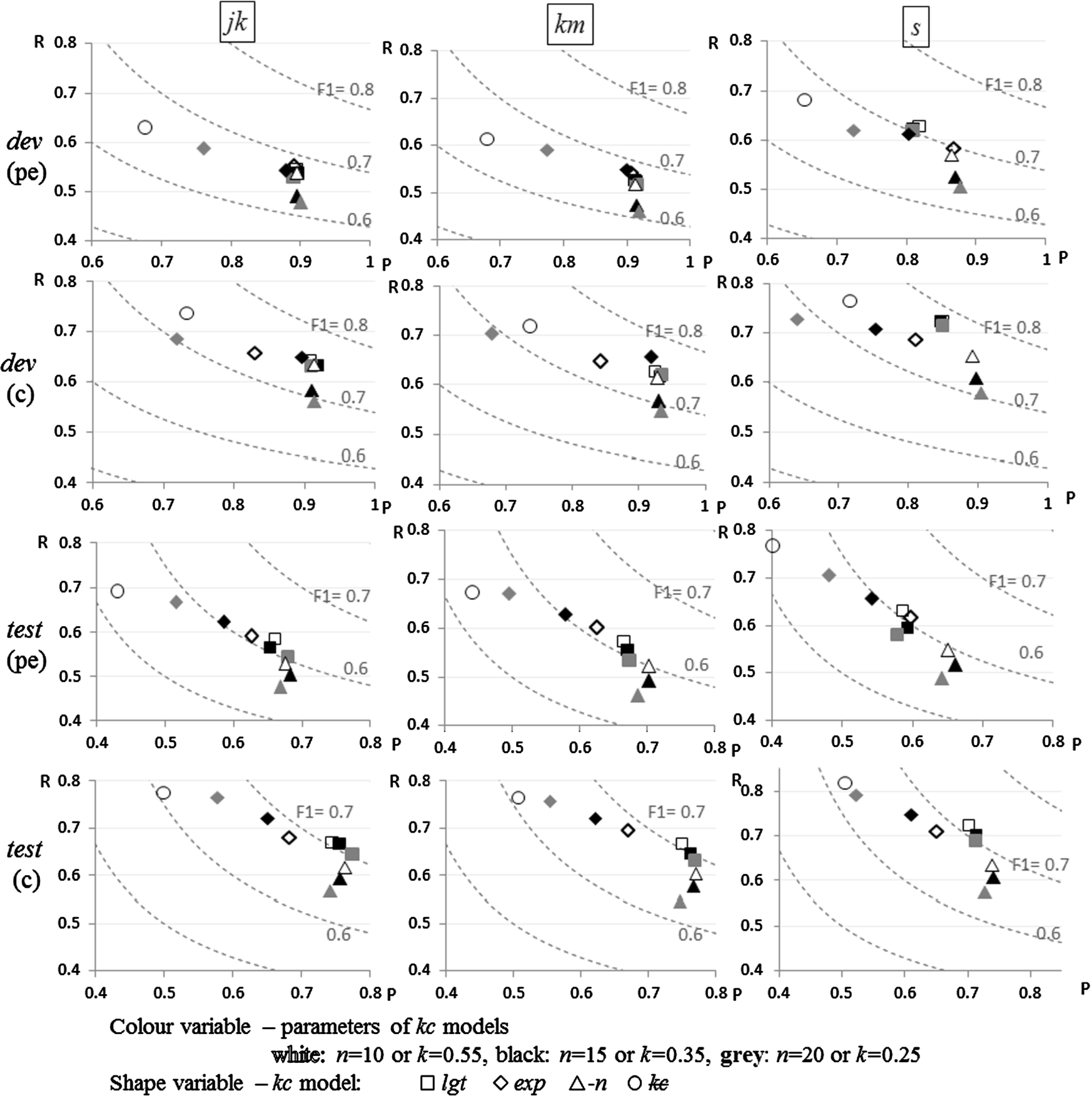
Balance between precision and recall for the proposed method and baselines on (a) the dev set; (b) the test set. pe – pair equivalence, c – clustering. The dotted lines are F1 references.
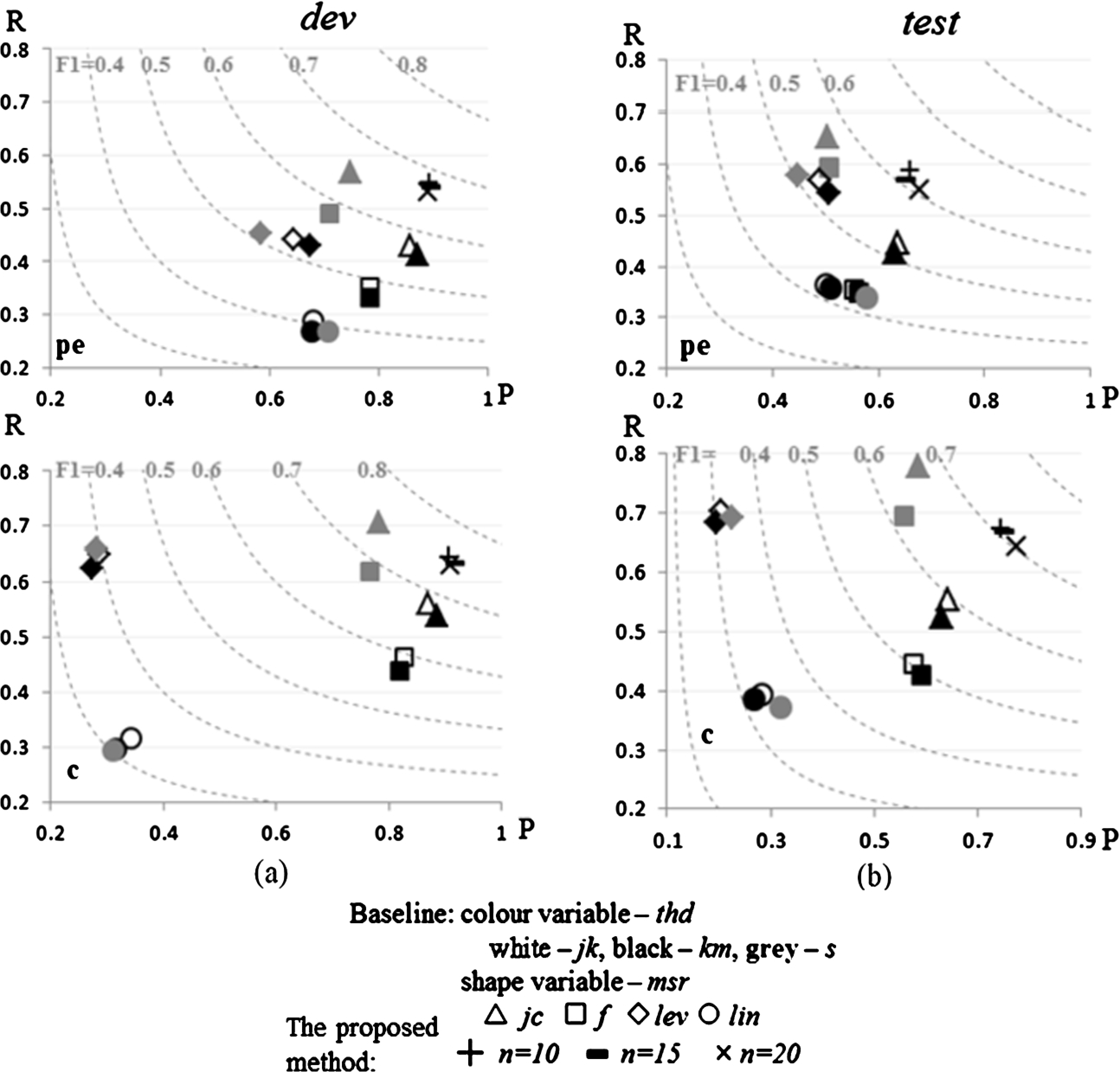
Figures 12(a) and 12(b) compares the balance between precision and recall of the proposed method against baselines on the
Interesting to note is the inconsistent performance of string similarity baselines (
Very similar pattern is also noted for the semantic similarity baselines (
5.3.Variants of the proposed method
In this section, we compare the proposed method against several alternative designs based on the alternative choices of knowledge confidence (
5.3.1.Alternative knowledge confidence models kc
Fig. 13.
Comparing variations of the proposed method by (a) alternating
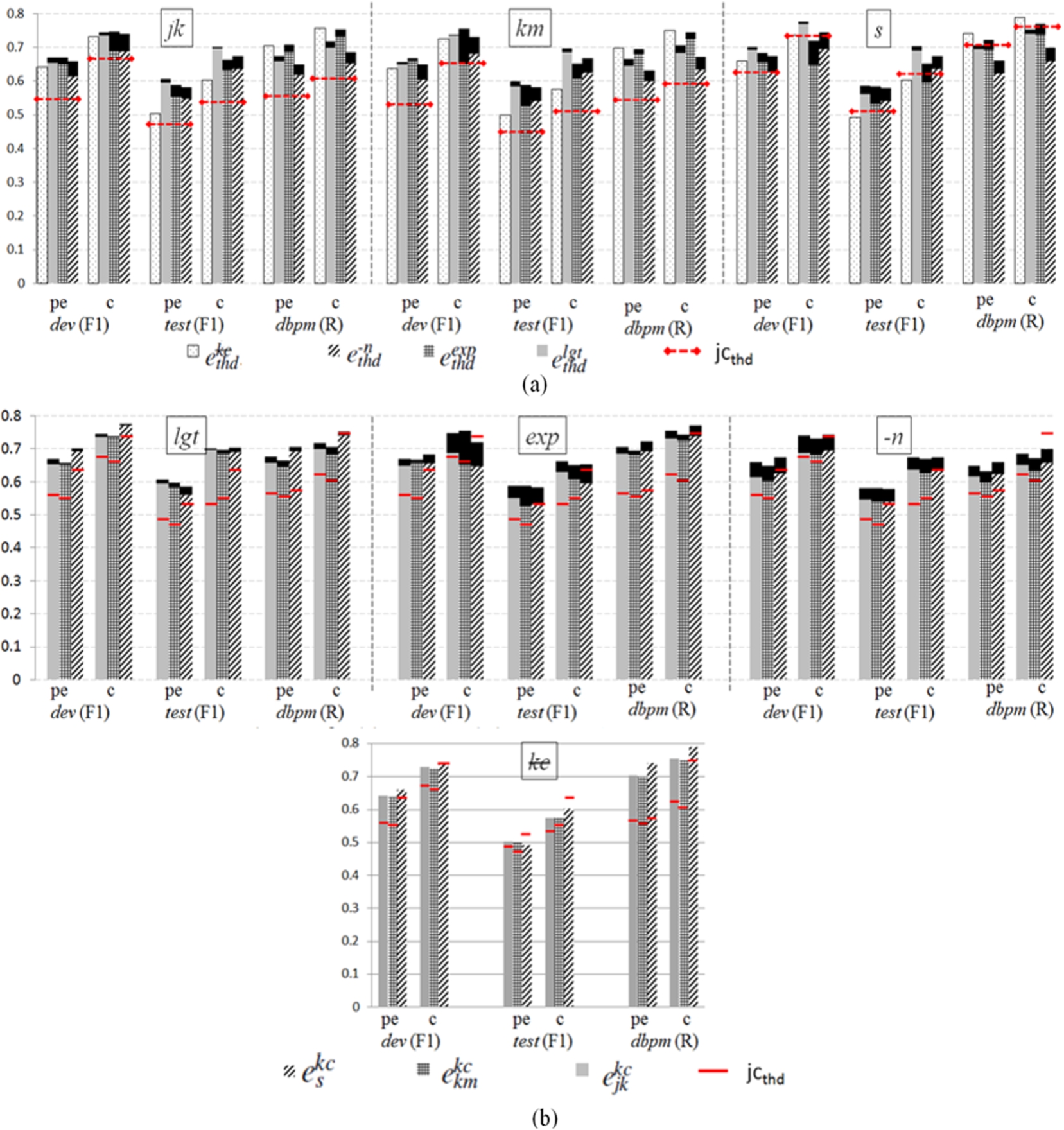
Figure 13(a) compares variants of the proposed method by alternating the
Firstly, under the same
By analyzing the precision and recall trade-off for different
5.3.2.Alternative threshold detection methods thd
Figure 13(b) is a re-arranged view of Fig. 13(a), in the way that it compares variants of the proposed method by alternating the
5.3.3.Limitations
The current version of the proposed method is limited in a number of ways. First and foremost, being an extensional matcher, it requires relations to have shared instances to work. This is usually a reasonable requirement for individual dataset, and hence experiments based on DBpedia have shown it to be very effective. However, in a cross-dataset context, concepts and instances will have to be aligned first in order to apply our method. This is because often, different datasets use different URIs to refer to the same entities; as a result, counting overlap of a relation’s arguments will have to go beyond syntactic level. A basic and simplistic solution could be a pre-process that maps concepts and instances from different datasets using existing sameAs mappings, as done by Parundekar et al. [38] and Zhao et al. [50].
However, when incorrect sameAs mappings are present, they can impact on the accuracy of the proposed method and hence this is our second limitation. Generally speaking, there are two cases of incorrect sameAs mappings, i.e., at concept level or instance level. Recall that the proposed similarity measure looks at relations of a specific concept and operates on a relation’s argument pairs (see triple agreement,
In the first case, suppose we have an incorrect concept mapping
In the second case, incorrectly mapped instances could indeed influence the method under two conditions. First, both
6.Conclusions
This article explored the problem of aligning heterogeneous relations in LOD datasets, particularly focusing on heterogeneity from within a single dataset. Heterogeneity decreases the quality of the data and may eventually hamper its usability over large scale. It is a major research problem concerning the Semantic Web community and significant effort has been made to address this problem in the area of ontology alignment. While most work studied mapping concepts and individuals in the context of cross-datasets, solving relation heterogeneity and in particular, in a single very large LOD dataset is becoming an increasingly pressing issue but still remains much less studied. The annotation practice undertaken in this work has shown that the task is even challenging to humans.
This article makes particular contribution to this problem with a domain- and language-independent and unsupervised method to align relations based on their shared instances in a dataset. In its current form, the method fits best with aligning relations from different schemata used in a single Linked Dataset, but can potentially be used in cross-dataset settings, provided that concepts and instances across the datasets are aligned to ensure relations have shared instances.
A series of experiments have been designed to thoroughly evaluate the method in two tasks: predicting relation pair equivalence and discovering clusters of equivalent relations. These experiments have confirmed the advantage of the method: compared to baseline models including both supervised and unsupervised versions, it makes significant improvement in terms of F1 measure, and always scores the highest precision. Compared to different variants of the proposed method, the logistic model of knowledge confidence achieves the best scores in most cases and is seen to give stable performance regardless of its parameter setting, while the alternatives suffer from a higher degree of volatility that occasionally causes them to underperform baselines. The Jenks Natural Breaks method for automatic threshold detection also proves to have slight advantage than the k-means alternative, and even outperformed the supervised method on the
As future work, we will explore the possibility of utilizing sameAs links between datasets to address cross-dataset relation alignment with focus on the previously discussed issues, and also aim to extend the method into to a full ontology alignment system.
Notes
1 http://stats.lod2.eu/, visited on 30-09-2015.
2 http://dbpedia.org/. All examples and data analysis based on DBpedia in this work uses its dataset in September 2013.
3 dbpp:http://dbpedia.org/property/.
4 foaf:http://xmlns.com/foaf/0.1/.
5 http://mappings.dbpedia.org/index.php/Mapping_en, visited on 01 August 2014.
6 To be clear, we will always use ‘object’ in the context of triples; we will always use ‘individual’ to refer to object instances of classes.
10 http://oaei.ontologymatching.org/2013/, visited on 01-11-2013. Some datasets were unavailable at the time.
11 dbr:http://dbpedia.org/resource/.
12 Notations have been changed.
13 We manually checked a random set of 40 concepts (approximately 17% of all) in our collection of datasets and found 38 show a strong pattern like this while the other two seem to be borderline.
14 Or the minimum in the smaller group. Practically there is no difference as the purpose of a threshold is to separate equivalent pairs from non-equivalent ones.
15 Readers may notice that we dropped the ‘cardinality ratio’ component from the prototype, since we discovered that component may negatively affect performance.
16 Based on the downloadable datasets as by 01-11-2013.
19 skos=http://www.w3.org/2004/02/skos/core#.
21 Not in formal ontology terms, but rather a Wikipedia terminology.
22 http://mappings.dbpedia.org/server/statistics/en/, visited on 15-09-2015.
25 Note that DBpedia by default returns a maximum of 50,000 triples per query. We did not incrementally build the exhaustive result set for each concept since we believe the data size is sufficient for experiment purposes.
26 http://staffwww.dcs.shef.ac.uk/people/Z.Zhang/resources/swj2015/data_release.zip. The cached DBpedia query results are also released.
27 Analysis based on the DBpedia SPARQL service as by 31-10-2013. Inconsistency should be anticipated if different versions of datasets are used.
Acknowledgements
Part of this research has been sponsored by the EPSRC funded project LODIE: Linked Open Data for Information Extraction, EP/J019488/1. We thank reviewers for their invaluable comments that have helped us improve this article substantially.
Appendices
Appendix A.
Appendix A.Precision and recall obtained with different knowledge confidence models kc
Figure 14 complements Fig. 13(a) by comparing the balance between precision and recall for different variants of the proposed method using the
Fig. 14.
Balance between precision and recall for the proposed method and its variant forms. pe – pair equivalence, c – clustering. The dotted lines are F1 references.
The
Appendix B.
Appendix B.Exploration during the development of the proposed similarity measure
In this section we present some earlier analysis that helped us during the development of the method. These analysis helped us to identify useful features for evaluating relation equivalence, as well as unsuccessful features which we abandoned in the final form of the proposed method. We analyzed the components of the proposed similarity measure, i.e., triple agreement
B.1.ta sa
We applied
Fig. 15.
Distribution of

B.2.Ranges of relations
We also explored several ways of deriving ranges of a relation to be considered in measuring similarity. One simplistic method is to use ontological definitions. For example, the range of dbo:birthPlace of the concept dbo:Actor is defined as dbo:Place according to the DBpedia ontology. However, this does not work for relations that are not defined formally in ontologies, such as any predicates with the dbpp namespaces, which are very common in the datasets.
Instead, we chose to define ranges of a relation based on its objects
SELECT ?o ?range WHERE {
?s [RDF Predicate URI] ?o .
?s a [Concept URI] .
OPTIONAL {?o a ?range .}
}
Next, we counted the frequency of each distinct value for the variable ?range and calculated its fraction with respect to all values. We found three issues that make this approach unreliable. First, if a subject s had an rdfs:type triple defining its type c, (e.g., s rdfs:type c), it appears that DBpedia creates additional rdfs:type triples for the subject with every superclass of c. For example, there are 20 rdfs:type triples for dbr:Los_Angeles_County,_California and the objects of these triples include owl:Thing, yago:Object10000 2684 and gml:_Feature (gml: Geography Markup Language). These triples will significantly skew the data statistics, while incorporating ontology-specific knowledge to resolve the hierarchies can be an expensive process due to the unknown number of ontologies involved in the data. Second, even if we are able to choose always the most specific class according to each involved ontology for each subject, we notice a high degree of inconsistency across different subjects in the data. For example, this gives us 13 most specific classes as candidate ranges for dbo:birthPlace of dbo:Actor, and the dominant class is dbo:Country representing just 49% of triples containing the relation. Other ranges include scg:Place, dbo:City, yago:Location (scg: schema.org) etc. The third problem is that for values of ?o that are literals, no ranges will be extracted in this way (e.g., values of ?range extracted using the above SPARQL template for relation dbpp:othername are empty when ?o values are literals).
For these reasons, we abandoned the two methods but proposed to use several simple heuristics to classify the objects of triples into several categories based on their datatype and use them as ranges. Thus given the set of argument pairs
We developed a measure called maximum range agreement, to examine the degree to which both relations use the same range in their data. Let
Fig. 16.
Distribution of
The intuition is that if two relations are equivalent, each of them should have a dominant range as seen in their triple data (thus a high value of
References
[1] | J. Artiles, J. Gonzalo and S. Sekine, The semeval-2007 weps evaluation: Establishing a benchmark for the web people search task, in: Proc. of the 4th International Workshop on Semantic Evaluations, SemEval ’07, Association for Computational Linguistics, Stroudsburg, PA, USA, (2007) , pp. 64–69. |
[2] | M. Atencia, J. David and J. Euzenat, Data interlinking through robust linkkey extraction, in: Proc. of the 21st European Conference on Artificial Intelligence (ECAI), T. Schaub, G. Friedrich and B. O’Sullivan, eds, IOS Press, Amsterdam, NL, (2014) , pp. 15–20. |
[3] | E. Blomqvist, Z. Zhang, A.L. Gentile, I. Augenstein and F. Ciravegna, Statistical knowledge patterns for characterizing linked data, in: Proc. of the 4th Workshop on Ontology and Semantic Web Patterns, at International Semantic Web Conference 2013, CEUR-WS.org, (2013) . |
[4] | T. Caliński and J. Harabasz, A dendrite method for cluster analysis, Communications in Statistics 3: (1) ((1974) ), 1–27. |
[5] | A. Carlson, J. Betteridge, B. Kisiel, B. Settles, E.R. Hruschka and T.M. Mitchell, Toward an architecture for never-ending language learning, in: Proc. of the 24th AAAI Conference on Artificial Intelligence, M. Fox and D. Poole, eds, AAAI Press, California, USA, (2010) , pp. 1306–1313. |
[6] | M. Cheatham and P. Hitzler, String similarity metrics for ontology alignment, in: Proc. of the 12th International Semantic Web Conference, H. Alani, L. Kagal, A. Fokoue, P. Groth, C. Biemann, J.X. Parreira, L. Aroyo, N. Noy, C. Welty and K. Janowicz, eds, Springer-Verlag, Berlin, Heidelberg, (2013) , pp. 294–309. |
[7] | I.F. Cruz, M. Palmonari, F. Caimi and C. Stroe, Towards ‘on the go’ matching of linked open data ontologies, in: Proc. of the Workshop on Discovering Meaning on the Go in Large and Heterogeneous Data, at the 22nd International Joint Conference on Artificial Intelligence, P. Shvaiko, J. Euzenat, F. Giunchiglia and B. He, eds, AAAI Press, California, USA, July (2011) . |
[8] | I.F. Cruz, M. Palmonari, F. Caimi and C. Stroe, Building linked ontologies with high precision using subclass mapping discovery, Artificial Intelligence Review 40: (2) (Aug (2013) ), 127–145. |
[9] | I.F. Cruz, C. Stroe, M. Caci, F. Caimi, M. Palmonari, F. Palandri Antonelli and U.C. Keles, Using agreementmaker to align ontologies for OAEI 2010, in: Proc. of the 5th International Workshop on Ontology Matching, at the 9th International Semantic Web Conference, CEUR-WS.org, (2010) . |
[10] | B. Cuenca Grau, Z. Dragisic, K. Eckert, J. Euzenat, A. Ferrara, R. Granada, V. Ivanova, E. Jimenez-Ruiz, A.O. Kempf, P. Lambrix, C. Meilicke, A. Nikolov, H. Paulheim, D. Ritze, F. Scharffe, P. Shvaiko, C. Trojahn and O. Zamazal, Preliminary results of the ontology alignment evaluation initiative 2013, in: Proc. of the 8th International Workshop on Ontology Matching, at the 12th International Semantic Web Conference, CEUR-WS.org, (2013) . |
[11] | R. Dewey, Chapter 7: Cognition, in: Psychology: An Introduction, (2007) , Psych Web, http://www.intropsych.com/. |
[12] | S. Duan, A. Fokoue, O. Hassanzadeh, A. Kementsietsidis, K. Srinivas and M.J. Ward, Instance-based matching of large ontologies using locality-sensitive hashing, in: Proc. of the 11th International Conference on the Semantic Web, P. Cudré-Mauroux, J. Heflin, E. Sirin, T. Tudorache, J. Euzenat, M. Hauswirth, J. Parreira, J. Hendler, G. Schreiber, A. Bernstein and E. Blomqvist, eds, Springer-Verlag, Berlin, Heidelberg, (2012) , pp. 49–64. |
[13] | J. Euzenat and P. Shvaiko, Ontology Matching, 2nd edn, Springer-Verlag, Heidelberg (DE), (2013) . |
[14] | A. Fader, S. Soderland and O. Etzioni, Identifying relations for open information extraction, in: Proc. of the 2011 Conference on Empirical Methods in Natural Language Processing, Association for Computational Linguistics, Stroudsburg, PA, USA, (2011) , pp. 1535–1545. |
[15] | L. Fu, H. Wang, W. Jin and Y. Yu, Towards better understanding and utilizing relations in DBpedia, Web Intelligence and Agent Systems 10: (3) ((2012) ), 291–303. |
[16] | A.L. Gentile, Z. Zhang, I. Augenstein and F. Ciravegna, Unsupervised wrapper induction using linked data, in: Proc. of the 7th International Conference on Knowledge Capture, ACM, New York, NY, USA, (2013) , pp. 41–48. |
[17] | T. Gruetze, C. Böhm and F. Naumann, Holistic and scalable ontology alignment for linked open data, in: Proc. of the 5th Workshop on Linked Data on the Web, at the 21th International World Wide Web Conference, C. Bizer, T. Heath, T. Berners-Lee and M. Hausenblas, eds, CEUR-WS.org, (2012) . |
[18] | L. Han, T. Finin and A. Joshi, GoRelations: An intuitive query system for dbpedia, in: Proc. of the 1st Joint International Conference on the Semantic Web, J. Pan, H. Chen, H.-G. Kim, J. Li, Z. Wu, I. Horrocks, R. Mizoguchi and Z. Wu, eds, Springer-Verlag, Berlin, Heidelberg, (2012) , pp. 334–341. |
[19] | S. Hertlingand and H. Paulheim, WikiMatch – using Wikipedia for ontology matching, in: Proc. of the 7th International Workshop on Ontology Matching, at the 11th International Semantic Web Conference, CEUR-WS.org, (2012) , pp. 37–48. |
[20] | G. Hripcsak and A. Rothschild, Agreement, the F-measure, and reliability in information retrieval, Journal of the American Medical Informatics Association 12: ((2005) ), 296–298. |
[21] | W. Hu, Y. Qu and G. Cheng, Matching large ontologies: A divide-and-conquer approach, Data and Knowledge Engineering 67: (1) (October (2008) ), 140–160. |
[22] | A. Isaac, L. Van Der Meij, S. Schlobach and S. Wang, An empirical study of instance-based ontology matching, in: Proc. of the 6th International Semantic Web and the 2nd Asian Semantic Web Conference, K. Aberer, K.-S. Choi, N. Noy, D. Allemang, K.-I. Lee, L. Nixon, J. Golbeck, P. Mika, D. Maynard, R. Mizoguchi, G. Schreiber and P. Cudré-Mauroux, eds, Springer-Verlag, Berlin, Heidelberg, (2007) , pp. 253–266. |
[23] | P. Jain, P. Hitzler, A.P. Sheth, K. Verma and P.Z. Yeh, Ontology alignment for linked open data, in: Proc. of the 9th International Semantic Web Conference, P. Patel-Schneider, Y. Pan, P. Hitzler, P. Mika, L. Zhang, J. Pan, I. Horrocks and B. Glimm, eds, Springer-Verlag, Berlin, Heidelberg, (2010) , pp. 402–417. |
[24] | P. Jain, P.Z. Yeh, K. Verma, R.G. Vasquez, M. Damova, P. Hitzler and A.P. Sheth, Contextual ontology alignment of LOD with an upper ontology: A case study with Proton, in: Proc. of the 8th Extended Semantic Web Conference, G. Antoniou, M. Grobelnik, E. Simperl, B. Parsia, D. Plexousakis, P. De Leenheer and J. Pan, eds, Berlin, Heidelberg, Springer-Verlag, (2011) , pp. 80–92. |
[25] | Y.R. Jean-Mary, E.P. Shironoshita and M.R. Kabuka, Ontology matching with semantic verification, Journal of Web Semantics: Science, Services and Agents on the World Wide Web 7: (3) (September (2009) ), 235–251. |
[26] | G. Jenks, The data model concept in statistical mapping, International Yearbook of Cartography 7: ((1967) ), 186–190. |
[27] | P. Lambrix and H. Tan, SAMBO – a system for aligning and merging biomedical ontologies, Journal of Web Semantics 4: (3) (September (2006) ), 196–206. |
[28] | J. Lehmann, R. Isele, M. Jakob, A. Jentzsch, D. Kontokostas, P.N. Mendes, S. Hellmann, M. Morsey, P. van Kleef, S. Auer and C. Bizer, DBpedia – a large-scale, multilingual knowledge base extracted from Wikipedia, Semantic Web Journal 6: (2) ((2015) ), 167–195. |
[29] | J. Li, J. Tang, Y. Li and Q. Luo, RiMOM: A dynamic multistrategy ontology alignment framework, IEEE Transactions on Knowledge and Data Engineering 21: (8) ((2009) ), 1218–1232. |
[30] | G. Limaye, S. Sarawagi and S. Chakrabarti, Annotating and searching web tables using entities, types and relationships, Proceedings of the VLDB Endowment 3: (1–2) ((2010) ) 1338–1347. |
[31] | D. Lin, An information-theoretic definition of similarity, in: Proc. of the 5th International Conference on Machine Learning, Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, (1998) , pp. 296–304. |
[32] | J.B. MacQueen, Some methods for classification and analysis of multivariate observations, in: Proc. of the 5th Berkeley Symposium on Mathematical Statistics and Probability, L.M. Le Cam and J. Neyman, eds, Vol. 1: , University of California Press, (1967) , pp. 281–297. |
[33] | F. Murtagh, Multidimensional Clustering Algorithm, COMPSTAT Lectures, Vol. 4: , Physica-Verlag, Wuerzburg, (1985) . |
[34] | M. Nagy, M. Vargas-Vera and E. Motta, Multi agent ontology mapping framework in the AQUA question answering system, in: Proc. of the 4th Mexican International Conference on Advances in Artificial Intelligence, A. Gelbukh, Á. de Albornoz and H. Terashima-Marín, eds, Springer-Verlag, Berlin, Heidelberg, (2005) , pp. 70–79. |
[35] | M. Nagy, M. Vargas-Vera and E. Motta, DSSim – managing uncertainty on the semantic web, in: Proc. of the 2nd International Workshop on Ontology Matching, at the 6th International Semantic Web Conference, CEUR Workshop Proceedings, CEUR-WS.org, (2007) . |
[36] | D. Ngo, Z. Bellahsene and R. Coletta, A generic approach for combining linguistic and context profile metrics in ontology matching, in: Proc. of the Confederated International Conference on the Move to Meaningful Internet Systems, R. Meersman, T. Dillon, P. Herrero, A. Kumar, M. Reichert, L. Qing, B.-C. Ooi, E. Damiani, D.C. Schmidt, J. White, M. Hauswirth, P. Hitzler and M. Mohania, eds, Springer-Verlag, Berlin, Heidelberg, (2011) , pp. 800–807. |
[37] | A. Nikolov, V. Uren, E. Motta and A. Roeck, Overcoming schema heterogeneity between linked semantic repositories to improve coreference resolution, in: Proc. of the 4th Asian Conference on the Semantic Web, A. Gómez-Pérez, Y. Yu and Y. Ding, eds, Springer-Verlag, Berlin, Heidelberg, (2009) , pp. 332–346. |
[38] | R. Parundekar, C.A. Knoblock and J.L. Ambite, Linking and building ontologies of linked data, in: Proc. of the 9th International Semantic Web Conference, P. Patel-Schneider, Y. Pan, P. Hitzler, P. Mika, L. Zhang, J. Pan, I. Horrocks and B. Glimm, eds, Springer-Verlag, Berlin, Heidelberg, (2010) , pp. 598–614. |
[39] | S. Pavel and J. Euzenat, Ontology matching: State of the art and future challenges, IEEE Trans. on Knowl. and Data Eng. 25: (1) (January (2013) ), 158–176. |
[40] | B. Schopman, S. Wang, A. Isaac and S. Schlobach, Instance-based ontology matching by instance enrichment, Journal on Data Semantics 1: (4) ((2012) ), 219–236. |
[41] | Md.H. Seddiqui and M. Aono, An efficient and scalable algorithm for segmented alignment of ontologies of arbitrary size, Journal of Web Semantics: Science, Services and Agents on the World Wide Web 7: (4) ((2009) ), 344–356. |
[42] | F. Shi, J. Li, J. Tang, G. Xie and H. Li, Actively learning ontology matching via user interaction, in: Proc. of the 8th International Semantic Web Conference, A. Bernstein, D.R. Karger, T. Heath, L. Feigenbaum, D. Maynard, E. Motta and K. Thirunarayan, eds, Berlin, Heidelberg, Springer-Verlag, (2009) , pp. 585–600. |
[43] | K. Slabbekoorn, L. Hollink and G.-J. Houben, Domain-aware ontology matching, in: Proc. of the 11th International Conference on the Semantic Web, P. Cudré-Mauroux, J. Heflin, E. Sirin, T. Tudorache, J. Euzenat, M. Hauswirth, J. Parreira, J. Hendler, G. Schreiber, A. Bernstein and E. Blomqvist, eds, Springer-Verlag, Berlin, Heidelberg, (2012) , pp. 542–558. |
[44] | F.M. Suchanek, S. Abiteboul and P. Senellart, PARIS: Probabilistic alignment of relations, instances, and schema, Proceedings of the VLDB Endowment 5: (3) (November (2011) ), 157–168. |
[45] | D. Symeonidou, V. Armant, N. Pernelle and F. Saïs, SAKey: Scalable almost key discovery in rdf data, in: Proc. of the 13th International Semantic Web Conference 2014, P. Mika, T. Tudorache, A. Bernstein, C. Welty, C. Knoblock, D. Vrandec˘ić, P. Groth, N. Noy, K. Janowicz and C. Goble, eds, Springer-Verlag, (2014) , pp. 33–49. |
[46] | J. Völker and M. Niepert, Statistical schema induction, in: Proc. of the 8th Extended Semantic Web Conference, G. Antoniou, M. Grobelnik, E. Simperl, B. Parsia, D. Plexousakis, P. De Leenheer and J. Pan, eds, Springer-Verlag, Berlin, Heidelberg, (2011) , pp. 124–138. |
[47] | Z. Zhang, A.L. Gentile, I. Augenstein, E. Blomqvist and F. Ciravegna, Mining equivalent relations from linked data, in: Proc. of the 51st Annual Meeting of the Association for Computational Linguistics – Short Papers (ACL Short Papers 2013), The Association for Computer Linguistics, (2013) , pp. 289–293. |
[48] | Z. Zhang, A.L. Gentile, E. Blomqvist, I. Augenstein and F. Ciravegna, Statistical knowledge patterns: Identifying synonymous relations in large linked datasets, in: Proc. of the 12th International Semantic Web Conference and the 1st Australasian Semantic Web Conference, H. Alani, L. Kagal, A. Fokoue, P. Groth, C. Biemann, J.X. Parreira, L. Aroyo, N. Noy, C. Welty and K. Janowicz, eds, Springer-Verlag, Berlin, Heidelberg, (2013) . |
[49] | Z. Zhang, A.L. Gentile and F. Ciravegna, Recent advances in methods of lexical semantic relatedness – a survey, Natural Language Engineering 19: (4) ((2012) ), 411–479. |
[50] | L. Zhao and R. Ichise, Mid-ontology learning from linked data, in: Proc. of the 1st Joint International Conference on the Semantic Web, J. Pan, H. Chen, H.-G. Kim, J. Li, Z. Wu, I. Horrocks, R. Mizoguchi and Z. Wu, eds, Springer-Verlag, Berlin, Heidelberg, (2011) , pp. 112–127. |
[51] | L. Zhao and R. Ichise, Graph-based ontology analysis in the linked open data, in: Proc. of the 8th International Conference on Semantic Systems, ACM, New York, USA, (2012) , pp. 56–63. |
[52] | L. Zhao and R. Ichise, Instance-based ontological knowledge acquisition, in: Proc. of the 10th Extended Semantic Web Conference, P. Cimiano, O. Corcho, V. Presutti, L. Hollink and S. Rudolph, eds, Springer-Verlag, Berlin, Heidelberg, (2013) , pp. 155–169. |