Factorizers for distributed sparse block codes
Abstract
Distributed sparse block codes (SBCs) exhibit compact representations for encoding and manipulating symbolic data structures using fixed-width vectors. One major challenge however is to disentangle, or factorize, the distributed representation of data structures into their constituent elements without having to search through all possible combinations. This factorization becomes more challenging when SBCs vectors are noisy due to perceptual uncertainty and approximations made by modern neural networks to generate the query SBCs vectors. To address these challenges, we first propose a fast and highly accurate method for factorizing a more flexible and hence generalized form of SBCs, dubbed GSBCs. Our iterative factorizer introduces a threshold-based nonlinear activation, conditional random sampling, and an
1.Introduction
Vector-symbolic architectures (VSAs) [10,11,22,39,41] are a class of computational models that provide a formal framework for encoding, manipulating, and binding symbolic information using fixed-size distributed representations. VSAs feature compositionality and transparency, which enabled them to perform analogical mapping and retrieval [12,21,40], inductive reasoning [6,45], and probabilistic abductive reasoning [18,19]. Moreover, the VSA’s distributed representations can mediate between rule-based symbolic reasoning and connectionist models that include neural networks. Recent work [18] has shown how VSA, as a common language between neural networks and symbolic AI, can overcome the binding problem in neural networks and the exhaustive search problem in symbolic AI.
In a VSA, all representations – from atoms to composites – are high-dimensional distributed vectors of the same fixed dimensionality. An atom in a VSA is a randomly drawn i.i.d. vector that is dissimilar (i.e., quasi-orthogonal) to other random vectors with very high probability, a phenomenon known as concentration of measure [32]. Composite structures are created by manipulating and combining atoms with well-defined dimensionality-preserving operations, including multiplicative binding, unbinding, additive bundling (superposition), and permutations. The binding operation can yield quasi-orthogonal results, which, counterintuitively, can still encode semantic information. For instance, we can describe a concept in a scene (e.g., a black circle) with two factors (color and shape) by binding quasi-orthogonal atomic vectors (
However, decomposing, or disentangling, a bound product vector into its factors is computationally challenging, requiring checking all the possible combinations of factors. Extending the previous example from two to F factors, each factor f having a codebook of
This paper provides the following contributions, which are divided into two main parts. In Part I, for the first time, we propose an iterative block code factorizer (BCF) that can reliably factorize blockwise distributed product vectors. The used codebooks in BCF are binary SBCs, which span the product space, while BCF can factorize product vectors from a more generalized sparse block code (GSBC). Hence, factorizing binary SBCs is a special case. BCF introduces a configurable threshold, a conditional sampling mechanism, and a new
In Part II, we present an application for BCF that reduces the number of parameters in fully connected layers (FCLs). FCLs are ubiquitous in modern deep learning architectures and play a major role by accounting for most of the parameters in various architectures, such as transformers [13,30], extreme classifiers [9,33], and CNNs for edge devices [42]. Given an FCL with respective input and output dimensions
2.VSA preliminary
VSAs define operations over (pseudo)random vectors with independent and identically distributed (i.i.d.) components. Computing with VSAs begins by defining a basis in the form of a codebook
For example, consider a VSA model based on the bipolar vector space [11], i.e.,
As an alternative, binary sparse block codes (binary SBCs) [29] induce a local blockwise structure that exhibits ideal variable binding properties [8] and high information capacity when used in associative memories [14,26,51]. In binary SBCs, the
3.Related work
3.1.Factorizing distributed representations
The resonator network [7,23] avoids brute-force search through the combinatorial space of possible factorization solutions by exploiting the search in superposition capability of VSAs. The iterative search process converges empirically by finding correct factors under operational capacity constraints [23]. The resonator network can accurately factorize dense bipolar distributed vectors generated by a two-layer perceptron network trained to approximate the multiplicative binding for colored MNIST digits [7]. Alternatively, the resonator network can also factorize complex-valued product vectors representing a scene encoded via a template-based VSA encoding [47] or convolutional sparse coding [28]. However, the resonator network suffers from a relatively low operational capacity (i.e., the maximum factorizable problem size given a certain vector dimensionality), and the limit cycles that impact convergence. To overcome these two limitations, a stochastic in-memory factorizer [31] introduces new nonlinearities and leverages intrinsic noise of computational memristive devices. As a result, it increases the operational capacity by at least five orders of magnitude, while also avoiding the limit cycles and reducing the convergence time compared to the resonator network.
Nevertheless, we observed that the accuracy of both the resonator network and the stochastic factorizer notably drops (by as much as 16.22%) when they are queried with product vectors generated from deep CNNs processing natural images (see Table 4). This challenge motivated us to switch to alternative block code representations instead of dense bipolar, whereby we can retain high accuracy by using our BCF. Moreover, compared to the state-of-the-art stochastic factorizer, BCF requires fewer iterations irrespective of the number of factors F (see Table 2). Interestingly, it only requires two iterations to converge for problems with a search space as large as
3.2.Fixing the final FCL in CNNs
Typically, a learned affine transformation is placed at the end of deep CNNs, yielding a per-class value used for classification. In this FCL classifier, the number of parameters is proportional to the number of class categories. Therefore, FCLs constitute a large portion of the network’s total parameters: for instance, in models for edge devices, FCLs constitute 44.5% of ShuffleNetV2 [35], or 37% of MobileNetV2 [50] for ImageNet-1K. This dominant parameter count is more prominent in lifelong continual learning models, where the number of classes quickly exceeds a thousand and increases over time [16].
To reduce the training complexity associated with FCLs, various techniques have been proposed to fix their weight matrix during training. Examples include replacing the FCL with a Hadamard matrix [20], or a cheaper Identity matrix [42], or vertices of a simplex equiangular tight frame [62]. Although partly effective, due to square-shaped structures, these methods are restricted to problems in which the number of classes is smaller than or equal to the feature dimensionality, i.e.,
Our BCF with two factors can reduce the memory and compute complexity to
4.Part I: Factorization of generalized sparse block codes
This section presents our first contribution: we propose a novel block code factorizer (BCF) that efficiently finds the factors of product vectors based on block codes. We first introduce GSBC, a generalization of the previously presented binary SBC. We present corresponding binding, unbinding, and bundling operations and a novel similarity metric based on the
4.1.Generalized sparse block codes (GSBCs)
Like binary SBCs, GSBCs divide the
Fig. 1.
Block code factorizer (BCF) for
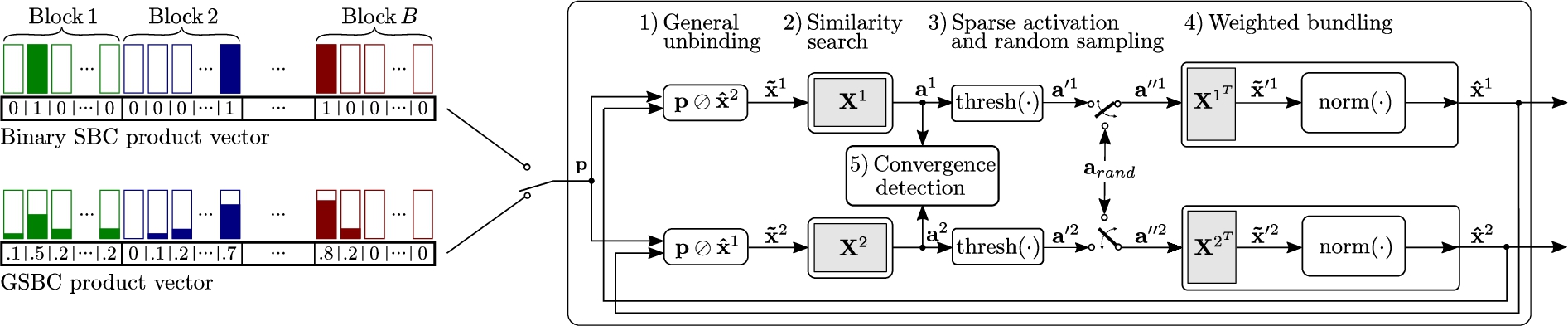
The individual operations for the GSBCs are defined as follows:
Binding/unbinding We exploit general binding and unbinding operations in blockwise circular convolution and correlation to support arbitrary block representations. Specifically, if both operands have blockwise unit
Bundling The bundling of several vectors is defined as their elementwise sum followed by a normalization operation, ensuring that each result block has unit
For any GSBC vectors a and b, it holds that
Table 1
Comparison of operations of binary SBCs and our GSBCs. All operations except for the similarity are applied blockwise
| Binary SBCs [29] | GSBCs (ours) | |
| Binding (⊛) | Modulo-L sum of nonzero indices | Blockwise circular convolution |
| Unbinding (⊘) | Modulo-L difference between nonzero indices | Blockwise circular correlation |
| Bundling (⊕) | Argmax of sum | Sum & normalization |
| Similarity | Dot-product |
4.2.Factorization problem
We define the factorization problem for GSBCs and our factorization approach for two factors. Applying our method to more than two factors is straightforward; corresponding experimental results will be presented in Section 4.6.
Given two codebooks,11
4.3.Block code factorizer (BCF)
Here, we introduce our novel BCF that efficiently finds the factors of product vectors based on GSBCs, shown in Fig. 1. The product vector decoding begins with initializing the estimate factors
Step 1: Unbinding. At the start of iteration
Step 2: Similarity search. Next, we query the associative memory, containing the codebook
Step 3: Sparse activation and conditional random sampling. Recent work on stochastic factorizers [31] demonstrated that applying a threshold function to the elements of the similarity vector can improve convergence speed and operational capacity. We deploy a similar idea in our BCF. In this step, the previously computed similarities are compared against a fixed threshold
This nonlinearity allows us to focus on the most promising solutions by discarding the presumably incorrect low-similarity ones. However, thresholding entails the possibility of ending up with an all-zero similarity vector, effectively stopping the decoding procedure. To alleviate this issue, upon encountering an all-zero similarity vector, we randomly generate a subset of equally weighted similarity values:
The novel threshold and conditional sampling mechanisms are simple and interpretable, and they lead to faster convergence. The stochastic factorizer [31] relied on various noise instantiations at every decoding iteration. The necessary stochasticity was supplied from intrinsic noise of phase-change memory devices and analog-to-digital converters of a computational analog memory tile. Instead, BCF remains deterministic in the decoding iterations unless all elements in the similarity vector are zero, in which case it activates only a single random source. This can be seen as a conditional restart of BCF using a new random initialization. The conditional random sampling could be implemented with a single random permutation of a seed vector in which A-many arbitrary values are set to
Step 4: Weighted bundling. Finally, we generate the next factor estimate
Step 5: Convergence detection. The iterative decoding is repeated until BCF converges or a predefined maximum number of iterations (N) is reached. We define the maximum number of iterations such that BCF does at most as many similarity searches as the brute-force approach [31]:
Fig. 2.
Optimal threshold and sampling width found using Bayesian optimization with
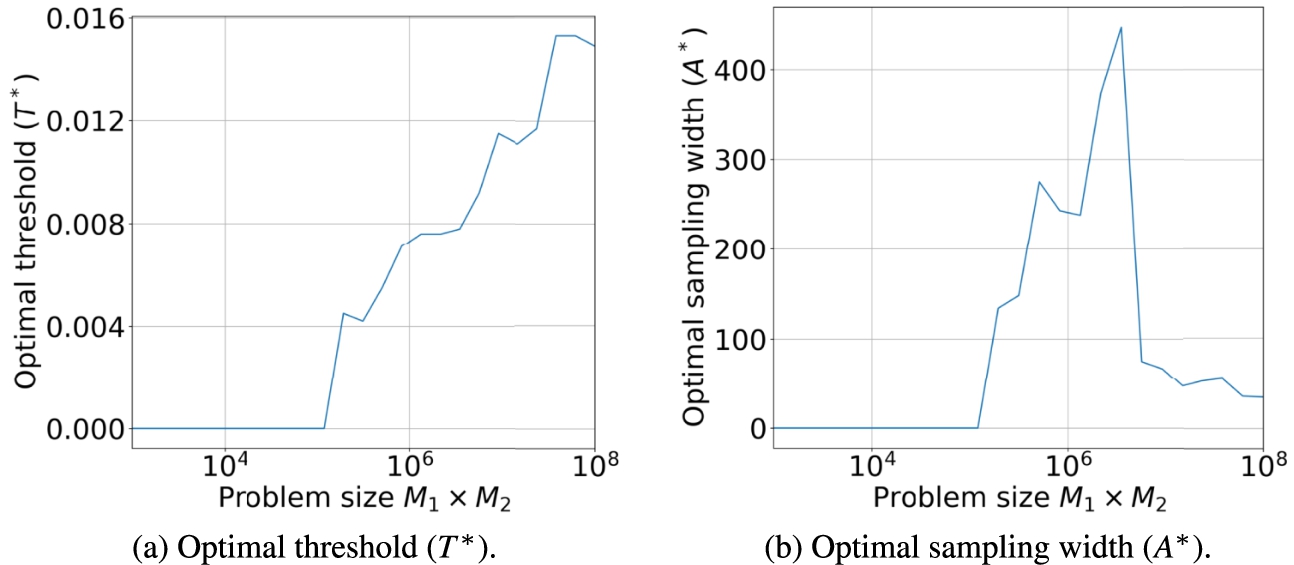
4.4.Hyperparameter optimization
This section explains the methodology for finding optimal BCF hyperparameters to achieve high accuracy and fast convergence. The optimal configuration is denoted by
The loss function is defined as the error rate given by the percentage of incorrect factorizations out of 512 randomly selected product vectors. To put a strong emphasis on fast convergence, we reduced the maximal number of the iterations to
For each problem (F,
Figure 2 shows the resulting threshold (T) and sampling width (A) over various problem sizes for
4.5.Experimental setup
Fig. 3.
Factorization accuracy (left) and number of iterations (right) of various BCF configurations on synthetic (i.e., exact) product vectors for different problem sizes (
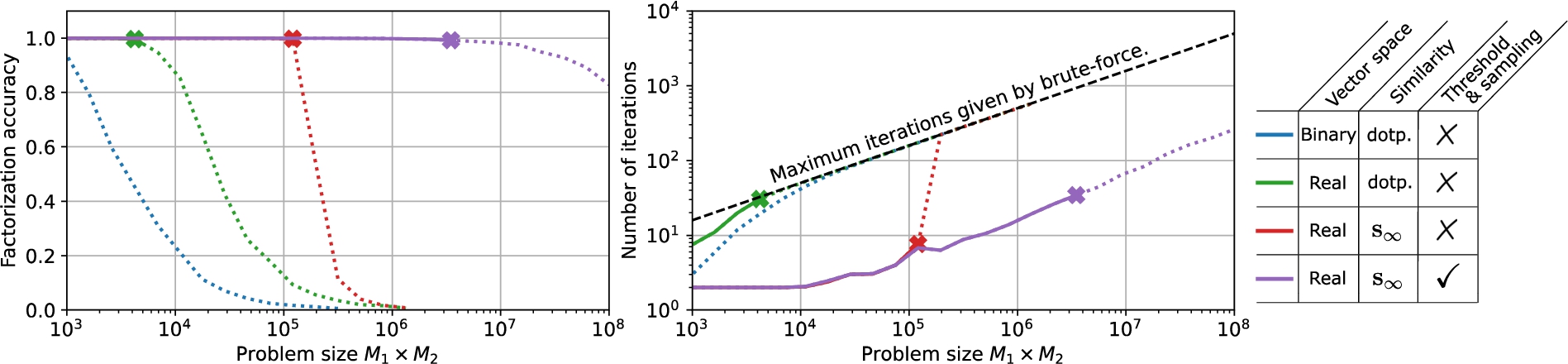
We evaluate the performance of our novel BCF on randomly selected synthetic product vectors. For each problem (F,
4.6.Comparative results
Figure 3 compares the accuracy (left) and the number of iterations (right) of various BCF configurations with
Fig. 4.
Effect of the dimension
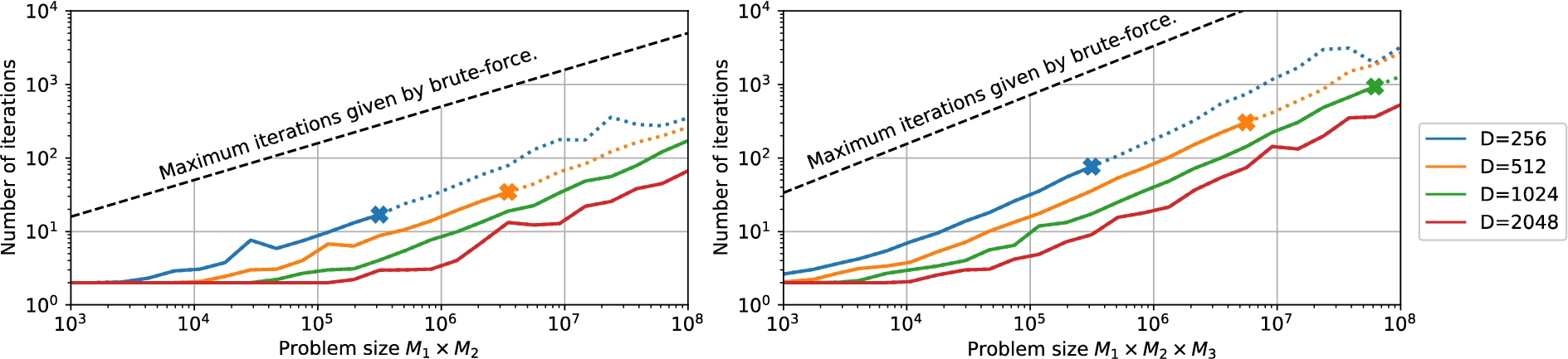
Fig. 5.
Effect of the number of blocks B on the number of iterations for BCF with
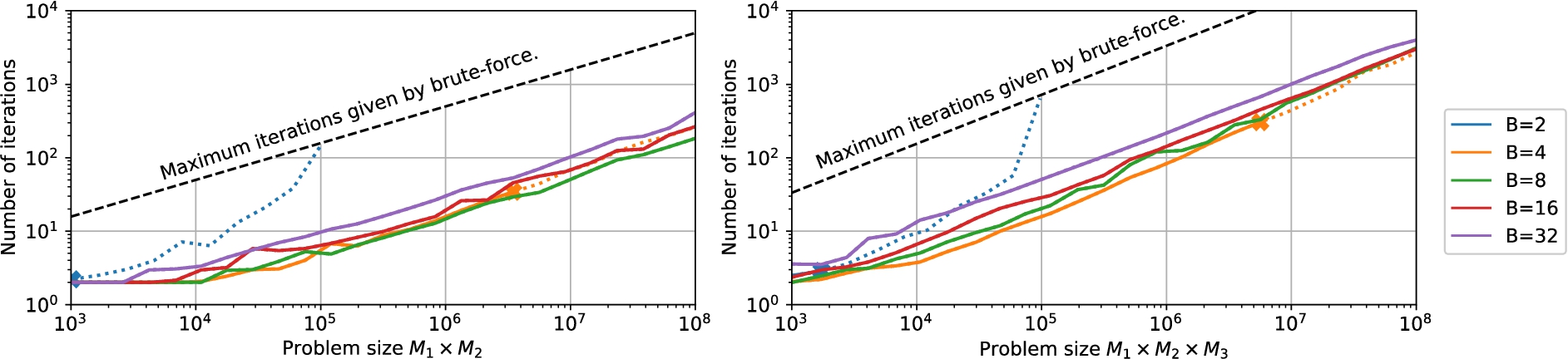
Next, we analyze BCF’s decoding performance for a varying number of blocks (B), vector dimensions (
Figure 5 shows BCF’s performance for a fixed
Finally, we compare our BCF with the state-of-the-art stochastic factorizer [31] operating with dense bipolar vectors. We fix the problem size to
4.7.Ablation study
This section provides more insights into BCF’s two main hyperparameters: the threshold (T) and the sampling width (A).
Effect of sampling width in an unconditional random sampler The sampling width (A) determines how many codevectors will be randomly sampled and bundled in case the thresholded similarity is an all-zero vector. Intuitively, we expect too low sampling widths to result in a slow walk over the space of possible solutions. Alternatively, suppose the sampling width is too large (e.g., larger than the bundling capacity). In that case, we expect high interference between the randomly sampled codevectors to hinder the accuracy and convergence speed due to the limited bundling capacity.
Fig. 6.
Number of iterations when BCF is configured as an unconditional random sampler with varying sampling width (A). We set
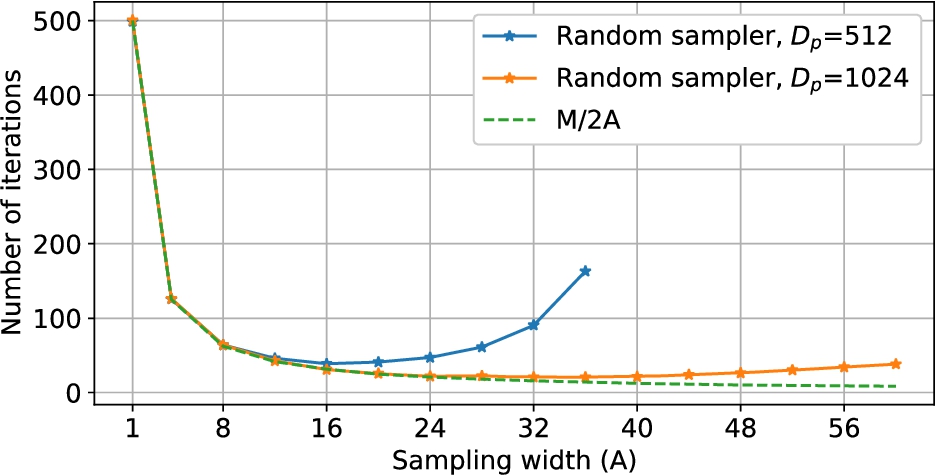
To experimentally demonstrate this effect, we run BCF with
Figure 6 shows experimental results with this factorizer mode for
Effect of sampling width (A) in BCF In this set of experiments, we do not restrict the threshold to be
Table 3 shows how the accuracy and the number of iterations change as we vary the sampling width (A) in
Table 3
BCF performance when varying the sampling width (A).
| A | Accuracy | Num. iters. | |
| 10 | 0.00602 | 99.4% | 39.16 |
| 50 | 0.00641 | 99.4% | 17.86 |
| 100 | 0.00641 | 99.4% | 15.73 |
| 500 | 0.00722 | 98.6% | 24.25 |
| 1000 | 0.00441 | 46.9% | 276.78 |
Similarity metric
Fig. 7.
Log-scale histograms of
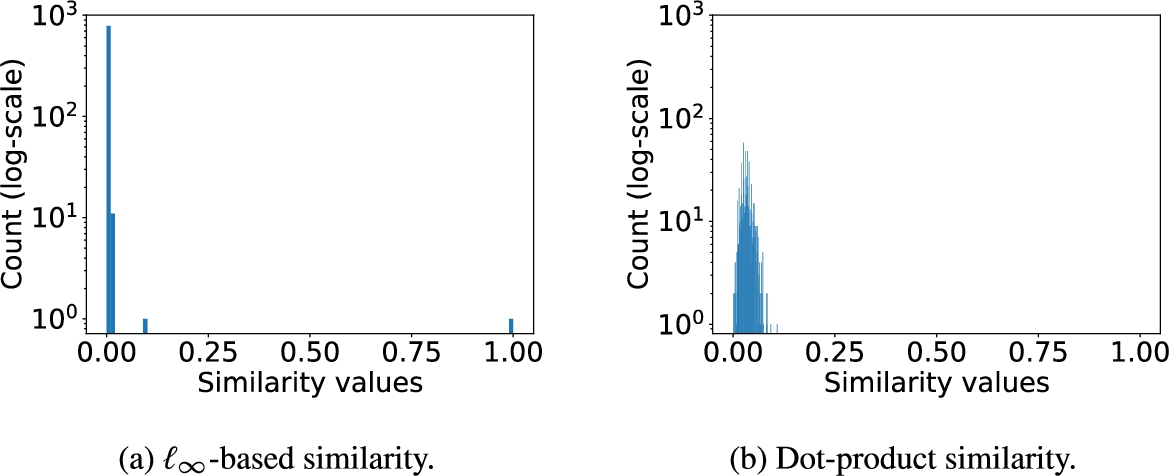
Here, we compare the
5.Part II: Effective replacement of large FCLs with block code factorizers
Fig. 8.
Replacement of a large FCL with our BCF (b) without or (c) with a projection
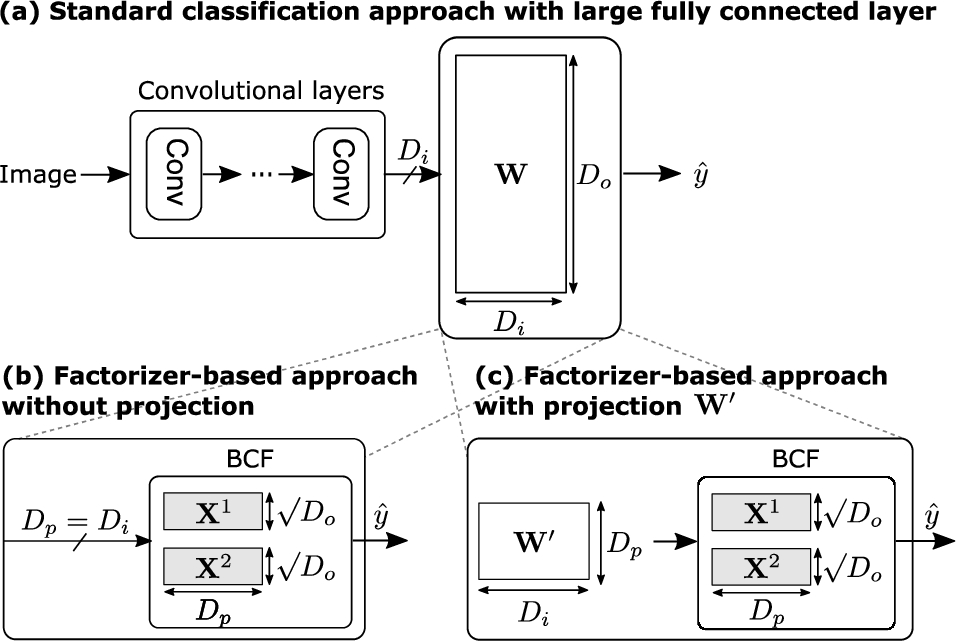
So far, we have applied our BCF on synthetic (i.e., exact) product vectors. In this section, we present our second contribution, expanding the application of our BCF to classification tasks in deep CNNs. This is done by replacing the large final FCL in CNNs with our BCF, as shown in Fig. 8. Instead of training C hyperplanes for C classes, embodied in the trainable weights
5.1.Casting classification as a factorization problem
First, we describe how the classification problem can be transformed into a factorization problem. The codebooks and product space are naturally provided if a class is a combination of multiple attribute values. For example, the RAVEN dataset contains different objects formed by a combination of shape, position, color, and size. Hence, we define four codebooks (
If no such semantic information is available, the codebooks and product space are chosen arbitrarily. When targeting two factors, we first define a product space
Fig. 9.
Training and inference with BCF.
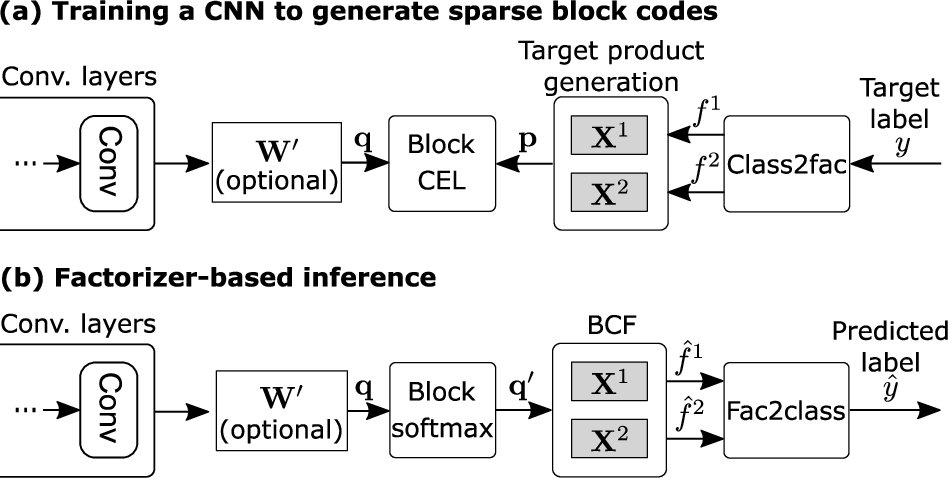
5.2.Training CNNs with blockwise cross-entropy loss
After defining the product space, we train a function
A typical loss function for binary sparse target vectors is the binary cross-entropy loss in connection with the sigmoid nonlinearity. However, we experienced a notable classification drop when using the binary cross-entropy loss; e.g., the accuracy of MobileNetV2 on the ImageNet-1K dataset dropped below 1% when using this loss function. To this end, we propose a novel blockwise loss that computes the sum of per-block categorical cross-entropy loss (CEL). For each block b, we extract the L-dimensional block
5.3.BCF-based inference
The BCF-based inference is illustrated in Fig. 9b. We pass a query image (I) through the CNN, yielding the query product (q), which can be interpreted as a “noisy” version of the ground-truth product vector p. We then search for the product vector
We pass the output of the CNN through a blockwise softmax function with an inverse softmax temperature
5.4.Experimental setup
Datasets We evaluate our new method on three image classification benchmarks.
ImageNet-1K. The ImageNet-1K dataset [3] is a large-scale image classification benchmark with colored images from
CIFAR-100. The CIFAR-100 dataset [27] contains colored images with a resolution of
RAVEN. The RAVEN dataset [59] contains Raven’s progressive matrices tests with gray-scale images with a resolution of
Architectures ShuffleNetV2 [35], MobileNetV2 [50], ResNet-18, and ResNet-50 [15] serve as baseline architectures. In addition to our BCF-based replacement approach, we evaluate each architecture with the bipolar dense resonator [7,23], the Hadamard readout [20], and the Identity readout [42]. For the FCL replacement strategies without the intermediate projection layer, we removed the nonlinearity and batch norm of the last convolutional layer of all CNN architectures. This notably improved the accuracy of all replacement strategies; e.g., the accuracy of MobileNetV2 with the Identity replacement improved from
Training setup The CNN models are implemented in PyTorch (version 1.11.0) and trained and validated on a Linux machine using up to 4 NVIDIA Tesla V100 GPUs with 32 GB memory. We train all CNN architectures with SGD with architecture-specific hyperparameters, described in Appendix A.1. For each architecture, we use the same training configuration for the baseline and all replacement strategies (i.e., Hadamard, Identity, resonator networks, and our BCF). We repeat the main experiments five times with a different random seed and report the average results and standard deviation to account for training variability.
Table 4
Comparison of approaches which replace the final FCL without any projection layer (
| Dataset/architecture | ( | Baseline acc. | FCL replacement approach | |||||||||
| Had. acc. | Id. acc. | Bipolar dense | Our BCF ( | |||||||||
| BF acc. | Res. acc.∗ | Avg. iter.∗ | BF acc. | Fac. acc. | Avg. iter. | Param. saving↑ | FCL comp. saving↑ | |||||
| ImageNet-1K | ||||||||||||
| ShuffleNetV2 | (1024, 1k) | 68.02 | 67.62 | 66.17 | 54.54 | 150 | 7 | 44.5% | ||||
| MobileNetV2 | (1280, 1k) | 71.30 | 70.72 | 70.64 | 60.83 | 150 | 6 | 37.6% | ||||
| ResNet-18 | (512, 1k) | N/A | N/A | 68.65 | 54.17 | 150 | 7 | 4.4% | ||||
| ResNet-50 | (2048, 1k) | 75.30 | 74.65 | 75.80 | 67.98 | 150 | 5 | 8.0% | ||||
| CIFAR-100 | ||||||||||||
| ResNet-18 | (512, 100) | 77.21 | 76.56 | 76.63 | 71.15 | 150 | 2 | 0.5% | ||||
| RAVEN | ||||||||||||
| ResNet-18 | (512, 4.2k) | N/A | N/A | 99.89 | 94.92 | 45 | 16 | 16.2% | ||||
| p-value | – | – | 0.125 | 0.125 | 0.063 | 0.031 | – | 0.094 | 0.063 | – | – | – |
Acc. = Accuracy (%); N/A = Not applicable; Had. = Reproduced Hadamard [20]; Id. = Reproduced Identity [42]; BF = Brute-force; Res. = Resonator nets [7]; Fac. = Block code factorizer whereby it sets
∗ Maximum number of iterations was increased to
5.5.Comparative results
Table 4 compares the classification accuracy of the baseline with various replacement approaches without projection, namely Hadamard [20], Identity [42], bipolar dense [7], and our BCF. On ImageNet-1K, BCF reduces the total number of parameters of deep CNNs by 4.4%–44.5%,33 while maintaining a high accuracy within
Table 5
Classification accuracy when interfacing the last convolution layer with BCF using a projection layer with
| Dataset/architecture | Baseline | Our BCF ( | ||||||
| ( | # Param. | Acc. | BF acc. | Fac. acc. | Avg. iter. | Param. saving↑ | FCL comp. saving↑ | |
| ImageNet-1K | ||||||||
| ShuffleNetV2 | (1024, 1k) | 2.3 M | 6 | 21.7% | ||||
| MobileNetV2 | (1280, 1k) | 3.4 M | 6 | 18.4% | ||||
| ResNet-18 | (512, 1k) | 11.5 M | 6 | 2.2% | ||||
| ResNet-50 | (2048, 1k) | 25.5 M | 5 | 3.9% | ||||
| RAVEN | ||||||||
| ResNet-18 | (512, 4.2k) | 13.3 M | 16 | 14.2% | ||||
| p-value | – | – | – | 0.465 | 0.313 | – | – | – |
On CIFAR-100, BCF matches the baseline within
Considering the other FCL replacement approaches, Hadamard consistently outperforms Identity. However, both the memory and computation requirements of Hadamard are
We compare our approach to weight pruning techniques, which usually sparsify the weights in all layers, whereas we focus on the final FCL due to its dominance in compact networks. Such pruning can be similarly applied to earlier layers in addition to our method. Pruning the final FCL of a pretrained MobileNetV2 with iterative magnitude-based pruning [61] yields notable accuracy degradation as soon as more than 95% of the weights are set to zero. In contrast, our method remains accurate (69.76%) in high sparsity regimes (i.e., 99.98% zero elements). See Appendix A.6 for more details.
Furthermore, we compare our results with [54], which randomly initialize the final FCL and keep it fixed during training. On CIFAR-100 with ResNet-18, they could show that fixing the final FCL layer even slightly improves the accuracy compared to the trainable FCL (
Table 5 shows the performance of our BCF when using the projection layer (
5.6.Ablation study
We give further insights into the BCF-based classification by analyzing the effect of the number of blocks, the projection dimension, the number of factors, and the initialization of the CNN weights.
Number of blocks B Table 6 shows the brute-force and BCF classification accuracy for block codes with different numbers of blocks. The brute-force accuracy degrades as the number of blocks (B) increases, particularly in networks where the final FCL is dominant (e.g., ShuffleNetV2). These experiments demonstrate that deep CNNs are well-matched with very sparse vectors (e.g.,
Projection dimension
Table 6
Classification accuracy (%) on ImageNet-1K for the baseline and the block code-based replacement approaches (
| Classification approach | B | ShuffleNetV2 | MobileNetV2 | ResNet-18 | ResNet-50 | ||||
| BF | Fac. | BF | Fac. | BF | Fac. | BF | Fac. | ||
| Baseline | – | – | – | – | – | ||||
| GSBCs | 4 | ||||||||
| 8 | 64.30 | 63.65 | 69.53 | 69.20 | 67.90 | 67.76 | 76.69 | 76.48 | |
| 16 | 63.22 | 62.04 | 69.34 | 68.83 | 67.02 | 64.98 | 76.52 | 76.27 | |
| 32 | 61.96 | 59.74 | 69.12 | 68.35 | 65.09 | 61.39 | 76.08 | 75.62 | |
Table 7
Loading a pretrained ResNet-18 model improves accuracy and training time. Classification accuracy (%) on ImageNet-1K using BCF with ResNet-18 (with projection
| Pretrained model | Training epochs | BF acc. | Fac. acc. | |
| Baseline | ✗ | 100 | – | |
| GSBCs | ✗ | 100 | ||
| GSBCs | ✓ | 50 | ||
| ✓ | 75 | |||
| ✓ | 100 |
Number of factors F So far, we have evaluated BCF with two factors, each having codebooks of size
Initialize ResNet-18 with pretrained weights Finally, we show that the training of BCF-based CNNs can be improved by initializing their weights from a model that was pretrained on ImageNet-1K. Table 7 shows the positive impact of pretraining of ResNet-18 (with projection) on ImageNet-1K. The pretraining improves the accuracy of BCF by
6.Discussion
BCF is a powerful tool to iteratively decode both synthetic and noisy product vectors by efficiently exploring the exponential search space using computation in superposition. As one viable application, this allowed us to effectively replace the final large FCL in CNNs, reducing the memory footprint and the computational complexity of the model while maintaining high accuracy. If the classes were a natural combination of multiple attribute values (e.g., the objects in RAVEN), we cast the classification as a factorization problem by defining codebooks per attribute, and their combination as vector products. In contrast, the codebooks and product space were chosen arbitrarily if the dataset did not provide such semantic information about the classes (e.g., ImageNet-1K or CIFAR-100). Instead of this random fixed assignment, one could use an optimized dynamic label-to-prototype vector assignment [49]. It would be also interesting if a product space could be learned, e.g., by gradient descent, revealing the inherent structure and composition of the individual classes. Besides, other applications may benefit from a structured product representation, e.g., representing birds as a product of attributes in the CUB dataset [57]. Indeed, high-dimensional distributed representations have already been proven to be helpful when representing classes as a superposition of attribute vectors in the zero-shot setting [48]. Representing the combination of attributes in a product space may further improve the decoding efficiency.
This work focuses on decoding single vector products; however, efficiently decoding superpositions of vector products with our BCF would be highly beneficial. First, it would allow us to decode images with multiple objects (e.g., multiple shapes in an RPM panel on RAVEN). Second, it enables the replacement of arbitrary FCL in neural networks, which usually involve activating multiple neurons. This limitation has been addressed in [17] albeit for dense codes, where a mixed decoding method efficiently extracts a set of vector products from their fixed-width superposition. The mixed decoding combines sequential and parallel decoding methods to mitigate the risk of noise amplification, and increases the number of vector products that can be successfully decoded. However, the number of retrievable vector products in the superposition still needs to be higher to be able to replace arbitrary FCLs in neural networks. Therefore, future work into advanced decoding techniques could improve this aspect of BCF.
Finally, our BCF could enhance Transformer models [56] on different fronts. First, large embedding tables are a bottleneck in Transformer-based recommendation systems, consuming up to 99.9% of the memory [5]. Replacing the embedding tables with our fixed-width product space would reduce the memory footprint as well as the computational complexity in inference when leveraging our BCF. Second, the internal feedforward layers in Transformer models could be replaced by BCF, specifically the first of the two FCLs which can be viewed as key retrieval in a key-value memory [13]. As elaborated in the previous paragraph, the number of decodable vector products in superposition is still limited. Hence, sparsely activated keys would be beneficial. It has been shown that these sparse activations can be found in the middle layers of Transformer models [44].
7.Conclusion
We proposed an iterative factorizer for generalized sparse block codes. Its codebooks are randomly distributed high-dimensional binary sparse block codes, whose number of blocks can be as low as four. The multiplicative binding among the codebooks forms a quasi-orthogonal product space that represents a large number of class categories, or combinations of attributes. As a use-case for our factorizer, we also proposed a novel neural network architecture that replaces trainable parameters in an FCL (aka classifier) with our factorizer, whose reliable operation is verified by accurately classifying/disentangling noisy query vectors generated from various CNN architectures. This quasi-orthogonal product space not only reduces the memory footprint and computational complexity of the networks working with it, but also can reserve a huge representation space to prevent future classes/combinations from coming into conflict with already assigned ones, thereby further promoting interoperability in a continual learning setting.
Notes
1 In our experiments, the codebooks consist of binary SBC codewords, but they could be GSBC vectors too.
2 If
3 The relative parameter reduction depends on the size of the overall network and the final FCL, which we replace with our method.
Acknowledgements
This work is supported by the Swiss National Science foundation (SNF), grant no. 200800.
Appendices
Appendix
AppendixEffective replacement of large FCLs
This appendix provides more details on the effective replacement of large FCLs using the proposed BCF.
A.1.Overall CNN training setup
We train all CNN architectures with SGD with architecture-specific hyperparameters, summarized in Table 8. The training setups for the different networks mainly differ in the chosen learning rate schedule. ShuffleNetV2 was trained for 400 epochs using a learning rate initially set to 0.5 and linearly decreased towards 0 at every epoch. MobileNetV2 was trained with a cosine learning rate schedule [34], where the learning rate is decreased based on a cosine function (single cycle) from 0.04 to 0 within 150 epochs. An additional warmup period of 5 epochs was used. ResNet-18 and ResNet-50 were trained with an exponential decaying learning rate schedule. For training the ResNet-18 on the RAVEN dataset, we started with a pre-trained model from the ImageNet-1k dataset [63].
Table 8
Hyperparamters for CNN training
| Dataset/architecture | Ep. | Bs. | Mmt. | Wd. | Learning rate schedule | |||
| Init. value | Type | Decay rate | Step size | |||||
| ImageNet-1K | ||||||||
| ShuffleNetV2 | 400 | 2048 | 4e-5 | 0.9 | 0.5 | lin | – | – |
| MobileNetV2 | 150 | 256 | 4e-5 | 0.9 | 0.04 | cos | – | – |
| ResNet-18 | 100 | 256 | 1e-4 | 0.9 | 0.1 | exp | 0.1 | 30 |
| ResNet-50 | 100 | 256 | 1e-4 | 0.9 | 0.1 | exp | 0.1 | 30 |
| CIFAR-100 | ||||||||
| ResNet-18 | 200 | 128 | 5e-4 | 0.9 | 0.1 | exp | 0.2 | 60 |
| RAVEN | ||||||||
| ResNet-18 | 100 | 256 | 1e-4 | 0.9 | 0.1 | exp | 0.1 | 50 |
Ep. = Epochs; Bs. = Batch size; Mmt. = Momentum; Wd. = Weight decay.
A.2.Loss functions for the bipolar dense resonator network integration
We evaluated different loss functions for replacing FCL with the bipolar dense resonator networks. A standard cross-entropy loss operating on the cosine similarities between the query vector and the fixed bipolar vectors, scaled with a trainable inverse softmax temperature s [20], yielded good brute-force accuracies but notable drops when integrating the resonator networks. For example, when replacing the final FCL of ShuffleNetV2 on ImageNet-1K, we achieved a brute-force accuracy of
Instead, we found that the fixed but configurable arcface [4] loss function is the most suitable for the resonator network integration. Arcface computes the angle of the target logit, adds an additive angular margin (m) to the target angle, and gets the target logit back again by the cosine function. Finally, the logits are rescaled by a fixed scaling factor (s) before applying the cross-entropy loss. To find the optimal hyperparameters (s, m), we conducted a grid search across a wide range of configurations (
A.3.Projection dimension D p
The main results of BCF using the projection layer are reported for GSBC vectors with a dimension of
Table 9
Classification accuracy (%) on ImageNet-1K when replacing the FCL in MobileNetV2 with BCF using a projection layer with variable
| BF | Fac. | Param. saving↑ | ||
| Baseline | – | – | 0.0% | |
| GSBCs | 128 | 32.8% | ||
| 256 | 28.0% | |||
| 512 | 18.4% | |||
| 768 | 8.7% | |||
| 1000 | 0.0% |
A.4.Maximum number of iterations N
On ImageNet-1K, the maximum number of iterations of BCF with 2 codebooks is set to
Table 10
BCF-based replacement approach without and with projection (
| Baseline acc | GSBCs (B = 4) | |||||
| BF acc. | BCF ( | BCF ( | ||||
| Acc. | Avg. iter. | Acc. | Avg. iter. | |||
| No projection | ||||||
| ShuffleNetV2 | 7.3 | 2.4 | ||||
| MobileNetV2 | 6.2 | 2.3 | ||||
| ResNet-18 | 6.7 | 2.4 | ||||
| ResNet-50 | 4.8 | 2.2 | ||||
| Projection | ||||||
| ShuffleNetV2 | 6.0 | 2.4 | ||||
| MobileNetV2 | 5.5 | 2.3 | ||||
| ResNet-18 | 6.2 | 2.4 | ||||
| ResNet-50 | 4.6 | 2.2 | ||||
A.5.Number of factors F
So far, we have evaluated BCF with two factors, each having codebooks of size
Table 11
Classification accuracy (%) on ImageNet-1K when replacing the FCL in MobileNetV2 with BCF using a projection with
| F | BF | Fac. | Avg. iter. | FCL comp. saving↑ | |
| Baseline | – | – | – | 0.0% | |
| GSBCs | 2 | 6 | 33.4% | ||
| 3 | 11 | 35.6% |
A.6.Comparison with weight pruning
We compare our approach to weight pruning techniques, which mostly sparsify the weights in all layers, whereas we focus on the final FCL due to its dominance in compact networks. Such pruning can be similarly applied to earlier layers in addition to our method. For a one-to-one comparison, we prune the final FCL weights of a pretrained MobileNetV2 using iterative magnitude-based pruning [61]. As shown in Table 12, the accuracy of the magnitude-based pruning method quickly degrades as soon as more than 95% of the weights are set to zero. In fact, this susceptibility forced related works to prune the final FCL only to 90% [52]. In contrast, our method remains accurate in high sparsity regimes: the codebooks store only
Table 12
Comparison of BCF with pruning of final FCL weights of a pretrained MobileNetV2 on ImageNet-1K
| Approach | Zero elements (%) | Accuracy (%) |
| Baseline | – | |
| BCF | 99.98 | |
| FCL pruning | 80.00 | 71.13 |
| 90.00 | 70.44 | |
| 95.00 | 69.48 | |
| 99.00 | 65.82 | |
| 99.98 | 18.38 |
References
[1] | G. Bent, C. Simpkin, Y. Li and A. Preece, Hyperdimensional computing using time-to-spike neuromorphic circuits, in: International Joint Conference on Neural Networks (IJCNN), (2022) . |
[2] | Y. Cui, S. Ahmad and J. Hawkins, The HTM spatial pooler – a neocortical algorithm for online sparse distributed coding, Frontiers in Computational Neuroscience 11: ((2017) ). doi:10.3389/fncom.2017.00111. |
[3] | J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li and L. Fei-Fei, Imagenet: A large-scale hierarchical image database, in: IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2009) , pp. 248–255. |
[4] | J. Deng, J. Guo, N. Xue and S. Zafeiriou, ArcFace: Additive angular margin loss for deep face recognition, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2019) , pp. 4690–4699. |
[5] | A. Desai, L. Chou and A. Shrivastava, Random Offset Block Embedding (ROBE) for compressed embedding tables in deep learning recommendation systems, Proceedings of Machine Learning and Systems 4: ((2022) ), 762–778. |
[6] | B. Emruli, R.W. Gayler and F. Sandin, Analogical mapping and inference with binary spatter codes and sparse distributed memory, in: International Joint Conference on Neural Networks (IJCNN), (2013) . |
[7] | E.P. Frady, S.J. Kent, B.A. Olshausen and F.T. Sommer, Resonator networks, 1: An efficient solution for factoring high-dimensional, distributed representations of data structures, Neural Computation 32: (12) ((2020) ), 2311–2331. doi:10.1162/neco_a_01331. |
[8] | E.P. Frady, D. Kleyko and F.T. Sommer, Variable binding for sparse distributed representations: Theory and applications, IEEE Transactions on Neural Networks and Learning Systems ((2021) ). |
[9] | A. Ganesan, H. Gao, S. Gandhi, E. Raff, T. Oates, J. Holt and M. McLean, Learning with holographic reduced representations, in: Advances in Neural Information Processing Systems (NeurIPS), (2021) . |
[10] | R.W. Gayler, Multiplicative binding, representation operators & analogy, in: Advances in Analogy Research: Integration of Theory and Data from the Cognitive, Computational, and Neural Sciences, (1998) . |
[11] | R.W. Gayler, Vector symbolic architectures answer Jackendoff’s challenges for cognitive neuroscience, in: Joint International Conference on Cognitive Science (ICCS/ASCS), (2003) , pp. 133–138. |
[12] | R.W. Gayler and S.D. Levy, A distributed basis for analogical mapping, in: New Frontiers in Analogy Research: Proceedings of the Second International Analogy Conference-Analogy, (2009) . |
[13] | M. Geva, R. Schuster, J. Berant and O. Levy, Transformer feed-forward layers are key-value memories, in: Conference on Empirical Methods in Natural Language Processing, (2021) . |
[14] | V. Gripon and C. Berrou, Sparse neural networks with large learning diversity, IEEE Transactions on Neural Networks 22: (7) ((2011) ), 1087–1096. doi:10.1109/TNN.2011.2146789. |
[15] | K. He, X. Zhang, S. Ren and J. Sun, Deep residual learning for image recognition, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2016) , pp. 770–778. |
[16] | M. Hersche, G. Karunaratne, G. Cherubini, L. Benini, A. Sebastian and A. Rahimi, Constrained few-shot class-incremental learning, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (2022) , pp. 9057–9067. |
[17] | M. Hersche, Z. Opala, G. Karunaratne, A. Sebastian and A. Rahimi, Decoding superpositions of bound symbols represented by distributed representations, in: Proceedings of the 17th International Workshop on Neural-Symbolic Learning and Reasoning (NeSy), (2023) . |
[18] | M. Hersche, M. Zeqiri, L. Benini, A. Sebastian and A. Rahimi, A neuro-vector-symbolic architecture for solving Raven’s progressive matrices, Nature Machine Intelligence ((2023) ), 1–13. |
[19] | M. Hersche, M. Zeqiri, L. Benini, A. Sebastian and A. Rahimi, Solving Raven’s progressive matrices via a neuro-vector-symbolic architecture, in: Proceedings of the 17th International Workshop on Neural-Symbolic Learning and Reasoning (NeSy), (2023) . |
[20] | E. Hoffer, I. Hubara and D. Soudry, Fix your classifier: The marginal value of training the last weight layer, in: International Conference on Learning Representations (ICLR), (2018) . |
[21] | P. Kanerva, Large patterns make great symbols: An example of learning from example, in: Hybrid Neural Systems, S. Wermter and R. Sun, eds, Springer, Berlin Heidelberg, (2000) , pp. 194–203. ISBN 978-3-540-46417-4. doi:10.1007/10719871_13. |
[22] | P. Kanerva, Hyperdimensional computing: An introduction to computing in distributed representation with high-dimensional random vectors, Cognitive Computation 1: (2) ((2009) ), 139–159. doi:10.1007/s12559-009-9009-8. |
[23] | S.J. Kent, E.P. Frady, F.T. Sommer and B.A. Olshausen, Resonator networks, 2: Factorization performance and capacity compared to optimization-based methods, Neural Computation 32: (12) ((2020) ), 2332–2388. doi:10.1162/neco_a_01329. |
[24] | D. Kleyko, D.A. Rachkovskij, E. Osipov and A. Rahimi, A survey on hyperdimensional computing aka vector symbolic architectures, part I: Models and data transformations, ACM Comput. Surv. ((2022) ). |
[25] | D. Kleyko, A. Rahimi, D.A. Rachkovskij, E. Osipov and J.M. Rabaey, Classification and recall with binary hyperdimensional computing: Tradeoffs in choice of density and mapping characteristics, IEEE Transactions on Neural Networks and Learning Systems 29: (12) ((2018) ). |
[26] | A. Knoblauch and G. Palm, Iterative retrieval and block coding in autoassociative and heteroassociative memory, Neural Computation 32: (1) ((2020) ), 205–260. doi:10.1162/neco_a_01247. |
[27] | A. Krizhevsky, Learning multiple layers of features from tiny images, (2009) . |
[28] | C.J. Kymn, S. Mazelet, A. Ng, D. Kleyko and B.A. Olshausen, Compositional factorization of visual scenes with convolutional sparse coding and resonator networks, (2024) , arXiv preprint arXiv:2404.19126. |
[29] | M. Laiho, J.H. Poikonen, P. Kanerva and E. Lehtonen, High-dimensional computing with sparse vectors, in: 2015 IEEE Biomedical Circuits and Systems Conference (BioCAS), (2015) . |
[30] | G. Lample, A. Sablayrolles, M.A. Ranzato, L. Denoyer and H. Jegou, Large memory layers with product keys, in: Advances in Neural Information Processing Systems (NeurIPS), (2019) . |
[31] | J. Langenegger, G. Karunaratne, M. Hersche, L. Benini, A. Sebastian and A. Rahimi, In-memory factorization of holographic perceptual representations, Nature Nanotechnology ((2023) ). |
[32] | M. Ledoux, The Concentration of Measure Phenomenon, American Mathematical Society, (2001) . |
[33] | J. Liu, W.-C. Chang, Y. Wu and Y. Yang, Deep learning for extreme multi-label text classification, in: International ACM SIGIR Conference on Research and Development in Information Retrieval, (2017) . |
[34] | I. Loshchilov and F. Hutter, SGDR: Stochastic gradient descent with warm restarts, (2016) , arXiv preprint arXiv:1608.03983. |
[35] | N. Ma, X. Zhang, H.-T. Zheng and J. Sun, ShuffleNet V2: Practical guidelines for efficient CNN architecture design, in: Proceedings of the European Conference on Computer Vision (ECCV), (2018) . |
[36] | N.Y. Masse, G.C. Turner and G.S.X.E. Jefferis, Olfactory information processing in drosophila, Current Biology 19: (16) ((2009) ). |
[37] | P. Mettes, E. van der Pol and C. Snoek, Hyperspherical prototype networks, Advances in Neural Information Processing Systems (NeurIPS) 32: ((2019) ). |
[38] | B.A. Olshausen and D.J. Field, Natural image statistics and efficient coding, Network: Computation in Neural Systems 7: (2) ((1996) ), 333–339. doi:10.1088/0954-898X_7_2_014. |
[39] | T.A. Plate, Holographic reduced representations, IEEE Transactions on Neural Networks 6: (3) ((1995) ), 623–641. doi:10.1109/72.377968. |
[40] | T.A. Plate, Analogy Retrieval and Processing with Distributed Vector Representations, Expert Systems, (2000) . |
[41] | T.A. Plate, Holographic Reduced Representations: Distributed Representation for Cognitive Structures, Center for the Study of Language and Information, Stanford, (2003) . |
[42] | Z. Qian, T.L. Hayes, K. Kafle and C. Kanan, Do we need fully connected output layers in convolutional networks? (2020) , arXiv preprint arXiv:2004.13587. |
[43] | D.A. Rachkovskij and E.M. Kussul, Binding and normalization of binary sparse distributed representations by context-dependent thinning, Neural Computation 13: (2) ((2001) ), 411–452. doi:10.1162/089976601300014592. |
[44] | H. Ramsauer, B. Schäfl, J. Lehner, P. Seidl, M. Widrich, L. Gruber, M. Holzleitner, T. Adler, D. Kreil, M.K. Kopp, G. Klambauer, J. Brandstetter and S. Hochreiter, Hopfield networks is all you need, in: International Conference on Learning Representations (ICLR), (2021) . |
[45] | D. Rasmussen and C. Eliasmith, A neural model of rule generation in inductive reasoning, Topics in Cognitive Science 3: (1) ((2011) ), 140–153. doi:10.1111/j.1756-8765.2010.01127.x. |
[46] | A. Renner, Y. Sandamirskaya, F.T. Sommer and E.P. Frady, Sparse vector binding on spiking neuromorphic hardware using synaptic delays, in: International Conference on Neuromorphic Systems (ICONS), (2022) . |
[47] | A. Renner, L. Supic, A. Danielescu, G. Indiveri, B.A. Olshausen, Y. Sandamirskaya, F.T. Sommer and E.P. Frady, Neuromorphic visual scene understanding with resonator networks, (2024) , Nature Machine Intelligence 641–652. |
[48] | S. Ruffino, G. Karunaratne, M. Hersche, L. Benini, A. Sebastian and A. Rahimi, Zero-shot classification using hyperdimensional computing, in: 2024 Design, Automation and Test in Europe Conference and Exhibition (DATE), IEEE, (2024) . |
[49] | M.S.E. Saadabadi, A. Dabouei, S.R. Malakshan and N.M. Nasrabad, Hyperspherical Classification with Dynamic Label-to-Prototype Assignment, (2024) , arXiv preprint arXiv:2403.16937. |
[50] | M. Sandler, A. Howard, M. Zhu, A. Zhmoginov and L.-C. Chen, MobileNetV2: Inverted residuals and linear bottlenecks, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2018) . |
[51] | K. Schlegel, P. Neubert and P. Protzel, A comparison of vector symbolic architectures, Artificial Intelligence Review 55: (6) ((2022) ), 4523–4555. doi:10.1007/s10462-021-10110-3. |
[52] | J. Schwarz, S. Jayakumar, R. Pascanu, P.E. Latham and Y. Teh, Powerpropagation: A sparsity inducing weight reparameterisation, Advances in Neural Information Processing Systems (NeurIPS) 34: ((2021) ), 28889–28903. |
[53] | T.R. Scott, A.C. Gallagher and M.C. Mozer, von Mises-Fisher loss: An exploration of embedding geometries for supervised learning, in: Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), (2021) . |
[54] | G. Shalev, G.L. Shalev and Y. Keshet, Redesigning the Classification Layer by Randomizing the Class Representation Vectors, (2021) , arXiv preprint arXiv:2011.08704. |
[55] | J. Snoek, H. Larochelle and R.P. Adams, Practical Bayesian optimization of machine learning algorithms, Advances in Neural Information Processing systems (NeurIPS) 25: ((2012) ). |
[56] | A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A.N. Gomez, Ł. Kaiser and I. Polosukhin, Attention is all you need, Advances in Neural Information Processing Systems (NeurIPS) 30: ((2017) ). |
[57] | C. Wah, S. Branson, P. Welinder, P. Perona and S. Belongie, The Caltech-UCSD Birds-200-2011 Dataset, (2011) . |
[58] | D.J. Willshaw, O.P. Buneman and H.C. Longuet-Higgins, Non-holographic associative memory, Nature 222: (5197) ((1969) ), 960–962. doi:10.1038/222960a0. |
[59] | C. Zhang, F. Gao, B. Jia, Y. Zhu and S.-C. Zhu, RAVEN: A dataset for relational and analogical visual REasoNing, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2019) . |
[60] | X. Zhang, R. Zhao, Y. Qiao, X. Wang and H. Li, AdaCos: Adaptively scaling cosine logits for effectively learning deep face representations, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (2019) . |
[61] | M. Zhu and S. Gupta, To prune, or not to prune: exploring the efficacy of pruning for model compression, (2017) , arXiv preprint arXiv:1710.01878. |
[62] | Z. Zhu, T. Ding, J. Zhou, X. Li, C. You, J. Sulam and Q. Qu, A geometric analysis of neural collapse with unconstrained features, in: Advances in Neural Information Processing Systems (NeurIPS), (2021) . |
[63] | T. Zhuo and M. Kankanhalli, Solving Raven’s Progressive Matrices with Neural Networks, (2020) , arXiv preprint arXiv:2002.01646. |




