Inconsistencies in countries COVID-19 data revealed by Benford’s law

1.Introduction

COVID-19 outbreak was declared as a Public Health Emergency of International Concern by World Health Organization (WHO) in January, 30th. As the outbreak gained pandemic proportions, many efforts to test communities and to report positive cases have been carried out by almost every country. Data on daily new cases and deaths of COVID-19, among other information provided by countries health authorities, represent one of the main tools for analyzing the disease dynamics and to compare distinct mitigation strategies carried out by each country. However, it is undoubted that registration and reporting of COVID-19 new cases and deaths may be biased by many political and economic factors, causing both intentional and unintentional errors.

Benford’s Law (also called “first digit phenomenon”) is a statistical phenomenon that describes the frequency of a given integer, from 1 to 9, to be in the first significant digit in the numbers of a large data set. This phenomenon was discovered by Simon Newcomb in 1881 (Newcomb, 1881) and rediscovered and detailed by Frank Benford in 1938 (Benford, 1938). The law states that the expected proportion of numbers in a data set that have a leading digit “n” is an exponential distribution given by:

The Benford’s law has been most practically used to detect fraud or rounding errors in real world numbers. This is possible by examining departures in the frequencies of individual digits from those predicted by Benford. This only makes sense once it is established (often empirically) that the data follow the law under normal circumstances (Sambridge et al., 2011). This is true because human pseudo-random productions are in many ways different from true randomness (Nickerson, 2002). As a consequence, fabricated data might fit to the Benford’s Law to a lesser extent than genuine data (Banks & Hill, 1974; Gauvrit et al., 2017).

Many real-world data sets were shown to conform to this distribution, including the distance between earth and known stars (Alexopoulos & Leontsinis, 2014) or exoplanets (Aron, 2013), crime statistics (Hickman & Rice, 2010), the number of daily-recorded religious activities (Mir, 2014), earthquake depths (Sambridge et al., 2011), interventional radiology dose-area product data (Cournane et al., 2014), financial variables (Clippe & Ausloos, 2012), and internet traffic data (Arshadi & Jahangir, 2014). As pseudo-random numbers generated by humans often fail to conform to Benford’s law, it has been extensively used to detect fabricated data (Gauvrit et al., 2017), including frauds in international trade (Cerioli et al., 2019; Lacasa, 2019), money laundering (Badal-Valero et al., 2018), falsified science articles (Hüllemann et al., 2017), irregularity in payment for medical services (Park et al., 2016), etc.

Figure 1.

First digit density distribution of daily new cases data from countries that indubitably conform to the Benford’s law (p> 0.05). Each bar represents the density probability of a given number, from 1 to 9, to be in the first digit position in the data set of daily new cases. Red curve represents the density of Benford’s distribution (Eq. (1)). RMSD, log (Likelihood) and Chi-square tests were calculated comparing those two distribution (see Material and Methods). Countries in this Figure are Afghanistan, Armenia, Austria, Belgium, Bolivia, Bulgaria, Canada, China, Costa Rica, Croatia, Czech Republic, Denmark, Dominican Republic, Ethiopia, France, Georgia, Germany, Ghana, Guatemala, Hungary, Ireland, Israel, Italy, Jordan, Kazakhstan, Kyrgyzstan, Lebanon, Libya, Moldova, Morocco, Myanmar, Nepal, Netherlands, Oman, Paraguay, Portugal, Singapore, Slovakia, Slovenia, South Africa, Spain, Sweden, Switzerland, Tunisia, United Arab Emirates, United Kingdom and Venezuela.

Figure 2.

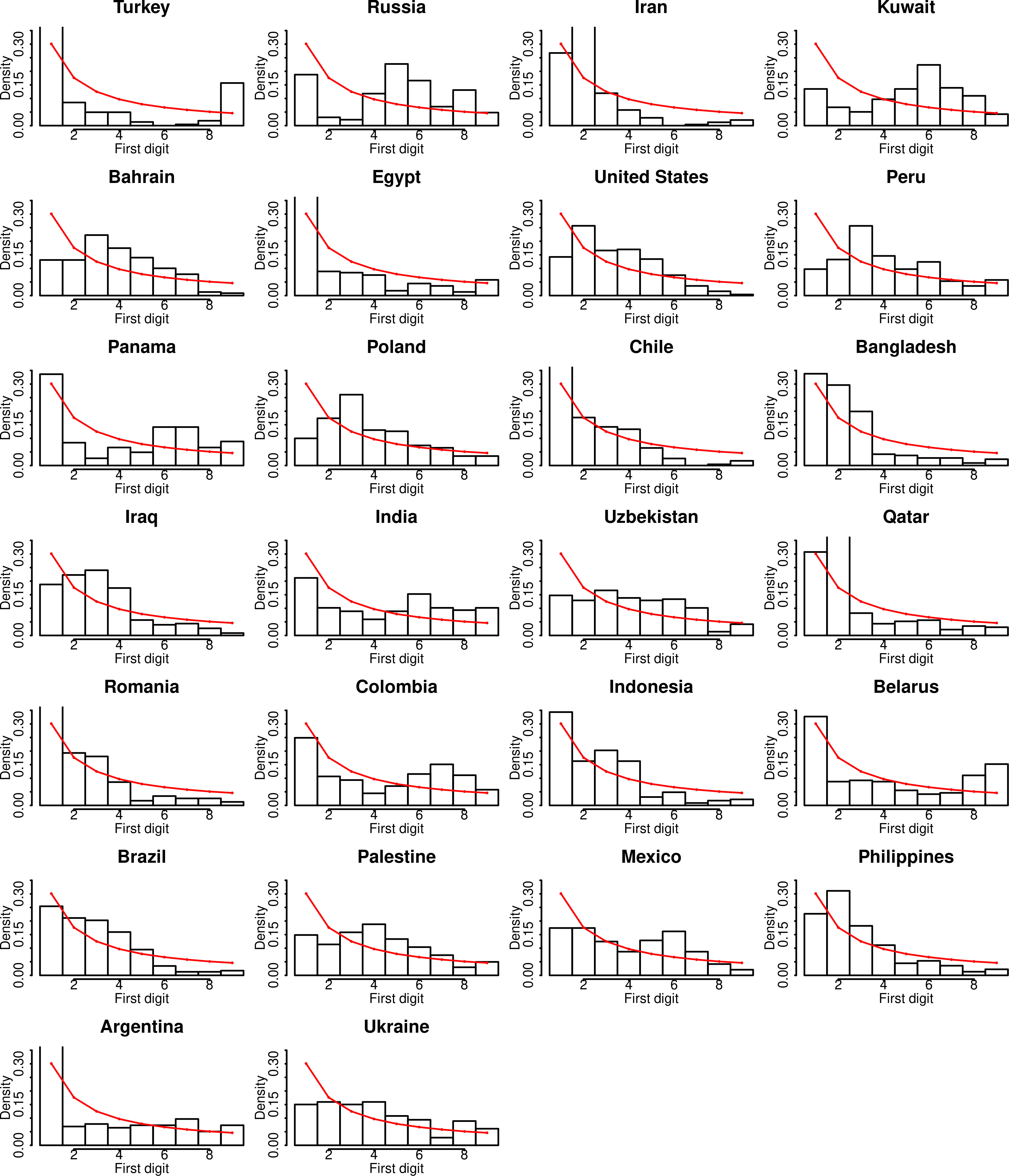
First digit density distribution of daily new cases data from countries that clearly do not conform to the Benford’s law (p< 0.01). Each bar represents the density probability of a given number, from 1 to 9, to be in the first digit position in the data set of daily new cases. Red curve represents the density of Benford’s distribution (Eq. (1)). RMSD, log (Likelihood) and Chi-square tests were calculated comparing those two distribution (see Material and Methods). Countries in this Figure are Argentina, Bahrain, Bangladesh, Belarus, Brazil, Chile, Colombia, Egypt, India, Indonesia, Iran, Iraq, Kuwait, Mexico, Palestine, Panama, Peru, Philippines, Poland, Qatar, Romania, Russia, Turkey, Ukraine, United States and Uzbekistan.

Here, we used the Benford’s law to analyze a data set of daily new cases of COVID-19 reported by 80 countries. Data analysis were carried out by root mean square deviation (RMSD), Likelihood of the fitted data and Chi-square test. Benford’s law may be an efficient screening methods for detecting fraudulent or misconducting procedures in the COVID-19 data collection, compilation and reporting.

2.Materials and methods

Data sets containing the number of daily new cases from every country were extracted from Our World in Data project (Roser et al., 2020) as comma-spaced values (CSV) files, processed with R (R Core Team, 2013), using Rstudio 1.2.5042 (RStudio Team, 2020) for Linux. Data sets used in this work contained information on the number of daily new cases by day, for each country, since the very first registered COVID-19 case, in date-integer formats. Depending on the date in which the first case was registered, the number of positive (not zero) registers for each country varies from 156 to 280 date-cases pairs (median = 225). Countries with less than 150 positive daily registers were removed from the data analysis because the Chi-square test produced uncertain results (data not shown).

Data were subset to select countries that registered more than 1,000 cases in, at least, one single day. This sub setting was performed because real-world data sets that ranges for more than three orders of magnitude conform better to the Benford’s law than those that ranges for just one or two orders of magnitude (Fewster, 2009). First digits of every register in the data set were counted and stored for each studied country. Densities of Benford’s distribution among integer numbers were calculated from Eq. (1) to give the following proportions for each number, from 1 to 9, respectively: 0.301, 0.176, 0.125, 0.097, 0.079, 0.067, 0.058, 0.051 and 0.046. Root mean square deviation (RMSD), log of the Likelihood and Chi-square tests were calculated comparing the first digit distribution of each country (Figs 1 and 2, bars) with the Benford’s distribution (Figs 1 and 2, lines).

RMSD were calculated with a simple math routine in R and the log of Likelihoods were calculated as the “goodness-of-fit” of first digit distribution within Benford’s distribution as product of the single likelihoods of each data point, taking a normal distribution with the Benford’s density as mean and the standard deviation of the country’s first digit distribution.

Chi-square tests were performed with the R function “chisq.test”.

All procedures, data retrieving and manipulation, as well as graphics plotting can be reproduced using the R script “moreau.benford.r” available at Code Ocean (codeocean.com).

3.Results

A data set containing the daily number of cases registered and reported by countries (owid-covid-data.csv) was retrieved from Our World in Data project (Roser et al., 2020) and processed in order to evaluate their conformity to the Benford’s law. Countries that have not presented more than 1,000 cases in a single day, as well as those ones that presented less than 150 positive daily registries were excluded from the processed data set, as described in Material and Methods. Histograms depicting density distributions were built and plot together to the Benford’s density distribution. Figure 1 shows the first digit density distributions for countries in which the COVID-19 daily new cases data clearly conform to the Benford’s law (p> 0.05) as evaluated by Chi-square test. 47 countries are in this condition: Afghanistan, Armenia, Austria, Belgium, Bolivia, Bulgaria, Canada, China, Costa Rica, Croatia, Czech Republic, Denmark, Dominican Republic, Ethiopia, France, Georgia, Germany, Ghana, Guatemala, Hungary, Ireland, Israel, Italy, Jordan, Kazakhstan, Kyrgyzstan, Lebanon, Libya, Moldova, Morocco, Myanmar, Nepal, Netherlands, Oman, Paraguay, Portugal, Singapore, Slovakia, Slovenia, South Africa, Spain, Sweden, Switzerland, Tunisia, United Arab Emirates, United Kingdom and Venezuela.

Figure 2 shows first digit density distributions for countries in which the COVID-19 daily new cases data clearly do not conform to the Benford’s law (p< 0.01) as evaluated by Chi-square test. 26 countries are in this condition: Argentina, Bahrain, Bangladesh, Belarus, Brazil, Chile, Colombia, Egypt, India, Indonesia, Iran, Iraq, Kuwait, Mexico, Palestine, Panama, Peru, Philippines, Poland, Qatar, Romania, Russia, Turkey, Ukraine, United States and Uzbekistan.

Eight countries layed in the group with disputable evidences to be in conformity to the Benford’s law, as evaluated by the Chi-square test (p< 0.05, but p> 0.01): Bosnia and Herzegovina, Ecuador, Honduras, Japan, Pakistan, Puerto Rico, Saudi Arabia and United Arab Emirates.

Analysis of conformity to the Benford’s law were carried out by calculating RMSDs, Likelihoods em Chi-square tests for data of each country (bars), in comparison to the proportions of the Benford’s distribution (lines). Table 1 summarizes the calculated parameters for each country, sorted by the RMSD. As shown, countries with the highest 20 RMSD values presented p< 0.01 in Chi-square test.

Figure 3.

Correlation between RMSD and log (Likelihood) calculated by fitting of the first digit distribution of daily new cases data from studied countries into the Benford’s distribution (Eq. (1)). The line traces the linear regression (R2= 0.6254). White stars over the symbols represent countries in which data clearly have not conformed to the Benford’s law, as evaluated by Chi-square tests (p< 0.01).

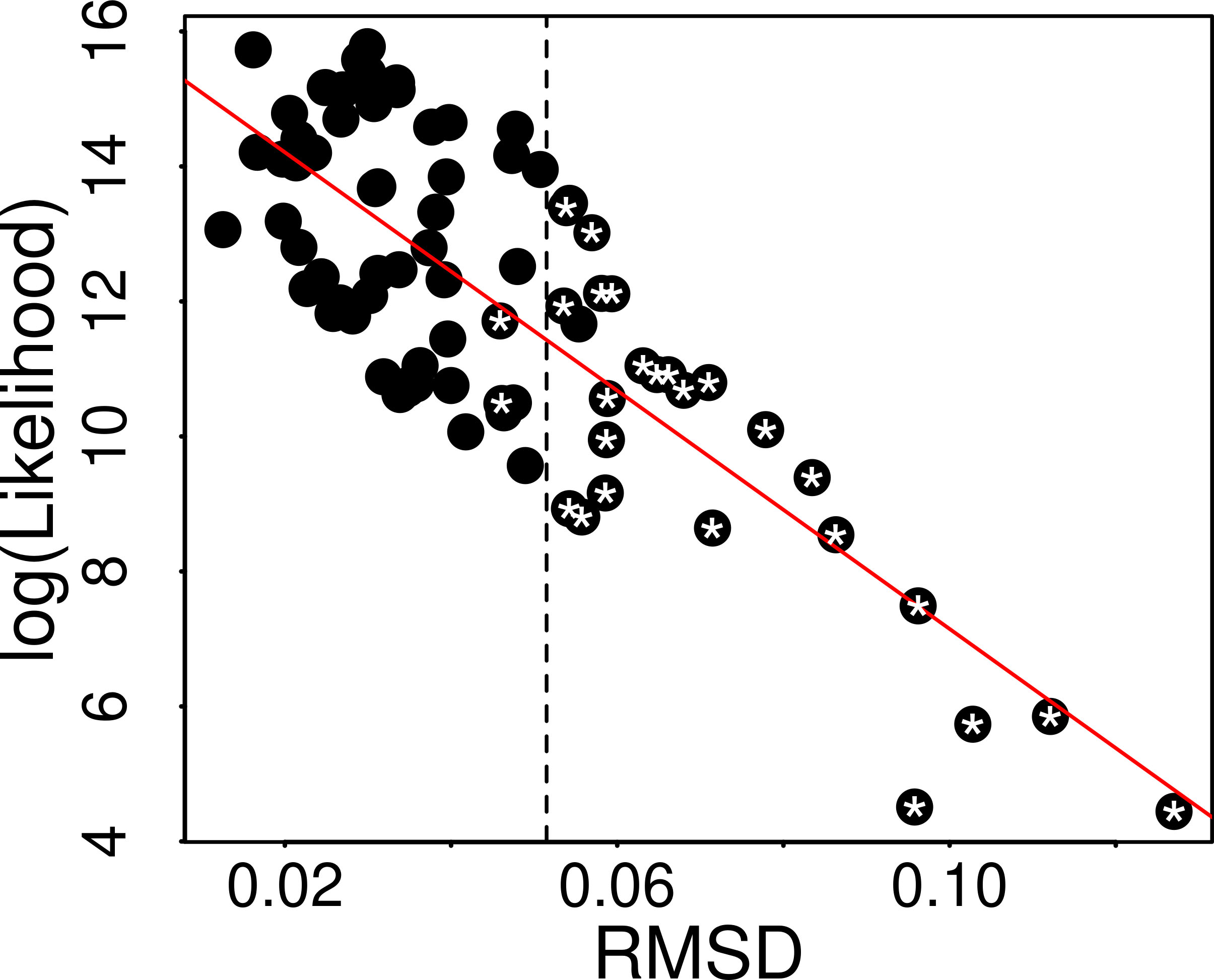
Figure 3 shows the correlation between RMSD and log (Likelihood) for studied countries. As Shown, there is a good correlation between these two parameters (R2= 0.6299). Additionally, Chi-square test demonstrated non-depedence to the Benford’s distribution (p< 0.01) in most of those countries that have higher RMSD (data points marked with white stars). The vertical dashed line drawn in Fig. 3 indicates RMSD = 0.051. With exception of four countries, every country in which the data clearly has not conformed to the Benford’s law, as evaluated by the Chi-square test (p< 0.01), has also presented RMSD higher than 0.051 (Fig. 3). However in a small extension, there is a good correlation between log of Likelihoods and Chi-square test too (data not shown). Although each country presented different number of registers, i. e., distinct number of dates with daily new cases registered, what could account to the differences observed among the conformity of their data to the Benford’s law, no correlation between the number of positive registers and RMSD (R2=-0.1116), log of the Likelihoods (R2=-0.0597) or p (R2= 0.0840) could be observed.

4.Discussion

Although a good accordance between Chi-square tests, log of Likelihoods and RMSD of the analysis of data conformity of countries daily new cases of COVID-19 to the Benford’s law could be observed, some divergences were noted from those three analytical tools. For instance, data from Bosnia and Herzegovina and Puerto Rico presented RMSD values above 0.051 (dashed vertical line in Fig. 3), though the result of Chi-square tests rejected the hypothesis of non association to the Benford’s law (p> 0.01; Table 1). On the other hand, data from Brazil and Indonesia presented RMSD values below 0.051, though the Chi-square tests did not rejected the non association hypothesis to the Benford’s law (P< 0.01). We were not able, from the present data analysis, to determine what was the origin of such divergences and more detailed studies must be performed on this issue in order to reach this objective.

Data on the daily new cases of COVID-19 from 26 countries clearly have not conformed to the Benford’s law, as evaluated by Chi-square test (p< 0.01). In addition, cluster analysis of all the 80 countries data denoted a good correlation among the three used parameters. Countries in which the data display severe non conformity to the Benford’s law detected by Chi-square test presented high RMSD from Benford distribution and, also, low Likelihoods (Fig. 3). These results suggest that Chi-square, RMSD and Likelihood converge to act together as affordable tools to evaluate the conformity of the COVID-19 daily new cases data to the Benford’s law.

Benford’s analysis has been used to evaluate COVID-19 data in a preprint paper (Wei & Vellwock, 2020) that evaluates the “Benfordness” using the Euclidian distance between the country numbers and Benford’s distribution - what was called “d-factor”. Although Euclidian distance is not a hypothesis test, the authors argued that a d-factor smaller than 0.25 – an arbitrarily set value - denotes conformity to the Benford’s law. Here, I used Chi-square test, which I believe to be more likely to be used - such it is a hypothesis test. Additionally, the present data have shown good correlation between Chi-square test and RMSD for the used data sets, reinforcing its use.

Results presented here open room to the possibility of data corruption in the reported data of COVID-19 from many countries. Specially in those countries where the lack of democratic principles can restrain the free access to information, both economic and political criteria might superimpose technical and scientific ones. This data corruption may exert a huge impact on the decision taking and on the management of COVID-19 pandemic all over the world.

5.Disclosure statement

Author declare no commercial associations that might create a conflict of interest in connection with submitted manuscripts.