Polarity and Variable Selection Heuristics for SAT-Based Anytime MaxSAT

1.Introduction

Weighted Partial MaxSAT (known simply as MaxSAT) is a well-studied optimization problem having a plethora of applications [11,14,18].

A MaxSAT instance comprises a set of hard satisfiable clauses H and a set of n weighted soft clauses T={tn−1,tn−2,…,t0}, where each soft clause ti is associated with a strictly positive integer weight wi. The weight of a variable assignment (model) μ is w(T,μ)=∑i=0n−1¬μ(ti)×wi, that is, the overall weight of T’s bits, falsified by μ. The expected output of a MaxSAT algorithm is a model having the minimum possible weight. For the rest of this paper, for convenience and without restricting generality, it is assumed that every soft clause is a unit clause (an arbitrary soft clause C can be transformed into a unit clause v′, where v′ is a fresh variable, by adding the clause ¬v′∨C to H). Thus, the set of the soft clauses T can be thought of as a bit-vector, where t0 is its Least Significant Bit (LSB) and tn−1 is its Most Significant Bit (MSB). T is called the target bit-vector, or, simply, the target and every ti∈T is called a target bit.

Anytime MaxSAT algorithms are expected to find an improving set of models {μ1,μ2,…,μn} over time, that is, for every j>i, it must hold that w(T,μj)<w(T,μi). The anytime property can be critical for industrial usage because it allows users to get an approximate solution even for very difficult instances [14]. Anytime MaxSAT algorithms have been evaluated at MaxSAT Evaluations since 2011, when the so-called incomplete tracks emerged.

Most existing anytime MaxSAT algorithms apply an incremental SAT solver to find an improving set of models. Typically, the first model μ1 is found by applying the SAT solver over the hard clauses only. Then, different strategies are used, depending on the algorithm. Consider, for example, the Linear Search SAT-UNSAT (LSU) algorithm [10]. After LSU finds each new model, it blocks all the solutions of weight ⩾w(T,μi) using Pseudo-Boolean (PB) or cardinality constraints and invokes the SAT solver again to find a better model. Other examples are the recently introduced Open-WBO-Inc-BMO [8] and WMB [14] algorithms that guide the solver towards better models by approximating MaxSAT with Bounded Multilevel Optimization (BMO) [3] and Bit-Vector Optimization (OBV) [15], respectively.

This paper serves as a system description of the anytime MaxSAT solver TT-Open-WBOInc, which won the 60-second and the 300-second incomplete tracks of MaxSAT Evaluation 2019 (MSE19). TT-Open-WBO-Inc was created by applying a few simple modifications to the BMO-based Open-WBO-Inc-BMO algorithm in the open-source solver Open-WBO-Inc [9]. Specifically, we implemented the Target-Optimum-Rest-Conservative (TORC) polarity selection heuristic and a modified version of the Target-Score-Bump (TSB) variable selection heuristic. Both TORC and TSB were recently introduced in [14]. Despite the simplicity of our modifications, the solver became substantially more efficient. In principle, both heuristics are applicable to any SAT-based anytime MaxSAT algorithm. We chose to implement them in Open-WBO-Inc-BMO because it is a relatively simple high-performing anytime algorithm, implemented in an open-source solver.

The contributions of this work are as follows. First, our implementation of TORC and TSB is open-sourced, whereas the original implementation in [14] is closed-sourced. Second, our results confirm the usefulness of both heuristics in an independent implementation. Third, we introduce some improvements to the original TSB heuristic. Fourth, we provide an empirical comparison of the impact of various heuristics on the Open-WBO-Inc-BMO algorithm within the Open-WBO-Inc solver.

The rest of this paper is organized as follows. Section 2 reviews polarity selection heuristics for anytime SAT-based MaxSAT (including TORC). Section 3 is about TSB. Section 4 is dedicated to experimental results. Section 5 concludes our work.

2.Polarity Selection for Anytime MaxSAT

Recall that modern SAT solvers apply phase saving [16] as their polarity selection heuristic. In phase saving, after the variable decision heuristic picks a variable, the literal is chosen according to its latest value. As we review below, it has been shown that overriding phase saving in the context of anytime MaxSAT is advantageous [2,5,7,14,17].

Let v be a variable. Fixing the value of v to σ∈{0,1} means assigning v the value σ whenever v is chosen by the SAT solver’s decision strategy. Fixing the values of all the variables to some assignment ρ causes the SAT solver to carry out a local search near ρ [5], hence any encountered model is likely to be highly similar to ρ. This observation was first used to guide a SAT solver to generate a solution near a given assignment in [1,13] in the context of generating diverse solutions in SAT.

The best-performing polarity selection heuristics for anytime MaxSAT take advantage of the fixing technique. The optimistic approach [7] fixes the polarity of the target bits to 1. This strategy works well when the actual solution is close to an ideal assignment (where an assignment is ideal iff it assigns 1 to all the target bits). The conservative approach [2,5,17] fixes the polarity of all the variables to the previous best solution, and thus the solver looks for a solution near the previous best one (applicable only after μ1 is found).

Target-Optimum-Rest-Conservative (TORC) [14] polarity selection heuristic was designed to leverage the best of both the conservative and the optimistic approaches. Before the initial SAT invocation, TORC fixes the polarity of all the target variables to 1. Then, after each new improving model μi is encountered, the polarity of all the non-target variables is fixed to their values in μi. In other words, whenever the variable decision heuristic chooses: a) A target variable: TORC sets its polarity to 1 (to be optimistic). b) A non-target variable: TORC sets its polarity to its value in the best model so far (to be conservative; only after the first SAT invocation is completed). Note that after the initial SAT call, TORC sets the polarity every time a new decision variable is picked. TORC was shown to significantly outperform other polarity selection heuristics in [14]. Our experiments, described in Section 4, confirm this result.

It is also possible to apply a weaker version of fixing the polarity selection by setting the polarity of variables to a certain value only once before each SAT invocation [10,15], but such an approach is less efficient in the context of anytime MaxSAT [14].

3.Target-Score-Bump (TSB) Decision Heuristic

Target-Score-Bump (TSB) [14] is a modification to the SAT solver’s variable selection heuristic for anytime SAT-based MaxSAT.

Since the introduction of the VSIDS variable decision heuristic [12], modern SAT solvers associate a score with each variable. The decision strategy prefers variables with greater scores. VSIDS increases the scores for variables participating in the derivation of a new conflict clause. It is also possible to alter the reward mechanism. For example, Glucose [4] bumps up the score twice for any variable, propagated in a clause having a small LBD value. All scores are decayed over time to give preference to variables that participated in recent conflicts.

TSBbumps up the variable scores of target bit variables, so as to improve their chances of being picked early. In [14], for each target bit variable, the score is bumped as if the variable participated in a conflict clause. TSB is applied only once prior to the initial SAT invocation. The intuition is that applying it in conjunction with TORC should improve the likelihood of the initial model to be close to an ideal assignment.

In the original TSB implementation, all scores are bumped by the same factor. We implemented TSB in Open-WBO-Inc, which uses Glucose 4.1 [4] as the underlying SAT solver. Glucose has a function varBumpActivity(v,b) that bumps up the score of variable v by bump-up score factor b, where the greater b is the more likely the decision strategy will pick v. Glucose’s decision heuristic initializes the bump-up score factor b to 1. The variable decay strategy is implemented in Glucose by multiplying b by a factor of d after each conflict. Initially, Glucose sets d to 1.25. Glucose’s heuristics change d on-the-fly. More specifically, d is periodically decreased until it reaches the threshold value of 1÷0.95, unless Glucose’s adaptive strategy is triggered.

The fact that the bump-up score factor b is modifiable in Glucose can be used to regulate the impact of TSB and to give some preference to target bits having greater weights. Let the minimal weight be min=min(w0,…,wn−1) and the maximal weight be max=max(w0,…,wn−1). For every variable t of target bit literal ti of weight wi, we apply the function varBumpActivity(t,b) prior to the first SAT invocation, where b is:

Both weightBump and varBump are user-given parameters. Based on preliminary experiments on instances from MaxSAT Evaluation 2018 (MSE18), we use weightBump = 113 and varBump = 552. Therefore, the solver bumps up the score of a target bit having the maximal or the minimal weight as if it participated in log1.25(552+113)≈29 or log1.25(552)≈28 conflicts, respectively. Note that even after these first conflicts are derived, target variables that impacted conflict clause derivation are likely to continue to be picked more frequently. A target having a larger weight has an advantage over a target having a smaller weight only at the very beginning of the search. TT-Open-WBO-Inc winning MSE19 is evidence that our magic numbers work well on the MSE19 instances too.

4.Experimental Results

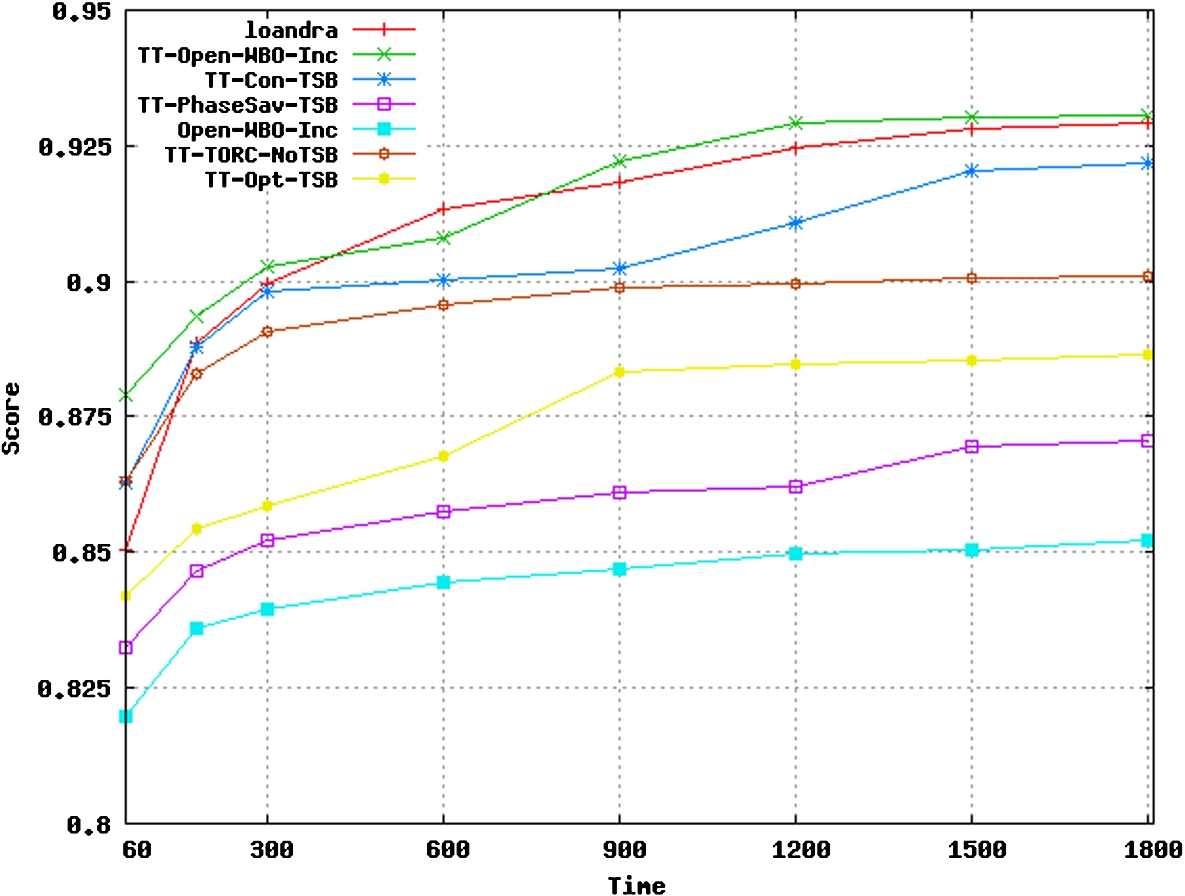
The goal of this section is to study the impact of TORC and TSB on the performance of Open-WBO-Inc-BMO. To carry out our study, we ran several configurations of the Open-WBOInc-BMO algorithm, summarized in Table 1. The first column shows the name of the configuration. The second column displays the polarity selection strategy. The third column specifies whether or not TSB is applied. Comments appear in the last column. In addition, we ran the loandra [6] anytime MaxSAT solver, which came in second after TT-Open-WBO-Inc in both of the weighted incomplete categories at MSE19. loandra combines between complete and anytime algorithms. We used machines with 32 Gb of memory running Intel^® Xeon^® processors with 3 Ghz CPU frequency. We decided to run the solvers for 30 minutes and to measure the average score at the following intervals: 60, 180, 300, 600, 900, 1200, 1500 and 1800. This allowed us to study the performance of the solvers over time. We updated both TT-Open-WBO-Inc and loandra to print out the time of discovery of each new model μi. The code of both solvers as well as instructions on how to reproduce our experiments are available on the journal website. We used benchmarks from the weighted incomplete tracks of MSE18 (the benchmarks from MSE19 were not available at submission time). The criteria for comparing anytime MaxSAT solvers during evaluations is their score, defined as follows for a particular solver S and i instances: ∑i(1+the minimal weight of the unsatisfied target bits found by any participating solver)∕(1+the weight of the unsatisfied target bits found by S). This criteria depends on the participating solvers. Following [14], we decided to calculate an absolute score against the best result, achieved by the top 6 solvers in MSE18 in 24 hours. Hence, we define the score as follows: ∑i(1+the best result of the 6 top solvers in 24 hours)∕(1+the weight of the unsatisfied target bits found by S).

The results are shown in Fig. 1. Several observations can be made: a) TORC is the best polarity heuristic for every timeout. The conservative heuristic is second best, followed by the optimistic heuristic. Phase saving is the least efficient of the polarity heuristics; b) The impact of TSB is positive for every timeout; c) The original Open-WBO-Inc is the less efficient algorithm; d) TT-Open-WBO-Inc is more efficient than loandra for all timeouts but that of 600 seconds. Note that since loandra was created by combining a complete algorithm and an anytime algorithm, our heuristics can be integrated into the anytime component of loandra, potentially making the solver more efficient.

Figure 1.

Comparing the average score of solvers over time.

5.Conclusion

We described the anytime MaxSAT solver TT-Open-WBO-Inc, which won both of the weighted incomplete tracks of MaxSAT Evaluation 2019. TT-Open-WBO-Inc was created by implementing the polarity selection heuristic TORC and a modified version of the variable decision heuristic TSB in the Open-WBO-Inc-BMO algorithm within the open-source SAT-based anytime MaxSAT solver Open-WBO-Inc. Our results provide additional evidence that applying TORC and TSB is expected to be advantageous for anytime MaxSAT and, more broadly, for solving any discrete optimization problem with a SAT-based anytime algorithm.