Optimizing dual energy X-ray image enhancement using a novel hybrid fusion method
Abstract
BACKGROUND:
Airport security is still a main concern for assuring passenger safety and stopping illegal activity. Dual-energy X-ray Imaging (DEXI) is one of the most important technologies for detecting hidden items in passenger luggage. However, noise in DEXI images, arising from various sources such as electronic interference and fluctuations in X-ray intensity, can compromise the effectiveness of object identification.
OBJECTIVE:
To address the challenge of noise interference in DEXI, this study aims to develop and validate a robust denoising technique using the Discrete Wavelet Transform (DWT) and Stationary Wavelet Transform (SWT).
METHODS:
The proposed method targets and removes background and Poisson noise in DEXI images, improving object recognition accuracy. During the denoising process, images are decomposed into several subbands, and thresholding techniques are applied to minimize noise while preserving important information. The images are then reconstructed to provide a cleaner and more accurate depiction of scanned objects.
RESULTS:
Experimental results demonstrate the effectiveness of the DWT and SWT-based denoising strategy in preserving critical data while suppressing noise in DEXI. The performance of the denoising technique is quantified using Peak Signal-to-Noise Ratio (PSNR) and Mean Squared Error (MSE). The proposed system achieved an average PSNR of 35.23 and an MSE of 19.52 for 256×256 DEXI images, and an average PSNR of 36.01 and an MSE of 16.29 for 512×512 DEXI images.
CONCLUSION:
The results highlight the achievement of the proposed approach in enhancing the quality of DEXI for improved security screening, demonstrating its potential application in airport security systems.
1Introduction
In many applications, including airport security screening, dual-energy X-ray imaging (DEXI) has become a vital tool for distinguishing different. Even though DEXI is widely used, noise interference such as background noise and Poisson often impairs its ability to detect objects accurately and dramatically lowers image quality. These difficulties demand for the creation of sophisticated image enhancement methods that can successfully reduce noise while maintaining important image information.
One of the most favorable fields for product quality inspection is image processing, which is developing in attractiveness daily. The tough part of image processing is extracting features from the image and categorizing the object [1–3]. Images, printouts, 3D models, and the necessary data can be processed using image processing techniques [4]. Image processing can reduce computational costs and memory requirements by extracting valuable insights from images.
Conventional image processing methods seem unable to handle massive amounts of image data despite their modest success [5–7]. The concept underlying digital image processing is using digital computers to practice digital images. Digital images are, in fact, a certain arrangement of a small number of components. Each element is referred to as a pixel, image, or image element with a specific location and value. Nowadays, X-ray images are the most frequently utilized images, and the term “pixel” is generally used to refer to any constituent of a digital image [8].
1.1Background
In the real world, X-rays are a form of electromagnetic radiation wave that is widely utilized to capture images of bodily structures via a variety of materials. The image is captured on a computer by the methods listed below. An established technology, X-ray imaging is utilized extensively in a variety of fields, including medical imaging and aviation security. The physics professor Dr. Roentgen is credited with discovering X-rays in 1895 [9]. To ensure public safety at transportation hubs and other high-risk places, object detection for complicated X-ray cargo and X-ray imaging-based baggage inspection have become standard practices [10, 11]. One of the most popular security procedures for preserving airport and transportation security is X-ray imaging security screening, where manual screening by human operators is essential [12–17].
The screening processes for airport security make extensive use of dual-energy X-ray imaging. It is an essential piece of equipment for passenger baggage inspections, allowing security guards to distinguish between various materials easily. This distinction makes it easier to spot forbidden objects and possible security risks. Due to their capability to distinguish between different materials inside passenger baggage, X-ray security scanners based on dual-energy transmission imaging have been used for aviation security screening at ports and airports [18–20]. Dual-energy X-ray imaging is used in the medical field for various purposes, including assessing bone density, vascular imaging, and identifying pathological conditions in organs and tissues. To guarantee accurate diagnosis, treatment planning, and patient care, noise reduction in medical images is essential.
1.2Problem statement
The presence of noise in (DEXI) can be attributed to multiple factors, such as electronic interference, oscillations in X-ray intensity, and inherent constraints of the detection system. The occurrence of noise interferences frequently undermines the efficacy of DEXI, posing a significant challenge in accurately discerning objects. Various forms of noise might conceal crucial features in the images, hindering the accurate detection and categorization of objects during security screening. Much information is contained in these X-ray dual-energy transmission imaging images. The DEXI of 256×256 and 512×512 resolution of low-energy and high-energy images are used for baggage inspection at the Airport for security screening. However, because this information is veiled a little, people are less likely to examine it. More importantly, getting actual changes in information properties like texture, color, intensity, etc, is exceedingly hard.
Therefore, we require an efficient color image segmentation technique to study them. However, the image quality determines how well any color image segmentation algorithm performs. Specifically, during transmission, acquisition, low lighting, or high temperatures, noise is created in the radiography image of the luggage and is typically regarded as undesired [21]. As a result, sounds typically present during the capture, transmission, and image acquisition procedures cause the image quality to decline. As a result, segmenting such noisy images does not yield useful analysis results [22]. Therefore, before going on to the next analytic stage, we require preprocessing techniques to eliminate artefacts, outliers, or, noises in images.
The study integrates in situ X-ray imaging and numerical modeling to analyze damage evolution in C/SiC composites at temperatures up to 1200°C, enhancing understanding of their failure behavior [23]. The fusion of the image and the creation of the fusion rule are the two components of the multiscale decomposition fusion technique, Image Feature Extraction Network (CEFormer) as an enhancement [24, 25]. The research introduces a personalized recommendation model combining Stacked Denoising Auto Encoder and OCEAN personality traits, enhancing accuracy by leveraging user behavior correlations with personality traits [26].
1.3Brief literature review
Wavelet-based image fusion has therefore been developed recently as an image processing technique to integrate complementary information from images since it integrates well into a variety of image fusion techniques [27, 28].
1.4Objectives of the study
Image enhancement is a preprocessing technique in which our goal is to suppress noise while preserving contour integrity and other detailed information [29].
To improve the image, denoising, deblurring, and producing high-quality images are ineffective uses of conventional techniques such as histogram equalization, etc. Thermal radiation information from infrared photos and fine-grained textures from visible images are combined in image fusion [30, 31]. In image fusion, complementary information from both photos is integrated into a single image, combining the high-energy and low-energy images to produce a visually appealing and complex image.
1.5Motivation
The motivation behind this research stems from the need to improve the reliability and accuracy of DEXI in high-security environments. Traditional denoising methods often fail to address the complex noise patterns encountered in X-ray images, leading to suboptimal performance. Therefore, there is a critical need for a robust denoising approach that can enhance image clarity without compromising the integrity of the underlying data.
The novelty of this research lies in the integration of DWT and SWT for dual-energy X-ray image enhancement, a combination that, to the best of our knowledge, has not been previously explored. This approach not only improves noise reduction but also enhances the retention of critical image features, making it particularly valuable for high-stakes applications such as airport security screening.
1.6Contributions of the paper
In this research paper for denoising purposes an image fusion algorithm is used that is Discrete Wavelet Transform (DWT) to remove background and Stationary Wavelet Transform (SWT) to reduce Poisson noises in DEXIs. The proposed DWT and SWT algorithms decompose the developed image into multiple subbands, then apply thresholding techniques to minimize noise while retaining image features, and subsequently reconstructing original and enhanced image. In Experimental results for DWT and SWT-based denoising strategy in DEXI objective metrics like PSNR and MSE measured to check the quality of the enhanced images.
• Innovative Hybrid Image Enhancement Technique: Our proposal involves a combination of Discrete Wavelet Transform (DWT) and Stationary Wavelet Transform (SWT) to remove noise and enhance the clarity of DEXI effectively.
• Thorough Performance Evaluation: We assess the efficiency of the suggested approach using objective measurements like Peak Signal-to-Noise Ratio (PSNR) and Mean Squared Error (MSE), showcasing its higher performance compared to current methods.
• Application to Real-World Scenarios: The improved technique is used on actual X-ray images taken in airport security situations, demonstrating its practical significance in enhancing the accuracy of object identification.
• Enhanced Image Fusion Technique: We propose a novel fusion decision approach in the wavelet domain that improves the quality of the fused image by preserving important image features while efficiently decreasing noise.
2Related work
Over the past two decades, image fusion has evolved into a sophisticated image-processing technique of considerable significance, particularly wavelet-based image fusion, which has emerged as a prominent avenue of research due to its effective integration into various image fusion algorithms [27, 28]. In most instances, wavelet transformations exhibit superior performance compared to traditional approaches in merging images with varying resolutions. Among the most proficient methods for image fusion is the discrete wavelet transform (DWT), surpassing alternative techniques and providing more distinct information [32]. There exist diverse approaches and techniques for carrying out image enhancement. In this context, a methodology relying on the DWT was introduced by a researcher in [33] to mitigate impulse and Poisson noise. They aim to mitigate disturbances such as impulse noise, particle noise, and distorted X-ray images’ sharpness and blurriness. A study in [34] highlighted the utilization of the discrete wavelet transform (DWT) along with an area of interest-based strategy to improve dual-energy X-ray images. The specific interest area within the image was enhanced by applying the area of interest technique, followed by enhanced image quality achieved through wavelet-based fusion [35].
About [36], a novel hybrid framework is introduced to reduce noise in digital color images effectively. This filter combines elements of both Gaussian and impulse noise suppression techniques. A recently developed approach presents a two-stage filtering technique that leverages the principles of quaternion theory to effectively mitigate impulse noise in RGB images [37]. The original technique is introduced, centering on rank-weighted cumulated pixel change measure [38]. This technique is specifically designed to eliminate impulsive noise from color images effectively. It uses the digital route idea to remove impulse pollution from color images [39]. The boundary and centre pixels of a filtering window is connected via the digital path notion.
Pursuant to the fundamental goal of mitigating noise and enhancing X-ray image quality, which holds critical significance for the accurate analysis and behavior of a comprehensive medical environments spectrum, an adaptive image denoising algorithm is strategically implemented [40]. A professional approach is introduced, which utilizes segmentation and classification techniques to identify fractures in X-ray images effectively. The proposed method aims to detect and categorize fractures accurately by employing advanced image segmentation algorithms and classification models [41]. A weighted average filtering technique effectively eliminates both Gaussian and impulse noise from RGB images. The proposed method utilizes a procedure that assigns appropriate weights to the neighboring pixels to achieve efficient noise reduction while preserving the integrity of the image [42].
The author provides a broad review of existing research on the application of X-ray imaging for baggage inspection at airports. It debates various X-ray imaging systems used for detecting dangerous objects within baggage. Additionally, it explores the concept of dual-energy X-ray image fusion and factors related to image enhancement. This paper also delves into different types of digital image noise and provides detailed explanations of noise models. Diagrams are included to illustrate the impact of Poisson and Impulse noise on intensity values [9].
Using a limited number of X-rays in dual-energy X-ray radiography (DXA) results in noise, which affects the image quality of both high and low-energy images. To enhance the accuracy of bone mineral density mapping, it is crucial to employ denoising techniques on DXA images [43]. Within the context of the research paper, a sophisticated hybrid framework is introduced, meticulously designed to elevate X-ray image quality. This innovative framework seamlessly integrates essential components including the DWT, Wiener, and Gaussian filter, as expounded upon comprehensively in reference [27]. This paper examines the performance of DWT and SWT in denoising electromyography (EMG) signals and detecting muscle fatigue. Both DWT and SWT are based on wavelet analysis and decompose the signals into frequency bands [30]. The paper proposes a hybrid approach for enhancing “X Ray” images by utilizing discrete wavelet transform and area of concentration (ROI) enhancement. The aim is to address issues such as background noise, blurriness, and low contrast in corrupted “X Ray” images, which can affect the accuracy of object detection and decision-making processes [35]. The suggested approach utilizes wavelet-based image fusion to progress degraded X-ray images and the SWT algorithm to effectively eliminate noise from the images. With this framework, the same contaminated X-ray image is processed to reduce noise, remove blurriness, and enhance sharpness. By uniting the X-ray images from different sources utilizing a specific method, such as DWT in the wavelet domain, we obtain an enhanced X-ray image. Results obtained indicate that our projected hybrid solution enhances both distorted and contaminated X-ray images.
3Proposed system
The proposed framework is structured into two distinct phases: the initial stage involves the acquisition of high-energy as well as low-energy X-ray images, that are subsequently subjected to fusion using various fusion guidelines within the wavelet domain via DWT. Subsequent to it, bonded images undergo a process of background noise reduction, accomplished through the application of inverse Discrete Wavelet Transform (iDWT) for reconstruction. MAX, MIN, MEAN, and other fusion rules are some examples. To obtain the fused image in this study, we employed MAX:- MAX as the detail and approximation coefficients. Then, to eliminate the Poisson noise from the merged image, the SWT algorithm is applied. This method utilizes different wavelet families and levels, significantly enhancing noise reduction. Specifically, DWT effectively mitigates background noise, while SWT, applied with thresholding and selective coefficient adjustments, robustly reduces Poisson noise. This improves the image’s quality while reducing blurriness and removing Poisson noise. The MSE and PSNR values utilized to evaluate images quality demonstrate that our suggested approach produces superior results. Experimental results demonstrate that the suggested hybrid framework significantly improved contrast and accuracy while reducing noise and blurriness.
3.1DWT (Discrete Wavelet Transform)
The (DWT) stands for discrete wavelet transform, serves as a technique that effectively combines frequency as well as time domains. Specifically, the DWT technique offers an amalgamation of these domains, analogous to the time-frequency representation of non-stationary signals. While short time Fourier transform is also able to extract time-frequency data, wavelet transform presents a superior approach by effectively addressing the inherent fixed resolution issue that the short-time Fourier transform encounters. A variety of basic functions are produced as a result of the signal or indication being split during the wavelet transform process. According to some, the wavelet transform serves a variety of purposes. One of the most common words used in image processing is WAVELETS [44]. The WAVELET transformation is used to first transform the entire image, and then the complete set of WAVELET coefficients is encoded. We may examine the image’s surface using the multiresolution image distribution technique known as a wavelet. Wavelet coefficients are used for classification, just like feature vectors are. A wavelet is produced from an image’s pixels via the DWT method [32]. The wavelets produced are then used for wavelet-based coding and compression.
Low-cost, streamlined, low-productivity DWT approach can resolve reciprocal highlights from computer images [45, 46]. In the suggested hybrid system, highlights are extracted including low and high energy X-ray images using DWT approach. A better variant of continuous wavelet transform (CWT) method is the DWT, also known as the mother wavelet transform [47].
The linear transformation process known as the DWT divides frequency elements of image into two distinct parts: approximation and widely detailed segments. These segments grant access to image data across horizontal, diagonal, and vertical subbands. This is accomplished by employing low-pass as well as high-pass filters [45]. The primary functions within the DWT framework consist of wavelet and scaling functions. The scaling functions are predominantly executed by the low-pass filter, while the wavelet functions are chiefly governed by the high-pass filter. The efficacy of these functions is intrinsically linked to the filters employed in the DWT process [32]. These two orthogonal roles split function space into orthogonal regions including both low as well high frequencies. Detail coefficients, linked to wavelet functions, gather high-frequency information whereas approximation coefficients, linked to scaling functions, collect low-frequency data. The following elements are expressed by Equation (1):
(1)
(2)
Equation (1) represents the mathematical formulation of the Discrete Wavelet Transform (DWT). It is used for processing high-energy X-ray images. dj + 1 [p] represents the output of the DWT at scale j + 1 and position p. g [i - 2p] is a wavelet filter function, used to analyze the image. aj [i] represents the input image or wavelet coefficients at scale j. The Equation essentially decomposes the input image into wavelet coefficients at a higher scale. Similar to Equations (1, 2) represents the DWT, but it is used for low-energy X-ray images. The difference here is the use of a different wavelet filter function represented by l [-2p] aj [i]. The wavelet function’s detailed and approximate coefficients are denoted by the letters dj and aj in the equations, functions g [i - 2p] and l [i - 2p] signify coefficients of the low and high pass filters, respectively. In order to build a fusion decision map, the wavelet transform function is first supplied toward low also high-energy x-ray images using DWT. The fused wavelet coefficient chart is bent using the source X-ray images wavelet coefficient [47].
3.2Reconstruction of wavelet transform
The wavelet reconstruction constitutes the final phase of the fusion process. In this step, fused x-ray image is derived from the estimated and detailed coefficients using the iDWT. This fusion procedure significantly diminishes background interference. After the fusion process is finished, The SWT method is used to decrease Poisson noise and also improve x-ray image value.
3.3SWT – Stationary Wavelet Transform
The Stationary Wavelet Transform (SWT) algorithm seems to be a powerful tool in image processing for tasks such as denoising, feature extraction, and image compression. It provides a high-resolution time-frequency representation of the image while preserving its spatial information. The SWT algorithm in image processing is particularly useful for denoising images. Poisson noise can be effectively reduced by thresholding the detail coefficients obtained from the SWT. The SWT preserves the image details while reducing the noise, resulting in a denoised image with improved visual quality. Additionally, the SWT is used for feature extraction in image processing tasks. By analyzing detail coefficients at different scales, important image features such as edges, textures, or patterns can be extracted. This can be beneficial for things such as image classification, object recognition, or image segmentation.
3.4Filtering techniques
Filtering holds a significant role in every signal processing system, encompassing the evaluation of signal degradation and the proficient restoration of the signal while preserving its inherent features. Over the passage of time, a variety of filtering methods suitable for diverse applications have been elucidated in the literature [48, 49]. There are two types of filtering algorithms: non-linear and linear. The most often used linear filtering algorithms are Poisson, mean, and enhanced algorithms, while nonlinear filtering approaches include bilateral, median, and enhanced algorithms. Each algorithm is recommended for a certain kind of noise and has its own advantages and disadvantages. Numerous noise creation approaches have demonstrated that there isn’t a single filtering algorithm that can be used for all types of image filtering [50].
Here, in this suggested hybrid framework, a DWT algorithm is utilized to merge the DEXI and improve image quality and eliminate background noise while a SWT algorithm is employed to minimize Poisson noise in X-ray images. The widespread use of wavelet transforms in the analysis of bio-signals such as electromyography (EMG) is due to its ability to simultaneously access time and frequency information. Methods like DWT and SWT are commonly employed for wavelet-based analysis in this context [27].
The Wiener filter stands out as the prevailing technique for mitigating blurriness in images corrupted by noise. The central objective of Wiener filtering is the attenuation of signal noise. In terms of mean square error, Wiener filtering emerges as the optimal choice. In essence, it achieves an overall reduction in mean square error by simultaneously performing inverse filtering and noise smoothing [51].
3.5Image enhancement algorithm
This study is centered on the issue of noise in medical imaging, which includes speckle noise in ultrasound, Rician noise in MRI imaging and Poisson noise in X-ray imaging. Specifically, the paper focuses on the problem of denoising X-ray images. While one possible solution to enhance the quality of X-ray images is to increase the dose value, doing so may lead to adverse effects such as cell death or other related problems [52, 53]. The method’s efficacy was determined by assessing image quality metrics on reconstructed and decomposed images. Simulated noisy projection data was introduced under comparable conditions, incorporating Poisson noise as a simulation factor [54, 55]. In contrast to other types of digital images, noise in X-ray images significantly impacts the pixel intensity values and object boundaries. This introduces uncertainty, making it exciting for the system to differentiate amongst various objects and for the administrator to carry out informed judgments [56]. A hybrid approach based on the Wavelet algorithm was recommended to get the required results. The recommended hybrid technique, which is based on Wavelet, is paired with the SWT algorithm to get the chosen results.
(3)
In our research, we used the Wavelet to decompose the input matrix X using the 2-D Stationary Wavelet Transform (SWT). Specifically, the Haar wavelet was used to do a three-level decomposition. In addition to the horizontal (hdc), vertical (vdc), and diagonal (ddc) detail coefficients for each decomposition level, the output of this operation gave us the approximation coefficients at the third level (ca). Each set of detail coefficients is included within a cell array, with chd1 standing for the horizontal details acquired from the first level of decomposition, etc.
(4)
In our approach, the original matrix was reconstructed using the 2-D Inverse Stationary Wavelet Transform (iSWT), utilizing the Wavelet function iswt2. It takes as input the approximation coefficients (A), horizontal (H), vertical (V), and diagonal (D) detail coefficients, as well as the low-pass (LoR) and high-pass (HiR) filters used in the SWT organised in cell arrays corresponding to each decomposition level are the inputs for this function. The” I “is the reconstructed image as an output. The function efficiently combines these coefficients such that the original 2D matrix is gradually reconstructed using the selected low-pass (LoR) and high-pass (HiR) reconstruction filters. The reconstruction filters must align with those used during the decomposition stage for a precise and exact reconstruction of the original data.
Thus, our proposed hybrid approach is employed to address the issue of background and Poisson noise in deteriorated X-ray images. On the other hand, although sharpening can’t significantly increase image contrast, it may drastically improve border details by using various Laplace operator approaches. As a result, visual enhancement results from the interaction of the Stationary Wavelet Transform as well as the Discrete Wavelet Transform. The proposed hybrid approach employs both wavelet transforms to reduce background and Poisson noise. The proposed technique of DWT and SWT offers a simultaneous solution for de-blurring, removing background noise and Poisson noise and enhancing the boundaries of damaged X-ray images. This is achieved by incorporating the mentioned consistent feature through image fusion. Figure 1 depicts the block diagram of the suggested hybrid framework, and the next section explains its process flow.
Fig. 1
Block Diagram illustrating the structure of the suggested hybrid framework.
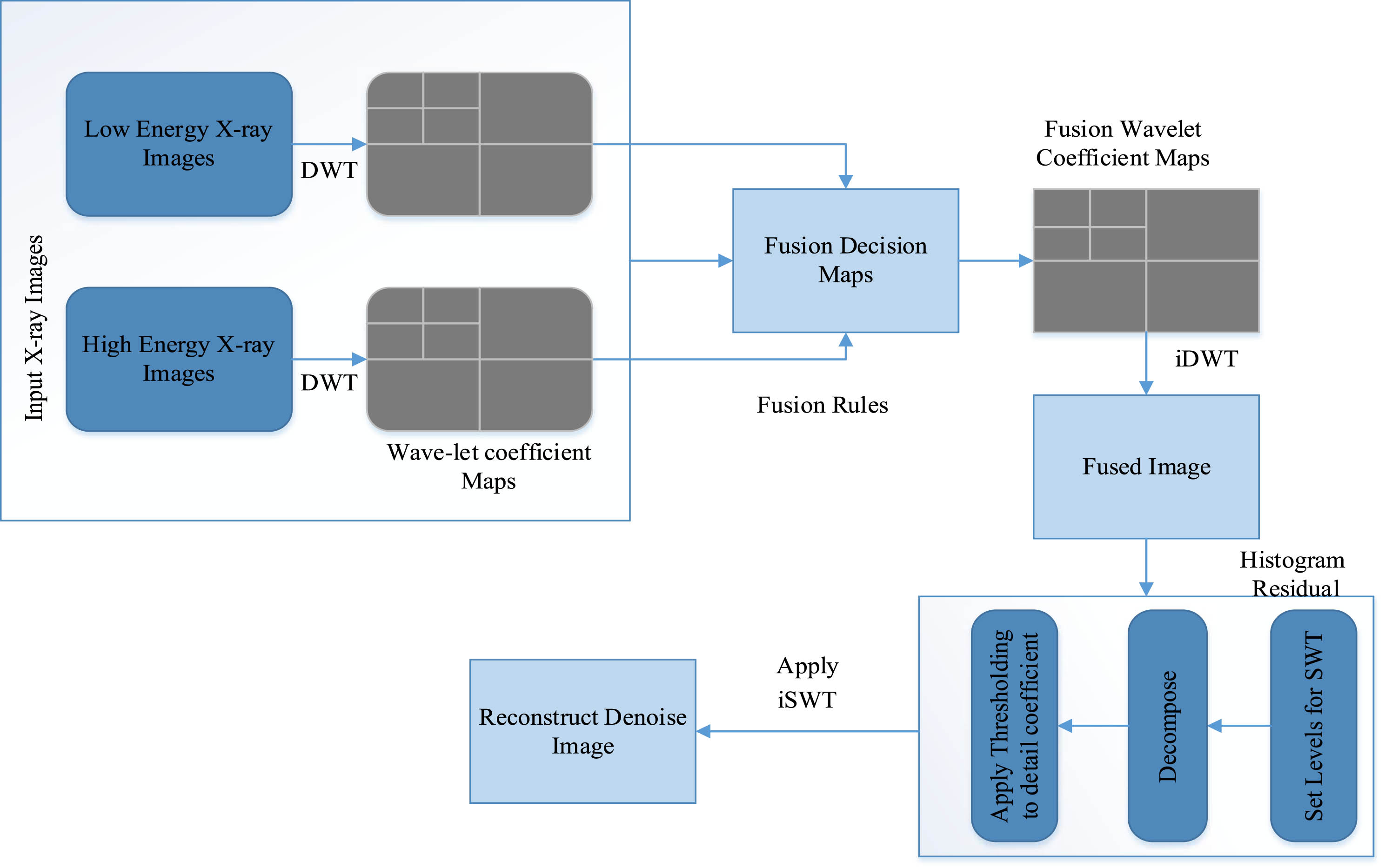
The two input images low and high energy as well as the wavelet coefficient maps that were generated by DWT are shown in the first box of this figure. The fusion decision maps of the images are then built using fusion rules following DWT. The fused wavelet coefficient map is subsequently employed to integrate the images. The fused image is then acquired using iDWT. The two input images are merged to create a fused image, which is then run through the SWT algorithm. The DWT is used to reduce background noise, blurriness, whereas the SWT algorithm is used to remove Poisson noise. After using the two algorithms, a Gray-scale de-noised image is finally produced.
Image De-Noising Algorithm / Pseudo Code
Here is pseudo-code of projected image denoising algorithm:
Algorithm Dual Energy X-Ray Image Enhancement
| Start |
| # Phase 1: Import X-ray noisy image of low-energy. |
| # Phase 2: Import the X-ray noisy image of high-energy. |
| # Phase 3: Specify the wavelet family and decomposition |
| levels for image |
| # Phase 4: Perform image fusion using Discrete Wavelet Transform (DWT). |
| # Phase 5: For the inverse DWT (iDWT), provide the desired coefficients. |
| # Phase 6: Apply the inverse DWT to rebuild the fused image. |
| # Phase 7: Read and obtain the recreated fused image. |
| # Phase 8: Establish the wavelet coefficient and levels |
| # Phase 9: Perform Stationary Wavelet Transform (SWT) dec |
| # Phase 10: Using thresholding, calculate the detail coefficients. |
| # Phase 11: Calculate histogram residual. |
| # Phase 12: Analyze histogram residual. |
| # Phase 13: Utilize residual information for denoising. |
| # Phase 14: Apply iSWT to reconstruct the image. |
| # Phase 15: End |
| Low_energy_xray = import_low_energy_xray() |
| high_energy_xray = import_high_energy_xray() |
| wavelet_family = choose_wavelet_family() |
| decomposition_levels = specify_decomposition_levels() |
| low_energy_coefficients = DWT(low_energy_xray, wavelet_family, decomposition_levels) |
| high_energy_coefficients = DWT(high_energy_xray, wavelet_family, decomposition_levels) |
| fused_coefficients = fuse_coefficients(low_energy_coefficients, high_energy_coefficients) |
| desired_coefficients = specify_desired_coefficients() |
| reconstructed_image = iDWT(fused_coefficients,wavelefmily,decomposition_levels,desired_coefficients) |
| fused_image = read_and_obtain_fused_image(reconstructed_image) |
| wavelet_coefficient_levels = establish_coeficient_levels() |
| swt_coefficients = SWT(fused_image, wavelet_family, wavelet_coefficient_levels) |
| thresholded_coefficients = threshold_swt_coefficients(swt_coefficients) |
| histogram_residual = calculate_histogram_residual(thresholded_coefficients) |
| analysis_results = analyze_histogram_residual(histogram_residual) |
| denoised_coefficients = denoise_coefficients(thresholded_coefficients, analysis_results) |
| denoised_image = iSWT(denoised_coefficients, wavelet_family, wavelet_coefficient_levels) |
4Experimental analysis and discussion
The recommended approach involves utilizing the DWT to restore the image. The initial and critical step in the proposed scheme is detecting background noise in the damaged pixels. Image fusion is utilized to effectively remove background noise from X-ray images. To solve difficulties like separating between high energy and low energy x-ray images, the researcher uses the image fusion technique that can improve complexity and dispensation time.
In the second stage or iteration, the DWT algorithm is implemented on each pixel. This generates approximation and detail coefficients by decomposing the low and high-energy X-ray images using DWT. Fusion techniques are placed following the decomposition to create fused estimation and detail coefficients. The fused X-ray image is then obtained using the iDWT. In some cases, after the fusion process, a noise reduction technique may be employed, which may involve additional image enhancement. The SWT algorithm is used after the image is processed by DWT to remove Poisson noise. The histogram residual in the Stationary Wavelet Transform (SWT) algorithm refers to the change between the histogram of the original image and the histogram of approximation coefficients obtained from the SWT. This residual information can be utilized for denoising strategies within the SWT algorithm. In earlier research, histogram equalization was commonly utilized as a method for image enhancement. However, this method has a drawback in that it tends to amplify the brightness of the brighter regions in the image by increasing the brightness of each pixel uniformly. To address this limitation, the researcher previously employed the histogram specification approach to enhance the contrast in the image. However, this approach also has its own drawbacks and problems, as it uniformly adjusts the intensity of every pixel in the image, resulting substantially boosting the brightness of the image’s already-bright parts [56, 57].
Another histogram-based approach that can be considered is adaptive histogram equalization. However, this method has one disadvantage that it can just enhances image, but similarly amplifies the noise present in image [42]. In projected hybrid scheme, after fusion procedure, fused image undergoes the Stationary Wavelet Transform (SWT) approach to address this issue. The SWT approach aims to eliminate the noise and develop overall image quality.
To evaluate the effectiveness of the proposed image enhancement method, we worked with X-ray images that had noise variations ranging from 10% to 90%, all anchored around a mean of zero. The test set consisted of images with two main dimensions, 256×256 and 512×512. The dataset encompasses X-ray images captured at 256×256 and 512×512 resolutions, featuring low-energy and high-energy scans. These images are sourced from Pakistan Civil Aviation Authority (PCAA) Pakistan, airport security scenarios, designed explicitly for luggage inspection and containing concealed illicit objects. Within these categories, the images were either single high-energy or low-energy images or their combined fused version. Due to the unique noise variance in each image, resulting primarily from background noise and Poisson noise intensities, it was critical to subject each image to a comprehensive set of noise reduction techniques. This intensive process inevitably resulted in a large amount of output data. In order to present our results in a comprehensible way, we have presented the images in 256×256 and 512×512 resolutions and divided them into low-energy, high-energy and fusion images. Each process step performed for these resolutions is meticulously recorded in Figs. 2 and 4 datasets 1 and 2 respectively. To further explain, Fig. 2 contains images with different noise ratios and denoised for 256×256 resolution, while Fig. 4 contains similarly treated images of 512×512 resolution.
Fig. 2
Contain the images with the different noise ratio and processed images of size 256×256.

Fig. 3
Noisy and denoised images of size 256×256: MSE and PSNR Analysis.
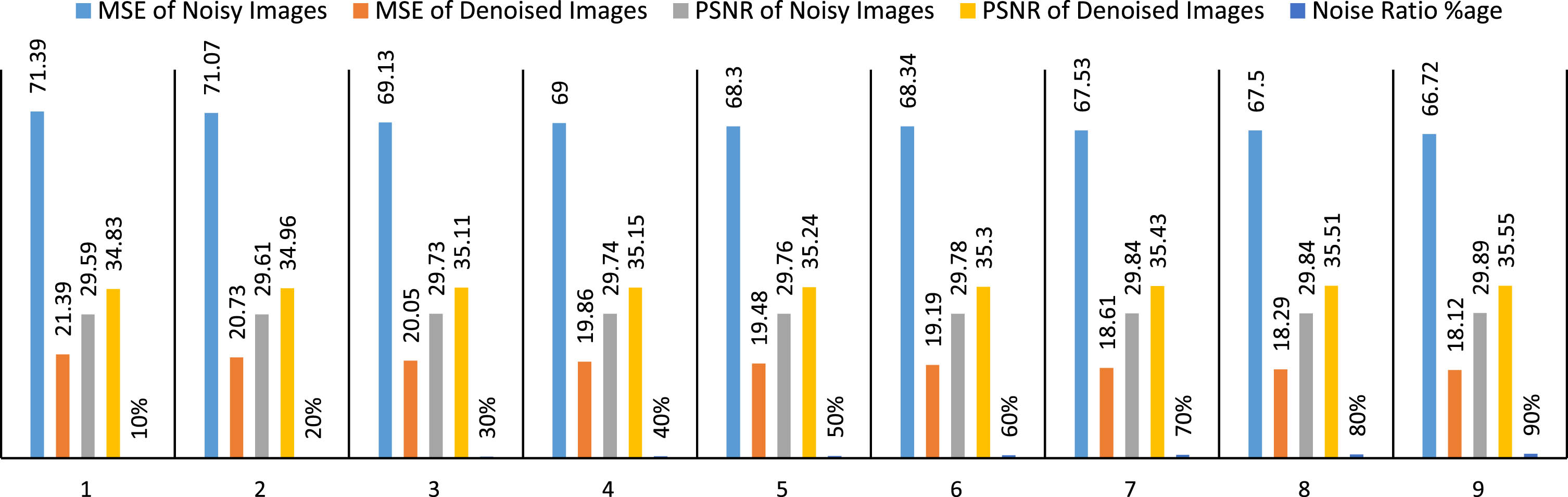
Fig. 4
Dataset 2. Contains different images with different noise ratios and processed images 512×512.

Fig. 5
MSE and PSNR Analysis of Noisy and Denoised images of size 512×512.
4.1Experimental results
4.2256×256 images dataset
The images data is clearly displayed in the above Fig. 2. The first row consists of DEXI of size 256×256. These images are impacted by background noise and Poisson noise. In the second row, high-energy x-ray images has been displayed. Moving to third row, Background noise has been significantly reduced in these images by processing using the DWT method. The last row has the final resulted images that have undergone the SWT algorithm and successfully reduced the Poisson noise. MSE and PSNR are two often used metrics when evaluating noise and denoised DEXI of size 256×256. The MSE calculates the average squared difference between the original and denoised images, with lower values indicating.
4.3MSE and PSNR analysis of 256×256 resolution images
The graph above shows the statistical analysis of MSE and PSNR of noisy and denoised 256×256 resolution images. This data shows the results of applying a denoising algorithm to noisy images. The results are given in terms of MSE and PSNR. MSE measures how much the denoised Image deviates from the original image, while PSNR measures the quality of the denoised image.
The data shows that denoising effectively improves the quality of noisy images. The MSE of the noisy images is 71.39, while the MSE of the denoised images is 21.39, a 70% reduction. The PSNR of noisy images is 29.59, while the PSNR of denoised images is 34.83, an increase of 17.24%. As the percentage of denoising increases, the MSE and PSNR of the denoised images continue to improve. At 90% denoising, the MSE is 18.12, which is a 74.4% decrease, and the PSNR is 35.55, which is a 20.05% increase. This shows that the denoising algorithm can effectively improve the quality of noisy images.
4.4MSE and PSNR values for 256×256 resolution images
The table above contains the MSE and PSNR values for both noisy and denoised images, along with the noise ratio in the percentage column for each pair. These values indicate the performance of a denoising algorithm or technique applied to noisy images. The first column represents the mean square error of the original noisy images compared to some reference images. A high MSE value indicates a larger difference between the noisy and the denoised images. The second column shows the mean square error of the denoisy images (obtained with the proposed denoising technique) compared to the same reference images. A lower MSE value indicates that the denoising process has reduced the change between the denoised images and the original images. The third column shows the PSNR value of the noisy images. A higher PSNR value indicates that the noisy original images are closer to the reference-only images in terms of quality. The 4th column represents the PSNR value of the denoised images. A higher PSNR value indicates that the denoised images are qualitatively closer to the pure reference images after applying the denoising technique. The 5th column indicates the percentage of noise in the original noisy images. The results of the proposed approach for denoising DEXI are clear and show better results in terms of MSE and PSNR.
4.5512×512 resolution images dataset
The image data in Fig. 4 provides an in-depth analysis of the images being studied. Dual-energy single X-ray images with background and Poisson noise are displayed in the first row. They are each 512×512 in size. The second row then displays high-energy X-ray images. As we go on to the third row, it is clear that the use of the DWT method has significantly reduced background noise in these images. The final row displays the final results after the SWT technique used to lessen noise in images excellently.
4.6MSE and PSNR analysis of 512×512 resolution images
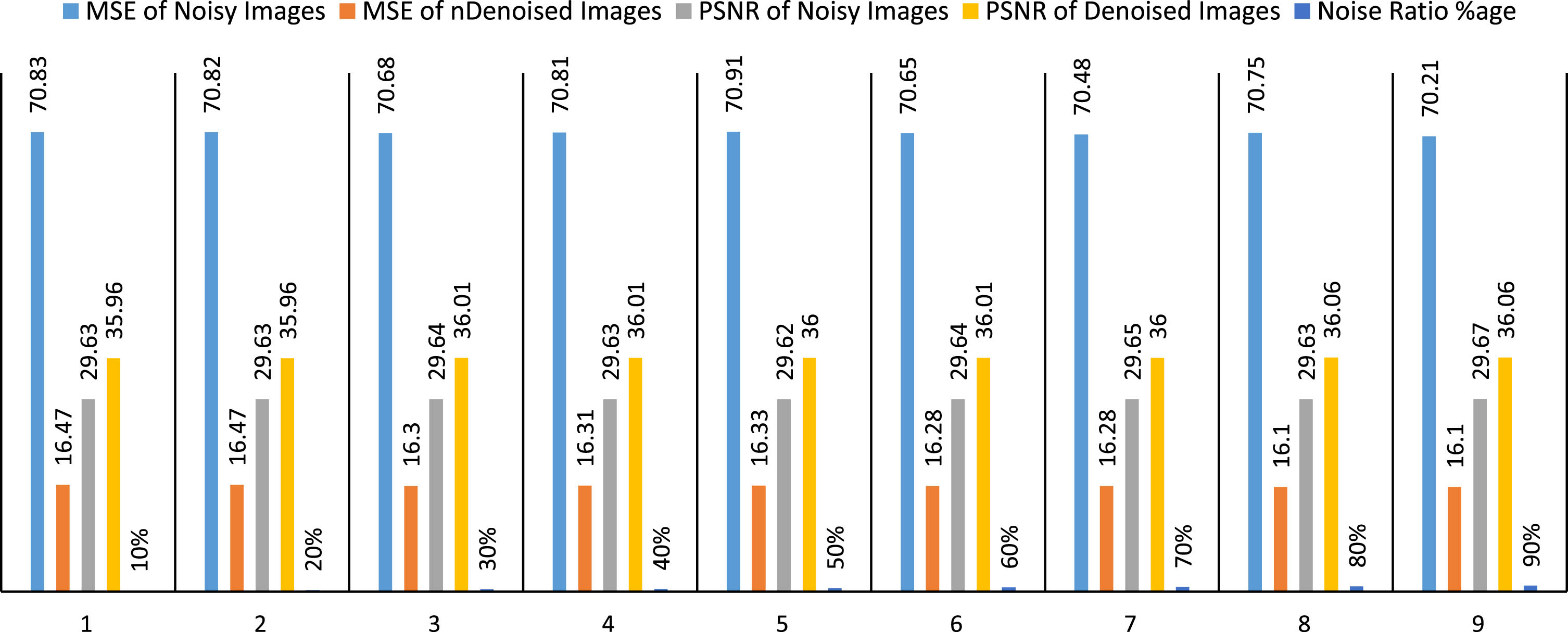
The chart below shows the MSE and PSNR statistical analysis of noisy and denoised images of 512×512 resolution.
In analyzing noisy and denoised DEXI of 512×512 resolution, MSE and PSNR are commonly used as metrics to evaluate the quality of the denoising process. MSE calculates the average squared change between the original and the denoised images, with lower values indicating better denoising performance. On the other hand, PSNR quantifies the ratio of the original images maximum likely performance to the residual noise’s performance, expressed in decibels. A good result in terms of MSE and PSNR means that the denoising algorithm has effectively reduced the noise in the dual-energy X-ray images while preserving important image details, resulting in realistic and visually appealing results. At 10% noise removal, the MSE of the noisy image was 70.83, and the MSE of the denoised image was 16.47. The PSNR of the noisy image was 29.63, and the PSNR of the denoised image was 35.96. As the percentage of noise removal increased, the MSE of the noisy image decreased, and the MSE of the denoised image increased. The PSNR of the noisy image remained relatively constant, but the PSNR of the denoised image increased. At 90% denoising, the MSE of the noisy image was 70.21 and the MSE of the denoised image was 16.10. The PSNR of the noisy image was 29.67 and the PSNR of the denoised image was 36.06. This shows that denoising successfully removed significant noise from the image while maintaining a high PSNR. The evaluation of the results involves using PSNR and MSE as evaluation metrics. These metrics are used to evaluate the results. The quality of the images is assessed using these two parameters. To reveal the effectiveness of our projected technique, we equated evaluation results with those obtained from individual X-ray images. Table 1 presents the judgmentof MSE and PSNR values obtained from the projected method using single high and low-energy x-ray images.
Table 1
MSE and PSNR analysis of 256×256 resolution of fused noisy images and proposed approach
| MSE of Noisy Images | MSE of Denoised Images | PSNR of Noisy Images | PSNR of Denoised Images | Noise Ratio % age |
| 71.39 | 21.39 | 29.59 | 34.83 | 10% |
| 71.07 | 20.73 | 29.61 | 34.96 | 20% |
| 69.13 | 20.05 | 29.73 | 35.11 | 30% |
| 69.00 | 19.86 | 29.74 | 35.15 | 40% |
| 68.30 | 19.48 | 29.76 | 35.24 | 50% |
| 68.34 | 19.19 | 29.78 | 35.30 | 60% |
| 67.53 | 18.61 | 29.84 | 35.43 | 70% |
| 67.50 | 18.29 | 29.84 | 35.51 | 80% |
| 66.72 | 18.12 | 29.89 | 35.55 | 90% |
| 68.78 | 19.52 | 29.75 | 35.23 | Average |
4.7MSE and PSNR values for 512×512 resolution images
The PSNR measure, which assesses the image quality, was another assessment technique utilized to evaluate the experience. An image enhancement is 10% greater compared to a single iamges, according to high PSNR values. PSNR values of the recommended method are higher compared to single X-ray images, as revealed in Tables 1 and 2.
Table 2
MSE and PSNR values for proposed method and fused images 512×512
| MSE of Noisy Images | MSE of Denoised Images | PSNR of Noisy Images | PSNR of Denoised Images | Noise Ratio % age |
| 70.83 | 16.47 | 29.63 | 35.96 | 10% |
| 70.82 | 16.47 | 29.63 | 35.96 | 20% |
| 70.68 | 16.30 | 29.64 | 36.01 | 30% |
| 70.81 | 16.31 | 29.63 | 36.01 | 40% |
| 70.91 | 16.33 | 29.62 | 36.00 | 50% |
| 70.65 | 16.28 | 29.64 | 36.01 | 60% |
| 70.48 | 16.28 | 29.65 | 36.00 | 70% |
| 70.75 | 16.10 | 29.63 | 36.06 | 80% |
| 70.21 | 16.10 | 29.67 | 36.06 | 90% |
| 70.68 | 16.29 | 29.64 | 36.01 | Average |
The single luggage x-ray image PSNR values and suggested fusion-based method are shown in dataset 1 and 2. According to the findings from these datasets, projected fused X-ray images have greater PSNR values than individual X-ray images. Obtained results indicate the images with higher PSNR values demonstrate enhanced precision and are measured as more revealing. It is important to remember that greater PSNR values are a sign of better performance.
The results shown in the above-mentioned figures show how well the recommended hybrid image development system works when compared to competing approaches. According to the evaluation’s findings, each image’s PSNR values are improved by applying our suggested hybrid framework for X-ray image enhancement that combines the DWT and SWT.
The following are the limitations:
• The method works effectively for dual energy grey scale X-ray images. To complete the work, X-ray images with both high and low energies are needed.
• This approach requires together high as well low energy images for fusion.
• This method remains applicable to use in radiographic mode.
5Conclusion
Electronic interference, intensity variations, and detector system limitations cause noise in DEXI. DEXI is typically hampered by noise, making object identification difficult. Noise may hide important image information, making security screening item detection and categorization difficult. This study effort has provided an innovative, trustworthy, and effective method for lowering blurriness, improving the quality of the image as well eliminating both Poisson noise and background noise. An empirical, innovative, and effective technique based on image fusion was used to explore regressive effects that affect DEXI quality, including visual sharpness or blurriness, background noise, and other effects. To compare the fused images to single images shows that the suggested hybrid approach creates clear, noise-free images. The achieved hybrid method was assessed using MSE and PSNR values. According to research, suggested hybrid architecture enhances image quality while lowering background, and Poisson noise, all without adding any complexity or time constraints. Due to its simplicity, the proposed hybrid framework offers several advantages over older ones. This hybrid architecture maybe put to use as a practical application for image analysis at security checkpoints, airports and in medical imaging.
Future work
Future study might expand the hybrid technique to handle additional noise types as image technology advances and explore its suitability for real-time processing in high-throughput security applications.
Acknowledgment
We are thankful to Prince Sattam bin Abdulaziz University, Alkharj, KSA, for supporting this study.
Declaration of competing interest
The authors declare that they have no conflict of interest.
Funding
This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445).
References
[1] | Prakash D. , et al., A study on image processing with data analysis, 2393: ((2022) ), 020225. |
[2] | Monteiro A.C.B. , et al., Metaheuristics applied to blood image analysis, in Metaheuristics and Optimization in Computer and Electrical Engineering, Springer, (2020) , pp. 117–135. |
[3] | Karimi N. , Kondrood R.R. , Alizadeh T. , An intelligent system for quality measurement of Golden Bleached raisins using two comparative machine learning algorithms, Measurement 107: ((2017) ), 68–76. |
[4] | Prabaharan T. , Periasamy P. , Mugendiran V. , Studies on application of image processing in various fields: An overview, in IOP Conference Series: Materials Science and Engineering, IOP Publishing, (2020) . |
[5] | Ali W.A. , et al., A review of current machine learning approaches for anomaly detection in network traffic, Journal of Telecommunications and the Digital Economy 8: (4) ((2020) ), 64–95. |
[6] | Ranjbarzadeh R. , Baseri Saadi S. , , Corrigendum to” Automated liver and tumor segmentation based on concave and convex points using fuzzy c-means and mean shift clustering" [Measurement 150 (2020) 107086], Measurement 151: ((2020) ), 107230. |
[7] | Li Z. , et al., Large-scale retrieval for medical image analytics: A comprehensive review, Medical Image Analysis 43: ((2018) ), 66–84. |
[8] | Pourasad Y. , Cavallaro F. , A novel image processing approach to enhancement and compression of X-ray images, International Journal of Environmental Research and Public Health 18: (13) ((2021) ), 6724. |
[9] | Khan S.U. , et al., A review of airport dual energy X-ray baggage inspection techniques: Image enhancement and noise reduction, Journal of X-ray Science and Technology 28: (3) ((2020) ), 481–505. |
[10] | Velayudhan D. , et al., Recent advances in baggage threat detection: A comprehensive and systematic survey, ACM Computing Surveys 55: (8) ((2022) ), 1–38. |
[11] | Viriyasaranon T. , Chae S.-H. , Choi J.-H. , MFA-net: Object detection for complex X-ray cargo and baggage security imagery, Plos One 17: (9) ((2022) ), e0272961. |
[12] | Akcay S. , Breckon T. , Towards automatic threat detection: A survey of advances of deep learning within X-ray security imaging. arXiv 2020, arXiv preprint arXiv:2001.01293. |
[13] | Vukadinovic D. , Osés M.R. , Anderson D. , Automated detection of inorganic powders in X-ray images of airport luggage, Journal of Transportation Security 16: (1) ((2023) ), 3. |
[14] | Oulhissane L. , et al., Enhanced detonators detection in X-ray baggage inspection by image manipulation and deep convolutional neural networks, Scientific Reports 13: (1) ((2023) ), 14262. |
[15] | Wu J. , Xu X. , Yang J. , Object detection and X-ray security imaging: A survey, IEEE Access ((2023) ). |
[16] | Otabir S.A.G. , et al., X-Ray Baggage Object Detection Using Neural Networks Approach for Safety Purpose, in Advances in Intelligent Manufacturing and Mechatronics: Selected Articles from the Innovative Manufacturing, Mechatronics & Materials Forum (iM3F 2022), Pahang, Malaysia, Springer, (2023) . |
[17] | Wang B. , et al., Detect occluded items in X-ray baggage inspection, Computers & Graphics 115: ((2023) ), 148–157. |
[18] | Park J. , An G. , Seo H. , Design optimization of X-ray security scanner based on dual-energy transmission imaging with variable tube voltage, Journal of Instrumentation 18: (01) ((2023) ), C01063. |
[19] | Zaliskyi M. , et al., Shadow image processing of X-ray screening system for aviation security, International Journal of Image, Graphics and Signal Processing (IJIGSP) 14: (6) ((2022) ), 26–46. |
[20] | Isaac-Medina B.K. , et al., Cross-modal Image Synthesis within Dual-Energy X-ray Security Imagery, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, (2022) . |
[21] | Shah A. , et al., Comparative analysis of median filter and its variants for removal of impulse noise from gray scale images, Journal of King Saud University-Computer and Information Sciences 34: (3) ((2022) ), 505–519. |
[22] | Chouai M. , et al., Dual-energy x-ray images enhancement based on a discrete wavelet transform fusion technique for luggage inspection at airport, in 2019 6th International Conference on Image and Signal Processing and their Applications (ISPA), IEEE, (2019) . |
[23] | Qian W. , et al., In situ X-ray imaging and numerical modeling of damage accumulation in C/SiC composites at temperatures up to 1200°C, 197: ((2024) ), 65–77. |
[24] | Gong X. , et al., Multispectral and SAR image fusion for multi-scale decomposition based on least squares optimization rolling guidance filtering, ((2024) ). |
[25] | Yin L. , et al., Convolution-transformer for image feature extraction. |
[26] | Wang B. , et al., Stacked noise reduction auto encoder–OCEAN: A novel personalized recommendation model enhanced, 12: (6) ((2024) ), 188. |
[27] | Ullah B. , et al., A novel hybrid framework to enhance dual-energy X-ray images, Journal of Sensors 2023: ((2023) ). |
[28] | Pajares G. , De La Cruz J.M. , A wavelet-based image fusion tutorial, Pattern Recognition 37: (9) ((2004) ), 1855–1872. |
[29] | Dimitrov A.G. , Spike sorting the other way, Neurocomputing 52: ((2003) ), 741–745. |
[30] | Zhao Z. , et al., DDFM: Denoising diffusion model for multi-modality image fusion supplementary materials, mij (yij–xij) 2: (2), 2. |
[31] | Zhao Z. , et al., DDFM: denoising diffusion model for multi-modality image fusion, arXiv preprint arXiv:2303.06840 ((2023) ). |
[32] | Gonzales R.C. , Woods R.E. , Eddins S.L. , Digital image processing using MATLAB, (2004) : Pearson Prentice Hall. |
[33] | Khan S.U. , et al., X-ray image enhancement using a boundary division wiener filter and wavelet-based image fusion approach, J Inf Process Syst 12: (1) ((2016) ), 35–45. |
[34] | Arnal J. , Súcar L. , Hybrid filter based on fuzzy techniques for mixed noise reduction in color images, Applied Sciences 10: (1) ((2019) ), 243. |
[35] | Fahad M. , Ahmed S. , Ullah B. , Dual energy “X ray” image enhancement using hybrid approach. |
[36] | Chanu P.R. , Singh K.M. , A two-stage switching vector median filter based on quaternion for removing impulse noise in color images, Multimedia Tools and Applications 78: (11) ((2019) ), 15375–15401. |
[37] | Smolka B. , Malik K. , Malik D. , Adaptive rank weighted switching filter for impulsive noise removal in color images, Journal of Real-Time Image Processing 10: ((2015) ), 289–311. |
[38] | Smolka B. , Malinski L. , Impulsive noise removal in color digital images based on the concept of digital paths, in 2018 13th International Conference on Computer Science & Education (ICCSE), IEEE, (2018) . |
[39] | Mandic I. , et al., Denoising of X-ray images using the adaptive algorithm based on the LPA-RICI algorithm, J Imaging 4: (2) ((2018) ), 34. |
[40] | Hržić F. , et al., Local-entropy based approach for X-ray image segmentation and fracture detection, Entropy 21: (4) ((2019) ), 338. |
[41] | Dev R. , Verma N.K. , Generalized fuzzy peer group for removal of mixed noise from color image, IEEE Signal Processing Letters 25: (9) ((2018) ), 1330–1334. |
[42] | Georgieva V. , Kountchev R. , Draganov I. , An adaptive enhancement of X-Ray images, Advances in Intelligent Analysis of Medical Data and Decision Support Systems ((2013) ), 79–88. |
[43] | Al-Antari M.A. , et al., Denoising images of dual energy X-ray absorptiometry using non-local means filters, Journal of X-ray Science and Technology 26: (3) ((2018) ), 395–412. |
[44] | Salve S. , Chakkarwar V. , Classification of mammographic images using gabor wavelet and discrete wavelet transform, International Journal of Advanced Research in Electronics and Communication Engineering (IJARECE) 2: (5) ((2013) ). |
[45] | Pei L. , Zhao Y. , Luo H. , Application of wavelet-based image fusion in image enhancement, in 2010 3rd International Congress on Image and Signal Processing, IEEE, (2010) . |
[46] | Demirel H. , Anbarjafari G. , Discrete wavelet transform-based satellite image resolution enhancement, IEEE Transactions on Geoscience and Remote Sensing 49: (6) ((2011) ), 1997–2004. |
[47] | Ionela N.A. , Monica B. , Satellite image improvement using phase information and wavelet transform, in 2010 8th International Conference on Communications, IEEE, (2010) . |
[48] | Pushpavalli R. , Sivaradje G. , Switching median filter for image enhancement, International Journal of Scientific & Engineering Research 3: (2) ((2012) ), 1–5. |
[49] | Anwar S. , Rajamohan G. , Improved image enhancement algorithms based on the switching median filtering technique, Arabian Journal for Science and Engineering 45: (12) ((2020) ), 11103–11114. |
[50] | Yu L. , Image noise preprocessing of interactive projection system based on switching filtering scheme, Complexity 2018: ((2018) ), 1–10. |
[51] | Kumar S. , et al., Performance comparison of median and wiener filter in image de-noising, International Journal of Computer Applications 12: (4) ((2010) ), 27–31. |
[52] | Göreke V. , A novel method based on Wiener filter for denoising Poisson noise from medical X-Ray images, Biomedical Signal Processing and Control 79: ((2023) ), 104031. |
[53] | Kirti T. , Jitendra K. , Ashok S. , Poisson noise reduction from X-ray images by region classification and response median filtering, Sādhanā 42: ((2017) ), 855–863. |
[54] | Komolafe T.E. , et al., Hybrid Optimization Method (HOM) Reconstruction with limited angle in Dual Energy Breast CT, in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), IEEE, (2019) . |
[55] | Komolafe T.E. , et al., Material decomposition for simulated dual-energy breast computed tomography via hybrid optimization method, Journal of X-Ray Science and Technology 28: (6) ((2020) ), 1037–1054. |
[56] | Bhosale N. , Manza R. , Kale K. , Analysis of effect of Gaussian, salt and pepper noise removal from noisy remote sensing images, in Second International Conference on Emerging Research in Computing, Information, Communication and Applications (ERCICA 2014), Elsevier (August 2014. |
[57] | Khan S.U. , et al., A close assessment of x-ray image enhancement techniques for contraband detection, International Journal of Computer Science and Information Security (IJCSIS) 14: (8) ((2016) ). |




