Analysis of competitive surfing tournaments with generalized Bradley-Terry likelihoods
Abstract
Here we analyse competitive surfing, specifically the 2019 Men’s World Surf League, using formal statistical methods. We use generalized Bradley-Terry likelihoods to assess a number of hypotheses of interest to the surfing community. We quantify the dominance of the top competitors using likelihood techniques, and go on to study the “Brazilian storm” phenomenon using reified entities in two ways. Firstly we assess the supposed Brazilian preference for beach break and point break wave types; and secondly we consider results from the perspective of tournament theory and test for competitors modifying their strategy in the presence of compatriot rivals. We quantify the evidence for these commonly assumed features of contemporary competitive surfing and suggest further avenues of research.
1Introduction
Surfing is a popular and growing activity in terms of both participation and viewing (Warshaw, 2010). Competitive surfing involves surfers competing against one or more other surfers in heats lasting 30-50 minutes (Booth, 1995). Points are awarded on a 10-point scale: each of five judges awards points to a surfer riding a particular wave. The World Surf League (WSL) is the main governing body for professional surfers (World Surf League, 2021). The WSL conducts a world tour in which the best ranked 34 surfers compete; in addition, at each tour venue, two “wildcard” surfers also enter the competition, who are ignored here due to their generally poor performance.
The 2019 WSL tour saw competitive events held at eleven different surf locations. The typical format is as follows. Up to four surfers—the competitors—are in the water simultaneously, watched by up to five judges. Subject to surfing etiquette, competitors are free to catch a wave at their discretion within the heat’s time window. The judges rate each wave ride and award points to the surfer based on a range of subjective criteria such as stylish execution and transition of manoeuvres, but also credit elements such as the difficulty and novelty of the performance. The top score and bottom score among the five judges are removed and the remaining three judges’ scores are averaged to give the final score for the surfer for that wave. Each surfer’s aggregate score is given by the average of the two highest-scoring waves. The winner is the surfer with the highest aggregate score.
Such scoring systems are designed to account for the random nature of wave quality while reflecting competitors’ abilities fairly. Differences in wave quality between successive days mean that direct comparison of scores between one day and another are not informative about competitors’ abilities as they are strongly dependent on details of wave quality at the time of the competition. However, for a particular heat, the order statistic—that is, which competitor scored most highly, second highest, and third—is informative about competitors’ abilities: the wave environment is common to each surfer.
We note in passing that Lemoore had a different format from the other venues in the championship, being held in an artificial wave pool in which every wave was essentially identical (up to a mirror reflection). Statistically, there were seven heats of either 2, 4, 8, or 16 surfers. We show below how to incorporate the information present in such observations with the remainder of the championship using a consistent and intuitive statistical model.
2Previous statistical analysis of competitive surfing
Farley et al. (2015) analyse surfing results using one-way ANOVA techniques and report comparisons between the top 10 and bottom 10 surfers in the 2013 World Championship Tour (WCT) and conclude that the top-ranked athletes are more consistent than the lower-ranked group. They report that “to date, only a limited number of research studies have reported on the results of competitive surfing” [p44], and the analysis presented here fills some of this gap.
Other statistical research into competitive surfing appears to focus on the scoring of aerial manoeuvres compared with other manoeuvres in events. Lundgren et al. (2014), for example, report that aerial manoeuvres scored higher than other stunts but had a lower completion rate, a theme we return to below.
3Likelihood-based systems and points-based systems
Table ref resultstable shows the official results table from the tour. We see that Ferreira places first with 59740 points, Medina second with 56475, and so on. The overall ranking of the surfers is determined by summing the season’s points.
Table 1
Conventional league table for the top five competitors in the WCT 2019 tour. Thus at WCT01 (Coolangatta, QLD) we see Ferreira coming first, Andino second and Smith third label resultstable
| competitor | nationality | WCT | points | |||||
| 01 | 02 | 03 | … | 10 | 11 | |||
| Ferreira | BRA | 1 | 5 | 17 | … | 1 | 1 | 59740 |
| Medina | BRA | 5 | 5 | 17 | … | 9 | 2 | 56475 |
| Smith | ZAF | 3 | 3 | 17 | … | 2 | 17 | 49985 |
| Toledo | BRA | 9 | 2 | 5 | … | 5 | 17 | 49145 |
| Andino | USA | 2 | 17 | 5 | … | 5 | 9 | 46655 |
| ⋮ | ⋮ |
As in many subjective sports, points are awarded to competitors on the basis that a better performance attracts a higher number of points. However, such systems are difficult to analyse statistically, because the points awarded are intrinsically arbitrary: provided that better performances attract more points, the precise number of points awarded does not change the competitors’ behaviour. Competitors will endeavour to earn the maximum number of points possible, and to do this will deliver the best performance they are able to give.
As discussed above, analysis of order statistics does not suffer from this particular defect (Aldous, 2017). Order statistics can be analysed using a number of formal statistical methods, but here we focus on one method that has been successfully applied in many competitive sporting contexts: here we suggest that Plackett-Luce likelihood functions furnish an objective and coherent method for ranking competitors. Further, likelihood-based methods offer one signal advantage over points-based systems: the ability to conduct statistically rigorous tests of meaningful nulls.
4The Bradley-Terry class of probability models for order statistics
The Bradley-Terry model (Bradley, 1954) assigns non-negative strengths p1, …, pn to each of n competitors in such a way that the probability of i beating j ≠ i in pairwise competition is
(1)
and this would be a forward ranking Plackett-Luce model in the terminology of Johnson et al. (2020). We now use a technique due to Hankin (2010, 2017) and introduce fictional (reified) entities whose nonzero Bradley-Terry strength helps certain competitors or sets of competitors under certain conditions. The original example was the home-ground advantage in football. If players (teams) 1, 2 with strengths p1, p2 compete, and if our observation were a home wins and b away wins for team 1, and c home wins and d away wins for team 2, then a suitable likelihood function would be
(2)
where pH is a quantification of the beneficial home ground effect. Similar techniques have been used to account for the first-move advantage in chess (Hankin, 2020), and here we apply it to assess the supposed Brazilian preference for particular wave types.
5The dataset and likelihood function
Table ref rawresults shows the first few and last few entries in the dataset we use, drawn from 2019 WCT. The first line shows that, at one of the heats in WCT01 (Coolangatta, QLD), Colapinto came first, Bailey hfilneg hrule hrule second, and Wright came third: we write Colapinto ≻ Bailey ≻ Wright. The last line shows that, at WCT11 (Banzai Pipeline), Ferreira came first and Medina second: Ferreira ≻ Medina. We can convert this dataset into a Plackett-Luce likelihood function but first have to remove the wildcards whose strength is typically very low. We also remove De Vries who, while not a wildcard, competed only twice in 2019 and came last each time, thus having zero maximum likelihood strength. For the first line we would have a Plackett-Luce likelihood function of
(3)
The entire dataset has a likelihood function that incorporates all 477 lines of Table ref rawresults, but it includes:
(4)
Table 2
Extract from observations: raw resultslabel rawresults from WCT 2019. Thus the first heat at WCT01 (Coolangatta, QLD) shows competitors Colapinto, Bailey, and Wright in the water at the same time, the competition order being Colapinto ≻ Bailey ≻ Wright; as discussed in the text we use only the competition order for our likelihood function
| WCT01 Colapinto Bailey Wright |
| WCT01 Freestone Lau Smith |
| WCT01 Dora Ferreira Slater |
| WCT01 Duru Toledo Ibelli |
| WCT01 Moniz Heazlewood Wilson |
| . . . |
| WCT11 Medina Florence |
| WCT11 Colapinto Bourez |
| WCT11 Ferreira Slater |
| WCT11 Medina Colapinto |
| WCT11 Ferreira Medina |
5.1Bradley-Terry and pairs
Paired comparisons are particularly favourable to Bradley-Terry because the likelihood function is exponential family and as such is amenable to analysis via general linear models (Turner and Firth, 2012). However, this is not applicable when more than two entities are compared; and indeed here we see comparisons between three surfers and, in the case of Jeep Surf Freshwater Pro WCT08, many more. It is natural to ask how much information is contained in the observations where more than two surfers are in the water.
To answer this, we directly calculate the observed information matrix for the log-likelihood function in equation ref complete_likelihood_function. Observing that differentiation is linear, we may calculate second derivatives by summing individual terms of the support function and further observing that, for a typical term of the form log(∑k∈Kpk) n [where the sum is over some subset K of strengths] we have
(5)
The hyper2 package includes function hessian() which returns this matrix for any given support function. For equation ref complete_likelihood_function we find that the determinant is about 4.3 × 1071. Compare this with 2.9 × 1069 for the pairs considered in isolation, a ratio of about 146.4. This ratio shows that there is considerable information loss in considering only the paired comparisons. We are thus motivated to consider the whole dataset, not just the part which involves paired comparisons.
6Results
For any likelihood function, one important diagnostic is the maximum likelihood estimate. The hyper2 package facilitates the finding of maximum likelihood estimates using the bespoke maxp() function, which uses standard optimization techniques. Derivatives are available which ensures rapid convergence to the evaluate.
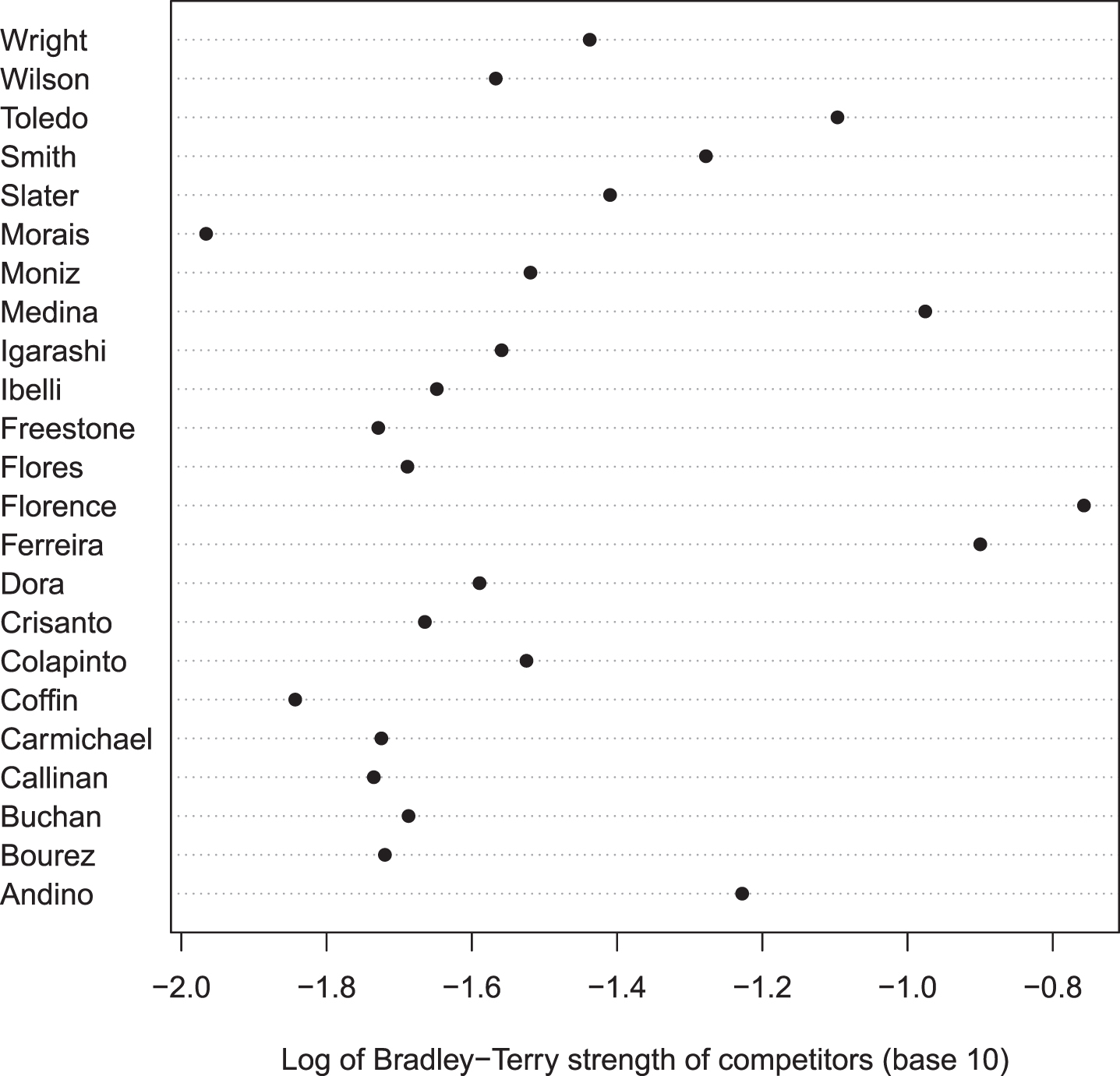
Fig. ref dotchartmax shows the maximum likelihood estimate for the 23 competitors’ strengths, which appears to show a wide range from Florence at about 0.175 down to Morais at about 0.01. The hyper2 software (Hankin, 2017) may be used to formally assess one plausible null: that the competitors all have equal skill, that is
Fig. 1
Dot chartshowing maximum likelihood strengths of the 23 competitors in alphabetic order, logarithmic axis. Note the dominance of Ferreira, Florence, and Medina
However, points awarded may be compared with likelihood estimates, and one would expect high points totals to be associated with high likelihoods. Fig. ref compare_likelihood_points shows a loose correlation (R2 = 0.71; p = 4 ×10-7) and Fig. ref compare_likelihood_points_rankings shows how the rankings differ when calculated by the points and likelihood systems. Note the anomalous position of Florence, who did not compete in five venues due to injury: this strongly affecting his points total but not his likelihood-based ranking.
Fig. 2
Scatterplot of points scored (horizontal axis) against maximum likelihood estimates (vertical axis). One would expect a positive correlation as high Bradley-Terry strength would lead to a high probability of earning more points; with these axes the correlation is moderate at about R2 = 0.71. Florence, at (37700, 0.175), is something of an anomaly. He did not compete at five venues due to injury, this affecting his points total but not his likelihood-based ranking
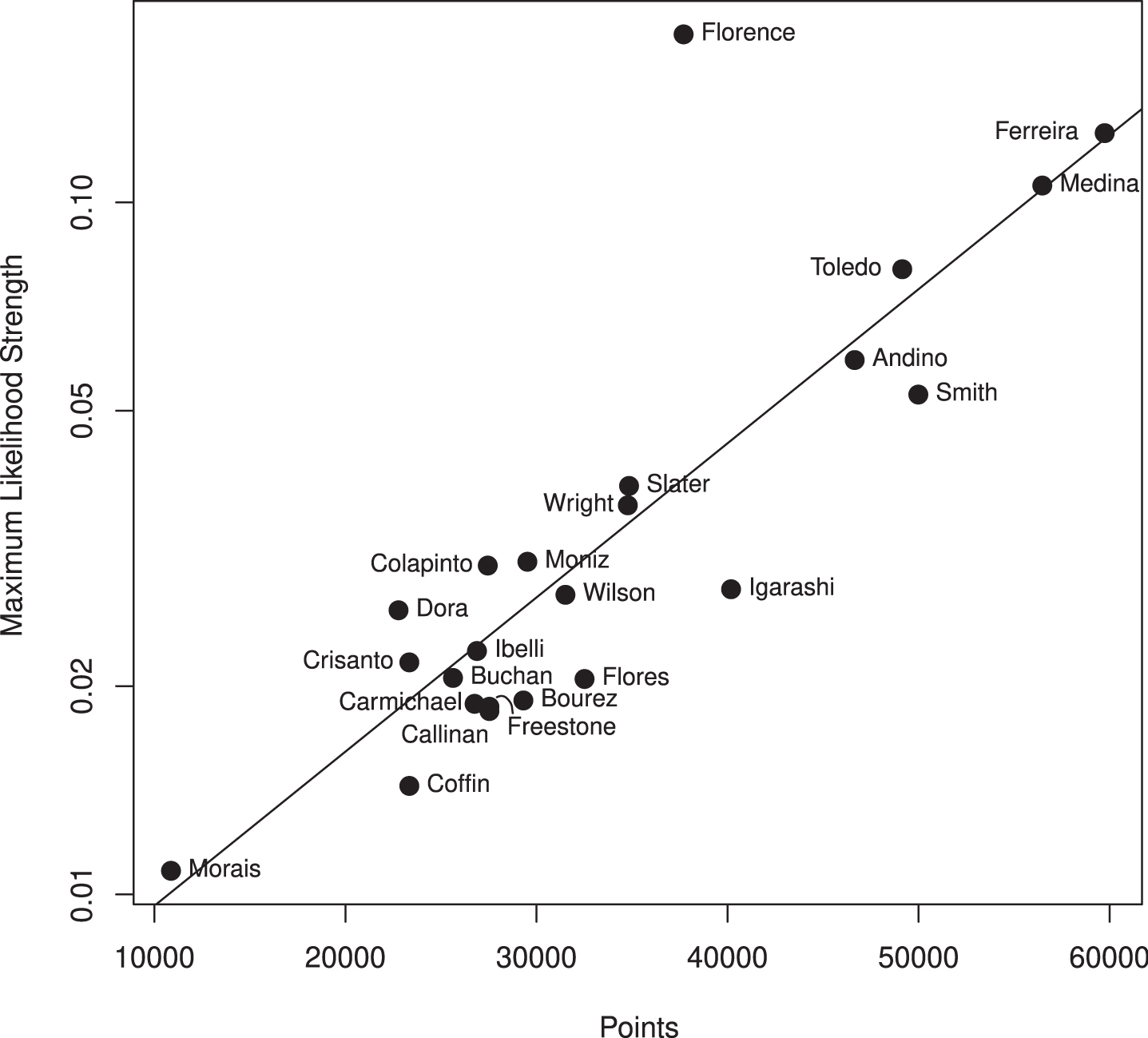
Fig. 3
Scatterplot of ranks of points-based ranking against likelihood-based ranking. Note the anomalous position of Florence

We may ask whether the top two officially ranked competitors, Medina and Ferreira, have different strengths. To test the null of equal strength, we maximize the likelihood subject to the null, and compare with the global maximum likelihood (Hankin, 2010); package idiom is to use samep.test() which reports its findings in a standardised format. This gives a support difference of about 0.05, well short of Edwards’s 2 units of support criterion. Alternatively, we could observe that
Medina’s performance was startlingly good at Freshwater Pro (WCT08). Indeed, Medina came first at only two venues (the other was at Jeffries Bay, South Africa) and it is natural to enquire whether there is statistical evidence to support the assertion that he performed better under the more controlled conditions of the Lemoore Surf Ranch. To do this, we create an artificial surfer, Medina_wct08, who competes at Lemoore, and test the null that Medina has the same competitive strength as Medina_wct08. We reject this null at a p-value of 0.043 and conclude that Medina’s performance at Lemoore is significantly better than his performance at natural venues. From an inferential perspective, this test is interesting because competitor Medina never faces Medina_wct08. It is as though competitor A consistently beats B, and B consistently beats C in pairwise competition, but A has never directly competed against C. Nevertheless we may assert with some confidence that the Bradley-Terry strength of A exceeds that of C in the absence of nontransitive effects (West and Hankin, 2008), via indirect comparison.
7The Brazilian storm
In surfing lore, the “Brazilian storm” refers to the emergence of Brazil as a dominant nation of elite surfers. The term was first used to describe the fact that six out of eight quarterfinalists at the 2011 Nike Lowers Pro were Brazilian; it rose in public consciousness following the victories of Medina and de Souza in the WSL championships in 2014 and 2015 respectively. The storm shows no signs of abating, with commentators such as Douglas opining that this generation “represents a seismic shift for Brazilian competitors onto an entirely new plane” (Douglas-Rosa, 2020).
Here, we study two aspects of this sporting phenomenon: the suggested Brazilian preference for beach break and point break wave types; and the noncompetitive effect of compatriot rivalry.
7.1Brazilian wave type preferences
The statistical method described here can test many different hypotheses inspired by surfing lore. For example, one frequent suggestion (Burgess, 2020, Ho, 2021) is that Brazilian surfers tend to have skillsets that favour point and beach break wave types, readily accessible to these surfers’ native Brazil; see Scarfe et al. (2003) for a scientific overview of surf break characteristics, and Butt et al. (2004) for a surfer’s perspective.
We now assess the null that Brazilians perform equally well on all types of wave types. To that end, we create a reified surfer, “Brazilian wavetype", whose strength helps all Brazilian surfers when surfing on their (putative) preferred wave type, an analogue of the “home ground monster" who helps the home team as per equation ref home_ground_advantage. Here we modify the likelihood function only when a single Brazilian is in the water, thus avoiding possible interaction with the compatriot issue discussed in section ref compatriot.
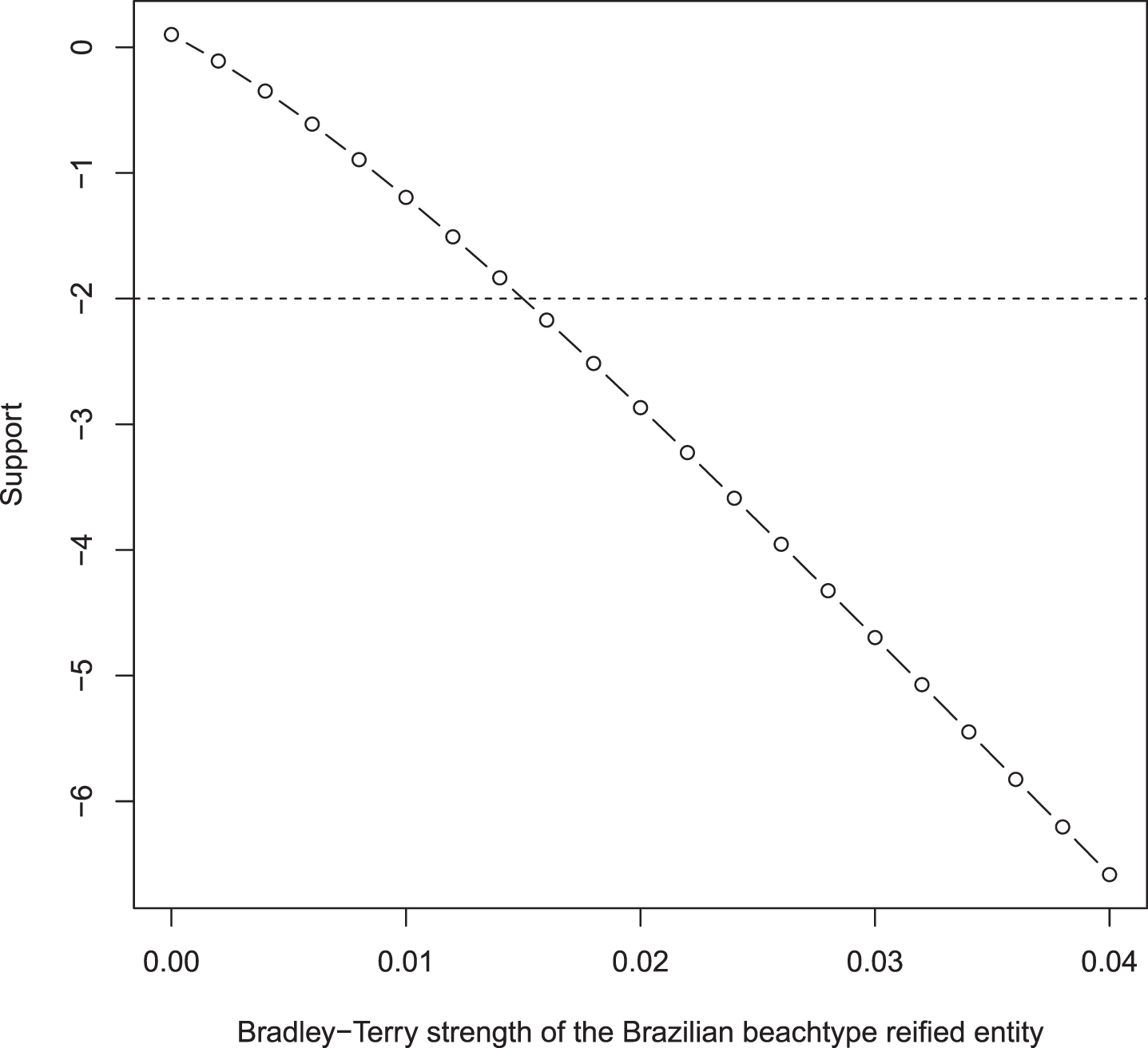
To illustrate the concept, we show a simple likelihood function in Table ref probabilitybrazilian. The null would be that this reified entity has zero strength. We fail to reject this null (differential support = 0.035; p = 0.79) and conclude that there is no evidence to suggest that Brazilians’ performance is better on their preferred wave types than one would expect by chance. We may go further using the method of support: not only is the maximum likelihood estimate for Brazilian wavetype very small (about 0.002), but in addition we may reject the proposal that the strength of this entity exceeds about 0.015 (Fig. ref brazilian_wavetype_support): at this value of the strength or greater, we may gain two or more units of support by moving to the evaluate (Edwards, 1992).
Fig. 4
Profile support for the Brazilian wavetype reified entity. The horizontal axis specifies a particular strength for Brazilian wavetype, and the height of the curve gives the support conditional on the x-axis. At a strength of 0.015 we see the support is -2 and we could thus be reasonably confident that the strength does not exceed this value
8Differential label compatriot behaviour toward compatriotic competitors
One measure of the rising popularity of surfing is its inclusion in the 2020 Summer Olympics (Tulloch, 2019), and it is natural to ask whether this would affect the competition in some way (Ho, 2021). One suggestion would be that competitors become more focussed on beating compatriots than surfers from other countries, the thinking being that admission to a country’s Olympic team would be of more importance to a competitor than their overall standing in the tournament. One might expect competitors to value their ranking when restricted to within their country more than their international ranking. If this is the case then we would expect competitors to change their behaviour if they are in the water with another surfer of the same nationality. Specifically, if we have three surfers in the water of whom two are of one nationality and the third of another, we would expect the compatriots to adopt a style calculated to beat their countryman, possibly at the expense of performance relative to the odd man out. In this context, risk sensitivity is likely to be become important. One example might be aerial manoeuvres which are risky but, if successful, attract high scores (Lundgren et al., 2014). Such strategies are known to occur in chess (Hankin, 2020): players suffering a sequence of defeats adopt a high-risk (all-or-nothing) approach, while players in a winning streak hunker down, play defensively, and entrench their lead. Such hypotheses are difficult to test with conventional techniques as the competitors’ strengths themselves are nuisance parameters (Basu, 1977).
argethispage2pt
Consider, as an example, the case of Smith, Buchan, Freestone who were simultaneously in the water at Bells Beach, Australia. Now, Buchan and Freestone are Australian, and Jordy Smith is South African. It is reasonable to ask whether Buchan and Freestone, who are in direct competition with one another for a place in the Australian Olympic surfing team, would be more motivated to beat each other than to come ahead of Smith. This would be a rational response, but arguably noncompetitive. How would such a strategy manifest itself in scorelines? We would suggest that Smith is able to modify his strategy to benefit from the mutual rivalry between Buchan and Freestone; and indeed we see Smith winning that particular heat. We tentatively interpret this as a Nash-type equilibrium: there is no incentive for either Buchan or Freestone to deviate from their prioritization of defeating their compatriot; and indeed neither Buchan nor Freestone were selected for the 2020 Olympic team.
The reified Bradley-Terry technique furnishes an intuitive statistical test for such mechanisms, that automatically controls for competitors’ strengths. Noting that the compatriots effectively place themselves at a disadvantage when compared with the odd man out, we introduce a compatriot monster whose strength pC helps the odd man out. Writing p1, p2 for the strengths of the compatriots and q for the odd man out, we construct likelihood functions for the six possible orderings when two compatriots and an odd man out are in the water at the same time in Table ref likelihoodcompatriot (if we have either three different nationalities or three identical nationalities, we revert to the standard Plackett-Luce likelihood). Note that all six likelihood functions in Table ref likelihoodcompatriot are informative about p1, p2, q in addition to being informative about the object of inference, pC.
Table 3
The label likelihoodcompatriot six possible finishing orders (“≻” means “scored more points than”) for the case where two compatriot surfers and an odd man out are in the water at the same time, with associated likelihood function for strengths p1, p2, q, pC. Here p1, p2 are the strengths of two compatriot surfers, q the strength of the odd man out, pC the strength of the compatriot monster. and nationality and a third are in the water at the same time
| order |
|
| p1 ≻ p2 ≻ q |
|
| p2 ≻ p1 ≻ q |
|
| p1 ≻ q ≻ p2 |
|
| p2 ≻ q ≻ p1 |
|
| q ≻ p1 ≻ p2 |
|
| q ≻ p2 ≻ p1 |
|
Table 4
Likelihood function for results between surfer 1 (Brazilian) and surfer 2 (non-Brazilian) with label probabilitybrazilian Bradley-Terry strengths p1, p2 respectively, and a “Brazilian wavetype" entity with strength B that quantifies the enhanced Brazilian performance on reef wave types
| wave type | Prob (p1 ≻ p2) |
|
| beach |
|
|
| point |
|
|
| reef |
|
|
Table 5
Simplified payoff table label valuetable for Buchan (B), Freestone (F), and Smith (S). Buchan and Freestone, being Australian, have a payoff that reflects their likelihood of being picked for the national Olympic squad: they are interested in whether or not they beat their countryman. Thus Buchan’s payoff shows whether or not he beat Freestone, and vice versa. Smith, being South African, is motivated by his ranking against his competitors and here we show Smith with a Borda-type payoff. Smith observes that both Buchan and Freestone are indifferent between outcomes {B≻ F ≻ S, B ≻ S ≻ F, S ≻ B ≻ F }, and may be able to exploit this indifference by strategies increasing the probability of his desired outcome, S ≻ B ≻ F
| order\value | B | F | S |
| B ≻ F ≻ S | 1 | 0 | 0 |
| B ≻ S ≻ F | 1 | 0 | 1 |
| F ≻ B ≻ S | 0 | 1 | 0 |
| F ≻ S ≻ B | 0 | 1 | 1 |
| S ≻ B ≻ F | 1 | 0 | 2 |
| S ≻ F ≻ B | 0 | 1 | 2 |
We can now apply the Method of Support to the hypothesis that pC = 0, that is, that such noncompetitive behaviour is absent. We find that the maximum likelihood estimate for pC is about 0.017, weaker than the “real” surfers, but the support for a nonzero pC is about 0.59 [asymptotic p = 0.28], insufficient to reject our null. We conclude that there is no strong evidence to suggest that such noncompetitive behaviour occurred—at least not from the order statistics we considered.
9Conclusions and further work
We analysed results from the 2019 WCT using reified Bradley-Terry likelihoods to assess a number of hypotheses of interest to the surfing community. Reified Bradley-Terry allows the use of formal statistical methods in ways that analysing points scored does not. For example, we can be confident that the results reflect differences in skill (rather than random variation); there is no statistical difference in strength between the top two officially ranked competitors, Medina and Ferreira; but we may reject the hypothesis that Medina and Wilson are equal in strength.
We discuss and assess the “Brazilian storm” phenomenon using reified Bradley-Terry techniques, and show that there is no strong evidence to support the supposed Brazilian preference for point and beach break wave types. We also suggest that surfing’s being included in the 2020 Summer Olympics might result in modified strategies to bolster intranational ranking at the expense of WCT performance; we quantify this phenomenon by introducing a reified Bradley-Terry entity: a “compatriot monster” with an estimated strength of about 0.017.
Further work might include incorporation of more tournament results into our likelihood function, and possibly to investigate priority infringements between compatriots. One suggestion, made by an anonymous JSA referee, was to apply the methodology used in Section 7 to events that occurred prior to the announcement that surfing would be in the Olympics. This would allow the quantification of any change in non-competitive behaviour between compatriots.
References
1 | Aldous, D. , (2017) , Elo ratings and the sports model: A neglected topic in applied probability? Statistical Science 32: (4), 616–629. |
2 | Basu, D. , (1977) , On the elimination of nuisance parameters, >Journal of the American Statistical Association 77: , 355–366. |
3 | Booth,D , (1995) , Ambiguities in pleasure and discipline: The development of competitive surfing, Journal of Sport, 22: (3),189–206. |
4 | Bradley,R.A , (1954) , Incomplete block rank analysis: On the appropriateness of the model for a method of paired comparisons, Biometrics, 10: (3),375–390. |
5 | Burgess,A , (2020) ,Why Brazilians dominate the world of surfing?, online; Red Bull Surfing. https://www.youtube.com/watch?v=JI9F0y4V-38&ab_channel=RedBull. |
6 | Butt,T , Russell,P , Gregg,R 2004, Surf science: an introduction to waves for surfing, University of Hawaii Press. |
7 | Douglas-Rosa,A , (2020) , The perfect storm, Surfer, 61: (2), 70–79. |
8 | Edwards,A.W.F. , 1992, Likelihood (Expanded Edition), John Hopkins. |
9 | Farley,O.R.L. , Raymond,,E. , Secomb,,J.L. , Ferrier,,B. , Lundgren,,L. , Tran,,T.T , Abbiss,,C. , Sheppard,,J.M. , (2015) , Scoring analysis of the Men’s World Championship Tour of Surfing, The International Journal of Aquatic Research and Education, 9: (1), 38–48. |
10 | Hankin,,R.K.S. , (2010) , A generalization of the Dirichlet distribution, Journal of Statistical Software 33: (11), 1–18. |
11 | Hankin,,R.K.S. , (2017) , Partial rank data with the hyper package: Likelihood functions for generalized Bradley-Terry models, The R Journal 9: (2), 429–439. |
12 | Hankin,,R.K.S. , (2020) , A generalization of the Bradley-Terry model for draws in chess with an application to collusion, Journal of Economic Behavior and Organization 180: , 325–333. |
13 | Ho,,S , (2021) , The ugly truths surfing’s Olympic debut can’t hide, Online, https://www.stuff.co.nz/sport/olympics//the-ugly-truths-surfings-olympic-debut-cant-hide. |
14 | Johnson,,S.R , Henderson,D.A , Boys,,R.J , 2020, On Bayesian inference for the extended Plackett–Luce model. |
15 | Luce,,R , 1959, Individual choice behaviour: A theoretical analysis, Wiley, New York. |
16 | Lundgren,,L.E. , Newton,,R.U , Trin,,T.T , Dunn,M , Simphius,,S , (2014) , Analysis of manoeuvres and scoring in competitive surfing, International Journal of Sports Science and Coaching 9: (4), 663–669. |
17 | Plackett,R.L. , (1975) , The analysis of permutations, Applied Statistics 24: , 193–202. |
18 | Scarfe,B.E. , Elwany,M.H.S , Mead,S.T , Black,K.P , 2003, The science of surfingwaves and surfing breaks –a review, Technical Report https://escholarship.org/uc/item/6h72j1fz,ScrippsInstitutionofOceanography.. |
19 | Tulloch,A , 2019, Italo Ferreira clinches first WSL world title and Tokyo 2020 berth, Olympic News (IOC), https://olympics.com/en/news/surfing-italo-ferreira-wsl-world-title-olympic-berth. |
20 | Turner,H , Firth,D , (2012) , Bradley–Terry models in R: The BradleyTerry2 package, Journal of Statistical Software 48: (9), 1–21. |
21 | Warshaw,M , 2010, A brief history of surfing, Chronicle Books. |
22 | West,L.J , Hankin,,R.K.S , (2008) , Exact tests for two-way contingency tables including structural zeros, Journal of Statistical Software 28: (11), 1–19. |
23 | World Surf League , 2021, Rules and regulations, online,https://www.worldsurfleague.com/pages/rules-and-regulations. |




