An alternative ranking system for biathlon pursuit races
Abstract
Biathlon is an Olympic sport combining cross-country skiing with rifle shooting, giving a penalty for each target miss. The biathletes ran different race formats, including the pursuit race. During this race, the biathletes chase the leader with a start time identical to the result of the sprint race previously achieved. So, pursuit involves different skills (such as tactics or management of emotional pressure) that are not present during races with an interval-start procedure like sprint. Nevertheless, final pursuit rankings are strongly correlated to sprint ones, which prevents a spectacular comeback after a disappointing sprint race. We present here an alternative pursuit ranking system that is nearly decorrelated to sprint rankings. This simple ranking system is based on comparisons with previous pursuit results. The current and the alternative rankings were then compared on different pursuit rankings, using a database of 148 results from men pursuit world cups. The alternative ranking was shown to strongly modify a single pursuit ranking but these modifications were smoothed on a whole world cup season. Advantages and limitations of the alternative ranking system are discussed, paving the way to a fairer modification of the current pursuit ranking to increase surprise and suspense in biathlon pursuit races.
1Introduction
Biathlon is an Olympic sport combining 3 to 5 laps of cross-country skiing with rifle shooting. Between each skiing lap, biathletes complete a shooting session in which they attempt to hit five targets placed at a distance of 50 m, alternating between the prone and standing shooting positions between laps. A penalty (time or skiing distance) is given for each target miss. The biathlete with the shortest overall time wins the race (International Biathlon Union, 2020). Several different biathlon events exist, in which the individual distance was included as an official Olympic event in 1960, followed by sprint (1980), pursuit (2002), and mass start (2006) (International Biathlon Union, 2020). More precisely, in pursuit races, the 60 best biathletes from the sprint race chase the leader with a start time identical to the result of the sprint race achieved a few days before (i.e. if the second biathlete arrives 12s after the winner of the sprint race, he will start 12s after the first for the pursuit race and so on). So, two of the four current individual Olympic biathlon races involve direct confrontation (mass-start and pursuit), where biathletes are fighting against each other, not versus time. In these events, tactics play a major role and the final ranking is often decided during the last shooting and/or the final skiing sprint. Furthermore, tight duels during the shootings and the subsequently increased emotional pressure (Vickers et al., 2007) influence shooting times and accuracies differently than for races with an interval-start procedure. During pursuit or mass-start races, drafting behind other skiers, locating oneself optimally in the crowd also helps maximize the utilization of individual skills (Laaksonen et al., 2018b). Finally, in pursuit races, the skiing speed exerts less impact on the overall performance than in sprint, since the pursuit event involves four bouts of shooting with shorter skiing loops between (Laaksonen et al., 2018b). The pursuit race is therefore expected to reward different skills than sprint or individual races.
Nevertheless, and despite its increasing public audience (EBU, 2019), the biathlon has been sparsely studied, as highlighted by the fact that a search in PubMed with “biathlon” as a keyword currently results in 107 hits, whereas a similar search with “cross-country skiing” (resp. “sport shooting”) yields almost 8 (resp. 7) times as many hits. Among these references, the impact of different parameters on shooting accuracy (Gallicchio et al., 2019; Josefsson et al., 2020) or the influence of the different biathlon phases on sprint or individual results (Laaksonen et al., 2018a; Luchsinger et al., 2019) were extensively examined. Despite their specific aspects, the pursuit and the mass-start races are almost unexplored. Recently, Luchsinger et al. (2020) investigated the contribution from cross-country skiing, sprint race performance, and shooting components to the pursuit race performance. Sprint race performance was found to be the most influential factor, explaining more than 50% of the final pursuit performance. This result and the fact that the sprint races are the most numerous events (approximatively 40% of the events, 30% being pursuits, 20% mass-starts, and 10% individual races) during a world cup season involve that more than 55% of the final overall world cup results are due to sprint races, which seems very high. Also, the specific skills needed for the pursuit races (tactics, management of emotional pressure . . .) are not rewarded by the current pursuit ranking, mostly hidden by the importance of the sprint performances. By consequence, decreasing the correlation between sprint and pursuit results is desirable to decrease the influence of the sprint results in the world cup ones, to reward the pursuit specific skills, and to increase suspense and surprise by allowing biathletes that poorly performed during the sprint race to obtain a good pursuit result. An alternative pursuit ranking which minors the influence of the sprint results would therefore be of high interest for biathletes and organizers of international biathlon events. Different rankings than official ones have been recently developed in numerous sports, for example for football teams (Gásquez & Rovuela, 2016), for football players (Wolf et al., 2020), for tennis (Kovalchik, 2020), for basketball (Barrow et al., 2013) . . . We refer the interested reader to the review of Wunderlich and Memmert (2020) for more details. But, to our knowledge, none of the previous works could be easily adapted to our specific biathlon pursuit problem. Therefore, the current paper aimed to propose an alternative, simple, and fairer ranking for the biathlon pursuit and to investigate its impact on pursuit races and world cup pursuit rankings.
2Materials and methods
2.1Data collection
The final results of all sprint and pursuit races are publicly available on the datacenter webpage of the IBU: https://biathlonresults.com/. The results were collected on the 15th December 2020 starting from the 2001/2002 season. All the results taken into account for the men’s pursuit world cup were gathered, including world championships and Olympic games before 2014. It provides us 148 different pursuit results. All these results provide us an important database of pursuit results in different conditions that are considered to give an appropriate representation of the different possible pursuit scenarios.
2.2Alternative pursuit ranking
As explained previously, during pursuit races, biathletes are racing each other in real-time for a better rank and not racing against time. Therefore, we chose to work using final ranks, not final times. All the pursuit results were gathered to compute final pursuit ranks according to the starting pursuit rank. This global information is given in Fig. 1 for all sprint ranking positions and the distributions of the final pursuit ranks are provided in Fig. 2 for some starting ranks.
Fig. 1
Final pursuit ranks according to starting pursuit ranks.
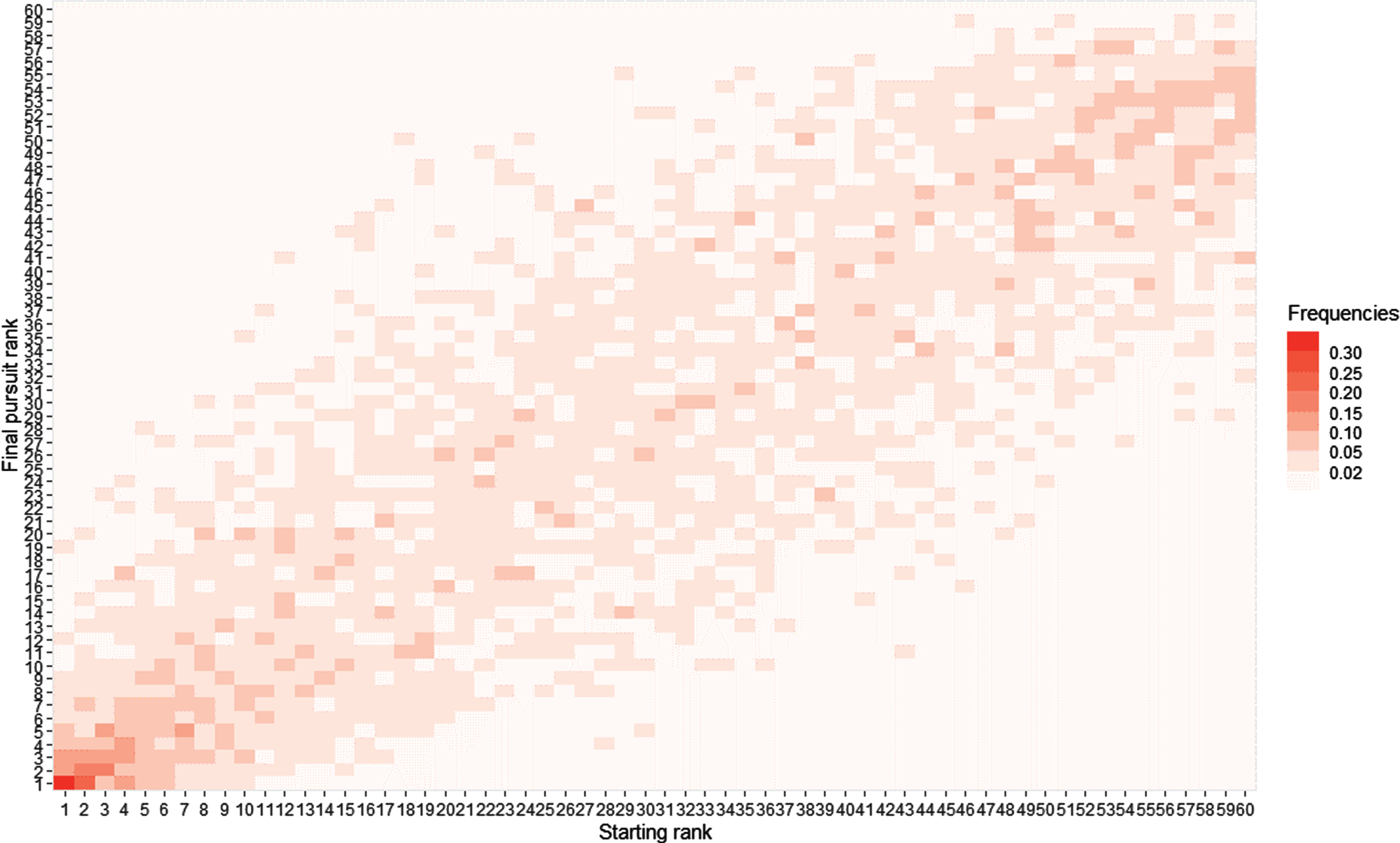
Fig. 2
Barplots of the final pursuit ranks according to six different starting pursuit ranks.
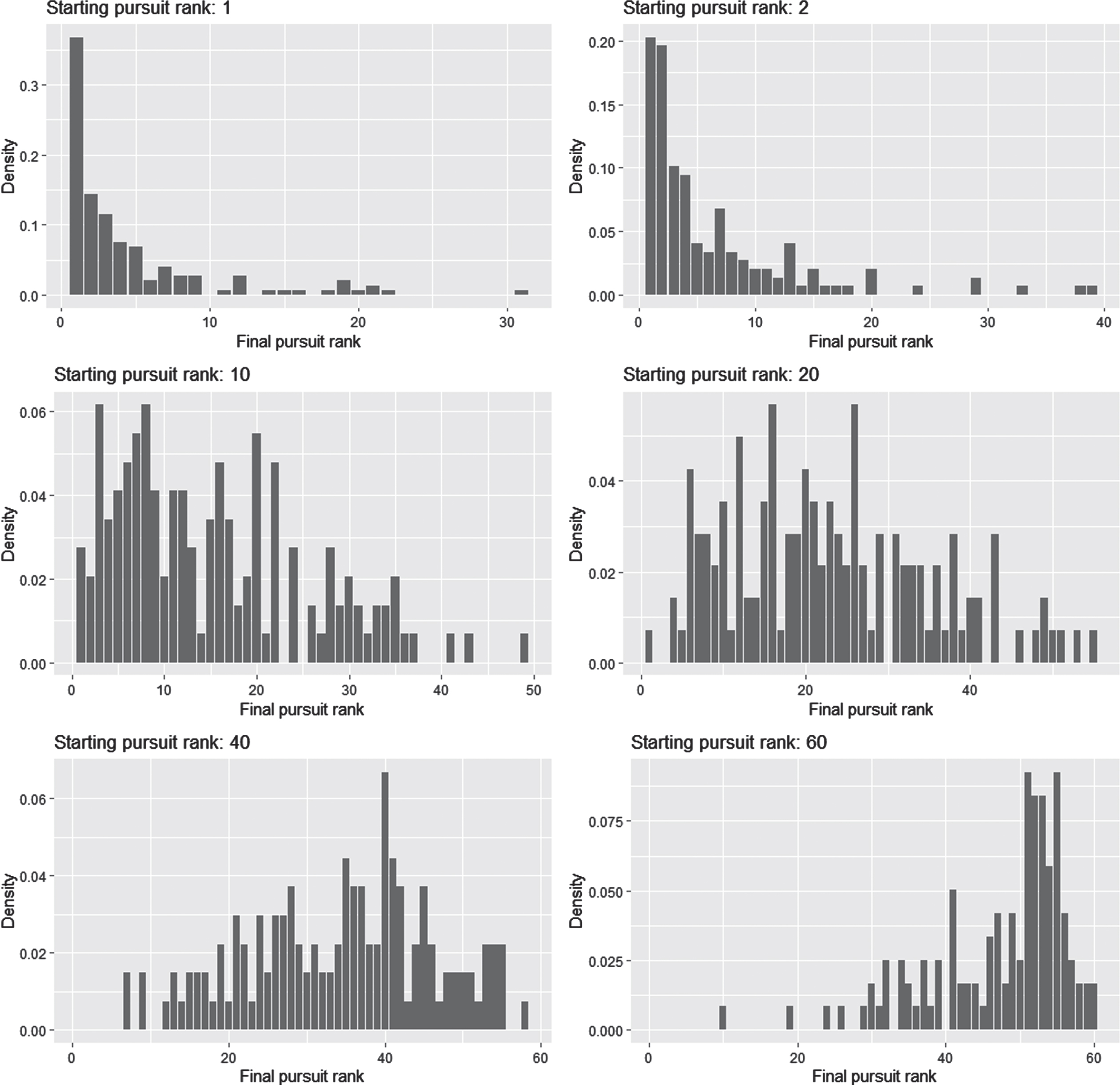
These figures emphasize the results of Luchsinger et al. (2020), highlighting the importance of the starting pursuit rank in the final pursuit result.
We propose an alternative approach to define a fairer pursuit final ranking that will decrease this correlation. For each starting biathlete at a pursuit race k, a quantity qki is calculated according to the position of his final results fki in the final result distribution of all previous starters with the same rank i. Some of these distributions are plotted in Fig. 2. This quantity is given by the following formula
This formula is somewhat natural and explainable: indeed, if qki is equal to zero, it means that, during the previous 148 pursuit races, no biathlete with starting rank i achieved a final better (i.e. smaller) rank fki and so, for all j, fji ≥ fki. So, this biathlete deserves a good alternative final pursuit rank, whatever his starting rank. On the contrary, if qki is equal to one (i.e. for all j, fji < fki), then fki is the worst final pursuit rank achieved by any of the 148 biathletes with this starting rank i and it must lead to a poor alternative final pursuit rank.
Estimating a quantity (here a performance during a pursuit race) using comparisons to existing distributions (such as the previous pursuit results) is a common approach in non-parametric statistics (Wasserman, 2006). It prevents making false assumptions on the underlying distributions but requires an important number of datasets. In this application, with 148 datasets of previous biathlon pursuit results, this framework seems adapted. All the different pursuit scenarios (including extreme ones) will by consequence be taken into account according to their previous occurrences. Note that, if we consider each of the 148 pursuit races as a ballot, a connection can be made with the well-known Borda count ranking (Borda, 1781) for the use of all the pursuit races with strong differences for the other part of the alternative ranking computations. We can also notice that there exists a continuum of possible ranking functions between the non-parametric alternative one defined above and the current one. So, if needed, the alternative method could be modified to bring fewer modifications to the pursuit rankings. But this will complicate the formula provided above and, thus, is beyond the scope of this paper.
2.3Data analyses
All the data analyses were performed using the R freeware, version 3.5.1 (R Core Team, 2019). The correlations were calculated using Spearman’s rank correlation coefficient. For the world cup rankings, we remind that only the first forty biathletes of each race score points, according to the current rules of IBU (International Biathlon Union, 2020). Note that all the races are taken into account to compute all the alternative rankings, even those that took place in the future. This will ensure a good estimation of the different distributions of the final rankings according to the starting ranks.
3Results
3.1Study of a specific pursuit race
We first choose to study a specific pursuit race to illustrate the modifications induced by our alternative ranking. We choose the pursuit race that took place at Annecy –Le Grand Bornand (21 December 2019). The results are given in Table 1.
Table 1
Sprint ranks, current and alternative final pursuit rank for the pursuit race in Annecy-Le Grand Bornand in 2019. The gain is the difference between the alternative and the current pursuit rank
| Current pursuit rank | Name | Sprint rank | Alternative pursuit rank | Gain |
| 1 | BOE Johannes Thingnes | 4 | 1 | 0 |
| 2 | FILLON MAILLET Quentin | 3 | 5 | –3 |
| 3 | CHRISTIANSEN Vetle Sjaastad | 13 | 2 | 1 |
| 4 | BOE Tarjei | 2 | 25 | –21 |
| 5 | DOLL Benedikt | 1 | 42 | –37 |
| 6 | JACQUELIN Emilien | 20 | 4 | 2 |
| 7 | FOURCADE Martin | 12 | 12 | –5 |
| 8 | BJOENTEGAARD Erlend | 5 | 24 | –16 |
| 9 | PEIFFER Arnd | 21 | 10 | –1 |
| 10 | SCHEMPP Simon | 32 | 3 | 7 |
| 11 | HORN Philipp | 25 | 7 | 4 |
| 12 | DALE Johannes | 6 | 38 | –26 |
| 13 | LOGINOV Alexander | 11 | 23 | –10 |
| 14 | KRCMAR Michal | 17 | 15 | –1 |
| 15 | DESTHIEUX Simon | 8 | 35 | –20 |
| 16 | EBERHARD Julian | 10 | 29 | –13 |
| 17 | WINDISCH Dominik | 7 | 48 | –31 |
| 18 | ILIEV Vladimir | 22 | 14 | 4 |
| 19 | PONSILUOMA Martin | 15 | 30 | –11 |
| 20 | PIDRUCHNYI Dmytro | 18 | 27 | –7 |
| 21 | LAPSHIN Timofei | 19 | 26 | –5 |
| 22 | CLAUDE Florent | 23 | 20 | 2 |
| 23 | KUEHN Johannes | 14 | 41 | –18 |
| 24 | HOFER Lukas | 9 | 49 | –25 |
| 25 | TRSAN Rok | 47 | 9 | 16 |
| 26 | EDER Simon | 26 | 21 | 5 |
| 27 | PRYMA Artem | 34 | 17 | 10 |
| 28 | LABASTAU Mikita | 46 | 11 | 17 |
| 29 | DUDCHENKO Anton | 31 | 19 | 10 |
| 30 | ELISEEV Matvey | 28 | 33 | –3 |
| 31 | PORSHNEV Nikita | 24 | 37 | –6 |
| 32 | BORMOLINI Thomas | 60 | 6 | 26 |
| 33 | RASTORGUJEVS Andrejs | 36 | 22 | 11 |
| 34 | CLAUDE Fabien | 35 | 31 | 3 |
| 35 | FEMLING Peppe | 56 | 8 | 27 |
| 36 | GARANICHEV Evgeniy | 30 | 40 | –4 |
| 37 | SEPPALA Tero | 33 | 34 | 3 |
| 38 | BOCHARNIKOV Sergey | 29 | 43 | –5 |
| 39 | SAMUELSSON Sebastian | 27 | 44 | –5 |
| 40 | NELIN Jesper | 42 | 32 | 8 |
| 41 | VACLAVIK Adam | 37 | 39 | 2 |
| 42 | STVRTECKY Jakub | 16 | 52 | –10 |
| 43 | GUIGONNAT Antonin | 59 | 13 | 30 |
| 44 | WEGER Benjamin | 58 | 16 | 28 |
| 45 | LEITNER Felix | 49 | 36 | 9 |
| 46 | LATYPOV Eduard | 55 | 18 | 28 |
| 47 | TKALENKO Ruslan | 39 | 45 | 2 |
| 48 | NORDGREN Leif | 38 | 46 | 2 |
| 49 | WIESTNER Serafin | 57 | 28 | 21 |
| 50 | BAUER Klemen | 44 | 47 | 3 |
| 51 | MALYSHKO Dmitry | 41 | 53 | –2 |
| 52 | STENERSEN Torstein | 43 | 51 | 1 |
| 53 | CHENG Fangming | 45 | 50 | 3 |
| 54 | DOHERTY Sean | 40 | 57 | –3 |
| 55 | LANDERTINGER Dominik | 52 | 54 | 1 |
| 56 | DOVZAN Miha | 50 | 56 | 0 |
| 57 | GUZIK Grzegorz | 54 | 55 | 2 |
| 58 | DOLDER Mario | 48 | 58 | 0 |
| 59 | HARJULA Tuomas | 51 | 59 | 0 |
| 60 | BURKHALTER Joscha | 53 | 60 | 0 |
The correlation between the starting rank and the current pursuit rank (resp. the alternative pursuit rank) is equal to 0.82 (resp. 0.20) which highlights the decreased influence of the sprint results on the alternative ranking. If we look at the main modifications we could see that T. Boe, B. Doll, E. Bjoentegaard, or J. Dale are losing more than 15 ranks with the alternative pursuit ranking. This is due to the fact that they had lost ranks during the pursuit and, therefore, their current good pursuit ranks are mainly due to their good performances in the sprint race. So, it seems logical that they lose ranks with the alternative ranking. On the contrary, E. Jacquelin, S. Schempp, and T. Bormolini performed very well during the pursuit race (resp. 14, 22, 28 ranks won during the pursuit race) and deserve their better pursuit rank using the alternative ranking. For example, T. Bormolini will be ranked 6th with the alternative pursuit ranking whereas it never happened on all the past 148 pursuit races with the current ranking system for a biathlete with the 60th starting rank, as it could be seen on the last plot of Fig. 2.
The computer code used to obtain the results of Table 1 is provided as Supplementary Material with the corresponding dataset. This code could be reused with any pursuit result to compute the alternative rankings in less than a second on an ordinary laptop.
3.2Study of the 2019/2020 pursuit world cup ranking
As explained above, the alternative pursuit ranking can lead to major modifications on a specific pursuit race. Then, we chose to study the 2019/2020 pursuit world cup to analyze the modifications at the scale of a whole season. The first ten biathletes using the two pursuit rankings on all the 2019/2020 races are given in Table 2.
Table 2
The current and the alternative rankings for the 2019/2020 pursuit world cup. The winner of a pursuit race scores 60 points, the second 54 points, the third 48 points, etc. . . . until the fortieth who scores one point (IBU, 2020)
| Rank | Name | Alternative points | Name | Official points |
| 1 | JACQUELIN Emilien | 219 | JACQUELIN Emilien | 232 |
| 2 | FOURCADE Martin | 188 | FOURCADE Martin | 230 |
| 3 | BOE Johannes Thingnes | 171 | FILLON MAILLET Quentin | 230 |
| 4 | PEIFFER Arnd | 160 | BOE Johannes Thingnes | 217 |
| 5 | FILLON MAILLET Quentin | 154 | LOGINOV Alexander | 197 |
| 6 | GARANICHEV Evgeniy | 153 | BOE Tarjei | 178 |
| 7 | CHRISTIANSEN Vetle | 141 | DESTHIEUX Simon | 171 |
| 8 | BJOENTEGAARD Erlend | 138 | CHRISTIANSEN Vetle | 169 |
| 9 | LOGINOV Alexander | 128 | PEIFFER Arnd | 167 |
| 10 | KRCMAR Michal | 114 | BJOENTEGAARD Erlend | 147 |
First, we could see that there is only a small modification on the podium, J. Boe who was 4th with the current ranking is now 3rd whereas Q. Fillon-Maillet who was 3rd is now 5th. There is no modification for the first two ranks and eight biathletes are in the two top 10. The strong modifications of the rankings of each pursuit race (as seen in the previous subsection) lead to non-negligible but with less impact world cup ranking modifications. Nevertheless, we can note some important individual modifications for example for E. Garanichev (26th with the current ranking and 6th with the alternative) or M. Krcmar (resp. 21st and 10th) who benefit from the alternative ranking unlike T. Boe (resp. 6th and 11th) or S. Desthieux (resp. 7th and 18th).
The number of points with the alternative ranking seems lower than the current one. Indeed, that is an important property of the alternative ranking: the points are awarded to most biathletes as they are less linked to the sprint results (71 biathletes with the current ranking and 81 with the alternative one). But there is a strong correlation of 0.83 between the number of points of each biathlete with the current or the alternative ranking which could explain the relatively small modifications between the two rankings, as mentioned above.
Note that these small modifications could have a major impact on the overall world cup ranking. Indeed, J. Boe won the overall world cup with 2 points ahead of M. Fourcade. With the alternative ranking, M. Fourcade would have won the overall world cup with the same margin. Obviously, this is science fiction as the application of the alternative ranking would probably modify the pursuit races. Nevertheless, it could highlight the importance of the sprint results in the overall world cup ranking (J. Boe won 4 of them this season) and the potential impact of the alternative ranking on the overall world cup rankings, mainly when there are few points of difference.
3.3Study of the last ten pursuit world cup seasons
We then studied the pursuit world cup seasons of the ten last years to analyze if the previous remarks could be extended. First, on the pursuit races, the correlations between the starting ranks and the pursuit ranks decreased as seen in the first results subsection: the correlation mean is equal to 0.74 with the current ranking and to 0.06 with the alternative one. Then, we analyzed the last ten pursuit world cup rankings. For all the rankings, there are more biathletes with points with the alternative ranking than with the current one with a mean increase of 11 biathletes. The mean of the difference of points between the first rank and the ranks from 2 to 10 are also all smaller for the alternative pursuit ranking. This would have led to, in most of the cases, closer rankings and more suspense in the last races of the season.
As seen in the previous subsection, the modifications on the podiums of the pursuit world cup rankings are small but not negligible. For 7 seasons we have the same winner, two times the first and the second invert their rankings and for the last one, the 4th becomes 1st with the alternative ranking. There are only two identical podiums but, if we compare the name of the first three biathletes, 23 above 30 are shared by the two different rankings. It highlights some important common traits between the two rankings even if some individual rankings could be strongly modified, for example, a biathlete who was 3rd with the current ranking is 16th with the alternative one highlighting the importance of his sprint results in his good current pursuit ranking.
4Discussion
4.1Advantages of the alternative ranking
First, the main advantage of this alternative ranking is obviously that the correlation with the starting rank is very low. Therefore, even the 60th ranked at the end of the sprint had a chance to be on the podium which is not the case with the current ranking. In other words, a biathlete with high pursuit skills who had a bad sprint result has an increased chance of obtaining a good pursuit result with the alternative ranking. But we have to keep in mind that the best pursuit biathlete is still the one that cut the finish line first. It will result in more surprising and contested pursuit races, at each stage of the races, which is desirable for gaining audience (Bizzozero et al., 2016). More generally, it will also decrease the importance of the sprint races on the overall world cup rankings.
Second, even if the alternative ranking deeply modifies each pursuit ranking, each season pursuit world cup ranking is less modified than each single pursuit race. It sounds natural as, even if tactics and head-to-head are of major importance in pursuit races, it remains biathlon with cross-country skiing and shootings. So, the best biathletes are globally the same, the alternative pursuit ranking allows to define the pursuit as a whole discipline with real specialists, not just as a relatively small perturbation of the sprint ranking (as proven in Luchsinger et al., 2020).
4.2Limitations of the alternative ranking
The first criticism that could be made to the alternative ranking is that it is more complicated than the current one. Nowadays, when you cross the finish line of the pursuit race in 3rd place, you are ranked 3rd, whereas with the alternative ranking you need to wait for all the biathletes to finish the race. Even if the alternative ranking is calculated in less than one second at the end of the race, it could be seen as a limiting factor. Nevertheless, this argument needs to be mitigated. First, the winner of the pursuit race is necessarily the winner of the alternative pursuit ranking and is therefore known immediately as he crosses the finish line. Then, for the sprint or individual biathlon races or for other sports such as the decathlon (where you need to refer to a complex points system to see how many points you score, see Cox et al. (2002) for further details) the final ranks are unknown until the last athlete crosses the finish line. This could induce important cliffhangers when biathletes are waiting in the finish area to wait and see if they are or not on the podium. Finally, at each split time, a ranking based on the alternative pursuit ranking could be quickly calculated to inform the biathletes of their rankings.
Another limitation is that, when you have several biathletes that did not start or did not finish the pursuit race despite their presence on the first 60 biathletes of the sprint, it artificially increases the alternative rankings of biathletes that are at the end of the ranking. That could induce unmerited good alternative pursuit rankings for biathletes that have not performed well during the pursuit race but who improved their final rankings thanks to those who gave up. It could be solved by integrating the number of finishers of each pursuit race in the formula to calculate the quantity qki for example by dividing fji and fki by the number of finishers of each pursuit race. But, to keep a very simple formula and as it is uncommon and does not impact the more important highest ranks, it was not taken into account in this paper.
5Conclusion
The alternative pursuit ranking presented in this paper is less correlated to the starting ranking than the current one. Some minor limitations remain but, if considered as important, could be easily corrected. This paper paves the way to a fairer modification of the current pursuit ranking that will also increase surprise and suspense in the pursuit races.
Acknowledgments
The author thanks Benoît Rey-Robert for fruitful comments and English corrections and the anonymous reviewer for his/her fruitful comments that helped us to improve the paper.
Declaration of interest statement
No potential conflict of interest was reported by the author.
SUPPLEMENTARY MATERIAL
[1] The computer code and the dataset of the pursuit of Annecy-Le Grand Bornand 2019 are provided as Supplementary Material.
References
1 | Barrow D. , Drayer I. , Elliott P. , Gaut K. , Osting B. , (2013) . Ranking rankings: An empirical comparison of the predictive power of sports ranking methods. Journal of Quantitative Analysis in Sport, 9: (2), 187–202. doi: 10.1515/jqas-2013-0013. |
2 | Bizzozero P. , Flepp R. , Franck E. , (2016) . The importance of suspense and surprise in entertainment demand: Evidence from Wimbledon. Journal of Economic Behavior & Organization, 130: , 47–63. doi: 10.1016/j.jebo.2016.07.006. |
3 | Borda J.C. , Mémoire sur lesálections au scrutin, Histoire de l’Acadámie Royale des Sciences. |
4 | Dunn C. , Ryan T.F. , (2002) . An analysis of decathlon data. Journal of the Royal Statistical Society:. Journal of the Royal Statistical Society: Series D (The Statistician), 51: (2), 179–187. doi: 10.1111/1467-9884.00310. |
5 | EBU. 2019. European Broadcasting Union. https://www.ebu.ch/news/2019/03/eurovision-sport-brings-biathlon-to-theworld (accessed on 8 January 2021). |
6 | Gallicchio G. , Finkenzeller T. , Sattlecker G. , Lindinger S. , Hoedlmoser K. , (2002) . The influence of physical exercise on the relation between the phase of cardiac cycle and shooting accuracy in biathlon. European Journal of Sport Science, 19: (5), 567–575. doi: 10.1080/17461391.2018.1535626. |
7 | Gásquez R. , Royuela V. , (2016) . The determinants of international football success: A panel data analysis of the elo rating. Social Science Quarterly, 97: (2), 125–141. doi: 10.1111/ssqu.12262. |
8 | International Biathlon Union. 2020. IBU event and competition rules. http://www.biathlonworld.com/downloads/ (accessed on 8 January 2021). |
9 | Josefsson T. , Gustafsson H. , Iversen Rostad T. , Gardner F. L. , Ivarsson A. , 2020. Mindfulness and shooting performance in biathlon. A prospective study. European Journal of Sport Science, Forthcoming. doi: 10.1080/17461391.2020.1821787. |
10 | Kovalchik S. , Extension of the Elo rating system to margin of victory. International Journal of Forecasting, 36: (4), 1329–1341. doi: 10.1016/j.ijforecast.2020.01.006. |
11 | Laaksonen M.S. , Finkenzeller T. , Holmberg H.-C. , Sattlecker G. , (2018) . The influence of physiobiomechanical parameters, technical aspects of shooting, and psychophysiological factors on biathlon performance: A review. Journal of Sport and Health Science, 7: (4), 394–340. doi: 10.1016/j.jshs.2018.09.003. |
12 | Laaksonen M.S. , Jonsson M. , Holmberg H.-C. , (2018) b. The olympic biathlon –recent advances and perspectives after pyeongchang. Frontiers in Physiology , 9: , 796. doi: 10.3389/fphys.2018.00796. |
13 | Luchsinger H. , Kocbach J. , Ettema G. , Sandbakk Ø. , (2019) . The contribution from cross-country skiing and shooting variables on performance-level and sex differences in biathlon world cup individual races. International Journal of Sports Physiology and Performance, 14: (2), 190–195. doi: 10.1123/ijspp.2018-0134. |
14 | Luchsinger H. , Kocbach J. , Ettema G. , Sandbakk Ø. , 2020. Contribution from cross-country skiing, start time and shooting components to the overall and isolated biathlon pursuit race performance. PLoS One, 15: (9), e0239057. doi: 10.1371/journal.pone.0239057. |
15 | RCoreTeam. 2019. R:ALanguage and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/. |
16 | Vickers J.N. , Williams A.M. , (2007) . Performing under pressure: The effects of physiological arousal, cognitive anxiety, and gaze control in biathlon. Journal of Motor Behavior, 39: (5), 381–394. doi: 10.3200/jmbr.39.5.381-394. |
17 | Wasserman L , (2006) . All of nonparametric statistics. Springer Science & Business Media. |
18 | Wolf S. , Schmitt M. , 2020. A football player rating system, Journal of Sports Analytics, Forthcoming. doi: 10.3233/JSA-200411. |
19 | Wunderlich F. , Memmert D. , 2020. Forecasting the outcomes of sports events: A review. European Journal of Sport Science, Forthcoming. doi: 10.1080/17461391.2020.1793002. |




