“Choose your opponent”: A new knockout design for hybrid tournaments†
Abstract
We present a new, simple knockout format for sports tournaments, that we call “Choose Your Opponent”, where the teams that have performed best during a preliminary group stage can choose their opponents during the subsequent knockout stage. The main benefit of this format is that it essentially solves a recently identified incentive compatibility problem when more than one teams from a group advance to the knockout stage, by effectively canceling the risk of tanking. This new design also makes the group stage more exciting, by giving teams a strong incentive to perform at their best level, and more fair, by limiting the risk of collusion and making sure that the best group winners are fairly rewarded in the knockout round. The choosing procedure would add a new, exciting strategic component to the competition. Advancing teams would choose their opponent during new, much anticipated TV shows which would attract a lot of media attention. We illustrate how this new format would work for the round of 16 of the UEFA Champions League, the most popular soccer club competition in the world.
1Introduction
Many sports tournaments consist of a group stage played as a round-robin, followed by a single-elimination knockout stage. Often, the best k teams1 in each group advance to the knockout stage, and the knockout stage follows a predetermined bracket route that depends only on group labels (e.g., A, B, C, etc.) and group ranks (group winner, group runner-up, etc.). Usually, for the teams that advance, a better group rank means facing an opponent with a worse group rank during the first round of the knockout stage. Since group rank is supposed to reflect team abilities, the bracket gives, on paper, an incentive to advance with the best group rank. Probably the most famous example of a competition using such a format is the FIFA World Cup (soccer). The knockout bracket of the 2018 FIFA World Cup is shown in Figure 1; the 8 groups are labeled A to H; C1 denotes the winner of Group C, F2 denotes the runner-up of Group F, etc. Some variations exist; for instance, when the number of groups is not a power of 2, the best k teams in each group advance to the knockout stage, as well as the best of the teams ranked k + 1 in their group (compared across groups), so as to populate a bracket with 2N teams. For example, the 1986, 1990, 1994 FIFA World Cups, as well as the UEFA Euros since 2016, use a format with n = 6 groups of 4, where the best k = 2 teams in each group advance to the round of 16 (2N = 16), together with the best 2N - kn = 4 third-placed teams; see (Guyon, 2016) for details.
Fig. 1
Bracket of the knockout stage of the 2018 FIFA World Cup.
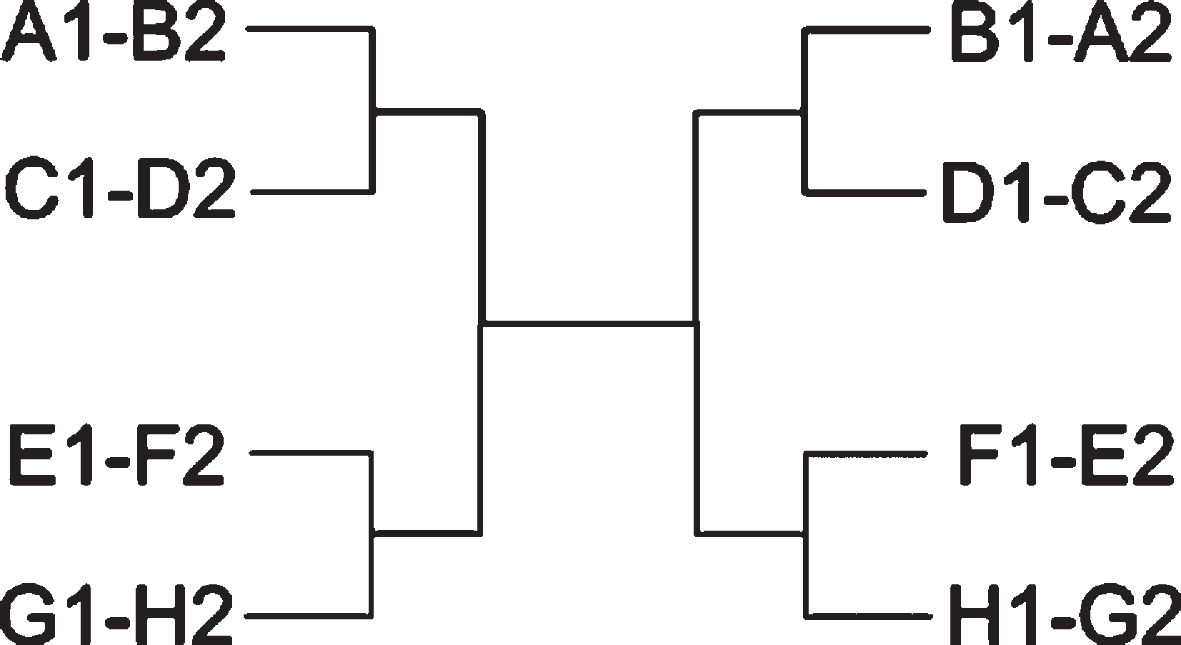
Compared to a pure round-robin tournament involving all teams, this hybrid format made of a group stage followed by a knockout stage has more outcome uncertainty, but it has much less matches, so it can fit in a given calendar frame. It also has a much smaller proportion of noncompetitive matches. Compared to a pure knockout tournament, this hybrid format has less outcome uncertainty, and it gives all teams a minimum number of matches (at least two) and a chance to advance even if they lose their first game.
Those traditional designs suffer from well-known and well-documented flaws. Fairness issues include the risk of collusion, the risk of tanking/shirking, the possible absence of win incentive in the last group games, and group winners being poorly rewarded in the knockout stage despite a great performance in the group stage. Those flaws are discussed in detail in Section 2.
In this article, in order to eliminate these flaws, we suggest a new knockout format. In this new format, that we call “Choose Your Opponent”, the teams that have performed best during the group stage can choose their opponent during the subsequent knockout stage. The main benefit of this format is that it makes the group stage more exciting, by giving teams a strong incentive to perform at their best level. It also makes the group stage more fair, by limiting the risk of collusion, effectively canceling the risk of tanking, and making sure that the best group winners are fairly rewarded for their group stage performance and do not meet strong opponents in the first knockout round.
In particular, one of the remarkable benefits of this design is that it practically solves the problem identified by Vong (2017), who has shown that in the classical design of hybrid tournaments, i.e., when bracket routes are predetermined based on group labels and group ranks, in order to exclude the risk of tanking, it is both necessary and sufficient to allow only the top-ranked team in each group to advance. That is crucially important because regulations that allow only one qualifier from each group may not be desirable, as they tend to produce many stakeless games. Though the “Choose Your Opponent” design cannot fully cancel the risk of tanking, it makes tanking irrelevant in practice, since in all realistic situations tanking can only decrease a team’s probability of achieving its goal, whether it be winning the tournament or reaching a particular round.
Moreover, advancing teams would pick their opponent during new, much anticipated TV shows which would attract a lot of media attention; the picking strategies of the teams would certainly be highly debated by the media and among fans.
The “Choose Your Opponent” knockout format appears to have been used in the Austrian ice hockey league since the 2012–2013 postseason “Playoff Pick” (Austrian ice hockey league website; Matisz, 2020). The top three teams in the league can choose their opponent from the playoff spots 5 to 8. For instance, in 2016–17, the first-placed Vienna Capitals chose the fifth-placed HC TWK Innsbruck and the second-placed EC Red Bull Salzburg picked the seventh-placed Graz 99ers (Wikipedia, 2016–17 Austrian Hockey League season). In 2017–18, Vienna Capitals also finished in first place and again picked HC TWK Innsbruck, this time six-placed (Wikipedia, 2017–18 Austrian Hockey League season). In 2019–20, they finished in third place and preferred the fifth-placed EC Graz 99ers to the seventh-placed Black Wings Linz (Wikipedia, 2019–20 Austrian Hockey League season).
The “Choose Your Opponent” design has also been used in the Southern Professional Hockey League in the U.S. under the name “Challenge Round” in 2017–18 and 2018–19 (Southern Professional Hockey League website).2 The English rugby league applied it under the name “Club Call” in 2009–14 for semifinals only (Wikipedia, Super League play-offs). The format has also recently been used in bridge (Canadian Bridge Federation; The United States Bridge Federation), chess (Chess.com website), sailing (2015 World Match Racing Tour), and in the multiplayer online battle arena video game Dota 2 (The International Dota 2 Championships).
However, it seems that it has never been used in the most popular sports tournaments. It could be used in many major tournaments, including:
• Soccer: FIFA World Cup, UEFA European Championship, Copa America, African Cup of Nations, UEFA Champions League, UEFA Europa League, playoffs of European qualifiers to the FIFA World Cup, etc.
• Football (NFL), basketball, baseball, ice hockey: playoffs of the regular domestic season.
• Handball, basketball, volleyball: World Cup, continental championships, European club competitions.
• Rugby: World Cup, European club competitions, playoffs of the regular domestic season.
• Tennis: ATP Finals.
• Cricket: the ICC Cricket World Cup.
Fig. 2
Ideal bracket, when teams have been ranked from 1 (the best group winner) to 2N after the group stage is over. Here N = 4.
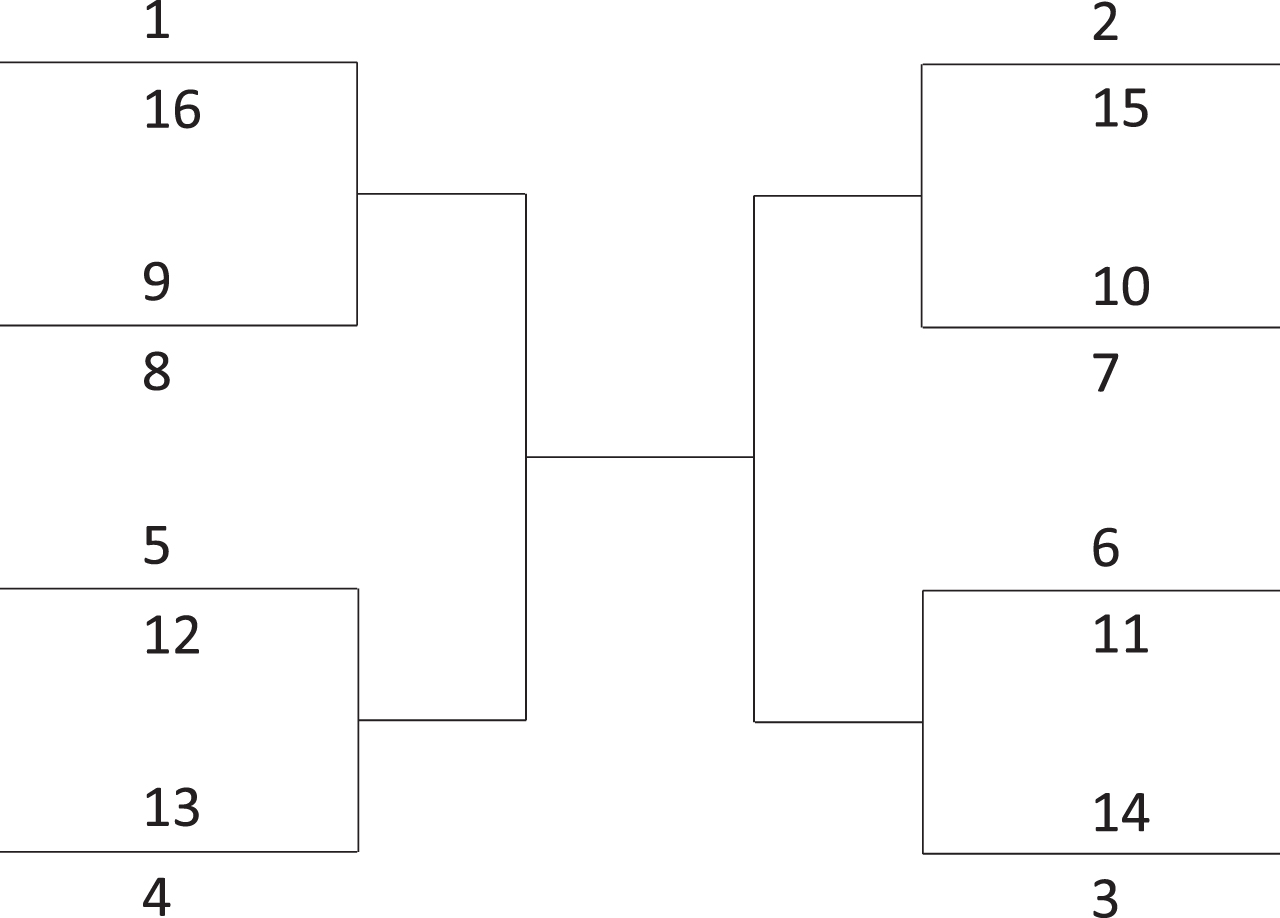
There exists a vast literature on knockout tournament design. Several theoretical studies have attempted to find a best seeding and formalize different goals of seeding. Hwang (1982) defines a bracket to be monotone if the probability of winning the tournament increases with team skill. He shows that the canonical knockout bracket (see Figure 2) is not necessarily monotone and suggests an adaptive reseeding method that he proves to be monotone. Schwenk (2000) suggests three axioms for fair seeding (delayed confrontation, sincerity rewarded, favoritism minimized). He proves that the canonical knockout bracket fails to satisfy the second axiom and suggests a variant that satisfies all three seeding axioms, in which subgroups of teams are randomly shuffled. Vu and Shoham (2011) introduce two alternative criteria for fairness (envy-freeness and order preservation) and investigate several impossibility results. Groh et al. (2012) aim to find optimal seedings in elimination tournaments for three different criteria: (1) maximization of total tournament effort; (2) maximization of the probability of a final among the two top ranked teams; (3) maximization of the win probability for the top player. They also identify the seedings ensuring that higher-ranked players have a higher winning probability. Pauly (2014) develops a mathematical model of strategic manipulation in complex sports competition formats. Karpov (2016, 2018) develops an axiomatic theory of knockout tournaments, gives axiomatic justification for various seedings methods, suggests two new seeding methods (equal gap seeding and increasing competitive intensity seeding), and provides many useful references. Dagaev and Suzdaltsev (2018) study optimal ways to seed a knockout tournament in order to maximize the overall spectator interest in it, assuming that neutral spectators tend to prefer to watch close and intense matches and matches that involve strong teams. As it has already been mentioned, Vong (2017) has shown that in the classical design of hybrid tournaments, in order to exclude the risk of tanking, it is necessary and sufficient that only the top-ranked team in each group advances. Arlegi and Dimitrov (2020) study the impact of two basic principles of fairness on the structure of elimination-type competitions: that stronger players should have a larger chance of winning than weaker players, and that equally strong players should have the same chances of being the final winner. They find that a new competition structure that they call antler plays a referential role in the design of fair knockout brackets.
Our new format is radically different from the ones studied in those papers, as in our approach teams are not placed in a bracket using a predefined mechanism. Rather, the teams that have performed best so far during the tournament decide against who they will play in the next knockout round, while the teams that are chosen have no say. This new feature practically solves the win incentive issues raised in the abovementioned papers.
Numerous statistical and simulation studies aim at comparing tournament designs. Glickman (2008) assumes only partial information about competitors’ relative rankings and develops Bayesian locally-optimal design of adaptive knockout tournaments to maximize the probability that the best team advances to the next round. Recently, Glickman and Hennessy (2016) have extended this approach in order to identify the overall best team in fixed knockout tournament brackets. Other utility functions are also considered. Scarf, Yusof, and Bilbao (2009) propose tournament metrics that can be used to measure the success of a sporting tournament, and describe how these metrics may be evaluated for a particular tournament design. This allows them to compare competing designs, such as round-robin, pure knockout and hybrids of these designs. They use the UEFA Champions League (soccer) to illustrate their methodology, while Scarf and Yusof (2011) use the FIFA World Cup Finals (soccer). Csató (2021a) compares four hybrid designs for the World Men’s Handball Championships. Other relevant literature includes Adler et al. (2017), Annis and Wu (2006), Appleton (1995), Baumann, Matheson, and Howe (2010), Csató (2021b), Dagaev and Rudyak (2019), Edwards (1998), Goossens, Beliën, and Spieksma (2012), Lasek and Gagolewski (2018), Marchand (2002), McGarry and Schutz (1997), and Ross and Ghamami (2008). Fair draws of round-robin groups are investigated in (Cea et al., 2020; Guyon, 2014a, 2015a; Laliena and López, 2019). Another recent line of research is concerned with fixing a knockout tournament (Aziz et al., 2014; Stanton and Vassilevska Williams, 2011; Vassilevska Williams, 2010; Vu, Altman, and Shoham, 2009).
In a sense, the “Choose Your Opponent” policy is a “reversed” draft allocation mechanism as the former prefers the best teams and the latter prefers the worst teams. Draft allocation has a very large literature, see, e.g., Banchio and Munro (2021), Fornwagner (2019), Kazachkov and Vardi (2020), Lenten (2016), Lenten, Smith, and Boys (2018), Price et al. (2010), and Taylor and Trogdon (2002).
Note that academic research has already led to changing tournament designs in soccer. Let us mention three examples:
• Inspired by Guyon (2014a, 2015a), the draw for the 2018 FIFA World Cup—unlike the previous editions of this championship—has determined all pots by positions in the FIFA World Ranking in order to increase balancedness across the groups while still satisfying geographic constraints;
• UEFA has followed the proposal of Guyon (2016) to reduce the biases in the design of the knockout bracket of the 2020 UEFA European Championship;
• Durán et al. (2017) have constructed an alternative schedule for the FIFA World Cup South American Qualifiers, which overcomes the main drawbacks of the previous policy and has unanimously been approved by all CONMEBOL (South American Football Confederation) members to be used in the qualifier for the 2018 FIFA World Cup; see also (Alarcón et al., 2017).
The remainder of this article is structured as follows. Section 2 discusses the main flaws of the traditional hybrid designs. In Section 3, we describe the “Choose Your Opponent” knockout format and investigate its main benefits and drawbacks. Section 4 investigates how this new format would work for the round of 16 of the UEFA Champions League. Finally, Section 5 concludes.
2Flaws of the traditional hybrid tournament design
The hybrid tournament design, though it is widely used, has serious fairness issues:
• Risk of collusion: When k ≥ 2, two teams may be tempted to collude if they play against each other during the last match day of the group stage, and if a given result satisfies both of them, whatever the result of the other group matches. For instance, one team may be satisfied by securing the first position in the group, while the other team may be satisfied by securing qualification to the knockout stage, even in second position. Collusion does not have to be explicit, it may be tacit and simply take the form of two teams refusing to attack each other when the current score of the match satisfies both of them.
One of the most famous examples of collusion in sports is the “disgrace of Gijón” (see, e.g., (Kendall and Lenten, 2017)). It refers to the match between West Germany and Austria who refused to attack each other during 80 minutes, satisfied by the 1-0 Germany win that let both teams advance to the second round of the 1982 FIFA World Cup at the expense of Algeria, who had played their last group game the day before. To prevent this to happen again, FIFA, soccer’s world governing body, decided that all teams in a given group would play their last group match at the same time.
However, playing the last two group games at the exact same time does not fully prevent collusion. Denmark-France (0-0 on June 26, 2018 during the 2018 FIFA World Cup) is a recent example of tacit collusion in this context: both teams knew that a draw would let them both advance to the knockout stage whatever the result of the other game in the group, Australia-Peru. They did little effort to attack each other, which resulted in a boring game and the only goalless match of the 2018 World Cup. The crowd made its displeasure known, as well as football fans around the world on social media (The Sun, 2018). Denmark’s manager Åge Hareide said after the game: “We just needed one point, we were up against one of the best teams in the world at counterattacks, so we would have been stupid to open up a lot of space. We stood back and got the result we needed, it was a 0-0 and we’re very pleased with that” (The Guardian, 2018).
The last 10 minutes of the 2018 World Cup match between Japan and Poland is another example of tacit collusion. Poland, already eliminated, was leading 1-0 and happy to leave the tournament on a win. When Senegal, which was playing at the same time against Colombia, conceded a goal at the 74th minute, Japan was perfectly even with Senegal in the group ranking on points, goal difference, and goals scored. The next tie-breaker was fair-play. With two yellow cards less than Senegal during the group stage, Japan would advance at the expense of Senegal. Even though Senegal could still score, Japan was happy with a 0-1 loss. Japan and Poland then suddenly stopped to attack each other, in scenes reminiscent of the disgrace of Gijón (BBC, 2018).
Another recent example of tacit collusion in soccer was the last minutes of the Peru-Colombia World Cup qualifying game (1-1) in October 2017. The current score saw both sides progress in World Cup qualifying. With results elsewhere going in their favor, Colombia knew a draw would see them finish in fourth place and qualify automatically, while Peru would advance to a playoff against New Zealand after finishing fifth. Both teams then stopped to attack each other. The Independent (2017) reported that, following allegations of match-fixing, Radamel Falcao, the Colombian striker and captain, admitted that he discussed playing for a draw with his opponents, as could be seen on TV.
Denmark-Sweden at UEFA Euro 2004 is another example of a tacit collusion situation (Kendall and Lenten, 2017): a 2-2 tie would qualify both teams at the expense of Italy, whatever the result of the game between Italy and Bulgaria. The game indeed ended as a 2-2 draw, raising complaints from the Italian team and fans, even though Sweden and Denmark seemed to attack each other without restraint and try to win the game.
The pre-2017 examples above are studied in Kendall and Lenten (2017) where the authors also provide other examples of tacit collusion in sports, and more generally examples where the rules of sports have led to unforeseen and/or unwanted consequences. Guyon (2020d) examines the risk of collusion in groups of 3, a format that FIFA considers using for the 48 team group stage of the 2026 World Cup. He explains how to build the match schedule so as to minimize the risk of collusion, and also quantifies how the risk of collusion depends on competitive balance and the point system. He also describes alternate formats for a 48 team World Cup that would eliminate or strongly decrease the risk of collusion. Stronka (2020) attempts to quantify the probability of match-fixing in groups of four teams under various match schedules and pair matching procedures. Schedules to reduce match-fixing opportunities have been recently studied in (Chater et al. 2021).
• Risk of tanking/shirking: When k ≥ 2 and the knockout bracket has predetermined routes (like in Figure 1), some teams may even be tempted to tank, i.e., to intentionally lose their last group stage match. (Tanking is also known as shirking.) This could for instance happen in the example of Figure 1 (k = 2) if Group B teams play their last group game after Group A has completed all its matches, and a team considered as one of the best in the world has finished second in Group A, due to bad luck or poor seeding (see Section 4.4) for instance. Imagine that two Group B teams have already secured their qualification to the knockout stage and play against each other in the last group game. Both teams may then be tempted to lose this game in order to finish second in Group B and thus avoid the runner-up of Group A.
Tanking famously happened in the badminton tournament of the 2012 Olympics in London. On August 1, 2012, four teams were ejected from the competition for “not using one’s best efforts to win a match” and “conducting oneself in a manner that is clearly abusive or detrimental to the sport” following round-robin matches the previous evening, during which the teams were accused of trying to lose in order to manipulate the knockout bracket.3 The decision was highly debated. Indeed it can be argued that the bad design of the tournament could be blamed more than the teams: while the teams have not been performing their best effort to win the game at hand, they have been in fact doing their best to win the tournament (Badminton at the 2012 Summer Olympics). Moreover, it is a common practice in every competitive sport to save forces in earlier matches in order to perform better in later stages of a tournament. The badminton tournament of the 2012 Olympics is discussed in (Kendall and Lenten, 2017, Section 3.3.1). It is also used as a motivating example by Pauly (2014).
The game between England and Belgium at the 2018 FIFA World Cup is another good illustration of the risk of tanking. England and Belgium were playing against each other in the last round of the group stage, and the winner could face a more difficult path to the final (Brazil in quarterfinals and France in semifinals) than the loser (England lost against Belgium and faced Sweden and Croatia instead). In the case of France-Denmark, it was not clear either whether winning the group was much of an advantage: the group winner could possibly face twice World Cup winners Argentina, while the runner-up would very likely face Croatia (and all this indeed happened).
Tanking also famously happened during the soccer game Thailand vs Indonesia at the 1998 AFF championship (Kendall and Lenten, 2017, Section 3.9.2), in which Indonesian defender Mursyid Effendi deliberately scored an own goal during injury time to secure a 2-3 loss that would allow Indonesia to play against Singapore in semifinals rather than against Vietnam, the hosts of the tournament. Csató (2020e) investigates an interesting example of tanking in soccer, where in a given match the two teams must not win in order to advance to the next stage, due to a bad tournament design. Other studies on incentive incompatibility or lack of strategy-proofness, i.e., the possibility that a team is strictly better off with a weaker performance, include (Csató, 2018, 2019, 2020b; Dagaev and Sonin, 2018; Vong, 2017); see also the references therein.
• Absence of win incentive: Some teams may have secured the first place of their group before their last group game. For instance, this was the case of Brazil and Nigeria during the 1998 FIFA World Cup, and of Italy during the UEFA Euro 2016. This happens more frequently in the UEFA Champions League and UEFA Europa League than in the FIFA World Cup or UEFA Euro because the former are played in a home-away round-robin format while the latter use a single round-robin format. When the knockout bracket has predetermined routes (like in Figure 1), teams that have already secured the first place of their group have no incentive at all to win their last group match and often send their B team to play this game, distorting the results of their group and the fairness of the competition. In the three examples mentioned above, Brazil, Nigeria, and Italy all lost their last group matches against Norway, Paraguay, and the Republic of Ireland, respectively, after securing the first place of their group after only two games.
Teams may also just need a draw in their last group game to secure the first place, and prefer securing a draw rather than taking risks and trying to win the game by playing attacking soccer. This usually results in more defensive, less attractive play.
Note that teams might have at least some financial incentives to win as many matches as possible in the group stage. This is the case for instance in UEFA club competitions, where the revenue distribution system incentivizes win even for teams that have no sporting win incentive, see for instance (Total Sportal website; UEFA website, 2019/20 UEFA club competitions revenue distribution system).
• Group winners may be poorly rewarded: When group winners are paired with runners-up during the first round of the knockout stage (FIFA World Cup, UEFA Champions League, rugby World Cup, rugby European cups, ATP Finals, etc.), they may face runners-up that they would not have picked if given the choice. They can feel poorly and unfairly rewarded for winning their group. This happens quite often during the draw of the round of 16 of the UEFA Champions League (see Section 4). In this case tanking is not an option, as the bracket is randomly drawn and does not have predetermined routes. A similar scenario could have occurred in the playoffs of the UEFA Euro 2020 qualifying tournament as a group winner in the UEFA Nations League might have faced stronger opponents than a non-group winner from the same league despite its better performance in the UEFA Nations League, see (Csató, 2020c).
Note that at UEFA European Championships, since 2016, some group winners face third-placed teams while other play runners-up, depending only on their group label (see a full study of the corresponding so-called “group advantage” in (Guyon, 2016)).
3The “Choose Your Opponent” knockout design
3.1Description of the format
In classical hybrid tournament designs, the teams that advance to the knockout round either
• follow a predetermined bracket route entirely decided by their group label and group rank, as illustrated for example in Figure 1; or
• follow the predetermined “ideal” bracket entirely decided by their rank during the regular season, like during the NBA playoffs (see Figure 2 for an illustration of the 16-team “ideal” bracket); or
• are automatically reseeded in the “ideal” bracket, like during the NFL Conference Championships, where the strongest remaining teams face the weakest remaining teams; or
• are randomly drawn against opponents, like during the draws of the knockout rounds of the UEFA Champions League and the UEFA Europa League.
First, the 2N teams that qualified for the knockout stage would be ranked from 1 to 2N, based on their group stage results. For instance, the n group winners would be ranked from 1 to n, compared across groups based on sporting criteria which depend on the sport in consideration. For example, in soccer, the criteria could be in order: number of points; goal difference; number of goals scored; fair-play score (based on the number of yellow and red cards received), etc. Then the n runners-up would be ranked from n + 1 to 2n, compared across groups based on the same criteria, and so on. We call the resulting ranking the “global ranking 1–2N”. For instance, UEFA uses this mechanism for its Nations League to build a global ranking of the 55 member associations from the rankings of the different groups of the different leagues; this overall ranking was used in the draw of the groups of the Euro 2020 qualifiers (Wikipedia, UEFA Euro 2020 qualifying). UEFA also used the suggested global ranking mechanism in the seeding of the Euro 2020 (Wikipedia, UEFA Euro 2020 qualifying).
Remark 1. Note that when there is one unique group in the group stage (n = 1), like in the NBA conferences for instance, the global ranking is trivially built from the group rankings.
Remark 2. Currently, in the NFL and MLB, the teams that advance to the postseason playoffs are the division winners, as well as “wild cards”, i.e., teams with the best records that did not win their division. The NHL uses a similar format, with wild cards advancing on top of the best teams in each division. A similar rule could be used to produce the global ranking, with division winners being ranked above wild cards.
At this point, one natural knockout format would consist of placing teams in the “ideal” bracket shown in Figure 2 in the case where N = 4 (see (Guyon, 2016) and the references therein). The ideal bracket is a perfectly balanced bracket, where the ranks (from 1 to 2N) of the two opponents sum to 2N + 1 in each of the 2N-1 matches of the first knockout round, and then, assuming the best ranked team always advances to the next round, sum to 2N-k+1 + 1 in the kth knockout round. It ensures that teams 1 to 8 cannot meet before the quarterfinals, in which case the quarterfinals are 1-8, 2-7, 3-6, and 4-5; that teams 1, 2, 3, and 4 cannot meet before the semifinals, in which case the semifinals are 1-4 and 2-3; and that teams 1 and 2 cannot meet before the final. This bracket is not only perfectly balanced, it is also free of any group advantage (see (Guyon, 2016)) and, compared to brackets built only on group labels and group ranks (like the one in Figure 1), it also increases win incentive during the group stage, as the more a team wins during the group stage, the weaker their opponents in the knockout stage will be, at least on paper, and the higher the probability is that it goes far in the tournament. Guyon (2016) has suggested two ways of modifying the “ideal” bracket to make sure that two teams from the same group cannot meet again before the semifinals.
However, it often happens that teams perceived as strong get quite poor results in the group stage and advance to the knockout round with a poor global ranking, maybe due to bad luck, or a bad seeding (see Section 4.4), or because their physical training aims at peak performance during the knockout round and players have suffered too much fatigue during the group stage. In such a case, a team advancing into the “ideal” knockout bracket with a good rank may end up facing an opponent that it perceives as stronger than other, better ranked opponents, and may feel unfairly rewarded for its good performance in the group stage. For example, if UEFA had adopted the “ideal” bracket for the UEFA Euro 2016, Germany would have been ranked 2nd after the group stage and therefore would have had to face Portugal, ranked 15th, a team generally considered as a soccer powerhouse (and, as a matter of fact, the future winner of the competition), in the round of 16. Germany may have preferred to play, say, against Ireland, Slovakia, Iceland, or Hungary, teams that finished the group stage with a better rank than Portugal but are considered weaker by many specialists (see (Guyon, 2016)). There exist numerous examples of teams unfairly rewarded for winning their group and having to face strong opponents in the first knockout round: Brazil having to face Argentina in the round of 16 of the 1990 FIFA World Cup; Arsenal and Napoli having to face Bayern Munich and Real Madrid in the round of 16 of the 2016–17 UEFA Champions League; Tottenham and Paris Saint-Germain, the best two group winners in the 2017–18 group stage of the UEFA Champions League, having to face Juventus and Real Madrid in the round of 16, etc.
The “Choose Your Opponent” knockout format precisely aims to avoid these situations by allowing the teams that have performed best during the group stage to choose their opponent during the final knockout stage among the pool of opponents that are still available.
• Full choice: The full choice implementation of this format would work as follows:
- Team 1 in the global rankings chooses their opponent among Teams {2, …, 2N}.
- Team 2, if not already picked, chooses their opponent among the remaining teams.
- Team 3, if not already picked, chooses their opponent among the remaining teams.
- And so on, until all matchups are formed.
• Restricted choice: The restricted choice implementation would protect Teams {2, …, 2N-1} (from the better half of the advancing teams), which could not be chosen:
For example, with the restricted choice implementation, Germany would not have been allowed to pick Hungary (ranked 6th out of 16) in the round of 16 of the UEFA Euro 2016; Hungary would have been protected by their good performance during the group stage. Other restrictions can easily be accomodated. For instance, in the UEFA Champions League, teams from the same country or group cannot play against each other during the round of 16 (see Section 4).4. Also, if the tournament organizer wants to avoid repeated matchups year after year, it may add the constraint that, if possible, a team cannot pick a team that it has selected in the previous edition (or p previous editions) of the tournament. The tournament organizer may also add a constraint to prevent two teams qualifying from the same city to play at home on the same day, as this may overload the infrastructure.- Team 1 would choose their opponent among Teams {2N-1 + 1, …, 2N} (the weaker half of the advancing teams).
- Team 2 would choose their opponent among the remaining teams in the weaker half of the advancing teams.
- Team 3 would choose their opponent among the remaining teams in the weaker half of the advancing teams.
- And so on, until all matchups are formed.
• Frozen rankings: In the frozen ranking implementation, the team rankings would not be updated after each round of the knockout stage; teams would be ranked based on their group stage performance during the whole knockout stage.
• Updated rankings: In the updated ranking implementation, the team rankings would be updated after each round of the knockout stage. For instance, teams qualified for the kth knockout round would be ranked from 1 (best ranked team) to 2N-k+1 (lowest ranked team) based on their results during the group stage and the previous knockout rounds, according to criteria similar to those used to rank advancing teams at the end of the group stage. For instance, in soccer, the criteria could be, in order: number of points; goal difference (per minute played); goals scored (per minute played); fair play (per minute played); etc. A win before extra-time during a knockout round could be awarded with 3 points, a win during extra-time with 2 points, and a win after penalty shootout with 1 point.5
Remark 3. (Alternatives for updated rankings) the teams that advance to the postseaOne could also consider an updated ranking version where the strengths of the opponents that a team has eliminated in the past knockout rounds are taken into account in its ranking. That could lead to interesting strategic debates: should a team pick an easy opponent to maximize the chances that it advances to the next round, or select a stronger opponent, which would improve its ranking in the following round if it advances? For instance, should Team 1 pick the the lowest-ranked advancing team, or select a higher-ranked team so that it still has the first pick in the next round if it advances? Taking the strength of the opponent into account would also reward more weaker teams for eliminating stronger teams. For instance this could be done using a dynamic Elo-like rating system.
Many variations of the “Choose Your Opponent” policy can be considered. A team may be awarded by the opportunity to choose not only its next opponent but also, for instance:
• Whether they play the first leg of the next knockout round at home or away, when applicable. Several papers analyze whether playing the second leg at home means a significant advantage or not (Amez et al., 2020; Eugster et al., 2011; Geenens and Cuddihy, 2018; Page and Page, 2007).
• The opponents of other teams or a set of possible opponents for other teams.
• Other features of its knockout bracket. For example, the team ranked first might choose its opponent not only in the Round of 16 but in the quarterfinals, too, if it wins all of its group matches.
Remark 4. (“Choose Your Opponent" in the draw of the groups) It is also possible to use the “Choose Your Opponent" policy in the draw of the groups. For instance, assume a tournament with n groups and n seeded teams, ranked 1 to n according to past performance. First, the unseeded teams are drawn into the n groups; usually this is done using a system of pots with the objective of achieving a good group balance. Then the n seeded teams would be allowed to pick their group, in order. Team 1 would first choose one of the n groups, then Team 2 would choose one of the n - 1 remaining groups, and so on. Here again, restrictions can easily be accomodated. For example, a seeded team may only be allowed to choose a group in which all teams come from a different country.
This procedure is a good way of rewarding the highest-ranked teams while ensuring group balance. It would actually ensure superior group balance compared to drawing seeded teams into groups, as the higher-ranked seeded teams would probably choose the weaker groups, while the lower-ranked seeded teams would end up in stronger groups.
3.2Benefits and drawbacks
The main benefits of the “Choose Your Opponent” knockout format are the following:
• Risk of tanking reduced to almost zero: In practice, teams would not be tempted to tank. It would always be better to score one more point, goal, etc., than not, because it can only give you more options: more chances to pick your opponent, and if you are already in a position to pick one, a wider range of teams to choose from. For example, with such a system, the 2012 Olympics badminton tournament scandal (see Section 2) would have been avoided, and England and Belgium would have exerted their best effort to win their last group match at the 2018 FIFA World Cup. In particular, the “Choose Your Opponent” format effectively solves the problem of strategic manipulation in tournaments identified by Vong (2017). The only (very unlikely but mathematically possible) situations where a team might still prefer to tank in the “Choose Your Opponent” format is when, by tanking, a team thinks that it increases its probability of reaching its final objective, be it winning the tournament or reaching a particular round. For instance a team would prefer to tank if the objective it wants to maximize is the probability of winning the tournament and if, by tanking, it still advances to the knockout stage, but eliminates another team that otherwise would have also advanced and (unrealistically) would have beaten every other advancing team with probability one (and then would have won the tournament with probability one), and as a result gets a non-zero probability of winning the tournament. More generally it may prefer to tank if, by tanking, the global rankings are modified in such a way that it increases its objective, say, the probability of reaching a particular round. Mathematically, this can only happen in the case of extreme, unrealistic win probability matrices. (Note that by tanking a team likely loses choosing rights, which typically negatively impacts its objective.) We cannot imagine a realistic situation where a team would benefit from tanking in the “Choose Your Opponent” format.
• Maximize win incentive during the group stage: Teams would have a strong incentive to win all group matches, even if they have already secured qualification to the knockout stage, and even if they have already secured the first place in the group. Indeed, even if a team is guaranteed to win its group before the last match day of the group stage (e.g., Italy during the UEFA Euro 2016), it still has a strong incentive to win this last match, and with the largest score, to improve its ranking within the n group winners and be one of the first teams to pick its opponent during the knockout stage.
• Decreased risk of collusion: For the same reasons, teams would be less tempted to collude during the last match day of the group stage. The great benefits of being one of the best group winners would deter teams from colluding and being satisfied with a draw or a loss. Note, however, that the risk of collusion would not be canceled. For instance, during the group stage, a team that has nothing to win or lose (this could happen during the last match days) could agree to lose by many goals/points, which would help its opponent increase its ranking among group winners and get a better picking position.
• Added strategic component: The procedure of choosing opponents would bring a new, exciting strategic component to the competition. It could give the tournament a whole new dynamics. The picking strategies of the teams would certainly be much commented upon in the media and among the fans, before and after the picking procedure.
• Exciting TV shows: The picking procedure would lend itself to exciting, much anticipated TV shows which would be scheduled right at the end of the group stage and knockout rounds.
• Schedule: Adopting the “Choose Your Opponent” design might lengthen tournaments:
The FIFA World Cup is a typical example of such tournaments. Indeed, consider a tournament with the three above characteristics. At the end of the group stage or at the end of a knockout round, a team who played its last game several days ago may pick a team who just finished playing. This implies that more match-free days may be needed between the end of the group stage and the first round of the knockout stage, and between consecutive rounds of the knockout stage, and could lengthen the tournament. Note, however, that adopting “Choose Your Opponent” is not problematic for tournaments that leave a lot of time between the end of the group stage and the first knockout round, and between consecutive knockout rounds, like the UEFA Champions League or the UEFA Europa League.– in which a minimum number of rest days, say r, is guaranteed to all teams between two games;
– in which match days and knockout rounds are spread over several days to maximize TV exposure and the value of media rights;
– that must be played over a short period of time.
Leaving r match-free days between the end of the group stage and the first round of the knockout stage, and between consecutive rounds of the knockout stage, is the obvious, simplest way of ensuring that all teams benefit from r rest days between two matches. By proper scheduling, it might be enough to schedule less than r match-free days. The minimum number of rest days can also be decreased by imposing additional constraints during the “Choose Your Opponent” procedure, but at the expense of fairness. For instance, a team having played its last group game early may only be allowed to pick an opponent having also played its last group game early. For example, in the case of the FIFA World Cup, group winners from the first half of the groups—those playing early—may only pick their opponents among runners-up from the same half.
Another scheduling drawback could be the advantage enjoyed by the teams that play the last group matches. In contrast to the teams from the groups that play early, they know which result will be sufficient to achieve a certain position in the global ranking. Since group labeling is arbitrary, this could be judged unfair—but can be handled to a certain degree by, for example, placing the titleholder automatically in a group that is finished the latest time. Theoretically, all groups can be finished simultaneously, but this would decrease the value of media rights.
• Travel plans and logistics: All advancing teams would have to wait until the end of a round to know when and where they would play the next game. For tournaments that must be played over a short period of time in distant cities, such as the FIFA World Cup,6 this can be seen as a drawback since teams and fans would have less time for planning their trip to the next game—or they would have more possible options to consider and plan for—than in the traditional system with predetermined bracket routes. But it can also be seen as a benefit, as all teams would then be put on an equal foot. Moreover, it would not be a problem for tournaments where consecutive rounds are played several weeks apart, such as the UEFA Champions League or UEFA Europa League, or that are played in one city or neighboring cities, such as Olympic Games tournaments, the final stages of basketball and handball national team championships, the “Final Eight” of the UEFA Champions League organized in Lisbon, Portugal in August 2020, or the “Major League Soccer is back” tournament organized in July 2020 in Orlando, Florida.
Note that the picking teams could also be allowed to choose the city/stadium where they will play their next game. This is illustrated in (Guyon, 2019a) in the case of the UEFA Euro 2020, where the rule could have been used to maximize the number of home games during the knockout stage.
• First picked teams possibly feeling offended or humiliated: The first teams chosen, as well as their fans, could feel offended or even humiliated to be perceived as one of the weakest teams remaining in the tournament. However, if a team is one of the first picks, it probably means that it really is one of the weakest remaining teams. Moreover, this can actually give those teams a very strong motivation to prove their pickers wrong when they face them on the pitch.
• No one wanting to take responsibility for the pick: It might be that no individual in a team/club wants to take the responsibility of picking the team’s opponent, fearing backlash if the team is actually eliminated by the chosen opponent. However, in such a situation, a team can easily organize their own draw and decide the rules for their draw. For instance, when a team does not want to make any decision, they can organize a uniformly distributed draw among all available opponents. A team may also collectively agree that they want to avoid some opponents, which they would exclude from the draw. If 2/3 of a team prefers Opponent A and 1/3 prefers Opponent B, then the team can set up a draw with a bowl containing three balls, two balls “A” and one ball “B”, etc.
• Distribution of choice options: In the case of the full choice implementation, the distribution of choice options may possibly seem unfair. For example, if Team 1 picks Team 5 in the round of 16 of the UEFA Champions League, and Team 6 has some choice, then Team 5 may feel aggrieved. Indeed, people usually like to choose even if it has no real effect.
Remark 5. (Importance of the seeding rules) Note that since in this system group winners would be compared across groups and the best group winners would be awarded big benefits, it is crucial that the groups be well balanced. This can be achieved by a seeding procedure that fairly reflects the quality of the teams.
A poor seeding may be the result of following a poor ranking, see for instance (Guyon, 2014b; Lasek et al. 2013; McHale and Davies, 2007) about pre-2018 FIFA rankings. A poor seeding may also be the result of not following a good ranking; Section 4.4 deals with an issue with the seeding of the group stage of the UEFA Champions League. And a poor seeding may be also the result of how (legitimate) draw constraints are handled. For instance, Guyon (2014a, 2015a) explains that until 2014, due to how FIFA enforced the geographic constraints that it puts on the draw, the group stage of the FIFA World Cup was poorly seeded and produced unbalanced groups. One of his solutions (Suggestion #1 in (Guyon, 2014)) was adopted by FIFA for the 2018 World Cup.
The fact that the “Choose Your Opponent” design requires the groups to be very well balanced can be seen both as a drawback and as a benefit. Indeed, it can be considered a drawback as tournament organizers sometimes fail to correctly seed the teams, as the above examples show. However, for many symmetric tournament designs, group balance should be a priority of all tournament organizers, and tournament designs that make group balance very important can be seen as a great way to ensure that the teams are correctly seeded. Note, however, that asymmetric designs with voluntarily unbalanced groups do also exist; they have been studied by Csató (2020a), who has shown potential benefits of those formats.
Remark 6. In tournaments such as the NBA, NFL, MLB, and NHL, where the “ideal” bracket (shown in Figure 2 in the case where N = 16)—or some variation of it—has been used for a long time, the first picking teams may be reluctant to choose a team that they were not supposed to meet in the traditional bracket, for that might be very embarrassing if they lose. In the example of Figure 2, Team 1 may not dare select a team ranked 15 or higher, as that bears the risk of people mocking their choice if they lose in the round of 16. However, if Team 1 chooses an opponent that is not the lowest-ranking team, it is probably because they have determined that they have more chances of beating them than beating the lowest-ranking team, and this might indeed be the case. Other factors, such as travel, might also weigh in the choice. Note that this remark does not apply to tournaments that do not currently follow the “ideal” bracket, such as the FIFA World Cup or the UEFA Champions League.
In the next section, we illustrate the “Choose Your Opponent” format by showing how it would work for the round of 16 of the UEFA Champions League.
4Application to the round of 16 of the UEFA Champions League
After describing the flaws of the current draw system of the round of 16 of the UEFA Champions League in Section 4.1, we explain how the “Choose Your Opponent” policy would work in practice in Section 4.2. In Section4.3_example we give a detailed example using the results of the group stage of the 2017-18 season of the Champions League; we consider both the full choice and restricted choice implementations. Finally, Section 4.4 discusses the importance of correctly seeding the group stage.
Table 1
Global rankings 1–16 at the end of the group stage of the 2017–18 UEFA Champions League. GD stands for “Goal Difference” and GF for “Goals For”. UEFA uses head-to-head results as the first tie-breakers
| Group winners | Runners-up | ||||||||||
| Rk | Team | Gp | Pts | GD | GF | Rk | Team | Gp | Pts | GD | GF |
| 1 | Tottenham (ENG) | H | 16 | +11 | 15 | 9 | Bay. Munich (GER) | B | 15 | +7 | 13 |
| 2 | Paris S.-G. (FRA) | B | 15 | +21 | 25 | 10 | Real Madrid (SPA) | H | 13 | +10 | 17 |
| 3 | Manchester C. (ENG) | F | 15 | +9 | 14 | 11 | Basel (SWI) | A | 12 | +6 | 11 |
| 4 | Manchester U. (ENG) | A | 15 | +9 | 12 | 12 | Sh. Donetsk (UKR) | F | 12 | 0 | 9 |
| 5 | Barcelona (SPA) | D | 14 | +8 | 9 | 13 | Chelsea (ENG) | C | 11 | +8 | 16 |
| 6 | Beşiktaş (TUR) | G | 14 | +6 | 11 | 14 | Juventus (ITA) | D | 11 | +2 | 7 |
| 7 | Liverpool (ENG) | E | 12 | +17 | 23 | 15 | Porto (POR) | G | 10 | +5 | 15 |
| 8 | Roma (ITA) | C | 11 | +3 | 9 | 16 | Sevilla (SPA) | E | 9 | 0 | 12 |
4.1Flaws of the current draw system
The “Choose Your Opponent” format could for instance be used in the UEFA Champions League in order to better reward group winners and make the group stage more attractive. In the current format, the group stage is made of 8 groups of 4 teams, with the best two teams in each group advancing to the round of 16. Every year in December, the draw of the round of 16 is a much anticipated event, which attracts a lot of media attention. In order to reward group winners for their group stage performance, they can only be drawn against runners-up. (Two other constraints apply: teams from the same group or from the same country cannot be drawn against each other. This yields interesting draw probability calculations, see (Guyon, 2017a, 2017b, 2018, 2019b, 2019c, 2020b, 2020c; Kloessner and Becker, 2013). The draw procedure has also been analyzed in (Boczoń, 2018).)
However, it often happens that some of the very best European clubs, considered to be consistently in the top 8 clubs over the past years, actually finish second in their group. In the recent years, this was the case of Real Madrid (2016–17, 2017–18, 2019–20), Bayern Munich (2016–17, 2017–18), Juventus Turin (2015–16, 2017–18), Atlético Madrid (2018–19, 2019–20), Manchester City (2016–17), and Paris Saint-Germain (2015–16, 2016–17). When group winners are drawn against one of those teams, they can feel bitter about the way they are rewarded for winning their group.
The flawed seeding system used by UEFA for the group stage since 2015 made those cases more likely (see Section 4.4). In the 5 years preceding the change, runners-up advanced to the quarterfinals 7 times out of 40 (17.5%), whereas in the 5 years following the change the proportion more than doubled, reaching 15 times out of 40 (37.5%).
4.2The “Choose Your Opponent” format for the round of 16 of the UEFA Champions League
The “Choose Your Opponent” format would solve this problem, and could easily be adapted to take the country and group constraints into account: UEFA would allow the group winners to choose their opponent, but group winners could not pick an opponent from the same country or the same group. The best group winner (based on the global ranking 1–16) would first pick their opponent, then the second best group winner would pick theirs, etc. It would make sense to protect the group winners by enforcing the restricted choice implementation, where group winners cannot be picked by other group winners. By contrast, the full choice implementation would allow group winners to choose other group winners as their opponents.
Exactly as is done today for the draw of the round of 16 of the UEFA Champions League, to make sure that a team’s choice is acceptable, i.e., does not lead to a dead end, a computer program would provide the list of admissible opponents ahead of each team pick. A team’s choice leads to a dead end if it makes it impossible that the above rules (no match between teams from the same country or from the same group) be met for all the remaining games. The backtracking algorithm is a nice recursive procedure that does just that; see (Guyon, 2014a) for an example.
Note that UEFA uses head-to-head results as the first tie-breaker. This is impossible to apply across groups. Consequently, it might happen that a runner-up has better performance measures in the global ranking compared to the winner of its group, which would be quite strange. That is a further argument for not using head-to-head results as a tie-breaking rule and preferring global goal difference within the group. Note that goal difference is more attractive from a theoretical point of view (Berker, 2014).
Table 2
Round of 16 draw of the 2017–18 UEFA Champions League
| Manchester United –Sevilla | Liverpool –Porto |
| Beşiktaş –Bayern Munich | Manchester City –Basel |
| Tottenham –Juventus | Barcelona –Chelsea |
| Paris Saint-Germain –Real Madrid | Roma –Shakhtar Donetsk |
4.3An example
Let us take the 2017–18 season of the UEFA Champions League as an example. The results of the group stage are reported in Table 1, and the outcome of the draw of the round of 16 in Table 2. Tottenham and Paris Saint-Germain were the two best group winners that year, but in the round of 16 they were respectively drawn against Juventus and Real Madrid, two clubs which, despite being 1st and 5th in the UEFA club coefficient ranking at the time, finished second in their group. Despite collecting 13 points in Group H, Real Madrid finished behind Tottenham which performed exceptionally well that year (16 points); Juventus finished second in Group D behind another soccer powerhouse, Barcelona (3rd in the UEFA club coefficient ranking at the time). Both Tottenham and Paris Saint-Germain must have felt bitter and poorly and unfairly rewarded for their excellent group stage performance.
Table 3
Elo ratings of the 16 teams participating in the round of 16 of the 2017–18 UEFA Champions League as of December 11, 2017, day of the draw
| Group winners | Runners-up | ||||||
| Elo Rk | Team | Gp | Elo rating | Elo Rk | Team | Gp | Elo rating |
| 1 | Barcelona (SPA) | D | 2025 | 2 | Real Madrid (SPA) | H | 2024 |
| 3 | Manchester C. (ENG) | F | 1968 | 4 | Bay. Munich (GER) | B | 1947 |
| 7 | Manchester U. (ENG) | A | 1910 | 5 | Juventus (ITA) | D | 1945 |
| 8 | Tottenham (ENG) | H | 1909 | 6 | Chelsea (ENG) | C | 1910 |
| 9 | Paris S.-G. (FRA) | B | 1895 | 12 | Sevilla (SPA) | E | 1789 |
| 10 | Liverpool (ENG) | E | 1875 | 13 | Porto (POR) | G | 1769 |
| 11 | Roma (ITA) | C | 1865 | 14 | Sh. Donetsk (UKR) | F | 1754 |
| 15 | Beşiktaş (TUR) | G | 1733 | 16 | Basel (SWI) | A | 1710 |
4.3.1Restricted choice implementation
Let us look at how the “Choose Your Opponent” design would have possibly worked. We first consider the restricted choice version. Here, we assume that teams pick their opponent based on the prevailing Elo ratings at the time, see Table 3. Elo ratings, introduced for chess by Arpad Elo in the 1960s, are a reliable measure of team skills. For European soccer clubs, they are maintained by the website clubelo.com.
• First, Tottenham (Team 1) would choose their round of 16 opponent among runners-up. The available teams for Tottenham are: Bayern Munich, Basel, Shakhtar Donetsk, Juventus, Porto, and Sevilla. Tottenham cannot choose Real Madrid, as both teams were in the same group. They cannot play against Chelsea either, due to the country constraint. For instance, Tottenham picks Basel (the runner-up with the lowest Elo rating at the time, see Table 3).
• Then it is Team 2’s turn (Paris Saint-Germain) to choose their opponent among the remaining runners-up. The available teams for Paris Saint-Germain are: Real Madrid, Shakhtar Donetsk, Chelsea, Juventus, Porto, and Sevilla. Paris Saint-Germain cannot choose Bayern Munich, as both teams were in the same group. For instance, Paris Saint-Germain picks Shakhtar Donetsk.
• The following team to choose their opponent is Manchester City. The available opponents are: Bayern Munich, Real Madrid, Juventus, Porto, and Sevilla. Manchester City cannot choose Chelsea, another English team. For instance, they pick Porto.
• Then it is Team 4’s turn (Manchester United). The available teams are: Bayern Munich, Real Madrid, Juventus, and Sevilla. Manchester United cannot choose Chelsea either, because of the country constraint. For instance, they pick Sevilla.
• Then it is Barcelona’s turn (Team 5). They can only pick Bayern Munich or Chelsea. They cannot play against Real Madrid, another Spanish team, nor against Juventus, which was in the same group as Barcelona. For instance, Barcelona chooses Chelsea.
• Then Beşiktaş (Team 6) can choose among: Bayern Munich, Real Madrid, and Juventus. For instance, they pick Juventus.
• Next, Team 7 (Liverpool) must choose between Bayern Munich and Real Madrid. For instance, they pick Bayern Munich.
• Finally, the last round of 16 matchup is Roma–Real Madrid.
Table 4
Possible round of 16 of the 2017–18 UEFA Champions League under the “Choose Your Opponent” design with restricted choice
| Tottenham –Basel | Barcelona –Chelsea |
| Paris Saint-Germain –Shakhtar Donetsk | Beşiktaş –Juventus |
| Manchester City –Porto | Liverpool –Bayern Munich |
| Manchester United –Sevilla | Roma –Real Madrid |
The resulting round of 16 table is shown in Table 4 In this example, the backtracking algorithm does not detect any future dead end. However, if Beşiktaş (Team 6) chose Real Madrid instead of Juventus, then Liverpool (Team 7) would have had no choice: they would have had to play against Juventus. Indeed, the backtracking algorithm would not allow Liverpool to choose Bayern Munich, as in this case the last match-up would be Roma–Juventus, which is prohibited by the country constraint.
4.3.2Full choice implementation
As for the full choice implementation, it may have worked this way:
• First, Tottenham (Team 1) would choose their round of 16 opponent among all other qualified teams (group winners or runners-up). The available teams for Tottenham are: Paris Saint-Germain, Barcelona, Beşiktaş, Roma, Bayern Munich, Basel, Shakhtar Donetsk, Juventus, Porto, and Sevilla. Tottenham cannot choose Real Madrid, as both teams were in the same group. They cannot play against the 4 other qualified English teams either (Manchester City, Manchester United, Liverpool, Chelsea). For instance, Tottenham picks Basel.
• Then it is Team 2’s turn (Paris Saint-Germain) to choose their opponent among the remaining teams. The available teams for Paris Saint-Germain are: Manchester City, Manchester United, Barcelona, Beşiktaş, Liverpool, Roma, Real Madrid, Shakhtar Donetsk, Chelsea, Juventus, Porto, and Sevilla. Paris Saint-Germain cannot choose Bayern Munich, as both teams were in the same group. For instance, Paris Saint-Germain picks Shakhtar Donetsk.7
• The following team to choose their opponent is Manchester City. The available opponents are: Barcelona, Beşiktaş, Roma, Bayern Munich, Real Madrid, Juventus, Porto, and Sevilla. Manchester City cannot choose the other English teams. For instance, they pick Porto.
• Then it is Team 4’s turn (Manchester United). The available teams are: Barcelona, Beşiktaş, Roma, Bayern Munich, Real Madrid, Juventus, and Sevilla. Manchester United cannot choose the other English teams. For instance, they pick Beşiktaş, a group winner, whereas in the restricted choice version they had picked Sevilla.
• Then it is Barcelona’s turn (Team 5). They can pick among: Roma, Bayern Munich and Chelsea. They cannot play against the other Spanish teams (Real Madrid and Sevilla), nor against Juventus, who was in the same group as Barcelona. For instance, Barcelona chooses Roma.
• Since Beşiktaş (Team 6) has already been picked, it is directly Team 7’s turn (Liverpool). They can only choose between Bayern Munich, Real Madrid, and Sevilla, since they cannot play against Chelsea. For instance, they pick Sevilla.
• Roma (Team 8) has already been chosen, therefore it is Team 9’s turn (Bayern Munich). They can play against Real Madrid, Chelsea, and Juventus. For instance, they pick Chelsea.
• Finally, the last round of 16 matchup is Real Madrid–Juventus.
4.3.3Comparison
In the full choice version, powerful clubs that failed to win their group would probably not be picked by group winners, and as a result they would have to face each other in the round of 16 (in our example, Bayern Munich–Chelsea and Real Madrid–Juventus). Therefore in the full choice version it would be extremely important for soccer powerhouses to win their group; otherwise they would likely eliminate each other in the round of 16, and also possibly in the following rounds. This is because the full choice version gives more options to the group winners, who are given the possibility to avoid a strong runner-up and prefer picking a group winner that they believe they have more chances to eliminate. This is for instance the choice made by Manchester United and Barcelona in our example, who avoid Sevilla and Chelsea and prefer Beşiktaş and Roma, respectively.
Therefore, by giving more choice options to the group winners, the full choice implementation maximizes win incentive in the group stage, and might seem preferable in this regard.
Table 5
Champions League under the “Choose Your Opponent” design with full choice
| Tottenham –Basel | Barcelona –Roma |
| Paris Saint-Germain –Shakhtar Donetsk | Liverpool –Sevilla |
| Manchester City –Porto | Bayern Munich –Chelsea |
| Manchester United –Beşiktaş | Real Madrid –Juventus |
4.4Importance of the seeding rules
The above example highlights the importance of correctly seeding the group stage and illustrates one of the important flaws of the current seeding system of the UEFA Champions League. UEFA modified the seeding system of the group stage in 2015–16. Before the 2015–16 season, the 32 teams participating in the group stage would be placed in 4 pots of 8 teams, with Pot 1 being made of the 8 best teams (based on the UEFA club coefficient, which measures performance in European club competitions in the last 5 years), Pot 2 the following 8, etc. Since each group of 4 is made of one team drawn from each pot, this procedure guaranteed that groups were well balanced, and two top 8 teams could not face each other in the group stage. Since the 2015–16 season, in order to reward domestic champions, Pot 1 is made of the domestic champions of the 8 highest ranked domestic leagues (even if they have a low UEFA coefficient, i.e., a poor performance in European club competitions in the last 5 years), while Pots 2 to 4 are still built based on decreasing UEFA club coefficient.8 This means that two top 8 teams (based on the UEFA coefficient) can now face each other in the group stage, and in this case it is likely that one top 8 club will finish second in their group. The group winner facing that team in the round of 16 (under the current draw system) will feel unfairly rewarded for winning its group.
For example, in 2017–18, despite being ranked 3rd and 5th in the UEFA club coefficient ranking, Barcelona (Pot 2) and Juventus (Pot 1) were placed in the same group. As a consequence it was very likely that during the draw of the round of 16 one of the runners-up would be from the top 5 of the UEFA club coefficient ranking, either Barcelona or Juventus, and one group winner would have to face a very strong opponent in the round of 16. Juventus finished second in the group behind Barcelona, and Tottenham, despite being the best group winner with 16 points, had to face a strong Juventus in the round of 16—and were eliminated.
As noted in Remark 3.2, it would also be very important that groups be well balanced in the “Choose Your Opponent” design. For instance, under the current seeding rules of the UEFA Champions League, there is usually at least one Pot 1 team (the champions of the domestic leagues ranked 6th or beyond) with a UEFA club coefficient or Elo rating much lower than those of the other Pot 1 teams (both numbers measure team skills based on performances in the past few years). For instance, in 2017–18, Spartak Moscow (Russia) was seeded in Pot 1, as the champions of the 6th highest ranked domestic league, despite the fact that their UEFA club coefficient was only 18.6, much lower than those of the other Pot 1 teams (the average of the 7 other club coefficients in Pot 1 was 120), and as a matter of fact the third lowest UEFA club coefficient of the 32 clubs that qualified for the group stage. No Russian team had a club coefficient larger than 87.1 at the time. As a result, under “Choose Your Opponent”, the winner of the group of Spartak Moscow would have been awarded an undue advantage: since it faced a weak Pot 1 opponent due to the poor seeding, it could have more easily been ranked as one of the best group winners and thus been one of the first teams to choose their round of 16 opponent. This again underlines the importance of adopting seeding rules that fairly reflect team abilities.
Guyon (2015b) suggested a better way of seeding the UEFA Champions League group stage that would reward the European leagues whose teams performed best in Europe in the past years, and for each country would also reward the teams that performed best in their domestic league the previous year. Corona et al. (2019) have simulated the UEFA Champions League under the pre-2015 and post-2015 seeding regimes. Dagaev and Rudyak (2019) have also obtained numerical estimates for competitiveness changes in the UEFA tournaments caused by the 2015–16 seeding reform. Note that Engist et al. (2021) find no evidence that seeding itself contributes positively to a team’s success in the UEFA Champions League. Remark 7. The implementation of the “Choose Your Opponent" policy in the UEFA Europa League Round of 32 is nontrivial because 24 teams come from the Europa League and 8 come from the Champions League. Currently, the twelve group winners and the four third-placed teams from the Champions League group stage with the better group records are seeded. To decide the Round of 32, a draw is organized that matches up seeded teams with unseeded teams, with the restriction that teams from the same group or the same association cannot be drawn against each other. In one simple implementation, the 12 Europa League group winners would be ranked 1–12 based on their group stage performance, and the 4 best third-placed teams from the Champions League would be ranked 13–16; and similarly for ranks 17–32. Alternatively, teams coming from the Champions League could get ranks 25–32, or ranks 1–8, or ranks 1, 5, 9, 13, 17, 21, 25, 29, or ranks 4, 8, 12, 16, 20, 24, 28, 32, etc.
5Conclusion
In this article, we have introduced and investigated a new, exciting, and simple design for hybrid tournaments, in which the teams that have performed best during a preliminary group stage can choose their opponent in the subsequent knockout rounds. The main benefit of this format is that it significantly increases win incentive during the group stage, by rewarding the best group winners with first picks, thus making the group stage more exciting. It also increases fairness, by deterring teams from colluding or tanking during the last game of the group stage, and by making sure that the best group winners are fairly rewarded for their group stage performance and do not meet a strong opponent in the first round of the knockout stage. The “Choose Your Opponent” format would also lend itself to new, much anticipated TV shows during which advancing teams would pick their opponent. These events are likely to attract a lot of media attention, and the picking strategies of the teams would probably be highly debated by the media and among fans. This format would bring an interesting strategic component to the tournament.
We have illustrated how this new format would work for the round of 16 of the UEFA Champions League, the most popular soccer club competition in the world; the “Choose Your Opponent” easily adapts to the constraints that UEFA currently puts on the draw. In (Guyon, 2019a), we have also studied how the “Choose Your Opponent” format could have naturally been adapted in order to maximize the number of home games during the knockout round of the UEFA Euro 2020, which for the first time will be hosted by 12 countries.
This new knockout format could create logistics issues for tournaments that are played in distant cities over a short period of time, such as the FIFA World Cup, but it looks particularly well suited to competitions where knockout draws/picks can be organized well ahead of the knockout matches, like the UEFA Champions League or the UEFA Europa League; or to competitions that are organized in one city or in close cities. We encourage sports governing bodies and leagues around the world to consider it as a way to build fairer, more exciting tournaments.
Acknowledgments
We are very grateful to László Csató, Dries Goossens, and Frits Spieksma for their interesting comments on the preprint (Guyon, 2019a), and to two anonymous referees for their very helpful comments on a first version of this article. We would also like to thank Nicholas Hall for pointing out to us (very unrealistic but mathematically possible) situations in which teams may still be tempted to tank under the “Choose Your Opponent” knockout design.
References
1 | Adler, I. , Cao, Y. , Karp, R. , Pekoz, E. , & Ross, S. (2017) , Random knockout tournaments, Operations Research 65: (6), 1589–1596. |
2 | Alarcón, F. , Durán, G. , Guajardo, M. , Miranda, J. , Muñoz, H. , Ramírez, L. , Ramírez, M. , Sauré, D. , Siebert, M. , Souyris, S. , Weintraub, A. , Wolf-Yadlin, R. , & Zamorano, G. (2017) , Operations research transforms the scheduling of Chilean soccer leagues and South American World Cup Qualifiers, Interfaces 47: (1), 52–69. |
3 | Amez, S. , Baert, S. , Neyt, B. , & Vandemaele, M. (2020) , No evidence for second leg home advantage in recent seasons of European soccer cups, Applied Economics Letters 27: (2), 156–160. |
4 | Annis D. H. , & Wu S. S. , (2006) , A comparison of potential playoff systems for NCAA I-A football, The American Statistician 60: (2), 151–157. |
5 | Appleton, D. R. , (1995) , May the best man win? Journal of the Royal Statistical Society: Series D (The Statistician) 44: (4), 529–538. |
6 | Arlegi, R. , & Dimitrov, D. , (2020) , Fair elimination-type competitions, European Journal of Operational Research 287: (2), 528–535. |
7 | Austrian ice hockey league website: Game mode. Available at http://www.ice.hockey/en/league-info/information/game-mode. |
8 | Aziz, H. , Gaspers, S. , Mackenzie S. , Mattei, N. , Stursberg, P. , & Walsh T. , 2014, Fixing a balanced knockout tournament. Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence (AAAI-14), 552–558. |
9 | Banchio, M. , & Munro, E. , (2021) , An incentive-compatible draft allocation mechanism. Manuscript. Available at https://www.evanmunro.ca/files/targeting.pdf. |
10 | Baumann, R. , Matheson V. A. , & Howe, C. A. . (2010) , Anomalies intournament design: the madness of March Madness, Article, Journal ofQuantitative Analysis in Sports 6: (2), Article 4. |
11 | BBC: World Cup 2018: Japan go through but final group game ends in ‘mind-boggling farce’. June 28, 2018. Available at http://www.bbc.com/sport/football/44649668. |
12 | Berker, Y. , (2014) , Tie-breaking in round-robin soccer tournaments andits in influence on the autonomy of relative rankings: UEFA vs. FIFAregulations, European Sport Management Quarterly 14: (2), 194–210. |
13 | Boczoń, M. , & Wilson, A. J. , Goals, constraints, and public assignment: A field study of the UEFA Champions League. Technical Report 18/016, University of Pittsburgh, Kenneth P. Dietrich School of Arts and Sciences, Department of Economics, 2018. |
14 | Canadian Bridge Federation: General conditions of contest for all Canadian national bridge championships. Available at http://cbf.ca/wp-content/uploads/ConditionsofContest/CBC-General-Conditions-of-Contest-Eng.pdf. |
15 | Cea, S. , Durán, G. , Guajardo, M. , Sauré, D. , Siebert, J. , & Zamorano, G. (2020) , An analytics approach to the FIFA ranking procedure and the World Cup final draw, Annals of Operations Research 286: (1-2), 119–146. |
16 | Chater, M. , Arrondel, L. , Gayant, J.-P. , & Laslier, J.-F. , (2021) , Fixing match-fixing: Optimal schedules to promote competitiveness, European Journal of Operational Research 294: (2), 673–683. |
17 | Chess.com website: PRO chess league announces returning teams, new qualifiers. Available at http://www.chess.com/news/view/pro-chess-league-announcesreturning-teams-new-qualification-system-8669. |
18 | Corona, F. , Forrest, D. , Tena, J. D. , & Wiper, M. , (2019) , Bayesianforecasting of UEFA Champions League under alternative seedingregimes, International Journal of Forecasting 35: (2), 722–732. |
19 | Csató, L. , (2018) , Was Zidane honest or well-informed? How UEFA barely avoided a serious scandal, Economics Bulletin 38: (1), 152–158. |
20 | Csató, L. , (2019) , UEFA Champions League entry has not satisfied strategyproofness in three seasons, Journal of Sports Economics 20: (7), 975–981. |
21 | Csató, L. , (2020) , Optimal tournament design: lessons from the menshandball Champions League, Journal of Sports Economics 21: (8), 848–868. |
22 | Csató, L.. , (2020) , The incentive (in)compatibility of group-basedqualification systems, International Journal of GeneralSystems 49: (4), 374–399. |
23 | Csató, L. , (2020) , Two issues of the UEFA Euro 2020 qualifyingplay-offs, International Journal of Sport Policy and Politics 12: (3), 471–484. |
24 | Csató, L. , (2020) , The UEFA Champions League seeding is not strategy-proof since the 2015/16 season, Annals of Operations Research 292: (1), 161–169. |
25 | Csató, L. , (2020) , When neither team wants to win: A flaw of recent UEFA qualification rules, International Journal of Sports Science & Coaching 15: (4), 526–532. |
26 | Csató, L. , (2021) , A simulation comparison of tournament designsfor the World Men’s Handball Championships, InternationalTransactions in Operational Research 28: (5), 2377–2401. |
27 | Csató, L. , (2021) , Tournament Design: How Operations Research Can Improve Sports Rules. Palgrave Pivots in Sports Economics, Palgrave Macmillan, Cham, Switzerland. |
28 | Dagaev, D. , & Suzdaltsev A. , (2018) , Competitive intensity and qualitymaximizing seedings in knock-out tournaments, Journal ofCombinatorial Optimization 35: (1), 170–188. |
29 | Dagaev, D. , & Sonin, K. , (2018) , Winning by losing: Incentiveincompatibility in multiple qualifiers, Journal of SportsEconomics 19: (8), 1122–1146. |
30 | Dagaev, D. , & Rudyak, V. , (2019) , Seeding the UEFA Champions Leagueparticipants: Evaluation of the reform, Journal of QuantitativeAnalysis in Sports 15: (2), 129–140. |
31 | Durán, G. , Guajardo, M. , & Sauré, D. , (2017) , Scheduling theSouth American qualifiers to the 2018 FIFA World Cup by integerprogramming, European Journal of Operational Research 262: (3), 1109–1115. |
32 | Edwards C. T. , (1998) , Non-parametric procedure for knockouttournaments, Journal of Applied Statistics 25: , 375–385. |
33 | Engist, O. , Merkus, E. , & Schafmeister, F. , (2021) , The effect ofseeding on tournament outcomes: Evidence from aregression-discontinuity design, Journal of Sports Economics 22: (1), 115–136. |
34 | Eugster, M. J. A. , Gertheiss, J. , & Kaiser, S. , (2011) , Having thesecond leg at home - Advantage in the UEFA Champions League knockoutphase? Journal of Quantitative Analysis in Sports 7: (1), 2011. |
35 | Fornwagner, H. , (2019) , Incentives to lose revisited: The NHL and itstournament incentives, Journal of Economic Psychology 75: (Part B), 102088. |
36 | Geenens, G. , & Cuddihy, T. , (2018) , Non-parametric evidence ofsecond-leg home advantage in European football, Journal of theRoyal Statistical Society: Series A (Statistics in Society) 181: (4), 1009–1031. |
37 | Goossens, D. R. , Beliën, J. , Spieksma, F. C. R. (2012) , Comparingleague formats with respect to match importance in Belgian football, Annals of Operations Research 194: (1), 223–240. |
38 | Glickman, M. E. , (2008) , Bayesian locally optimal design of knockouttournaments, Journal of Statistical Planning and Inference 138: (7), 2117–2127. |
39 | Glickman, M. E. , & Hennessy J. (2016) , Bayesian optimal design offixed knockout tournament brackets, Journal of QuantitativeAnalysis in Sports 12: (1), 1–15. |
40 | Groh, C. , Moldovanu, B. , Sela, A. , & Sunde, U. , (2012) , Optimalseedings in elimination tournaments, Economic Theory 49: (1), 59–80. |
41 | Guyon, J. 2014, Rethinking the FIFA World Cup final draw. Preprint, 2014. Available at http://www.ssrn.com/abstract=2424376. |
42 | Guyon, J. 2014, A Better Way to Rank Soccer Teams in a Fairer World Cup. The New York Times, June 13, 2014. Available at http://www.nytimes.com/2014/06/14/upshot/a-better-way-to-rank-soccer-teams-in-a-fairer-world-cup.html. |
43 | Guyon, J. (2015) , Rethinking the FIFA World Cup final draw, Journal of Quantitative Analysis of Sports 11: (3), 169–182. |
44 | Guyon, J. 2015, Champions League: How to Solve the Seeding Problem. The New York Times, January 21, 2015. Available at http://www.nytimes.com/2015/01/22/upshot/champions-league-how-to-solve-the-seeding-problem.html. |
45 | Guyon, J. (2018) , What a fairer 24 team UEFA Euro could look like, Journal of Sports Analytics 4: (4), 297–317. Preprint “What a fairer UEFA Euro could look like” available at http://www.ssrn.com/abstract=2714199, 2016. |
46 | Guyon, J. 2017, Ligue des champions : pourquoi le PSG a presque une chance sur trois de rencontrer Chelsea. Le Monde, December 10, 2017. Available at http://www.lemonde.fr/ligue-des-champions/article/2017/12/10/ligue-des-champions-pourquoi-le-psg-a-une-chance-sur-trois-de-rencontrer-chelsea_5227638_1616944.html. |
47 | Guyon, J. 2017, Por qué el Barcelona tiene un, 41,3% de emparejarse con el Chelsea en octavos. El País, December 17, 2017. Available at https://elpais.com/deportes/2017/12/07/actualidad/1512643772_372491.html. |
48 | Guyon, J. 2018, Ligue des champions : Atlético Madrid ? Dortmund ? Qui seront les adversaires du PSG et de Lyon en 8e de finale ? Le Monde, December 13, 2018. Available at http://www.lemonde.fr/football/article/2018/12/13/ligue-des-champions-les-adversaires-les-plus-probables-pour-le-psg-et-lyon-en-8e-de-finale_5396808_1616938.html. |
49 | Guyon, J. 2019, “Choose Your Opponent”: A new knockout format for sports tournaments. Application to the round of 16 of the UEFA Champions League and to maximizing the number of home games during the UEFA Euro 2020. Preprint, 2019. Available at http://www.ssrn.com/abstract=3488832. |
50 | Guyon, J. 2019, Champions League last-16 draw probabilities: Why Chelsea are more likely to get Barcelona and what fates await Liverpool, Man City and Tottenham. Four Four Two, December 12, 2019. Available at http://www.fourfourtwo.com/features/champions-league-last-16-draw-probabilities-liverpool-chelsea-tottenham-man-city-real-madrid-barcelona. |
51 | Guyon, J. 2019, Ligue des champions : quels sont les adversaires les plus probables pour le PSG et Lyon ? Le Monde, December 15, 2019. Available at http://www.lemonde.fr/sport/article/2019/12/15/ligue-des-champions-de-football-quels-sont-les-adversaires-les-plus-probables-pour-le-psg-et-lyon_6022954_3242.html |
52 | Guyon, J. 2019, Ligue des champions : et si les vainqueurs de groupe choisissaient leur adversaire pour les les huitièmes de finale ? Le Monde, December 17, 2019 (in French). Available at http://www.lemonde.fr/sport/article/2019/12/17/ligue-des-champions-et-si-les-vainqueurs-de-groupe-choisissaient-leur-adversaire-pour-les-8es-de-finale_6023186_3242.html. |
53 | Guyon, J. 2020, Champions League knockout draw: What if group winners could choose their opponents? Four Four Two, December 11, 2020. Available at http://www.fourfourtwo.com/features/champions-league-knockout-draw-what-if-group-winners-could-choose-their-opponents. |
54 | Guyon, J. 2020, Champions League knockout draw: Who are the most likely opponents for Liverpool, Manchester City and Chelsea? Four Four Two, December 11, 2020. Available at http://www.fourfourtwo.com/features/champions-league-knockout-draw-who-are-the-most-likely-opponents-for-liverpool-manchester-city-and-chelsea. |
55 | Guyon, J. 2020, Ligue des champions : Borussia M’Gladbach, adversaire le plus probable du PSG en huitième de finale. Le Monde, December 12, 2020. Available at http://www.lemonde.fr/football/article/2020/12/12/ligue-des-champions-borussia-m-gladbach-adversaire-le-plus-probable-du-psg-en-huitieme-de-finale_6063134_1616938.html. |
56 | Guyon, J. , (2020) , Risk of collusion: Will groups of 3 ruin the FIFA World Cup? Journal of Sports Analytics 6: (4), 259–279. |
57 | Hwang, F. K. , (1982) , New concepts in seeding knockout tournaments, American Mathematical Monthly 89: (4), 235–239. |
58 | International Hockey Wiki website: Liiga. Available at https://internationalhockey.fandom.com/wiki/Liiga. |
59 | Karpov, A. , (2016) , A new knockout tournament seeding method and its axiomatic justification, Operations Research Letters 44: (6), 706–711. |
60 | Karpov, A. , (2018) , Generalized knockout tournament seedings, International Journal of Computer Science in Sport 17: (2), 113–127. |
61 | Kazachkov, A. E. , & Vardi, S. , On tanking and competitive balance: reconciling conicting incentives. Manuscript, 2020. Available at https://akazachk.github.io/pubs/tanking.pdf. |
62 | Kloessner, S. , & Becker, M. , (2013) , Odd odds: The UEFA ChampionsLeague round of sixteen draw, Journal of Quantitative Analysis in Sports 9: (3), 249–270. |
63 | Kendall G. , & Lenten, L. , (2017) , When sports rules go awry, European Journal of Operational Research 257: (2), 377–394. |
64 | Laliena, P. , & López, F. J. , (2019) , Fair draws for group roundsin sport tournaments, International Transactions in Operational Research 26: (2), 439–457. |
65 | Lasek, J. , Szlávik, Z. , & Bhulai, S. , (2013) , The predictive powerof ranking systems in association football, International Journal of Applied Pattern Recognition 1: (1), 27–46. |
66 | Lasek, J. , & Gagolewski, M. , (2018) , The efficacy of league formats in ranking teams, Statistical Modelling 18: (5-6), 411–435. |
67 | Lenten, L. J. A. , (2016) , Mitigation of perverse incentives in professional sports leagues with reverse-order drafts, Reviewof Industrial Organization 49: (1), 25–41. |
68 | Lenten, L. J. A. , Smith, A. C. T. , & Boys, N. , (2018) , Evaluating analternative draft pick allocation policy to reduce ‘tanking’ in theAustralian Football League, European Journal of OperationalResearch 267: (1), 315–320. |
69 | Marchand, E. , (2002) , On the comparison between standard and randomknockout tournaments, The Statistician 51: , 169–178. |
70 | Matisz, J. , 2020, What if NHL playoff teams picked their opponents? The Score, December 4, 2020. Available at https://www.thescore.com/nhl/news/2059087. |
71 | McGarry, T. , & Schutz, R. W. , (1997) , Efficacy of traditional sporttournament structures, Journal of the Operational ResearchSociety 48: (1), 65–74. |
72 | McHale, I. , & Davies, S. , (2007) , Statistical analysis of the effectiveness of the FIFA world rankings. Statistical Thinking in Sports, edited by Jim Albert and Ruud H. Koning, Chapman & Hall/CRC. |
73 | Page, L. , & Page, K. , (2007) , The second leg home advantage: Evidencefrom European football cup competitions, Journal of SportsSciences 25: (14), 1547–1556. |
74 | Pauly, M. , (2014) , Can strategizing in round-robin subtournaments beavoided? Social Choice and Welfare 43: (1), 29–46. |
75 | Price, J. , Soebbing, B. P. , Berri, D. , & Humphreys, B. R. , (2010) , Tournament incentives, league policy, and NBA team performancerevisited, Journal of Sports Economics 11: (2), 117–135. |
76 | Ross, S. , & Ghamami, S. , (2008) , Efficient simulation of a randomknockout tournament, Journal of Industrial and SystemsEngineering 2: (2), 88–96. |
77 | Scarf, P. , Yusof, M. M. , & Bilbao, M. , (2009) , A numerical study ofdesigns for sporting contests, European Journal of OperationalResearch 198: (1), 190–198. |
78 | Scarf, P. A. , & Yusof, M. M. , (2011) , A numerical study of tournamentstructure and seeding policy for the soccer World Cup Finals, Statistica Neerlandica 65: (1), 43–57. |
79 | Schwenk, A. , (2000) , What is the correct way to seed a knockout tournament? American Mathematical Monthly 107: (2), 140–150. |
80 | Southern Professional Hockey League website: The SPHL. Available at http://www.thesphl.com/the-sphl. |
81 | Stanton I. , & Vassilevska Williams V. , 2011, Rigging tournament brackets for weaker players. Proceedings of the 22nd International Joint Conference on Artificial Intelligence (IJCAI), 357–364. |
82 | Stronka, W. , (2020) , Anti-tanking pair matching before an eliminationphase of a two-phase tournament, Economies 8: (3), 66. |
83 | Taylor, B. A. , & Trogdon, J. G. , (2002) , Losing to win: Tournamentincentives in the National Basketball Association, Journal ofLabor Economics 20: (1), 23–41. |
84 | The Guardian: Denmark join France in last 16 after first goalless draw of World Cup. June 26, 2018. Available at http://www.theguardian.com/football/2018/jun/26/denmark-france-world-cup-group-c-match-report |
85 | The Independent: Radamel Falcao makes revealing admission following match-fixing allegations in Peru vs Colombia draw. October 12, 2017. Available at http://www.independent.co.uk/sport/football/international/radamel-falcao-match-fixing-colombia-peru-draw-world-cup-south-america-qualifying-renato-tapia-a7996226.html. |
86 | The International Dota 2 Championships: Rules. Available at http://www.dota2.com/international/rules/?l=english, 2019. |
87 | The Sun: “So Obviously Fixed” World Cup 2018: France and Denmarkspark fix” claims on social media after first 0-0 draw of the tournament. June 27, 2018. Available at http://www.thesun.co.uk/world-cup-2018/6631385/france-denmark-world-cup-2018-fix-social-media. |
88 | The United States Bridge Federation: Conditions of contest for 2019 mixed United States bridge championship. Available at http://usbf.org/docs/COC/2019-Mixed-USBC-COC-Draft1.pdf. |
89 | UEFA website: Regulations of the UEFA Champions League 2012–15 Cycle. 2014/15 Season. Available at http://web-old.archive.org/web/20200927130546/https://www.uefa.com/MultimediaFiles/Download/Regulations/uefaorg/Regulations/02/14/11/74/2141174DOWNLOAD.pdf. |
90 | Total Sportal website: UEFA Champions League 2020-21 revenue sharing (confirmed). Available at http://www.totalsportal.com/football/uefa-champions-league-revenue-distribution, 2020. |
91 | UEFA website: 2019/20 UEFA club competitions revenue distribution system. Available at http://www.uefa.com/insideuefa/stakeholders/news/0253-0f8e6d83afa2-0904576faee6-1000–2019-20-uefa-club-competitions-revenue-distribution-system, 2019. |
92 | Vassilevska Williams V. , 2010, Fixing a tournament. Proceedings of the 24th AAAI Conference on Artificial Intelligence (AAAI), 895–900. |
93 | Vong, A. I. , (2017) , Strategic manipulation in tournament games, Games and Economic Behavior 102: , 562–567. |
94 | Vu T. , Altman, A. , & Shoham Y. , 2009, On the complexity of schedule control problems for knockout tournaments, Proceedings of the 8th International Joint Conference on Autonomous Agents and Multi-Agent Systems (AAMAS), 225–232. |
95 | Vu T. , & Shoham Y. , (2011) , Fair seeding in knockout tournaments,no, ACM Transactions on Intelligent Systems and Technology 3: (1), no 9, 2011. |
96 | Wikipedia: 1997-98 UEFA Champions League group stage. Available at https://en.wikipedia.org/wiki/1997-98_UEFA_Champions_League_group_stage. |
97 | Wikipedia: 2010-11 SM-liiga season. Available at https://en.wikipedia.org/wiki/2010-11_SM-liiga_season |
98 | Wikipedia: Badminton at the 2012 Summer Olympics. Available at https://en.wikipedia.org/wiki/Badminton_at_the_2012_Summer_Olympics_-_Women%27s_doubles. |
99 | Wikipedia: 2016-17 Austrian Hockey League season. Available at https://en.wikipedia.org/wiki/2016-17_Austrian_Hockey_League_season. |
100 | Wikipedia: 2017-18 Austrian Hockey League season. Available at https://en.wikipedia.org/wiki/2017-18_Austrian_Hockey_League_season. |
101 | Wikipedia: 2019-20 Austrian Hockey League season. Available at https://en.wikipedia.org/wiki/2019-20_Austrian_Hockey_League_season. |
102 | Wikipedia: Super League play-offs. Available 1844 at https://en.wikipedia.org/wiki/Super_League_play-offs. |
103 | Wikipedia: UEFA Euro 2020 qualifying. Available at https://en.wikipedia.org/wiki/UEFA_Euro_2020_qualifying. |
104 | World Match Racing Tour: Standard Tour Rules. Available at https://issuu.com/awmrt/docs/2015_wmrt_standard_tour_rules_v1.2. |
Notes
2 Note that between 2010 and 2013 the Finnish ice hockey league made a surprising use of “Choose Your Opponent”, allowing the lowest-ranked teams at some point during the 14-team regular season to pick their opponent among the best-ranked teams for an additional two games in the regular season (International Hockey Wiki website; Wikipedia, 2010–11 SM-liiga season). The 14th-placed team at the time was the first picking team, followed by the 13th-placed team, etc. The restricted choice version was used: the picking teams could only choose opponents ranked between the first and seventh place.
3 It seems that the teams wanted to avoid one half of the bracket (Badminton at the 2012 Summer Olympics).
4 Currently, Ukrainian and Russian teams are not allowed to play against each other either.
5 For knockout rounds played over two legs, one at home and one away, a team advancing thanks to the away goals rule may also be awarded less points than one advancing after scoring strictly more goals than its opponent over the two legs.
6 The 2022 FIFA World Cup in Qatar is an exception, as all stadiums used for the tournament will be close to each other.
7 Beşiktaş had a lower Elo rating than Shakhtar Donetsk at the time, but Paris Saint-Germain would maybe have considered that it is more difficult to get a good result when they play the first leg in Turkey, due to the famous “hot” ambiance in Turkish stadiums, rather than in Ukraine. Paris Saint-Germain may also have considered that if they chose Beşiktaş, many Beşiktaş fans would have attended the second leg in Paris, as there are many football fans of Turkish descent living in the Paris area. For similar reasons, Manchester City (Team 3) may have also preferred to choose Porto.
8 To be precise, in both seeding systems, the Champions League title holder is seeded in Pot 1, as an exception. Since the 2018–19 season, the Europa League title holder is also seeded in Pot 1. For instance, when none of the two title holders have won one of the 6 highest ranked domestic leagues, only the domestic champions of the 6 highest ranked domestic leagues are seeded in Pot 1, along with the two title holders. A good summary of the UEFA Champions League seeding policy is (Csató, 2020d), which also identifies an issue of incentive incompatibility in the current rule. The Champions League titleholder was automatically allocated into Pot 1, independently of its UEFA club coeffcient even before the 2015–16 season (UEFA website, Regulations of the UEFA Champions League 2012–15 Cycle, 2014/15 Season). This advantage enjoyed by the title holder dates back to at least the 1997–98 season (Wikipedia, 1997–98 UEFA Champions League group stage).




