Forecasting serve performance in professional tennis matches
Abstract
Many research papers on tennis match prediction use a hierarchical Markov Model. To predict match outcomes, this model requires input parameters for each player’s serving ability. While these parameters are often computed directly from each player’s historical percentages of points won on serve and return, doing so fails to address bias due to limited sample size and differences in strength of schedule. In this paper, we explore a handful of novel approaches to forecasting serve performance that specifically address these limitations. By applying an Efron-Morris estimator, we provide a means to robustly forecast outcomes when players have limited match data over the past year. Next, through tracking expected serve and return performance in past matches, we account for strength of schedule across all points in a player’s match history. Finally, we demonstrate a new way to synthesize historical serve data with the predictive power of Elo ratings. When forecasting serve performance across 7,622 ATP tour-level matches from 2014-2016, all three of these proposed methods outperformed Barnett and Clarke’s standard approach.
1Introduction
Statistical prediction models have been applied to tennis for decades, often to predict the winner of a match. Laying the groundwork for research on point-based models, Klaassen and Magnus (2001) first tested the assumption that points in a tennis match are independent and identically distributed, or i.i.d. While this was proven false, they concluded deviations are small enough that the i.i.d. assumption provides a reasonable approximation. By estimating each player’s probability of winning a point on serve and computing win probability from these parameters, they demonstrated a new way to forecast matches under this assumption (Klaassen and Magnus, 2003).
In the time since, we have seen a variety of ways to forecast serve performance. Barnett and Clarke (2005) estimated these parameters by adjusting historical tournament statistics by the performance of the server and returner, relative to the average player. Assuming that serve and return performances follow a normal distribution on a match-by-match basis, Newton and Aslam (2009) ran Monte Carlo simulations to predict the winner of a match. Adapting Barnett and Clarke’s approach, Spanias and Knottenbelt (2012) predicted serve performance by modeling the probabilities of specific point outcomes (e.g. ace, rally win on first serve, etc.) within a service game. In order to reduce bias from variations in strength of schedule, Knottenbelt et al. (2012) then proposed the Common-Opponent Model, which measures performance relative to common adversaries in their respective match histories. More recently, Kovalchik and Reid (2018) demonstrated a way to calibrate serve parameters to the win probability implied by each player’s Elo rating.
Building upon previous work in serve performance prediction, this exploration serves two purposes. Following a previous assessment of 11 different pre-match prediction models on 2014 ATP tour-level matches (Kovalchik, 2016), we evaluate serve performance prediction methods across the same dataset as a benchmark for future work. We also introduce several new methods to more robustly compute expected serve performance. When forecasting thousands of matches, the previously stated methods tend to run into problems with limited match data and differences in strength of schedule.1 To avoid these pitfalls, we explore variations of Barnett and Clarke’s approach that specifically address these issues.
In section 2, we review the hierarchical Markov Model and Elo ratings, two of the most often-cited methods for predicting tennis match outcomes. In section 3, we review Barnett and Clarke’s formula and explore further approaches to serve performance prediction. Section 3.1.1 introduces a Bayesian estimator to more robustly predict serve performance from limited match data. Section 3.1.2 demonstrates an approach that tracks expected serve and return performances in every match, allowing us to consider strength of schedule over the course of a player’s entire match history. Section 3.2 harnesses Elo ratings’ predictive power to more accurately predict serve performance while maintaining the overall serve ability between two players. In section 4, we present several case studies to examine how each approach informs predictions for individual matches. In section 5, we evaluate all proposed methods alongside established prediction models. Section 6 summarizes findings and suggests future steps for research with point-based models.
Effective serve performance prediction holds strong implications for both player analytics and in-match forecasting. With more effective forecasts, coaches can better understand how their players match up with opponents on serve and return, and adjust their strategies accordingly. By using the hierarchical Markov Model, we can also compute win probability as a function of each player’s expected serve performance from any score. Therefore, improving existing methods will provide means to more confidently predict match outcomes while play is in progress, a problem with significant application to betting markets and real-time sports analytics.
2Models for match win prediction
Newly proposed methods will require the context of two popular match prediction models. The hierarchical Markov Model computes win probability directly from point-level probabilities, while Elo ratings infer player ability solely from match outcomes.
2.1Hierarchical markov model
Consider a tennis match between player i and player j, where fij estimates the probability that player i wins a point on serve against player j in a given match. Given serve parameters fij, fji we can calculate the probability that player i wins the match, πij, from any score. To do so, consider how scores are composed of points, games, and sets. With player i serving to player j, let ai, aj represent each player’s within-game score. Then we compute the probability of player i winning the current game from score ai - aj as follows:
Following this approach, one may calculate player i’s probability of winning the current set, Ps(gi, gj), and then the match, Pm(si, sj), through similar recursive relationships. Barnett et al. (2002) describe the recursion in full detail.
2.2Elo ratings
Elo was originally developed as a head-to-head rating system for chess players (Elo, 1978). Recently, FiveThirtyEight’s Elo variant has gained prominence in the media (Bialik et al., 2016). For a match at time t between player i and player j with Elo ratings Ei(t) and Ej(t), player i is forecasted to win with probability:
For the following match, player i’s rating is then updated accordingly:
Wi(t) is an indicator for whether player i won the given match at time t, while Kit is the learning rate for player i at time t.
According to FiveThirtyEight’s analysts, Elo ratings perform optimally when allowing Kit to decay slowly over time (Bialik et al., 2016). With mi(t) representing the number of player i’s career matches at time t, we update the learning rate as follows2:
This variant updates a player’s Elo rating most quickly when we have no information about them and makes smaller changes as mi(t) accumulates. To apply this rating system to all ATP tour-level matches, we initalize each player’s Elo rating at Ei(0) =1500 and match history mi(0) =0. Then, we iterate through all tour-level matches from 1968-present in chronological order, storing Ei(t) , Ej(t) for each match and updating each player’s Elo rating accordingly.3
3Predicting serve performance
A significant portion of research in tennis match prediction concerns estimating each player’s probability of winning a point on serve. We present several variations to Barnett and Clarke’s approach in Section 3.1 and a way to reconcile Elo ratings with these point-based methods in Section 3.2.
3.1Barnett-Clarke formula
Given players’ historical serve/return performance, Barnett and Clarke (2005) demonstrated a method to calculate fij, fji.
fij = ft +(fi - fav) -(gj - gav)
fji = ft +(fj - fav) -(gi - gav)
In a match between player i and player j, each parameter estimates one player’s probability of winning a point on serve against the other. fi represents player i’s historical percentage of points won on serve, while gi corresponds to their percentage of points won on return. ft denotes the percentage of points won on serve at the match’s given tournament and fav, gav represent tour-level averages for the percentages of points won on serve and return, respectively.
While Barnett and Clarke’s dataset was limited to year-to-date statistics, we may calculate fi, gi with the past twelve months of match data for any given match. Where
wik denotes the number of service points won by player i in match k and nik the total number of service points played by player i in match k.
Next, we calculate ft for a given tournament and year, where
wk and nk represent the number of service points won and played in match k, respectively.
Finally, we calculate fav, gav where
gav(y, m) =1 - fav(y, m) .
Overall, Barnett and Clarke’s formula assumes that differences between player serve and return ability are additive. Next, we explore variations to this approach.
3.1.1Efron-Morris estimator
In the case of players who do not regularly compete in tour-level events, fi, gi must be calculated from limited sample sizes. Consequently, match probabilities based on these estimates can be skewed by noise. To address this, we turn to the Efron-Morris estimator to provide alternative parameters of the form:
Rather than directly apply the estimator to fij, fji, we normalize the serve/return parameters fi, gi which constitute Barnett and Clarke’s equations.
Decades ago, Efron and Morris (1977) described a method to estimate a group of sample means with unequal variances. The Efron-Morris estimator shrinks sample means toward the overall mean by a magnitude proportional to each sample mean’s uncertainty, producing a mean-squared error favorable in expectation to that of Maximum-Likelihood Estimation. While Barnett and Clarke use raw historical averages of serve and return points won, we can instead use this estimator to feed more reliable parameters into their equations. Just as Efron and Morris estimated toxoplasmosis rates across hospitals with uneven populations, we will apply this method to serve performance prediction.
Consider our match dataset
To model serve performance according to a Bayesian distribution, we consider each
θi ∼ N(μ, τ2) .
Put together, the above statements imply the following (Efron and Morris, 1975):
Normalization coefficient Bi depends on both τ2, the variance of true service ability, and
Then, using maximum likelihood estimation, we estimate Bi and
When ni is large, our uncertainty in fi decreases and shrinkage coefficient
While Barnett and Clarke’s original paper computed fi, gi with sample means, using an Efron-Morris estimator will produce more robust forecasts across large datasets, where the amount of available data for a given match varies significantly. In addition, this estimator can be applied to other variations of Barnett and Clarke’s approach, as we will observe when evaluating methods in Section 5.
3.1.2Opponent-adjusted ratings
While Barnett and Clarke’s equation considers the opponent’s serve and return ability, it does not track strength of schedule throughout each player’s match history. This is important, as a player’s win percentages on serve/return may become inflated from playing weaker opponents or vice versa. In this section, we propose a variation to Barnett and Clarke’s equation which replaces fav, gav with opponent-adjusted averages
Once again, nik denotes the number of service points played by player i in match k. In calculating
Since the formula considers each player’s opponent-adjusted ratings at the time of each match, we must compute ratings in chronological order. Similarly to Elo, we initialize all players’ opponent-adjusted ratings to fav, gav before iterating through all tour-level matches 1968-present and calculating player ratings for each match accordingly.
3.2Klaassen-Magnus elo ratings
Before Barnett and Clarke’s approach, Klaassen and Magnus (2001) suggested a method to infer serving probabilities from a pre-match win forecast πij. As b = fij + fji represents the overall serve ability between two players, they impose the constraint that any new serve parameters
As this paper was published in 2002, Klaassen and Magnus produced serve parameters from ATP rank-based forecasts. However, given that Elo has since been demonstrated to outperform ATP rank in predicting match outcomes, we apply this method with Elo forecasts.
Even when we impose the constraint fij + fji = b, our hierarchical Markov Model’s match probability equation has no analytical solution to its inverse. Therefore, we turn to the following approximation algorithm to generate serving percentages that correspond to a win probability within ε of our Elo forecast:
| Algorithm 1 Klaassen-Magnus Elo Serve Parameters |
| procedure EloServeProbabilities(π, b, ε) |
| f ← b/2 |
| diff ← b/4 |
| currentProb ← . 5 |
| while |currentProb - π| > ε do: |
| If currentProb < πthen |
| f += diff |
| else |
| f -= diff |
| diff = diff/2 |
| currentProb ← matchProb(f, b - f) |
| return f, b, - f |
To generate serve probabilities for a given match, we first compute πij as player i’s chance of victory against player j given their Elo ratings and fij, fji as specified by any Barnett-Clarke variation in section 3.1. Then we run the above algorithm with π = πij, b = fij + fji, and ε set to a desired precision level.6 At each step, we call matchProb() to compute the win probability from the start of the match if player i and player j had serve parameters fij = f, fji = b - f, respectively. Then we compare currentProb to prob and increment f by diff, which halves at every iteration. This process continues until the serve parameters f, b - f correspond to a win probability within ε of πij, taking
Given any pre-match forecast πij, we can produce
Most importantly, this approach allows us to generate serve parameters from forecasts that are not point-based. While Kovalchik (2016) explored a variety of point-based methods specific to tennis’ scoring system, none outperformed Elo ratings in predicting match outcomes. However, Elo ratings alone lack sufficient context to predict outcomes at a point level. Using the above approach, we significantly expand the possibilities when producing serve parameters for a given match. Should methods superior to Elo arise in the future, we may similarly intuit
4Case studies
The following examples illustrate applications of newly proposed methods in several ATP tour-level matches.
4.1Efron-Morris estimator
To see how the Efron-Morris estimator makes our model robust to small sample sizes, consider the following match. When Daniel Elahi (COL) and Ivo Karlovic (CRO) faced off at ATP Bogota 2015, Elahi had played only one tour-level match in the past year. From a previous one-sided victory, his year-long percentage of service points won, fi = .7969, was abnormally high compared to the year-long tour-level average of fav = .6423.
| player name | Daniel Elahi | Ivo Karlovic |
| service points won | 51 | 3516 |
| service points | 64 | 4654 |
| fi | .7969 | .7555 |
| return points won | 22 | 1409 |
| return points | 67 | 4903 |
| gi | .3284 | .2874 |
| Elo rating | 1585.93 | 1952.86 |
Following Barnett and Clarke’s method, we predict Elahi to win 89.25% of points on serve, which eclipses Karlovic’s forecast of 81.01%.
fij = ft +(fi - fav) -(gj - gav) = .8925
fji = ft +(fj - fav) -(gi - gav) = .8101
Given that Karlovic is one of the most effective servers in the history of the game, this estimate seems unrealistic. From the serving stats, our hierarchical Markov Model computes Elahi’s win probability as πij = .8095, mainly in consequence of only having collected his player statistics for one match. On the other hand, Karlovic becomes a strong favorite when we calculate Elahi’s win probability via Elo ratings:
This leads us to further question validity of this approach when using limited historical data. Thus, we turn to the Efron-Morris estimator to shrink Elahi’s serve and return parameters toward fav, gav.
Above, we can see that the Efron-Morris estimator shrinks Elahi’s stats far more than Karlovic’s, since Karlovic has played many more tour-level matches in the past year. Given
Fig.1
Strength of Bi against number of points played with fi =.64,
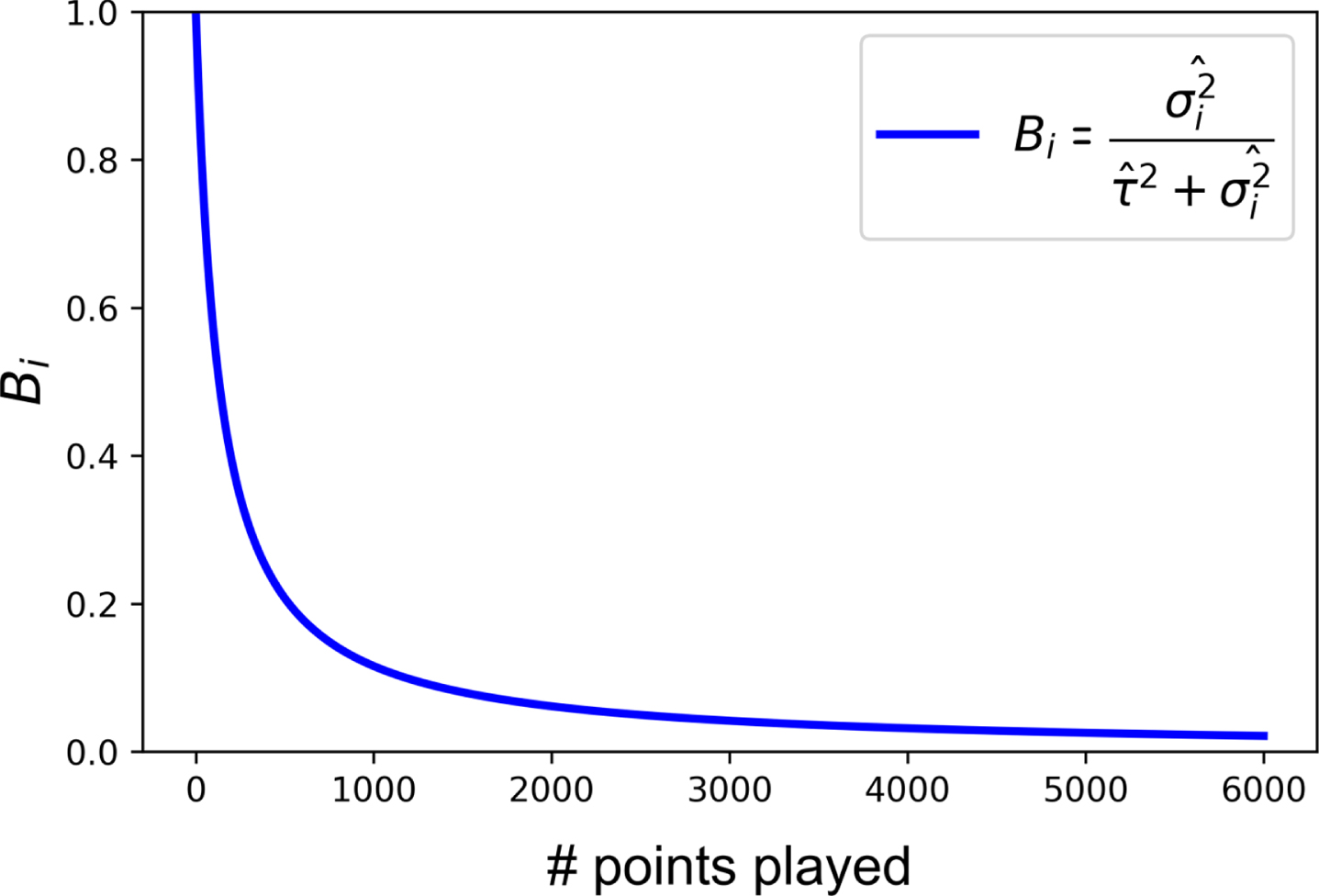
Figure 1 illustrates how normalization coefficient Bi varies with n throughout our dataset. When n is small, as in Elahi’s case, the Efron-Morris estimator strongly shrinks estimates toward the mean. Over the first one thousand points of play, however, Bi sharply declines in strength, approaching zero as match history accumulates further.
4.2Opponent-adjusted ratings
To illustrate the effect of tracking opponent-adjusted statistics, we consider the 2014 US Open first-round match between Mikhail Youzhny (RUS) and Nick Kyrgios (AUS).
| player name | Mikhail Youzhny | Nick Kyrgios |
| service points won | 1828 | 900 |
| service points | 2960 | 1370 |
| fi | .6176 | .6569 |
| return points won | 1145 | 424 |
| return points | 2947 | 1323 |
| gi | .3885 | .3205 |
| Elo rating | 1941.65 | 1931.07 |
From the standard approach, with ft = .6583, we compute fij = .6446, fji = .6159. To then calculate opponent-adjusted statistics, we must consider each player’s expected performance given their past opponents. As we observe, Kyrgios has faced slightly stronger opponents than Youzhny over the past twelve months.
| player name | Mikhail Youzhny | Nick Kyrgios |
|
| .4332 | .4486 |
|
| 1677.62 | 755.44 |
|
| .0508 | .1055 |
|
| .6982 | .7237 |
|
| 889.32 | 365.59 |
|
| .0868 | .0441 |
In the above table,
Using regular serve parameters, Youzhny is favored to win with πij = .6410. With opponent-adjusted serving percentages, we factor in the stronger opponents in Kyrgios’ match history and Youzhny’s win probability drops to πij = .4334. As we see, opponent-adjusted ratings can turn around forecasts when one player has faced tougher opponents over the past twelve months.
4.3Klaassen-Magnus elo ratings
Finally, we demonstrate the use of Klaassen-Magnus Elo ratings. In the quarterfinals of the 2016 Olympics at Rio de Janeiro, Kei Nishikori (JP) faced off against Gael Monfils (FRA).
| player name | Kei Nishikori | Gael Monfils |
| service points won | 3309 | 2345 |
| service points | 5069 | 3533 |
| fi | .6528 | .6637 |
| return points won | 2103 | 1433 |
| return points | 5229 | 3608 |
| gi | .4021 | .3972 |
| Elo rating | 2295.56 | 2140.56 |
Though Elo ratings clearly favored Nishikori, serve/return statistics over the past twelve months put Monfils at a slight advantage.
fij = ft +(fi - fav) -(gj - gav) = .6204
fji = ft +(fj - fav) -(gi - gav) = .6263
To produce serve parameters that reflect Nishikori’s Elo advantage and the pair’s overall serve ability, we implement the approach from Section 3.3 with πij = .7094, fij = .6204, fji = .6263.
Now we can forecast match outcomes with the hierarchical Markov Model, using serve parameters that respect each player’s Elo rating.
5Results
We evaluated methods across three years of tour-level matches, including Barnett and Clarke’s standard approach and Knottenbelt’s Common-Opponent Model, outlined in Appendix A, as benchmarks. Across the board, Klaassen-Magnus Elo ratings fared the best, while Efron-Morris estimators improved performance to a varying degree.
5.1Dataset
This project drew from a publicly available match dataset (Sackmann, 2018). Match summary statistics cover over 150,000 ATP tour-level matches dating back to 1968. Relevant features included:
match date, tournament, surface type, player names
match serve/return statistics
The matches in this repository comprised dataset
5.2Evaluation
All methods produced parameters fij, fji to estimate each player’s probability of winning a point on serve in a given match. We evaluated methods by predicting both the winner of every match and each player’s percentage of points won on serve. To evaluate serve performance prediction, we considered the RMSE (root-mean-square-error) between each method’s parameters and observed performance. By observing the proportion of points won on serve by each player for a single match k, we obtained sik, sjk and realized error terms eik, ejk:
eik = |sik - fij|, ejk = |sjk - fji| .
Over test set
To produce match win forecasts, we returned to the hierarchical Markov Model. As a function of a method’s parameters fij, fji we calculated match win probability πij recursively from the probabilities of winning sets and games, as described in Section 2.1. Then we computed accuracy and log loss by comparing these forecasts with observed wins or losses for each match in
5.3Discussion
We evaluated methods across 7,622 ATP tour-level matches from 2014-16. To compute Klaassen-Magnus Elo ratings, we set the constraint b = fij + fji, where fij, fji were computed with the Efron-Morris Estimator, as described in Section 3.1.1. Because a player’s performance can vary significantly across surfaces, we included a Barnett and Clarke variation which only considers performance on the given match’s surface.8 In Table 1 and Table 2, “EM” denotes a variation that used the Efron-Morris estimator to compute fi, gi in Barnett and Clarke’s equation.
Table 1
Serve performance prediction of 2014-16 ATP matches
| Variation | 2014 | 2015 | 2016 |
| n=(2,488) | (n=2,540) | (n=2,594) | |
| RMSE | RMSE | RMSE | |
| Barnett-Clarke | .0846 | .0916 | .0845 |
| Barnett-Clarke EM | .0823 | .0909 | .0823 |
| Barnett-Clarke surface | .0883 | .0968 | .0904 |
| Barnett-Clarke surface EM | .0850 | .0944 | .0872 |
| Barnett-Clarke opponent-adjusted | .0829 | .0898 | .0825 |
| Barnett-Clarke opponent-adjusted EM | .0821 | .0894 | .0818 |
| Klaassen-Magnus Elo | .0804 | .0890 | .0798 |
| Common-Opponent | .0957 | .1046 | .0943 |
Table 2
Match win prediction of 2014-16 ATP matches
| Variation | 2014 | 2015 | 2016 | |||
| n=(2,488) | (n=2,540) | (n=2,594) | ||||
| Accuracy | Log Loss | Accuracy | Log Loss | Accuracy | Log Loss | |
| Barnett-Clarke | 64.8 | .648 | 65.0 | .634 | 64.6 | .663 |
| Barnett-Clarke EM | 65.6 | .613 | 65.2 | .609 | 64.7 | .628 |
| Barnett-Clarke surface | 63.3 | .705 | 63.2 | .712 | 62.0 | .742 |
| Barnett-Clarke surface EM | 63.5 | .628 | 62.9 | .628 | 62.5 | .645 |
| Barnett-Clarke opponent-adjusted | 67.8 | .637 | 68.0 | .613 | 67.4 | .641 |
| Barnett-Clarke opponent-adjusted EM | 67.8 | .625 | 68.1 | .605 | 67.6 | .632 |
| Klaassen-Magnus Elo | 69.1 | .589 | 69.3 | .579 | 69.7 | .594 |
| Common-Opponent | 63.6 | .628 | 64.5 | .627 | 63.4 | .650 |
Table 1 displays each method’s RMSE in predicting the proportion of points won on serve. Of all Barnett-Clarke variations, the surface-based estimator fared worst. This was likely due to decreased sample sizes, as filtering matches by surface limited the amount of available data. Its Efron-Morris variant performed significantly better in all years, suggesting there may be value in a surface-specific approach when bias from limited data is offset. However, this variant only came close to reaching parity with the standard Barnett-Clarke model in the year 2014.
While it was intended to address issues with varying strength of schedule, the Common-Opponent Model underperformed all other methods in predicting serve performance. When two players shared few opponents across their match histories, this approach proved fairly susceptible to bias. Furthermore, while Barnett-Clarke variants considered the past twelve months of data, this approach considered all historical matches, curbing its ability to express recent trends as players’ match histories accumulated. On the other hand, opponent-adjusted ratings demonstrated an improvement to both Barnett-Clarke and the Common-Opponent Model. By estimating serve and return ability on a continuous scale, opponent-adjusted ratings allowed us to consider all matches within the last twelve months and avoid a major shortcoming of the Common-Opponent Model.
Overall, Klaassen-Magnus Elo ratings proved most effective in forecasting serve performance. As Elo ratings were already known to estimate player ability more effectively than point-based models, it follows that adjusting serve parameters in accordance with these ratings would significantly improve forecasts. In contrast, Barnett-Clarke variations still appear to leave out important information by ignoring match outcomes and forecasting strictly from point-level data. While point-based models have often proven necessary for predicting more granular outcomes (Barnett et al., 2006), Klaassen-Magnus Elo ratings reconciled point-based models’ expressivity with Elo ratings’ predictive power. Following the recent work of Kovalchik and Reid (2018), this further demonstrated the effectiveness of synthesizing Elo ratings with point-level models specific to tennis’ scoring system.
When applied to Barnett-Clarke variants, the Efron-Morris estimator improved performance to varying degrees. Presumably, this stemmed from robustness with respect to small sample sizes. To better understand its application to our tour-level match dataset, we consider the distribution of points within player match histories.
Fig.2
Number of points played on serve by players i, j in the past twelve months before every match in
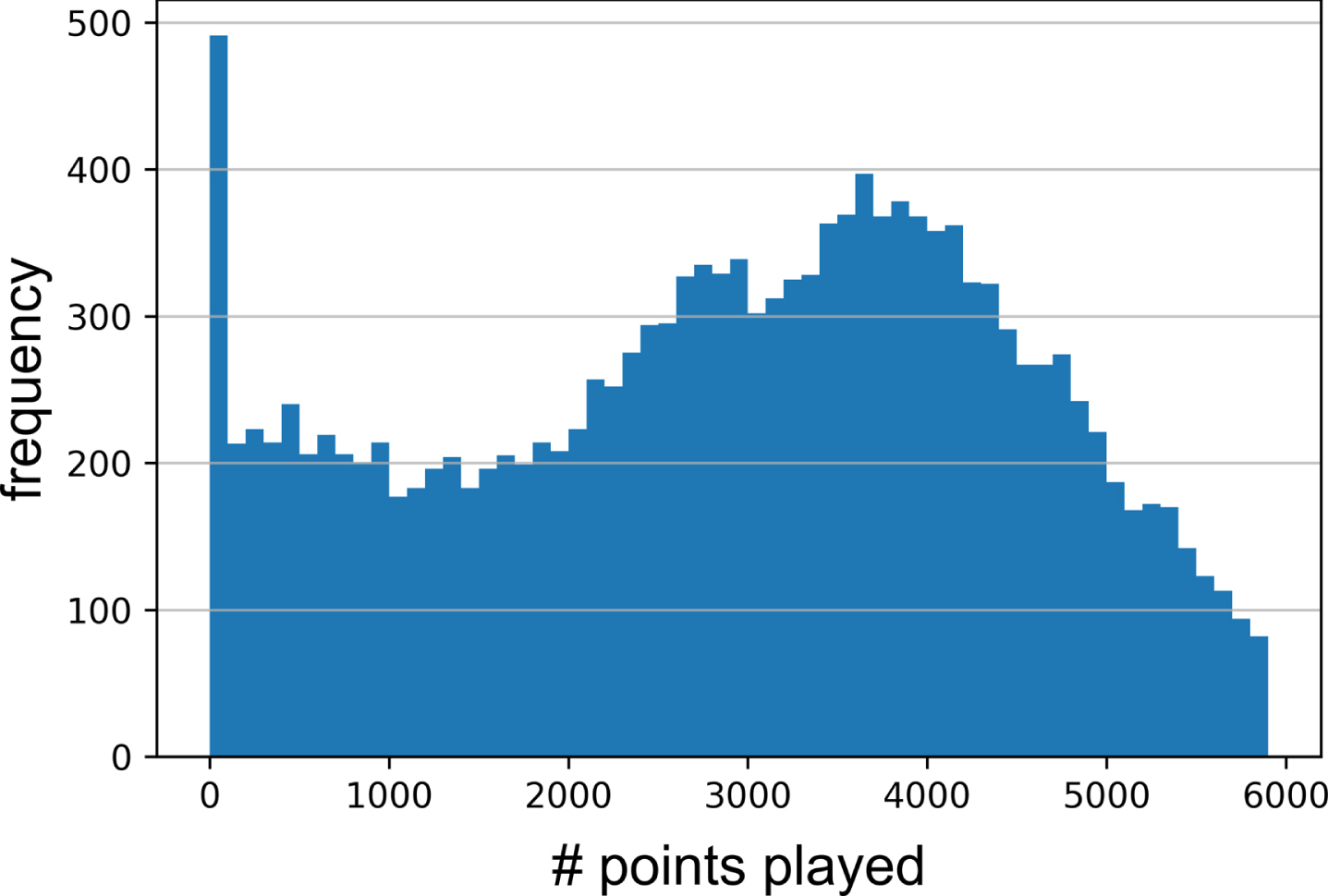
Figure 2 illustrates the distribution of sample sizes when computing fi, fj with an Efron-Morris estimator.9 Following Barnett and Clarke’s original approach, estimates produced with sample sizes from the leftmost range of the distribution were particularly susceptible to bias. However, recalling normalization strength from Figure 1, we know the Efron-Morris estimator reduced bias by shrinking these estimates furthest toward the mean. Since players accumulate return points over time at approximately the same rate, we can assume the estimator normalized gi, gj in a similar manner. If only by reducing errant predictions in this range, the Efron-Morris estimator succeeded in helping all Barnett-Clarke variants more effectively predict serve performance.
Table 2 details each method’s performance in predicting match winners, where many of the same trends surfaced. Once again, variations with an Efron-Morris estimator outperformed their counterparts. In most cases, the improvement in log loss was greater than that of accuracy, supporting the notion that this estimator mitigates extreme results when faced with limited data. The opponent-adjusted model performed several percentage points better than Barnett and Clarke’s original approach across all years, establishing itself as the most effective point-based method surveyed in this exploration. Once again, Klaassen-Magnus Elo ratings predicted outcomes most effectively. However, it is worth noting that its output produced win probabilities identical to those of the Elo ratings fed into the model. In that regard, its relative performance confirmed results from previous studies noting Elo’s dominance in match prediction (Kovalchik, 2016).
6Conclusion
Although Barnett and Clarke’s approach has long been established in tennis match prediction, there are many ways to forecast serve performance. In order to extract more information from historical match data, we outlined a handful of novel approaches to generating the parameters in their equation. Using an Efron-Morris estimator improved performance across the board, emphasizing the need to address scenarios with limited match data. The opponent-adjusted model demonstrated a new way to quantify strength of schedule through point-level data, resulting in significantly improved performance over Barnett-Clarke and the Common-Opponent Model. Finally, Klaassen-Magnus Elo ratings synthesized historical serve data with the predictive power of Elo ratings while maintaining the overall serve ability between two players.
A clear next step to this exploration would involve applying these methods to in-match prediction. With point-by-point datasets available today, we can use these same methods to forecast match outcomes while play is in progress and set similar benchmarks with tour-level match data.
Acknowledgments
I would like to thank Kevin Rader for his guidance on earlier iterations of this research. I amalso grateful to Jeff Sackmann for making all relevant match data publicly available.
References
1 | Barnett, T. and Clarke, S. R. (2005) , Combining player statistics topredict outcomes of tennis matches, IMA Journal of ManagementMathematics 16: (2), 113–120. |
2 | Barnett, T. J. , Clarke, S. R. , et al., (2002) , Using microsoft excel to model a tennis match. In 6th Conference on Mathematics and Computers in Sport, pages 63-68. Queensland, Australia: Bond University. |
3 | Barnett, T. J. , et al., (2006) Mathematical modelling in hierarchical games with specific reference to tennis. PhD thesis, Swinburne University of Technology. |
4 | Bialik, C. , Morris, B. , and Boice, J. (2016) , How we’re forecasting the 2016 u.s. open. http://fivethirtyeight.com/features/how-were-forecasting-the-2016-us-open/. Accessed: 2017-10-30. |
5 | Efron, B. and Morris, C. (1975) , Data analysis using stein’s estimatorand its generalizations, Journal of the American StatisticalAssociation 70: (350), 311–319. |
6 | Efron, B. and Morris, C. N. (1977) , Stein’s paradox in statistics. WH Freeman. |
7 | Elo,A. E. (1978) , The rating of chessplayers, past and present. Arco Pub. |
8 | Klaassen, F. J. and Magnus, J. R. (2003) , Forecasting the winner of atennis match, European Journal of Operational Research 148: (2), 257–267. |
9 | Klaassen, F. J. G. M. and Magnus, J. R. (2001) , Are points in tennisindependent and identically distributed? evidence from a dynamicbinary panel data model, Journal of the American StatisticalAssociation 96: (454), 500–509. |
10 | Knottenbelt, W. J. , Spanias, D. , and Madurska, A. M. (2012) , Acommon-opponent stochastic model for predicting the outcome ofprofessional tennis matches, Computers & Mathematics withApplications 64: (12), 3820–3827. |
11 | Kovalchik, S. and Reid, M. (2018) , A calibration method with dynamic updates for within-match forecasting of wins in tennis, International Journal of Forecasting. |
12 | Kovalchik, S. A. (2016) , Searching for the goat of tennis winprediction, Journal of Quantitative Analysis in Sports 12: (3), 127–138. |
13 | Newton, P. K. and Aslam, K. (2009) , Monte carlo tennis: a stochasticmarkov chain model, Journal of Quantitative Analysis inSports 5: (3). |
14 | Sackmann, J. (2018) , Tennis atp. https://github.com/JeffSackmann/tennis_atp. |
15 | Spanias, D. and Knottenbelt, W. J. (2012) , Predicting the outcomes oftennis matches using a low-level point model, IMA Journal ofManagement Mathematics 24: (3), 311–320. |
Appendices
Appendix A: Common-Opponent Model
Consider a match between players i and j, who share N common opponents throughout their entire match histories. To quantify their relative performance against opponent Ck, let spw(i, Ck) denote the percentage of service points won by player i against opponent Ck and rpw(i, Ck) the corresponding percentage of return points won. We may quantify player i’s advantage over player j with respect to opponent Ck as follows:
Then we approximate match win probability in terms of this relative advantage.
In the above equation, M3(f, g) denotes player i’s win probability in a best-of-three match with f, g representing their probability of winning a point on serve and return, respectively. To compute πij via the Common-Opponent Model, we average the win probability over all N common opponents shared:
While Knottenbelt did not originally use this model to predict serve performance, we inferred parameters fij, fji from the model’s win probability equation as followed:
fij = .6 + Δij/2
fji = .6 - Δij/2 .
Following the above steps, we may predict the winner and serve performance of any match using the Common-Opponent Model.
Notes
1 Knottenbelt’s Common-Opponent model addresses strength of schedule at the cost of reducing the amount of available match data. Kovalchik and Reid’s approach indirectly addresses both of these issues through the use of Elo ratings.
2 The constants in this equation are parameter values that FiveThirtyEight’s team chose after fitting this model on decades of tour-level match data.
3 Tennis’ Open Era began in 1968, when professionals were allowed to enter grand slam tournaments.
4 For current month m, we only collect month-to-date matches.
5 The number of player j’s service points in match k is equal to the number of player i’s return points in match k.
6 For this project, we set ε = .001.
7 Davis cup matches frequently involve lower-ranked players.
8 All matches occurred on hard, clay, or grass courts.
9 For given match k with serve parameters




