Using multi-class classification methods to predict baseball pitch types
Abstract
Since the introduction of PITCHf/x in 2006, there has been a plethora of data available for anyone who wants to access to the minute details of every baseball pitch thrown over the past nine seasons. Everything from the initial velocity and release point to the break angle and strike zone placement is tracked, recorded, and used to classify the pitch according to an algorithm developed by MLB Advanced Media (MLBAM). Given these classifications, we developed a model that would predict the next type of pitch thrown by a given pitcher, using only data that would be available before he even stepped to the mound. We used data from three recent MLB seasons (2013-2015) to compare individual pitcher predictions based on multi-class linear discriminant analysis, support vector machines, and classification trees to lead to the development of a real-time, live-game predictor. Using training data from the 2013, 2014, and part of the 2015 season, our best method achieved a mean out-of-sample predictive accuracy of 66.62%, and a real-time success rate of over 60%.
1Introduction
Ever since Bill James published his work on sabermetrics four decades ago, Major League Baseball (MLB) has been on the forefront of sports analytics. While the massive amount of statistical data is generally used to examine historical player performance on the field in an effort to make coaching and personnel decisions, there is great potential for predictive models that has largely gone unnoticed. The implementation of the PITCHf/x system and distribution of large amount of pitching data publicly over the internet has sparked the use of machine learning methods for prediction, not just analysis.
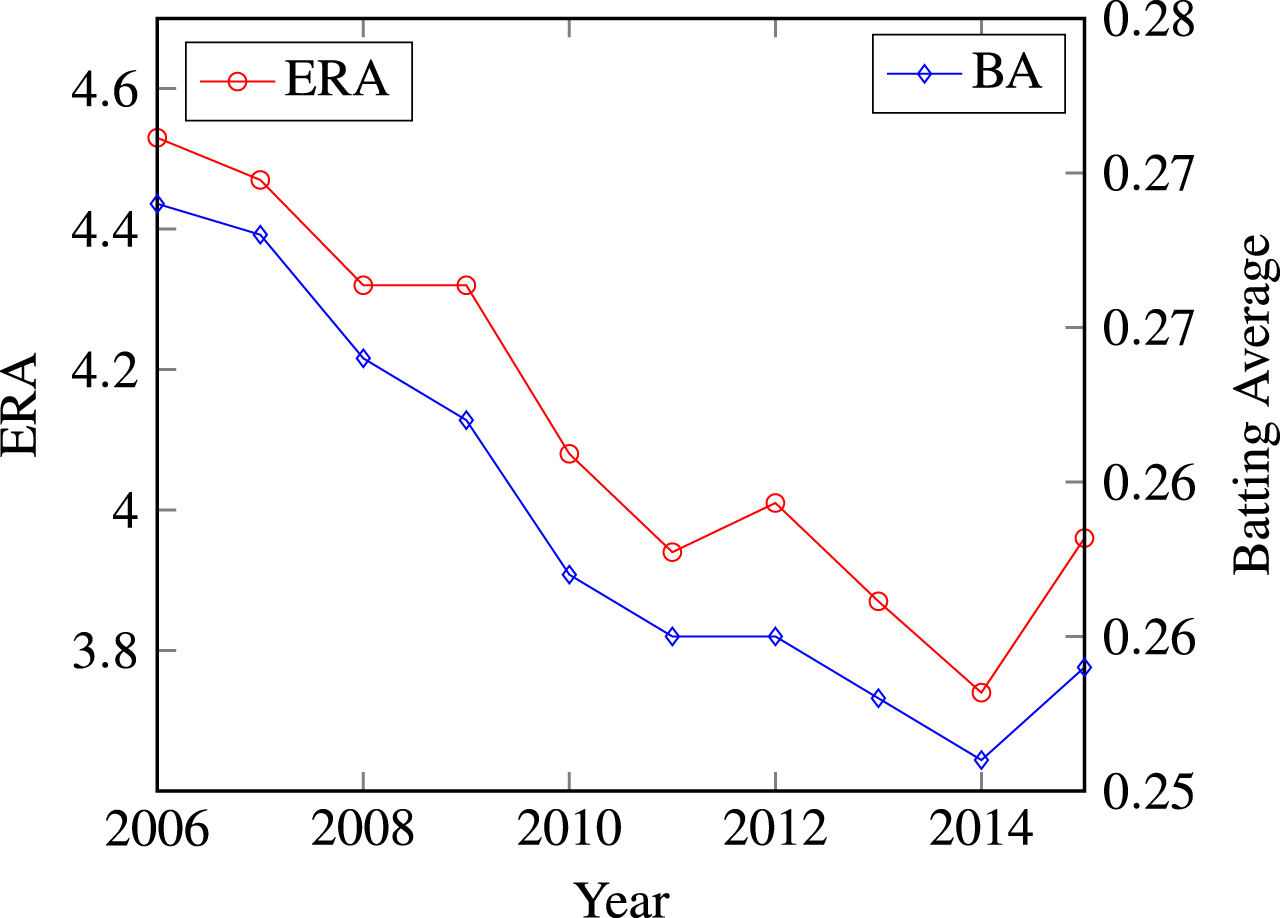
As shown in Fig. 1, pitchers have been getting better and better at preventing hits, lowering the average ERA and batting average across the league. While hitting a major league pitch will always be an incredibly difficult task, in this work we hypothesize that knowing what type of pitch is coming next may help the batter decide to swing or not and work to get him on base. In this paper, we compare three different machine learning techniques and their predictive abilities, seeking to find what feature inputs are the most informative and to develop a blind prediction in an attempt to anticipate the next pitch type. By comparing different techniques, we were able to find which would work best in a live game environment, attempting to predict the next type of pitch as before it would be thrown.
1.1Literature review
Previous research has mostly focused on a binary prediction, commonly a fastball vs. non-fastball split. This prediction has resulted in accuracy around 70% (Ganeshapillai and Guttag, 2012), with varying degrees of success for individual pitchers and different methods. This binary classification using support vector machines was expanded upon using dynamic feature selection by Hoang (2015), improving the results by approximately 8 percent. Because many classification methods were originally designed for binary classification, this prediction method makes sense, but we wish to expand it further into predicting multiple pitch types.
Very limited attempts have been made at multi-class prediction prior to our work. Bock (2015) used a support vector machine approach with a linear kernel function, focusing mostly on finding a measure of predictability for a pitcher and comparing that predictability against long-term pitcher performance. The authors only examined four pitch types, and had a very limited out-of-sample testing set, looking at the methods accuracy on 14 pitchers during a single World Series, with an average accuracy of just under 61%. Woodward (2014) used decision trees to again only predict up to four different types of pitches, and only shows results for two individual pitchers. We expand on their work by considering up to seven different pitch types and apply machine learning to many more pitchers over a longer amount of time. Along with a much larger test set, we also investigate which methods perform the best, if our results share any correlation with standard pitching statistics, what variables are most important for prediction, and finally our ability to predict the next pitch type in a live game situation.
Fig.1
League-wide Batting Average and ERA over the past decade.
2Methods
2.1Data
The introduction of PITCHf/x was a revolutionary development in baseball data collection. Cameras, installed in all 30 MLB stadiums, record the speed and location of each pitch at 60 Hz, and data is made available to the public through a variety of online resources. MLB Advanced Media uses a neural-network based algorithm to classify those pitches, giving a confidence in the classification along with the type of pitch (Fast, 2010). This information is added to the PITCHf/x database, along with the measure characteristics of the pitch and details about the game situation. Using the pitch data provided at gd2.mlb.com, we were able to retrieve every pitch from the 2013, 2014, and 2015 seasons. Using 22 features from each pitch, we created data sets for every individual pitcher, adding up to 81 additional features to each data set, depending on how many types of pitches the individual threw. Here we consider seven pitch categories (with given integer values), fastball (FF, 1), cutter (CT, 2), sinker (SI, 3), slider (SL, 4), curveball (CU, 5), changeup (CH, 6), and knuckleball (KN, 7), and those that had a type confidence (the MLBAM algorithm’s confidence that its classification is correct) greater than 80%.
We restricted our data set only to pitchers who threw at least 500 pitches in both the 2014 and 2015 seasons, which left us with 287 total unique pitchers, 150 starters and 137 relievers as designated by ESPN. The average size of the data set for each pitcher was 4,682 pitches, with the largest 10,343 pitches and the smallest 1,108 pitches. Because each pitcher threw a different number of unique pitch types, not all the datasets are the same size. At the most, a pitcher could have 103 features associated with each pitch and at the minimum he could have 63. The average pitcher had 81 features.
Table 1 gives a list of the features used, both those that can be taken from the immediate game situation and the features we generated using the historical data on for both pitcher and batter. Because of the size of the feature set, similar features are grouped together in the table, i.e. group 16 contains the previous pitch’s type, result, break angle, break length, break height, and the zone where it crossed the plate. Groups 19–26 have variable sizes due to the number of types of pitches each pitcher throws. Groups 27–29 are unique for each batter, containing the percent of each type of pitch he puts in play, has a strike on, or takes a ball on.
Table 1
Feature groups for each pitch. Tendency refers to the percentage of each pitch type
| Number | Feature Group | Type of Variable |
| 1 | Inning | Categorical |
| 2 | Top or Bottom | Binary |
| 3 | Outs | Categorical |
| 4 | Order Position | Categorical |
| 5 | Total At-Bat | Categorical |
| 6 | Score Spread | Categorical |
| 7 | Time of Day | Categorical |
| 8 | Batter Handedness | Binary |
| 9 | Strikes | Categorical |
| 10 | Balls | Categorical |
| 11 | On Base | Binary |
| 12 | Base Score | Categorical |
| 13 | Previous At-Bat Result | Categorical |
| 14 | Previous Pitch Result | Categorical |
| 15 | Previous Pitch Type | Categorical |
| 16 | Previous Pitch Location | Categorical |
| 17 | Pitch Number | Categorical |
| 18 | Previous Pitch Speed, Break Angle, Break Length, Break Height | Continuous |
| 19 | Previous 5 Pitch Tendency | Continuous |
| 20 | Previous 10 Pitch Tendency | Continuous |
| 21 | Previous 20 Pitch Tendency | Continuous |
| 22 | Previous 5 Pitch Strike Tendency | Continuous |
| 23 | Previous 10 Pitch Strike Tendency | Continuous |
| 24 | Previous 20 Pitch Strike Tendency | Continuous |
| 25 | Pitcher Historical Tendency | Continuous |
| 26 | Pitcher Tendency vs. Batter | Continuous |
| 27 | Batter Strike Tendency | Continuous |
| 28 | Batter In-Play Tendency | Continuous |
| 29 | Batter Ball Tendency | Continuous |
2.2Model development
We decided to employ three different classification-based methods to compare and contrast results from all 287 pitchers in our data set. First, we used multi-class Linear Discriminant Analysis because its speed and efficiency. Then, to compare results to Bock (2015) and Woodward (2014) we used support vector machines and classification trees. In an effort to reduce model variance between different models and increase accuracy, we employed a committee method, using ten of each model type and taking the majority vote as output.
2.3Linear Discriminant Analysis
Linear Discriminant Analysis (LDA) is a method descended from R.A. Fisher’s linear discriminant first introduced by Fisher (1936). Assuming two classes of observations have respective mean covariance pairs
where the maximum separation between the classes is found when
To go from the linear discriminant to LDA, we use the assumption that the class covariances are the same, i.e. Σ0 = Σ1 = Σ, then the proportional equation leads to
and so the decision of which class
where
We use a regularization parameter to shrink the covariance matrix closer to the average eigenvalue of Σ. In the MATLAB implementation of LDA, N (N - 1)/2 separations are made, making it comparable to the one-vs-one (OvO) technique for support vector machines. The final class decision is made by minimizing the sum of the misclassification error (MathWorks, 2016a).
2.4Multi-class Support Vector Machines
Support vector machines (SVM) were first designed as a method of binary classification. The extension of binary SVMs to a multi-class method has led to two common approaches to multi-class classification. Unlike Unlike Bock (2015), however, we employed a C-SVM formulation with the radial basis kernel function. For a problem with N distinct classes, the one-vs-all (OVA) method creates N SVMs, and places the unknown value in whatever class has the largest decision function value.
For our model, we used the one-vs-one (OVO) method, which creates N (N - 1)/2 SVMs for classification. For a set of p training data, (x1, y1) , …, (xp, yp) where xl ∈ Rn, l = 1, …, p and yl ∈ {1, …, N} is the class label for xl, then the SVM trained on the ith and jth classes solves
where φ (x) = eγ||xi-xj|| is the radial basis function used to map the training data xi,j to a higher dimensional space and C is the penalty parameter. After all comparisons have been done, the unknown value is classified according to whichever class has the most votes from the assembled SVMs.
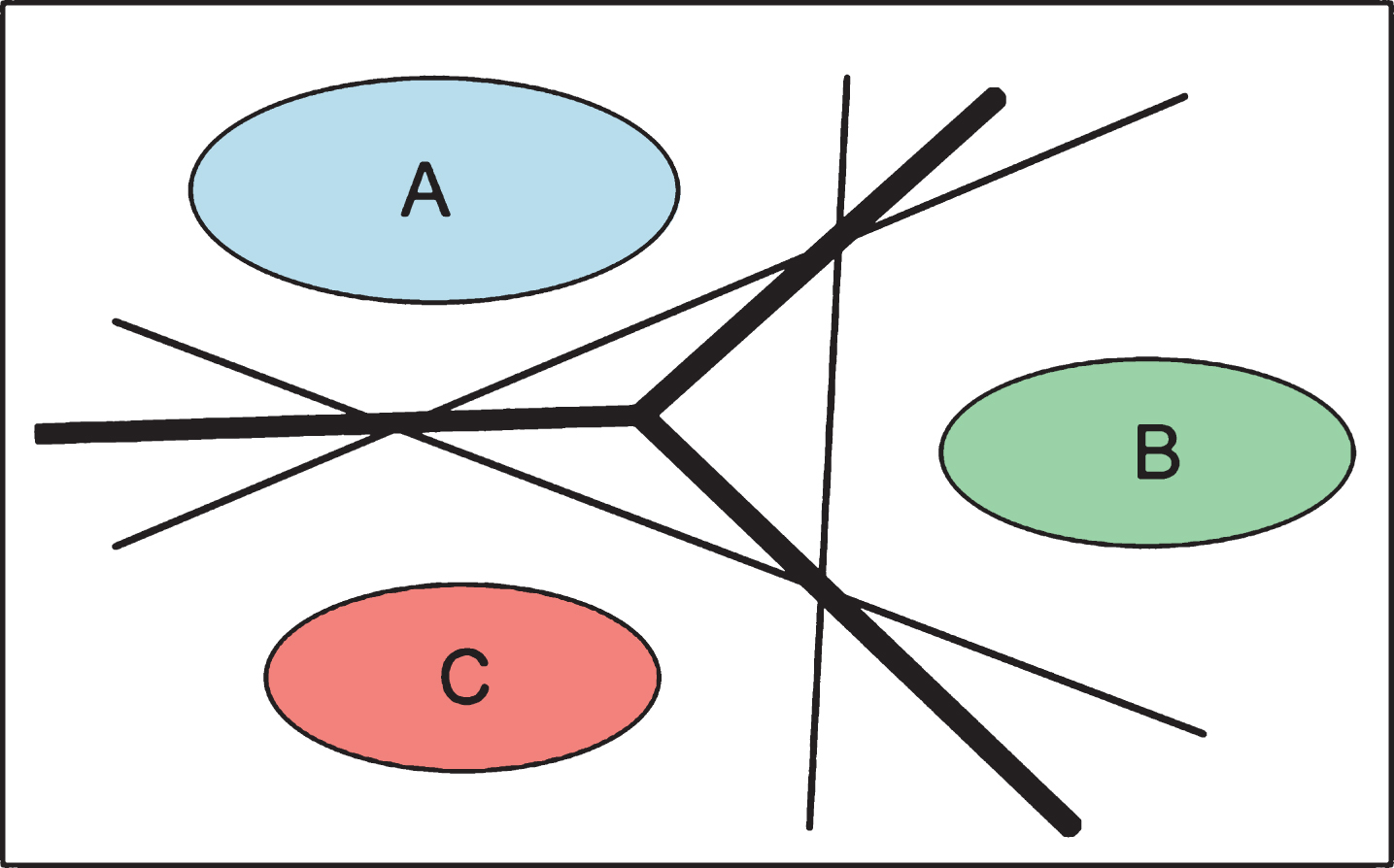
Figure 2 shows a basic representation of the differences between the OVA and OVO methods. The middle triangle formed by the OVA method leaves a gap where the classification algorithm can fail to place an unknown value, but since the OVO method does not have any blind spots, we used it for our classification. We used a modified grid search from Finkel (2003) to optimize for both parameters C and γ, using the five-fold cross-validation accuracy of the training set to find the optimal parameters.
2.5Classification trees
In order to compare our results to Woodward (2014), we also implemented classification trees, using random forests. We used the MATLABCART (Classification And Regression Trees) implementation that creates aggregate random forests of trees, known as TreeBagger.
Fig.2
A visual representation of the one-vs-all method (thin lines) compared to the one-vs-one method (thick line) from (Aisen, 2006).
Classification Trees are a specific type of binary decision tree that give a categorical classification as an output. The input set is used in the nodes of the tree, determining which feature to split at each node and what criterion to base that decision on. To determine node impurity, MATLAB classification trees use the Gini diversity index (gdi), given by
For each node, the tree first computes the impurity at the node, then sorts the observation to determine what features can be used as splitting criteria or cut points. For all splitting points, the tree seeks to maximize the decrease in impurity, ΔI, by splitting the observations at the node into two child nodes, then measuring ΔI for each node with different cut points. Once a feature is chosen as the best splitting candidate, then the feature is split using the best cut point, and the process is repeated until the total impurity is minimized and the end leaf nodes are found. To combat overfitting, however, classification trees are pruned by merging leaves that have the most common class per leaf (MathWorks, 2016b).
3Results
3.1Overall prediction accuracy
To establish a value for comparison, we found the best “naive” guess accuracy, similar to that used by Ganeshapillai and Guttag (2012). We define this naive best guess to be the percent of time each pitcher throws his preferred pitch from the training set in the testing set. Consider some pitcher who throws pitch types 1, 2, 4, and 5 with distribution P = {p1, p2, p4, p5} where ∑pi = 1, and his preferred training set pitch is max(Ptrain) = p2, then the naive guess for the pitcher is Ptest (p2). For example, since Jake Arrieta threw his sinker the most in the training set (26.31%), we would take the naive guess as the percentage of the time he threw a sinker in the testing set, which gives a naive guess of 34.03%. With the random forest method, we predicted 48.33% of his pitches correctly, so we beat the naive guess by 14.30% in his case. For all 287 pitchers, the naive guess was 54.38%.
Table 2 shows a breakdown of each type of pitch predicted for Odrisamer Despaigne by the random forest method, as well as the accuracy for each specific pitch, showing that for each pitch type, the accuracy of the model prediction improves the naive guess. We take this style of comparison from Woodward (2014), who gives an outline of a decision tree based prediction model, but does not go into detail or use more than a handful of examples, so we cannot fully compare to his results.
Table 2
100 CT pitch-specific model predictions for Odrisamer Despaigne, overall accuracy 53.30%
| Predicted Pitch Type | ||||||||||
| FF | CT | SI | SL | CU | CH | KN | % Thrown | % of Each Correct | ||
| Actual Type | FF | 330 | 5 | 77 | 2 | 17 | 2 | 0 | 28.60 | 76.21 |
| CT | 55 | 42 | 19 | 2 | 1 | 8 | 3 | 8.59 | 32.31 | |
| SI | 108 | 5 | 312 | 2 | 19 | 10 | 0 | 30.12 | 68.42 | |
| SL | 31 | 2 | 23 | 10 | 2 | 6 | 2 | 5.02 | 13.16 | |
| CU | 36 | 2 | 43 | 3 | 54 | 3 | 1 | 9.38 | 38.03 | |
| CH | 72 | 1 | 34 | 0 | 2 | 33 | 2 | 9.51 | 22.92 | |
| KN | 63 | 3 | 30 | 3 | 5 | 3 | 26 | 8.78 | 19.55 | |
Table 3 shows the prediction results from each individual method. On average accuracy alone, Classification Trees had the best prediction accuracy of 66.62%. The number of pitchers we predicted better than naive is given, as well as the percentage of the 287 total pitchers that number represents. The average prediction accuracy is shown in Table 4, given along with the overall average improvement over the naive guess, denoted
Table 3
Average values to compare support vector machines (SVM), random forests of 100 classification trees (100 CT), and linear discriminant analysis (LDA), with average naive accuracy 54.38%.
| Value | LDA | SVM | 100 CT |
| Prediction Accuracy (%) | 65.08 | 64.49 | 66.62 |
| # of Predictions > Naive | 263 | 251 | 282 |
| % of Predictions > Naive | 91.64 | 87.46 | 98.26 |
|
| 10.70 | 10.11 | 12.24 |
|
| 13.26 | 12.38 | 12.52 |
|
| –9.08 | –5.40 | –1.15 |
| Range of Committee (%) | 1.52 | 3.02 | 2.22 |
| Time (s) | 22.75 | 2,383.8 | 72.05 |
Table 4
Average Prediction accuracy for each pitch count for the Classification Tree method. Pitcher favored counts are shown in bold, batter-favored counts in italics.
| Count (B-S) | 100 CT |
| 0-0 | 71.48 |
| 0-1 | 64.77 |
| 0-2 | 62.27 |
| 1-0 | 70.01 |
| 1-1 | 61.15 |
| 1-2 | 58.94 |
| 2-0 | 74.78 |
| 2-1 | 67.43 |
| 2-2 | 59.84 |
| 3-0 | 83.00 |
| 3-1 | 75.62 |
| 3-2 | 67.53 |
We also give the average range of accuracy between the most and least accurate members of each committee as well as the average time for each pitcher’s model to be trained and tested. As shown in Table 3, the random forests of classification trees outperformed both LDA and SVM by a wide margin. Basing the judgement solely on how many pitchers were predicted better, the random forests were near-perfect, leading the average prediction accuracy and improvement to also be higher. LDA outperforms the random forests only when we examine the average improvement for those pitchers who we are able to beat the naive guess for, but conversely also has much worse performance for the pitchers we do not beat the naive guess for. At this stage, we undertook further comparative analysis to determine if the random forests were the best method overall.
3.2Prediction by count
A common analysis in any pitch prediction is breaking down prediction success rate by each pitch count. There are twelve possible counts for any at-bat, three where the batter and pitcher are even, three where the pitcher is ahead in the count (more strikes than balls), and six where the batter is ahead (more balls than strikes). Similar to other works, On the very batter-favored count of 3-0, we were able to predict 104 pitchers (36.24% of 287 pitchers) totally correct, i.e. for every pitch they threw on a 3-0 count, we predicted them all exactly. The total counts and average success rates for the random forest classification tree method are given in Table 4. Pitcher ahead counts are bolded, batter-favored counts are italicized.
The high success rate on counts in which the batter is ahead is not surprising, given that a pitcher is more likely to throw a controllable pitch in order to even the count or to avoid a walk. Batter-behind counts give the pitcher much more freedom, which explains the lower average predictability.
3.3Comparison with standard statistics
In an effort to determine if the prediction success correlated with any standard measure of pitcher success, we ran a linear regression analysis to find the correlations between the random forest model prediction accuracy and the improvement over the naive guess to the pitchers’ wins-above-replacement (WAR) and fielding-independent-pitching (FIP) statistics. FIP is an extension of a pitchers’ earned run average (ERA) that examines only outcomes over which the pitcher had control. To find a measure of the diversity a pitcher’s pitch selection, we also compared the prediction accuracy, improvement, WAR, and FIP to the Herfindahl-Hirschman Index (HHI). HHI is inversely proportional to the diversity of pitch selection, and can be expressed as
Table 5
Linear regression R2 values, slopes, intercepts, p-values, and t-statistics for the given random forest model accuracy (Acc) and improvement (Imp) values and standard statistics
| X Var | Y Var | R2 | Slope | Intercept | Slope P-val | Slope T-stat | Int. P-val | Int. T-stat |
| HHI | Acc | 0.777 | 0.747 | 0.332 | 0.000 | 31.323 | 0.000 | 29.897 |
| HHI | Imp | 0.069 | –0.279 | 0.248 | 6.752e-6 | –4.588 | 0.000 | 8.744 |
| HHI | FIP | 0.039 | –1.437 | 4.512 | 0.001 | –3.370 | 0.000 | 22.699 |
| Acc | FIP | 0.039 | –1.703 | 5.002 | 0.001 | –3.382 | 0.000 | 14.711 |
| Acc | WAR | 0.014 | –1.824 | 2.358 | 0.042 | –2.039 | 1.191e–4 | 3.903 |
| Imp | WAR | 0.012 | –1.335 | 1.305 | 0.063 | –1.865 | 0.000 | 10.023 |
| HHI | WAR | 0.001 | –0.399 | 1.321 | 0.602 | –0.523 | 2.455e–4 | 3.714 |
| Imp | FIP | 7.997e–6 | 0.019 | 3.865 | 0.962 | 0.047 | 0.000 | 51.733 |
| Imp | FIP | 0.041 | –0.363 | 4.602 | 0.368 | –0.902 | 0.000 | 20.526 |
| HHI | –1.539 | 0.001 | –3.479 | |||||
| Acc | FIP | 0.041 | –0.927 | 4.819 | 0.385 | –0.870 | 0.000 | 11.870 |
| HHI | –0.745 | 0.410 | –0.825 | |||||
| Acc | WAR | 0.040 | –6.311 | 3.416 | 0.001 | –3.371 | 2.699e–6 | 4.791 |
| HHI | 4.313 | 0.007 | 2.719 | |||||
| Imp | WAR | 0.016 | –1.541 | 1.703 | 0.039 | –2.077 | 2.645e–5 | 4.273 |
| HHI | –0.829 | 0.293 | –1.054 |
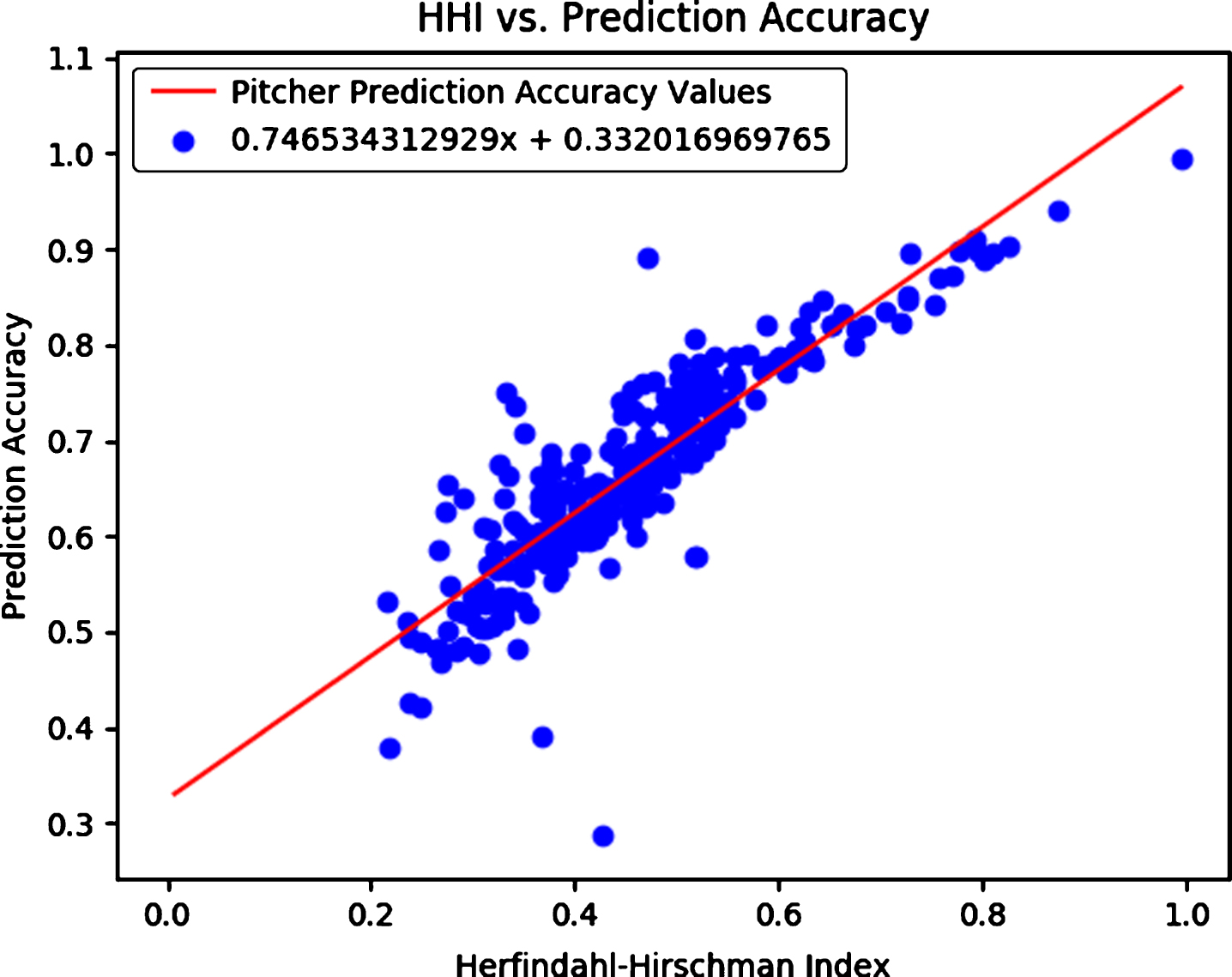
Overall, given the very low R2 values for most pairs of variables we examined, the only correlation that we can draw any conclusions from is between the HHI and overall model accuracy, shown in Fig. 3. The higher the HHI (and therefore the less diversity in pitch selection), the more accurate the model is, most likely due to the fact that the pitcher is throwing a single pitch type a lot. While the regression slopes of the other pairings might suggest interesting correlations, due to the excessively small R2 values there is little to no mathematical strength to any conclusions we could draw.
Fig.3
Linear regression fit line between the Herfindahl-Hirschman Index and the random forest model prediction accuracy, with intercept 0.332 and correlation 0.746.
4Variable importance
Post-processing techniques can be used to determine what features are the most important in a model, so we used the models created for the results previously discussed to find measures of variable importance with the permuted variable delta error (PVDE) for the random forests of classification trees. The PVDE is found during the construction of each random forest for each variable by first finding the expected error (EOi) against a hold-out validation set, similar to the cross-validation used for the parameter optimization. The values for a particular variable xi are then randomly permuted across every observation in the subset of the training data used for the tree construction, and the expected error value (EPi) is found against the same holdout set.
Table 6 gives the ranks of the permuted variable delta error for each input feature group (with 29 feature groups, total), respectively. The ranks were found by first averaging the values for each pitcher, then sorting those averages by magnitude, and then averaging each rank across each variable in the group. Once the group ranks were found, we sorted the averaged group ranks to find the overall importance. The results of the analysis are mostly unsurprising, but again are helpful to show that the model works the way we would expect it to. The pitch number can be a measure of how tired a pitcher is, which would greatly affect his pitch choice. As shown by the results by count, the number of balls and strikes can also affect the pitch selection, so the inputs being second and third most important is unsurprising.
Table 6
Variable Importance for Permuted Variable Delta Error for all pitchers. 1 means highest importance, 29 means lowest importance
| Feature Group | PVDE |
| Inning | 16 |
| Top or Bottom | 29 |
| Outs | 27 |
| Order Position | 18 |
| Total At-Bat | 6 |
| Score Spread | 21 |
| Time of Day | 25 |
| Batter Handedness | 7 |
| Strikes | 2 |
| Balls | 3 |
| On Base | 28 |
| Base Score | 19 |
| Previous At-Bat Result | 24 |
| Previous Pitch Result | 10 |
| Previous Pitch Type | 4 |
| Previous Pitch Location | 8 |
| Pitch Number | 1 |
| Previous Pitch Stats | 5 |
| Previous 5 Pitch Tendency | 13 |
| Previous 10 Pitch Tendency | 17 |
| Previous 20 Pitch Tendency | 14 |
| Previous 5 Pitch Strikes | 11 |
| Previous 10 Pitch Strikes | 15 |
| Previous 20 Pitch Strikes | 20 |
| Pitcher Historical Tendency | 26 |
| Pitcher Tendency vs. Batter | 23 |
| Batter Strike Tendency | 22 |
| Batter In-Play Tendency | 12 |
| Batter Ball Tendency | 9 |
5Live pitch prediction
At the start of this research, one of the reasons we examined different machine learning methods of prediction was to determine what would work best in real time in a live game environment. The previous experiments were all done in a “bulk” setting, i.e. predicting all of the testing set all at once. While this gives a way to measure the effectiveness of each method, the construction of the testing datasets was not reflective of the way a dataset would be built during an actual baseball season. Any live prediction training set could only be updated with after each game, and would only show historical pitcher or batter tendencies up to the day before a game was played.
The data for the live predictions was parsed appropriately, creating pitcher preferences and batter performance measures up until the day being predicted. We examined the games in the regular season of September and October 2016, creating models for each pitcher for not only predicting the type of pitch thrown, but also the speed of the pitch and the location of the pitch. Models were created for every pitcher who pitched in September and October, as long as he had pitched at some point after the All-Star break (mid-July) and before September 1st. There was a large amount of data available to test on, and the characteristics of the data are shown in Table 7.
Table 7
Python live pitch predictions for September 1st through October 2nd, 2016, with overall accuracy 59.07%
| Predicted Pitch Type | ||||||||||
| FF | CT | SI | SL | CU | CH | KN | % Thrown | % of Each Correct | ||
| Actual Type | FF | 52774 | 329 | 871 | 2124 | 1300 | 681 | 22 | 52.13 | 90.83 |
| CT | 2688 | 1353 | 203 | 24 | 190 | 127 | 3 | 4.12 | 29.49 | |
| SI | 693 | 171 | 5381 | 417 | 211 | 101 | 0 | 6.26 | 77.16 | |
| SL | 12243 | 59 | 1475 | 3110 | 90 | 98 | 0 | 15.32 | 18.21 | |
| CU | 9775 | 340 | 650 | 183 | 2092 | 232 | 0 | 11.91 | 15.76 | |
| CH | 8539 | 165 | 982 | 318 | 307 | 911 | 0 | 10.07 | 8.12 | |
| KN | 9 | 0 | 0 | 0 | 0 | 0 | 183 | 0.17 | 95.31 | |
While the overall prediction accuracy for all the pitches thrown was 59.07%, the average accuracy across each pitcher in each game was 60.69%.
6Conclusion and future work
Because Bock (2015) and Woodward (2014) are the only examples of multi-class pitch prediction we have found, they are the standard for comparison. An example of pitch prediction using Markov Chains was done by Malter (2016), but it is not a situational-based model. Our model takes data that is available in the moments before the next pitch is thrown and gives the batter and manager better knowledge of what is coming than he would have had beforehand. Our results are better than any other purely predictive model of a multi-class pitch type thus far.
Moving forward, we plan to employ a feature selection method similar to one used by Hoang (2015) to find which inputs are the most important to the prediction, or even if reducing the size of the feature vectors may improve the prediction, as we may work to avoid the curse of dimensionality. Due to the construction of the multi-class problem, implementing pre-processing techniques such as F-score or ROC curve analysis may require the introduction of classification using a Directed Acyclic Graph. Using these pre-processing techniques along with the information learned from the variable importance may help improve the live pitch predictors as well.
References
[1] | Aisen B. , (2006) , A Comparison of Multi-Class SVM Methods. http://courses.media.mit.edu/2006fall/mas622j/Projects/aisen-project/. |
[2] | Bock J.R. , (2015) , Pitch Sequence Complexity and Long-Term Pitcher Performance, Sports, 40–55. |
[3] | Fast M. , (2010) , The Internet cried a little when you wrote that on it, The Hardball Times. |
[4] | Finkel D. , (2003) , DIRECT Optimization Algorithm User Guide, Centerfor Research in Scientific Computation, NCSU. |
[5] | Fisher R. , (1936) , The use of multiple measurements in taxonomic problems, Annals of Eugenics 2: , 179–188. |
[6] | Ganeshapillai G. and Guttag J. , (2012) , Predicting the Next Pitch, Proceedings of the MIT Sloan Sports Analytics Conference. |
[7] | Hoang P. , (2015) , Supervised Learning in Baseball Pitch Predictionand Hepatitis C Diagnosis, NC State University, Ph.D.Thesis. |
[8] | Malter D. , (2016) , Using Markov Chains to Predict Pitches. URL: http://danmalter.github.io/r/2016/03/28/Markov-chains.html. |
[9] | MathWorks (2016) a, Discriminant Analysis. URL: http://www.mathworks.com/help/stats/discriminant-analysis.html. |
[10] | MathWorks (2016) b, fitctree.m documentation. URL: http://www.mathworks.com/help/stats/fitctree.html. |
[11] | Woodward N. , (2014) , A Decision Tree Approach to Pitch Prediction, The Hardball Times. |




