Using PITCHf/x to model the dependence of strikeout rate on the predictability of pitch sequences
Abstract
We develop a model for pitch sequencing in baseball that is defined by pitch-to-pitch correlation in location, velocity, and movement. The correlations quantify the average similarity of consecutive pitches and provide a measure of the batter’s ability to predict the properties of the upcoming pitch. We examine the characteristics of the model for a set of major league pitchers using PITCHf/x data for nearly three million pitches thrown over seven major league seasons. After partitioning the data according to batter handedness, we show that a pitcher’s correlations for velocity and movement are persistent from year-to-year. We also show that pitch-to-pitch correlations are significant in a model for pitcher strikeout rate and that a higher correlation, other factors being equal, is predictive of fewer strikeouts. This finding is consistent with experiments showing that swing errors by experienced batters tend to increase as the differences between the properties of consecutive pitches increase. We provide examples that demonstrate the role of pitch-to-pitch correlation in the strikeout rate model.
1Introduction
The act of hitting a pitch in major league baseball places extraordinary demands on the batter’s visuomotor system. A typical fastball travels from the pitcher to the batter in about 400 milliseconds and, in order to initiate a swing on time, the batter must estimate the time and location for contact during the first 150–200 milliseconds of the pitch trajectory (Gray, 2002a). Even small errors in time or space will lead to failure and, as a result, major league batters frequently swing and miss. Pitchers endeavor to make the batter’s task even more challenging by throwing pitches with a wide variety of characteristics. A pitcher can change speeds by mixing fastballs and off-speed pitches. He can also change the batter’s eye level by mixing pitches that are high and low or disrupt the batter’s balance by locating pitches inside and outside. In addition to changing speed and location, pitchers can impart different spins on the ball which alters its trajectory. Given the difficulty of the hitting task, batters can benefit from being able to predict the characteristics of an upcoming pitch. Consequently, the pitcher’s team expends significant effort involving, for example, elaborate sign sequences and players covering their mouths when discussing strategy to keep the parameters of the next pitch a secret.
A batter’s success in predicting and reacting to the characteristics of a pitch depends on the distribution of pitches that might be thrown. Experiments with experienced batters on simulated pitches have shown, for example, that contact rates improve significantly when pitches are limited to two speeds rather than drawn from a wide range of speeds (Gray, 2002a). Another study has shown that major league strikeout rates increase as a pitcher’s number of distinct pitch types increases (Arthur, 2014a). An important question for the pitcher’s team is the optimal distribution of pitches that should be utilized. This distribution depends on a number of variables including the relative quality of the pitcher’s array of pitches, the batter’s strengths and weaknesses, the count, the score, the inning, the number of outs, the baserunners, and the identity of the following batters. Researchers (Gassko, 2010) (Tango et al., 2007) have proposed the use of game theory to derive an optimized distribution of pitches for a given situation.
In addition to striving for an optimized pitch distribution, a pitcher can also seek advantage by adjusting his sequence of pitches. Gray (2002a, 2002b) performed experiments with college batters to show that the average spatial and temporal error in a batter’s swing for a given pitch has a significant dependence on the speed of the preceding pitches. In particular, the errors are larger when there is a significant difference between the speed of the current pitch and the speed of the prior pitches. Several studies of major league matchups have also demonstrated that pitchers benefit from varying speed and movement from pitch-to-pitch. Bonney (2015) showed that pitchers achieve better results when they reduce velocity by at least five miles per hour after a first-pitch fastball. Glaser (2010) showed that, on average, following an off-speed pitch with the same off-speed pitch is not a good choice. Roegele (2014) showed that pitchers benefit when consecutive pitches have different movement after following the same tunnel (Long et al. 2017) during the first part of their path to the batter. These results are consistent with the strategy of using setup pitches (Greenhouse, 2010) which aim to enhance the probability of a pitcher’s success on a subsequent pitch.
More than half of the pitches thrown in major league baseball in 2014 were some variant of a fastball. The popularity of the fastball stems from its high velocity which limits a batter’s reaction time and from the ability of most major league pitchers to control the fastball with more accuracy than their offspeed pitches. Several studies (Arthur, 2014a) (Cameron, 2009) have found a positive correlation between a pitcher’s fastball velocity and his strikeout rate and we might reasonably expect that pitchers also benefit from fastball movement. Thus, the properties of a pitcher’s fastball will play an important role in determining his strikeout rate. In addition to the intrinsic characteristics of his fastball and other pitches, the previous discussion suggests that distribution and sequencing will also play a role in a pitcher’s success. Lichtman (2013) has shown, for example, that pitchers who throw a high fraction of fastballs suffer a larger decline in performance when they face batters for the second or third time in a game as compared to other pitchers.
In this paper we introduce a set of pitch-to-pitch correlation measures for a pitcher which quantify his tendency to throw consecutive pitches with similar properties and which quantify the degree to which the location, velocity, and movement of his next pitch can be predicted from the characteristics of the previous pitch. Since these measures are derived from estimates of continuous-valued variables, they avoid the loss of information that occurs during classification in methods that analyze pitch type sequences (Arthur, 2014b) (Weinstein, 2015). The utility of the correlation measures is investigated using PITCHf/x (Fast, 2010) parameter estimates for nearly three million pitches thrown by a set of pitchers over the years from 2008 to 2014. Since the handedness (left or right) of the batter and pitcher plays an important role in pitch selection, the pitch-to-pitch correlations are computed separately for each applicable platoon configuration (LHP vs LHB, LHP vs RHB, RHP vs LHB, RHP vs RHB) for each pitcher and year. We show that these pitcher descriptors are repeatable from year-to-year and that the measures derived from velocity and movement provide more year-to-year consistency than the measures derived from location. We also evaluate the use of the correlation measures as explanatory variables within a model for pitcher strikeout rate. The model reveals that, as expected, a pitcher’s strikeout rate increases as his fastball velocity and vertical movement increase. The model also shows that, other factors equal, a pitcher’s strikeout rate decreases as his fastball fraction and pitch-to-pitch correlation increase. We use the example of James Shields and Bartolo Colon to demonstrate the dependence of strikeout rate on these measures of predictability.
2PITCHf/x data
PITCHf/x is a system that uses two cameras to capture a set of images of pitches thrown in baseball games (Fast, 2010). The system was developed by Sportvision and was available in all thirty major league stadiums at the start of the 2008 season. The PITCHf/x images can be used to estimate the three-dimensional path of a pitch and to derive information about its speed and movement. Pitch information is publicly distributed in real-time by Major League Baseball Advanced Media (MLBAM) using the GameDay application.
Our analysis of PITCHf/x data considers several of the reported attributes for each pitch. The pair (px,pz) specifies the location of a pitch as it crosses home plate where px is the horizontal coordinate and pz is the vertical coordinate relative to an origin at the back vertex of home plate. The positive x-axis points to the right from the catcher’s perspective, the positive y-axis points toward second base, and the positive z-axis points up. The coordinates px and pz are typically reported in feet. The movement of a pitch (pfx_x,pfx_z) is defined as the difference between the pitch location (px,pz) and the theoretical location of a pitch thrown at the same speed that does not deviate from a straight path due to spin (Nathan, 2012). The movement parameters pfx_x and pfx_z are typically reported in inches. The start-speed is an estimate of pitch speed in three dimensions near the release point in miles per hour. Brooks Baseball (www.brooksbaseball.net) improves the accuracy of the MLBAM reported values by making small adjustments to the calculations.
Different pitch types have different characteristics. For a right-handed major league pitcher, for example, a four-seam fastball typically has a start-speed above 90 miles per hour with a negative pfx_x and a positive pfx_z while a curveball typically has a start-speed below 80 miles per hour with a positive pfx_x and a negative pfx_z. For a left-handed pitcher, the sign of pfx_x will reverse for these pitch types. In addition to the measured parameters, MLBAM also assigns a label to each pitch such as FF for a four-seam fastball or CU for a curveball.
3Pitch-to-pitch correlation
3.1Definitions
We use the measurements described in section 2 to define a vector of descriptors for a pitcher that quantifies the relationship between consecutive pitches in location, movement, and velocity. For a given pitcher in a given season, say Clayton Kershaw in 2014, we consider separately the pitches thrown to left-handed and right-handed batters after intentional balls are removed. Let
(1)
where
We can also let
A correlation coefficient r has several important properties. The value of r is always between -1 and +1 with the sign of r being the same as the sign of the slope of the regression line for the set of N points
3.2Data
In section 4 we will examine the dependence of a pitcher’s strikeout rate on the correlation coefficients defined in section 3.1. As with the correlation coefficients, we compute each pitcher’s strikeout rate separately for each applicable platoon configuration for each year. Before the rate is computed, however, we remove all plate appearances that resulted in a bunt or an intentional walk and we also remove all plate appearances with a pitcher as a batter. The number of remaining plate appearances is referred to as adjusted plate appearances. A pitcher’s strikeout rate PK is then defined as the ratio of strikeouts to adjusted plate appearances. Using considerations (Healey, 2015) that were derived from reliability studies (Carleton, 2013), we consider a pitcher’s strikeout rate to be reliable for a season and platoon configuration if the pitcher had at least 150 adjusted plate appearances for that season and platoon configuration. For this study, we also removed all pitchers that were used strictly as relievers during a season as well as all pitchers who had at least twenty percent of their pitches classified as knuckleballs. Table 1 summarizes the total number of pitcher seasons that satisfy these criteria for each of the four platoon configurations over the years from 2008 to 2014 for which PITCHf/x data was widely available.
Table 1
Number of pitcher seasons for each platoon configuration, 2008 to 2014
| LHP vs LHB | LHP vs RHB | RHP vs LHB | RHP vs RHB |
| 180 | 394 | 814 | 796 |
Table 2
Pitch-to-pitch correlation statistics for RHP versus RHB, 2008–2014
| Var. | Mean | Std. Dev. | Minimum | Pitcher/Year | Maximum | Pitcher/Year |
| rx | 0.076589 | 0.051952 | –0.074098 | J. Westbrook/2013 | 0.265521 | I. Kennedy/2013 |
| rz | 0.060740 | 0.046061 | –0.077553 | C. Morton/2010 | 0.220789 | N. Tepesch/2014 |
| rmx | 0.082631 | 0.082353 | –0.148586 | D. Bush/2010 | 0.383200 | J. Marquis/2013 |
| rmz | 0.099813 | 0.089800 | –0.130765 | M. Pineda/2011 | 0.554724 | C.-M. Wang/2008 |
| rs | 0.072066 | 0.088115 | –0.164595 | M. Estrada/2011 | 0.515570 | B. Colon/2013 |
Table 3
Pitch-to-pitch correlation statistics for RHP versus LHB, 2008–2014
| Var. | Mean | Std. Dev. | Minimum | Pitcher/Year | Maximum | Pitcher/Year |
| rx | 0.088363 | 0.051648 | –0.081521 | B. Bannister/2009 | 0.262060 | L. Hernandez/2010 |
| rz | 0.057892 | 0.048850 | –0.098732 | B. Tomko/2008 | 0.236806 | D. Pauley/2010 |
| rmx | 0.091798 | 0.081257 | –0.121566 | H. Iwakuma/2014 | 0.428561 | J. Marquis/2013 |
| rmz | 0.088761 | 0.089713 | –0.127830 | J. Duchscherer/2008 | 0.456142 | M. Batista/2008 |
| rs | 0.060686 | 0.089174 | –0.152202 | N. Figueroa/2010 | 0.438098 | B. Colon/2014 |
The (rx, rz, rmx, rmz, rs) correlation coefficients were computed for all of the cases represented in Table 1 using the Brooks Baseball adjustments to the PITCHf/x measurements. Tables 2, 3, 4, and 5 present the mean, standard deviation, and minimum and maximum values for each coefficient over the pitcher seasons for each platoon configuration. The Tables also provide the pitcher and year for each minimum and maximum value. We see that the coefficients that are based on movement and speed (rmx, rmz, rs) have larger ranges and standard deviations across pitchers than the coefficients that are based on location (rx, rz).
Table 4
Pitch-to-pitch correlation statistics for LHP versus RHB, 2008–2014
| Var. | Mean | Std. Dev. | Minimum | Pitcher/Year | Maximum | Pitcher/Year |
| rx | 0.079737 | 0.050875 | –0.063483 | C. Friedrich/2012 | 0.217846 | C. Kershaw/2010 |
| rz | 0.053402 | 0.040659 | –0.089965 | R. Rowland-Smith/2009 | 0.170210 | W. Smith/2012 |
| rmx | 0.105860 | 0.075576 | –0.150204 | E. Bedard/2011 | 0.340786 | T. Glavine/2008 |
| rmz | 0.093271 | 0.077765 | –0.137182 | E. Bedard/2011 | 0.308426 | M. Hampton/2009 |
| rs | 0.051189 | 0.079572 | –0.215225 | J. Outman/2009 | 0.250635 | J. Garcia/2013 |
Table 5
Pitch-to-pitch correlation statistics for LHP versus LHB, 2008–2014
| Var. | Mean | Std. Dev. | Minimum | Pitcher/Year | Maximum | Pitcher/Year |
| rx | 0.058538 | 0.060958 | –0.079173 | B. Chen/2013 | 0.236886 | J. Garcia/2011 |
| rz | 0.058783 | 0.056556 | –0.078295 | J. Vargas/2013 | 0.235601 | B. Duensing/2011 |
| rmx | 0.076101 | 0.082671 | –0.135050 | C.J. Wilson/2010 | 0.334654 | S. Diamond/2013 |
| rmz | 0.110630 | 0.083982 | –0.055096 | J. Vargas/2014 | 0.365518 | J. Danks/2011 |
| rs | 0.066918 | 0.080587 | –0.111602 | C.C. Sabathia/2011 | 0.300316 | W. Miley/2014 |
3.3Year-to-year analysis
An important question is the degree to which the statistics defined in section 3.1 represent distinctive and repeatable characteristics of a pitcher. One way to answer this question is to compute year-to-year correlations which measure the consistency of a statistic for pitchers from year-to-year. Specifically, for each platoon configuration we identified the instances of pitchers who satisfied the criteria described in section 3.2 for consecutive seasons. These instances were used to form pairs of consecutive pitcher seasons for each platoon configuration where the second year of a pair was allowed to be the first year of another pair. The total number of pairs for each platoon configuration is given in Table 6. For each of the statistics defined in section 3.1 we computed the year-to-year correlation coefficient for each platoon configuration using these pairs. The results are shown in Table 7. If each pitcher has the same value of a statistic for every pair of consecutive years, then the correlation coefficient will be one. The observed value of the correlation coefficients is less than one due to variation in the statistic measurements that originate from the use of limited sample sizes and from actual changes in pitcher tendencies over time. We see that the year-to-year correlations for statistics derived from movement and speed measurements (rmx, rmz, rs) are larger than the year-to-year correlations for statistics derived from location measurements (rx, rz).
Table 6
Number of pairs of pitcher seasons for each platoon configuration, 2008 to 2014
| LHP vs LHB | LHP vs RHB | RHP vs LHB | RHP vs RHB |
| 89 | 244 | 489 | 469 |
Table 7
Year-to-year correlations for each variable
| Variable | LHP vs LHB | LHP vs RHB | RHP vs LHB | RHP vs RHB |
| rx | 0.2522 | 0.3444 | 0.3327 | 0.3600 |
| rz | 0.0609 | 0.2199 | 0.3306 | 0.2543 |
| rmx | 0.5477 | 0.4971 | 0.5522 | 0.5940 |
| rmz | 0.4286 | 0.4623 | 0.6182 | 0.5737 |
| rs | 0.4683 | 0.5005 | 0.6342 | 0.6115 |
4Modeling strikeout rate
4.1Variables
4.1.1Fastball velocity and movement
The large majority of major league pitchers throw a two-seam or four-seam fastball and these pitches are typically assigned one of the four labels FA (fastball), FF (four-seam fastball), FT (two-seam fastball), or SI (sinker) by MLBAM. We computed the average of the variables start-speed, pfx_x, and pfx_z for the pitches with each of these labels for each pitcher in our study for each applicable platoon configuration and year. The variable velo for a pitcher, year, and configuration refers to the largest average start-speed over the four labels. Similarly, the variable max_pfx_z refers to the largest average pfx_z over these labels. For right-handed pitchers, pfx_x is typically negative for these labels and we define min_pfx_x as the minimum value of the average pfx_x over the four labels. The variable max_pfx_x is defined in a similar way for left-handed pitchers for which pfx_x is typically positive for these pitches. The variables velo, max_pfx_z, min_pfx_x (for RHP), and max_pfx_x (for LHP) characterize the velocity and movement of a pitcher’s fastball.
4.1.2Pitch mix and sequencing
In addition to the intrinsic properties of individual pitches, a pitcher’s effectiveness also depends on pitch distribution and sequencing. A single parameter that provides a high-level description of pitch distribution is the fastball fraction f . For each pitcher,year, and platoon configuration we define f as the ratio of pitches with a label of FA, FF, FT, or SI to the total number of pitches. The variables rx, rz, rmx, rmz, rs provide a measure of pitch sequencing by capturing pitch-to-pitch correlation in location, movement, and velocity. As defined in section 3.1, these five variables are based on correlations that are computed using all pitches regardless of type.
4.2Model estimation
We use a separate linear regression model for each platoon configuration to approximate pitcher strikeout rate PK using the variables defined in section 4.1. The number of observations for each configuration is given by Table 1. We considered approximations of the form
(2)
for right-handed pitchers and
(3)
for left-handed pitchers where F1 and F2 are a linear combination of their component variables and first-order cross terms. Tables 8–11 present the models of this form for each platoon configuration that have the most significant variables where significance is defined by a p-value below 0.01. Each table includes the coefficient, standard error, t-statistic, and p-value for each significant variable along with the R2 for the fit. We observe that off-speed pitches typically have a larger impact on same-sided (RHP vs. RHB, LHP vs. LHB) matchups. Therefore, the limited treatment of off-speed pitches by the model may explain the larger R2 values for opposite-sided (RHP vs. LHB, LHP vs. RHB) matchups. Due to considerations presented in section 3.1, we also examined the use of variables defined by the absolute value of the pitch-to-pitch correlation coefficients. Using the original signed values of the coefficients, however, led to models with less error which suggests that a negative correlation benefits a pitcher’s strikeout rate more than a zero correlation.
Table 8
RHP versus RHB, 796 observations, R2 = 0.240
| Variable | Coefficient | Std. Error | t-Statistic | p-value |
| 1 | –0.842891 | 0.075632 | –11.14470 | 0.0000 |
| velo | 0.010035 | 0.000750 | 13.37231 | 0.0000 |
| max_pfx_z | 0.018526 | 0.003066 | 6.04299 | 0.0000 |
| min_pfx_x | –0.018046 | 0.003693 | –4.88639 | 0.0000 |
| max_pfx_z*min_pfx_x | 0.002107 | 0.000377 | 5.58362 | 0.0000 |
| f | –0.106535 | 0.015137 | –7.03811 | 0.0000 |
| rmz | –0.050764 | 0.017670 | –2.87297 | 0.0042 |
Table 9
RHP versus LHB, 814 observations, R2 = 0.342
| Variable | Coefficient | Std. Error | t-Statistic | p-value |
| 1 | –0.780316 | 0.061231 | –12.74385 | 0.0000 |
| velo | 0.010417 | 0.000685 | 15.20755 | 0.0000 |
| max_pfx_z | 0.007929 | 0.000829 | 9.56582 | 0.0000 |
| f | –0.122944 | 0.012643 | –9.72435 | 0.0000 |
| rmz | –0.046995 | 0.016197 | –2.90152 | 0.0038 |
Table 10
LHP versus RHB, 394 observations, R2 = 0.383
| Variable | Coefficient | Std. Error | t-Statistic | p-value |
| 1 | –0.802541 | 0.069079 | –11.61780 | 0.0000 |
| velo | 0.011132 | 0.000802 | 13.87884 | 0.0000 |
| max_pfx_z | 0.004040 | 0.001300 | 3.10859 | 0.0020 |
| f | –0.123172 | 0.020833 | –5.91227 | 0.0000 |
| rmx | –0.093860 | 0.025214 | –3.72254 | 0.0002 |
Table 11
LHP versus LHB, 180 observations, R2 = 0.332
| Variable | Coefficient | Std. Error | t-Statistic | p-value |
| 1 | –0.985737 | 0.128364 | –7.679242 | 0.0000 |
| velo | 0.014176 | 0.001512 | 9.372694 | 0.0000 |
| f | –0.165529 | 0.041024 | –4.034951 | 0.0001 |
Table 12 presents the mean and maximum absolute error
Table 12
Mean and maximum of absolute difference
| Configuration | obs. | Mean(|D|) | Max(|D|) | Pitcher/Year |
| RHP vs RHB | 796 | 0.033049 | 0.176470 | Y. Darvish/2013 |
| RHP vs LHB | 814 | 0.031604 | 0.110285 | F. Hernandez/2013 |
| LHP vs RHB | 394 | 0.028972 | 0.113404 | C. Kershaw/2014 |
| LHP vs LHB | 180 | 0.036079 | 0.155823 | C. Kershaw/2013 |
We see from Tables 8–11 that the variable velo is significant for each platoon configuration with a positive coefficient which indicates that a one mile per hour increase in velocity corresponds to an increase in
For the three configurations with the most observations (Tables 8–11) the fastball vertical movement variable max_pfx_z is significant along with one of the pitch-to-pitch correlation variables. Specifically, rmz is significant for the two configurations involving right-handed pitchers and rmx is significant for the LHP versus RHB configuration. As expected, increased vertical movement and lower pitch-to-pitch correlation are associated with higher strikeout rates. The horizontal movement variable min_pfx_x and the cross term max_pfx_z*min_pfx_x are also significant for the RHP versus RHB configuration.
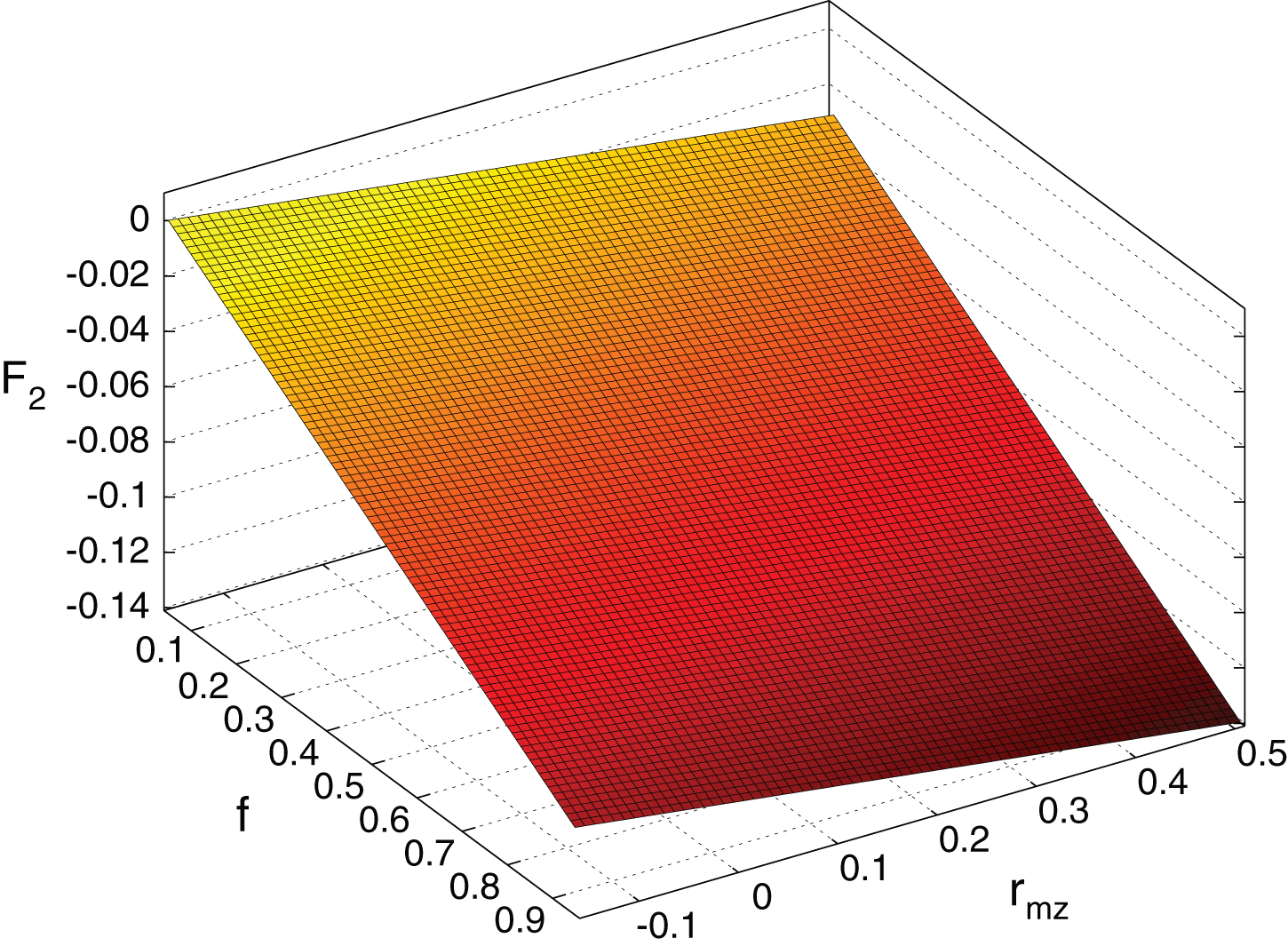
Figures 1 through 4 illustrate the distribution of the explanatory variables and the estimated F1 and F2 surfaces for the RHP versus LHB platoon configuration considered in Table 9. Figure 1 plots the joint distribution of fastball velocity and vertical movement for the 814 observations for this configuration. The variables are nearly uncorrelated with a correlation coefficient of 0.05. Figure 2 plots F1(1,velo,max_pfx_z) and shows that strikeout rate increases as fastball velocity and vertical movement increase. Figure 2 plots the joint distribution of fastball fraction and pitch-to-pitch correlation in vertical movement. These variables are also nearly uncorrelated with a correlation coefficient of 0.09. Figure 3 plots F2 (f, rmz) and shows that strikeout rate decreases as fastball fraction and pitch-to-pitch correlation in vertical movement increase. The shape of the F1 and F2 surfaces will be similar for the other platoon configurations for which these variables are significant.
Fig.1
Joint distribution for maxpfxz and velo for RHP versus LHB.
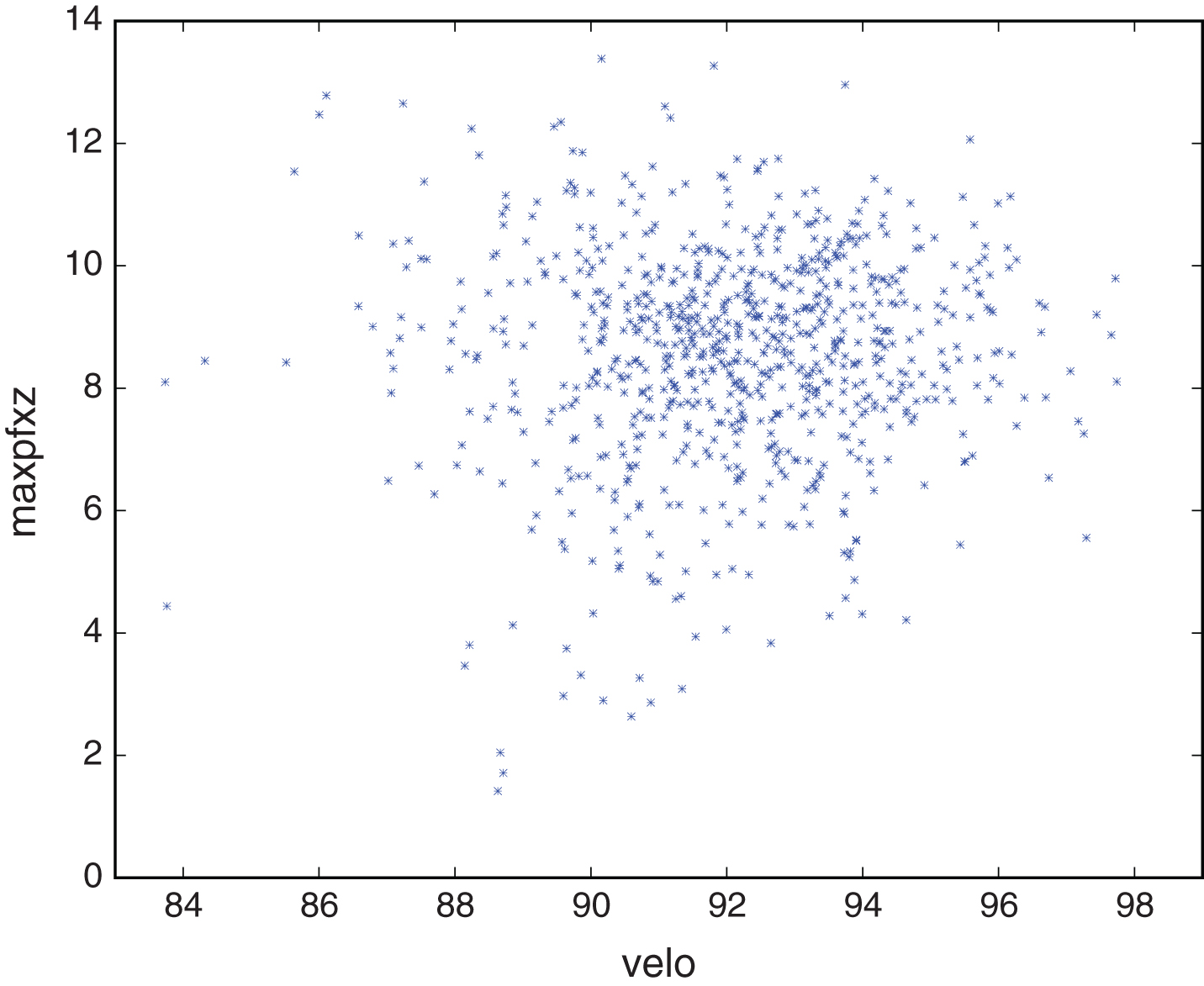
Fig.2
F1 surface for RHP versus LHB.
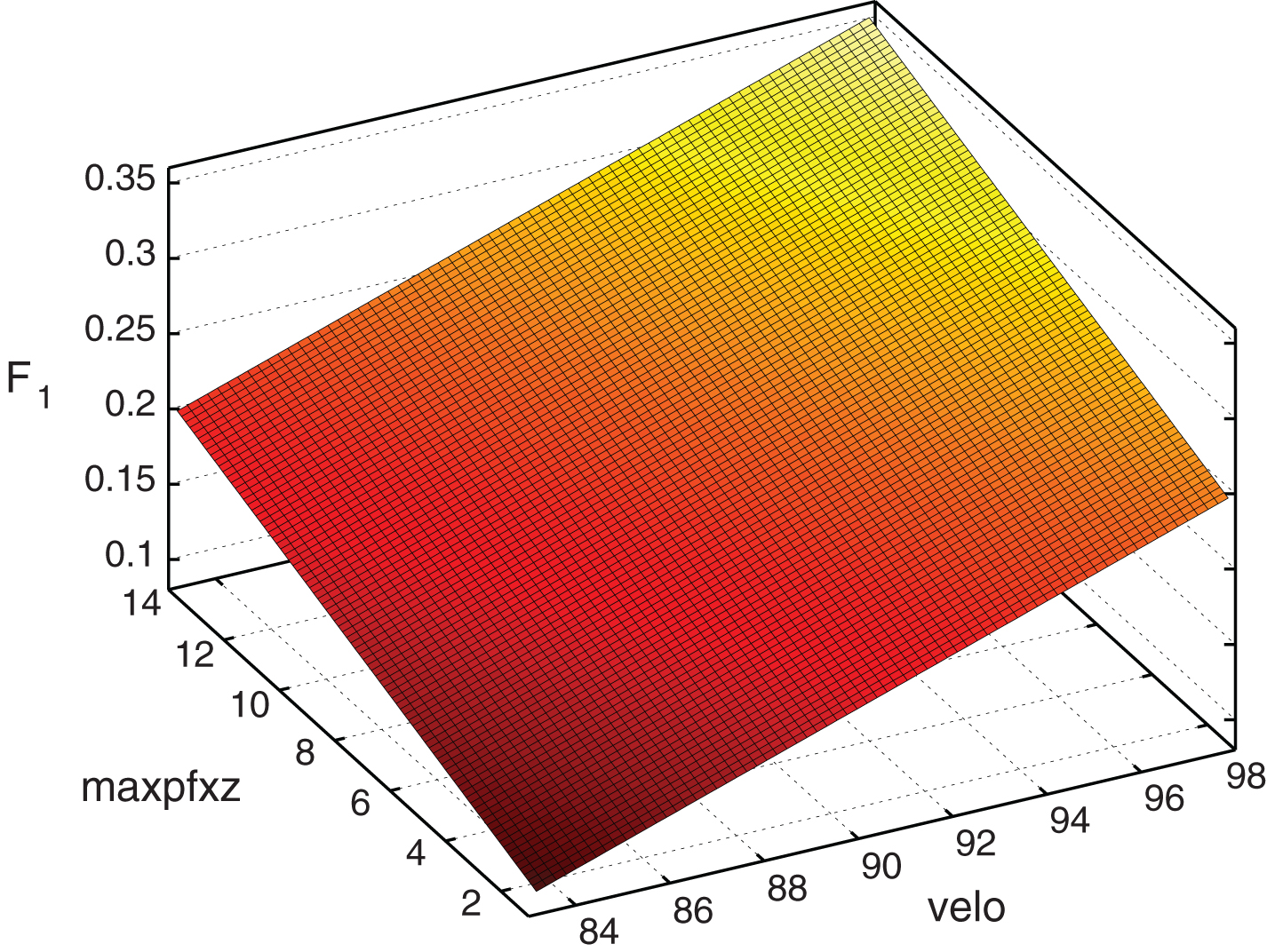
Fig.3
Joint distribution for f and rmz for RHP versus LHB.
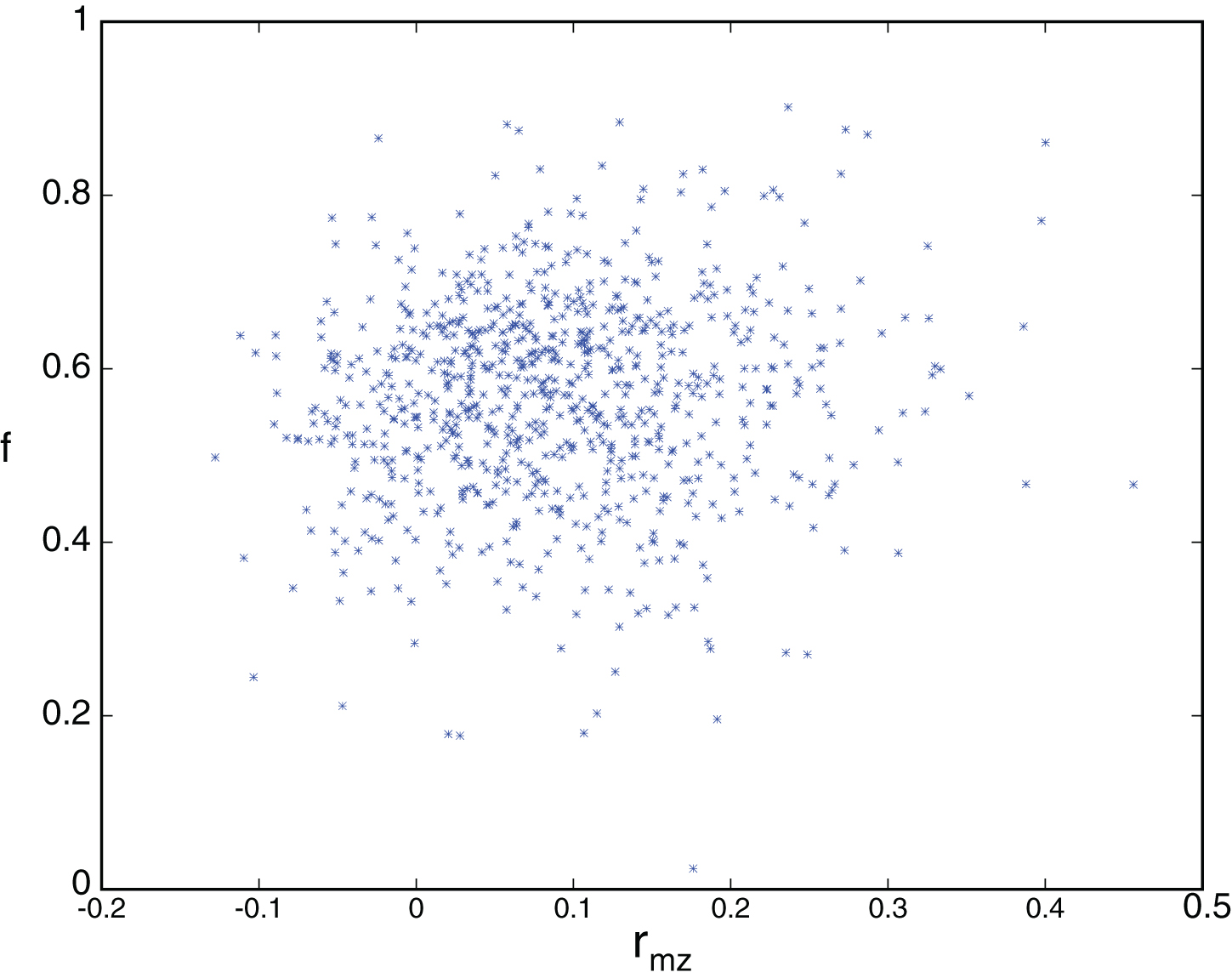
Fig.4
F2 surface for RHP versus LHB.
4.3Impact of pitch-to-pitch correlation
In this section, we examine the role of the pitch-to-pitch correlation variables on strikeout rate in more detail. Table 13 considers the three platoon configurations for which a correlation variable is significant. The value c is the coefficient for the correlation variable and platoon configuration from one of Tables 8–10. The values σ and maxdiff represent the standard deviation and maximum difference over pitchers for the correlation variable and platoon configuration from one of Tables 2–4. The constant 38 is the average number of batters faced per nine innings in major league baseball in 2014. Thus, c * σ * 38 and c * maxdiff * 38 are the changes in the number of strikeouts per nine innings associated with changes of σ and maxdiff in the correlation variable if the other variables are held constant. We see that c * maxdiff * 38 is between one and two strikeouts per nine innings depending on the platoonconfiguration.
Table 13
Dependence of strikeouts per nine innings on correlation variables
| Configuration | variable | c * σ * 38 | c * maxdiff * 38 |
| RHP vs RHB | rmz | –0.173 | –1.322 |
| RHP vs LHB | rmz | –0.160 | –1.043 |
| LHP vs RHB | rmx | –0.270 | –1.751 |
Table 14
RHP versus LHB Models for James Shields 2011 and Bartolo Colon 2012
| Pitcher/Year | velo | max_pfx_z | F1 | rmz | f | F2 |
| J. Shields/2011 | 91.886 | 8.923 | 0.248 | 0.177 | 0.325 | –0.048 |
| B. Colon/2012 | 92.173 | 8.579 | 0.248 | 0.237 | 0.902 | –0.122 |
4.4The Shields/Colon example
As an example of the importance of pitch mix and sequencing we present the case of right-handed pitchers James Shields (2011) and Bartolo Colon (2012) against left-handed batters. The pitchers had similar values for the fastball parameters velo and max_pfx_z which led to identical values for F1 for this configuration as shown in Table 14. Colon’s pitches, however, were much more predictable with a fastball fraction f = 0.902 and a vertical movement correlation rmz = 0.237 compared to f = 0.325 and rmz = 0.177 for Shields. As a result, F2 and the overall
5Conclusion
The success of a major league pitcher depends on many factors including the velocity and movement of his pitches and on his ability to utilize an effective pitch distribution and sequencing strategy. We have examined the use of pitch-to-pitch correlations for location, velocity, and movement as a measure of pitch sequencing. These correlations characterize the degree to which the properties of an upcoming pitch can be predicted from the properties of the previous pitch. We have derived the pitch-to-pitch correlations for a set of pitchers using PITCHf/x measurements for nearly three million pitches thrown from 2008 to 2014. The data for each pitcher was partitioned according to the handedness of the batter but, in order to maximize sample size, other contextual variables such as the count and inning were not considered. We showed that there is significant year-to-year consistency in the pitch-to-pitch correlation of velocity and movement for all four platoon configurations. We also presented a model that describes the dependence of a pitcher’s strikeout rate on a number of variables that include fastball velocity and movement as well as a fastball fraction descriptor for pitch distribution and the pitch-to-pitch correlation descriptors for pitch sequencing. We showed that a pitcher’s strikeout rate increases as his fastball velocity and vertical movement increase. We also showed that a pitcher’s strikeout rate decreases, other factors equal, as his predictability in terms of fastball fraction and pitch-to-pitch correlation increases.
Since the fastball is the most common pitch in major league baseball, our fastball-centric model was able to capture a significant fraction of the variance in strikeout rate while allowing evaluation of the role of the new pitch-to-pitch correlation descriptors. As might be expected, the largest errors in the model occurred for pitchers with an exceptional offspeed pitch since the benefit of these pitches is not explicitly captured by the model. Thus, a more detailed model could include information about the number, frequency, and physical properties of a pitcher’s offspeed pitches and how well these pitches complement each other and the pitcher’s fastball. Pitch location is another important factor which affects a pitcher’s strikeout rate that could be incorporated into future models. The current model also neglects the impact of a pitcher’s delivery which can be beneficial if, for example, he hides the ball well or detrimental if he inadvertently provides clues about the identity of the upcoming pitch.
Acknowledgments
We thank Arunav Singh for help with data processing. The PITCHf/x data was obtained from www.brooksbaseball.net and the data used for computing strikeout rate was obtained from www.retrosheet.org.
References
[1] | Arthur R. , (2014) , Entropy and the eephus [Online]. Available: www.baseball.prospectus.com/article.php?articleid=22758. |
[2] | Arthur R. , (2014) , The art and science of sequencing [Online]. Available: www.baseball.prospectus.com/article.php?articleid=23023. |
[3] | Bonney P. , (2015) , Defining the pitch sequencing question [Online]. Available: www.hardballtimes.com/defining-the-pitch-sequencing-question. |
[4] | Cameron D. , (2009) , Velocity and K/9 [Online]. Available: www.fangraphs.com/blogs/velocity-and-K9. |
[5] | Carleton R. , (2013) , Should I worry about my favorite pitcher? [Online]. Available: www.baseballprospectus.com/article.php?articleid=20516. |
[6] | Fast M. , (2010) , What the heck is PITCHf/x? In Distelheim J. , Tsao B. , Oshan J. , Bolado C. and Jacobs B. , editors, The Hardball Times Baseball Annual, pages 153–158. The Hardball Times, (2010) . |
[7] | Gassko D. , (2010) , When a pitcher meets a hitter [Online]. Available: www.hardball-times.com/when-a-pitcher-meets-a-hitter. |
[8] | Glaser C. , (2010) , The influence of batters’ expectations on pitch perception [Online]. Available: www.hardballtimes.com/tht-live/the-influence-of-batters-expectations-on-pitch-perception. |
[9] | Gray R. , (2002) , Behavior of college baseball players in a virtual batting task, Journal of Experimental Psychology: Human Perception and Performance 28: (5), 1131–1148. |
[10] | Gray R. , (2002) , Markov at the bat: A model of cognitive processing in baseball batters, Psychological Science 13: (6), 542–547. |
[11] | Greenhouse J. , (2010) , Lidge’s pitches [Online]. Available: www.baseballanalysts.com/archives/2010/05/brad_lidges_out.php. |
[12] | Healey G. , (2015) , Modeling the probability of a strikeout for a batter/pitcher matchup, IEEE Transactions on Knowledge and Data Engineering 27: (9), 2415–2423. |
[13] | Lichtman M. , (2013) , Pitch types and the times through the order penalty [Online]. Available: www.baseball.prospectus.com/article.php?articleid=22235. |
[14] | Long J. , Judge J. and Pavlidis H. , (2017) , Introducing pitch tunnels [Online]. Available: www.baseball.prospectus.com/article.php?articleid=31030. |
[15] | Nathan A. , (2012) , Determining pitch movement from PITCHf/x data [Online]. Available: www.baseball.physics.illinois.edu/Movement.pdf.. |
[16] | Roegele J. , (2014) , The effects of pitch sequencing [Online]. Available: www.hardballtimes.com/the-effects-of-pitch-sequencing. |
[17] | Tango T. , Lichtman M. and Dolphin A. , (2007) , The Book: Playing the Percentages in Baseball. Potomac Books, Dulles, Virgina. |
[18] | Weinstein M. , (2015) , Finding value in fastball mixing [Online]. Available: www.hardballtimes.com/finding-value-in-fastball-mixing. |




