Ranking and prediction of collegiate wrestling
Abstract
College wrestling rankings have a major impact upon the sport, as they are one of the criteria used to determine advancement to postseason championships and seeding, thereby benchmarking individual, team, and program success. In addition to ordering athletes based upon past performance, rankings may function as predictors for future match outcomes. This research identifies potential biases in traditional ranking methodologies and offers alternatives based on the network-based PageRank and Elo ratings. Using data from the 2013-2014 NCAA Division I wrestling season, we evaluate both existing and our new rankings on the basis of predictive accuracy. Our new methods significantly improve upon a baseline of 67% accuracy and several of the existing ranking methods. These results and follow-up analyses suggest that Elo presents an especially attractive alternative to current ranking systems for college wrestling, with potential extensions to the prediction of point differentials, ensemble methods, and generalizability to other combat sports.
1Introduction
Wrestling has received very little attention in the forecasting literature in comparison to other sports, such as baseball, basketball, and football. However, the nature of the sport adds many interesting dimensions to the ranking and forecasting problem. Collegiate wrestling in the United States (the variety known as folkstyle or scholastic wrestling) consists of individuals divided into ten weight classes, ranging from 125 pounds to 285 pounds (heavyweight), competing against opponents in the same weight class. Unlike sports where the only possible outcomes are win-lose-draw, there are no draws in folkstyle wrestling, and several types of victories are awarded. These may be determined by the point differential between competitors, match-terminating maneuver, or match termination by default, forfeit, or disqualification, as defined by NCAA rules (NCAA, 2009). Wrestling matches occur in the context of dual or tournament competitions. During the 2013-2014 season, NCAA Division I wrestling comprised nine conferences (ACC, Big Ten, Big 12, EIWA, EWL, MAC, Pac 12, SoCon, and WWC) and 78 schools.
These unique features of college wrestling— diversity of competition type (dual, tournament), multiple victory types (e.g. decision, fall, technical fall), organization of competitors into weight classes, and frequency of weight class changes— complicate the ranking process and are handled by existing wrestling rankings with differing degrees of success. There are currently several published rankings for individual college wrestlers, each with their own methods of construction, criteria under consideration, and thresholds for inclusion. These existing systems may produce widely varying rankings for the same wrestler during the same period.
Understanding the potential for bias and inaccuracy in current rankings is critical, as wrestling rankings have several important impacts upon the sport. The NCAA Coaches’ Panel1 and NCAA RPI2 are crucial components of post-season championship tournament selection and seeding, described in the NCAA pre-tournament manual (NCAA, 2013b). The Division I wrestling season culminates at the NCAA Division I Wrestling Championships in March, where 33 wrestlers compete in each of the 10 weight classes and the top eight finishers in each weight are named “All-Americans.” A wrestler may qualify for the NCAA Championship Tournament in one of two ways: automatic qualification or at-large bid. Automatic qualifiers are the top-k finishers in each weight class from each qualifying conference’s championship tournament, determined by the number of ranked wrestlers per weight class in each conference. For example, if the ACC has 6 wrestlers at 133 pounds ranked by the NCAA prior to the post-season, their conference tournament may receive up to 6 automatic qualifying bids, which will be awarded to the top six finishers in the ACC tournament in the 133 pound weight class. For the 2013-2014 season, 290 automatic qualifying bids were allotted, and the remaining 40 spots went to at-large bids, awarded by the Division I Wrestling Committee with consideration of winning percentage, RPI, Coaches’ Panel ranking, and head-to-head record. For the 330 wrestlers that advance to the NCAA Championship Tournament, seeds determine their placement in the brackets and thus their first round opponents. Again, the Coaches’ Panel and RPI rankings play an important role in NCAA Tournament seeding, determined by the Division I Wrestling Committee with consideration of several factors, including the final NCAA rankings, winning percentage, and head-to-headrecord.
Rankings are also used as benchmarks of individual, team, and program success. In addition to evaluating competitors based upon past performances, rankings may also be used as predictors of future outcomes. Stefani (2011) describes the use of athletic rankings for prediction, based on the assumption that the higher-ranked opponent is expected to defeat the lower- or unranked opponent. The question of accurate rankings is non-trivial. As individuals in a given weight class do not wrestle a complete tournament each season (meaning a wrestler does not face every other wrestler at his weight), rankings are an important basis of comparison and prediction for wrestlers with no previous matches.
This research is the first work of its kind addressing wrestling rankings. While there is currently no empirical research on the methodology of ranking collegiate or Olympic wrestling, sports ranking systems have been well-studied in the fields of mathematics, statistics, and management sciences. Our research evaluates several existing wrestling rankings for predictive accuracy on the matches of the NCAA Championship Tournament, drawing upon earlier work from Stefani (2011), which surveys the rating systems of 159 international sports. Although the scope of analysis is limited to international (non-collegiate) sports, and focuses solely on systems with published ratings (a numerical value assigned to competitor or team) as opposed to rankings (ordinal placement based upon ratings), his method for evaluating the predictive accuracy of rating systems is utilized in this project. This method is predicated on the assumption that for a system to be considered predictive, higher-rated opponents should defeat lower-rated opponents approximately 17% more often than random chance. It is from this premise that Stefani (2011) proposes the baseline of 67% accuracy for systems predicting win/loss outcomes (based upon 50% as a random prediction) that is utilized in this project. Although wrestling awards several victory types, matches result in binary win/loss outcomes. Barrow et al. (2013) expand upon previous work evaluating predictive accuracy in sports rankings, assessing eight approaches over 4 datasets (NBA, MLB, Division I men’s basketball, Division I football) in their paper. While the authors do not find any “best” method, they conclude that systems incorporating point differentials are usually more predictive than those only using win-loss data, which informs our approach.
Our research also investigates two new methods for wrestling ranking individual wrestlers, PageRank and Elo ratings. Our application of PageRank to a wrestling competition network draws upon the original work by Brin and Page (1998), but more specifically the application of the PageRank algorithm to directed sports competition networks, as seen in Govan and Meyer (2006). The authors investigate the feasibility of using the PageRank algorithm to rank NFL teams, and their analysis shows that a point differential weighted PageRank outperformed comparison methods including human predictions. Our project also builds upon work related to dynamic link weighting, including a study of tennis and mixed-martial arts competition networks featuring exponentially decaying weights by Procopio et al. (2012) which is of special interest as it includes data on combat sports, which have received less attention in the literature in comparison to other sports (football, basketball, soccer, baseball, etc.). Motegi and Masuda (2012) investigate the predictive accuracy of dynamic link weighting, finding that PageRank models incorporating dynamic link weights outperform both non-dynamic and official rankings. Our Elo method, which considers the relative strength of competitors when calculating rankings, is inspired by the system for chess rating created by Arpad Elo (1978). Based upon investigations of the accuracy of the Elo system (Glickman & Jones, 1999), we have adopted a context-specific parameterization of the formula. Hvattum and Arntzen (2010) also evaluate the accuracy of Elo ratings, focusing on the economic impacts of match predictions in association football (soccer). The authors find that Elo methods outperform all tested comparisons except betting odds. Differences in the performance of our methods and previous systems against human predictions will be discussed in Section 5.
The results of our evaluation of existing ranking systems indicate that all five existing methods perform below or similarly to the 67% baseline proposed by Stefani (2011) when evaluated over all eligible matches of the NCAA tournament, indicating that there is room for improvement in the construction of predictive rankings for Division I college wrestling. As some methods have large numbers of matches between unranked wrestlers, potential adjustments to accuracy evaluations are also discussed. In contrast, our highest-performing PageRank and Elo models significantly exceed the 67% accuracy level and two of the current objective methods. These results and follow-up analyses show promise for the construction of wrestling rankings with more predictive accuracy for match results, and the Elo method in particular presents an attractive alternative to current ranking system, with the potential for extension to prediction of margin of victory and team rankings, ensemble methods, and generalizability to other combat sports.
We describe the dataset and methodology in Section 2. Sections 3 and 4 present the results and follow-up analysis, respectively. Section 5 contains a discussion of results and limitations. Section 6, conclusions and suggestions for further research.
2Material and methods
2.1Dataset
The National Wrestling Coaches Association is the professional organization for all levels of scholastic and collegiate wrestling, and provides support and information for coaches, including the NWCA Scorebook3, an online database of wrestler and team statistics. Information on all Division I college wrestlers and matches was extracted from the NWCA College Scorebook for the 2013-2014 wrestling season (1 November 2013-22 March 2014). The raw wrestler dataset contains 2528 unique Division I wrestlers, including fields such as ID, weight class, eligibility year, school, and end-of-season record. The raw match dataset contains 17,316 unique matches between Division I wrestlers. The dataset was cleaned to remove match records that are not considered in the final ranking (outcomes such as medical forfeits, disqualifications, and defaults), resulting in the removal of 609 matches and 291 wrestlers who had no matches against Division I opponents or whose only matches ended in removed victory types. This results in a final dataset of 2236 unique wrestlers and 16,707 unique matches, with fields including match ID, date, competitor IDs, competitor rankings, result (W or L), win type (technical fall, decision, etc.), points, event ID, event type (tournament, dual), and location (home, away, neutral).
We select the 149-pound weight class as the training dataset for our ranking system design. As Table 1 displays, the 149-pound weight class has the largest total number of matches and wrestlers. Defining which wrestlers belong in a given weight class is itself a data problem. Although each wrestler is assigned a certified weight class as a part of NCAA health and safety regulations (NCAA, 2009), and a weight class is listed in the individual record and team roster, it is not uncommon for a wrestler to compete at a weight one or even two classes up or down from their original weight at the start of the season. Indeed, in the final dataset, 471 wrestlers (21%) competed at two or more weight classes during the 2013-2014 season. The issue of weight changes is extremely relevant to the issue of creating and evaluating rankings for individual wrestlers, as all existing systems and those proposed in this research rank wrestlers by weight class.
Table 1
Number of wrestlers and matches, by weight class
| Weight (lb) | Wrestlers (%) | Matches (%) |
| 125 | 221 (9%) | 1501 (9%) |
| 133 | 263 (10%) | 1576 (9%) |
| 141 | 314 (12%) | 1713 (10%) |
| 149 | 339 (13%) | 1972 (12%) |
| 157 | 319 (13%) | 1909 (11%) |
| 165 | 306 (12%) | 1744 (10%) |
| 174 | 290 (11%) | 1713 (10%) |
| 184 | 261 (10%) | 1562 (9%) |
| 197 | 253 (10%) | 1525 (9%) |
| 285 | 200 (8%) | 1492 (9%) |
| 2766 (100%)* | 16,707 (100%) |
*Wrestlers appear in more than one weight class (2236 unique wrestlers total).
2.2Existing ranking systems
Although wrestling rankings have received little attention in the research literature, both official and unofficial methods abound. The unique features of college wrestling, namely weight classes, weight and roster changes, multiple win types, and multiple competition types, are handled with differing degrees of success by these systems. The focus of our preliminary investigation is an assessment of the predictive accuracy of several existing systems for ranking collegiate wrestling, comparing them to both the 67% benchmark and each other. First, an evaluation of the official rankings and statistics of NCAA Division I wrestling is vital, as they play a large role in determining advancement to the postseason championships and position at the tournament.
As described in the pre-tournament guidelines (NCAA, 2013b), The NCAA RPI (ratings percentage index) is calculated as the product of a wrestler’s winning percentage (WP) and strength of schedule, i.e., the winning percentages of a wrestler’s opponents (OWP) and their opponents (OOWP), as shown in Equation (1):
(1)
Only Division I matches are included in the calculation of the RPI, and to be eligible for ranking, a wrestler must have at least 17 Division I matches in the weight class being ranked. Thus, the RPI may disadvantage wrestlers with a period of inactivity due to injury and the substantial proportion of individuals wrestling at two or more weight classes during a single season, as they are less likely to meet the threshold for inclusion. Due to the high number of Division I matches per wrestler required to calculate the RPI, it is only released twice per season, one week and three weeks preceding the qualifying conference tournaments. In addition, the RPI ranks only 33 wrestlers in each weight class, and only one wrestler in each weight class per school. Attempts to use the RPI for match prediction are hampered by cold-start problems; it cannot be consulted early in the season and only a small proportion of all wrestlers eventually receive an RPI ranking. In addition, the likelihood of excluding wrestlers who change weight classes (21% of all Division I wrestlers) represents a potential area of bias.
The NCAA Coaches’ Panel (CP), compiled by a vote of coaches representing each of the nine Division I wrestling conferences, is the other official ranking published by the NCAA. The match threshold for the CP is smaller than the RPI at only 5 Division I matches in the weight class being ranked. Therefore, the CP presents less of a barrier to ranking for wrestlers who have entered the lineup mid-season or changed weight classes. However, there is the additional eligibility requirement that a wrestler have been active in the past 30 days. Three CP rankings are released per season, one, three, and six weeks prior to the conference tournaments. As wrestlers are not ranked until the second half of the season, the CP cannot be used for match prediction prior to January. The CP ranks 33 wrestlers per weight class, and only one wrestler in each weight class per school. Thus, while the requirements for consideration in the CP suggest less bias toward those who have changed weight class, it is still available for only a small proportion of Division I wrestlers.
In the context of a tournament, seeds determine the placement of athletes in the bracket as well as their first round matchups. Seeds, like other rankings may also be used as match predictors. The seeds of the NCAA Tournament often represent the most up-to-date standings, with consideration of the most recent matches prior to the tournament. In comparison, the final NCAA RPI and CP rankings are published three weeks prior to the championships. However, only 16 wrestlers in each weight class receive seeds (48% of all tournament competitors), creating a similar scarcity problem that makes prediction of tournament matches based upon seeds alone difficult. Potential errors in the other official ranking methods trickle down into tournament seeds, which are determined by committee, with consideration of the final RPI and CP rankings, winning percentage, and head-to-head record.
With the official NCAA RPI and CP rankings only released near the end of the season, it is not surprising that many unofficial rankings for individual Division I wrestlers have become widely accepted. For example, Wrestling Insider Magazine (WIN Magazine)4, InterMat5, FloWrestling6, and Amateur Wrestling News (AWN)7 are leading sources of news and rankings for college, high school, and international wrestling. Due to the availability of archived rankings, WIN Magazine’s TPI (Tournament Power Index) was selected for evaluation. The TPI is based on a projection of the placement of wrestlers at the NCAA tournament using human judgments of current results, past performance, and schedule strength, as well as consideration of a wrestler’s consistency, to create its predictions. However, the TPI ranks only 20 wrestlers in each weight class weekly throughout the season. As with the NCAA rankings, the large proportion of wrestlers not receiving rankings may limit the effectiveness of the TPI for predicting matches between unranked opponents. In addition, the RPI, CP, and TPI rank only one wrestler in each weight class per school, making prediction based on these rankings ineffective in situations when a backup or redshirt wrestler is competing. In wrestling, athletes who are redshirting (attending classes and training, but not using NCAA eligibility by officially competing for the team) may still compete “unattached” at certain tournaments. Although such wrestlers cannot advance to the postseason without “pulling the redshirt”, the production of accurate rankings and predictions for this group is a need unmet by current systems.
Finally, one of the simplest methods for comparing competitors is to use only winning percentage (WP). This avoids both potential for bias introduced by the minimum match threshold of other systems, and the issue of ranking only one wrestler per weight class per institution. However, WP ignores the critical strength of schedule element present in the other ranking methods. Schedule strength is particularly relevant in wrestling, as schedules are non-standard. While additional scheduling rules may be imposed by conferences (e.g., number of intra-conference duals), only the minimum number of contests each Division I team must schedule per season (13) and proportion of contests vs. Division I opponents (at least 50%) are mandated by the NCAA (NCAA, 2013a). This creates an opportunity for wide variation in the number and quality of team contests. The level of opponents faced by individual athletes is also greatly impacted by participation in invitational tournaments. A simple WP runs the risk of rewarding teams and individuals who accumulate wins versus weaker opponents. Incorporating strength of schedule into rankings is vital due to the fact that wrestlers do not compete in a complete tournament throughout a season, creating a problem of incomplete pairwise comparisons (Jech, 1983).
2.3Evaluation
Following Stefani (2011), we use the following definition for predictive accuracy:
(2)
We consider a match “correctly predicted” by a ranking system if the higher-ranked opponent defeats the lower (or unranked) opponent, operating under the assumption that an unranked opponent has a lower probability of victory than a ranked opponent.
However, as noted in Section 2.2, many existing methods have restrictive thresholds for inclusion and rank only a small proportion of all competitors, reducing their accuracy under this measure. The issue of fairly evaluating accuracy for methods that cannot make a prediction for each match bears some similarity to the problem of assessing non-response in information retrieval and question-answering systems. Assigning unanswered questions according to random chance is one method discussed in the question-answering literature. Other measures from this domain include confidence weighted scoring (CWS), where systems self-assign a weight to each question according to their confidence in the answer, as well as the c@1 measure proposed by Penas and Rodrigo (2011), which assigns a probability to each unanswered question following the accuracy rate achieved on previously answered questions.
The motivation for such alternative methods of assessing accuracy comes from domains where different types of error carry their own cost. For ranking and prediction of collegiate wrestling, the cost of error and non-response may depend on one’s perspective and intended application. Reducing the scope of evaluation to only those matches where one or both wrestlers are ranked is a useful way to assess the performance of each method over the matches for which it has the most confidence, and a system that is highly accurate under this measure may be useful for sports betting, where the cost of non-response is less than the cost of an incorrect prediction. It should be noted that this form of evaluation runs the risk of rewarding methods that rank very few wrestlers. The most extreme case of this is ranking only one wrestler, but one that always wins. Assigning “unpredictable” matches according to chance may be viewed as a compromise, as it gives each method credit for the matches that it has made informed predictions about, while not overly rewarding methods that rank only a small proportion of total competitors. However, we view Equation (2) as the most appropriate measure if the ability to apply a method to every match is a high priority. Achieving high accuracy under this measure may be particularly crucial in forecasting important individual and team events, such as the post-season. Moreover, the consequence of omission from an official ranking may be more serious than inaccurate match prediction, as the RPI and CP are the primary determinants for both automatic qualifying allotments and at-large bids to the NCAA Championships. For comparisons between existing rankings and our new methods, we evaluate accuracy over all matches (counting “unknowns” as incorrect predictions), as producing a system that is able to make a better-than-random prediction for every match is a goal of this project. This is a need that is not satisfactorily met by any of the current systems, as most rank a small number of wrestlers in each weight class, and those that produce a ranking for all competitors (i.e. WP) do not include strength of schedulecalculations.
We evaluate five existing metrics and rankings for Division I college wrestling: winning percentage (WP), the two official NCAA rankings (RPI and CP), NCAA Tournament seeds, and the TPI published by WIN Magazine. As different rankings are updated at varying intervals, and each has its own criterion for inclusion, it is difficult to define a common scope for assessment that does not introduce bias. Thus, we evaluate both existing and new methods based upon their performance over the matches of the 2014 NCAA Division I tournament. For each method, we use the last ranking compiled prior to the tournament. As victories by forfeit, default, and disqualification are not considered in the training of our new ranking methods, we eliminate them from the evaluations of predictive accuracy. For the NCAA tournament dataset, this results in the removal of 11 matches, leaving 629. Table 2 summarizes the number of matches of each victory type in the NCAA Tournament.
Table 2
Number of matches by win type (2014 NCAA Championships)
| Victory type | Number of matches (%) |
| Decision | 390 (61%) |
| Major decision | 88 (14%) |
| Fall | 77 (12%) |
| Technical fall | 16 (3%) |
| Overtime | 58 (9%) |
| Forfeit, Default | 11 (2%) |
| 640 (100%) |
2.4PageRank
PageRank is an appealing method for ranking individual wrestlers because of its flexibility, ease of computation, and unique consideration of strength of schedule. PageRank divides importance or power in a network proportionally among the nodes according to number of links. In the context of wrestling, an individual accumulates power in the network by having few losses and many wins over wrestlers who also have few losses.
As mentioned in Section 2.1, we organize our proposed rankings of individual wrestlers by weight class. Therefore, from the full dataset of 16,707 matches and 2236 wrestlers, we create ten weight class networks with nodes representing wrestlers and links representing matches between wrestlers. Wrestlers who changed weights during the season receive a ranking in each class where they contested matches. Links are directed from loser to winner.
To calculate the PageRank (PR) of a wrestler Wi:
(3)
M (Wi) = set of wrestlers defeated by Wi
PR (Wj) = PageRank of wrestler Wj
L (Wj) = number of losses by wrestler Wj
d = damping factor
In Brin and Page’s (1998) original development of the PageRank algorithm for ranking hyperlinked web pages, the damping factor models the probability of random surfing, and the complement (1 - d) corresponds to the probability that a web user terminates the browsing process and “jumps” pages. Important for ranking wrestlers, the damping factor plays a role in combatting the sink effect when a wrestler encounters an opponent with no losses. Undefeated athletes receive an artificial outgoing link with a very small weight calculated as a function of the damping factor, ensuring a non-zero denominator to Equation (3). We execute the network analysis, visualization, and PR calculations using Gephi.
In addition to unweighted PageRank (UW), variations are calculated with links weighted by the margin of victory of the match. Weighting links by point differential is intended to differentiate the most dominant wrestlers. We explore two strategies for weighting links in the wrestling competition network(s).
Simple point differential (SPD): We calculate link weight as the difference between the points awarded to the winner and loser. If no points are allotted to either wrestler in the record, as is the case with falls, certain overtime victories, and records with missing data, then point differentials are awarded by victory type according to the following system: 1 point for regular decisions and overtime victories, 8 points for major decisions, 15 points for technical falls, and 18 points for falls. These figures follow the minimum point differential required to award each victory type, according to NCAA rules (NCAA, 2013a). To simplify multiple, parallel directed links between nodes, i.e., multiple victories by one wrestler over another, we consider three approaches for condensing multiple links in the same direction between a pair of nodes into a single weighted, directed link. The first is cumulative point differential of all parallel directed links between a pair of wrestlers, the second, the average of the point differentials, and the third, point differential from only the most recent match. We jointly test these three methods for condensing multiple links with the effect of different damping factors on the 63 149-pound matches of the NCAA tournament. As Table 3 shows, predictive accuracy is relatively stable regardless of the link-condensing method and damping factor. We select a damping factor of d = 0.85 to be applied in all subsequent PageRank modeling. To condense multiple, parallel links between a pair of wrestlers, we use the arithmetic average of the point differentials. For example, if Wrestler A has beaten Wrestler B three times, by 7, 4, and 4 points, then the directed link between them would have a weight of 5. If Wrestler B has defeated Wrestler A in one match by 2 points, the link in the opposite direction has a weight of 2.
Table 3
Predictive accuracy of multi-link weighting methods (149-pound weight class)
| Link weight | d = 0.65 | d = 0.75 | d = 0.85 | d = 0.95 |
| UW | 0.65 | 0.67 | 0.68 | 0.7 |
| SPD_cumulative | 0.62 | 0.62 | 0.62 | 0.62 |
| SPD_mean | 0.65 | 0.67 | 0.65 | 0.59 |
| SPD_mostRecent | 0.62 | 0.67 | 0.65 | 0.57 |
| DPD_cumulative | 0.6 | 0.62 | 0.67 | 0.67 |
| DPD_mean | 0.65 | 0.67 | 0.68 | 0.68 |
| DPD_mostRecent | 0.65 | 0.67 | 0.67 | 0.67 |
Discounted point differential (DPD): We incorporate time-awareness into link weighting to differentiate wins that occur early in the season from more recent results, with the expectation that recent data are more predictive of current match outcomes. We adopt a discounting method from the work of Park and Sharpe-Bette (1990) that mimics how temporal sequences of cash flows are discounted to yield present value. For the wrestling network, the point differential from a match is discounted at a rate increasing in the amount of time since the match. Equation (4) displays the formula for computing the discounted pointed differential of a match.
(4)
Dm = point differential of match m
t = number of days since match m
i = discount rate
Larger i values give more preference toward recent match results. We test the effect of different discount rates on predictive accuracy. While the difference is not statistically significant, i = 0.01 yielded the only increase in accuracy over the benchmark (Table 4). The success of smaller i values may be due to the span of the data and discounting unit selected (139 days). As we use only one year of competition data, we select days as the discounting unit. With more seasons of data, it may prove advantageous to use weeks or months as the discounting unit. After calculating the DPD link weights, we condense multiple links in the same direction between a pair of nodes in the same manner as SDP link-weighting. Therefore, a condensed link now represents a weighted average of the point differentials, with more weight on recent match results. Extending the previous example of the directed link from B to A— the matches resulting in point differentials of 7, 4, and 4 occurred in November, December, and January, respectively. Using the DPD method, the January match would contribute more to the final weight of the link than the December match, despite having the same margin of victory.
Table 4
Predictive accuracy of DPD discount factor (i)
| i | Accuracy |
| 0.005 | 0.67 |
| 0.01 | 0.68 |
| 0.05 | 0.64 |
| 0.1 | 0.64 |
| 0.2 | 0.65 |
| 0.3 | 0.62 |
| 0.4 | 0.62 |
2.5Elo
Elo is also a computationally simple, yet highly flexible method. Developed for rating competitors in chess (Elo, 1978), it has primarily been applied to “mind sports”, such as Go, Scrabble, Backgammon, and video games, but has also been implemented in more traditional sports, most notably as the official rating system of international women’s soccer (FIFA, 2012). Interestingly, there has been little, if any, use of Elo ratings in combat sports, and this project represents a novel addition to this literature. Elo approaches the issue of strength of schedule differently than PageRank, treating prior ratings as a proxy for player strength, with the difference in ratings between competitors at the time of a match is used to compute an expected probability of victory. Ratings after the match are computed based upon the disparity between this expected result and the actual result, with more rating points earned for an upset than a predictable win. Due to this non-uniform ratings update, the Elo system has been dubbed an “adjustive” rating.
The formula for calculating the Elo rating of a wrestler has three main components, displayed in Equations (5–7). The first is the scaled difference in ratings between competitors prior to the match (x):
(5)
Rbef = wrestler rating before match
Obef = opponent rating before match
H = “home advantage” correction
c = scaling factor
Under the assumption that the pre-match rating is an indicator of competitor’s relative strengths, the difference in ratings between wrestlers is used to compute an expected result (Sexp):
(6)
The expected result (Sexp) , represents the proportion of points predicted to be won by each opponent and may also be interpreted as the probability of victory plus half the probability of drawing. A wrestler’s rating after the match (Raft) is based upon the difference in the expected result and the actualresult:
(7)
K = match weight
M = match importance factor
Sact = actual result
The K-factor represents that maximum possible ratings adjustment, with larger values making the rating more sensitive to recent match outcomes. The match importance factor allows the marginal effect of a match on the calculated Elo rating to depend on the type of competition. For instance, the FIFA Women’s World Rankings (FIFA, 2012) for international soccer assigns a larger value of M to a World Cup match than to “friendly” (exhibition) match.
The Elo system is an attractive method for ranking college wrestlers as prediction is “built-in” to the method, and it offers flexibility in selecting ranking periods (ratings may be updated every match, tournament, week, etc.). Applications of Elo in this project re-calculate rankings after each match. Like the PageRank method described in Section 2.4, an Elo rating is calculated for each weight class, with wrestlers who changed weights receiving a ranking for each class in which they have competed during the season. The Elo system also offers a great degree of customization in parameters, and the first concern in implementing the Elo system for wrestling is parameterization. We test several values for each parameter upon the 149-pound weight class, holding others constant.
Initial rating and scaling factor (c): We select a value of 1000 for the default rating received by all individuals prior to competition. In his original chess rating system, Elo (1978) proposes an initial rating of 1400 for all competitors, but as this project uses only a single season of wrestling data, with 1–41 matches per wrestler, we select a smaller initial rating. For scaling factor, we select a value of 300. Neither initial rating nor scaling factor impacts predictiveaccuracy.
K-factor: In our testing, the match weight has the largest impact on predictive accuracy. While the original K-factor proposed by Elo is 10, our initial testing on the matches of the 149-pound weight class indicates that a much higher K-factor may be appropriate for Division I wrestling. As shown in Table 5, K = 225 results in the highest predictive accuracy, 69%. In addition to the K-factor being higher than is traditional for chess, the proportion of K-factor to c is over four times that used in other applications. While the accuracy of large match weight values may be due to possessing only one season of data, it may also indicate that the number and quality of individual wins and losses may have a large impact on match prediction in wrestling.
Table 5
Predictive accuracy of Elo rating K-factor (c = 300, initial value = 1000)
| K | Accuracy |
| 50 | 0.67 |
| 75 | 0.67 |
| 100 | 0.65 |
| 125 | 0.67 |
| 150 | 0.67 |
| 175 | 0.68 |
| 200 | 0.68 |
| 225 | 0.69 |
| 250 | 0.69 |
Other parameters: Our preliminary testing with the 149-pound weight class reveals that the match importance factor, M, and the “home advantage” correction, H, do not affect predictive accuracy. Therefore, we set H = 0 and M = 1 to effectively ignore these effects. The absence of a “home advantage” in wrestling is an expected finding, as a high proportion of Division I matches (67%) occur at neutral sites, including invitational tournaments and championships.
2.6Ensemble methods
In the domain of machine learning, ensemble methods combine multiple algorithms to improve predictive accuracy. Applied to the problem of ranking and predicting collegiate wrestling, we assemble ensembles of existing and new ranking methods. Common approaches for ensemble methods include bagging, boosting, and stacking. In this project, we utilize a simple ranking approach, where methods are ranked based upon a specific criterion, and then applied in rank-order. For each of the ensemble methods we construct, methods are applied in order of predictive accuracy. Each subsequent method is applied to the matches for which the previous method(s) were unable to produce a prediction, i.e. matches where both wrestlers were unranked or equally ranked. We explore the effectiveness of two ensemble approaches, a combination of the existing methods discussed in Section 2.2, and the ensemble of the WIN Magazine TPI and our methods.
3Results
On the basis of predictive accuracy, we evaluate the five existing methods for ranking NCAA Division I wrestlers as well as PageRank and Elo methods.
3.1Assessment of existing rankings
We use the 629 matches of the 2014 NCAA tournament to evaluate the predictive accuracy of the five existing methods: the ratings percentage index (RPI), the NCAA Coaches’ Panel (CP), winning percentage (WP), tournament seed (Seed), and the Tournament Power Index (TPI). Table 6 summarizes the results.
The Correct and Incorrect columns of Table 6 indicate the number of matches for which each method correctly and incorrectly predicts the winner, given one or both competitors have received a ranking. The Unknown column in Table 6 shows the number of matches occurring between two unranked or equally-ranked competitors, where a prediction cannot be made based upon ranking. Given the fairly large numbers of “unknown” matches for some methods, we consider three ways to count matches for the purpose of measuring predictive accuracy, as discussed in Section 2.3. The All category for predictive accuracy follows Equation (2) exactly, and represents the percentage of correctly predicted matches out of all 629 matches contested (counting an unknown match as an incorrect prediction). The Predicted category reduces the scope of evaluation for predictive accuracy to only matches where at least one wrestler is ranked, i.e. removing “unknown” matches from the count. The Random category for predictive accuracy assumes a 50% chance of predicting “unknown” matches correctly.
Table 6
Predictive accuracy of existing rankings (2014 NCAA Championships)
| Count | Accuracy | |||||
| Method | Correct | Incorrect | Unknown | All | Predicted | Random |
| RPI | 419 | 191 | 19 | 0.67 | 0.69 | 0.68 |
| CP | 435 | 189 | 5 | 0.69 | 0.7 | 0.7 |
| WP | 412 | 209 | 8 | 0.66 | 0.66 | 0.66 |
| Seed | 391 | 137 | 101 | 0.62∧ | 0.74** | 0.7 |
| TPI | 424 | 145 | 60 | 0.67 | 0.75** | 0.72* |
* = statistically superior to WP, ** = statistically superior to WP and RPI, ∧= statistically inferior to benchmark and other rankings.
Using the most recent NCAA RPI prior to the championship tournament (27 February 2014), 59 of the 330 competitors at the NCAA tournament did not receive a ranking in the second and final RPI (18%), resulting to 19 matches between unranked wrestlers. As Table 6 shows, depending on the counting method, the predictive accuracy ranges from 67% to 69% and does not significantly exceed the 67% accuracy benchmark or any of the other methods. The RPI’s fair performance may be due to the fact that— although the RPI includes consideration of strength of schedule—it suffers from lack of up-to-date information. The final RPI is released three weeks prior to the NCAA Tournament and does not incorporate match results from the conference tournaments.
We evaluate the other official ranking for Division I wrestling, the Coaches’ Panel (CP), for accuracy over the matches of the NCAA tournament. The CP ranking performs slightly better than the RPI, with 69% to 70% of matches correctly predicted, depending on counting method. Interestingly, while the third and final CP ranking is only as current as the RPI (also released three weeks prior to the NCAA Championship) and ranks the same number of competitors, it correctly identifies more of the NCAA qualifiers. This result may be due to the lower match threshold or its more subjective nature. Only 36 of the 330 wrestlers competing at the 2014 NCAA Tournament were unranked by the Coaches’ Panel (11%). Consequently, only 5 tournament matches are “unknown” using CP. Among the five current methods reviewed, CP has the highest predictive accuracy over all the matches of the championship tournament although it does not significantly exceed the 67% baseline.
We evaluate the predictive accuracy of each wrestler’s winning percentage (WP) over the matches of the NCAA Tournament. At 66%, the predictive accuracy of WP is lower than RPI, CP, and the 67% benchmark. This result is notable as WP is the one of components of the RPI formula. The lower performance of WP is likely due to the fact that WP does not include consideration of strength of schedule. While WP was available for all competitors in the NCAA Tournament, 8 matches occurred between individuals with equal WP (marked as “unknown” Table 6).
The seeding of the NCAA Division I wrestling championships is also assessed as a predictor of match outcomes. Because seeds are assigned to only the top 16 wrestlers in each weight, Seed has the highest proportion of “unknown” matches of all existing methods (16%). While Seed has 74% accuracy on the relatively small field of 528 matches where one or both opponents are seeded, applying Seed to all matches results in only 62% accuracy, a level significantly lower than the 67% benchmark and the other methods (at α = 0.05 significance level). It should be noted that the accuracy of Seed is impacted by the tournament bracket structure. The accuracy of tournament seeds is boosted by initial bracket assignments, which pair seeded wrestlers randomly with unseeded competitors. Indeed, the first round of the NCAA Championships resulted in only 23 upsets (14%). The impact of inaccuracies in tournament seeds grows over the course of the competition as unseeded competitors move on in the bracket or consolation rounds, and 6 unseeded wrestlers finished as “All Americans” in 2014. While seeds reflect up-to-date information on tournament participants and incorporate expert, human judgments, they alone may not be sufficient predictors of NCAA Tournament success, owing to the fact that 52% of competitors do not receive a seed ranking.
We evaluate the latest WIN Magazine Tournament Power Index (TPI) rankings prior to the tournament (published 10 March 2014). Of the 629 NCAA tournament matches not resulting in a forfeit, disqualification, or default, 424 (67%) are correctly predicted (Table 6). TPI only ranks 20 wrestlers in each weight class, with 131 of the 330 NCAA competitors (40%) unranked in the final TPI, resulting in 60 “unknown” matches to which it cannot make a prediction. However, for the 569 matches with at least one TPI-ranked wrestler, it achieves 75% accuracy. When assuming 50% accuracy on unknown matches, TPI is still the most accurate of the existing methods, and significantly exceeds the benchmark and WP. In Table 6 we footnote the predictive accuracies which distinguish themselves as statistically significant (α = 0.05) relative to their peers within each category.
Finally, we also create an ensemble ranking by combining the five existing rankings in an ordered fashion. We order the ranking methods by their accuracy in the Predicted category: TPI, Seed, CP, RPI, WP. We apply the first ranking method to all matches for which one or both wrestlers have a ranking, count the number of correct and incorrect matches, and then remove these matches from future consideration. Then we move on to the next ranking method and repeat this process on the remaining matches (those that were “unknown” for the previous methods). This ensemble ranking is able to produce a prediction for all 629 tournament matches and correctly predicts 458 of them (73%). Evaluated over all tournament matches, this is a significant difference from the benchmark 67% accuracy and the existing methods of RPI, WP, Seed, and TPI (at α = 0.05significance level). Admittedly, this ensemble method is very simple and suffers the limitation of using “future information”, i.e. methods are ordered according to their accuracy levels on the future event that they will predict. It is possible for another ensemble approach to be utilized (or another ordering method), to avoid this issue. Yet the success of this preliminary investigation of ensembles suggests the promise of combining several ranking systems to produce more accurate and complete rankings and predictions.
3.2PageRank
After initial parameter testing on the wrestlers and matches of the 149-pound weight class, PageRank using each link-weighting method is applied to all weight classes. The results for each weight class are displayed in Table 7. We aggregate the results over weight classes, with accuracy calculated as the sum of correctly predicted matches at all weights divided by the total number of matches (Table 7). Note we use the PageRank calculated using matches prior to the NCAA Championships and do not update the ratings during the tournament.
Table 7
Predictive accuracy of PageRank methods (2014 NCAA Championships)
| Weight | Matches | UW | SPD | DPD |
| 125 | 64 | 46 (0.72) | 45 (0.7) | 43 (0.67) |
| 133 | 64 | 47 (0.73) | 51 (0.8) | 47 (0.73) |
| 141 | 63 | 38 (0.6) | 46 (0.73) | 46 (0.73) |
| 149 | 63 | 43 (0.68) | 41 (0.65) | 43 (0.68) |
| 157 | 62 | 41 (0.66) | 42 (0.68) | 43 (0.69) |
| 165 | 64 | 48 (0.75) | 45 (0.7) | 44 (0.69) |
| 174 | 63 | 44 (0.7) | 45 (0.71) | 42 (0.67) |
| 184 | 64 | 40 (0.63) | 42 (0.65) | 46 (0.72) |
| 197 | 58 | 40 (0.69) | 39 (0.67) | 40 (0.69) |
| 285 | 64 | 48 (0.75) | 44 (0.69) | 47 (0.73) |
| 629 | 435 (0.69) | 440 (0.7) | 441 (0.7) |
When applied to all weight classes, only discounted point differential (DPD) represents a statistically significant improvement over the benchmark of 67% accuracy (p = 0.04851). In addition, as Table 7 shows, none of the ten weight classes have an accuracy rate lower than 67% when using DPD link-weighting, demonstrating a high level of consistency. Indeed, DPD has the lowest variance over the 10 weight classes compared to the other PageRank methods (σ2 = 0.0007). Nevertheless, there are no significant differences in the accuracy rates of DPD, SPD, and UW, with DPD and SPD performing almost identically.
Using the All accuracy metric for evaluating the existing ranking methods for NCAA Division I wrestling (WP, RPI, CP, TPI, and Seed), all proposed PageRank methods represent statistically significant improvement over tournament seeds. Both methods using margin of victory (SPD and DPD) are significantly more predictive than WP. Interestingly, none of the PageRank methods created in this project are significantly more predictive than the official rankings compiled by the NCAA (RPI and CP) or the WIN Magazine TPI.
Another approach to evaluating rankings, other than predictive accuracy, is the comparison of ordinal placements across different methods (Procopio et al., 2012). For ranking and prediction of Division I wrestling, the final tournament placement is a particularly salient comparison, with the NCAA recognizing the top-8 finishers in each weight class at the NCAA Tournament as “All-Americans.” Our PageRank methods succeed in identifying more of the 80 All-Americans than the existing ranking methods, with DPD PageRank correctly identifying 57 (71%). RPI places only 49 All-Americans in the top 8, CP 53, WP 51, and Seed and TPI both correctly identify 54. Indeed, for the 174-pound weight class, DPD identifies 7 of the placing wrestlers, with 3 in the exact same ordinal position. Figure 1 displays the network visualization for the 174-pound weight class and allows us to see that the issue of isolated ranking pools is likely not serious for collegiate wrestling. Although the graph is disconnected (there are a few isolated components), the majority of wrestlers are weakly connected, allowing PageRank to pass through the network. This visualization does demonstrate the issue of ranking “sinks” in competition networks, as the two top-ranked wrestlers had losses only to each other. While corrections such as the one discussed in Section 2.4 may be sufficient to handle some of the mathematical issues created by undefeated wrestlers, the application and evaluation of rankings over more seasons of data may also be useful.
Fig.1
Visualization of 174-pound wrestler network. Nodes sized and colored by DPD PageRank, light = low, dark = high.

3.3Elo ratings
We calculate Elo ratings for all weight classes using the parameters determined from testing on the 149-pound weight class (c = 300, k = 225, initial rating = 1000). We evaluate the Elo ratings on the matches of the Division I Championship tournament (using the last rating prior to the tournament as the predictor). While draws are not awarded in Division I wrestling, matches that are predicted as draws by the Elo rating (expected result = 0.5) would be counted as “Unknown.”
Aggregated over all weight classes, the Elo rating method correctly predicts 449 out of 629 matches (Table 8). Elo does not predict draws for any of the tournament matches, as no wrestlers competing have equal ratings by that point in the season. Using the All accuracy category, Elo displays a significant increase in accuracy over Seed, WP, and RPI, and the 67% benchmark (p = 0.009697). Although the Elo ratings display slightly higher accuracy than the three PageRank methods, the difference is not statistically significant. The Elo rating also identifies more of the NCAA All-Americans than the existing methods, 56 out of 80 (70%). However, as seen in Table 8, the accuracy of the Elo rating method is less consistent across weight classes than DPD PageRank (σ2 = 0.008).
Table 8
Predictive accuracy of Elo ratings (NCAA Division I Championships)
| Weight | Matches | Elo |
| 125 | 64 | 57 (0.89) |
| 133 | 64 | 45 (0.7) |
| 141 | 63 | 47 (0.75) |
| 149 | 63 | 36 (0.57) |
| 157 | 62 | 45 (0.73) |
| 165 | 64 | 42 (0.66) |
| 174 | 63 | 49 (0.78) |
| 184 | 64 | 42 (0.66) |
| 197 | 58 | 44 (0.76) |
| 285 | 64 | 42 (0.66) |
| 629 | 449 (0.71) |
3.4Ensemble methods
We perform preliminary investigation into the accuracy of an ensemble method combining our methods with existing rankings. Although the TPI of WIN Magazine ranks only 20 wrestlers per weight class, it had the highest accuracy for matches where one or both wrestlers had a TPI ranking (the Predicted category discussed in Section 3.1). For each match of the NCAA tournament, we first apply the TPI to matches where one or both wrestlers have a ranking and remove those matches from further consideration. If neither wrestler is ranked, we use one of the new methods (DPD, Elo). Achieving 73% accuracy, the TPI+Elo method performs slightly better than the TPI+DPD method (Table 9). This represents a significant improvement over the 67% benchmark and all of the existing methods, including the use of TPI alone, when evaluated over all 629 tournament matches (p = 0.02839). The TPI+Elo method also outperforms using the TPI and “guessing” on unknown matches (Random accuracy category) and the ensemble created from the five existing ranking systems (TPI, Seed, CP, RPI, WP), although the improvement is not statistically significant. As with the application of DPD and Elo alone, TPI+DPD is more consistent across all weight classes (σ2 = 0.001), while Elo has a slightly higher variance in accuracy rates (σ2 = 0.002). While these approaches have the limitation of using “future information”— TPI was selected to combine with new methods based upon its accuracy level over the matches of the NCAA Tournament— this issue may be easily avoided in future implementations. The results of these ensemble methods show promise for the construction of more predictive rankings because of their integration of methods that are diverse— our methods use computational techniques while the TPI uses a combination of subjective evaluation and computational techniques— as well as accurate on their own. In addition, these results suggest that expert human predictions, which are often expensive and limited in scale, may be effective leveraged in combination with a more widely applicable method.
Table 9
Predictive accuracy of ensemble ratings (NCAA Division I Championships)
| Weight | TPI + DPD | TPI + Elo |
| 125 | 44 (0.69) | 46 (0.72) |
| 133 | 51 (0.8) | 49 (0.77) |
| 141 | 47 (0.75) | 47 (0.75) |
| 149 | 44 (0.7) | 41 (0.65) |
| 157 | 44 (0.69) | 45 (0.73) |
| 165 | 45 (0.7) | 50 (0.78) |
| 174 | 46 (0.73) | 49 (0.78) |
| 184 | 46 (0.72) | 47 (0.73) |
| 197 | 42 (0.72) | 40 (0.69) |
| 285 | 46 (0.72) | 47 (0.73) |
| 455 (0.72) | 461 (0.73) |
4Follow-up analysis
While both PageRank and Elo show improvements compared to several current ranking methods in terms of predictive accuracy for the NCAA Division I Championships, several questions remain as to their effectiveness in dealing with the unique challenges of ranking and predicting collegiate wrestling, namely their effectiveness in situations of data scarcity created by weight and roster changes and their performance over the entire 2013-2014 season. We also perform a preliminary investigation regarding the accuracy of our methods in a “composite” ranking as opposed to the weight class-specific rankings created by existing systems and those proposed above.
As we have discussed above, the criterion for inclusion for each ranking method may disadvantage certain individuals. Several current methods for ranking individual wrestlers have specific requirements for consideration. For instance, the NCAA Coaches’ Panel requires 5 Division I matches at the weight being ranked and that a wrestler must have been active in the 30-day period prior to ranking. While computational methods like the RPI often require a certain number of matches to ensure the stability of their rankings, such criteria disproportionately affect wrestlers who have experienced weight changes, roster changes, or been injured, and may lead to rankings that are not good proxies for ability level, and subsequently to inaccurate predictions. As proposed by Stefani (2011), a match is correctly predicted if the higher-ranked opponent defeats the lower or unranked opponent. When an athlete is unranked not owing to low ability level, but due to an arbitrary threshold, this assumption for using rankings as match predictors is violated. It is difficult to track roster changes and injuries from available data, but wrestlers who have experienced injury or weight changes are likely to have fewer matches. As a follow-up investigation of our methods’ effectiveness at handling the unique challenges faced by the context of collegiate wrestling, we may compare the predictive accuracy of existing and proposed rankings for wrestlers with only a small number of Division I matches. We identify wrestlers with fewer than 17 Division I matches prior to the NCAA Tournament (17 was chosen as it is the threshold for inclusion in the NCAA RPI ranking). At the outset of the Championships, 15 out of the 330 competitors (5%) had fewer than 17 matches.
Table 10 compares the accuracy of existing methods and two of our new methods (DPD, Elo) on the 64 matches wrestled by these individuals. It is unsurprising that RPI has the lowest predictive accuracy for matches involving these 15 wrestlers, as they do not meet the requirements for inclusion in the ranking. Indeed, for matches that include wrestlers with fewer than 17 matches, RPI performs significantly below baseline (p = 6.291×10–8) and all of the other methods. This performance, significantly worse than the estimated 50% accuracy of random guessing (p = 0.01679), supports the existence of bias affecting predictive accuracy. When limiting the scope of evaluation to matches where at least one competitor received an RPI ranking (as with the Predicted category discussed in Section 3.1), the RPI only achieves 47% accuracy. This suggests that in many cases, the wrestlers who received an RPI ranking were not significantly better than those who did not. Beyond match predictions, RPI rankings have important impacts on tournament selection and seeding. Noted in Section 1, the RPI is used to calculate the number of automatic qualifiers allotted to each conference as well as being considered in awarding the remaining at-large bids. Thus, the exclusion of individuals with few matches from the RPI may decrease the likelihood of advancement to the post-season. WP and TPI have the highest accuracy for these 64 matches, but there are no statistically significant differences between any of the other rankings or the benchmark (at α = 0.05 level). The WP performs well, likely due to being able to produce a prediction for all wrestlers (0 matches “unknown”), and its relatively high accuracy suggests that it has less bias than other methods toward individuals with few matches. The success of TPI may be due to its combination of subjective human judgments with data-driven methods, but the utility of TPI is limited by its scope (4 of the 15 wrestlers did not receive a TPI ranking, leading 3 matches with an “Unknown” prediction). Although a very small test, these results indicates that most of the existing and proposed ranking methods may have difficulty predicting the performance of wrestlers with little prior match information. Despite the low performance of Elo and DPD, this result is interesting, as our methods use only data from the 2013-2014 season, while subjective rankings like the TPI may carry over information from previous seasons, especially helpful for wrestlers with few current matches due to recovery from injury or weight changes.
Table 10
Predictive accuracy for wrestlers with <17 matches (2014 NCAA Championships)
| Method | Correct | Incorrect | Unknown | Accuracy |
| RPI | 23 | 26 | 15 | 0.36 |
| CP | 40 | 21 | 3 | 0.63 |
| WP | 47 | 17 | 0 | 0.73 |
| Seed | 41 | 14 | 9 | 0.64 |
| TPI | 46 | 15 | 3 | 0.72 |
| DPD | 40 | 24 | 0 | 0.63 |
| Elo | 43 | 21 | 0 | 0.67 |
Further exploring the performance of our new methods under different conditions, we also investigate the accuracy of PageRank and Elo over the entire 2013-2014 season. Using the data from the 149-pound weight class, we compute a weekly PageRank by including all matches and wrestlers from week 1 through the current week, and then assess the accuracy of these PageRank values for predicting the matches occurring in the next week. For Elo, we update each wrestler’s rating after every match and evaluate predictive accuracy by using the final rating of the current week to predict the matches of the next week.
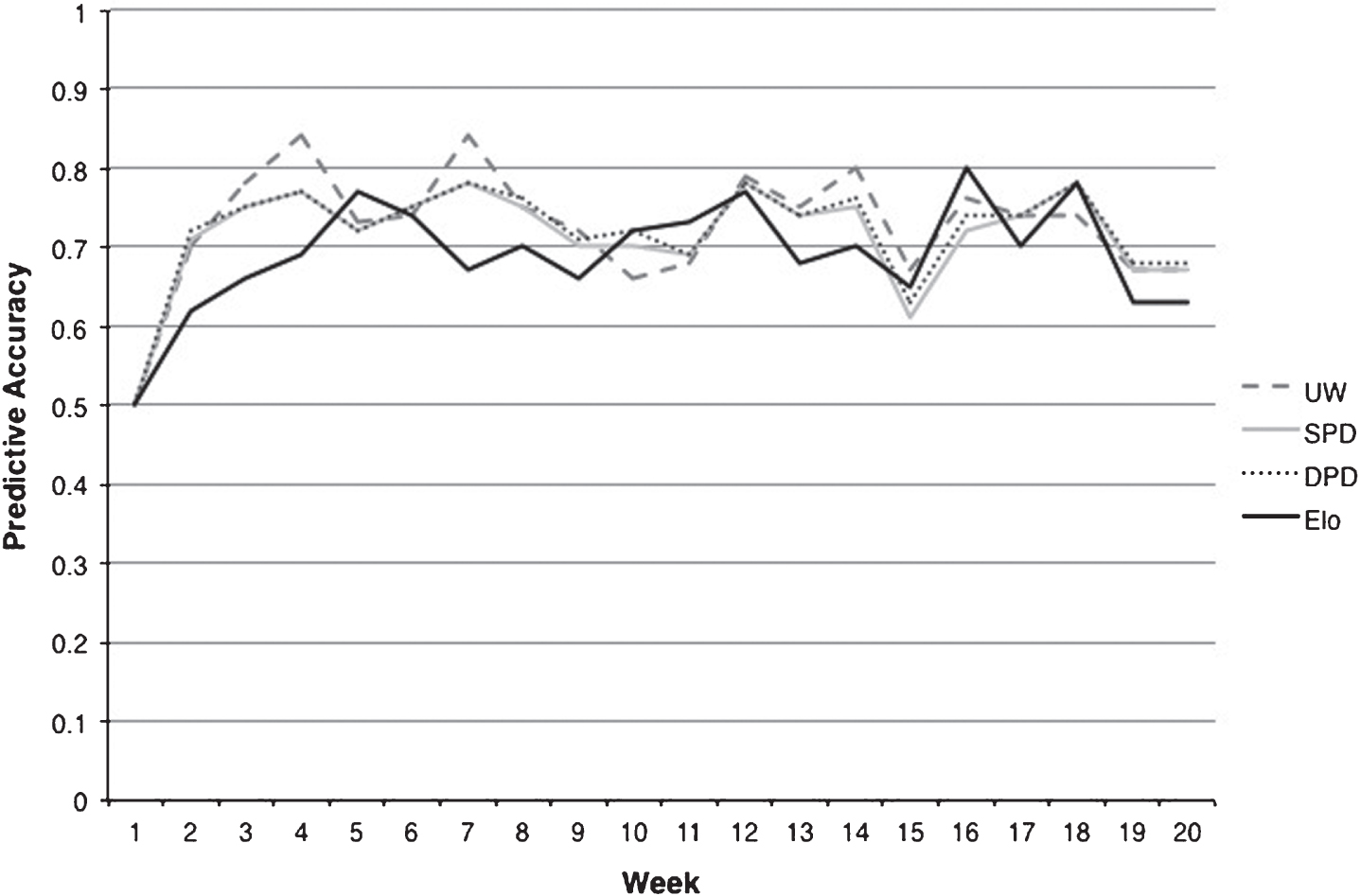
We discover that all three PageRank methods (UW, SPD, DPD) are able to achieve a high level of accuracy after only two weeks (Fig. 2). For Elo, accuracy increases at a slower rate, but exhibits a consistently high level (∼70%) after the fourth week of the season. In addition, this chart shows that the PageRank methods using point differentials (DPD and SPD) display very similar patterns, with DPD slightly outperforming SPD in the final weeks of the season. The unweighted PageRank (UW) has the highest accuracy in the early weeks, but parallels the other PageRank methods after the midpoint of the season. The lower accuracy of weighted PR methods may be due to the scheduling differences between Division I wrestling teams influencing the magnitude of early-season victories. While this analysis is limited to only the wrestlers and matches of the 149-pound weight class, it indicates that the methods proposed in this paper can be implemented on a weekly update schedule to predict the next week of competition with a high rate of accuracy. Even through DPD and Elo were not the top methods for predicting the tournament performance of wrestlers with fewer than 17 prior matches, the early-season success demonstrated in this test suggests that they are able to create accurate predictions with very little match information for each wrestler. Although the size of our dataset is limited, the ability of our methods to provide accurate rankings and predictions based only upon match information from the current season represents a strength. It is especially notable as other systems, like the RPI and CP, are not available until much later in the season.
Fig.2
Predictive accuracy of weekly rankings (2013-2014season).
The frequency of weight class changes is another unique data problem facing existing ranking methods for college wrestling. As stated in Section 2, 471 of the 2246 wrestlers in the dataset competed in more than one weight class during the 2013-2014 season. Weight class changes often disadvantage wrestlers under existing rankings methods, as all current and proposed approaches rank individuals by weight class, and, except for the TPI (which incorporates human evaluations) they do not have a mechanism for “carrying” a wrestler’s rank from one weight class to another. Additionally, methods using match thresholds for inclusion may possess a systematic bias against individuals who change weight classes during the regular season. At the NCAA Championships, 22 of the 330 competing wrestlers (7%) had changed weight classes at least once during the 2013-2014 season. To investigate whether our methods have improved success in ranking and predicting the performance of individuals who change weight class, we compare the predictive accuracy of the current rankings (WP, RPI, CP, TPI, and Seed) and two of our new methods (DPD, Elo) for the 78 matches of the NCAA Championships that involved these 22 wrestlers.
For the wrestlers competing at the NCAA Tournament who changed weight classes during the 2013-2014 season, Table 11 shows that WP and DPD achieve the highest accuracy when evaluated over all 78 matches (as with the All category discussed in Section 3.1). None of these methods display a significant improvement on the 67% baseline for the matches evaluated (at α = 0.05 level). Using tournament seeds alone for prediction continues to be the least accurate method, and is significantly less than the benchmark (p = 0.02335). The poor performance of Seed may be explained by its limited scope— 11 of the 22 wrestlers who experienced a weight change did not receive a tournament seed, resulting in 12 “unknown” matches whose outcome could not be predicted— and dependence on RPI, a method whose threshold for inclusion (at least 17 Division I matches at the ranking weight) is likely to exclude wrestlers who change weight class. Both WP and DPD display a significant improvement in accuracy over seeds (p = 0.04879), and both produce a rating for all 22 weight-changing wrestlers. While only a small test, this evaluation indicates that DPD is at least as accurate as current methods and the baseline for predicting the tournament performance of wrestlers who have changed weight classes. However, as it performs identically to a simpler existing method (WP), more investigation is needed into the effective handling of weight class changes for new methods.
Table 11
Predictive accuracy for matches involving weight class changes (2014 NCAA Championships)
| Method | Correct | Incorrect | Unknown | Accuracy |
| RPI | 49 | 27 | 2 | 0.63 |
| CP | 53 | 25 | 0 | 0.68 |
| WP | 54 | 24 | 0 | 0.69 |
| Seed | 44 | 22 | 12 | 0.56 |
| TPI | 52 | 18 | 8 | 0.67 |
| DPD | 54 | 24 | 0 | 0.69 |
| Elo | 51 | 27 | 0 | 0.65 |
As a final follow-up analysis, we extend upon the analysis of the impact of weight class-specific rankings and weight changes on predictive accuracy and investigate whether rank may effectively be “carried” from one weight class to another. Previously, only systems incorporating subjective human judgments (e.g. TPI) have included this feature. Forecasting performance in one weight class to another may introduce error, as the physiological impacts of weight changes are experienced differently for individual wrestlers (and may also depend on the direction of the weight change). In addition, wrestlers will face an entirely new set of competitors in a different weight class, amplifying the problem of incomplete pairwise comparisons. However, as a preliminary exploration of whether rank can effectively be “carried” to a different weight class, we organize all wrestlers and matches into one network— as opposed to the previous method of dividing competitors into 10 weight class-specific networks, described in Section 2.4. We apply the PageRank models built earlier (UW, SPD, DPD) to this composite network, resulting in a single ranking for each wrestler. Similarly, a single Elo rating is calculated for each athlete based on all matches contested.
Displayed in Table 12 is the accuracy of the composite ranking over the matches of the NCAA Division I Tournament. All PageRank methods based upon the composite network demonstrate a significant increase in accuracy over the 67% benchmark (at α = 0.05 significance level). In addition, UW and SPD significantly outperform all existing methods except CP, while DPD significantly outperforms all existing methods except TPI and CP. This is an improvement over the weight class-specific PageRank, where none of the proposed approaches exceeded the NCAA RPI or TPI. Comparing each composite PR method to its weight class-specific counterpart, each shows a small gain in accuracy. Interestingly, the composite Elo ranking shows a 3% decrease in accuracy from the weight class-specific version, with correctly predicted 449 of 629 matches. Since our Elo method was trained on the matches of a single weight class, it is possible that re-parameterization is necessary to utilize it when including “out of class” match data. However, the network structure used by PageRank may also provide an explanation, with the links between weight classes serving to further direct the flow of rank in the network toward the most dominant competitors. These results show promise for the use of network ranking methods to “carry” rank from one weight to another. More investigation into appropriate link-weighting schemes is warranted, i.e. whether an “in class” link should carry a different weight than an “out of class” link, or whether upward and downward links between weight classes should be weighted differently.
Table 12
Predictive accuracy for composite network ranking (2014 NCAA Championships)
| Method | Correct |
| UW | 448 (0.71) |
| SPD | 449 (0.71) |
| DPD | 442 (0.7) |
| Elo | 428 (0.68) |
5Discussion
College wrestling rankings have several important impacts upon the sport. Rankings serve as comparative indicators of individual and team success, and may be used as predictors of future match outcomes. Through an evaluation of existing ranking systems, the application of new approaches to ranking wrestling, as well as follow-up analyses investigating the predictive accuracy of these methods in relation to the specific issues presented by collegiate wrestling, several overall findings emerge.
First, existing ranking systems experience difficulty with some of the unique characteristics of collegiate wrestling, and PageRank and Elo, as implemented here, improve on many of these weaknesses. For example, the small rankings field of all existing methods (except winning percentage) restricts their applicability. Both the PageRank and Elo methods can rank the entire field of wrestlers competing in a weight class, enabling a better than random prediction for every match. Related to the issue of the small ratings field, most current methods rank only one individual per weight per school, ignoring backup and redshirt wrestlers. Our methods rank all Division I wrestlers in the effort to give more accurate predictions for matches involving such competitors. This total ranking also allows a wrestler to be ranked at more than one weight, which helps deal with the prediction problem created by the frequent weight changes in collegiate wrestling. Current systems do not possess this feature, and some have thresholds for inclusion that disadvantage these individuals and negatively impact accuracy. PageRank and Elo also include consideration of strength of schedule, which is not a part of calculating WP. This is especially important in wrestling, as schedules are non-standard. Finally, PageRank and Elo have a great deal of flexibility in their parameterization, allowing for wrestling-specific tuning. While this analysis focuses mainly on end-of-season rankings with the goal of predicting outcomes at the championship tournament, PageRank and Elo may be updated after each match, week, or other interval. Although PageRank and Elo showed high early-season performance, they did not improve upon the accuracy of existing methods in regards to wrestlers who had changed weight classes or wrestlers with few matches. Future work could include adjusting our new methods to deal with problems of data scarcity. To this end, gathering more data on past seasons may be especially useful. Although our rankings were able to achieve fairly high accuracy using only one season of data, investigating the utility of past season matches and whether rank can be “carried” over seasons cannot be achieved without more seasons of match data. In addition, more data is necessary to test the robustness of our proposed methods.
Second, out of the existing ranking methods for college wrestling, those incorporating subjective human evaluations (CP, TPI) tend to outperform those depending simply upon computational techniques (WP, RPI). However, it is likely that not all human judgments are created equal. While Govan and Meyer (2009) find that their PageRank method exceeds human predictions, it is important to note that the authors’ sample was drawn from graduate students, professors, family, and friends, and not experts on professional football, with many participants basing predictions simply upon intuition. The accuracy of human prediction has been associated with several factors, recent research has highlighted the impact of domain knowledge (Mellers et al., 2015). Thus, the “lay” human predictions compiled by Govan and Meyer (2009) are likely to achieve a different level of accuracy than “expert” human predictions, such as those generated by oddsmakers (Hvattum & Arntzen, 2010). These findings may explain the success of the TPI system, which combines the subjective judgments of rankings experts with computational techniques. While it may be possible to incorporate human evaluation into the new methods proposed (e.g. parameterization), obtaining human judgments is costly and may necessitate reducing the scope of the ranking— the TPI ranks only 25 wrestlers per week in each weight class.
However, ensemble methods show promise for the construction of more accurate rankings and predictions. Combining multiple, diverse methods (i.e. human/subjective and computational) may expand the scope and improve the accuracy of any single method. The ensemble constructed from the existing ranking systems correctly predicts 8% more matches than the best-performing single method (TPI). The TPI+DPD and TPI+Elo ensembles experience a 3% increase over DPD and Elo alone. Although our approach to constructing these ensemble methods was fairly simple, these methods present an opportunity to leverage a small number of human predictions through combination with a more broadly applicable computational method. It is especially notable that the TPI+Elo achieved the highest accuracy of all of the ensemble methods, correctly predicting 461 out of 629 matches.
While this analysis indicates that both PageRank and Elo present viable alternative to the current ranking methods in terms of predictive accuracy, the Elo method may have several advantages. Elo achieved higher accuracy across all weight classes than DPD PageRank, as well as a more consistent performance on the weekly ranking calculated for the 149-pound weight class. In addition, PageRank was not designed for match prediction, and does not have the adjustment feature of Elo, where upset wins are rewarded differently in the ratings than predictable ones. Moreover, Elo ratings enable a more complete view of a wrestler’s record by taking into consideration an individual’s losses as well as wins, while PageRank rewards an wrestler for wins over highly-ranked opponents, but does not punish him for losses to unranked opponents.
One of the most important potential advantages of the Elo rating system over PageRank that may be further explored is its potential to predict not only match outcomes (W/L), but point differentials. In this paper, we use the Elo’s expected score probability only for predicting win/loss match results. However, this probability may be interpreted as the expected proportion of points earned by each competitor, a probability that may be transformed to the expected point differential between competitors. This is especially exciting for the sport of wrestling, as point differentials determine all victory types except falls and forfeits, and teams accrue points according to the victories of individual wrestlers. While the focus of this project is the ranking and prediction of individual performance, a method that can accurately predict victory type may be generalized to team performance. As no other existing ranking system for collegiate wrestling possesses this capability, this is a promising are for future research. Additionally, the compilation of team rankings based upon individual rankings is a possible extension of this research.
The formulation of the Elo rating system described in Equation (5–7), which yields an expected proportion of points allotted to each competitor, is modified to output an expected point differential(PDexp).
(8)
σPD = standard deviation of point differentialc = scaling factor
Rbef = wrestler rating before match
Obef = opponent rating before match
H = “home advantage” correction
It should be noted that past research by Glickman and Jones (1999) indicates that the expected score proportion often underestimates the lower-rated opponent’s scoring, and further investigation is needed into the use of Elo as a predictor of margin of victory in collegiate wrestling.
6Conclusion
This project represents a novel investigation of ranking and prediction in the context of college wrestling. In addition to performing the first empirical analysis of the accuracy of collegiate wrestling rankings, we propose two new methods, PageRank and Elo ratings, which demonstrate significant improvement over the benchmark accuracy rate and several of the existing ranking methods.
We conclude that Elo presents promise for future work on the ranking and prediction of collegiate wrestling. The capability for Elo to yield not only expected proportion of points scored, but expected point differentials, is an exciting area for future research, as margin of victory has special importance in wrestling, determining victory type and team points. We also find preliminary evidence that Elo may be combined with subjective, human predictions to improve accuracy. These results suggest that work on ensemble methods incorporating small-scale, expensive human evaluations and automated computational methods may be a fruitful area for further research. Additionally, wrestling represents a unique application of the Elo method, which has previously been utilized primarily in “mind sports”, and this project demonstrates that Elo can effectively be used for the ranking and prediction of combat sports. This work may be generalized to similarly structured combat sports, including freestyle wrestling, judo, karate, and mixed martial arts. The unique findings regarding parameterization of Elo in this project, specifically the success of large K-factors, may also inform the use of Elo in othersports.
Notes
References
1 | Barrow D. , Drayer I. , Elliott P. , Gaut G. , & Osting B. (2013) . Ranking rankings: an empirical comparison of the predictive power of sports ranking methods, Journal of Quantitative Analysis in Sports 9: (2), 187–202. doi: 10.1515/jqas-2013-0013 |
2 | Bastian M., Heymann S., Jacomy M., (2009) . Gephi: an open source software for exploring and manipulating networks, in International AAAI Conference on Weblogs and Social Media, San Jose, California, May, 17–20. |
3 | Brin S. , & Page L. (1998) . The anatomy of a large scale hypertextual web search engine, in Proceedings of the seventh International Conference on the World Wide Web (WWW 1998), pp. 107–117. doi: 10.1016/S0169-7552(98)00110-X |
4 | Elo A.E. (1978) . The Rating of Chess Players Past and Present, Arco Publishing, New York. |
5 | FIFA., 2012. FIFA/Coca-Cola Women’s World Ranking, viewed 25 March 2015, http://resources.fifa.com/mm/document/fifafacts/r%26a-wwr/52/00/99/fs-590_06e_wwr-new.pdf |
6 | Glickman M.E. , Jones A.C. (1999) . Rating the chess rating system, Chance 12: , 21–28. |
7 | Govan A.Y. , Meyer C.D. (2006) . Ranking national football league teams using Google’s PageRank. Center for Research in Scientific Computing, North Carolina State University, Raleigh, NC, viewed 25 March 2015, http://www.ncsu.edu/crsc/reports/ftp/pdf/crsc-tr06-09.pdf |
8 | Grant R.R. , Leadley J.C. , & Zygmont Z.X. (2013) . Just win baby? Determinants of NCAA Football Bowl Subdivision coaching compensation, International Journal of Sport Finance 8: (1), 61–74. |
9 | Hvattum L.M. , & Arntzen H. (2010) . Using Elo ratings for match result prediction in association football, International Journal of Forecasting 26: (3), 460–470. doi: 10.1016/j.ijforecast.2009.10.002 |
10 | Jech T. (1983) . The ranking of incomplete tournaments: A mathematician’s guide to popular sports, The American Mathematical Monthly 90: (4), 246–266. |
11 | Mellers B. , Stone E. , Atanasov P. , Rohrbaugh N. , Metz S.E. , Ungar L. , Bishop M.M. , Horowitz M. , Merkle E. , Tetlock P. (2015) . The psychology of intelligence analysis: drivers of prediction accuracy in world politics, Journal of Experimental Psychology: Applied 21: (1), 1–14. doi: 10.1037/xap0000040 |
12 | Motegi S. , Masuda N. (2012) . A network-based dynamical ranking system for competitive sports, Scientific Reports 2: (904). doi: 10.1038/srep00904 |
13 | National Collegiate Athletic Association., 2009. 2009 and 2010 NCAA wrestling rules and interpretations, viewed 25 March 2015, http://matref0.tripod.com/Articles/2010NCAA_Rules_Book.pdf |
14 | National Collegiate Athletic Association, 2013a. 2013-2014 NCAA Division I manual, viewed 25 March 2015, http://grfx.cstv.com/photos/schools/loyc/genrel/auto_pdf/2013-14/misc_non_event/NCAAManual.pdf |
15 | National Collegiate Athletic Association, 2013b. Prechampionships manual: 2014 Division I wrestling championships, viewed 25 March 2015, http://www.ncaa.org/sites/default/files/PreChamps_DI_Wrestling_2014_RevisedLinks.pdf |
16 | Park C.S. , Sharp-Bette G.P. (1990) . Advanced Engineering Economics, John Wiley & Sons, Inc., New York. |
17 | Penas A. , Rodrigo A. (2011) . A simple measure to assess non-response, in Proceedings of the th Annual Meeting of the Association for Computational Linguistics, Association for Computational Linguistics, East Stroudsburg, PA, pp. 1415–1424. |
18 | Procopio P.S. , Goncalves M.A. , Laender A.H.F. , Salles T. , Figueiredo D. (2012) . Time-aware ranking in sport socialnetworks, Journal of Information and Data Management 3: (3), 195–210. |
19 | Stefani R., (2011) . The methodology of officially recognized international sports ranking systems, article, Journal of Quantitative Analysis in Sports 7: (4), 9. doi: 10.2202/1559-0410.1347 |




