Why very cold neutrons could be useful for neutron-antineutron oscillation searches

1.Introduction

The search for neutron – antineutron oscillations (n−n‾) [2,4–6,11,12,18,20,29] is a flagship experiment considered at the European Spallation Source (ESS), Lund, Sweden. An observation of (n−n‾) oscillations, which violate baryon conservation, would constitute a scientific discovery of fundamental importance to both physics and cosmology. A stringent upper bound on its transition rate would be an important contribution to our understanding of the baryon asymmetry of the universe, eliminating the post-sphaleron baryogenesis scenario in the light quark sector. The latest reviews of scientific motivations and possible implementations for such experiments may be found in refs. [1,27]. We refer the reader to these detailed studies for any further information and describe here only the ideas presented during the aforementioned talk.

2.n and n‾ guides for n−n‾ oscillation experiments

An interesting option to simultaneously increase the sensitivity of such an experiment and decrease its cost is to implement the idea of a guide both for n and n‾ [21,23,24,28]. While n guides have been in common use since the beginning of the neutron research, the idea of n‾ guides seems counterintuitive; shouldn’t we expect an n‾ to annihilate immediately upon contact with matter? In fact, we should not. Just the opposite, an n‾ is totally reflected from a surface if its transverse velocity component is smaller than the surface critical velocity for n‾. This is in complete analogy to the interaction of n with a surface [13]. Moreover, typical n and n‾ scattering lengths, bnA and bn‾A, (and therefore also (anti)neutron-nuclei optical potentials and probabilities of (anti)neutron loss per bounce) are similar in many cases. To good accuracy, the scattering length is bn‾A[fm]∼1.54A3−i [23]. The real part Re(bn‾A) increases with the atomic number A of the nucleus, composing the material surface. The imaginary part Im(bn‾A)[fm]∼1 is the same for all materials. These properties of the scattering length can be easily understood within the framework of a model that treats a nucleus as a “black sphere” of a certain radius and with a certain diffuseness of the potential; that the internal nuclear structure is of little importance greatly simplifies this quantum-mechanical problem [8,28]. The typical optical Fermi potential of materials for n‾ is 50–100 neV; and the typical lifetime of n‾ in a properly designed n/n‾ guide is 1–3 s. To increase the critical velocity for n‾, one should select materials with large A. The guide wall material should also have a large critical velocity for n, and should be suitable for building guides and/or coatings. Aside from these requirements, the choice of material for a relatively short neutron guide, in which the time of flight is significantly shorter than the n‾ annihilation lifetime in the guide, is not heavily restricted; most of the n and n‾ can reach the end of the guide without losses, remaining in a coherent superposition of these two states.

The idea of using the reflection of n‾ from the surface was proposed already in several of the first publications on the search for n−n‾ oscillations [9,15,17]. We 1) extend this approach to higher n energies, thus increasing statistics and, thereby, sensitivity; 2) point out conditions for suppressing the phase difference for n and n‾ at reflection; 3) underline the importance of setting low transverse momenta of n and 4) make certain choices for the nuclei composing the guide material.

Compared to the classical quasi-free-neutron method, our approach has certain advantages. For the same installation length, the advantages include smaller transversal sizes, lower costs, and larger statistics, i.e., higher sensitivity. For a longer installation, our approach provides a large gain in sensitivity. In terms of the oscillation probability, the gain increases quadratically with the length. For the particular case of a copper (Cu) n/n‾ guide at the PF1B beam at ILL, a feasibility analysis of the complete experiment has recently been performed [16]. The interaction potential for n‾ and a Cu guide was assumed to be VF′(n‾Cu)=V0′−iW′=94−i27 neV. This is the most conservative estimate of the interaction potential, calculated in the following way: V0′=V0−5ΔV0, W0′=W0+5ΔW0, where V0 and W0 are the known real and imaginary parts of the potential, while ΔV0 and ΔW0 are the known uncertainties of these values [28]. Thus, we have decreased the real part (potential height) and increased the imaginary part (losses) by 5 standard deviations. The analysis showed that the overall gain factor over the best existing constraint [7] can be a factor of 3–10; background is below one event for the whole experiment duration; systematics are virtually absent.

An experiment at the ESS would provide much higher sensitivity. Compared to the best experiment performed to-date [7], the gain factors include the possibilities of a significantly larger guide length and a significantly larger solid angle from which to extract neutrons. Each factor corresponds to a quadratic increase in sensitivity. Compared to a design that doesn’t use an n‾ guide, advantages of the new method include a lower cost and a lower background in the annihilation detector, both of which are due to the smaller guide and detector sizes. However, an optimization of the experimental design and a sensitivity evaluation have not yet been performed. These are planned for the near future.

It is interesting to estimate the uncertainties in the experiment sensitivity associated with the uncertainty in the scattering length of n‾ on the guide wall material. For ref. [16], the time of flight is ∼0.05 s, much shorter than the predicted n‾ storage times. Thus, the uncertainty is negligible. For a hypothetical experiment with cold neutrons (CN) at the ESS, the time of flight might reach ∼0.4 s, which is a factor of ∼0.2 of the characteristic ∼2 s expected n‾ storage time in the guide. For a typical uncertainty of the scattering length, equal ∼0.1, and taking into account that n‾ can appear at any point in the guide with equal probability, a systematic uncertainty in the estimation of the oscillation time is as small as ∼0.5%.

3.Advantages of very cold neutrons for n−n‾ oscillations experiment

Such a hypothetical experiment would be entirely limited by statistics, and would have negligible systematics. Thus, one might try to further improve the statistical sensitivity even if systematic uncertainties increase. Roughly speaking, systematic and statistical uncertainties should be equal in a properly designed experiment. This argument, as well as the fact that the sensitivity to the n−n‾ oscillation rate increases quadratically with increasing observation times, prompts a question [26]: is there any advantage of using slower neutrons for such an experiment?

Let us assume for the sake of simplicity that the design of a n/n‾ guide enables the transportation of most of the initially available n and n‾ to the n‾ annihilation detector. Let us also assume that the initial spread of transverse velocities is the same for both cases, i.e., VCN and CN. Finally, let us assume that the phase-space densities of VCN and CN are the same, as would be the case if the VCN distribution corresponds to the tail of an equilibrium distribution of neutrons in a CN source. One would then conclude that the sensitivity to n−n‾ oscillations in experiments with VCN and CN are about the same. This conclusion follows from the compensation of two factors: (1) the sensitivity increases as the square of observation time (the square of reciprocal longitudinal velocity), (2) the neutron flux decreases as the square of longitudinal neutron velocity for the same phase-space density. Such a conclusion, however, is not correct if a dedicated VCN source having a higher phase-space density is used. This is an important difference because, while the phase-space density of CN sources can hardly be increased (these sources are already state-of-the-art), a better VCN source could be built quite easily. We give an example of such a source in Section 4.

What is the optimum VCN velocity for such an experiment? One can profit from the n/n‾ guide idea only when the observation time is smaller than or equal to a characteristic n‾ lifetime in the guide. While the lifetime is always close to ∼2 s, the observation time is a function of the experiment length and the neutron longitudinal velocity. If the maximum experiment were ∼250 m, then the characteristic neutron velocity for a n−n‾ experiment would be ∼125 m/s. This is, however, very close to a typical VCN velocity! Further decreasing the longitudinal neutron velocity would not increase the observation time, which is defined by the lifetime until annihilation. Although all these estimations are rough and have been performed for mean values, VCN would appear to be nearly ideal.

We now turn to an analyze of the main additional gain factor resulting from a larger phase-space density that can be achieved in a dedicated VCN source. The additional gain factor is simply proportional to the increase in the phase-space density.

4.A possible implementation of a dedicated VCN source at ESS

An optimization of the VCN n−n‾ experiment at the ESS is a multi-parametric task which includes both the VCN source and the n−n‾ experiment. The present note is only a proposal of the principle concept; and a detailed analysis will be carried out following the Workshop.

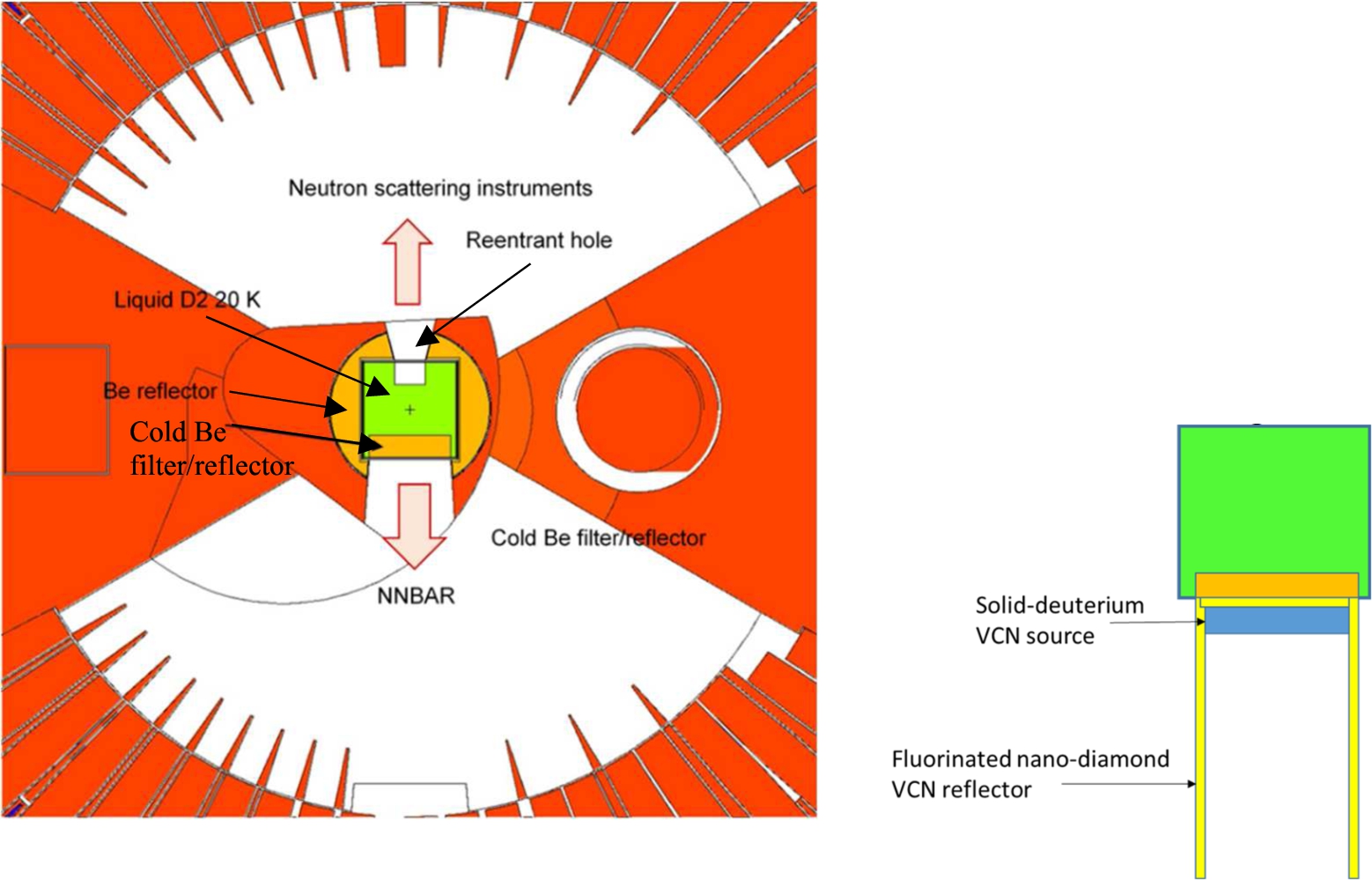
We propose the following implementation of the VCN source. In the current design, neutrons for the n−n‾ experiment will be provided by a large liquid-deuterium CN source placed under the main ESS target. A schematic of its implementation, kindly provided by Luca Zanini, is shown in Fig. 1. A VCN source dedicated to the n−n‾ experiment could be added to the current design without significant modification, as shown in the insert to Fig. 1. One option assumes a solid-deuterium VCN converter at a temperature of several Kelvin. Solid deuterium is a good candidate material as it has been studied in detail both theoretically and experimentally for the sources of ultracold neutrons (UCN) [3,14,30]. One advantage for VCN in comparison to UCN is that the former are not strongly scattered by inhomogeneities in the solid deuterium bulk, and are thus more easily extracted with minimal losses. Other converter/source materials might also be considered. The converter has a maximum square area in order to increase the total VCN flux. The source temperature and thickness are defined by the heat load acceptable at this position and can be optimized later. In order to place the solid deuterium converter at the position of maximum neutron flux, one might consider either removing the beryllium filter/reflector or placing the converter in a cavity in the liquid-deuterium source (provided these modifications do not penalize the total neutron flux). A fluorinated detonation nanodiamond (F-DND) reflector [19,22] increases the total flux of VCN by a large factor due to multiple reflections from the reflector walls and enhanced directional extraction to the experiment. On the other hand, as a thin F-DND layer between the liquid-deuterium source and the solid-deuterium converter is nearly transparent for CN, the incident CN are virtually unaffected. The nano-diamond sidewalls are also nearly transparent at large enough incidence angles. At very small grazing angles they might reflect neutrons quasi-specularly [10], thus increasing the neutron flux towards the n−n‾ experiment but reducing the flux to other directions.

Fig. 1.

Figure is taken from “L. Zanini et al., Very Cold and Ultra Cold Neutron Sources for ESS, these proceedings”. At left, the current design for the implementation of a large-volume liquid-deuterium source of CN. The green coloring indicates regions of 20 K. The downward facing arrow at bottom illustrates CN passing through a Be filter (orange) and feeding a n−n‾ experiment. A dedicated solid-deuterium VCN converter with an F-DND reflector could be added to this design, as is shown below.

5.Conclusion

We have motivated the use of very cold neutrons (VCN) for improving the sensitivity of n−n‾ searches at the ESS and have proposed a possible scheme for the implementation of a solid-deuterium VCN converter with a fluorinated detonation nano-diamond (F-DND) reflector. In the proposed position, the VCN source profits from a maximum cold neutron (CN) flux, an optimum incident neutron energy, and a very large cross-section of the extracted VCN beam. The VCN converter thickness and temperature should be defined by the acceptable heat load at this position, but might be close to 5 cm and 7–10 K, respectively. Such a VCN source could also be used to directly produce ultracold neutrons (UCN); in this case one profits from a mean (over time) UCN density in the converter. The option to extract a peak UCN density from the pulsed ESS neutron source was discussed in another talk presented at the same workshop [25]. The fact that one can accommodate CN, VCN and UCN energy ranges in the same neutron guide might be an important advantage.