Routines for optimizing neutron scattering instruments with McStas
Abstract
We present software routines for simulating the transport of thermal neutrons through materials relevant for neutron instrumentation. The elastic interactions in different types of textured polycrystals are modelled and implemented in the routines. Three limit cases of textures are explicitly considered: powder texture, with uniform distribution of grain orientations, mosaic single crystal texture, with a distribution of orientations sharply peaked about one direction, and ideal fibre textures. Sharp textures can be modelled as combinations of these three limit textures. For polycrystals with mild textures, a different method is used. The inelastic scattering is treated in the incoherent approximation, including multi-phonon terms of arbitrary large order. The routines have been implemented in the McStas software package.
1.Introduction
The use of neutron diffraction has been growing steadily during the last decades in material science research, especially because of the possibility to study magnetic structures and the possibility to resolve diffraction peaks at very high scattering angles, due to its constant form factor and the great penetration of neutron in matter. In reactor-based neutron sources, neutron diffractometers have been constructed optimized for specific applications: strain scanners, high-resolution diffractometer, high intensity diffractometer, etc. In these diffractometers, the polychromatic beam emerging from the reactor shielding is trimmed to generate a monochromatic beam with very narrow energy distribution that is then diffracted by the sample. The relative low flux of neutrons impinging on the sample in these diffractometers, compared to synchrotron or neutron spallation sources, make the signal-to-noise ratio (SNR) a critical factor in the design of the instrument and their sample environmental system.
Estimating the SNR at the time of designing a neutron scattering instrument is a difficult problem. All interactions between the neutrons and a sample that are not related to the experiment goal lead to an undesired background that is intrinsic to the sample. A second source of background is originated from the sample and its environment (that is, from neutrons that interact with the environment devices and perhaps also with the sample). This is a concern for sample environment, as this is the major source of background.
In general, the chemistry, shape, and texture of cryostats and furnaces can be improved so that the background that generate impair as less as possible the signal coming from the sample. Cryomagnets and pressure cells, however, can produce significant amounts of undesired scattering. The multiple scattering that results from the interaction between the sample and the devices of its environment is another source of background that has to be considered.
Over the years, methods and approximations have been developed to quantify these effects, as, for instance, the formulas to correct for the multiple scattering arising from the sample [12]. However, these methods remain limited in their capability to handle the complex scattering that takes place in sophisticated instruments and sample environments. The most accurate method for evaluating such contributions would be a Monte Carlo simulation that consider all aspects of interactions inside and around the sample. However, in Monte Carlo simulations of neutron instrument optics, one is usually interested in the signal at the detector, and therefore only the interactions that are relevant to this purpose are included. In contrast, when modelling the background, all neutron interactions may contribute, so that all of them have to be incorporated in the model. The complexity of estimating the background is exacerbated by the fact that some interactions depend strongly on the crystallographic texture of the material.
Monte Carlo simulations that help the instrument design would be much more useful if they could provide a reliable estimate of the SNR, for which the background has to be estimated. Reliable Monte Carlo simulations will also offer an invaluable help in data analysis for two reasons: (i) the empty-cell measurement, which is usually used to remove the impact of the environment, might be avoided, reducing beam-time losses; and (ii) they can help to redesign the geometry, thickness of the sample, container, and cryostat materials, to perform a successful experiment.
One of the most powerful software packages to simulate neutron optics is McStas [8,16,17], which provide a set of defined components (source, collimators, monochromators, sample, detector, etc.) that can be arranged in a prefixed sequence resembling the instrument to be modelled. Despite its wide range of applications, its capabilities to estimate the background are limited, since all existing components in McStas deal only with coherent scattering by materials that are either mosaic single crystals or powders. The same happens with other related software packages: none of them offers routines to deal with textured crystals. Thus, the background has to be evaluated assuming that the materials that form the sample environment devices are polycrystals with a uniform distribution of grain orientations. Nevertheless, in general, these materials are textured polycrystals with a non-trivial distribution of grain orientations. Hence, the integrated background estimated with the existing software is likely correct, but its spatial distribution, which is crucial regarding the influence on the SNR, can be grossly erroneous, as we will see in next section.
The development of routines suitable to estimate the background is not a problem of software development. There is no general method to deal with the complex neutron scattering that take place in materials other than mosaic single crystals and powders. Hence, we have to devise methods suitable to deal with textured polycrystals in Monte Carlo simulations before implementing them in software codes. The purpose of this paper is to summarize some developments in that direction and its implementation in the McStas software package.
2.Models of interactions and implementation in McStas
All interactions of neutrons with a material can potentially generate background. Thus, ideally, a program to estimate the background has to model the elastic scattering, both coherent and incoherent, the inelastic scattering, and the neutron absorption. Incoherent elastic scattering, being isotropic and energy independent, and neutron absorption, are trivial in comparison with the complexity of the other interactions, and are not included in the new routines, since they can be considered with existing McStas components.
The problem of the coherent elastic scattering in textured polycrystals, in spite of its complexity, is satisfactorily solved with the methods described below. The inelastic scattering is the major problem, due to its complexity. In this work, it is implemented in the incoherent approximation [10], which is good at large momentum transfer and may be good enough in some cases for polycrystalline materials [10]. However, this approximation gives only isotropic scattering and thus it suffers from the problems discussed in above, so that we expect that the integrated inelastic background will likely be well estimated, but the correlated energy-spatial distributions may have large errors. The modelling of coherent effects in the inelastic scattering by textured polycrystals is beyond the present capabilities.
2.1.Coherent elastic scattering
Many of the materials that generate the background in a neutron scattering instrument are textured polycrystalline materials whose texture is described by an Orientation Distribution Function (ODF) that gives the fraction of crystal grains oriented in a given direction [2]. There is no coherence in the scattering of neutrons by different grains, so that the macroscopic scattering cross section is simply the average over all the orientations, weighted by the ODF, of the single crystal cross section of a grain [13]. The effect of the grain mosaicity is completely masked by the effect of texture and therefore negligible. The effect of residual stresses can also be disregarded, since it only produces small shifts in Bragg peak positions. The coherent elastic scattering cross section can then be written as an average of the perfect single crystal cross section over all grain orientations, weighted by the ODF, and has the general form
The method for sharp textures consists in modelling them as a combination of three textures, which can be considered as limiting cases, and for which expressions for
Let us see the form of
Finally, for the ideal fibre texture we have
Fig. 1.
The
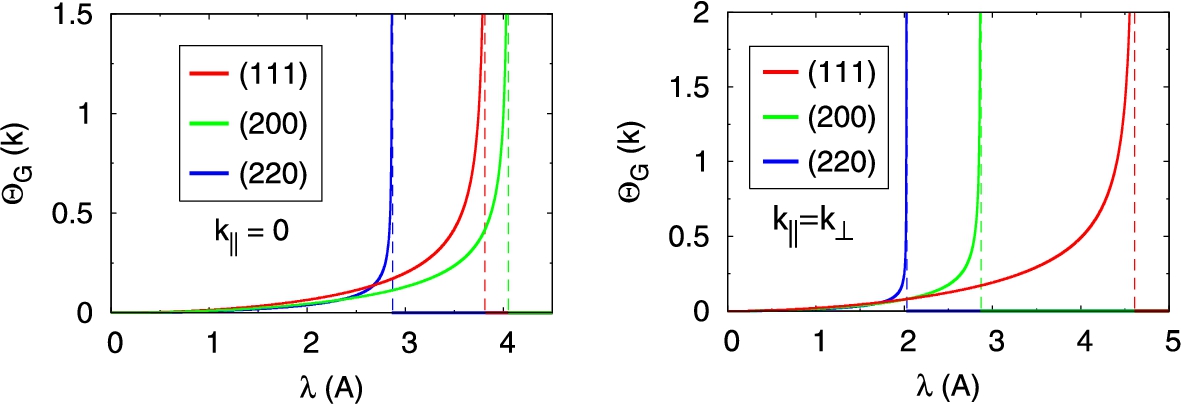
The meaning of the above equation is the following. It is assumed that we have chosen an orientation of the ideal crystal, which defines the reciprocal lattice vectors, and that we also have chosen an orientation of the ideal fibre texture, defined by its axis. Then the parallel and perpendicular components of the vectors entering the above formula are completely defined. Figure 1 displays
More complicated sharp textures can be simulated by combining these elementary textures with appropriate weights. That is, a texture can be described as a fraction of powder texture, plus a fraction of mosaic single crystal textures in different directions, and a fraction of ideal fibre textures with axes oriented in different directions.
As an example, a Monte Carlo simulation of the elastic scattering by an aluminum foil with an ideal fibre texture, with axis lying on the foil plane, has been carried out in two ways: 1) by using the scattering cross section corresponding to an ideal fibre texture; and 2) by modelling the ideal fibre texture as a combination of several mosaic single crystal textures, with different single crystals having the appropriate axis oriented along the fibre axis, and with the orientation in the perpendicular plane uniformly distributed. In, practice we use a sample of seven single crystals whose orientations in the perpendicular plane are uniformly distributed each 15°. To have overlapping Bragg peaks, we assign large mosaicity (of a few degrees) to the single crystals, what introduces a systematic error. Nevertheless, the results are reasonably good. The foil is irradiated with a neutron beam propagating along the perpendicular direction to the foil (hence, perpendicular to the fibre axis), with a divergence of 0.2° and a wide Gaussian spectrum centered at 2.02 Å, with a wavelength spread of 1.9 Å FWHW. The scattered neutrons are collected on a set of position sensitive planar detectors surrounding the sample with an octagonal geometry. The results are displayed in Fig. 2. The panels of each row show the number of counts collected by the eight detectors, which are located at angular positions ranging from 180° to 315° from the beam direction, 180° corresponding to the leftmost panel. The top and bottom panels correspond, respectively, to the exact ideal fibre texture, and to the ideal fibre texture approximated by the distribution of mosaic single crystal textures. We see a reasonable agreement. Additionally, these simulations constitute a test of the algorithm that implements the scattering by an ideal fibre texture.
Fig. 2.
An example of combination of elementary textures to represent a complex texture. Top panel: diffraction pattern in an octagonal detector system of an aluminium foil with a hypothetical ideal fibre texture. Bottom panel: same, with the texture represented by a distribution of mosaic single crystals with uniformly random orientations in the perpendicular plane to the aligned axis.

The method of simulating textured materials by combining distributions of the elementary textures is reasonable only for materials with very sharp textures, which have a few strongly preferred directions. In most cases, however, materials have mild textures, with preferred directions described by very wide peaks in the ODF, which cover tens of degrees. For these cases, a more powerful method has been developed [7]. It is based on the expansion of the ODF in generalized Fourier series, in terms of Wigner functions [2]. The scattering cross section can then be expressed as a series involving the Fourier coefficient of the ODF [7]. Such explicit expression can be used in Monte Carlo simulations. The method has been described in detail elsewhere [7], and has been implemented in a McStas component, called Texture.comp. As input, the component requires three files: one with crystallographic information, another one with the generalized Fourier coefficients of the ODF, and a third one that provides the orientation of the reference crystallographic axes with respect to the sample reference frame. Some optimization tricks, such as precomputing several quantities and using variance reduction techniques, have been implemented to improve the efficiency, making simulations feasible.
As an example of a McStas simulation using Texture.comp, we performed a simulation of the background generated by the scattering of a highly collimated neutron beam, with wavelength uniformly distributed between 2.0 Å and 3.0 Å, from a 18 mm diameter and 3 mm thick hollow cylinder made of the Zr2.5%Nb, with the texture reported by Malamud et al. [9]. For comparison, we performed also a similar simulation in which the texture is replaced by a uniform distribution of grain orientations (a powder). The scattered neutrons are collected in two banana shaped detectors, located at both sides of the beam axis, which are 4 m high and cover an angular range from 5° to 170° and from 190° to 355° respect to the beam propagation direction. These banana detectors are located at 2 m from the sample center line. Figure 3 displays the results. The left and right panels correspond to each banana detector. The top and middle panels show the results for the textured material and the powder, respectively. The bottom panels display the ratio between the signals produced by the textured material and the powder. The average value of this ratio is 1.02, which means that, as expected, the integrated signals are rather similar. The spatial distributions are however different: there are points where the signal produced by the textured material is 3.5 times larger than the signal produced by the powder. At those points, the SNR in the case of a container made from the textured material will be reduced by a factor 3.5 with respect to a container with a uniform distribution of grain orientations. Correspondingly, there are points at which the ratio is about 0.4, and there the SNR would be enhanced by a factor 2.5 due to the texture. This means that there would be some angular positions at the detector where the texture of the container will produce an increase of SNR and some other where will produce a reduction. The proper selection of the container orientation will then depend on the sample diffraction peak of interest. This decision has to be taken before setting the experimental setup and shows clearly the need of these new routines to estimate the background.
Fig. 3.
Simulation of the background generated by a hollow cylinder of Zr2.5%Nb with the texture reported in reference [9] (top panels) and with a uniform distribution of grain orientations (middle panels). In the bottom panels, the ratio between the results of the top and middle panels is shown.
![Simulation of the background generated by a hollow cylinder of Zr2.5%Nb with the texture reported in reference [9] (top panels) and with a uniform distribution of grain orientations (middle panels). In the bottom panels, the ratio between the results of the top and middle panels is shown.](https://content.iospress.com:443/media/jnr/2019/21-3-4/jnr-21-3-4-jnr190117/jnr-21-jnr190117-g003.jpg)
2.2.Inelastic scattering
Due to the complexity of the inelastic scattering, it has been treated using the incoherent approximation, which is good for large momentum transfer [10]. The momentum transfer, however, will not be large in general and thus systematic errors will be present due to this approximation. In particular, for cubic crystals the scattering in the incoherent approximation is isotropic. For non-cubic crystals is almost isotropic. Therefore, we expect that the integrated inelastic background will be well estimated, but the prediction of its spatial distribution might have important uncertainties due to the ignored coherent effects. The incoherent approximation has the advantage that, for cubic crystals, it depends only on the phonon density of states (DoS).
The inelastic scattering cross section in the incoherent approximation is computed in terms of the phonon expansion [6,10], as a sum over the number of phonons, p, emitted or absorbed in the scattering process. The sum is cut-off to a maximum number of phonons,
The total inelastic cross section depends only on the energy of the incoming neutron, and not on its direction (this is only rigorously true for simple cubic lattices). The contribution of each term of the phonon expansion to the total cross section are pre-computed as a function of energy and stored in simple tables. In the course of simulations, the total cross section for a given energy is obtained by interpolation from these tables. If the McStas kernel selects the inelastic scattering as interaction process, the scattered neutron is sampled as follows. First, the number of phonons p responsible for the scattering is sampled with a probability proportional to the contribution of the p-phonon term to the total inelastic cross section. Then, the energy and direction of the scattered neutron are sampled from the distribution corresponding to the p-phonon term of the phonon expansion, using a simple rejection method.
Fig. 4.
Transferred energy (
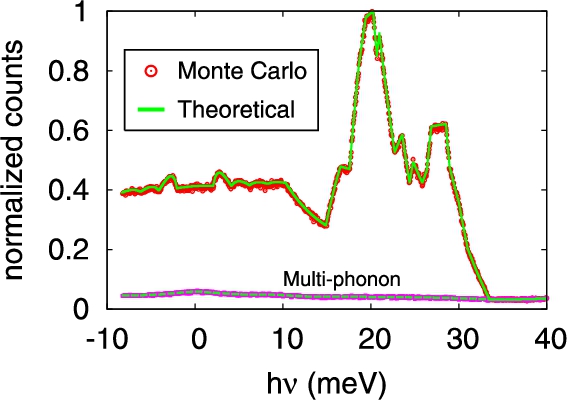
The code has been validated by performing many tests. Figure 4 displays the results of a simulation in ideal conditions, for which the result can be obtained theoretically by a numerical integration independent of the Monte Carlo simulation. The simulation setting is as follows: a point-like vanadium sample is irradiated with a perfectly collimated (zero divergence) neutron beam with infinitely narrow cross section, with energy uniformly distributed between 24.75 meV and 75 meV. As an input, the experimental DoS reported by Sears et al. [14] is used. The transferred energy distribution function is presented in Fig. 4. The red points are the results of the simulation; the pink points represent the multi-phonon contribution (two and three phonon scattering) obtained from the simulation. The green lines are the theoretical result. Notice the perfect agreement. We notice also a reasonably good agreement with the experimental results displayed in Fig. 2 of Sears et al. [14], especially considering the experimental uncertainties due to instrument resolution, background, multiple scattering, etc., which are absent in the ideal computation.
Fig. 5.
Left and middle panels: spatial distribution of neutrons scattered by a vanadium hollow cylinder considering inelastic scattering only. Right panel: distribution of transferred energy.
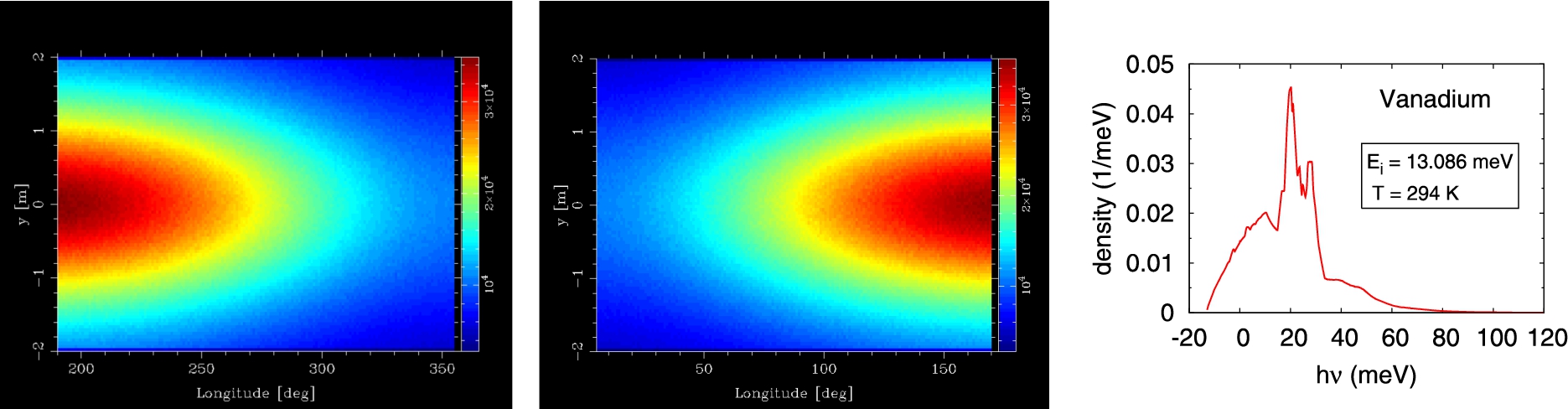
Figure 5 displays the results for the inelastic background generated by a hollow vanadium cylinder of 18 mm diameter and 3 mm thickness, irradiated by a neutron beam with divergence of 0.1° and energy of 13.086 meV (2.5 Å), with an energy spread of 25 μeV, at a temperature of 294 K. The left panels show the scattered neutron distribution detected by two banana detectors located at either side of the beam, that are 4 m high and cover an angular range from 190° to 355° (left panel) and from 5° to 170° (middle panel), measured with respect to the beam direction (0°) located at a distance of 2 m from the cylinder center line. The right panel shows the distribution of transferred energy. The shoulder and the long tail for
The inelastic scattering in the incoherent approximation may be also simulated with the existing McStas component Isotropic_Sqw.comp [4]. However, this requires as an input the whole scattering function as a function of transferred momentum and transferred energy, in some cases in a wide dynamical range. The scattering function, moreover, depends on temperature. The new component has the advantage that only requires as an input the phonon DoS, and can be used for any temperature in any dynamical range, with arbitrarily large number of multi-phonon terms.
The implementation of these developments as McStas components took advantage of the McStas Union component set, developed by M. Berteldsen [1], which separates components that describe physical processes from components that describe geometry and other aspects of neutron propagation, and automatically deals with multiple scattering. This way we could concentrate in the physical problem, using all the remaining capabilities of McStas.
3.Conclusion
To estimate the background generated at neutron scattering instruments it is necessary to consider the crystallographic texture of the materials used in the different parts of the instrument and to model the neutron interactions that take place in them. We have developed a method to take into account the crystallographic texture in Monte Carlo simulations that is based on modelling the actual texture as a combination of three elementary textures, for which closed expressions of the elastic coherent cross sections are available. The elementary textures are the powder texture, in which the grain orientations are uniformly distributed; the single crystal texture, in which the grain orientations are distributed according to a very narrow Gaussian function around a preferred direction; and the ideal fibre texture, in which the grains are perfectly aligned along one axis and the orientations on the perpendicular plane are uniformly distributed. This method of combining elementary textures is reasonable only for very sharp textures, that have a number of strongly preferred orientations besides a basically uniform orientation distribution. Most textures, however, are smooth, showing wide peaks, tens of degrees wide, around preferred directions. For these cases, we have developed a more suitable method, based on the generalized Fourier transform of the ODF [7]. It has been implemented in a McStas component called Texture.comp.
A method to simulate the inelastic scattering has also been implemented in a McStas component, called IncoherentPhonon_process.comp. In this case the incoherent approximation was used. Multiple-phonon excitations were incorporated in the model together with multiple neutron scattering. This new McStas component was validated for the case of a pointlike Vanadium sample by comparing the energy transferred distribution function predicted by the simulation with theoretical expressions. As an application of this routine, the spatial and energy distribution of neutrons scattered by a hollow vanadium cylinder was simulated using this component.
These new McStas components allow estimating the background through Monte Carlo simulations. They will be used in a near future to estimate the background generated by the walls of clamped pressure cells using the measurements reported in [5]. We expect they will contribute to the innovative, successful and cost-efficient use of beam time at the existing and future beamline at ESS and all other facilities.
Acknowledgements
We are grateful to the McStas gurus P. Willendrup and E. Farhi, and, especially, M. Berteldsen and E. Lelièvre-Berna, for the fruitful discussions. We acknowledge Grant No. PGC-2018-099024-B-I00 from Spanish Ministry of Science Innovation and Universities and funding from the project I-COOP B20319.
 This work was performed within the world class Science and Innovation with Neutrons in Europe 2020 (“SINE2020”) project, funded by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 654000.
This work was performed within the world class Science and Innovation with Neutrons in Europe 2020 (“SINE2020”) project, funded by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 654000.
References
[1] | M. Bertelsen, Software for simulation and design of neutron scattering instrumentation, PhD thesis, The Niels Bohr Institute, Faculty of Science, University of Copenhagen, 2017. |
[2] | H.-J. Bunge, Texture Analysis in Materials Science, Cuvillier Verlag, Göttingen, (1993) . ISBN 3-928815-81-4. |
[3] | G.J. Cuello and J.R. Granada, Thermal neutron scattering by Debye solids: A synthetic scattering function, Ann. Nucl. Energy 24: ((1997) ), 763–783. doi:10.1016/S0306-4549(96)00050-3. |
[4] | E. Farhi, V. Hugouvieux, M.R. Johnson and W. Kob, Virtual experiments: Combining realistic neutron scattering instrument and sample simulations, J Comp Phys 228: ((2009) ), 5251. doi:10.1016/j.jcp.2009.04.006. |
[5] | M. Kibble, V. Laliena, C.M. Goodway, E. Lelièvre-Berna, K.V. Kamenev, S. Klotz and O. Kirichek, Low-background materials for high pressure cells used in inelastic neutron scattering experiments, Journal of Neutron Research Pre-press ((2019) ), 1–12. doi:10.3233/JNR-190115. |
[6] | V. Laliena and J. Campo, arXiv:1807.07330. |
[7] | V. Laliena, M.A. Vicente Álvarez and J. Campo, in preparation. |
[8] | K. Lefmann and K. Nielsen, McStas, a general software package for neutron ray-tracing simulations, Neutron News 10: ((1999) ), 20. doi:10.1080/10448639908233684. |
[9] | F. Malamud, A. Moya Riffo, M.A. Vicente Alvarez, P. Vizcaino, M.J. Li, X. Liu, S.C. Vogel, M. Law, V.V. Sumin, V. Luzin, R.N. Vasin and J.R. Santisteban, Characterization of crystallographic texture of zirconium alloy components by neutron diffraction, Journal of Nuclear Materials 510: ((2018) ), 524–538. doi:10.1016/j.jnucmat.2018.08.003. |
[10] | G. Placzek and L. Van Hove, Nuov. Cim. 1: ((1955) ), 233. doi:10.1007/BF02731767. |
[11] | H. Sato, T. Kamiyama and Y. Kiyanagi, A Rietveld-type analysis code for pulsed neutron Bragg-edge transmission imaging and quantitative evaluation of texture and microstructure of a welded α-iron plate, Material Transactions 52: ((2011) ), 1294–1302. doi:10.2320/matertrans.M2010328. |
[12] | V.F. Sears, Slow-neutron multiple scattering, Adv. Phys. 24: ((1975) ), 1. doi:10.1080/00018737500101361. |
[13] | V.F. Sears, Neutron Optics, Oxford University Press, New York, (1989) . ISBN 0195046013. |
[14] | V.F. Sears, E.C. Svenson and B.M. Powell, Phonon density of states in vanadium, Can. J. Phys. 73: ((1995) ), 726–734. doi:10.1139/p95-107. |
[15] | S. Vogel, A Rietveld-approach for the analysis of neutron time-of-flight transmission data, PhD thesis, Christian-Albrechts-Universitat, Kiel, 1999. |
[16] | P. Willendrup, E. Farhi and K. Lefmann, McStas 1.7 a new version of the flexible Monte Carlo neutron scattering package, Physica B 350: ((2004) ), E735–E737. doi:10.1016/j.physb.2004.03.193. |
[17] | P.K. Willendrup and K. Lefmann, McStas (i): Introduction, use and basic principles for ray-tracing simulations, Journal of Neutron Research Pre-press ((2019) ), 1–16. doi:10.3233/JNR-190108. |




