Imaging nested-mirror assemblies – A new generation of neutron delivery systems?
Abstract
A mirror system for neutron transport with high brilliance transfer from a source or a divergent beam to an instrument is presented. The assembly of nested short elliptical (or very short flat) mirrors located halfway between two common focal points M and M′ images cold neutrons by single reflections from an area around M onto an area of similar size at M′. An absorber on the straight line MM′ blocks the direct view onto the source, with little impact on the transported solid angle. The simple geometry with well-defined, non-grazing angles of reflection off the individual mirrors opens up versatile possibilities to tailor beam size, divergence, wavelength spectrum and polarization to experimental needs. A common small-wavelength cut-off of the transported spectrum can be set by proper choice of the m values of supermirrors. Monochromatic beams can be generated using bandpass supermirrors. Adjustable apertures far away from the instrument define the size and the divergence of the beam at the sample, thus keeping background radiations low. The absence of mirrors in the harsh radiation environment close to an intense source simplifies the maintenance of beam tubes and increases mirror lifetimes.
1.Introduction
Small moderators of liquid para-hydrogen become increasingly popular as cold neutron sources in future facilities for neutron science, following the finding that a reduced moderator thickness in one or two dimensions may increase the brightness [3]. This motivates the implementation of a pancake shaped, flat moderator to feed multiple instruments at the European Spallation Source (ESS) with cold neutrons [33]. The Jülich High Brilliance Source (HBS) foresees “finger moderators” elongated in one dimension, which promise best performance for single user instruments [25].
The current technical design of the ESS target station includes a moderator with a height of only 3 cm, while neutron optical elements are demanded to start only at a minimum distance of 2 m. As pointed out in Ref. [2] “The beam extraction efficiency suffers when the source is reduced to a size similar or smaller than the opening of the neutron guide. This results in a trade-off when reducing the source size, between the resultant brightness increase and the loss of beam extraction efficiency”. This issue becomes crucial for instruments that offer best performance if fed by a cold-neutron beam of large divergence. An example is a potential in-beam UCN source at the ESS [22,36], for which the achievable UCN density is proportional to the transported solid angle. To keep this option alive for implementation at the ESS with its current moderator design, an appropriate neutron transport system is needed.
With this initial goal, a nested-mirror assembly has been proposed [37]. It promises to provide a high brilliance transfer from small neutron sources (moderators or guide exits), viewed under a large solid angle that is limited only by technically feasible mirror reflectivity. Beyond solving the issues raised in Ref. [2] it opens versatile possibilities for tailoring beam characteristics to experimental needs in neutron scattering. The purpose of this paper is to make instrument developers aware of these possibilities.
2.Design of nested-mirror neutron transport systems
The mirror assembly is shown in Fig. 1. Nested short elliptical (or very short flat) mirrors of identical length are placed halfway between two common focal points M and M′. They all image neutrons from a source area around M onto an area of similar size at M′. The assembly covers a seamless range of angles subtended from point M. A central absorber blocks the direct view onto the source along the axis MM′. The direction perpendicular to MM′ in Fig. 1 can be either taken as a radial or as a Cartesian component. This defines two variants of nested-mirror optics, with different dimensionality:
(1) Toroidal system
(2) Planar system
The toroidal system has cylindrical symmetry. With mirrors acting in radial direction, a single reflection transports a neutron from M to M′. The planar system on the other hand has translational symmetry in the direction out of the plane of Fig. 1. Correspondingly, it images neutrons only in the plane and usually has to be complemented by additional mirrors, to refocus or guide the neutrons in the orthogonal direction. There are two obvious options to do this:
(2a) Double planar system = two orthogonal planar systems
(2b) Hybrid system = planar system combined with orthogonal, guiding mirrors
Fig. 1.
Schematic of a nested elliptical multi-mirror system. M and M′ are common focal points of ellipses (the dashed line shows one of them), which after truncation to a common length define the mirror surfaces. See Ref. [37] for the construction of the ellipses.
![Schematic of a nested elliptical multi-mirror system. M and M′ are common focal points of ellipses (the dashed line shows one of them), which after truncation to a common length define the mirror surfaces. See Ref. [37] for the construction of the ellipses.](https://content.iospress.com:443/media/jnr/2018/20-4/jnr-20-4-jnr190101/jnr-20-jnr190101-g001.jpg)
The second planar multi-mirror optics in (2a) is rotated with respect to the first planar system by 90 degrees about the MM′ axis. The points M and M′ are thus connected by two reflections, one for each transverse dimension. A system where both sets of mirrors occupy the same region along the MM′ axis represents a nested version of Montel optics [20]. Technologically simpler seems an implementation reminiscent to Kirkpatrick–Baez optics [11], where two separate planar systems are placed consecutively along MM′ (note however, that this does not exactly correspond to the scheme in Fig. 1 and requires a reanalysis to be given in a forthcoming paper). Easy to implement seem also hybrid systems that consist of a planar multi-mirror optic combined with straight or ballistic reflective boundaries in the orthogonal direction. These mirrors must cover the whole area defined by the outermost rays in Fig. 1.
For a device designed to transport neutrons under a maximum solid angle to the instrument, large gains can be achieved with high-m supermirrors (m denoting the transfer wavenumber at the reflectivity cut-off, normalized to a mirror made of nickel with natural isotopic composition). Note that the relative loss of solid angle due to the central absorber scales as
Deviation of beams with lower divergence can be performed using a planar system with mirrors only on one side of the absorber (see Figs 2 and 3 for an illustration). This can be useful even if the primary neutron beam is delivered by a guide, notably for increasing the space available for instruments but also for taking advantage of the possibilities for further beam tailoring explained in the next section.
Fig. 2.
Effect of full-range supermirror coatings on the neutron wavelength spectrum transported by a nested-mirror system. Reflectivity curves shown in the upper left graph (with indication of the locations of the corresponding mirrors by straight lines) are designed to transport from the incident spectrum (dashed curve in the lower right graph) the part down to a common short-wavelength cut-off at about 6 Å (blue). An alternative set of mirrors (lower left graph) provides the cut-off at about 3 Å (red).
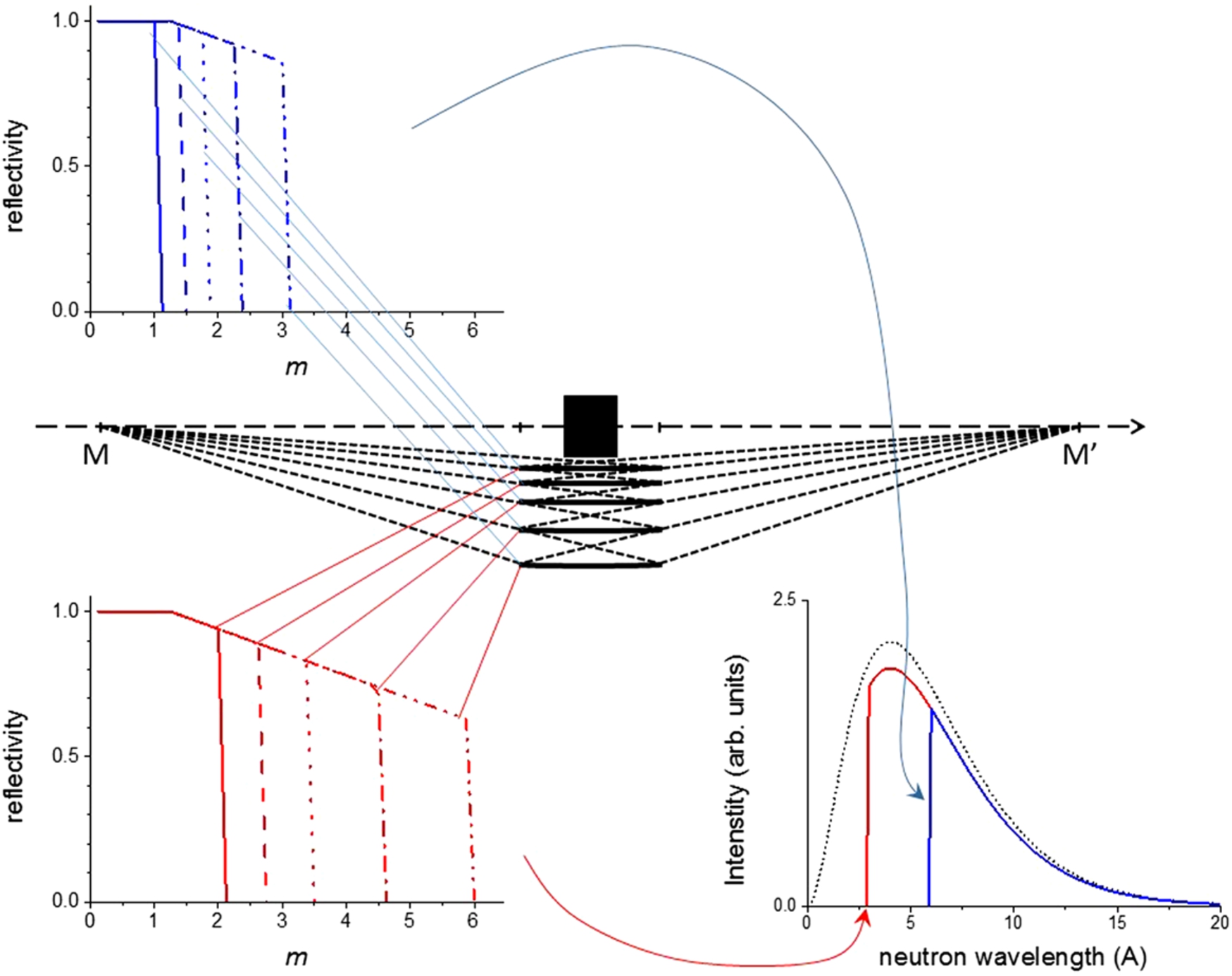
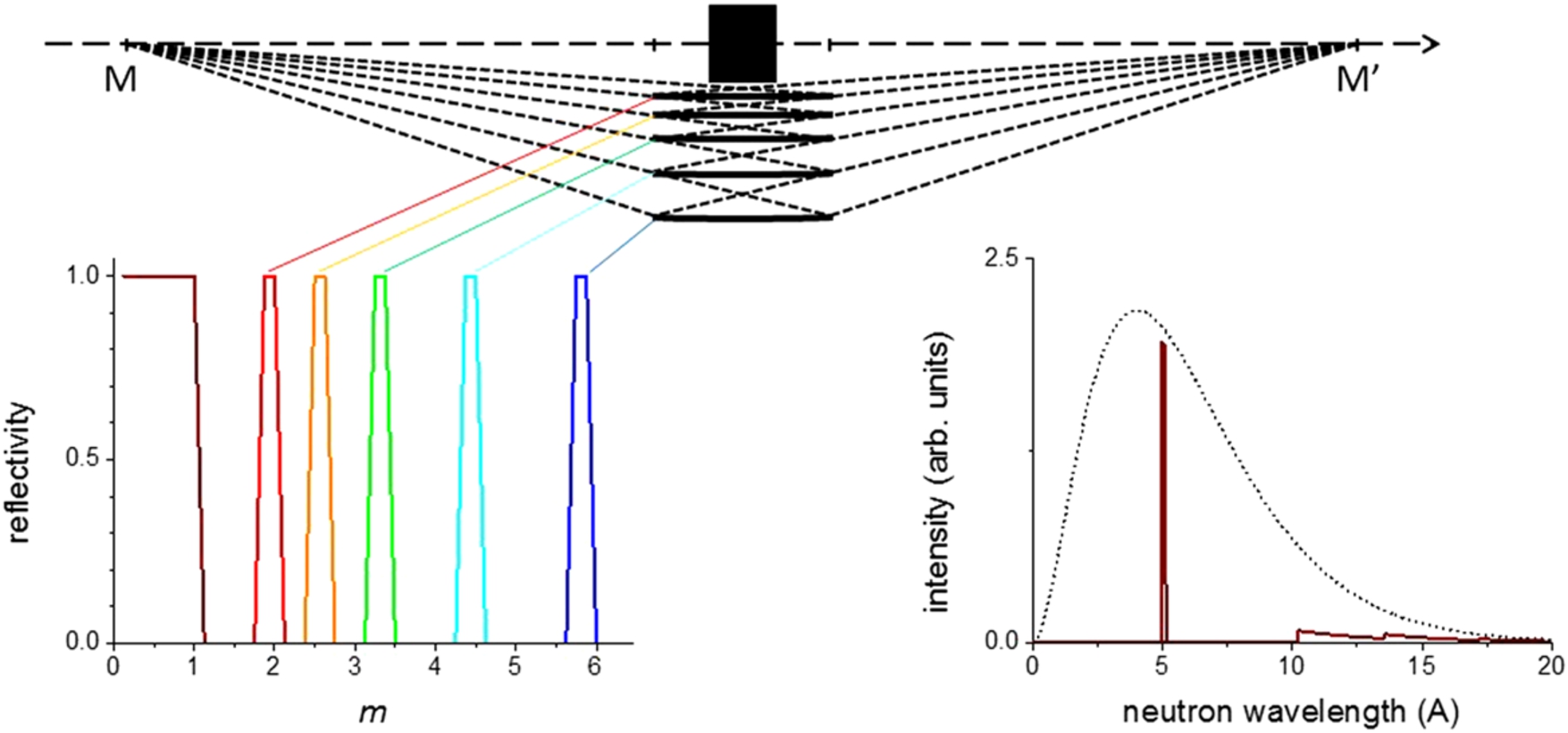
Fig. 3.
Effect of bandpass supermirror coatings on the neutron wavelength spectrum transported by a nested-mirror system. Reflectivity curves shown in the lower left graph (with indication of the locations of the corresponding mirrors by straight lines) are designed to transport from the incident spectrum (dashed curve in the lower right graph) a common narrow wavelength band at about 5 Å. Total reflectivity of the supermirrors (plateau for
3.Properties of the nested-mirror neutron transport systems
Key properties of the nested-mirror systems described in Section 2 are:
(a) They image a phase space element of a divergent neutron beam (from a source or the end of a guide) onto a phase space element of approximately equal size at the instrument. The smaller the ratio of mirror length over the distance MM′, the better defined is the image.
(b) They do (a) exclusively via single reflections (double reflections for the system 2a, one per transverse dimension) within a narrow range of reflection angles off each individual mirror. This range decreases with mirror length.
These two basic properties generate many possibilities to tailor main beam characteristics, including beam size and divergence, wavelength spectrum, and polarization. Taking advantage of these possibilities may significantly impact the quality of instruments for neutron scattering. Compared to a neutron delivery system where a guide ends close to the instrument, it becomes notably possible to maximize precisely the usable flux on the sample, while removing the useless flux far away from the instrument. This increases the signal-to-background ratio and hence also the sensitivity to weak scattering signals.
Beam size – As the mirror assemblies are imaging, the spatial part of beam phase space at the sample can be shaped by apertures close to the source (thus defining the “object” to be imaged). This blocks unwanted radiations the foremost beam upstream. Remotely controlled, these apertures can adapt the beam size to the sample in each individual experiment.
Beam divergence – The geometry of the mirror assembly defines the maximum divergence available for the instrument. Movable apertures in front or behind the mirrors can decrease the beam divergence in situ. This has two advantages: first, the transfer-momentum resolution can be selected in a well-defined manner to match the experimental needs and second, associated background radiations can be shielded far away from the detectors.
Anisotropic beam divergences may occur in various circumstances. They may originate from the source, due to moderator shape and/or geometrical constraints on beam tubes. Neutron scattering instruments often require anisotropic beams, notably if the detector array has a high unidimensional angular resolution. The primary beam divergence needs to be accordingly restricted in the scattering plane, whereas in the orthogonal direction the sample can be illuminated with a much larger divergence. Nested-mirror systems with movable apertures offer great versatility for trading resolution against intensity in experiments.
Neutron wavelength spectrum – The property (b) leads to interesting possibilities to tailor the spectrum. Due to reflection angles occurring in a narrow range about a finite value, each mirror provides a cut-off at short wavelength. By choosing appropriate m-values, one can set a common cut-off for the whole assembly, as illustrated in Fig. 2. In sharp contrast, a curved guide transports short-wavelength neutrons by garland reflections. Removal of these neutrons requires thicker shielding, due to the 1/v law for neutron absorption. They can even lead to false signals, such as due to second-order Bragg diffraction in crystal monochromators. Standard polycrystalline Bragg filters suppress them, however, at cost of some of the useful intensity and not without background. Nested-mirror imaging optics may supersede such devices.
If one needs neutrons only within a limited wavelength range, bandpass supermirrors can be used. In particular, as illustrated in Fig. 3, one can generate quasi-monochromatic spectra with a width of a few percent or less. This removes unwanted neutrons far beam upstream (e.g., in antireflection sublayers of the supermirrors). As a second advantage, bandpass supermirrors have a higher reflectivity at given m than full-bandwidth supermirrors and require by far less layers. An interesting option are quarter-wave bilayers which provide narrow spectra [17]. A double planar mirror system, as it involves two reflections, reduces the non-plateau reflectivity resulting from diffraction on the periodic superlattice. Nested-mirror systems might provide for many applications a spectral quality sufficient to avoid separate neutron velocity selectors or monochromators. However, total reflection at low m still contaminates the spectrum with long-wavelength neutrons. If this is a problem, one may consider the nested-mirror system be made of a stack of very short, flat mirrors deposited on highly transparent substrates that fill up the space between mirrors. The range of total reflection thus becomes reduced by a factor
As there is large freedom in the choice of the coatings of the individual mirrors, one can also imagine modulated beams with different wavelength spectra in different fractions of solid angle. One of the possibilities of such “angular-encoded multiplexed beams” is a device for monochromatic partial beams, providing high q resolution while simultaneously covering a wide range of neutron wavelengths.
Neutron polarization – Nested-mirror devices can also be equipped with polarizing supermirrors. As another consequence of the absence of garland reflections, total reflection has a weaker influence on the beam polarization so that such a device should perform better than a standard polarizing bender coupled to a neutron guide. Beam polarization values well beyond the current state of the art should be possible using the “crossed-polarizer” geometry [14], as long as depolarization in multilayers can be kept well under control [12]. A double planar nested-mirror system offers a natural implementation. A supermirror-based device for polarization analysis of divergent beams occurring in focusing neutron instruments can be found in Ref. [30]. Opaque spin filters can be used if extreme accuracy is required [13,35,40].
Neutron transfer losses of the nested-mirror systems originate partly from imperfect mirror reflectivity, partly from geometry and are partly due to gravity. As already discussed before, the impact of imperfect mirror reflectivity is smaller in a nested-mirror device than in an ordinary neutron guide, where multiple reflections may lead to quite drastic losses at high m. Geometrical losses are due to the finite size of the neutron source located at M; while the mirror assembly by construction covers a seamless range of angles subtended from the point M, a fraction of neutrons starting displaced by
4.Discussion and conclusions
As mentioned in the introduction, the initial motivation to consider nested-mirror optics was a neutron delivery issue for a potential in-beam UCN source at the ESS. Needed is a high brilliance transfer for neutrons with wavelengths around 9 Å from the small ESS moderator to the instrument. The solid angle should ideally be limited only by technically achievable mirror reflectivity. A simple ballistic guide would too much dilute the neutron phase space available at the moderator surface. The problem could be solved by optical imaging of the moderator to the UCN source, for which nesting of short elliptical (or very short flat) mirrors in a plane between two focal points was identified as a viable solution.
It turns out that, beyond initial intentions, nested-mirror systems offer interesting benefits also for neutron scattering instruments. They comply particularly well with the basic instrument design goal to transport only the neutrons actually needed (while removing distant from the instrument those neutrons that only create backgrounds). Imaging optics is able to tailor beam properties to match the size of the sample and properties of the instrument. It can thus deliver beams of higher quality than neutron guides. The situation is reminiscent to laser optics, where the analog of guides are optical fibers which deliver beams with less well defined properties.
Elliptic neutron guides [26] have been considered earlier as an extension of the ballistic-guide idea [10,18]. However, they do not provide an optical image of an extended source located in one of its mathematical focal points. Moreover, Monte-Carlo simulations showed that, even for a narrow beam, multiple reflections become increasingly common with increasing guide length [8]. Multiple reflections not only increase losses due to imperfect mirror reflectivity, but also generate complex structures in the divergence distribution. On the other hand, elliptic guides equipped with a central absorber were found to provide better background conditions than ordinary curved guides [6]. Improvement of beam homogeneities using concepts based on double elliptic guides is discussed in various papers [4,7,32,34]. Such schemes also reduce backgrounds which in a single elliptic guide with a central absorber were observed to stem from guide sections close to the sample with direct view on the moderator [5].
Imaging nested-mirror neutron transport systems involve less reflections than double elliptic guides. Beam size and divergence can be easily changed in situ by movable apertures close to the source and the mirrors. The signal-to-background ratio can thus be optimized for each experiment individually. This is also possible for elongated elliptic and/or Montel mirrors defining the phase space of neutrons at large distance from the sample, as pointed out in Ref. [5,29,31] in the context of delivering homogeneous neutron beams to study small samples. Truncation and nesting of long Montel or Kirkpatrick–Baez mirrors further increases the distance and reduces the spread of image magnifications which improves image quality. A change of the wavelength spectrum or switching between a polarized and a non-polarized beam is also possible. However, this would usually require an exchange of the whole mirror system, which is certainly an expensive option. Toroidal and planar systems described in this paper are even simpler in conception than (and involve only half of the reflections occurring in) Wolter imaging systems. These were first developed for x-rays and focus a parallel beam by double reflections off a combination of parabolic with hyperbolic or elliptical mirrors. Such systems were shown to be feasible for slow neutrons [19], for which a microscope based on three nested coaxial Wolter mirrors has already been demonstrated [16].
Opportunities that might follow from a pulse structure of the primary neutron beam were not in the focus of this paper and remain to be analyzed. For the implementation of pulse-tailoring choppers for instance, the only natural position seems close to the focal point M′ near the instrument. Another option would be, similar to double-elliptic guide schemes and accordingly adding more reflections, to use two nested-mirror systems with a shared intermediate focal point for the choppers.
Last but not least one should also not forget to mention purely practical advantages of the nested-mirror optics. As the mirrors are placed remote from the harsh environments close to an intense source, an exchange of beam tubes can be done without removal of neutron optical components. In addition, mirror lifetimes against degradation due to radiation will increase.
Coming finally back to a potential in-beam UCN source at the ESS, the projected ESS moderator brilliance of
In conclusion, imaging nested-mirror optics seem beneficial for various applications at reactor neutron sources and should also be further analyzed for future instrumentation at the European Spallation Source. Compact mirror systems might be interesting for neutron extraction from finger moderators of High Brilliance Sources [25] and in more exotic neutron source concepts [9].
References
[1] | K.H. Andersen, private communication. |
[2] | K.H. Andersen, M. Bertelsen, L. Zanini, E.B. Klinkby, T. Schönfeldt, P.M. Bentley and J. Saroun, Optimization of moderators and beam extraction at the ESS, J. Appl. Cryst. 51: ((2018) ), 264–281. doi:10.1107/S1600576718002406. |
[3] | K. Batkov, A. Takibayev, L. Zanini and F. Mezei, Unperturbed moderator brightness in pulsed neutron sources, Nucl. Instrum. Methods Phys. Res. A 729: ((2001) ), 500–505. doi:10.1016/j.nima.2013.07.031. |
[4] | P. Böni, New concepts for neutron instrumentation, Nucl. Instrum. Methods Phys. Res. A 586: ((2008) ), 1–8, Proceedings of the European Workshop on Neutron Optics (NOP2007). doi:10.1016/j.nima.2007.11.059. |
[5] | P. Böni, High intensity neutron beams for small samples, J. Phys.: Conf. Ser. 502: ((2014) ), 012047. |
[6] | P. Böni, F. Grünauer and C. Schanzer, Shielding of elliptic guides with direct sight to the moderator, Nucl. Instrum. Methods Phys. Res. A 624: ((2010) ), 162. doi:10.1016/j.nima.2010.09.015. |
[7] | L.D. Cussen, T. Krist and K. Lieutenant, A new guide concept for a homogenous neutron beam without direct line of sight, Nucl. Instrum. Methods Phys. Res. A 777: ((2015) ), 6–14. doi:10.1016/j.nima.2014.12.003. |
[8] | L.D. Cussen, D. Nekrassov, C. Zendler and K. Lieutenant, Multiple reflections in elliptic neutron guide tubes, Nucl. Instrum. Methods Phys. Res. A 705: ((2013) ), 121–131. doi:10.1016/j.nima.2012.11.183. |
[9] | D. Habs, M. Gross, P.G. Thirolf and P. Böni, Neutron halo isomers in stable nuclei and their possible application for the production of low energy, pulsed, polarized neutron beams of high intensity and high brilliance, Appl. Phys. B 103: ((2011) ), 485–499. doi:10.1007/s00340-010-4276-3. |
[10] | H. Häse, A. Knöpfler, K. Fiederer, U. Schmidt, D. Dubbers and W. Kaiser, A long ballistic supermirror guide for cold neutrons at ILL, Nucl. Instrum. Methods Phys. Res. A 485: ((2002) ), 453. doi:10.1016/S0168-9002(01)02105-2. |
[11] | P. Kirkpatrick and A.V. Baez, Formation of optical images by X-rays, Journal Opt. Soc. Am. 38: ((1948) ), 766–774. doi:10.1364/JOSA.38.000766. |
[12] | C. Klauser, T. Bigault, P. Böni, P. Courtois, A. Devishvili, N. Rebrova, M. Schneider and T. Soldner, Depolarization in polarizing supermirrors, Nucl. Instrum. Methods Phys. Res. A 840: ((2016) ), 181–185. doi:10.1016/j.nima.2016.09.056. |
[13] | C. Klauser, J. Chastagnier, D. Jullien, A. Petukhov and T. Soldner, High precision depolarisation measurements with an opaque test bench, J. Phys.: Conf. Ser. 340: ((2012) ), 012011. doi:10.1088/1742-6596/340/1/012011. |
[14] | M. Kreuz, V. Nesvizhevsky, A. Petukhov and T. Soldner, The crossed geometry of two supermirror polarisers – A new method for neutron beam polarisation and polarisation analysis, Nucl. Instrum. Methods Phys. Res. A 547: ((2005) ), 583–591. doi:10.1016/j.nima.2005.03.154. |
[15] | K.K.H. Leung, S. Ivanov, F.M. Piegsa, M. Simson and O. Zimmer, Ultracold neutron production and up-scattering in superfluid helium between 1.1 K and 2.4 K, Phys. Rev. C 90: ((2016) ), 025501. doi:10.1103/PhysRevC.93.025501. |
[16] | D. Liu, D. Hussey, M.V. Gubarev, B.D. Ramsey, D. Jacobson, M. Arif, D.E. Moncton and B. Khaykovich, Demonstration of achromatic cold-neutron microscope utilizing axisymmetric focusing mirrors, Appl. Phys. Lett. 102: ((2013) ), 183508. doi:10.1063/1.4804178. |
[17] | S. Masalovich, Analysis and design of multilayer structures for neutron monochromators and supermirrors, Nucl. Instrum. Methods Phys. Res. A 722: ((2013) ), 71. doi:10.1016/j.nima.2013.04.051. |
[18] | F. Mezei, The raison d’être of long pulse spallation sources, J. Neutron Res. 6: ((1997) ), 3. doi:10.1080/10238169708200095. |
[19] | D.F.R. Mildner and M.V. Gubarev, Wolter optics for neutron focusing, Nucl. Instrum. Methods Phys. Res. A 634: ((2011) ), S7. doi:10.1016/j.nima.2010.06.093. |
[20] | M. Montel, X-ray microscopy with catamegonic roof mirrors, in: X-Ray Microscopy and Microradiography, M. Montel, ed., Academic Press, New York, (1957) , pp. 177–185. |
[21] | H.A. Mook and J.B. Hayter, Transmission optical device to produce intense polarized neutron beams, Appl. Phys. Lett. 53: ((1988) ), 648. doi:10.1063/1.99840. |
[22] | J.M. Pendlebury and G.L. Greene, Considerations for an intense source of ultracold neutrons at the European long pulse Spallation Source, Phys. Procedia 51: ((2014) ), 78–84. doi:10.1016/j.phpro.2013.12.018. |
[23] | D.G. Phillips, W.M. Snow, K. Babu, S. Banerjee, D.V. Baxter, Z. Berezhiani, M. Bergevin, S. Bhattacharya, G. Brooijmans, L. Castellanos, M.-C. Chen, C.E. Coppola, R. Cowsik, J.A. Crabtree, P. Das, E.B. Dees, A. Dolgov, P.D. Ferguson, M. Frost, T. Gabriel, A. Gal, F. Gallmeier, K. Ganezer, E. Golubeva, G. Greene, B. Hartfiel, A. Hawari, L. Heilbronn, C. Johnson, Y. Kamyshkov, B. Kerbikov, M. Kitaguchi, B.Z. Kopeliovich, V.B. Kopeliovich, V.A. Kuzmin, C.-Y. Liu, P. McGaughey, M. Mocko, R. Mohapatra, N. Mokhov, G. Muhrer, H.P. Mumm, L. Okun, R.W. Pattie, C. Quigg, E. Ramberg, A. Ray, A. Roy, A. Ruggles, U. Sarkar, A. Saunders, A.P. Serebrov, H.M. Shimizu, R. Shrock, A.K. Sikdar, S. Sjue, S. Striganov, L.W. Townsend, R. Tschirhart, A. Vainshtein, R. Van Kooten, Z. Wang and A.R. Young, Neutron-antineutron oscillations: Theoretical status and experimental prospects, Phys. Rep. 612: ((2016) ), 1–45. doi:10.1016/j.physrep.2015.11.001. |
[24] | F.M. Piegsa, M. Fertl, S.N. Ivanov, M. Kreuz, K.K.H. Leung, P. Schmidt-Wellenburg, T. Soldner and O. Zimmer, New source for ultracold neutrons at the Institut Laue Langevin, Phys. Rev. C 90: ((2014) ), 015501. doi:10.1103/PhysRevC.90.015501. |
[25] | U. Rücker, T. Cronert, J. Voigt, J.P. Dabruck, P.-E. Doege, J. Ulrich, R. Nabbi, Y. Beßler, M. Butzek, M. Büscher, C. Lange, M. Klaus, T. Gutberlet and T. Brückel, The Jülich high-brilliance neutron source project, Eur. Phys. J. Plus 131: ((2016) ), 19. doi:10.1140/epjp/i2016-16019-5. |
[26] | C. Schanzer, P. Böni, U. Filges and T. Hils, Advanced geometries for ballistic neutron guides, Nucl. Instrum. Methods Phys. Res. A 529: ((2004) ), 63. doi:10.1016/j.nima.2004.04.178. |
[27] | P. Schmidt-Wellenburg, K.H. Andersen and O. Zimmer, Ultra-cold neutron production by multiphonon processes in superfluid helium under pressure, Nucl. Instrum. Methods Phys. Res. A 611: ((2009) ), 259. doi:10.1016/j.nima.2009.07.085. |
[28] | P. Schmidt-Wellenburg, J. Bossy, M. Fertl et al., Experimental study of ultracold neutron production in pressurized superfluid helium, Phys. Rev. C 92: ((2015) ), 024004. doi:10.1103/PhysRevC.92.024004. |
[29] | J. Stahn, U. Filges and T. Panzner, Focusing specular neutron reflectometry for small samples, Europ. Phys. J. Appl. Phys. 58: ((2012) ), 11001. doi:10.1051/epjap/2012110295. |
[30] | J. Stahn and A. Glavic, Efficient polarization analysis for focusing neutron instruments, J. Phys.: Conf. Ser. 862: ((2017) ), 012007. doi:10.1088/1742-6596/862/1/012007. |
[31] | J. Stahn, T. Panzner, U. Filges, C. Marcelot and P. Böni, Study on a focusing, low-background neutron delivery system, Nucl. Instrum. Methods Phys. Res. A 634: ((2011) ), S12–S16. doi:10.1016/j.nima.2010.06.221. |
[32] | S. Wechselbaumer, G. Brandl, R. Georgii, J. Stahn, T. Panzner and P. Böni, Tailoring phase-space in neutron beam extraction, Nucl. Instrum. Methods Phys. Res. A 793: ((2015) ), 75–80. doi:10.1016/j.nima.2015.05.003. |
[33] | L. Zanini, K. Batkov, E.B. Klinkby, F. Mezei, E. Pitcher, T. Schönfeldt and A. Takibayev, Proceedings of ICANS XXI, 29 September–3 October, Mito, Japan, 2014, pp. 126–133, http://www.neutronresearch.com/parch/2014/01/201401001260.pdf. |
[34] | C. Zendler, D. Nekrassov and K. Lieutenant, An improved elliptic guide concept for a homogeneous neutron beam without direct line of sight, Nucl. Instrum. Methods Phys. Res. A 746: ((2014) ), 39–46. doi:10.1016/j.nima.2014.01.044. |
[35] | O. Zimmer, A method for precise neutron beam polarisation analysis using an opaque spin filter, Phys. Lett. B 461: ((1999) ), 307. doi:10.1016/S0370-2693(99)00857-6. |
[36] | O. Zimmer, Superfluid-helium ultracold neutron sources: Concepts for the European Spallation Source? ESS Sci. Symp. Neutron Particle Physics at long pulse spallation sources, Phys. Procedia 51: ((2014) ), 85–88. doi:10.1016/j.phpro.2013.12.019. |
[37] | O. Zimmer, Multi-mirror imaging optics for low-loss transport of divergent neutron beams and tailored wavelength spectra, 2016, arXiv:1611.07353v1. |
[38] | O. Zimmer, K. Baumann, M. Fertl, B. Franke, S. Mironov, C. Plonka, D. Rich, P. Schmidt-Wellenburg, H.-F. Wirth and B. van den Brandt, Superfluid helium converter for accumulation and extraction of ultracold neutrons, Phys. Rev. Lett. 99: ((2007) ), 104801. doi:10.1103/PhysRevLett.99.104801. |
[39] | O. Zimmer and R. Golub, Ultracold neutron accumulation in a superfluid-helium converter with magnetic multipole reflector, Phys. Rev. C 92: ((2015) ), 015501. doi:10.1103/PhysRevC.92.015501. |
[40] | O. Zimmer, T.M. Müller, P. Hautle, W. Heil and H. Humblot, High-precision neutron polarization analysis using opaque spin filters, Phys. Lett. B 455: ((1999) ), 62. doi:10.1016/S0370-2693(99)00345-7. |
[41] | O. Zimmer, F.M. Piegsa and S. Ivanov, Superthermal source of ultracold neutrons for fundamental physics experiments, Phys. Rev. Lett. 107: ((2011) ), 134801. doi:10.1103/PhysRevLett.107.134801. |
[42] | O. Zimmer, P. Schmidt-Wellenburg, M. Assmann, J. Klenke and B. van den Brandt, Ultracold neutrons extracted from a superfluid-helium converter coated with fluorinated grease, Eur. Phys. J. C 67: ((2010) ), 589. doi:10.1140/epjc/s10052-010-1327-1. |




