A video processing algorithm using temporal intuitionistic fuzzy sets

1Introduction

The set theory devised by George Cantor is the foundation of modern mathematics and definitions of the most fundamental mathematical terms are based on sets. A set is a well-defined collection of objects. Here, well-defined means that there is a definite method to determine whether an object belongs to the set. Generally, a set is described by a two-valued function called characteristic function.

The real-world situations are often associated with built-in uncertainties. Hence, fuzzy sets, introduced by Lotfi A Zadeh –blurred, vague, indistinct quantities –this means that sets and their surroundings, their complement within the universe of discourse, are connected. In the usual diagrammatic notation of sets as circles, fuzzy sets appear to be sets with indistinct edges. There are objects at the boundaries of the circle that belongs to the fuzzy set and its complement, and hence the complement of a fuzzy set is again a fuzzy set [44]. A fuzzy set is characterized by its membership function. The membership grade in a fuzzy set is not a matter of affirmation or denial, but rather a matter of degree. In fuzzy set theory, the membership of an element to a fuzzy set is a single value between zero and one.

Due to the insufficiency in the availability of information, the evaluation of membership values is sometimes not possible up to our satisfaction. Therefore a generalization of fuzzy sets was introduced by Krassimir T Atanassov in 1983 as intuitionistic fuzzy sets (IFSs), which include both membership and non-membership of the element in the set, where the non-membership value equals one minus the membership value. However, in reality, it may not exist, because there remains a part indeterministic on which hesitation survives. This value is called the intuitionistic fuzzy index (hesitancy index). In such situations, the theory of IFS seems to be applicable to address this issue of uncertainty. In the case, when the degree of rejection is defined simultaneously with the degree of acceptance and when both these degrees are not complementary to each other, then IFS can be used as a more general tool for describing uncertainty. The authors got motivated from the following few open problems on the intuitionistic fuzzy set (IFS) and its extensions available in [24].

i. To investigate the properties of IFS in the field of image processing, pattern recognition, networks for finding the shortest route.

ii. Develop efficient algorithms for the construction of the degree of membership and non-membership of a given IFSs.

iii. To develop algorithms for defuzzification and comparison of IFSs.

Hence, an attempt has been made to work on these three problems to provide an IF logic tool for video processing.

Video processing tends to have uncertainties that vary each second. This tempts to propose the ‘temporal’ concept for the IFS. Video processing is a subset of image processing where the video is dissolved as frames and processed and again assembled to the output as a video. The process of dissolving and assembling takes time and hence many video processing algorithms tend to be slow and deviate in terms of accuracy. The video consists of a set of images/frames. The image/frame is defined with the help of pixels. TIFS are introduced in [27].

Function: Let two sets X and Y be given and suppose that to each element x ∈ X corresponds an element y ∈ Y which is denoted by f (x). Here, f is said to be a function given on X and written as f: X → Y.

Operator: An operator is a mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order relation). The general definition of an operator coincides with the definition of a mapping or function. Let X and Y be two sets. A rule or correspondence which assigns a uniquely defined element A (x) ∈ Y to every element x of a subset D ⊂ X is called an operator A from X into Y. Symbolically, A : D → Y where D ⊂ X.

The role of contrast intensification on sets, fuzzy sets, IFSs and TIFSs in image and video processing is discussed, in detail, in the forthcoming sections of this paper. In section 2, review of literature is given. In Section 3, the basic concepts of intuitionistic fuzzy sets and a few operations over them are defined. Also, image representation using sets, fuzzy sets and intuitionistic fuzzy sets are discussed. Section 4 deals with operations like Aⁿ, nA, contrast intensification, dilation and erosion on FSs and IFSs. Section 5 is dediacted to TIFSs. Intuitionistic fuzzy inference system is explained in Section 6. VIPROC algorithm, its implementation and results and discussion are given in Sections 7, 8 and 9 respectively. Section 10 concludes the paper.

2Literature review

Melo-pinto et al. described a thresholding technique using Atanassov’s intuitionistic fuzzy sets (A-IFSs). This approach uses Atanassov’s intuitionistic index values for representing the hesitance of the expert in determining whether the pixel belongs to the background or to the object. Segmentation experimental results and comparison with Otsu’s multilevel thresholding algorithm for the calculation of two and three thresholds are presented by them [34].

A new distance measure called intuitionistic fuzzy divergence, has been proposed and edge detection is carried out in [47].

In [16], the issue of moving object detection using a background subtraction technique is addressed. There are complex conditions in the real world video sequences that show multi-modal distributions of a scene. These multi-modal distributions cannot be modeled by just one feature. So, different image features should be extracted and fused to handle such conditions. The extracted features should be complement to each other. Hence, to efficiently model these multi-modal distributions, the authors propose fusing color and texture features using Choquet fuzzy integral. To capture spatial information, the spatial color features are extracted by Atanassov’s Intuitionistic Adaptive 3D Fuzzy Histon Rough-ness Index. Additionally, some texture features are extracted by a covariance matrix. Moreover, the authors proposed a novel model updating method than can cope with a number of challenges such as model initializing with moving objects, fast/slow moving object detection, and the moving objects that stop for a while. The proposed method is evaluated on a number of benchmark video sequences representing various real-world challenges. Results demonstrated that the proposed method can outperform the state-of-the-art methods in most of the experimented scenarios and challenges.

Pagola et al. present a valuable review of the recent works using extensions of fuzzy sets in image processing. The basics of the extensions of fuzzy sets are recalled. That is, type-2 fuzzy sets, interval-valued fuzzy sets and Atanassov’s IFSs. Also, a review on the proposed methods for noise removal, image enhancement, edge detection and segmentation is made [37].

In [21], a new construction method of IVFSs from fuzzy sets is presented. Also, the authors use these IVFSs for image processing. Concretely, in this contribution they introduced a new image magnification algorithm using IVFSs. This algorithm is based on block expansion and it is characterized by its simplicity.

Tizhoosh’s algorithm makes it possible to obtain additional information from commonly used fuzzy algorithms. In [3], the authors proved that Tizhoosh’s algorithm performs better than area algorithm. Therefore, the use of Tizhoosh’s algorithm in image processing and the use of interval-valued fuzzy sets is justified.

Research on video processing is a continuously explored area that is still finding immense applications in diverse domains. But its goal remains unchanged: Extraction of the desired target from the image frame is considered. There has been a huge increase in Internet Protocol (IP) based digital cameras from analog cameras. It has been estimated that 25% to 50% of the cameras have video analysis processors built in them. Some video analysis techniques such as extraction of features and categorization of objects are used for the desired target. Another important technique is pre-processing which results in more accuracy while analyzing the video in further stages of the processing [42].

Two-dimensional textures were studied to some extent in the past. Yet, there is relatively very less research and results on the three-dimensional dynamic textures that express certain time-varying properties in the video processing. In many frames, the regions have important structural similarities and exhibit high temporal correlations between image frames extracted from the actual video. The dynamic textures draw some disadvantages in motion detection and analysis. With the use of segmentation and exclusion of the dynamic textures in the image frames, the robust nature of the motion detection and action identification is improved [7]. The study introduces an optical flow-based to represent temporal video information. This type of approach is suited for the segmentation of the temporal video. This problem can be converted as a cut detection problem since it is the phase I of the content-based video information retrieval. In the first step, optical flow vectors are calculated and this representation is employed for the cut detection. The important aspect of the proposed idea is the way it solves the temporal video representation problem in a video information retrieval domain. Adding to the established results, this proposed way of representation acts as a solution for the dimensionality problem for the video data [44].

The main contents in the surveillance include the detection of human movements and the estimation of the population density and their tracking [19]. The study aims to extract and analyze different types of extraction of features from the video frames [10]. But, the problem of objective perspective deformation has more influence on the detection accuracy in all kinds of video monitoring analysis. Solving the problem of objective perspective deformation on the video feature extraction and analysis is an important aspect that has to be studied in several video analysis algorithms. The work proposes a perspective normalization weights that are compared with the linear perspective weights of the existing literature that is used in the moving object detection processing algorithms in the later stages. The results reveal that this method can solve the impact of the perspective distortion concerning the accuracy of the video analysis [2]. The recent developments in video processing that uses deep learning primitives have given way to several breakthroughs in the basic and important issues of video analysis such as classification of frames and detection of objects. These developments give way to a new list of applications. More particularly, Nick et al.introduce a set of approximate filters the speeds up issues involving the target objects in the particular video frame and their spatial relations. These filters can access fast if the issue predictions are true to proceed with more analysis for the frame or else leave for the next frame with minimizes the cost of the operations for the present frame. The work has proposed a set of filters for the estimation of the number of objects in a frame, the number of objects of a specific class in a frame as well as to assess an estimate of the spatial position of an object in a frame enabling us to reason out spatial constraints. These filters are ranked based on accuracy and their high accuracy in counting and their use for location estimation are proved experimentally with the help of real video data [36].

Based on fuzzy set modelling and fuzzy intensification operator, an implementation of contrast enhancement in the compressed domain is presented [13]. A Gaussian membership function to model image information in spatial domain has been proposed in [18]. Three enhancement techniques namely fuzzy rule based contrast enhancement, contrast enhancement using intensification (INT) operator, and contrast enhancement using fuzzy expected value (FEV) are presented for the low contrast grayscale images [45]. The contrast of Flat Electroencephalography (fEEG) image is enhanced by using a fuzzy approach. The fEEG image itself is a fuzzy object which is in grayscale. It is originated from a technique known as fEEG which mapped high dimensional signal into low dimensional space [46]. Detailed image analysis has been done using different qualitative attributes of the image in the simulation. The results show better enhancement in image contrast. It can be obtained by taking a different membership function for transformation of membership values in the fuzzy domain [32].

The contrast and sharpness of the images captured under water will be significantly deteriorated and diminished due to the low perceptibility of the image caused by the physical properties of water as a medium. An improved version of CLAHE mechanism is used to enhance color images by using dynamic histogram equalization technique [29]. In real-life situations, this type of document occurs as handwritten/printed text and historical documents. Contrast intensification operator on IFSs can be used to improve the quality of such degraded images [20]. Acquiring human gait data can be erroneous due to various factors and multimodal fusion of such erroneous gait data can be challenging. This work proposed a new decision fusion-based approach to solve the above problem. Gait data is recorded simultaneously using motion sensors and a visible light camera. The signals of the motion sensors are modelled using a Long Short Term Memory (LSTM) neural network and corresponding video recordings are processed using a 3D Convolutional Neural Network (CNN). GWO has been used to optimize the parameters during fusion. It has been chosen based on the underlying hunting strategy that leads to a better approximation of the solution and interestingly, in our case it converges quicker than other optimization techniques such as Genetic Algorithm (GA) or Particle Swarm Optimization (PSO) [29].

Object tracking from video sequences, although well researched, still faces difficulties under certain challenging situations. The work proposed a new particle filter-based tracking, where the fuzzy observation model exploits spatial correlation in a rough set-theoretic framework. It further improved certain critical steps of the particle filter such as mean state estimation and resampling [8]. A novel concept, namely, intuitionsistic entropy is introduced in [6] which consists of two new measures: neighborhood rough entropy and neighborhood probabilistic entropy to deal with the ambiguities that arise due to occurrence of overlapping/occlusion in a video sequence.

In [31], a novel system design framework for dynamic, data-driven processing of multispectral video streams using lightweight dataflow (LD) techniques is introduced. The authors of [40] made a survey on maritime object detection and tracking approaches are presented. In [9], an ensemble of three video processing techniques are benchmarked against each other and tested as viable options for the non-contact dynamic characterisation of slender beam-like structures. A novel 3D fuzzy method for the denoising of color videos corrupted by additive noise is presented [48]. Intuitionistic logic based on block matching techniques has been used to strongly and proficiently detect abandoned objects based on background subtraction is presented [41].

In a nutshell, the following are the two main reasons to introduce the proposed algorithm. (i) After making a thorough study/survey on video processing techniques/algorithms, it is observed that temporal IFS theory is not applied to design and develop an algorithm for processing videos. (ii) The authors are working on image processing and made a notable contribution in image processing using IFS theory. Therefore, the authors are interested to apply temporal IFS theory in video processing.

In this paper, the proposed VIPROC Algorithm is meant for contrast enhancement of a video using contrast intensification operator on TIFSs and this approach is first of its method.

3Image representation using sets, FSs and IFSs

In this section, an overview is given on geometric interpretation of Sets, FSs and IFSs. In addition, the mathematical representation of images using Sets, FSs and IFSs are also discussed.

A set A of a universal set X can be defined by its characteristic function χ_A as a mapping from the elements of the Universal set X to the values of the set {0, 1}: that is, χ_A: X → {0, 1}.

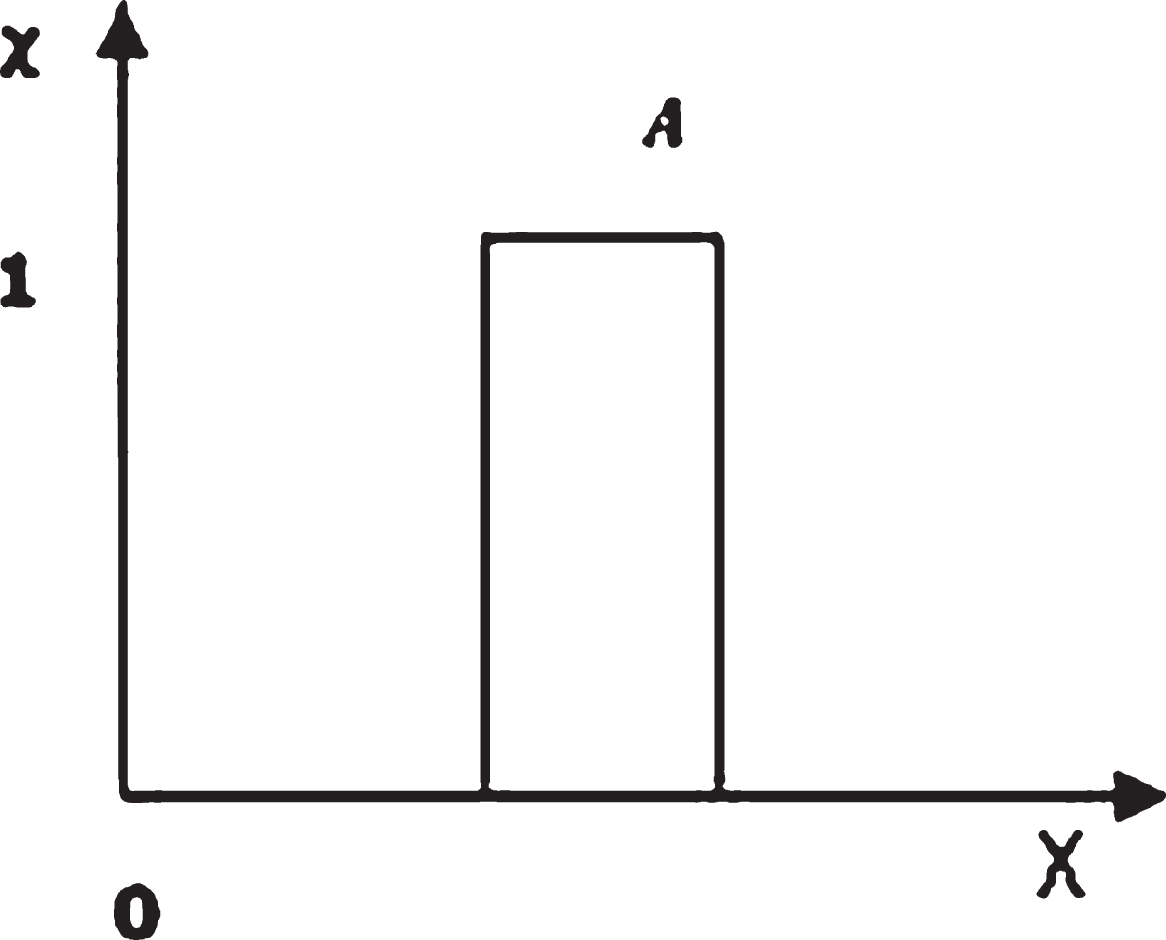
The mapping may be represented as a set of ordered pairs {(x, χ_A (x))} with exactly one ordered pair present for each element of X. The first element of the ordered pair is an element of the set X and the second is its value in {0, 1}. The value 0 is used to represent non-membership and the value 1 is used to represent the membership of the element of A. The truth or falsity of the statement ‘x is in A’ is determined by the ordered pair. The statement is true, if the second element of the ordered pair is 1, and the statement is false if it is 0. [Fig. 1].

Fig. 1

Sets.

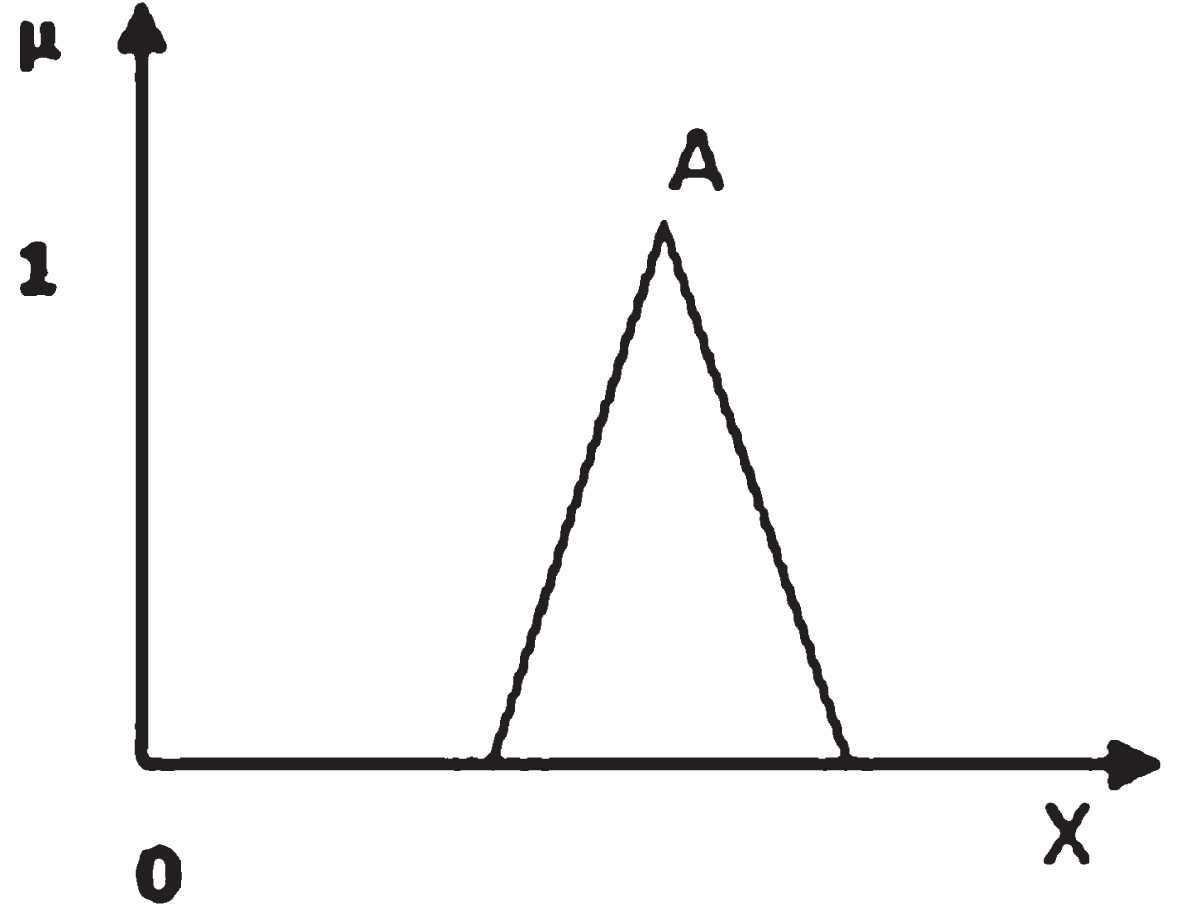
Let X be a non-empty set. A fuzzy set (FS) A in X is characterized by its membership function μ_A : X → [0, 1] and μ_A (x) is interpreted as the degree of membership of element x in fuzzy set A, for each x ∈ X. A is completely determined by, A = {(x, μ_A (x)) |x ∈ X}. [Fig. 2].

Fig. 2

Fuzzy Sets.

Let X be a non-empty set. An intuitionistic fuzzy set (IFS) A in X is defined as an object of the form A = {(x, μ_A (x)) , ν_A (x)) : x ∈ X} where μ_A : X → [0, 1] and ν_A : X → [0, 1] denote the membership and non-membership functions of A respectively, and 0 ≤ μ_A (x) + ν_A (x) ≤1, for each x ∈ X. The intuitionistic fuzzy set can also be written in the form A = 〈μ_A (x) , ν_A (x) 〉 or simply, A = (μ_A, ν_A). [Fig. 3].

Fig. 3

First geometrical interpretation of an IFS A [24].

For a clear understanding of intuitionistic fuzzy set, other similar diagrammatic representations are given in Figs. 4 and 5.

Fig. 4

An analogue of the first geometrical interpretation of an IFS A [24].

Fig. 5

Second geometrical interpretation of an IFS A [24].

An ordinary fuzzy set can also be written as A = {(x, μ_A (x)) , 1 - μ_A (x)) : x ∈ X}. That means all the fuzzy sets are IFSs, but the converse is not true. The value π_A (x) =1 - μ_A (x) - ν_A (x) is called the degree of non-determinacy (or the degree of uncertainty) of the element x ∈ X to the intuitionistic fuzzy set A.

A monochrome image, or simply, image (having various shades of gray) is represented mathematically by a spatial brightness function f (m, n) where (m, n) denotes the spatial coordinates of a point in the (flat) image. The value of f (m, n), 0< f (m, n) < ∞, is proportional to the brightness value or gray level of the image at the point (m, n). For computer processing, the continuous function f (m, n) has been discretized both in spatial coordinates and in brightness. Such an approximated image X (digitized) can be considered as an m × n array.

whose row and column indices identify a point (m, n) in the image and the corresponding matrix element value x_mn denotes the gray level at that point. The right side of the equation (1) represents what is called a digital image. Each element of the matrix, which is a discrete quantity, is referred to as an image element or picture element (pixel). From now on the terms ‘image’ and ‘pixel’ will be used to denote a digital image and its elements respectively. For processing, this image along with the coordinates of its pixels is stored in the computer in the form of an array of mn numbers.

Example: image –digital image: An image is a two-dimensional function f (x, y), where x and y are the spatial (plane) coordinates, and the amplitude of f at any pair of coordinates (x, y) is called the intensity of the image at that level. If x, y and the amplitude values of f are finite and discrete quantities, we call the image a digital image. A digital image is composed of a finite number of elements called pixels, each of which has a particular location and value.

In recent years, many researchers have applied the theories of fuzzy sets and intuitionistic fuzzy sets and their extensions to develop new techniques for contrast improvement.

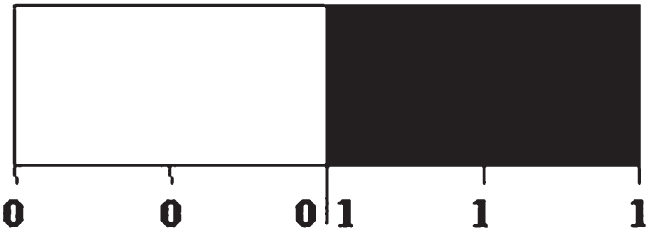
As discussed earlier, a crisp set A is described by its characteristic function χ_A : X → {0, 1}, which is a two valued logic. Hence, binary (Black and White) images are represented by the sets. In matrix notation, a binary image A with m rows and n columns is represented as,

A = [〈x_ij, χ_A (x_ij) 〉] _m×n .

Figure 6 depicts a binary image (white is assigned ‘0’ and black is assigned ‘1’).

Fig. 6

Binary Image.

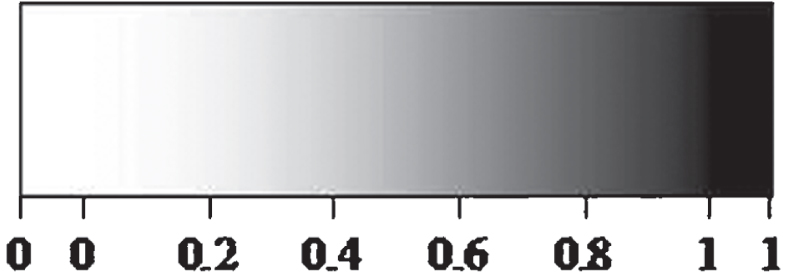
A fuzzy set, A is described by its membership function μ_A : X → [0, 1] which is many-valued logic. Hence, gray images are represented by fuzzy sets. Therefore, a gray image A with m rows and n columns is mathematically represented in matrix form as

A = [〈x_ij, μ_A (x_ij) 〉] _m×n .

Figure 7 shows a gray image scale with ‘0’ for white, ‘1’ for black and between ‘0’ and ‘1’ for gray.

Fig. 7

Grayscale Image

An intuitionistic fuzzy set, A is described not only by its membership function μ_A : X → [0, 1] but also by its non-membership function ν_A : X → [0, 1] such that 0 ≤ μ_A (x) + ν_A (x) ≤1. Specifically, degree of hesitency defined by the function, π_A : X → [0, 1] also plays role in describing IFS satisfying μ_A (x) + ν_A (x) + π_A (x) =1 for every x ∈ X.

Hence, it is noteworthy that a RGB image can be represented by an IFS, by taking three functions to define three colors. Therefore, a RGB image A is represented in matrix notation as

A = [〈x_ij, μ_A (x_ij) , ν_A (x_ij) , π_A (x_ij) 〉] _m×n .

This representation is given in Figs. 8 and 9.

Fig. 8

RGB Color map [19].

Fig. 9

Equilateral triangle geometrical interpretation of an IFS A [11].

4Contrast intensification operator

In this section, the basic concepts of intuitionistic fuzzy sets and operations like Aⁿ, nA and contrast intensification on these sets are defined and discussed.

Let X be a non-empty set. Let A and B be two IFSs such that A = {〈x, μ_A (x) , ν_A (x) 〉 : x ∈ X} and B = {〈x, μ_B (x) , ν_B (x) 〉 : x ∈ X} .

Define the following operations on A and B:

i. A . B = {〈x, μ_A (x) . μ_B (x) , ν_A (x) + ν_B (x) - ν_A(x) . ν_B (x) 〉 : x ∈ X}, [23]

ii. Aⁿ = {〈x, μ_A (x) ⁿ, 1 - (1 - ν_A (x)) ⁿ〉 : x ∈ X}, for any positive real n, [12]

iii. nA = {〈x, 1 - (1 - μ_A (x)) ⁿ, ν_A (x) ⁿ〉 : x ∈ X}, for any positive real n. [12]

Further, the operation contrast intensification has the effect of altering the intuitionistic fuzziness in an intuitionistic fuzzy set A.

Contrast intensification, as its name implies, reduces the fuzziness of A by increasing those of μ_A (x) which are above 0.5, and decreasing those which are below it.

The contrast intensification of a fuzzy set A of the Universe X, denoted by INTEN (A), is defined by INTEN (A) = {(x, μ_INTEN (x) : x ∈ X} , where

The contrast intensification of an IFS A of the Universe X, denoted by INTEN (A), is defined by INTEN (A) = {(x, μ_INTEN (x) , ν_INTEN (x)) : x ∈ X} , where μ_INTEN (x) =1 - (1 - μ_A (x)) ² and ν_INTEN (x) = [1 - (1 - ν_A (x)) ²] ².

5Temporal IFSs and their operations

In the previous section, IFSs and their role in image processing are dealt with. This section is dedicated to TIFSs and their operations. TIFSs give a possibility to trace the changes of the object considered for all the time moments from a time scale and permit more detailed estimations of the real time processes flowing in time.

Let X be the Universe and T be a non-empty set of time moments (T is a fixed set which we shall call ‘time-scale’ and it is strictly oriented by the relation ‘<’). Then a temporal intuitionistic fuzzy set is defined as A (T) = {〈 (x, t) , μ_A (x, t) , ν_A (x, t) 〉 : (x, t) ∈ X × T}, where

(1) A ⊂ X is a fixed set,

(2) 0 ≤ μ_A (x, t) + ν_A (x, t) ≤1 for all (x, t) ∈X × T,

(3) μ_A (x, t) and ν_A (x, t) denote the degrees of membership and non-membership respectively of the element x in X and at the time –moment t in T.

The geometrical representation of TIFS is given in Fig. 10.

Fig. 10

Geometrical interpretation of TIFS A (T) [25].

Hence, it is very important to note from Fig. 10 that each triangle represents a frame of a video. The operations on TIFSs are useful to enhance the quality of a video. They are defined as follows.

Let X be a non-empty set and T be a non-empty set of time-moments. Let A (T) and B (T) be two TIFSs such that A (T) = {〈 (x, t) , μ_A (x, t) , ν_A (x, t) 〉 : (x, t) ∈ X × T} and B (T) = {〈 (x, t) , μ_B (x, t) , ν_B (x, t) 〉 : (x, t) ∈ X × T} .

Define the following operations on A (T) and B (T):

(1) A (T) . B (T) = {〈 (x, t) , μ_A (x, t) . μ_B (x, t) , ν_A(x, t) + ν_B (x, t) - ν_A (x, t) . ν_B (x, t) 〉 : (x, t) ∈ X × T},

(2) A (T) ⁿ = {〈 (x, t) , μ_A (x, t) ⁿ, 1 - (1 - ν_A(x, t)) ⁿ〉 : (x, t) ∈ X × T}, for any positive real n,

(3) nA (T) = {〈 (x, t) , 1 - (1 - μ_A (x, t)) ⁿ, ν_A(x, t) ⁿ〉 : (x, t) ∈ X × T}, for any positive real n.

The contrast intensification of a TIFS A (T) of the Universe X, denoted by INTEN (A (T)), is defined by

INTEN (A (T)) = {〈 (x, t) , μ_INTEN (x, t) , ν_INTEN(x, t) 〉 : (x, t) ∈ X × T},

where μ_INTEN (x, t) =1 - (1 - μ_A (x, t)) ² and ν_INTEN (x, t) = [1 - (1 - ν_A (x, t)) ²] ².

6Intuitionistic fuzzy inference system

The design of the traditional logic controller [34] usually requires a mathematical model of the process involved. The construction of such a model is difficult for many real-world problems due to partial or unreliable information. The imprecise description of the problem can be handled as an alternative approach by expert human operations. This modeling leads to the usage of fuzzy concepts that are close to human perception than the traditional logical system. The basic structure of an intuitionistic fuzzy inference system is shown in Fig. 11.

Fig. 11

Structure of an intuitionistic fuzzy inference system.

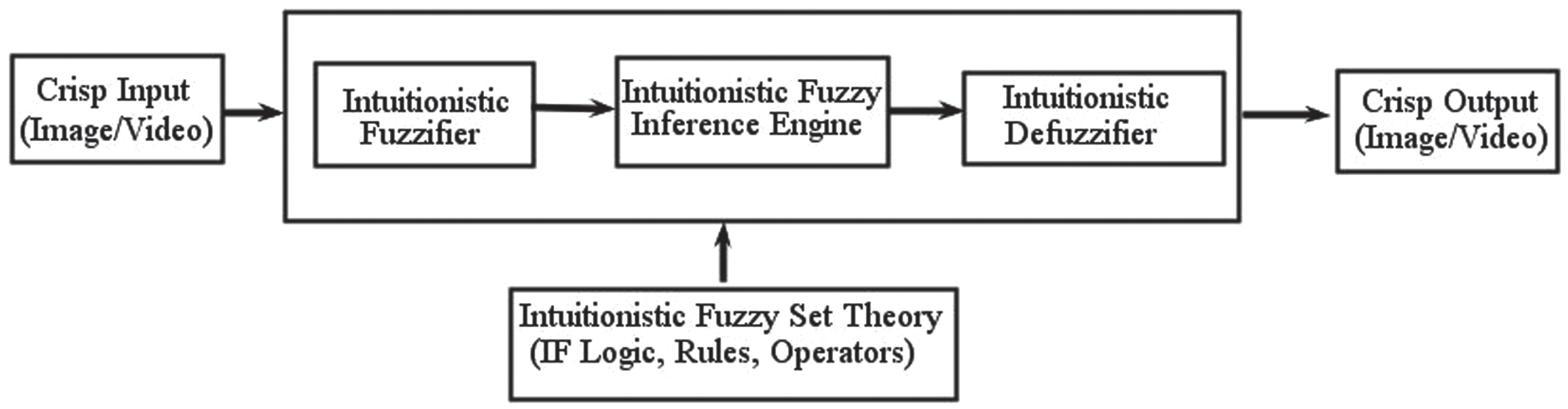
The system includes the following components.

(1) Intuitionistic fuzzifier: Intuitionistic fuzzification transforms input crisp values into intuitionistic fuzzy values. Nine types of intuitionistic fuzzification functions are defined based on different shapes of the membership and non-membership functions [31]. Appropriate intuitionistic fuzzy membership function can be selected for intuitionistic fuzzification.

(2) Intuitionistic fuzzy inference engine: Intuitionistic fuzzy values are then used by intuitionistic fuzzy inference engine where necessary modifications (using either intuitionistic fuzzy IF-THEN rules or intuitionistic fuzzy logic or intuitionistic fuzzy operations) are done to obtain the desired result. Here, the membership and non-membership functions are modified.

(3) Intuitionistic defuzzifier: Intuitionistic defuzzification function transforms intuitionistic fuzzy (output from inference engine) values into crisp values. Various types of intuitionistic defuzzification functions such as triangular, trapezoidal, L-trapezoidal, R-trapezoidal, Gaussian, S-shaped, Z-shaped functions are defined in [39]. A suitable intuitionistic fuzzy defuzzification function can be selected for defuzzification.

Remarks:

(1) If any of the defined fuzzification functions is not found suitable for the specific problem, the user can define a required fuzzification function, based on the requirement.

(2) Unlike defuzzification to a single value in the fuzzy controller, intuitionistic defuzzification gives a matrix of defuzzified values in [0,1], corresponding to the gray levels of the given image/video.

7VIPROC algorithm

The following notations are used in the proposed VIPROC Algorithm:

Notations:

t_k time-moment, k = 0,1,2...

xmnk = (x_mn, t_k) gray value of the (m, n) ^th pixel at time t_k

μmnk = μ (x_mn, t_k) membership value of the (m, n) ^th pixel at time t_k

νmnk = ν (x_mn, t_k) non-membership value of the (m, n) ^th pixel at time t_k

a, b the pixel range of the video frame considered at time t_kc, d the time range of the video considered at time t_k

r = a+b2

r′ = c+d2

ɛ degree of hesitancy

μmnk′ modified membership value of the (m, n) ^th pixel at time t_k

νmnk′ modified non-membership value of the (m, n) ^th pixel at time t_k

μ_INTEN (x_mn, t_k) contrast intensified membership value of (m, n) ^th pixel at time t_k

ν_INTEN (x_mn, t_k) contrast intensified non-membership value of (m, n) ^th pixel at time t_k

μ_CON (x_mn, t_k) concentrated membership value of (m, n) ^th pixel at time t_k

ν_CON (x_mn, t_k) concentrated non-membership value of (m, n) ^th pixel at time t_k

μ_DIL (x_mn, t_k) dilated membership value of (m, n) ^th pixel at time t_k

ν_DIL (x_mn, t_k) dilated non-membership value of (m, n) ^th pixel at time t_k

xmnk′ defuzzified new gray value of the (m, n) ^th pixel of the output video at time t_k

Algorithm 1 VIPROC Algorithm

Step 1: Read the input video in MATLAB Environment and split the video into frames using MATLAB built-in functions, xmnk = (x_mn, t_k)

Step 2: Using intuitionistic fuzzification functions, fuzzify the gray matrix of the frame(s)

While μmnk

If a<xmnk<r and c ≤ t_k < r′ xmnk+tk-(a+c)r+r′-(a+c)-(ɛ/2)

else If a<xmnk<r and r′ ≤ t_k < d xmnk+tk-(a+r′)r+d-(a+r′)-(ɛ/2)

else If r<xmnk≤b and c ≤ t_k < r′ b+r′-(xmnk+tk)b+r′-(r+c)-(ɛ/2)

Else b+d-(xmnk+tk)b+d-(r+r′)

While νmnk

If a<xmnk<r and c ≤ t_k < r′ r+r′-(xmnk+tk)r+r′-(a+c)-(ɛ/2)

a<xmnk<r and r′ < t_k ≤ d r+d-(xmnk+tk)r+d-(a+r′)-(ɛ/2) else If

r<xmnk<b and c ≤ t_k < r′ xmnk+tk-(r+c)b+r′-(r+c)-(ɛ/2) , else If

r<xmnk≤b and r′ ≤ t_k < d xmnk+tk-(r+r′)b+d-(r+r′)-(ɛ/2) ,

Else 1 - ɛ

Step 3: Apply the intuitionistic contrast intensification operator to the fuzzified gray matrix of the frame(s)

μ_INTEN (x_mn, t_k) , ν_INTEN (x_mn, t_k)

Step 4: Defuzzify the resultant gray matrix of the frame(s) using intuitionistic defuzzification functions

While xmnk′

μmnk′≤μmnk(a)

μmnk(a)<μmnk′≤μmnk(b) (μmnk′+∈)(b-a)+2a+(1-νmnk′)(b-a)2

μmnk(b)<μmnk′≤μmnk(c) (μmnk′+∈)(c-b)-(1-νmnk′)(c-b)2

else If μmnk′>μmnk

else c

Step 5: Merge the output frames by using MATLAB built-in functions and view the output video

8Implementation

The algorithm is developed and implemented using MATLAB 2018b.

To verify the algorithm, a test video of size “240 × 320 × 3” running for “10” seconds is taken for processing. There are totally 159 frames in the video. It is read frame by frame. For the implementation process, frame 1 is considered. It is shown in Fig. 12.

Fig. 12

Input frame 1.

Step 1:

After reading the video, frame 1 gray level extracted 5 × 5 matrix is given in (2) and corresponding video frame 1 is shown in Fig. 12.

Step 2:

Intuitionistic fuzzy membership and non-membership values are calculated for the matrix in (2) and displayed as follows in (3) and (4) respectively.

Step 3:

Contrast intensified membership (μ_INTEN) and non-membership (ν_INTEN) values are displayed in (5) and (6) respectively.

Step 4:

After defuzzification, the new gray level ( xmn′ ) matrix is obtained and displayed as follows:

Step 5:

The frame corresponding to the new gray level matrix obtained in Step 4 is depicted as output frame given in Fig. 13.

Fig. 13

Output frame 1.

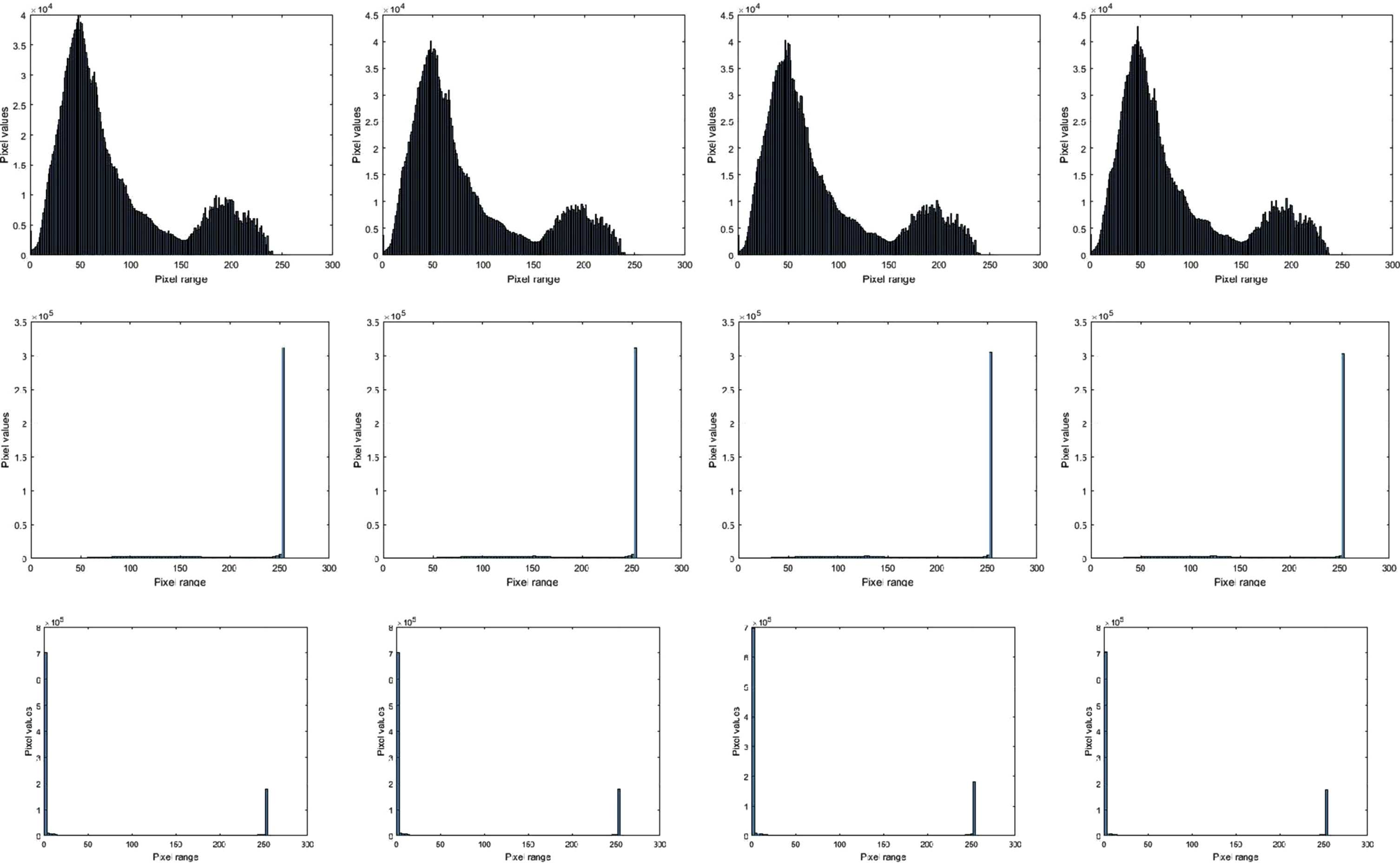
The input frames 1, 25, 50, 75, 100, 125, 150, 159 are shown along with the corresponding histograms in Figs. 14 and 15.

Fig. 14

Input frames.

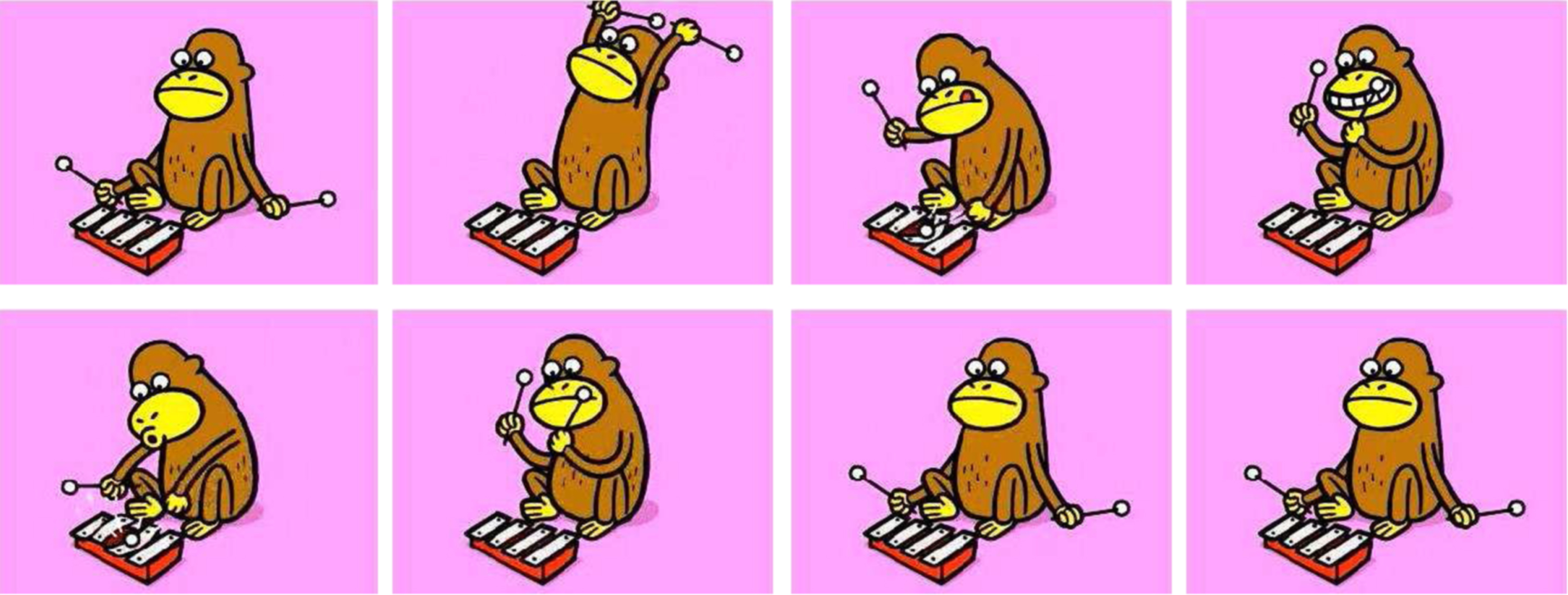
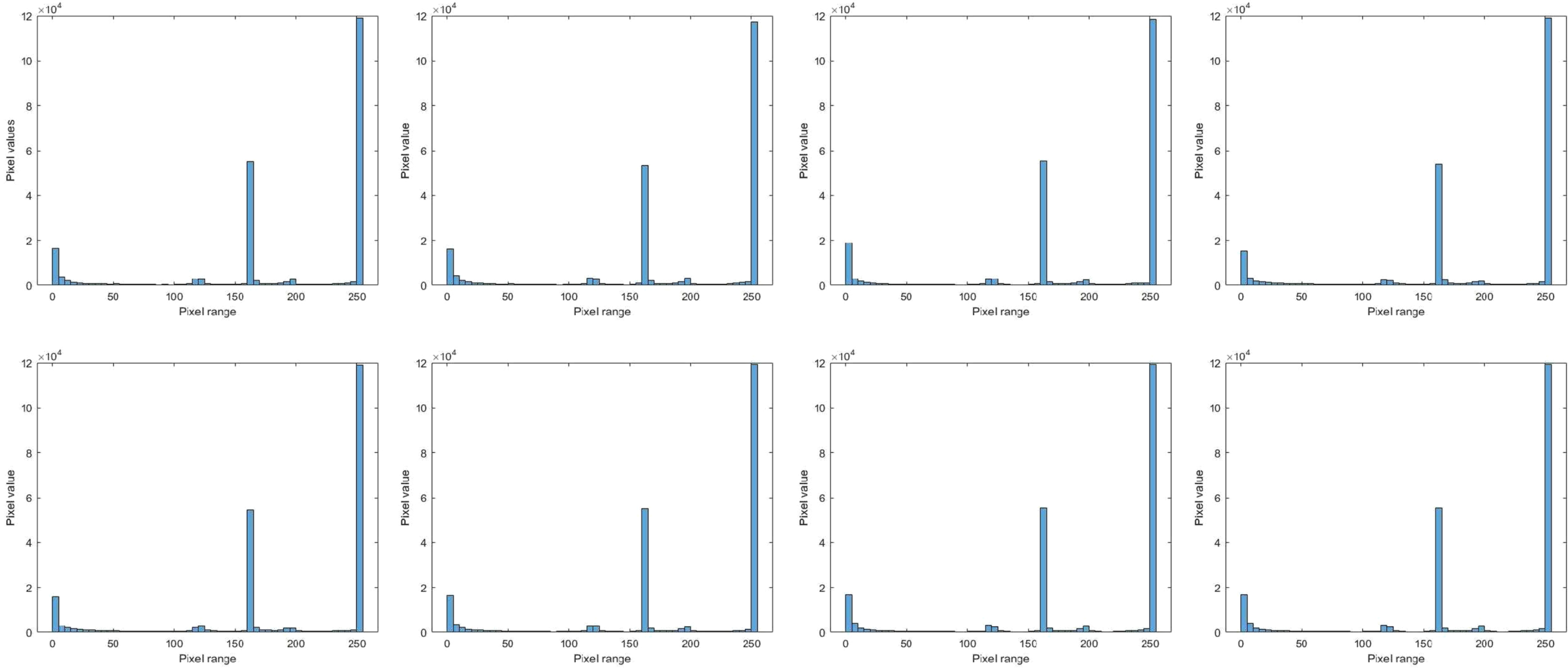
Fig. 15

Input frames histogram.

The output frames 1, 25, 50, 75, 100, 125, 150, 159 are shown along with the corresponding histograms in Figs. 16 and 17.

Fig. 16

Output frames.

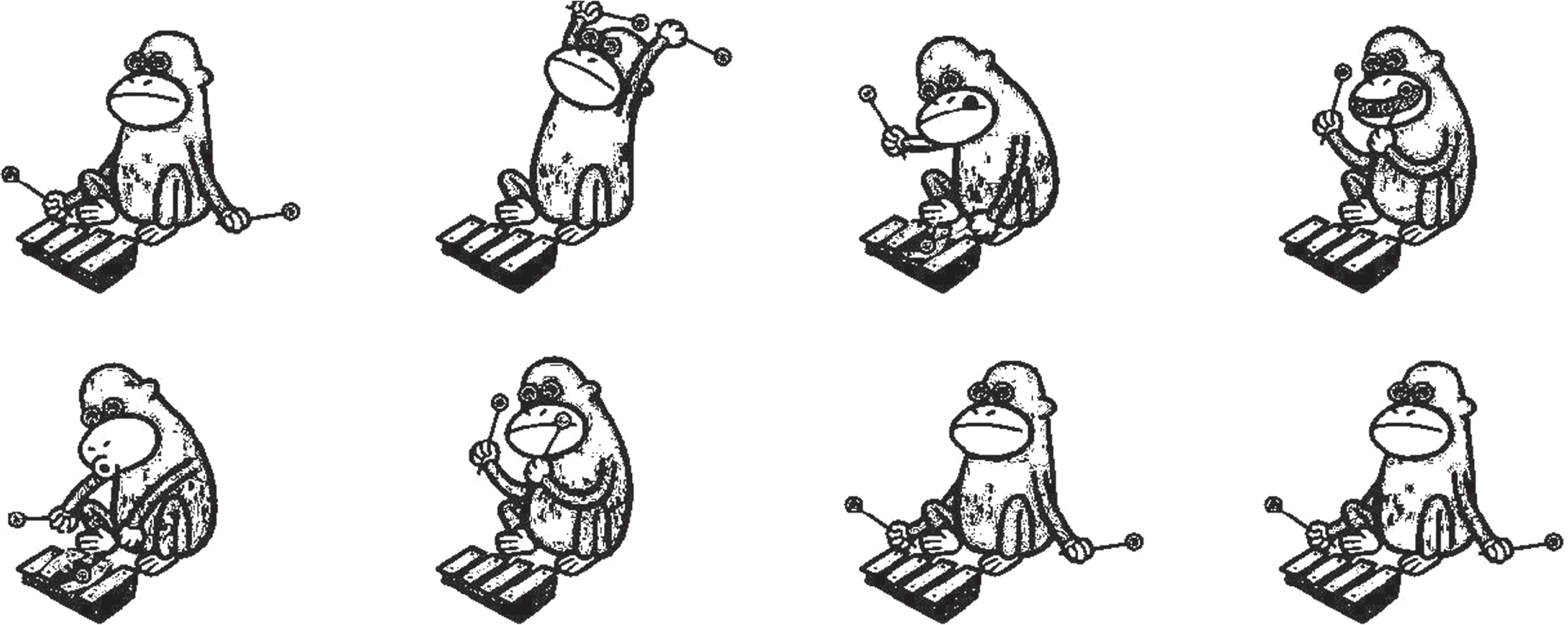
Fig. 17

Output frames histogram.

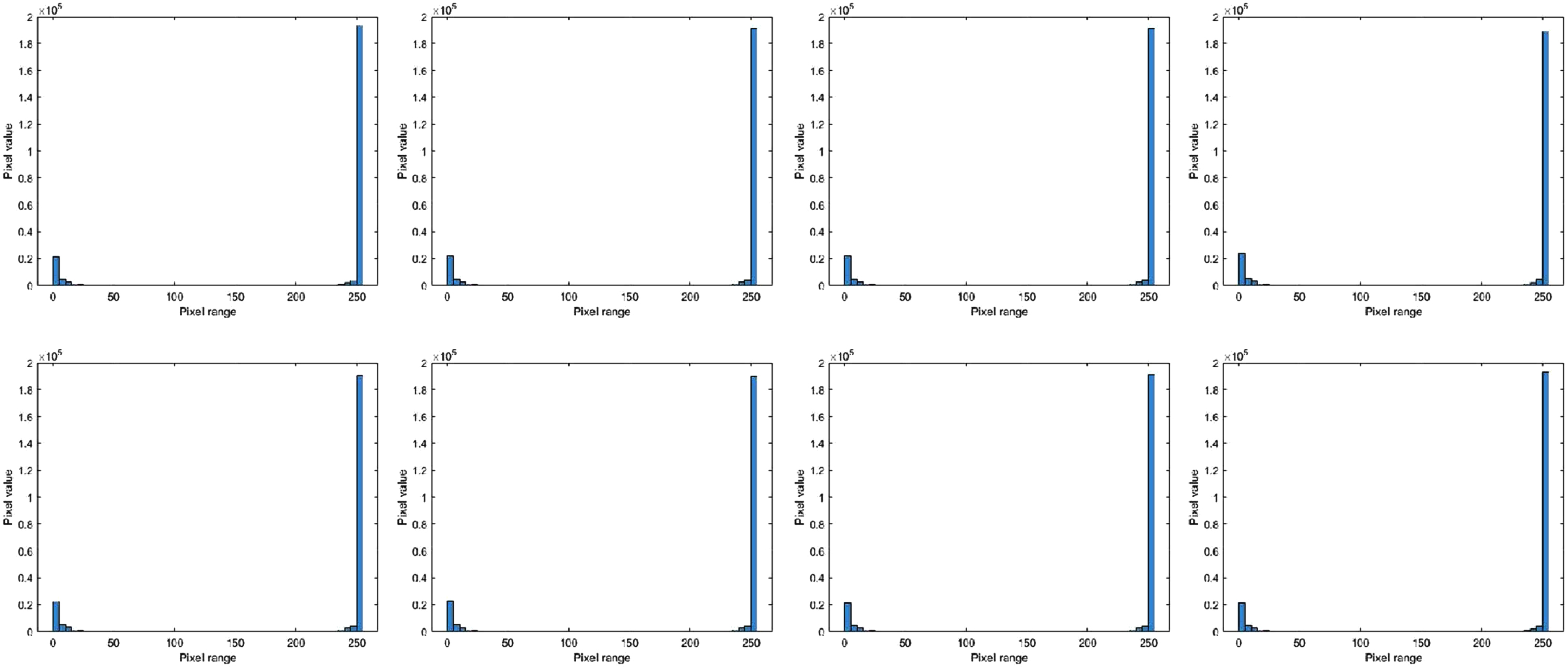
In Figs. 15 and 17, though the histograms look similar,they are not so. The justification can be made with a reference to image similarities. For example, in Fig. 17, the pixel difference of frame 1 and frame 25 is 2798 pixels. This value is too less compared to the total number of pixels of 230,400. This contributes only 1.2% of the total which is very less and so, it cannot be visualised in the histogram. Similarly in Fig. 15, the pixel difference between frame 1 and frame 25 is 5179 pixels which contributes only 2.24% of the total number of pixels of 230,400. Hence, the difference is minimal.

9Results and discussions

In this section, the comparison is made with fuzzy video processing and the proposed algorithm. A real-time video of size “720 × 1280” running for “12” seconds is taken for processing. There are a total of 295 frames in the video. Input frames and fuzzy contrast intensified output frames and our proposed algorithm’s output frames of this video are displayed in Fig. 18.

Fig.18

Input frames, Fuzzy contrast intensified image and the proposed algorithm’s output.

Fig.19

Input frames, Fuzzy contrast intensified image and the proposed algorithm’s output histogram.

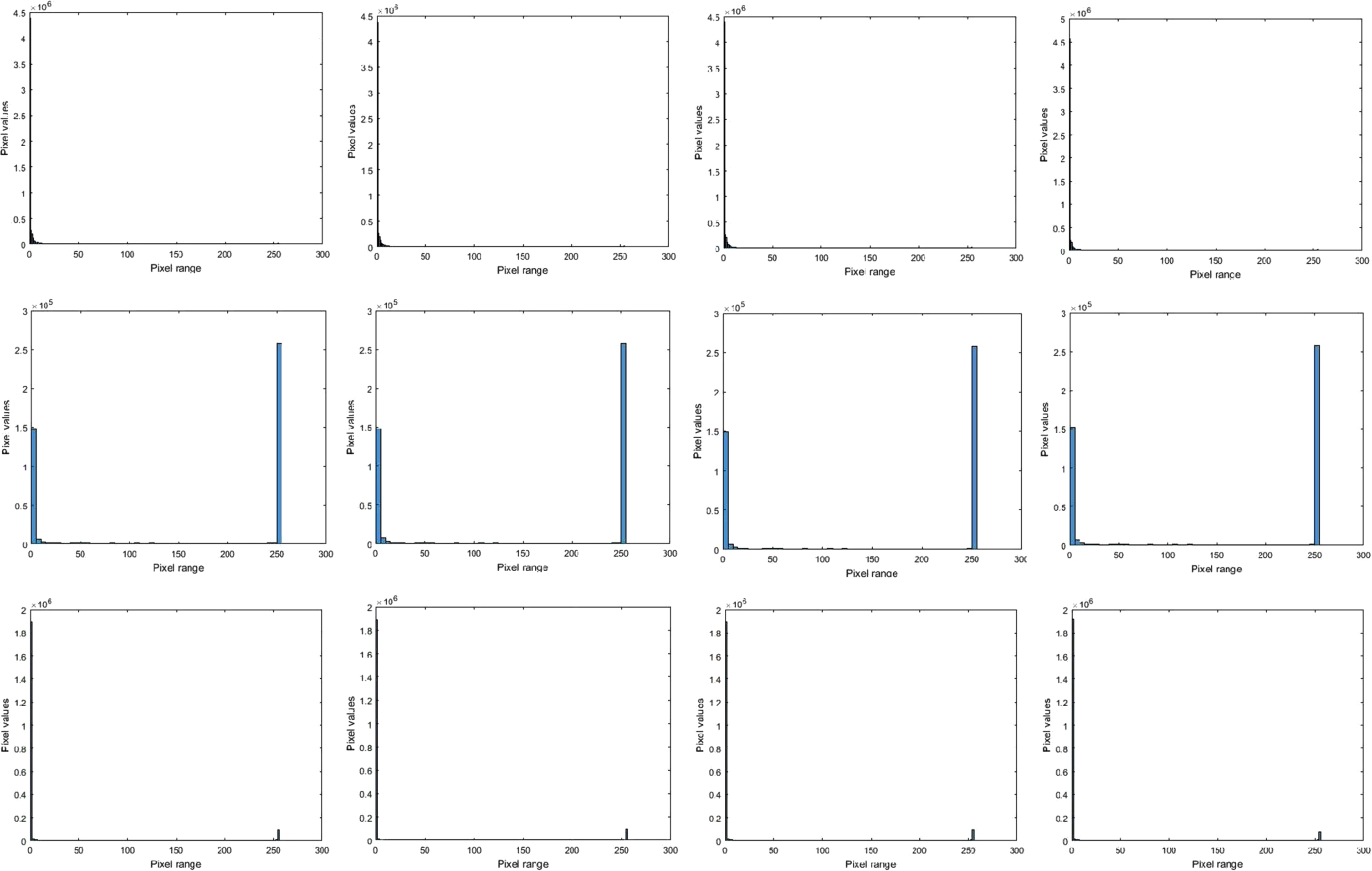
Another medical scan video [49, 50] of size “1080 × 1920” running for “3” seconds is taken for processing. There are a total of 90 frames in the video. It is read frame by frame. Input frames and fuzzy contrast intensified output frames and our proposed algorithm’s output frames of this video is displayed in Fig. 20. Also histograms of these frames are displayed in Fig. 21.

Fig. 20

Input frames, Fuzzy contrast intensified image and the proposed algorithm’s output.

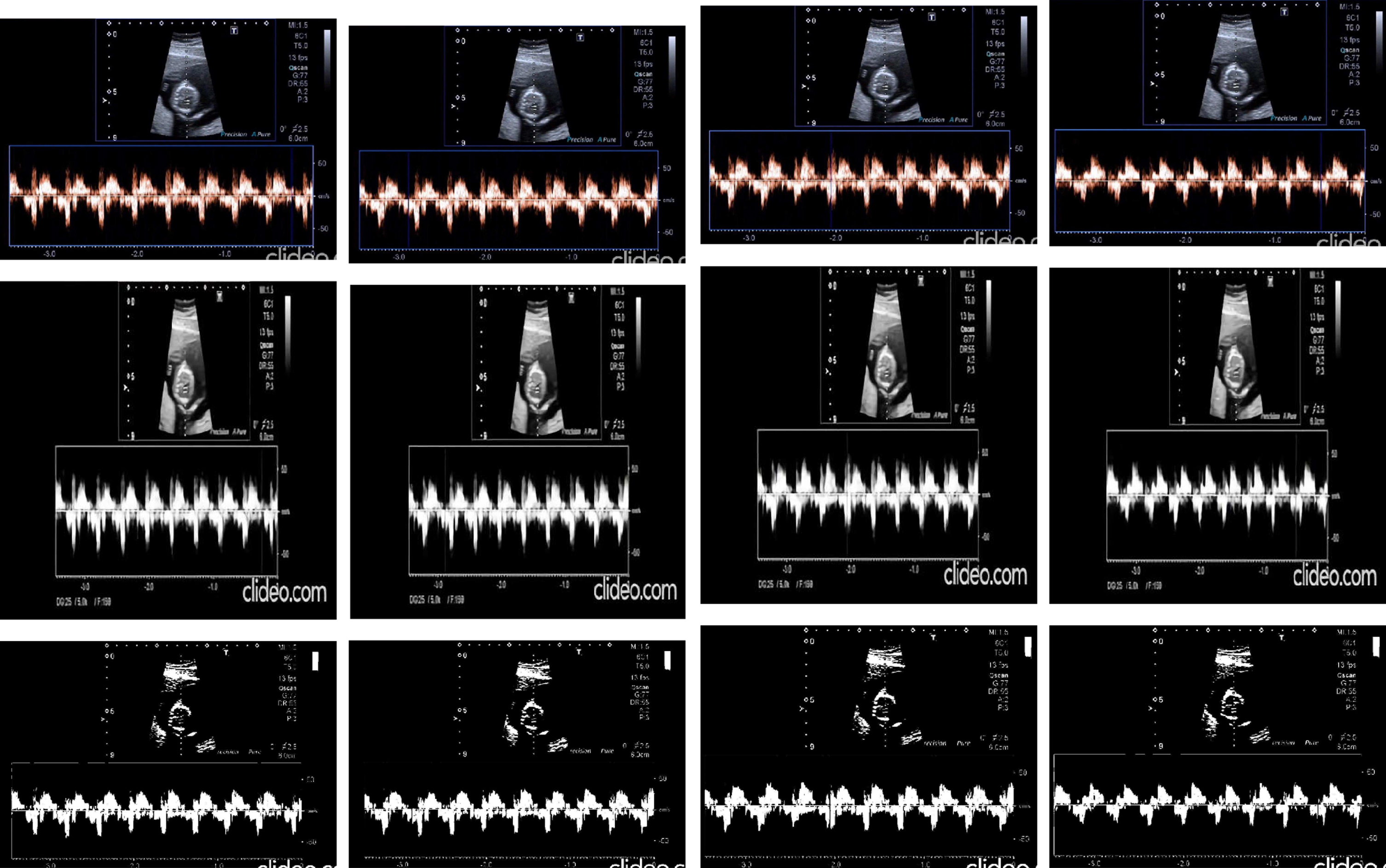
Fig. 21

Input frames, Fuzzy contrast intensified image and the proposed algorithm’s output frames histograms.

VIPROC algorithm is very useful in real-time and medical video processing to enhance the video quality. The proposed algorithm gives better result than the fuzzy video processing technique which is demonstrated in this section.

10Conclusion

Temporal intuitionistic fuzzy mathematical tools offer a new and flexible framework for designing and developing video enhancement algorithms. It is shown that the contrast intensification operator plays an important role in improving the quality of a video. The following are the major tasks done in this research work: (a) Representation of a video by a TIFS, (b) Video Processing (VIPROC) algorithm is designed and developed in MATLAB environment. The following are the ways by which the developed system is significant in video processing: (a) First attempt to use IFSs to represent RGB images and TIFSs to represent videos, (b) The intuitionistic fuzzy inference system is designed for the specific application, (c) A newly constructed defuzzification function is used. Further, it is proposed to analyze color videos without converting them into gray videos. For, it is necessary to extend this algorithm for red, green, blue separately and then be concatenated, which needs a vigorous parameter tuning. Also, the authors proposed to modify and improve the VIPROC algorithm, using the mathematical operations like dilation and erosion to improve the quality of a video, in their future work.