Intelligent traffic signal controller based on type-2 fuzzy logic and NSGAII
Abstract
Intelligent traffic signal control (TSC) system is important for the alleviation of traffic congestion. Usually, most of the researches about TSC focused on single intersection based on type-1 fuzzy set. Compared with type-1 fuzzy logic controller (FLC), type-2 FLC can deal with more uncertainties in the road traffic control system. Therefore, a type-2 FLC optimized by NSGAII (T2-NSGAII) is designed for TSC in a complex road network, in which the intersection’s traffic signal time is dynamically adjusted by its own and adjacent intersections’ traffic volumes to reduce global delay time and traffic congestion. In T2-NSGAII, the expert rule set and the parameters of the fuzzy membership functions are simultaneously optimized by NSGAII to achieve less time delay and traffic congestion. In the simulations of a six-intersection traffic network with different vehicular arrival rates, it is demonstrated that T2-NSGAII has better performance compared with vehicle actuated controller based on fixed-time control (FTC), type-1 FLC, type-2 FLC and isolatedly optimized Type-2 FLC and the total delay time could be reduced by 76.3% , 65.1% , 58.3% and 35.4% respectively.
1Introduction
OVER the past few years, there has been a steady growth of vehicles and total miles of road leading to an enormous increase in traffic congestion. Given that major road construction in cities are both difficult and costly, one of the most effective ways to alleviate congestion is to increase the capacity of the existing infrastructure using Traffic signal control (TSC). TSC can bring a substantial reduction to traffic congestion, leading to improved conditions both for the drivers and the environment [12].
TSC in the signalized traffic intersections can be either fixed-time signal control or adaptive control [5]. Generally, the fixed-time control is simple and the time of the signal light is fixed, therefore, it can not dynamically response to real-time fluctuations of traffic volumes. To overcome the limitations of the fixed-time control that using fixed time intervals, adaptive TSC was designed based on the real-time traffic information to make quickly adjustments to signal settings [3].
Nevertheless, controlling the traffic signals of a transportation network constitutes a significant challenge due to the complexity of the problem, especially the uncertain and dynamic behavior of the network [3]. The TSC system has many uncertainties, i.e., the trafficqueue length, collected by the auto loop detectors, is non-stationary, and it varies all the time. The traffic variations are impacted by many factors, including the length of cars, the road condition, the weather, the trafficrules, etc. Therefore, new intellectual approaches are needed to deal with the complexity and uncertainness of the TSC system [10].
Fortunately, Fuzzy logic control (FLC) provides such an intellectual approach for the TSC system, which is capable of mimicking human thought and holding the expert knowledge in the form of inference rules [1, 11]. It is well known that, Type-2 fuzzy sets can efficiently deal with large uncertainties based on its three-dimensional membership. Compared with Type-1 FLC, Type-2 FLC has better performance, but the performance is largely affected by the quality of the fuzzy rules and it is extremely difficult to select the optimal parameters for the membership functions of Type-2 FLC [7]. As an efficient and powerful stochastic parameter optimization method for multiple objects, Non-dominated Sorting-based Genetic Algorithm (NSGA-II) has shown better performance than traditional genetic algorithm (GA) and particle warm optimization (PSO) [6]. Furthermore, NSGAII is designed for the problems of multiple objects optimization [4], which makes it more suitable for the parameter optimization problem of type-2 fuzzy logic controlsystem.
In the paper, we proposed a type-2 fuzzy logic controller, optimized by NSGAII, for the real-time light control in the four phase intersections with turning vehicles taken into consideration. To achieve high vehicle throughput rate, both the expert rule set and the parameters of the membership functions were simultaneously optimized by NSGAII. Then the fuzzy controller was applied in a multi intersections traffic network, in which the light time was dynamically adjusted by the traffic volumes of each intersection and its adjacentneighbors.
2Simulation of the traffic
In the paper, as shown in Fig. 1, the common four phase traffic situation is considered in our work, including: W-E straight phase, W-E left turning phase, N-S straight phase and N-S left turning phase. Therefore, each intersection has four-phase and they alternately emergent, which is similar with the widely used intersections in real traffic network. Assume that l and f represent the distance between two adjacent intersections and the length of one vehicle respectively, and the average speed of vehicles is v km/h, then there are at most l/f vehicles in each lane. As shown in Equation (1), the time cost of vehicles to reach the next intersection consists of three parts: the intersection passing time l/v, the delay time for red signal t g and the delay time for congestion t c . Apparently, the length of the signal time should be dynamically adjusted based on the average moving speed of vehicles and the neighbor intersections’ queue length to reduce the delay time while raise the throughput rate. There are many sensing technologies to detect vehicles’ speed data at intersections. Accordingly, the number of vehicles in each lane can be estimated based on the sensed speed.
(1)
3Intelligent signal control based on type-2 FLC
3.1Input data
To design a FLC system, we need to choice the input and output variables firstly. As described in Fig. 1, there are four lane directions in each intersection: E-W straight, E-W left-turning, S-N straight, S-N left-turning. Apparently, the vehicles in the direction, which has more traffic volume, have high privilege to pass. And the traffic state of the straight or left-turning adjacent intersections should also be taken into consideration. Therefore, at the end of every green light time, in each intersection the queue length of the 4 directions and the traffic state of the target intersection are chosen to be two input variables to the fuzzy controller.
3.1.1The queue length
The queue length, throughput rate, average delay time and parking times are commonly used criteria to evaluate the traffic conditions. According to [13], we suppose that the minimum successive time unit is 1s, and the vehicles’ arrival time in each direction israndom, thus, in a time unit interval, the number of arrived vehicles q n is shown in Equation (2)
(2)
Let lq and rq represent the vehicle queue lengths during green light time and red light time respectively, the queue length is:
(3)
(4)
3.1.2The traffic state
As defined in Equations (5) and (6), the traffic state of the i-th intersection s i is denoted by the flow rate fr i , and fr i in each direction is calculated by the arriving rate of upstream minus downstream departure flow rates for each lane in that direction of the phase. Sampling of the vehicle data is done at a pre-given time interval, which can be about 10s (Minimum green time):
(5)
(6)
3.2The fuzzifier
The fuzzifier is utilized to map a numeric vector x=(x
1,...x
p
) ∈ X
1 × X
2 × ··· × X
p
≡ X into a type-2fuzzy set
In the paper, to fuzzify the input data and output result: queue length, traffic state and green time, four linguistic partitions are adopted: “Sparse (S)”, “Low (L)”, “Medium (M)” and “High (H)”. Interval type-2uncertain standard deviation Gaussian membership functions are employed, as illustrated in Fig. 2. The basic domain of green time is denoted as [0, 60], while the domain of queue length and neighbor status are [0, 15], [0, 100] respectively. The upper and lower boundary standard deviation can be calculated based on the recorded flow rates and queues at different period of time on different days in a week.
Usually, the rule base of FLC is expressed in the “if-then” form, which holds the expert knowledge. The structure of fuzzy rules in a type-1 FLC and a type-2 FLC is in the same manner, but in the type-2 FLC the antecedents and the consequents are denoted by type-2fuzzy sets. So assume that for a type-2 FLC with p inputs x 1 ∈ X 1...x p ∈ X p and one output y ∈ Y, there are M rules, and the l-th rule in the type-2 FLS can be written as:
(7)
According to common sense and the daily experience, the preliminary rule base is shown in Table 1.The rule base is optimized and validated based on a group of traffic network consisting of interconnectedintersections.
3.3Inference engine
The inference engine of the type-2 FLS is responsible for combining rules and mapping the input fuzzy sets to the output fuzzy sets. It is necessary to compute the join (unions) and the meet (intersections), as well as the extended sup-star compositions of type-2 relations. If
(8)
The inference result of the l-th fired rule R
l
is described by the membership function μ
R
l
(x,y)=μ
R
l
(x
1,...,x
p
, y) where μ
R
l
(x,y)=
(9)
In general, the p-dimensional input to R
l
is given by the type-2 fuzzy set
(10)
(11)
(12)
(13)
Then the inference result of the l-th triggered rule is simplified and shown in Equation (14):
(14)
Therefore, the final inference result of the all triggered rules in the fuzzy rule base is shown in Equation (15).
(15)
3.4Type-reducer and defuzzifier
After the fuzzy inference process, the output from an interval type-2 fuzzy set is acquired. Type-reducer is necessary to convert interval type-2 fuzzy set into type-1fuzzy set output, which is then converted in a numeric output through running the defuzzifier. For the case of our FLS center of sets (cos) type reduction is employed, Y cos , which is expressed as
(16)
In Equation (16), Y
cos
represent interval set calculated by y
l
and y
r
, y
i
= [y
l
, y
r
], which is the centroid of the result set
(17)
The output interval of the type-2 FLC system can be calculated by the values of y l and y r .After type-reduction, we get an interval set Y cos , which is applied to defuzzifier, and the crisp output is obtained as:
(18)
4Optimization process using NSGAII
In the paper, NSGAII is employed to optimize the fuzzy rule and parameters of the type-2 FLC system. NSGAII is a high efficient and powerful random search algorithm for solving multiple objects optimization problems. NSGII was first introduced by K. Deb [4]. For NSGAII, The optimal solutions lie on the non-dominated front (Pareto optimal front) in the feature space of multiple objectives.
4.1Introduction of NSGAII
Usually, the multi-objective optimization problem can be expressed as how to choice the correct map-ping of a set of n parameters to a set of m objectives. It can be described algebraically in Equation (19):
(19)
In Equation (19), x represents the set of decision variables, and y denotes the objective set. For an evolutionary algorithm with multiple objectives, f i (x) is the fitness function for the i-th objective. Specifically, if any object function f i (x) is originally designed to find a maximum value, and then it can be modified as -f i (x). Just as other evolutionary algorithms, NSGAII is also based on the idea of evolution of populations of possible candidate individuals, which represent possible solutions, and the evolution process includes mutation, crossover and selection. Furthermore, NSGAII introduced the concept of pareto dominate ≺ to classify the individuals into different pareto front based on the multi-objects values, accordingly the pareto domination is defined as:
If x A , x B are two possible solutions, if x A ≺ x B , then:
(20)
The solution x A ≺ x B means for each object function, x A is at least as good as x B , and at least for one object, x A is better than x B . When x A and x B are not pareto dominate each other, both solutions belong to the same non-dominated front, which means if x A is better than x B in some objectives, then it must be worse at least in one other objective.
When a possible solution s in the last generation is not dominated by any other feasible solutions, s is referred to as a pareto optimal solution of the m-objective minimization problem in Equation (19). The set of all pareto optimal solutions forms the tradeoff surface (pareto front) in the objective space.
4.2Encoding of the parameters and rules
In the paper, the fuzzy rule set and the MF parameters are simultaneously optimized by NSGAII. For the fuzzy inference rules, as shown in Table 1, there are 12 rules. Therefore, 12 codes are defined to denote the outputs of the fuzzy rules.
For example, the first four codes represent the output of the first row in Table 1, the linguistic Sparse (S), Low (L), Medium (M) and High (H) are denoted by numeric value 1,2,3 and 4 respectively. And the rules in Table 1 is expressed by chromosome, it equals [4,4,3,3;4,3,3,2;3,3,2,2].
In the rule base, as shown in Fig. 3, each linguistic degree in the Gaussian membership function of the queue length is decided by 7 parameters: σ L1,σ L2,σ M1,σ M2,σ H1,σ H2 and the mean value m. Consider the other input variable neighbor traffic state and the output variable green time, there are 31 parameters in all for the optimization of membership function. Finally, each individual of NSGAII is encoded as shown in Fig. 4.
4.3The multi object fitness function
The delay of multiple intersections is taken as the fit-ness function. Let D denotes the total delay in the last sampling period of an intersection A. And the number of the arrived vehicles is counted by the loop detectors. Suppose n represents the total number of the arrived vehicles at A. And the average delay of A is D/n. This value is an absolute delay because D only related to the number of the arrived vehicles. The average delay of other intersections can be calculated in a similar manner. Therefore, the multiple optimization objects of NSGAII is
(21)
During the evolution of NSGAII, the individuals of each generation is evaluated by the multiple fitness function defined in Equation (21), furthermore, to keep the diversity of the individuals, the crowding distance is also taken into consideration when we choice individuals into the next generation. The detail of NSGAII is described in [4].
5Simulation results
To evaluate the performance of the fuzzy controllers, type-2 fuzzy logic control optimized by NSGAII (T2-NSGAII), a network of six intersections is de-signed. All intersections are 4-way with four phases, as shown in Fig. 5. The proposed method and targets are tested in same traffic flow patterns and the results are compared and analyzed. The sequence of signal phasing, traffic flow information and signal plans are generated by the matrix of origin-destination of PARAMICS software. The bench mark objects include 4 kinds of commonly used methods, includes: simple fixed-time control (FTC) [2], fuzzy logic control based on type-1 (T1) [1], fuzzy logic control based on type-2 (T2) [8], fuzzy logic control based on type-2 isolatedly optimized by DE (T2-DE) [13].
The comparisons of the delay time of the intersections among different methods are shown in Figs. 6 to 11, where s represents the arrival rate of straight vehicles per second and l denotes the arrival rate of left-turning vehicles per second.
From the figures, we can see that T2-NSGAII has better performance compared with the benchmarks TFC, T1, T2, T2-DE, the average total delay time is reduced by 76.3% , 65.1% , 58.3% and 35.4% respectively. The average delay of T2-NSGAII is the smallest, while the simple FTC method gets the worst performance. Moreover, type-2 FLC methods optimized by DE or NSGAII perform better than the T2 without optimization, which demonstrates that the optimization can facilitate the FLC systems to get suitable parameters and further improve the throughput rate of the traffic system. The figures also show that T2-NSGAII is superior to T2-DE, that’s because the fuzzy rules and MF parameters of all the adjacent intersections of T2-NSGAII are simultaneously optimized, it makes sure that the rules and the MF parameters are compatible. However, in T2-DE, the fuzzy rules, MF parameters are optimized independently, which is prone to get trapped into local optimal solutions and make the rules and parametersincompatible.
The average queue lengths of intersections are shown in Table 2. At the boundary intersections such as A, C and D, the arrived vehicles can smoothly pass through them. Meanwhile, some intersections in the central blocks begin to get traffic jam. From Table 2 we can find that, the queue length of T2-NSGAII method is the smallest and the level of crowdedness is less than others. Furthermore, the results shows that the vehicle queue length of all the T2 method (T2, T2-DE, and T2-NSGAII) is less than that of T1, which demonstrates our theoretical analysis that type-2 FLC has the ability of deal with more uncertainties which exist in the traffic control system, because of its special three-dimensional membership functions holds more uncertainties. It should be noted that the communication and changing phase sequence information between intersections also facilitates the FLC system, especially when they are simultaneously optimized.
6Conclusion
In this paper, an intelligent traffic signal controller based on type-2 FLC and NSGAII was proposed. As the type-2 fuzzy logic can well model nonlinear systems, especially on the condition that only a small number of data or expert knowledge is available, it has better ability in tackling uncertainties and robustness than traditional type-1 FLC. Therefore, type-2 FLC is more suitable for traffic signal control. Then NSGAII was employed to optimize both the fuzzy rules and the MF parameters, as it can well optimize multiple objects simultaneously compared with other evolutionary algorithms. The proposed method and other benchmarks were applied to a six-intersection traffic network. Different traffic scenarios were simulated and compared with each other. The results showed that T2-NSGAII got better performance than the other methods, which demonstrated T2-NSGAII’s ability in the application of complicated traffic signal control.
Acknowledgments
This work is sponsored by the National NaturalScience Foundation of China (61402308).
References
1 | Chou CH, Teng JC (2002) A fuzzy logic controller for traffic junction signals Information Sciences 143: 1 73 97 |
2 | Robertson DI (1969) Transport Research Laboratory in the United Kingdom TRANSYT: A Traffic Network Study Tool, Technical Report |
3 | Zhao D, Dai Y, Zhang Z (2012) Computational intelligence in urban traffic signal control: A survey IEEE Transactions on Systems, Man, and Cybernetics Part C: Applications and Reviews 42: 4 485 494 |
4 | Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II IEEE Transactions on Evolutionary Computation 6: 2 182 197 |
5 | Trabia MB, Kaseko MS, Ande M (1999) A two-stage fuzzy logic controller for traffic signals Transportation Research Part C 7: 353 367 |
6 | Castillo O, Melin P (2012) A review on the design and optimization of interval type-2 fuzzy controllers Applied Soft Computing 12: 4 1267 1278 |
7 | Castillo O, Martinez RM, Melin P, Valdez F, Soria J (2012) Comparative study of bio-inspired algorithms applied to the optimization of type-1 and type-2 fuzzy controllers for an autonomous mobile robot Information Science 192: 1 19 38 |
8 | Balaji PG, Srinivasan D (2011) Type-2 fuzzy logic based urban traffic management Engineering Applications of Artificial Intelligence 24: 12 22 |
9 | Liu Q, Xu J (2012) Traffic Signal Timing Optimization for Isolated Untersections Based on Differential Evolution Bacteria Foraging Algorithm Proceeding of the 8th International Conference on Traffic and Transportation Studies 210 215 |
10 | Evers R, Proost S (2015) The myth of traffic-responsivesignal control: Why common sense does not always make sense Transportation Research Part A 77: 350 357 |
11 | Rahman SM, Ratrout TN (2009) Review of the fuzzy logic based approach in traffic signal control: prospects in saudi arabia Journal of Transportation Systems Engineering and Information Technology 9: 5 58 70 |
12 | Timotheou S, Panayiotou CG, Polycarpou MM (2013) Towards Distributed Online Cooperative Traffic Signal Control Using the Cell Transmission Model Proceedings of the 16th Intelligent Transportation Systems Conference 1737 1742 |
13 | Bi YR, Srinivasan D, Lu XB, Sun Z, Zeng WL (2014) Type-2 fuzzy multi-intersection traffic signal control with differential evolution optimization Expert Systems with Applications 41: 7338 7349 |
Figures and Tables
Fig.1
The four phase of an intersection.
Fig.2
Fuzzified antecedents and consequents. (a) Fuzzified neighbor status, neighbor status, (b)Fuzzified queue length, l(c)Fuzzified greentime.
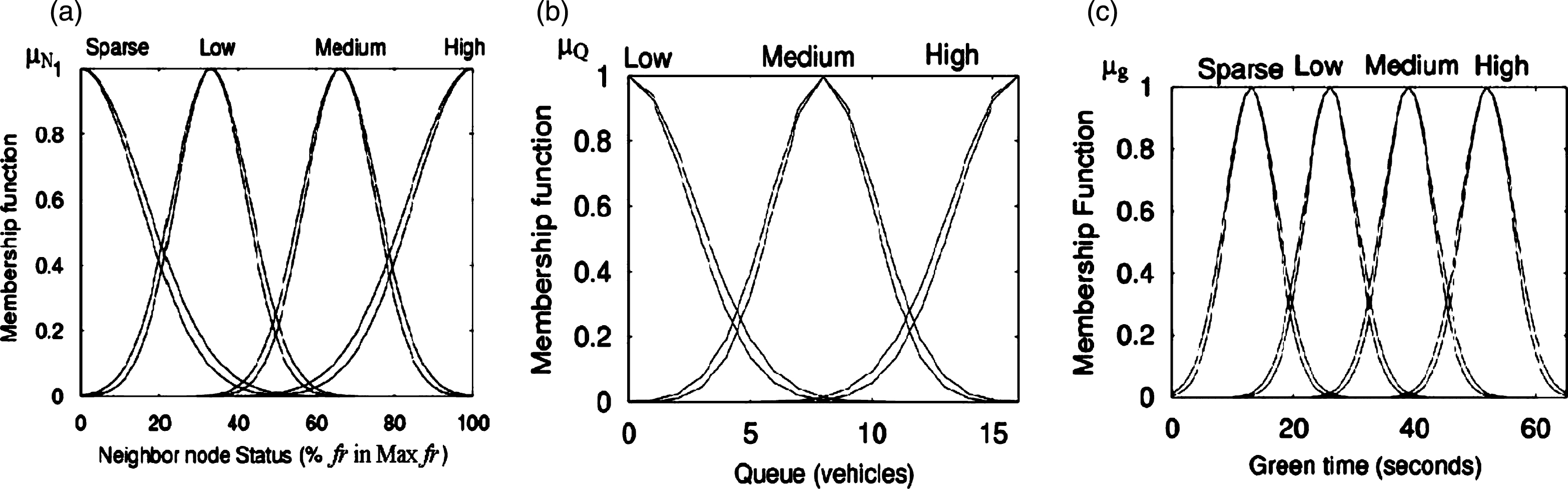
Fig.3
Coding for the MF parameters.
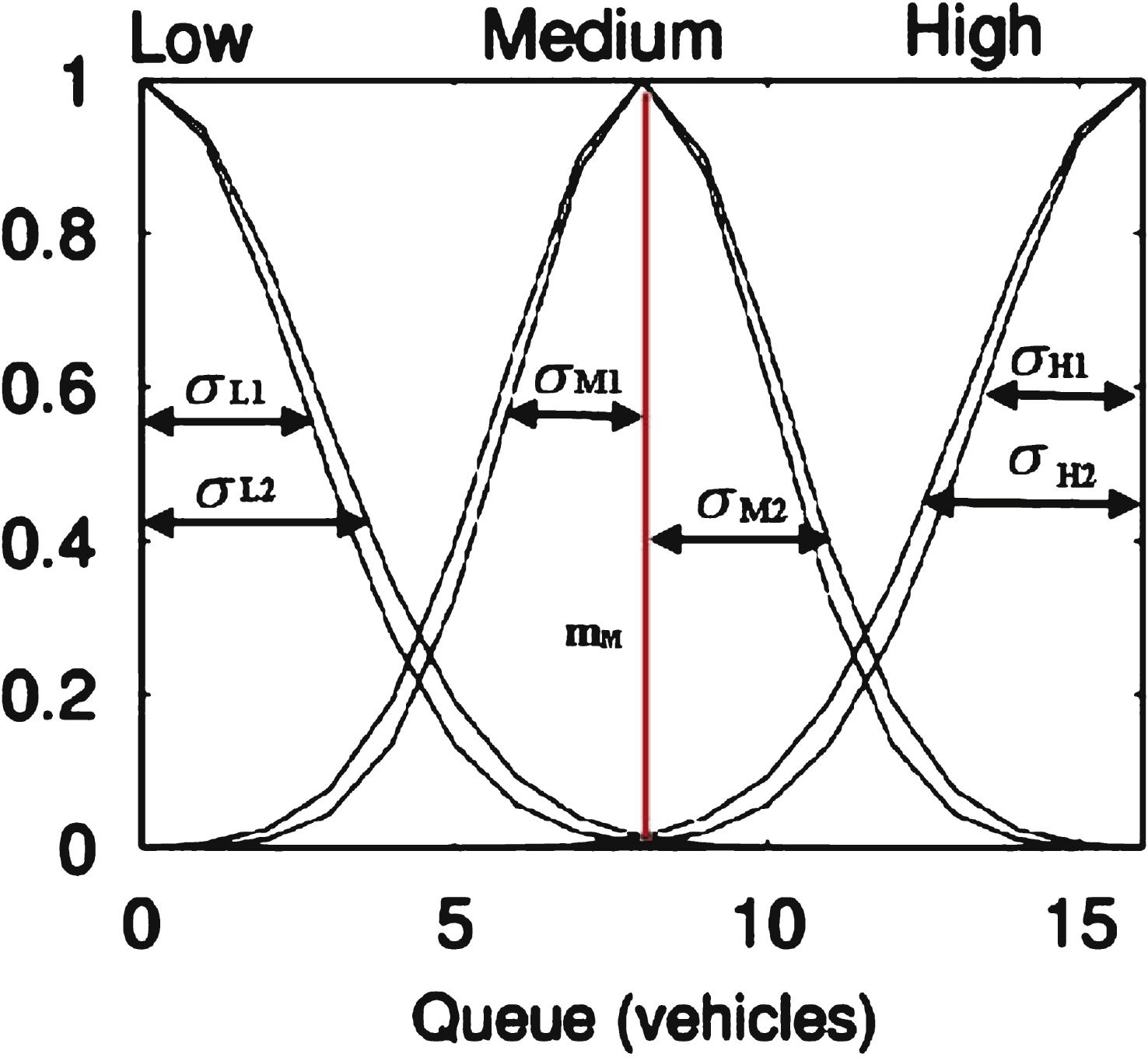
Fig.4
Coding for the MF parameters.
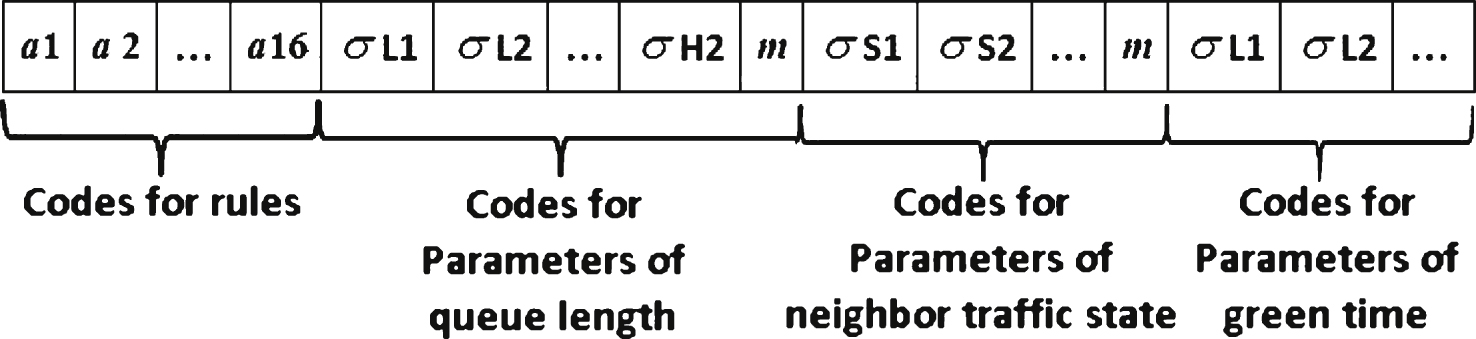
Fig.5
The traffic network in the simulations.
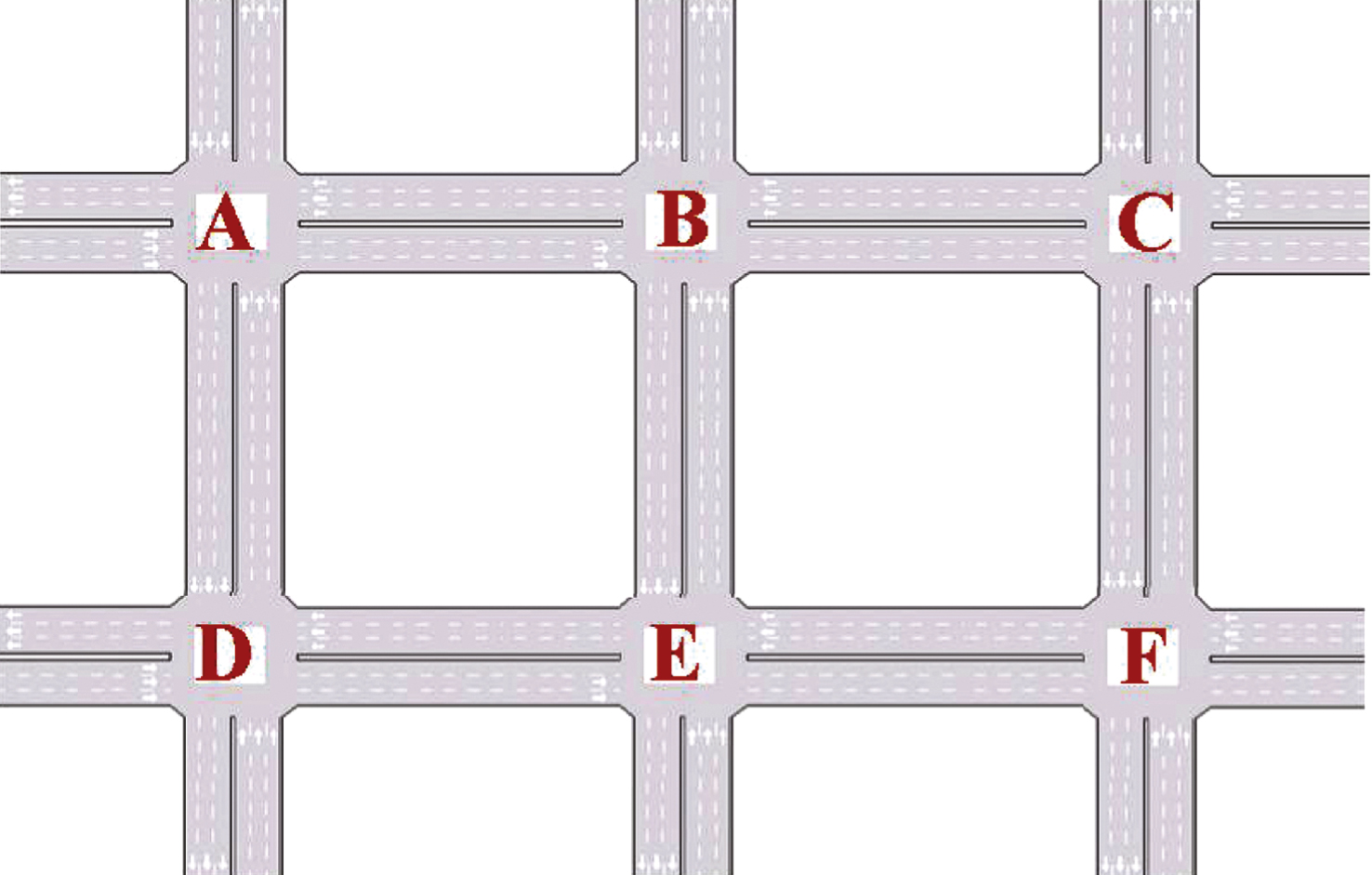
Fig.6
The delay time of intersection A.
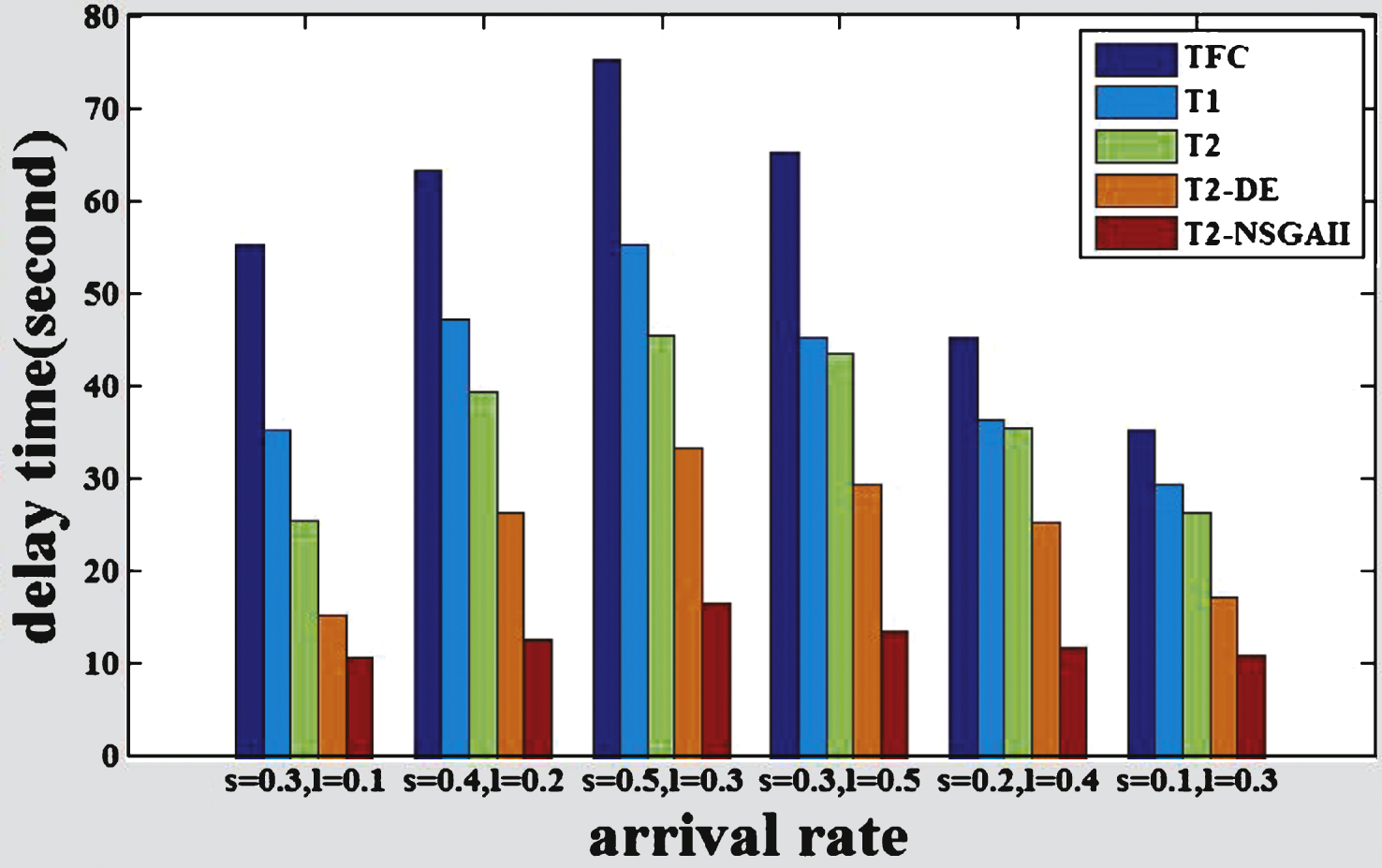
Fig.7
The delay time of intersection B.
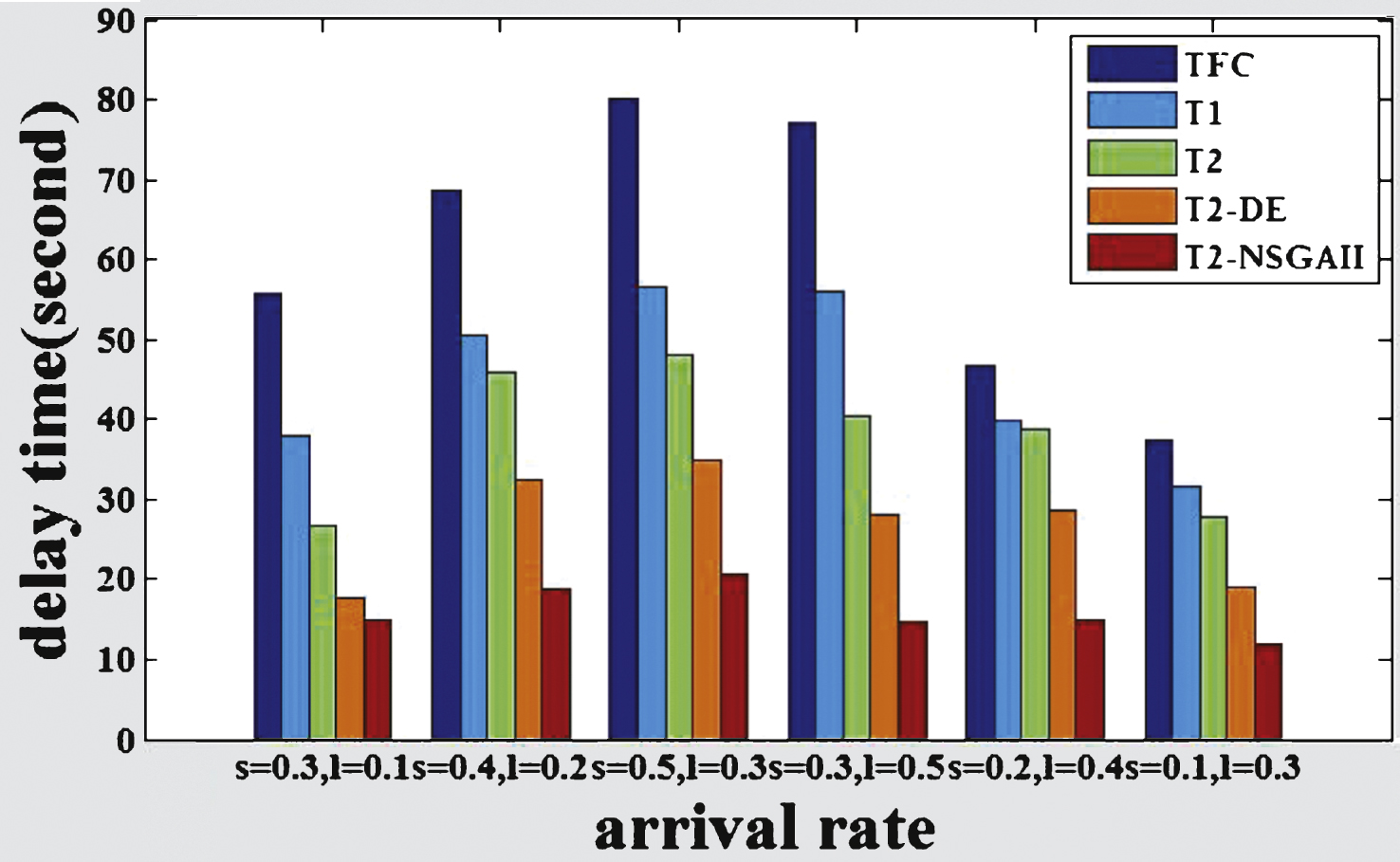
Fig.8
The delay time of intersection C.
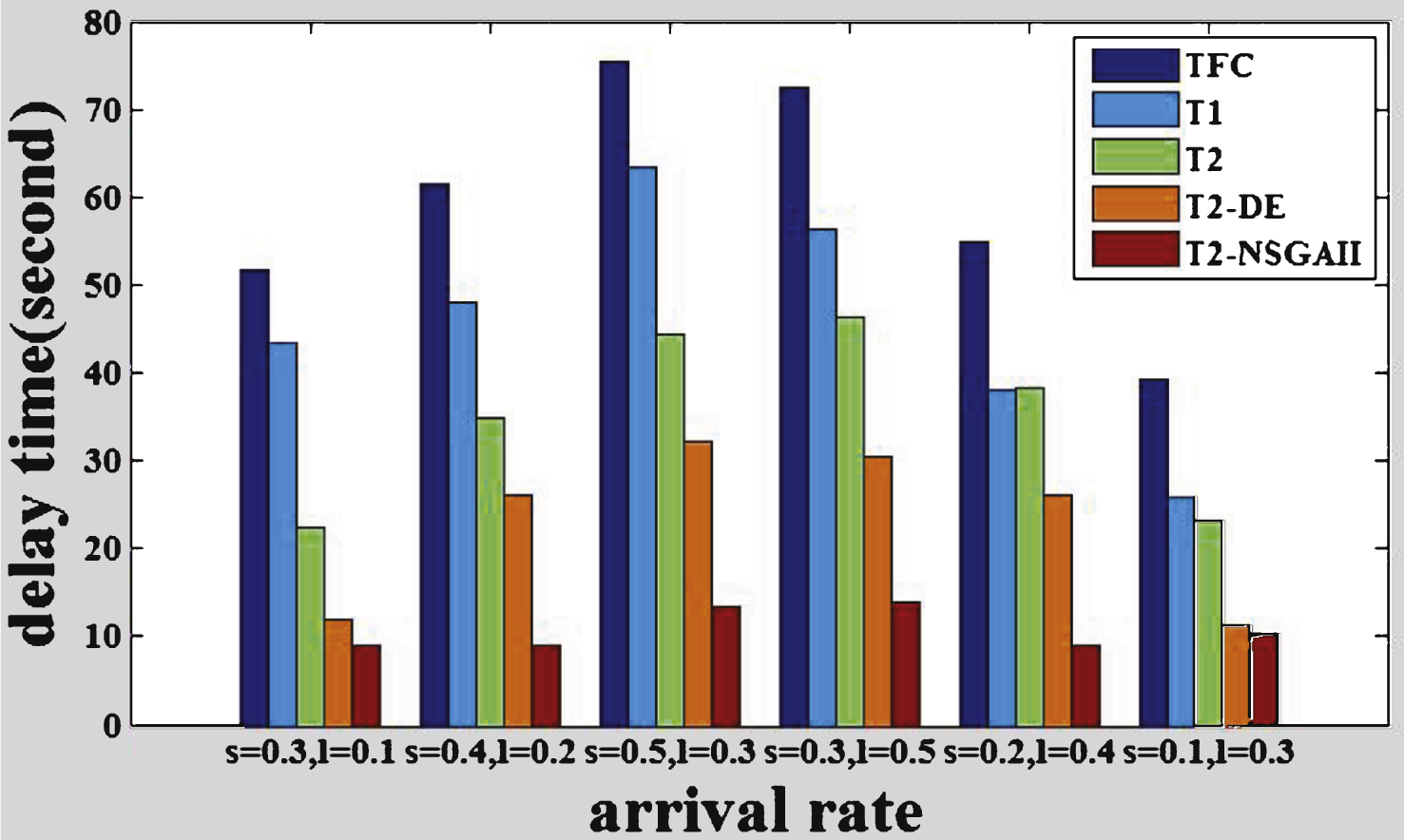
Fig.9
The delay time of intersection D.
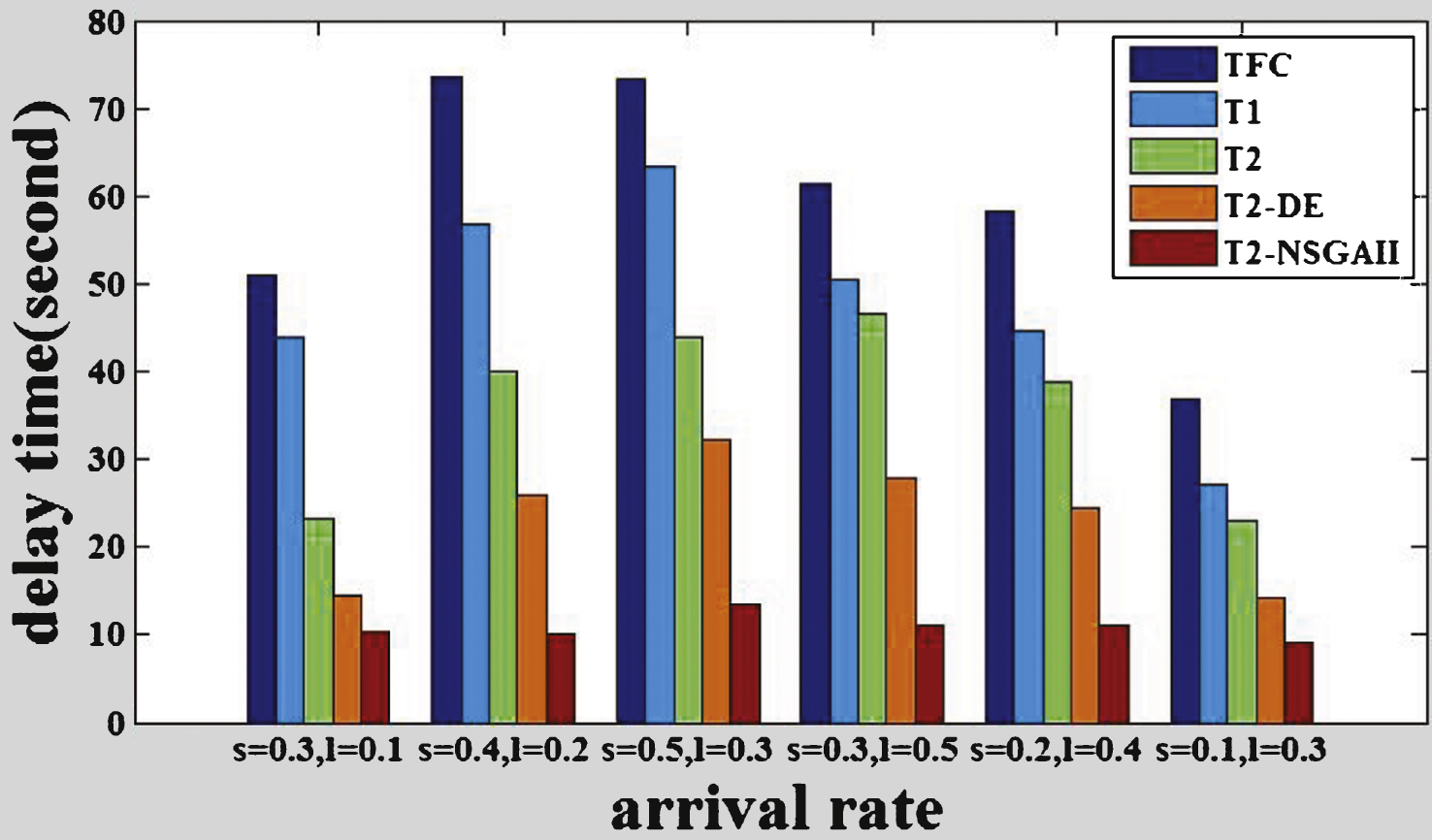
Fig.10
The delay time of intersection E.
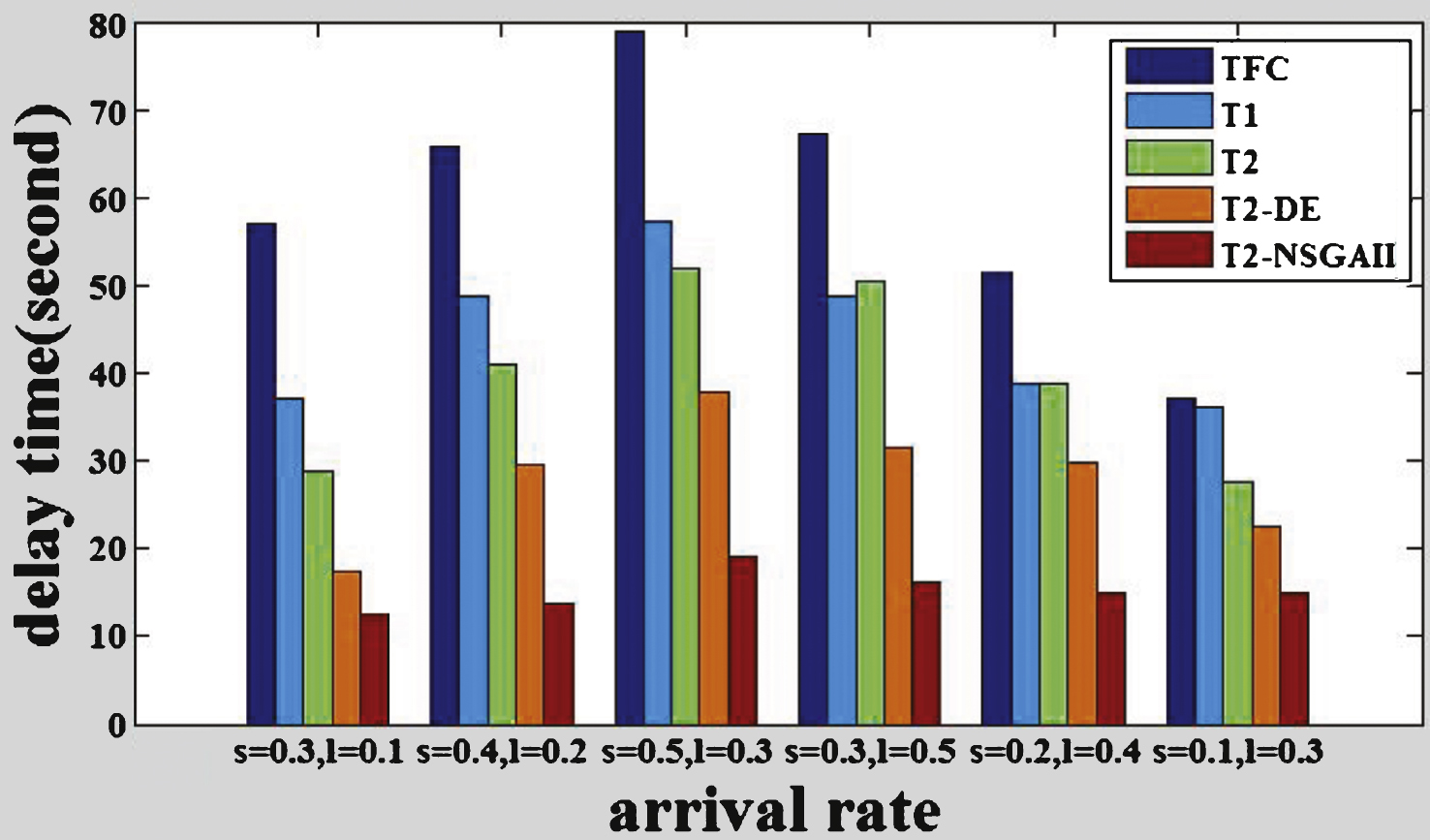
Fig.11
The delay time of intersection F.
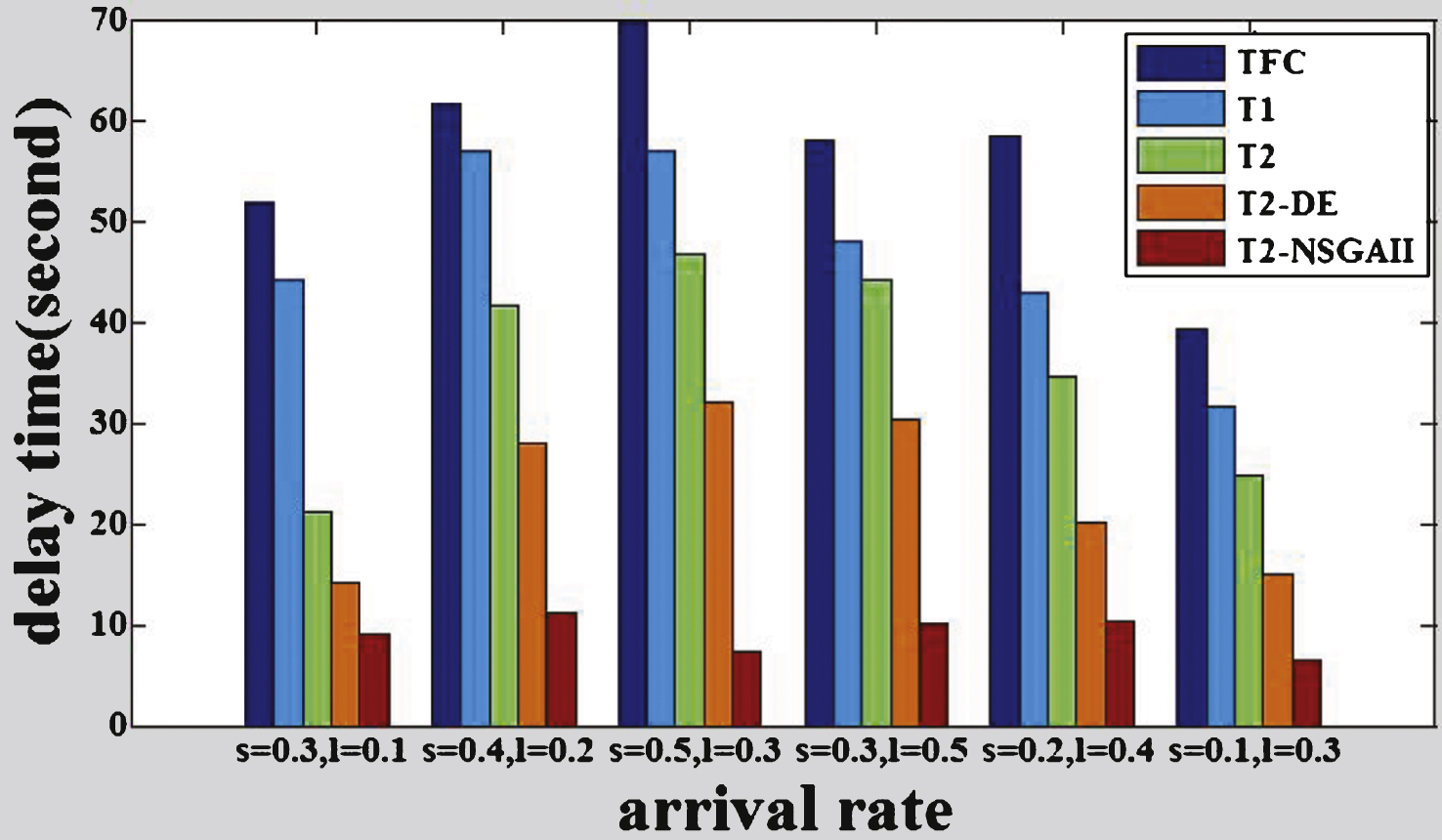
Table 1
Preliminary fuzzy rule base
| Queue length | Neighbor target intersection state | |||
| S | L | M | H | |
| L | H | H | M | M |
| M | H | M | M | L |
| H | M | M | L | L |
Table 2
The queue lengths of intersections (s =0.4, l=0.2)
| Model | A | B | C | D | E | F |
| FTC | 20.1 | 31.5 | 18.8 | 21.3 | 33.5 | 20.8 |
| T1 | 16.6 | 21.4 | 16.4 | 18.6 | 22.5 | 19.0 |
| T2 | 13.7 | 18.9 | 15.1 | 15.9 | 19.4 | 15.8 |
| T2-DE | 10.1 | 15.6 | 14.0 | 13.4 | 16.5 | 13.9 |
| T2-NSGAII | 6.9 | 11.5 | 9.6 | 9.8 | 12.2 | 6.5 |




