Matching method for emergency plans of highway traffic based on fuzzy sets and rough sets
Abstract
To deal with the problem in emergency plan matching of highway traffic that incident description is incomplete, incident properties are unclear, and plan matching is inaccurate, etc., a plan matching method is proposed based on fuzzy sets and rough sets. The property weight calculation method based on rough sets is used to reduce the dependency on prior knowledge; the structural similarity calculation is used to solve the problem of property missing and matching angle varying; the fuzzy set calculation method is adopted to solve the problem of fuzzy property similarity missing. The traffic emergency plan matching case for Changzhou section of Shanghai-Nanjing highway demonstrates that the proposed method can improve the accuracy and reliability of highway traffic emergency matching, reflecting the advantages of rough sets and fuzzy sets in emergency plan matching.
1Introduction
With the increase of vehicle traffic on highways, traffic emergencies continue to happen. It is an engineering problem urgently needed solving how to reduce the response time of traffic emergencies and increase the rescue efficiency. Practice has shown that the real-time acquisition of emergency plans is the key measure of reducing rescue decision time. Proposing automatic matching methods for emergency plans and developing corresponding application systems have important scientific and engineering value for improving emergency rescue decision efficiency.
Zografos [5] established a decision support system for emergency response to aid the dispatch decision of rescue resources. Logi, et al. designed a decision support system for traffic congestion incidents to implement the disposal decisions under congestion conditions. Alvear, et al. [3] designed a decision support system for highway tunnel emergency management to realize the command and decision of highway tunnel under incomplete information conditions. Konstantinos [6] developed a decision support system of the rescue resource scheduling for highway emergencies, which defines the rescue procedures for emergency incidents, and designs relevant databases and model bases to realize the optimal scheduling in rescue process. An emergency plan system was developed for Shanghai World Expo to improve the emergency response capabilities. Lu, et al. [9] adopted case-based reasoning (CBR) technology to develop an airport emergency plan management system. Yang, et al. [7] introduced CBR technology into highway emergency management and designed the retrieve, reuse, correct and save modules for cases, realizing plan matching based on nearest neighbor searching. There are still aspects that need improving in the above method and application system: 1) The property weights need manually determination in the plan matching process; 2) The information of historical cases is incomplete, the description of emergency incident information is incomplete, and the property missing affects the reliability of casematching; 3) The fuzziness of plan properties is not considered in the automatic retrieval of plans.
In this study, structural similarity is introduced to analyze the property structural characteristics of emergency incidents and historical cases. Different similarity calculation methods are adopted for different properties. The fuzziness of character properties is described by fuzzy sets and the similarity calculation methods of fuzzy properties are developed. The rough set theory is adopted to determine the property weights of emergency incidents, and design the algorithm process of emergency plan matching. We aim to propose an intelligent matching method for traffic emergency plan of freeway without prior knowledge, which can overcome the matching error caused by the uncertainty of emergency incidents to some degree, improving the accuracy and reliability of emergency plan matching.
2Overview of highway traffic emergency plan matching
2.1Incident character properties
According to the requirements of emergency rescue decision for highway traffic, emergency cases are divided into five parts, namely case character information, incident character properties, emergency command departments, decision plans and effect evaluation. The part playing a key role in rescue decision is incident character properties, including basic incident information and incident loss information. Basic incident information describes the traffic conditions and environmental conditions when the incident happens. Incident loss information describes the seriousness of emergency incidents, including fallouts, obstacles, the number of blocked lanes, the number and type of overturned vehicles, accident casualties, damaged condition of incident vehicles, etc. Incident character properties are divided into four classes [2]:
– Numerical properties: expressed by determined numbers, such as death toll, number of injured, etc.;
– Symbolic properties: expressed by clear terms, such as time of incident, site of incident, etc.;
– Fuzzy conceptual properties: conceptual variables are the properties. A term set consists of all homogeneous fuzzy variable properties, with each fuzzy variable property corresponding to each term in the set, such as traffic congestion condition,etc.;
– Fuzzy interval or fuzzy number properties: an interval without determined boundaries or an undetermined number. When the left and right boundaries of the fuzzy interval are equal, the fuzzy interval reduces to a fuzzy number. For example, accident duration, affecting scope, etc.
In this study, 24 highway incident character properties are extracted. Among them, there are four numerical properties shown in Table 1; fourteen symbolic properties shown in Table 2; four fuzzy conceptual properties shown in Table 3; and two fuzzy interval properties shown in Table 4.
2.2Matching method for traffic emergency plans
The traffic emergency plan matching is a calculation and comparing process of case similarity. By establishing a similarity measurement function, the current emergency incident is compared with the historical case in the case library. Then the case which is most similar to the current incident is retrieved and treated as the most suitable rescue plan for the current emergency incident. Therefore, choosing an appropriate similarity calculation method is the key factor of plan matching.
If we want to determine the similarity between an emergency incident and a historical case, we have to first determine the similarity between incident character properties. At present, commonly used similarity calculation method for character properties is nearest neighbor method [1], which is based on normalized distances between case properties. This method is inadequate for similarity calculation of qualitative case property description. For example, for qualitative properties “general” and “serious” levels of incidents, the similarity calculation result is 0 (which means dissimilar). However there is similarity between them, and only the extents of casualties and property losses are different. Other similarity calculation methods simply equalize fuzzy properties and determined properties, causing the loss of similarity calculation for qualitative description properties. Due to the uncertainty, complexity and fuzziness of highway traffic incidents, the character properties of incident sites are mainly fuzzy values. Therefore, using fuzzy sets to calculate similarity between properties can fully reveal the similarity between properties.
3Similarity calculation for emergency character properties
3.1Character weight calculation based on rough set theory
The importance of incident character properties in plan matching process is expressed by the weights in similarity calculation. Whether the property weights are reasonable directly affects the accuracy and reliability of plan matching. Current weigh assigning methods are mainly based on domain experts’ prior knowledge, which mainly depends on subjective decision and experience. In this study, rough set theory is used to determine each property weight of incidents. Only the data are compared and no other prior knowledge is needed. Therefore the method is objective [8]. Moreover, rough set theory has the ability to solve minimal invariant set (called kernel) and minimal rule sets (called reduction) in large-scale data. This ability can be used to simplify redundant properties and property values. The character properties of highway emergency incidents include quantitive properties and qualitative properties. The quantitive properties are firstly discretized. The discretization method is referred to literature [4].
According to the rough set theory, the knowledge expression system S = (U, R, F, V) is designed, where, U is the incident historical case set; R = {x 1, x 2, …, x n } is the incident feature property set; C = {c 1, c 2, …, c n-1} is the condition property set; D = {d} is the decision property set. Decision property is usually the “incident level” and R = C ∪ D. The dependency of decision property set D on condition property set C is given:
(1)
The importance r c-i of the i-th property is given:
(2)
The objective weigh w i1 of the i-th property is given:
(3)
The larger w i1 is, the more important the i-th property is to decisions. When property i is removed from condition property set, the positive region of class U/D is largely affected; when w i1 = 0, i.e., r c - r c-i = 0, which means removing the i-th property does not affect the positive region of class U/D. Therefore this property is redundant and should be removed.
The integrated weight w i of the i-th property is expressed by Equation (4):
(4)
3.2Calculating similarity between emergency incidents and historical case structures
The case properties corresponding to different incidents have different composition structures. There are numerous descriptive properties of highway emergency incidents. Therefore, it is inevitable that historical case information or case description is incomplete. Moreover, using structural similarity to choose historical cases not only increases the similarity between the chosen case and the emergency incident property, but also solves the property value missing problem, making the formed rescue plan more timely and useful [10].
Let the current emergency incident be P, and a certain historical case in case library be Q The structural similarity S (P, Q) equals to the weight sum of the intersection set property of P and Q, divided by the weight sum of the union set property of P and Q, shown in Equation (5):
(5)
3.3Property similarity calculation based on fuzzy sets
Fuzzy conceptual properties, fuzzy intervals and fuzzy numerical properties are collectively known as fuzzy properties. The similarities between fuzzy properties are special relation functions, such as trigonometric functions, trapezoidal function, Gaussian function, etc. The trapezoidal function is used in this study, the membership function S M (x) of element x in fuzzy set is expressed [2]:
(6)
The similarity between the fuzzy properties of incident P and historical case Q is calculated by summing areas. That is, to calculate the area overlapping ratio between the membership functions of two fuzzy properties, which is expressed by Equation (8):
(7)
Point
(8)
(9)
If
For similarity between numbers, a linear function is adopted for normalization, which is expressed:
(10)
Since there are only property values for symbolic properties and there is no real sense of similarity, the similarity measurement for symbolic properties only takes the value of 1 for identical properties and 0 for different properties, as shown:
(11)
3.4Overall similarity calculation
Integrating structural similarity, property similarity and corresponding weights, we obtain the overall similarity shown in Equation (13):
(12)
According to maximum similarity reuse strategy, select the case with maximum Sim (P, Q) as the best matched emergency plan.
4Case analysis
According to the some cases in the emergency case library of Changzhou section of Shanghai-Nanjing highway, the proposed similarity calculation method is used to match exemplar plans, as shown in Table 5.
– Determine the property weights
According to Equations (3) and (4), the property weights are:
W = {0.055, 0.034, 0.047, 0.047, 0.052, 0.050, 0.030, 0.028, 0.034, 0.036, 0.043, 0.048, 0.050, 0.053, 0.051, 0.033, 0.054, 0.056, 0.047, 0.038, 0.038, 0.037, 0.039}, and no redundant property exists.
- Calculate the structural similarity
According to Equation (5):
The calculation of S (A, B2) and S (A, B3) is similar. S (A, B2) = S (A, B3) =1.
It is clear that the property structure of emergency A is the same as historical cases B2 and B3, and is also similar to B1.
– Calculate the similarity between properties
* The similarity calculation steps for fuzzy conceptual properties are as follows:
Use daily traffic congestion index to reflect the road network traffic congestion level. The road congestion is classified into 5 classes, with a value range of [0, 10], as shown in Table 6. The similarity of road congestion level property between incident A and historical case B1 is calculated. Since there are only two situations in Table 5, namely clear and minor congestion, only the similarity between (2,4] and (4,6] needs calculation.
Road congestion level of emergency A correspond to fuzzy set p
1, historical case B1 is q
1. Then v
l
p1
= 4,and v
r
p1
= 6. Since k = 0.1, m
p1 = kv
lp1 = 0.4, n
p1 = kv
rp1 = 0.6. Similarly, v
lq
1
= 2, v
rq
1
= 4, with m
q1 = 0.2, n
q1 = 0.4. According to Equations (8) and (9)
According to Equation (7):
Similarly, the similarity between the road congestion level of A and B1, B2, B3 is calculated. The results are shown in Table 7.
* The calculation of the similarity of fuzzy interval properties, is in accordance with the similarity calculation of fuzzy properties. The similarity results are shown in Table 8.
* The similarity calculation for numerical properties and symbolic properties is according to Equations (11) and (12), as shown in Tables 9 and 10.
* The overall similarity is calculated according to Equation (12) and shown in Table 11:
According to Table 11, the similarity between incident A and historical case B2 is larger than that of A and B1, A and B3, which indicates that the solution plan of historical case B2 should be the rescue plan of emergency incident A.
5Conclusions
The proposed method reduces the dependency on prior knowledge and eliminates redundant properties. The integrated structural similarity calculation for emergency incidents and historical cases improves the reliability of case structure matching and reduces the effect of property missing on similarity calculation. The traffic incidents are classified into different types according to their properties, and different calculation methods are adopted for different tupes. The fuzzy set is specially used to calculate the similarity between fuzzy properties, solving the previous problem of similarity loss. The proposed highway traffic emergency plan matching method is able to adapt to the uncertainty of incident description in plan matching, improving the accuracy of plan matching.
Considering it is difficult to collect the character of freeway emergency incident, we will focus on how to deal with emergency plan matching with a large number of event properties missing.
References
1 | Yan A, Qian L, Wang P (2014) A comparative study of attribute weights assignment for case-based reasoning Acta Automatica Sinica 40: 9 1896 1902 |
2 | Zhang B, Yu Y (2002) Hybrid similarity measure for retrieval in case-based reasoning system Systems Engineering-Theory & Practice 22: 3 131 136 |
3 | Alvear D, Abreu O, Cuesta A, Alonso V (2013) Decision support system for emergency management: Road tunnels Tunnelling and Underground Space Technology 34: 13 21 |
4 | Miao D (2001) A new method of discretization of continuous attributes in rough sets Acta Automatica Sinica 5: 296 302 |
5 | Zografos GK, Vasilakis MG, Giannouli MI (2000) Methodological framework for developing decision support systems for hazardous materials emergency response operations Journal of Hazardous Materrals 71: 503 521 |
6 | Konstantinos GZ, Konstantinos NA, George MV (2002) A real-time decision support system for roadway network incident response logistics Transportation Research Part C 10: 1 18 |
7 | Yang S, Xiong C, Ni F (2008) Freeway incident management system based on case-based reasoning Journal of Southeast University 38: 5 878 883 |
8 | Cao X, Liang J (2002) Determination method of character weight based on rough sets theory Chinese Journal of Management Science 10: 5 98 100 |
9 | Lu Z, Hu X, Yang H (2010) Airport emergency preparednesss management based on case-based reasoning Journal of Civil Aviation University of China 28: 1 5 |
10 | Zhang Z, Wang X, Dang J, Min Y (2012) Research on CBR decision method of railway emergency rescue based on integral similarity degree Journal of the China Railway Society 34: 11 49 53 |
Figures and Tables
Fig.1
Functions of fuzzy sets p 1 and q 1.
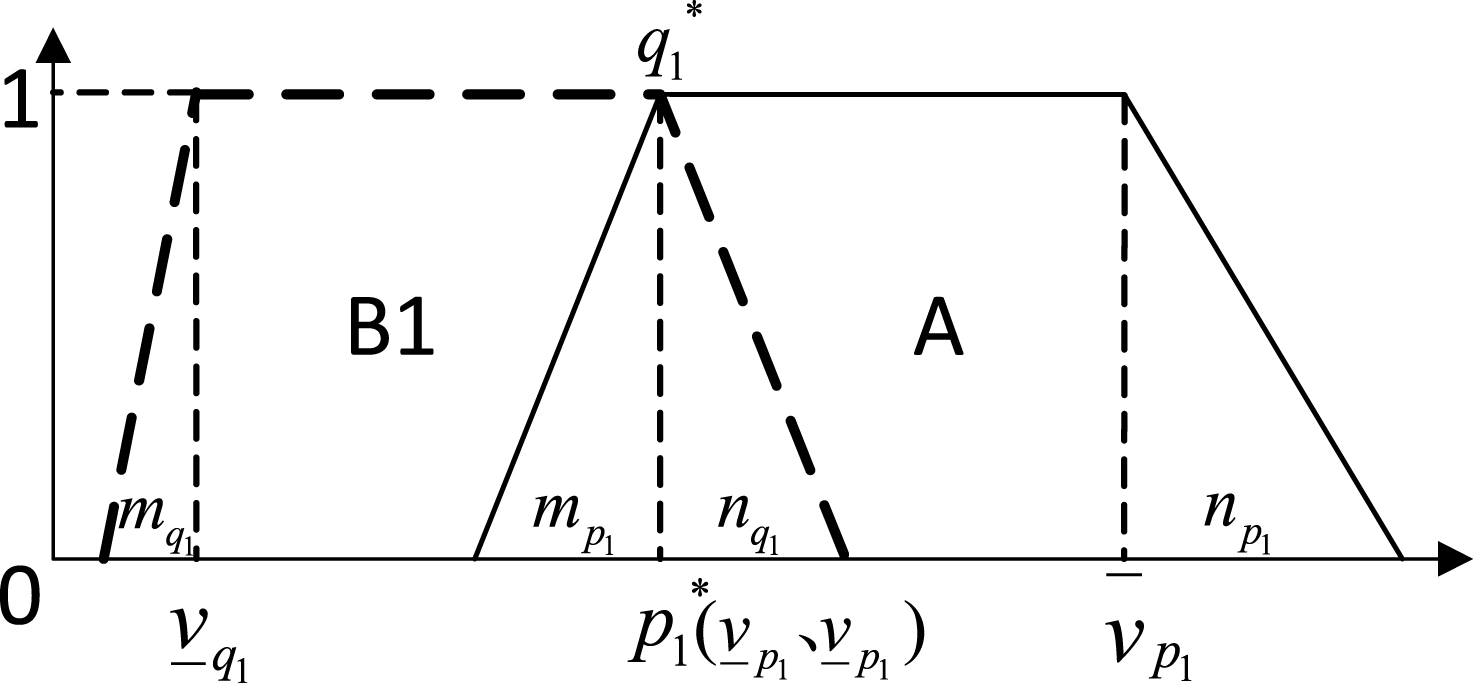
Table 1
Numerical properties
| Property name | Property value |
| No. of damaged vehicles | (determined number) |
| No. of injured | (determined number) |
| Death toll | (determined number) |
| No. of retained people | (determined number) |
Table 2
Symbolic properties
| Property name | Property value |
| Incident level | exceptional serious level I, serious level II, |
| general level III, minor level IV | |
| Incident data | 2008-12-31 (Specified date) |
| Incident section | Lianshui to Gaoyou (Specified section) |
| Incident time | workday daytime (night), holiday daytime |
| (night), activity day daytime (night) | |
| Weather condition | sunny, foggy, rainy, snowy |
| Road condition | dry, wet, icy |
| Road occupancy | one lane, two lanes, three lanes |
| Lane blocking | bidirectional, unidirectional |
| condition | |
| Vehicle type | motorcycle, bus, sedan, van, truck, |
| trailer, non-motor vehicle | |
| Fallout | yes, no |
| Road property loss | yes, no |
| Hazardous | yes, no |
| chemical leak | |
| Fire | yes, no |
| Explosion | yes, no |
Table 3
Fuzzy conceptional properties
| Property name | Property value |
| Precipitation | light rain, moderate rain, heavy rain, storm |
| Snow amount | light snow, moderate snow, |
| heavy snow, blizzard | |
| Icing area | large, small |
| Traffic congestion | busy, blocked, unblocked |
Table 4
Fuzzy interval properties
| Property name | Property value |
| Visibility | >500 m, 200–500 m, 100–200 m, |
| 50–100 m, <50m | |
| Incident duration | [1,3]h |
Table 5
Property values of emergency incidents and historical cases
| Property name | Case A | Case B1 | Case B2 | Case B3 |
| Incident level | level III | level III | level III | level IV |
| Incident date | 2015-01-20 | 2015-01-11 | 2014-12-02 | 2014-12-24 |
| Incident section | Changzhou-Zhenjiang | Changshu-Changzhou | Suchou-Changzhou | Danyang-Changzhou |
| Incident time | workday daytime | holiday daytime | holiday night | activity day daytime |
| Weather condition | sunny | sunny | sunny | foggy |
| Road condition | dry | dry | dry | wet |
| Precipitation | ———- | moderate | ———- | ——— |
| Snow amount | ———- | ———- | ———- | ——— |
| Icing area | ———- | ———- | ———- | ———- |
| Visibility | 300–400m | 200–300m | 300–400m | 100–200m |
| Incident duration | [2,4]h | [1,3]h | [1,4]h | [1,3]h |
| Road occupancy | one lane | one lane | one lane | one lane |
| Lane blocking condition | unidirectional | unidirectional | unidirectional | unidirectional |
| Traffic congestion | minor congestion | unblocked | minor congestion | unblocked |
| No. of damaged vehicles | 2 | 2 | 3 | 0 |
| Vehicle type | sedan | sedan | sedan | bus |
| No. of injured | 2 | 4 | 2 | 1 |
| Death toll | 0 | 0 | 1 | 0 |
| No. of retained people | 1 | 1 | 2 | 0 |
| Fallout | no | no | yes | no |
| Road property loss | no | yes | no | no |
| Fire | no | no | no | no |
| Explosion | no | no | no | no |
Table 6
Traffic congestion levels
| Daily traffic | [0,2] | (2,4] | (4,6] | (6,8] | (8,10] |
| congestion index | |||||
| Traffic congestion level | Very clear | clear | minor congestion | medium congestion | serious congestion |
Table 7
Similarity of road congestion property
| Property name | A and B1 | A and B2 | A and B3 |
| Road congestion | 0.0909 | 1 | 0.0909 |
Table 8
Fuzzy property similarity
| Property name | A and B1 | A and B2 | A and B3 |
| Visibility | 0.1304 | 1 | 0 |
| Incident duration | 0.3846 | 0.7077 | 0.3486 |
Table 9
Similarity of numeric properties
| Property name | A and B1 | A and B2 | A and B3 |
| No. of damaged vehicles | 1 | 0.667 | 0.333 |
| No. of injured | 0.333 | 1 | 0.667 |
| Death toll | 1 | 0 | 1 |
| No. of retained people | 1 | 0.5 | 0.5 |
Table 10
Similarity of symbolic properties
| Property name | A and B1 | A and B2 | A and B3 |
| Incident level | 1 | 1 | 0 |
| Incident date | 0 | 0 | 0 |
| Incident section | 0 | 0 | 0 |
| Incident time | 0 | 0 | 0 |
| Weather condition | 1 | 1 | 0 |
| Road conditions | 1 | 1 | 0 |
| Road occupancy | 1 | 1 | 1 |
| Lane blocking condition | 1 | 1 | 1 |
| Vehicle type | 1 | 1 | 0 |
| Fallout | 1 | 0 | 1 |
| Road property loss | 1 | 1 | 1 |
| Fire | 1 | 1 | 1 |
| Explosion | 1 | 1 | 1 |
Table 11
Overall similarity
| Name | A and B1 | A and B2 | A and B3 |
| Overall similarity | 0.6019 | 0.6329 | 0.4023 |




