A fast Algorithm for mining fuzzy frequent itemsets
Abstract
In this paper, a fuzzy frequent itemset (FFI)-Miner algorithm is developed to mine the complete set of FFIs without candidate generation. It uses a novel fuzzy-list structure to keep the essential information for later mining process. An efficient pruning strategy is also developed to reduce the search space, thus speeding up the mining process to directly discover the FFIs. Experiments are conducted to show the performance of the proposed FFI-Miner algorithm compared to the Apriori-based and tree-based approaches in terms of execution time and the number of traversal nodes for discovering FFIs under variants of membership functions.
1Introduction
Depending on the various requirements of the mined knowledge, association-rule mining (ARM) is the fundamental way to find the potential relationships among the items from the binary databases [10, 11, 13]. Agrawal et al. first presented the Apriori algorithm to mine association rules (ARs) in a level-wise way [11]. Han et al. then designed the frequent pattern (FP)-tree structure with a FP-growth mining algorithm to find FIs without candidate generation [5]. In real-life situations, it is difficult to handle the quantitative databases based on the crisp sets. Fuzzy-set theory was proposed to handle the quantitative databases [7]. In the past, Chan et al. proposed the F-APACS algorithm to discover the fuzzy association rules (FARs) [6]. Hong et al. stated the fuzzy data mining approach to discover fuzzy frequent itemsets (FFIs) in a level-wise way [14].Hong et al. then presented an efficient algorithm to merge the same fuzzy sets of the transformed transactions into smaller transformed databases, thus speeding up the computations for level-wisely mining the FARs [15].
Instead of the generate-and-test mechanism, fewer studies have been proposed to derive FARs or FFIs based on tree structures. Lin et al. respectively designed the fuzzy frequent pattern (FFP)-tree [1], compressed fuzzy frequent pattern (CFFP)-tree [2], and upper-bound fuzzy frequent pattern (UBFFP)-tree structures to mine FFIs [3]. Some studies for efficiently mining fuzzy association rules are still developed in progress [4, 8].
2Preliminaries and problem statement
2.1Preliminaries
Let I = {i 1, i 2, …, i m } be a finite set of m distinct items (attributes) in a quantitative database QD = {T 1, T 2, …, T n }, where each transaction T q ∈ QD is a subset of I, contains several items with its purchase quantities v iq and has an unique identifier, called TID.
An itemset X is a set of k distinct items {i 1, i 2, …, i k }, where k is the length of an itemset called k-itemset. An itemset X is said to be contained in a transaction T q if X ⊆ T q . A minimum support threshold is defined as δ. The user-specified membership functions is set as μ. A quantitative database is shown in Table 1 as a running example to illustrate the proposed approach. It consists of 8 transactions and 5 items, which are respectively denoted as (A) to (E). The minimum support threshold is initially set as δ (= 25%). The membership functions can be set as Fig. 1. Note that all items in the given example used the same membership functions to fuzzifier their quantitative values.
Definition 1. The linguistic variable R i is an attribute of a quantitative database whose value is the set of fuzzy terms represented in natural language as (R i1, R i2, …, R ih ) and can be defined in the membershipfunctions μ.
Definition 2. The quantitative value of i denoted as v iq , is the quantitative of the item i in transaction T q .
Definition 3. The fuzzy set, denoted as f iq , is the set of fuzzy terms with their membership degrees (fuzzy values) transformed from the quantitative value v iq of the linguistic variable i by the membership functionsμ as:
(1)
Thus, the Table 1 is then transformed by the membership functions shown in Fig. 1. Take TID (= 1) as an example to illustrate the process. In this process, the items with their quantitative values are transformed as: (
Definition 4. The support of the transformed fuzzy terms, denoted sup (R il ), is the summation of scalar cardinality of the fuzzy values of fuzzy term R il , which can be defined as:
(2)
Definition 5. The support of fuzzy k-itemsets (k ≥ 2),denoted as sup (X), is the summation of scalar cardinality of the fuzzy values for X, which can bedefined as:
(3)
2.2Problem statement
The problem of fuzzy frequent-itemset mining (FFIM) in this paper is to discover the complete set of fuzzy frequent itemsets (FFIs) as:
(4)
3Proposed list-based FFI-Miner algorithm
In this section, a new fuzzy-list structure is built to maintain the fuzzy information, which can be used to efficiently and effectively speed up the computations for directly discovering FFIs. The phases of the designed FFI-Miner algorithm are described below.
3.1Fuzzification phase
In the proposed algorithm, the maximum scalar cardinality strategy is adopted, thus making the number of transformed terms used in later processing equal to the number of the original items. This strategy can be used to find the most represented term of each item in the original databases.
Strategy 1. (Maximum scalar cardinality) For a linguistic variable i, the fuzzy terms R il with the maximum scalar cardinality (support) among the transformed fuzzy terms is used to present the linguistic variable (item) of FAM.
After that, the fuzzified quantitative database is then revised to keep the represented fuzzy terms if they are considered as the fuzzy frequent 1-itemsets. The kept transformed fuzzy terms of each transformed transaction are sorted in their support-ascending order. This strategy can be used to easier find the fuzzy values between the transformed fuzzy terms based on the designed fuzzy-list structures.
Strategy 2. (The support-ascending order) For the remaining fuzzy terms with their fuzzy values in a transaction T q , the fuzzy terms are sorted in their support-ascending order to perform the intersection operation for discovering their support values among the fuzzy k-terms (k≥ 2).
Based on the maximum scalar cardinality and the support-ascending order strategies, the original databases can be transformed as the fuzzified databases.
3.2Fuzzy-list structure
After the original quantitative database is transformed, the remaining fuzzy terms in L 1 are used to build their own fuzzy-list structures for keeping the fuzzy information. The definitions used in the fuzzy-list structure are respectively given below.
Definition 6. A fuzzy term R il in transaction T q , and R il ⊆ T q . The set of fuzzy terms after R il in T q is denoted as T q /R il .
Definition 7. The internal fuzzy value of a fuzzy term R il in transaction T q is denoted as if (R il , T q ).
Definition 8. The resting fuzzy value of a fuzzy term R il in transaction T q is denoted as rf (R il , T q ) by performing the union operation to get the maximum fuzzy value of all the fuzzy terms as the upper-bound value in T q /R il in T q , which is defined as:
(5)
In the constructed fuzzy-list structure, each element consists of three attributes as:
1. Transaction TID (tid), which indicates a transaction T q containing R il .
2. Internal fuzzy value (if), which indicates the fuzzy value of R il in T q .
3. Resting fuzzy value (rf), which indicates the maximum fuzzy value of the resting fuzzy terms after R il in T q .
The initial fuzzy-list structures of the fuzzy terms in L 1 are first constructed. Since the support-ascending order of the fuzzy terms in L 1 are (D . L < B . L < C . H < A . M), the results are shown in Fig. 2. The construction algorithm of fuzzy-list structure is shown in Algorithm 1.
| Algorithm 1 Fuzzy-list Construction |
| Input: P x . FL, the fuzzy-list of P x ; P y . FL, the |
| fuzzy-list of P y . |
| Output: P xy . FL the fuzzy-list of x and y. |
| 1: P xy . FL ← null. |
| 2: for each E x ∈ P x . FL do |
| 3: if ∃E y ∈ P y . FL and E x . tid = = E y . tid then |
| 4: E xy . tid ← E x . tid. |
| 5: E xy . if ← min (E x . if, E y . if). |
| 6: E xy . rf ← E y . rf. |
| 7: E xy ← < E xy . tid, E xy . if, E xy . rf >. |
| 8: append E xy to P xy . FL. |
| 9: end if |
| 10: end for |
| 11: return P xy . FL. |
Definition 9. The SUM . R il . if is to sum the fuzzy values of an itemset R il in D, which can be defined as:
(6)
Definition 10. The SUM . R il . rf is to sum the resting fuzzy values after R il in D, which can be defined as:
(7)
3.3Search space of fuzzy-list
Based on the designed fuzzy-list structure, the search space of the proposed FFI-Miner algorithm can be represented as an enumeration tree according to the developed support-ascending order strategy. In this example, the search space of the enumeration tree is shown in Fig. 3.
Since the complete search space of the enumeration tree is very huge for discovering all fuzzy frequent itemsets, it is necessary to reduce the search space but still can completely find the fuzzy frequent itemsets.
Strategy 3. For an itemset X, if its SUM . X . if is no less than the minimum support count, it is considered as a fuzzy frequent itemset. Also, if min(SUM.X.if, SUM.X.rf) of X is no less than the minimum support count, the supersets of X are required to be generated and determined.
Theorem. Given the fuzzy-list of a fuzzy term R il . If the sum of resting fuzzy values of R il is no less than minimum support count (δ × |QD|), any extensions of R il are not the fuzzy frequent itemsets.
Proof. For ∀T q ⊇ X′, suppose fuzzy term R il is denoted as X, and X’ is the extension of X, thus:
Thus, if the summation of the resting fuzzy values of the itemset X is no larger than the minimum support count, any extensions of X will not be a fuzzy frequent itemsets and can be directly ignored to avoid the construction phase of the fuzzy-list structures of the extensions of X. The proposed fuzzy-frequent itemset (FFI)-Miner algorithm is described in Algorithm 2.
| Algorithm 2 FFI-Miner |
| Input: FLs, fuzzy-list of 1-itemsets; δ. |
| Output: FFIs, the set of complete fuzzy frequent itemsets. |
| 1: for each fuzzy-list X in FLs do |
| 2: if SUM . X . if ≥ δ × |QD| then |
| 3: FFIs ← X ∪ FFIs. |
| 4: end if |
| 5: if SUM . X . rf ≥ δ × |QD| then |
| 6: exFLs ← null. |
| 7: for each fuzzy-list Y after X in FLs do |
| 8: exFL ← exFLs + Construct (X, Y). |
| 9: end for |
| 10: FFI-Miner(exFLs, δ). |
| 11: end if |
| 12: end for |
| 13: return FFIs. |
4Experimental evaluation
In this section, the proposed FFI-Miner algorithm is evaluated to compare the state-of-the-art FDTA [14], CFFP-tree [2], GDF [15], and UBFFP-tree [3] algorithms. Two real-life chess, mushroom datasets [9] and one synthetic c20d10k dataset [9] are used in the experiments. The quantities of items are randomly assigned in the range of [1, 11] interval in the used datasets by adopting normal distribution. In the conducted experiments, the linear membership functions for 3-terms were shown in Fig. 1 and the linear membership functions for 2-terms are respectively shown in Fig. 6.
4.1Runtime
The execution time of four algorithms compared to the designed FFI-Miner with different types membership functions under different minimum support thresholds in three datasets is conducted and shown in Fig. 4. From Fig. 4, it can be observed that the proposed algorithm is faster than the previous algorithms under varied minimum support thresholds in three datasets whether in 2-terms or 3-terms membership functions. The proposed FFI-Miner algorithm has almost up to one or two orders of magnitude faster than other algorithms. The reason is that the CFFP-tree algorithm is very sensitive of the transaction length since each node in the CFFP-tree structure requires more computations to attach an array. Although the UBFFP-tree algorithm uses an efficient structure to keep the FFIs, it still requires an additional database scan to find the actual counts of the remaining itemsets. The FDTA and GDF can efficiently mine the FFIs to handle the condense datasets but the sparse one since the number of remaining itemsets is not very large to perform the generate-and-test mechanism for mining the FFIs.
4.2Number of traversal nodes
The number of traversal nodes in the tree structure is evaluated. The FDTA and GDF algorithms perform the generate-and-test approach to mine FFIs. Thus, the proposed FFI-Miner algorithm only compares to the CFFP-tree and UBFFP-tree algorithms. The results are shown in Fig. 5. From Fig. 5, it can be observed that the number of traversal nodes of the designed FFI-Miner algorithm is much less than those of the CFFP-tree and UBFFP-tree algorithms under varied minimum support thresholds in three datasets. The proposed FFI-Miner algorithm requires less memory usage to keep the required information in the list structure. Besides, the number of tree nodes that required to be analyzed can be greatly pruned in the enumeration tree based on the designed pruning strategy. Thus, the amount of tree nodes and iterative operations for building subtree will be reduced compared to whether the CFFP-tree and UBFFP-tree algorithms.
5Conclusion
In this paper, we first propose a list-based FFI-Miner algorithm to efficiently discover FFIs from the quantitative databases. An efficient pruning strategy is also developed in the designed fuzzy-list structures to early prune the unpromising candidates for later mining process. From the conducted experiments, it can be easily observed that the proposed algorithm has better performance than the state-of-the-art algorithms for mining fuzzy frequent itemsets.
Acknowledgments
This research was partially supported by the Tencent Project under grant CCF-TencentRAGR20140114, by the Shenzhen Strategic Emerging Industries Program under grant ZDSY20120613125016389, by the National Natural Science Foundation of China (NSFC) under grant No. 61503092, and by the Natural Scientific Research Innovation Foundation in Harbin Institute of Technology under grant HIT.NSRIF.2014100.
References
1 | Lin CW, Hong TP, Lu WH (2010) Linguistic data mining with fuzzy fp-trees Expert Systems with Applications 37: 4560 4567 |
2 | Lin CW, Hong TP, Lin TC (2010) An efficient tree-based fuzzy data mining approach International Journal of Fuzzy Systems 12: 150 157 |
3 | Lin CW, Hong TP, Lu WH (2014) Mining fuzzy frequent itemsets based on UBFFP trees Journal of Intelligent & Fuzzy Systems 27: 535 548 |
4 | Lan GC, Hong TP, Lin YH, Wang SL (2015) Fuzzy utility mining with upper-bound measure Applied Soft Computing 30: 767 777 |
5 | Han J, Pei J, Yin Y, Mao R (2004) Mining frequent patterns without candidate generation: A frequent-pattern tree approach Data Mining and Knowledge Discovery 8: 53 87 |
6 | Chan KCC, Au WH (1997) Mining fuzzy association rules Proceedings of the International Conference on Information and Knowledge Management 209 215 |
7 | Zadeh LA (1965) Fuzzy sets Information and Control 8: 338 353 |
8 | Delgado M, Marin N, Sanchez D, Vila MA (2003) Fuzzy association rules: General model and applications IEEE Transactions on Fuzzy Systems 11: 214 225 |
9 | Fournier-Viger P, Gomariz A, Gueniche T, Soltani A, Wu CW, Vincent S (2014) Tseng, SPMF: A java open-source pattern mining library Journal of Machine Learning Research 15: 3389 3393 |
10 | Agrawal R, Imielinski T, Swami A (1993) Database mining: A performance perspective IEEE Transactions on Knowledge and Data Engineering 5: 914 925 |
11 | Agrawal R, Srikant R (1994) Fast algorithms for mining association rules in large databases Proceedings of the The International Conference on Very Large Data Bases 487 499 |
12 | Papadimitriou S, Mavroudi S (2005) The fuzzy frequent pattern tree Proceedings of the WSEAS International Conference on Computers 1 7 |
13 | Hong TP, Lin CW, Wu YL (2008) Incrementally fast updated frequent pattern trees Expert Systems with Applications 34: 2424 2435 |
14 | Hong TP, Kuo CS, Chi SC (1999) Mining association rules from quantitative data Intelligent Data Analysis 3: 363 376 |
15 | Hong TP, Lan GC, Lin YH, Pan ST (2013) An effective gradual data-reduction strategy for fuzzy itemset mining International Journal of Fuzzy Systems 15: 170 181 |
Figures and Tables
Fig.1
The used linear membership functions of linguistic 3-terms.
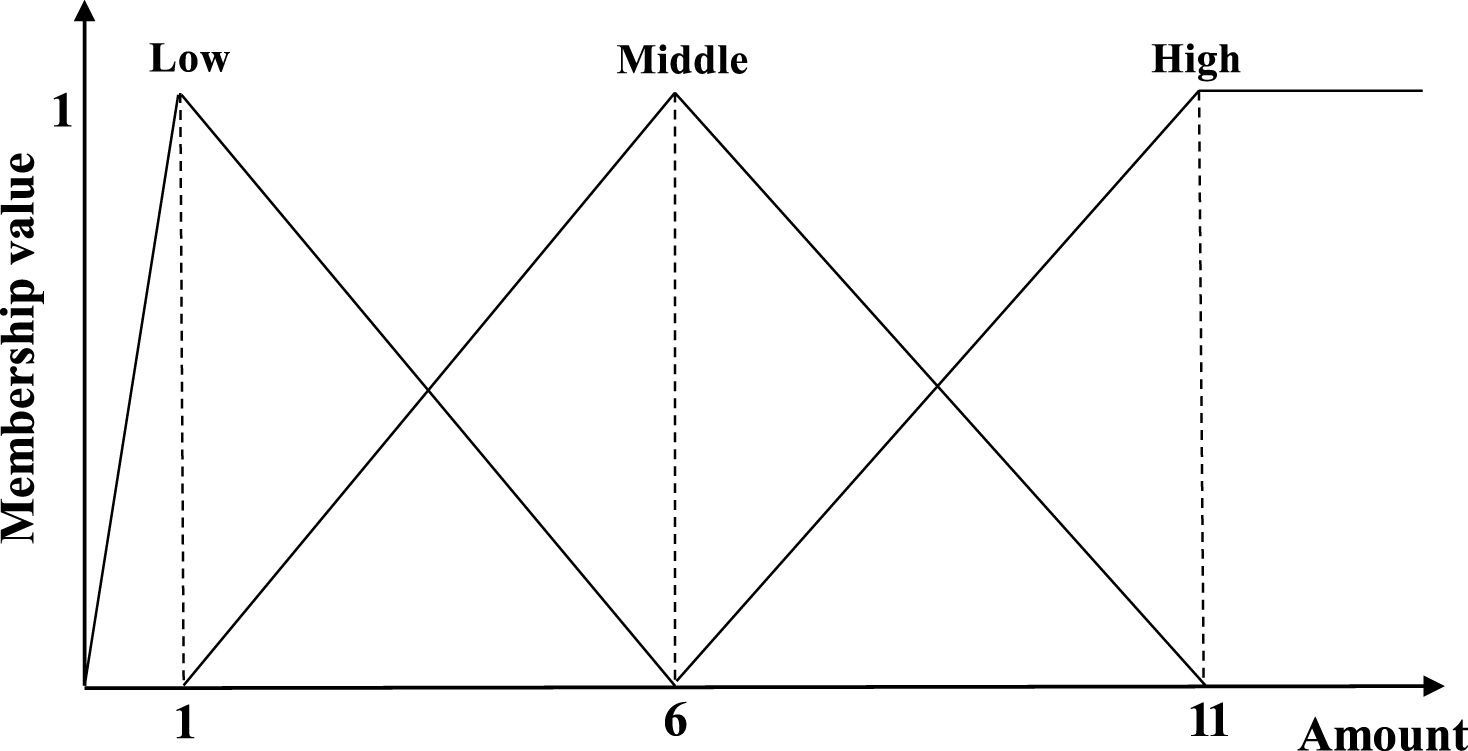
Fig.2
The initial constructed fuzzy-list structures.
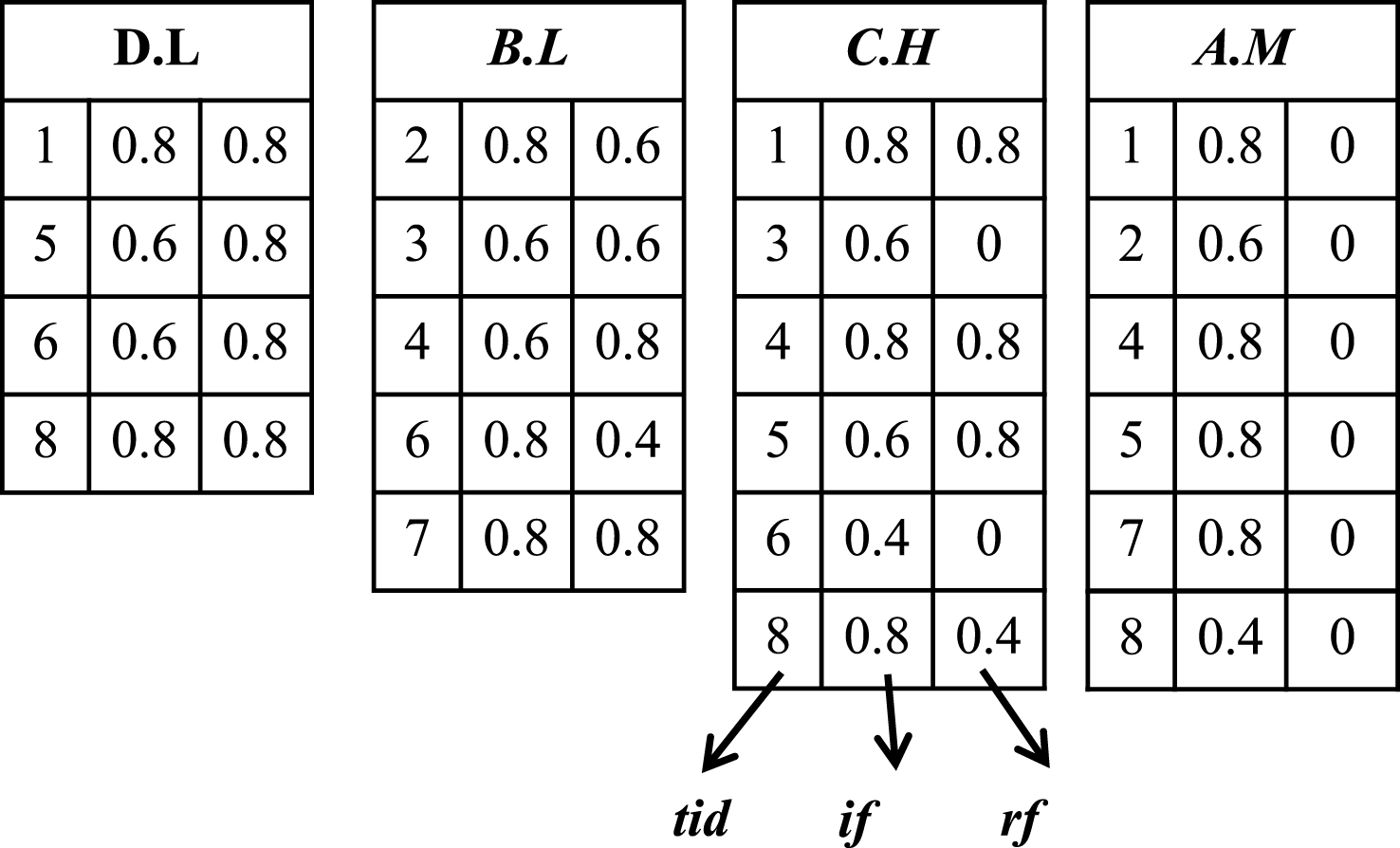
Fig.3
An enumeration tree of the used example.
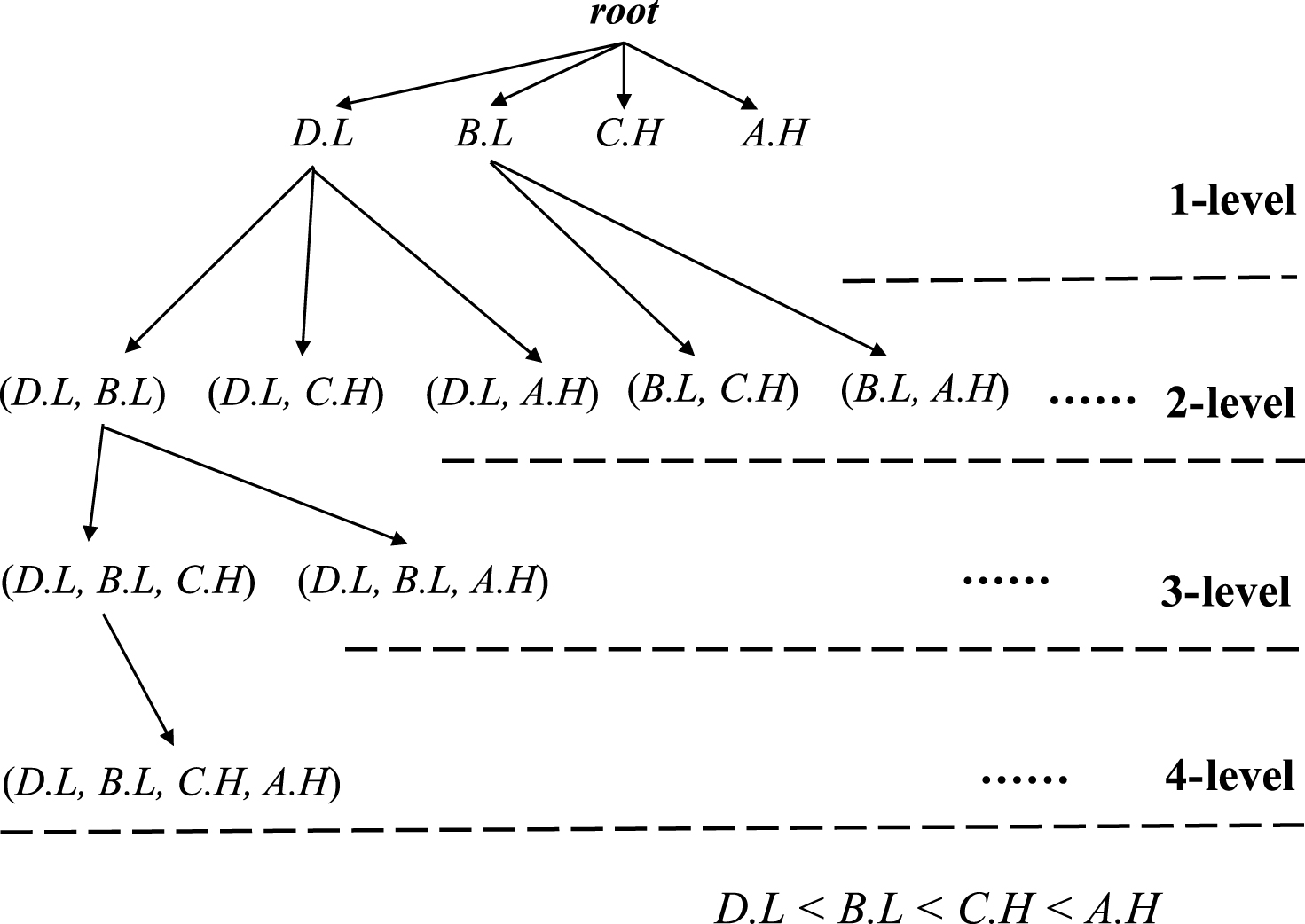
Fig.4
Runtime w.r.t. variant minimum support thresholds.
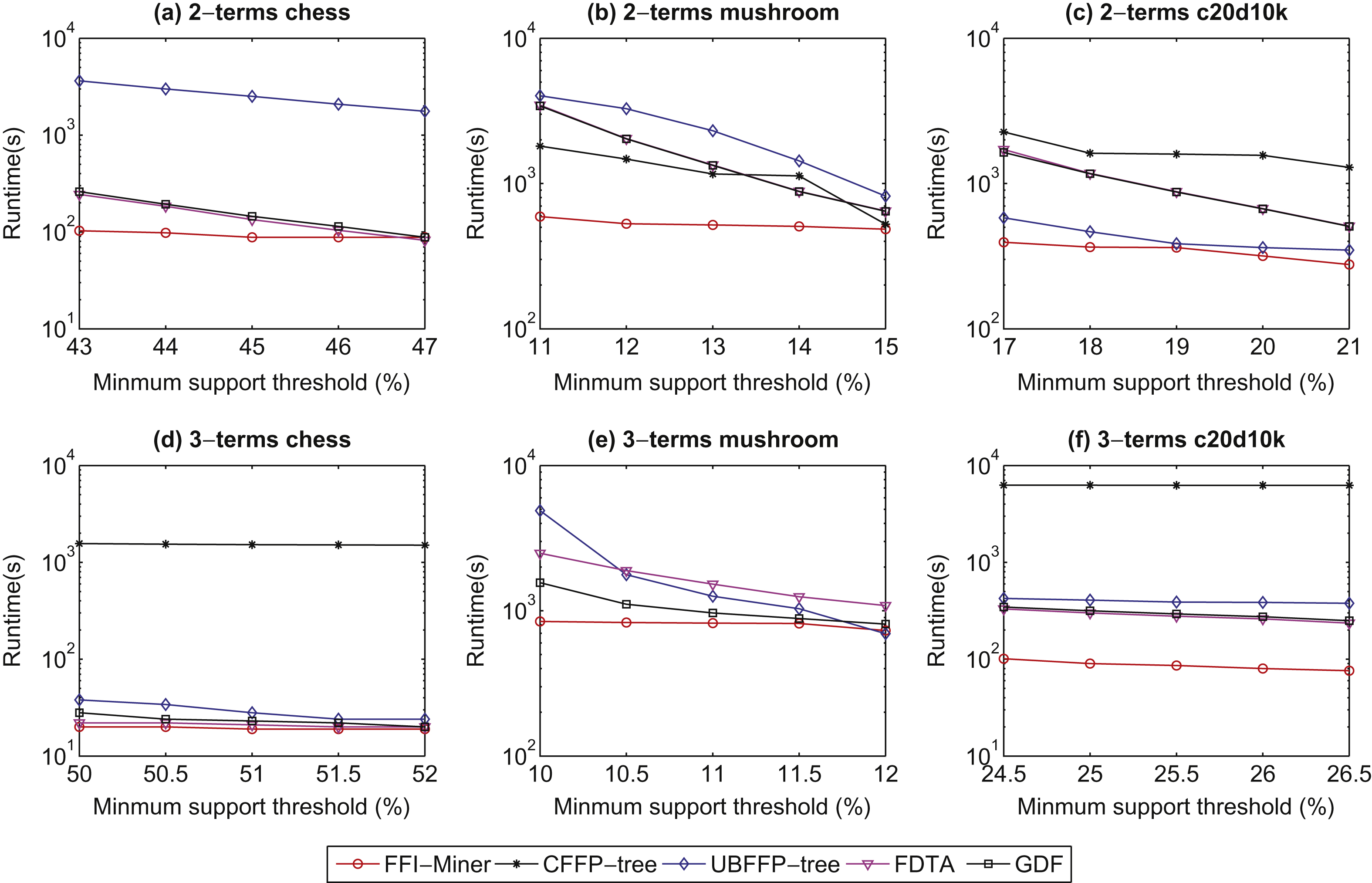
Fig.5
Number of traversal nodes w.r.t. variant minimum support thresholds.
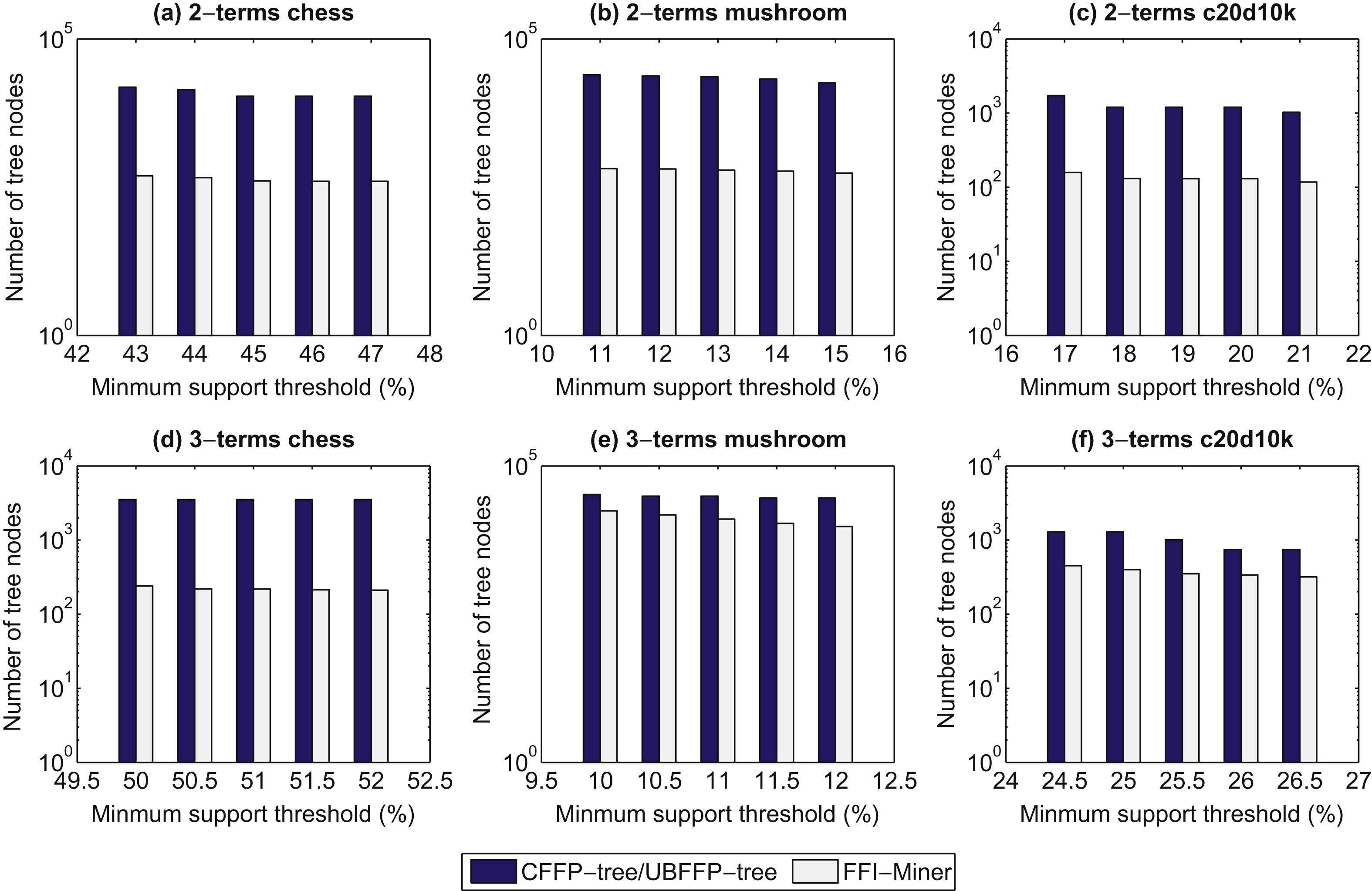
Fig.6
Linear membership functions for 2-terms.
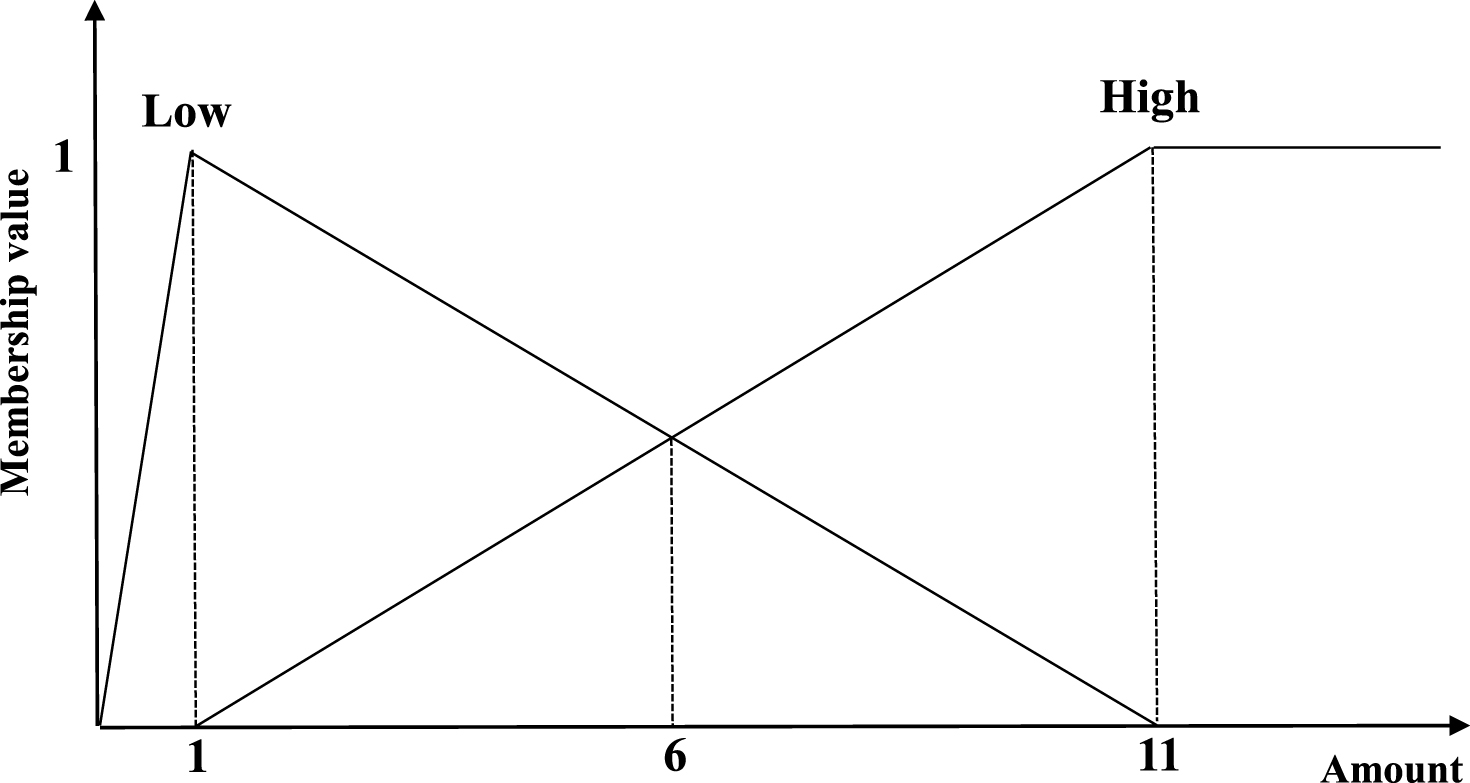
Table 1
A quantitative database
| TID | Items |
| 1 | A:5, C:10, D:2, E:9 |
| 2 | A:8, B:2, C:3 |
| 3 | B:3, C:9 |
| 4 | A:5, B:3, C:10, E:3 |
| 5 | A:7, C:9, D:3 |
| 6 | B:2, C:8, D:3 |
| 7 | A:5, B:2, C:5 |
| 8 | A:3, C:10, D:2, E:2 |




