Building cognizance rule knowledge for fault diagnosis based on fuzzy rough sets1
Abstract
With the continuous development of huge systems, dependence on the system is continually increasing. The failure of such systems will cause huge losses. The reason for system failure is often unclear, so that inconsistency and uncertainty between fault data will appear. In the actual application process, there is a process of change. If it is possible to predict the failure probability from the monitoring parameters, it will be very beneficial to system troubleshooting. Therefore, this paper proposes a new recognition algorithm based on fuzzy rough sets, in order to adapt to the processing of uncertain fault detection data. Additionally, the optimal direction of the dynamic information entropy increment is used to predict the fault information. This can quickly find the faults and provide important information for fault detection. It is verified that the proposed algorithm can improve the early warning and the accuracy of fault diagnosis information systems in the fault simulation analysis of a diesel engine.
1Introduction
With the quick development of modern industry and scientific technology, and with the large-scale, high-speed and automatic trends in modern equipment, people have become more concerned about the safety and reliability of equipment. In recent years, data techniques have become increasingly important to the development of modern industrial technology [19]. Faults of modern industrial production will result in disasters, once the fault has occurred. Recently, the disastrous accidents caused by critical equipment faults have inspired much research on equipment diagnosis, that have resulted in an emerging field of fault diagnosis of equipment, engineering structure and technological processes [26]. S. Yin introduces the application of data-driven methods in industrial monitoring, which has occurred in the last twenty years and promotes the rapid development of industrial automation [18]. Fault detection and diagnosis technology has been proposed as a new method to improve the reliability and safety of systems so that fault detection and diagnosis technologies within dynamic systems have become a rapid field of development. Existing fault diagnosis methods can be roughly divided into model-based methods, knowledge-based methods and methods based on image processing.
The residual between the measurable information and prior system information expressed by a model is used in the model-based method, which can achieve fault diagnosis by analyzing and processing the residual. This method must establish the mathematical model of diagnosed objects, and estimate the parameters using detective signals or by reconstructing the system state. The test for state estimation residual sequences and identification are used to forecast, locate and quantify the fault [24].
Due to the connection between the amplitude, phase, frequency and correlation of system I/O signals and the fault source, the fault can be detected and isolated by the application of a signal processing method and a characteristic extraction method after the fault has occurred. This method based on signal analysis theory provides multiple eigenvectors in the time domain and frequency domain, and exploits the connection between eigenvectors and fault sources to analyze and process the system signal so that the position of fault sources can be determined [9].
The knowledge-based method exploits expert diagnostic knowledge and diagnostic objects without establishing a quantitative mathematical model applied the fuzzy logic method to the adaptive adjustment of residual thresholds [7, 16]. M. Hemza proposed the automatic detection of faults using a neural network [11]. A. Bellini adopted a method based on pattern recognition to complete the automatic detection of non-linear system faults [1]. S. Yin derives the framework of data-driven design, which can be used for the monitoring of large-scale industrial processes [22]. S. Yin introduces an improved PLS (IPLS) method, which provides a high detection rate and can effectively diagnose the faults of KPI [20]. The expert system is also one algorithm of fault detection systems [13].
In spite of the fantastic results from state-of-the-art research on fault diagnosis, unsolved problems remain, as follows:
The unknown mechanism of faults from diagnostic equipment may result in ambiguity in the external manifestation of faults and unclear system states expressed by diagnostic information. Different faults may demonstrate similar performance, whereas the same fault may express differently at different times or under different environmental conditions. The ambiguity and inconsistency among failure data will have a major impact on the operating results of fault detection systems, which is not advantageous to the application of fault detective technology.
Shorter time of fault diagnosis will result in smaller losses caused by accidents. Therefore, the development of rapid diagnostic technology is very important, particularly rapid diagnostic technology that does not reduce the accuracy of fault diagnosis.
In this paper, a method based on cognitive rule extraction is used to achieve dynamic analysis and intelligent cognition of informative systems, monitored by a real-time system so that the fault is found more quickly. The continuous change of diagnostic information is considered, and the rule extraction is achieved by a cognitive rule in which the fuzzy rough set is adopted. The simulative analysis of a diesel engine fault demonstrates that the intelligent cognitive rules can achieve earlier warning regarding fault diagnosis information systems, and the improved accuracy of such systems.
This paper is organized as follows. Section 2 presents fuzzy rough set theory. Section 3 details the cognizance rule generation. Section 4 presents the simulation of a diesel engine fault for evaluation of the proposed method.
2Fuzzy rough set theory
As an extended rough set, fuzzy rough sets introduce fuzzy set theory, so that the rough set can effectively handle complex uncertain problems. The fuzzy decision table is defined in this section.
Definition 1. Let the fuzzy decision table be defined as DT = (U, A = C ∪ D, V, f). U is the discourse domain; A is the fuzzy attribute set, which includes condition attribute set C = {A
1, A
2, ⋯ , A
m
} and decision attribute set D = {A
m+1}, in which A
j
is the fuzzy attribute on domain U. U can be divided into p
j
fuzzy equivalence classes, namely
Since fuzzy rough sets introduce the fuzzy sets, the equivalent class, as well as the upper and lower approximation concepts in classical rough set theory are also extended to the fuzzy equivalence class, vague upper approximation, and lower fuzzy approximation, respectively.
Definition 2. Let R be defined as a fuzzy equivalence relation on domain U, namely the fuzzy attribute. For x ∈ U:
(1)
Definition 3. For the fuzzy decision table DT = (U, A = C ∪ D, V, f), R is a fuzzy attribute on domain U, and X ⊆ U. The lower approximation
(2)
(3)
(4)
(5)
The fuzzy lower approximation and upper approximation constructed binary pair
Definition 4. In rough set theory, the attribute set A in the domain partition can be expressed as follows:
(6)
If A = {α 1, α 2, ⋯ α m },
Through the definition of the fuzzy equivalence class of attribution set A, above, the membership function of an object belonging to such a fuzzy equivalence classes can be defined as follows:
(7)
In classical rough set theory, the positive region is defined as the union of the lower approximation. According to this rule, the membership function that one object belongs to in the fuzzy positive region of a rough fuzzy rough set can be defined.
Definition 5. Given a fuzzy decision table DT = (U,A~=C ∪ D,V,f),P ∈ C,Q ∈ D, define
(8)
(9)
3Cognizance rule development
The unknown mechanism of faults from diagnostic equipment may result in ambiguity in the external manifestation of faults and unclear system states expressed by diagnostic information. Different faults may demonstrate similar performance, whereas the same fault may express differently at different times or under different environmental conditions. The ambiguity and inconsistency in failure data will have great impact on the operating results of the fault detection system, which is not advantageous for the application of fault detective technology. Shorter detection times may reduce losses from accidents, and has thus become a primary research focus in the field. The cognitive rule intelligent extraction algorithm based on a rough set can deal with uncertain fault detection data, and detect fault information based on the optimum direction of the dynamic entropy increment to improve the accuracy and efficiency of detection.
For complex systems, many states can be expressed. There is inconsistency in these statistics under different environmental conditions. For example, for some states, a characteristic may be consistent under environmental conditions, but in some contradictory situations, system faults may occur after environmental changes. Therefore, the inevitable connection among system faults, states and different environments should be discussed dynamically to better obtain connection information between system states and faults. Based on the direction of maximum entropy, the cognitive rule states that the rule can be obtained in conjunction with the maximum dynamic information entropy of the fault detection system state, which can be analyzed under different environmental conditions.
The framework of cognizance rule acquirement is shown in Fig. 1.
The steps to achieve cognizance rule generation are as follows:
Build the fuzzy equivalence relation, which can be used to evaluate the correlation degree of two information system samples in the universe.
Determine the fuzzy judgment subjection degree, which must suit the information judgment table data. The cognizance rule defines the formula as follows:
(10)
Analyze the dynamic attribution importance, which considers the already-described attribute information.
(11)
(12)
The card is the member number of the set; a threshold can be set by the user, such as 0.8.
After computing all no-value attributes of dynamic importance, the cognizance rule can be generated based on the dynamic attribution importance. The cognizance rule form is as follows:
(13)
Then, the system can arrange the system state information in detection order for fault diagnosis.
After obtaining the new system states, the fault diagnosis system evaluates the fuzzy judgment. If the judgment subjection degree is beyond the threshold, the system accepts the judgment. Otherwise, the system regenerates the cognizance rule for the next information index in order.
4Simulation
To evaluate the cognizance rule generation framework for fault detection, this paper presents a simulation which compares the cognizance rule to attribution importance. Attribution importance is the statistical measurement, and is described as follows:
(14)
This simulation employs diesel engine malfunction as the fault detection system, which can discover eight malfunctions using eight detection parameters. These eight malfunctions are as follows: 100% offering (T1), 75% offering (T2), 25% offering (T3), idle consumption (T4), pin valve block (T5), valve jam (T6), pin valve leak (T7) and excess oil valve invalidation (T8). The eight detection parameters are as follows: greatest pressure (P1), hypo-greatest pressure (P2), wave range (P3), ascending edge width (P4), wave width (P5), greatest aftereffect width (P6), wave area (P7) and spout pressure (P8). According to the maximum and minimum detected by each sensor and normalized to the [–1,1] space, a data set will be recorded, which is then adapted to the output of various classifiers (or sensors). The diesel engine malfunction judgment information is listed in Table 1.
By analyzing this table, the statistic character can be determined. There are three cluster parameter centers:
The rule following fault detection information can be obtained from the intelligent extraction step and cognitive rule equations in Section 3. For example, in the known state P1 conditions and according to the attribute importance, the detection rule is as follows.
(15)
The cognitive rules based on the fuzzy rough set maximum dynamic information entropy in this paper are expressed as follows:
(16)
(17)
(18)
These cognitive rules distinguish the analysis direction of maximum dynamic information entropy of the fault detection system within the different initial values in state P1. Such directions are more suitable for the cognitive mechanism of the biosphere, so the fault detection accuracy and efficiency can be determined.
Results indicate that cognizance rules can offer more detail in order to control fault detection processing more intelligently and efficiently. The simulation system tests different dates with variant system noise to evaluate the result of the cognizance rules and attribute importance. Figure 2 shows the system judgment results with 0.21 system noise.
Figure 2 shows the system judgment results with 0.1 system noise.
Figure 3 shows the system judgment results on system noise 0.1.
This paper uses the Monte Carlo simulation method to test 300 experiments in order to evaluate the accuracy and efficiency of the variant index rule. Figure 4 shows discrimination accuracy result for 1,000 malfunction samples with [0.1, 0.2] system noise, averaging 300 Monte Carlo simulation. Figure 5 shows the discrimination efficiency result for 1000 mal-function sample on [0.1, 0.2] system noise averaging 300 Monte Carlo simulation.
For diesel engine fault detection data, different signal-to-noise of Monte Carlo simulation experiments show that the cognitive rules based on fuzzy rough set maximum dynamic information entropy discovery system failure better. Within the same signal-to-noise ratio data, the accuracy of the fault detection analysis based on maximum dynamic information entropy from cognitive rule that is higher than from regular attribute rules. This method could improve the fault detection efficiency. The cognitive rules based on fuzzy rough set maximum dynamic information entropy are also adaptive to deal with uncertain data for fault detection in more complicated systems.
5Conclusions
Due to the unknown mechanisms of faults in complex systems and the ambiguity and the inconsistency of system states and fault diagnosis, this paper proposes a method based on cognitive rule extraction to achieve dynamic analysis and intelligent cognition of informative systems monitored by a real-time system, so that the fault is found more quickly. Based on the direction of maximum entropy, the cognitive rule can improve the recognition rate resulting in earlier fault detection. The continuous change of diagnostic information is considered, so the rule extraction is achieved by cognitive rules which adopt the fuzzy rough set. The simulative analysis of a diesel engine fault indicates that the intelligent cognitive rules can achieve earlier detection in fault diagnosis information systems, with improved accuracy.
References
1 | Bellini A, Filippetti F, Tassoni C, Capolino G-A (2008) Advances in diagnostic techniques for induction machines IEEE Trans Ind Electron 55: 4109 4126 |
2 | Zeng A, Pan D, Zheng QL, Peng H (2006) Knowledge acquisition based on rough set theory and principal component analysis IEEE Intelligent Systems 21: 2 78 85 |
3 | Cornelis C, Cock MD, Radzikowska AM (2007) Vaguely quantified rough sets Proc Rough Sets, Fuzzy Sets, Data Mining Granular Compute (Lecture Notes in Artificial Intelligence) 4482: 87 94 |
4 | Wang CY (2015) Type-2 fuzzy rough sets based on extended t-norms Information Sciences 305: 165 183 |
5 | Yeung DS, Chen DG, Tsang ECC, Lee JWT, Wang XZ (2005) On the generalization of fuzzy rough sets IEEE Trans Fuzzy Syst 13: 343 361 |
6 | Lynn D, Nele V, Chris C, Llus G (2015) Comprehensive study of implicator-conjunctor-based and noise-tolerant fuzzy rough sets: Definitions, properties and robustness analysis Fuzzy Sets and Systems (2014) 275: 1 38 |
7 | Bouchikhi E, Houssin E (2015) Induction machine faults detection using stator current parametric spectral estimation Mechanical Systems and Signal Processing 52–53: 447 464 |
8 | Mi JS, Zhang WX (2004) An axiomatic characterization of a fuzzy generalization of rough sets Inf Sci 160: 235 249 |
9 | Lee KS, Park TG (2015) Robust fault detection observer design under fault sensitivity constraints Journal of the Franklin Institute 352: 1791 1810 |
10 | Maryam L, Shiratuddin S, Wong MF, Wai K (2015) Utilising fuzzy rough set based on mutual information decreasing method for feature reduction in an image retrieval system Lecture Notes in Electrical Engineering 313: 177 184 |
11 | Hemza M, Omar B, Djamel B (2015) Sliding mode based fault detection, reconstruction and fault tolerant control scheme for motor systems ISA Transactions 57: 340 351 |
12 | Quafafou M (2000) α -RST: A generalization of rough set theory Inf Sci 124: 301 316 |
13 | Talebi N, Sadrnia MA, Darabi A (2015) Fault detection of wind energy conversion systems using recurrent neural networks International Journal of Sustainable Energy 34: 52 70 |
14 | Parthalain NM, Shen Q, Jensen R (2010) A distance measure approach to exploring the rough set boundary region for attribute reduction IEEE Transactions on Knowledge and Data Engineering 22: 305 317 |
15 | Shen Q, Jensen R (2004) Selecting informative features with fuzzy-rough sets and its application for complex systems monitoring Pattern Recognit 37: 1351 1363 |
16 | Rubini R, Meneghetti U (2001) Application of the envelope and wavelet transform analysis for the diagnosis of incipient faults in ball bearings Mech Syst Signal Process 15: 287 302 |
17 | Jensen R, Shen Q (2007) Fuzzy-rough sets assisted attribute selection IEEE Transactions on Fuzzy Systems 15: 73 89 |
18 | Yin S, Li XW, Gao HJ, Okyay K (2015) Data-based techniques focused on modern industry: An overview IEEE Transactions on Industrial Electronics 62: 657 667 |
19 | Yin S, Huang Z (2015) Performance monitoring for vehicle suspension system via fuzzy positivistic C-means clustering based on accelerometer measurements IEEE/ASME Transactions on Mechatronics 20: 5 2613 2620 |
20 | Yin S, Zhu XP, Kaynak O (2015) Improved PLS focused on key-performance-indicator-related fault diagnosis IEEE Transactions on Industrial Electronics 62: 1651 1658 |
21 | Zhao SY, Tsang ECC, Chen DG (2009) The model of fuzzy Variable precision rough sets IEEE Transactions on Fuzzy Systems 17: 451 467 |
22 | Yin S, Ding SX, Xie XC, Luo H (2014) A review on basic data-driven approaches for industrial process monitoring IEEE Transactions on Industrial Electronics 61: 6418 6428 |
23 | Zhao SY, Tsang ECC, Chen DG, Wang XZ (2010) Building a rule-based classifier-A fuzzy-rough set approach IEEE Transactions on Knowledge and Data Engineering 22: 624 638 |
24 | Kochaski W, Boeff M, Hashemiyan Z, Staszewski WJ, Verma PK (2015) Modelling and numerical simulations of in-air reverberation images for fault detection in medical ultrasonic transducers: A feasibility study Journal of Sensors 2015: 14 |
25 | Li Y, Shiu SCK, Pal SK (2006) Combining feature reduction and case selection in building CBR classifiers IEEE Transactions on Knowledge and Data Engineering 18: 415 429 |
26 | Li ZL, Outbib R, Giurgea S, Hissel D, Li YD (2015) Fault detection and isolation for polymer electrolyte membrane fuel cell systems by analyzing cell voltage generated space Applied Energy 148: 260 272 |
27 | Li ZW, Xie TS (2015) Roughness of fuzzy soft sets and related results International Journal of Computational Intelligence Systems 8: 278 296 |
28 | Pawlak Z (1982) Rough sets Int J Comput Inf Sci 11: 341 356 |
29 | Pawlak Z, Skowron A (2007) Rough sets: Some extensions Information Sciences 177: 28 40 |
Figures and Tables
Fig.1
The framework for cognizance rule generation.
Fig.2
Discrimination results for 1,000 malfunction samples with 0.21 system noise.
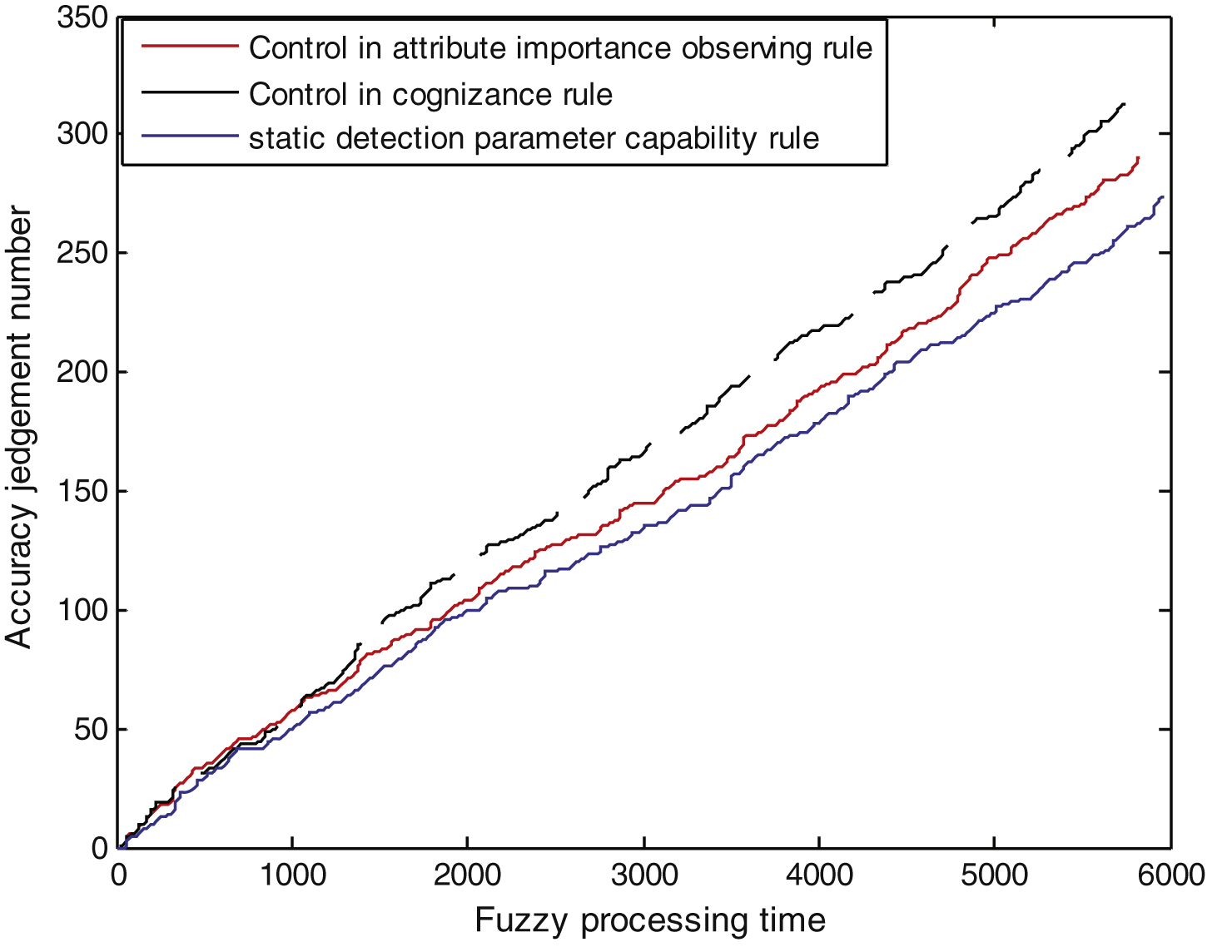
Fig.3
Discrimination results for 1,000 malfunction samples with 0.1 system noise.
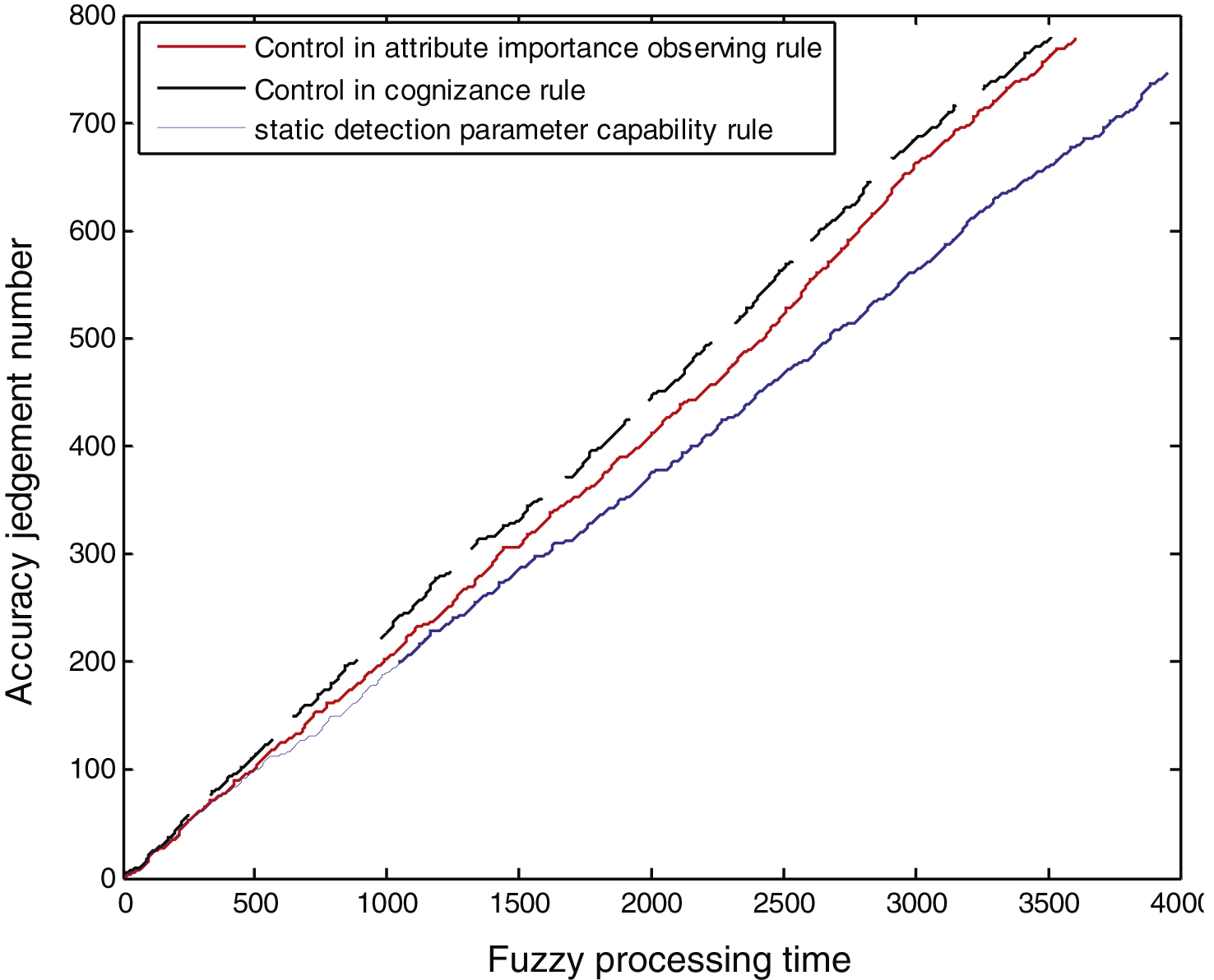
Fig.4
Discrimination accuracy result for 1,000 malfunction samples with [0.1, 0.2] system noise, averaging 300 Monte Carlo simulation.
![Discrimination accuracy result for 1,000 malfunction samples with [0.1, 0.2] system noise, averaging 300 Monte Carlo simulation.](https://content.iospress.com:443/media/ifs/2015/29-6/ifs-29-6-ifs1931/ifs-29-6-ifs1931-g004.jpg)
Fig.5
The discrimination efficiency result for 1000 malfunction sample on [0.1, 0.2] system noise averaging 300 Monte Carlo simulation.
![The discrimination efficiency result for 1000 malfunction sample on [0.1, 0.2] system noise averaging 300 Monte Carlo simulation.](https://content.iospress.com:443/media/ifs/2015/29-6/ifs-29-6-ifs1931/ifs-29-6-ifs1931-g005.jpg)
Table 1
Diesel engine malfunction judgment information table
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | |
| T1 | 0.9325 | 1.000 | 1.000 | –0.4526 | 0.3895 | 1.000 | 1.000 | 1.000 |
| T2 | –0.4571 | –0.2854 | –0.9024 | –0.9121 | –0.0841 | 1.000 | –0.2871 | 0.5647 |
| T3 | 0.5134 | 0.9413 | 0.9711 | –0.4187 | 0855 | 0.8546 | 0.9478 | 0.9512 |
| T4 | 0.1545 | 0.1564 | –0.500 | –0.6571 | –0.3333 | –0.6667 | –0.3333 | –0.500 |
| T5 | 0.1764 | 0.7648 | 0.4259 | –0.6472 | –0.0563 | 0.1726 | 0.5151 | 0.4212 |
| T6 | –0.6744 | –0.4541 | –0.8454 | 1.000 | –0.8614 | –0.6714 | –0.6279 | –0.6785 |
| T7 | 0.4647 | 0.5710 | 0.0712 | –0.7845 | –0.2871 | 0.8915 | 0.6553 | 0.6152 |
| T8 | 0.6818 | 1.000 | –0.625 | –0.8426 | –0.6215 | –0.1574 | 1.000 | 0.7782 |




