Mechanics of the red blood cell network
Abstract
Changes in the microstruture of blood caused by the red blood cell aggregation phenomenon affect the mechanical properties of the fluid. This fact has been extensively investigated in the past and it has been verified that the formation of rouleaux (the characteristic coin-pile like structures) and aggregates at low shear rates affect the flow and as a consequence the viscosity of the fluid is elevated. At physiological red blood cell concentrations and at low shear rates, however, in addition to rouleaux and aggregate formation an extended network is observed. The effects of network characteristics on the mechanical properties of blood have received relatively little attention in the literature and only a few studies provide quantitative data on this aspect of the blood flow. Quantitative data on network characteristics in view of the aggregation phenomenon illustrate that indeed different network configurations have different effects on the mechanical properties of the fluid. In this work, it is shown that changes in the viscosity of blood at specific flow conditions correlate with the changes in the mechanical characteristics of the red blood cell network.
1Introduction
The red blood cell aggregation phenomenon occurs when certain conditions are met; firstly, a suitable environment in terms of the proteins (mainly fibrinogen) and macromolecules is needed, secondly the cells should be subjected to flow conditions (normally below shear rates of approximately 50 s−1) where shear stresses are sufficiently low, and thirdly the intrinsic properties of the RBC should be appropriate, since they may influence aggregation independently of the suspension biochemistry [1, 2]. Intense aggregation is also observed at a number of pathological conditions [3]. Aggregated cells result in a cellular tube-like arrangement (rouleaux), which is very flexible due to the deformability of the cells. Combinations of rouleaux cause the formation of larger aggregates and at low shear rates the formation of a three dimensional cellular network [4]. In diabetic patients with elevated erythrocyte aggregation the flow of erythrocytes in capillaries is significantly decreased [5]. The aforementioned changes in the microstructure of the fluid affect its flow properties and consequently its apparent viscosity. Figure 1 shows the effect of aggregation to blood microstructure for RBCs suspended in a phosphate buffer saline (Fig. 1a) and for RBCs suspended in a Dextran 2000 solution (Fig. 1b).
The extent of RBC aggregation and other microstuctural characteristics at various RBC concentrations (hematocrit) and flow conditions have been explored and quantified by various techniques. Indirect techniques, such as erythrocyte sedimentation rate (ESR), light reflection/transmission, ultrasonic, or electrorheology techniques are popular due to their practicality and low cost. Unequivocal data may only be provided by optical microscopy techniques, in which digital image analysis may be employed for an efficient interpretation of the information appearing in the images. A summary of the indices proposed by researchers in the literature for the study of the microstructural characteristics of blood is provided in Table 1; a variety of indices have been utilized for the investigation of the aggregation effect, which provide information about the geometrical characteristics of aggregates (size and shape) and the extent of the aggregation phenomenon.
Main features of the microstructure analyzed in studies with physiological hematocrits include the area covered by the cells compared to the total image area [18], the size of the plasma gaps [16] and a network index, which was found to increase linearly with the aggregation extent [4].
The methods of assessment of the captured images have been evolved with the advance of the technology, with digital image analysis been mainly employed in the last three decades. The review presented in Table 1 shows also that the assessment of aggregation characteristics takes place at either static or steady flow conditions and that for steady flow studies the level of hematocrits was very low; this was necessary in order to improve quality of imaging and to avoid aggregate overlapping which occurs at relatively high concentrations of RBCs.
The main outcome of the studies presented in Table 1 in terms of the effect of aggregation in the mechanical properties of the fluid was that the increase of aggregate size and of the aggregation extent has as a result the elevation of the viscosity at low shear rates. In terms of clinical significance intense aggregation was found to be present in a variety of pathological conditions. However, studies in the literature indicate a counter-intuitive relationship between the increase of aggregation and viscosity [19, 20]. In addition, there is not sufficient information for samples with physiological hematocrits under flow and the effects of other microstructural characteristics, such as the network formation, are still not sufficiently understood [21].
The present paper reports on a development in the investigation of the effects of network characteristics of blood microstructure under specific dynamic flow conditions in order to enhance understanding of the effects of microstructure on the mechanical properties blood.
2Methodology
The optical shearing system used in the study has been described in [22] and [23]. In brief the system consists of a Linkam CSS-450 glass plate-plate arrangement, integrated to an Olympus BX51 microscope and a CCD camera (JVC TK-C1380). The analysis of the images was performed with specifically formulated algorithms (Matlab). The focus radius R, gap (30μm) and rotational speed determined the shear rate and the temperature for all measurements with both techniques was kept at 37°C. An aggregation index A α , similar to that used in [18], was defined according to the ratio of the RBC-free area (A RBC - Free ) observed in the image and the maximum expected RBC-free area according to hematocrit:
(1)
An aggregation integrity index, which would provide information about the strength of the developed network, was formulated based on the interaggregate branch characteristics and the size of the adjacent plasma gaps:
(2)
Samples were collected in EDTA (1.5% ) tubes from staff and students of the university (Ref. 04/05-15) and their hematocrit was adjusted to 45% by centrifugation unless otherwise stated. Shearing of the samples was performed in a range between 252 to 0.25 s−1, in this order, whereas the test duration was altered to produce five different flow conditions expressed by a flow number: C = 10 s/ Test duration. The 10 s was chosen as an aggregation relaxation time and the test durations were 10 and 20 seconds, where the shear rate was changed at an unsteady mode, and 70, 170 and 1140 seconds where shear rate was altered in a quasi-unsteady manner. The resulting five different C numbers were: 1, 0.5, 0.17, 0.06 and 0.01 respectively.
3Results
Figure 2 shows the increase of relative viscosity (η * = η/η p ) with the increase of the aggregation index A α for the different flow conditions (C numbers). The first observation is that the flow conditions affect the extent of the viscosity increase. Such a behavior is generally attributed to wall slip and sedimentation effects, however the data presented here were produced in rheometric tools with modified surfaces in order to minimize the slip effect [22]. In addition, the C flow number and total residual time in low shear rates imply that the sedimentation of the cells was also minimized. Based on the assumption of minimized slip and cell sedimentation the viscosity in Fig. 2 shows a counterintuitive behaviour as it decreases with the increase of aggregation; according to the current understanding the viscosity would be expected to rise with the increase of aggregation. The decline of the viscosity, as a result of the increase of aggregation, is revealed when the mean viscosity at specific aggregation states is considered; in Fig. 2 the heavier dashed line represents the mean value of viscosity from all viscosity values at a given A α .
For a better understanding of the behavior of viscosity is important to further analyze the effect of aggregation on blood microstructure and more specifically on the characteristics of the developed cell network. Indeed, it has been shown that the integrity of the microstructure is not a monotonically increasing function of aggregation [22]; the integrity index AI was found to decrease after a certain increase in the value of A α . The influence of both AI and A α on the measured viscosity is shown in Fig. 3, where the viscosity has been normalized by A α (panel (a)) and AI (panel (b)) and plotted against shear rate for three C numbers. The specific flow numbers and shear rates (below 10 s−1) where chosen as the conditions where slip and sedimentation are considered as negligible. As it can be observed, the difference in the viscosity behaviour is spread further for different C numbers when the aggregation index is related to viscosity (Fig. 3a). On the contrary, when the relative viscosity is normalized by the structural integrity index AI the viscosity curves collapse to a master curve (Fig. 3b). The same is observed for the two lower C flow numbers although not shown in the figure. This behaviour indicates that it is the structural integrity of the fluid that affects its viscosity behaviour, and more importantly that the changes in viscosity are directly proportional to the structural integrity for the particular flow cases.
In order to examine the effect of hematocrit on the behaviour of the structural integrity AI blood samples at three different hematocrits (25, 35 and 45% ) were subjected to different shear rates for a period of 30 seconds, after a period of 10 seconds at high shearing (100 s−1). The results (Fig. 4) showed that, although the coefficient of variation was relatively large, AI was affected by both the imposed flow and the hematocrit. In general, as the hematocrit decreases and the shear rate increases the changes in the integrity of the fluid are more pronounced; the hydrodynamic stresses acting on aggregates result at an increase of the size of the aggregates in the expense of the size of the interaggregate branches. As the shear rate increases further the aggregate size and integrity of network are reduced.
4Discussion and conclusions
The important information provided by the results presented in the previous section may be that the red blood network strength explains better the mechanical properties of blood in view of the aggregation phenomenon: a decrease of network integrity causes a decrease in the viscosity of blood. However, the data provided from optical microscopy techniques have been obtained in flow configurations with very small gaps (in the present case 30μm) which begs the question; do data provided by thin layers of blood reflect bulk fluid characteristics? To this extent the technique used for the development of the aggregation and integrity indices (equations 1 and 2) has been compared to other techniques and has been concluded that it can reveal features of blood microstructure identical to those obtained by other optical and electrorheology techniques [21, 23, 24]. In addition, direct comparison of data from optical shearing microscopy with results obtained from electrorheology techniques at identical flow conditions, but in different gaps (30 and 1000μm in optical microscopy and electrorheology respectively) have shown that there is an excellent agreement between the techniques for certain flow conditions, whereas discrepancies appear in the measurement with excessive aggregation [25].
Regarding the physiological relevance of the present work it may be useful to consider the behaviour of the mean viscosity shown in Fig. 2 (thick dashed line); the averaging of the viscosity from different shear rates at specific aggregation values may be compared to situations where viscosity is evaluated when the fluid is subjected to distribution of shearing forces. An example of such viscosity evaluation is the measurement of viscosity across a microchannel network, or in the in vivo conditions, across a whole organ [19]. Indeed, the mean viscosity shown in Fig. 2 behaves very similar to the vascular resistance measured across a whole organ as a function of aggregation [19]. The effects of the structural characteristics of blood on its viscosity have been illustrated also in a study where it was shown that the viscosity varies spatially because of the red blood cell network [26].
It may be concluded, therefore, that network characteristics play an important part in the mechanical properties of blood, behaving as a non-monotonic increasing function of aggregation, and that optical microscopy techniques may provide valid information, reflecting bulk fluid properties at certain flow conditions.
References
1 | Rampling M(1989) Red cell aggregation and yield stressClinical Blood Rheology1: 4563 |
2 | Rampling MW, Meiselman H, Neu B, Baskurt OK(2004) Influence of cell specific factors on red blood cell aggregationBiorheology41: 291112 |
3 | Gyawali P, Richards RS, Hughes DL, Tinley P(2014) Erythrocyte aggregation and metabolic syndromeClinical Hemorheology and Microcirculation57: 17383 |
4 | Picart C, Piau J-M, Galliard H, Carpentier P(1998) Blood low shear rate rheometry: Influence of fibrinogen level and hematocrit on slip and migrational effectsBiorheology35: 4-5335353 |
5 | Jung F, Mrowietz C, Hiebl B, Franke RP, Pindur G, Sternitzky R(2011) Influence of rheological parameters on the velocity of erythrocytes passing nailfold capillaries in humansClin Hemorheol Microcirc48: 1129139 |
6 | Engeset M, Stalker A, Matheson N(1966) Effects of dextran 40The Lancet7447: 11241127 |
7 | Chien S, Jan KM(1973) Ultrastructural basis ofn the mechanism of rouleaux formationMicrovascular Research5: 155166 |
8 | Schmid-Schoenbein H, Wells R, Schildkraut R(1969) Microscopy and viscometry of blood flowing under uniform shear rate (rheoscopy)Journal of Applied Physiology26: 5674678 |
9 | Schmid-Schoenbein H, Gaehtgens P, Hirsch H(1968) On the shear rate dependence of red cell aggregation in vitro Journal of Clinical Investigation47: 614471454 |
10 | Klose HJ, Volger E, Brechtelsbauer L, Schmid-Schoenbein H(1972) Microrheology and light transmission of blood. I. the photometric quantification of red cell aggregation and red cell orientationPflugers Archives - European Journal of Physiology333: 2126139 |
11 | Shiga T, Imaizumi K, Harada N, Misuzu S(1983) Kinetics of rouleaux formation using tv analyser. I. Human erythrocytesAmerican Journal of Physiology, Heart and Circulatory Physiology245: H252H258 |
12 | Mchedlishvili G, Beritashvili N, Lominandze D, Tsinamdzvrishvili B(1993) Technique for direct and quantitative evaluation of erythrocyte aggregability in blood samplesBiorheology30: 153161 |
13 | Chen S, Gavish B, Mahler Y, Yedgar S(1995) Monitoring of erythrocyte aggregate morphology under flow by computerised image analysisBiorheology32: 4487496 |
14 | Carpentier P, Imbert B, Picart C, Maltere C(2000) Morphometric analysis of erythrocyte aggregates in vitro: Pharmacological application with buflomedilJournal des Maladies Vasculaires25: 5356359 |
15 | Ben-Ami R, Barshtein G, Zeltser D, Goldberg Y, Shapira I, Roth A, Keren G, Miller H, Prochorov V, Eldor A, Berliner S, Yedgar S(2001) Parameters of red blood cell aggregation as correlates of the inflammatory stateAmerican Journal of Physiology - Heart280: 19821988 |
16 | Berliner S, Ben-Ami R, Samocha-Bonet D, Abu-Abeit S, Schechner V, Beigek Y, Shapira I, Yedgar S, Barshtein G(2004) The degree of red blood cell aggregation on peripheral blood glass slides corresponds to inter-erythrocyte cohesive forces in laminar flowThrombosis Research114: 3744 |
17 | Jayavanth S, Singh M(2004) Computerised analysis of erythrocyte aggregation from sequential video microscopic images under gravitational sedimentationInnovations and Technology in Biology and Medicine25: 6774 |
18 | Almog B, Gamzu R, Almog R, Lassing J, Shapira I, Berliner S, Pauzner D, Maslovitz I, Levin S(2005) Enhanced erythrocyte aggregation in clinically diagnosed pelvic inflammatory diseaseSexually Transmitted Diseases32: 8484486 |
19 | Baskurt OK(2008) In vivo correlates of altered blood rheologyBiorheology45: 6629638 |
20 | Shin S, Jang JH, Park MS, Ku YH, Suh JS(2006) Shear-dependent aggregation characteristics of red blood cells in a pressure driven microfluidic channelClinical Hemorheology and Microcirculation34: 353362 |
21 | Pribush A, Meyerstein D, Meyerstein N(2004) Conductometric study of shear-dependent processes in red cell suspensions. II. Transient cross-stream hematocrit distributionBiorheology41: 2943 |
22 | Kaliviotis E, Yianneskis M(2008a) On the effect of microstructural changes of blood on energy dissipation in Couette flowClinical Hemorheology and Microcirculation39: 1-4235242 |
23 | Kaliviotis E, Yianneskis M(2008) Fast response characteristics of red blood cell aggregationBiorheology b45: 6639649 |
24 | Snabre P, Bitbol M, Mills P(1987) Cell disaggregation behaviour in shear flowBiophysical Journal51: 795807 |
25 | Kaliviotis E, Ivanov I, Antonova N, Yianneskis M(2010) Erythrocyte aggregation at non-steady flow conditions: A comparison of characteristics measured with electrorheology and image analysisClinical Hemorheology and Microcirculation44: 4354 |
26 | Kaliviotis E, Dusting J, Balabani S(2011) Spatial variation of blood viscosity: Modelling using shear fields measured by a μPIV based techniqueMedical Engineering and Physics33: 824831 |
Figures and Tables
Fig.1
Non-aggregated RBCs, suspended in phosphate buffer saline, at a shear rate of 25 s−1 (a). Aggregated RBCs suspended in a Dextran 2000 solution, at 25 s−1 (b). The images have been converted to binary images (processed with the same parameters); the black structures are edges of cells and aggregates.

Fig.2
Relative viscosity η* = η/ηp against aggregation Aα plotted for all C numbers. The dashed lines are iso-shear rate lines presenting the values of viscosity at same shear rates. The heavier dashed line represents the mean value of viscosity from all viscosity values at a given Aα value (data adapted from [22]).
![Relative viscosity η* = η/ηp against aggregation Aα plotted for all C numbers. The dashed lines are iso-shear rate lines presenting the values of viscosity at same shear rates. The heavier dashed line represents the mean value of viscosity from all viscosity values at a given Aα value (data adapted from [22]).](https://content.iospress.com:443/media/jcb/2015/1-1/jcb-1-1-jcb15004/jcb-1-1-jcb15004-g002.jpg)
Fig.3
Relative viscosity normalized by Aα (panel a) and by AI (panel b) against shear rate for three flow conditions (data adapted from [22]).
![Relative viscosity normalized by Aα (panel a) and by AI (panel b) against shear rate for three flow conditions (data adapted from [22]).](https://content.iospress.com:443/media/jcb/2015/1-1/jcb-1-1-jcb15004/jcb-1-1-jcb15004-g003.jpg)
Fig.4
AI against time for three different hematocrits (25, 35 and 5% ) and different shear rates (0, 0.5, 1, 3, 6 and 10 s−1) after an initial period of high shearing at 100 s−1.
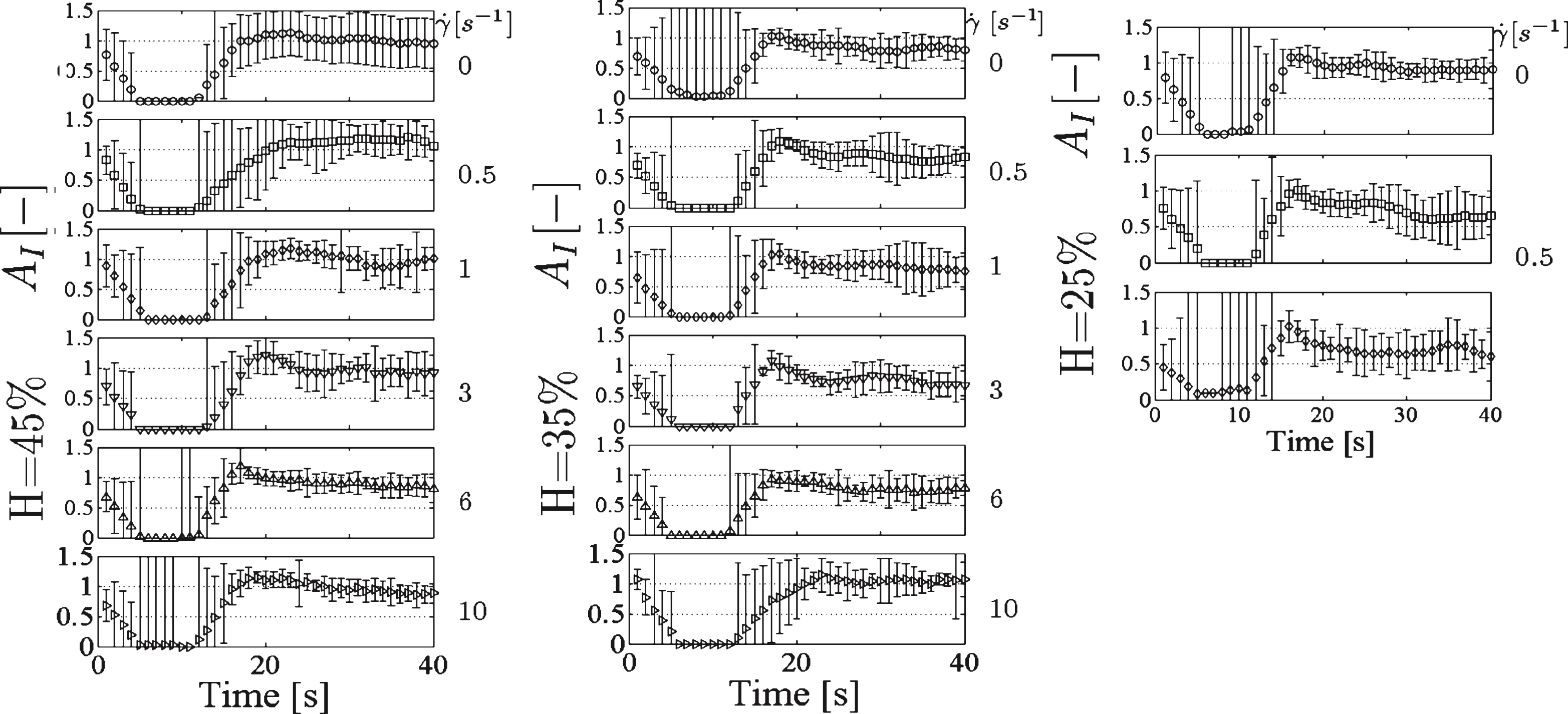
Table 1
A summary of the indices proposed in the literature for the study of blood microstructure. Bold italics indicate measurements taken at static conditions
| Direct Measurement | Digital image analysis | |
| Aggregate description and diameter, H = 45% [9, 10] | Vacuum radius (VR) - degree of aggregation, H = 35% [16]. | ≈1% |
| Length of rouleaux axes, and their ratio, H = 40% [14]. | ||
| Erythrocyte percent (EP), area covered by Erythrocytes, H = 35% [18]. | ||
| Network structure index as number of RBCs per aggregate, H = 44, 57% [4]. | ||
| Aggregate size, H = 7% [8] | Aggregate shape parameter = Aggregate projected area/Perimeter2, H = 1% [13]. | Hematocrit |
| Projected aggregate area (PPA), perimeter (PAP) and form factor (FF), H = 5% [17]. | ||
| MAI = Units in sample/Units in Ringer solution, H = 1% [7] | EAI = Total RBC-aggregate area/Area of aggregates, H = 0.5% [12]. | |
| Aggregate Count, Area and their ratio, H = 0.6% [11]. | ||
| Stalker method: grades from 1 to 4 [6] | Average (AAS), small, medium or large aggregate size (SAF, MAF and LAF), AUC area under the AAS/shear stress graph, H = 6% [15, 16]. | |
| 1960 | 1980 2000 | ≈45% |



