Fuzzy expert systems for prediction of ICU admission in patients with COVID-19
Abstract
The pandemic COVID-19 disease has had a dramatic impact on almost all countries around the world so that many hospitals have been overwhelmed with COVID-19 cases. As medical resources are limited, deciding on the proper allocation of these resources is a very crucial issue. Besides, uncertainty is a major factor that can affect decisions, especially in medical fields. To cope with these issues, we use fuzzy logic (FL) as one of the most suitable methods in modeling systems with high uncertainty and complexity. We intend to make use of the advantages of FL in decisions on cases that need to treat in ICU. In this study, an interval type-2 fuzzy expert system is proposed for the prediction of ICU admission in COVID-19 patients. For this prediction task, we also developed an adaptive neuro-fuzzy inference system (ANFIS). Finally, the results of these fuzzy systems are compared to some well-known classification methods such as Naive Bayes (NB), Case-Based Reasoning (CBR), Decision Tree (DT), and K Nearest Neighbor (KNN). The results show that the type-2 fuzzy expert system and ANFIS models perform competitively in terms of accuracy and F-measure compared to the other diagnosis systems.
1.Introduction
COVID-19 or Coronavirus has affected the public health and economics of many countries in the world due to its contagious nature and lack of effective medicine or vaccine [1]. It has spread to over 193 million people worldwide by the end of July 2021. According to medical reports, the mortality rate associated with this virus is low. However, the long duration of the disease and the disability of patients for a long time cause further spread of the disease and thus increase the mortality associated with this disease. It has killed over 4 million people by the end of July 2021 [2].
It is noteworthy that many COVID-19 patients will develop mild to moderate illness and recover without hospitalization. Fever, dry cough, and tiredness are the most common symptoms of COVID-19. These patients are advised to manage their symptoms at home. On the other hand, serious symptoms such as difficulty breathing and chest pain have appeared in some patients during the disease [3]. This condition can quickly get worse so that an emergency situation occurs. These critical situations can increase human decision-making errors leading to more financial and non-financial losses.
Besides, predicting the situation of patients is useful for hospitals and health centers due to the spread of this virus. It can help to design targeted tests of people, predict the number of required resources in hospitals and health centers, and inform medical plans for prioritizing the level of care, design-related policy about vaccination, and so on [4, 5]. In this way, health centers and hospitals can appropriately allocate their limited resources including treatment in intensive care units (ICUs), tests, and ventilators to the patients.
Therefore, to prevent human decision-making errors and to properly allocate the limited resources, it is a rational idea to design an expert system for the prediction of resource utilization in patients with COVID-19. In this study, the COVID-19 patient pre-condition dataset provided by the Mexican government is used [6]. To the best of our knowledge, there are a few expert systems for the prediction of a problem related to the COVID-19 patients. However, most of them use direct approach in which rules are extracted by an expert. In this paper, our expert system uses fuzzy modeling with an indirect approach, where the rules are extracted automatically by implementing a clustering approach. Furthermore, for the first time, an expert system is designed for the prediction of ICU admission in COVID-19 patients. In addition to developing a type-2 fuzzy expert system, an adaptive neuro-fuzzy inference system and some classification methods such as NB, CBR, DT, and KNN are implemented. Finally, we compare the results of these techniques in terms of accuracy and F-measure.
The structure of this paper is as follows: a literature review of different expert systems for medical diagnosis is presented in Section 2. The steps of designing the type-2 fuzzy expert system are presented in Section 3. In Section 4, the interval type-2 fuzzy expert system for ICU admission is presented. Classification methods and the developed fuzzy expert systems are evaluated in Section 5. Finally, conclusions and some directions for future studies are considered in Section 6.
2.Literature review
In this section, published research of Web of Science between the years 1980 and 2022 about the “COVID-19” or “Coronavirus” and “fuzzy expert systems” are analyzed using VOSviewer 1.6.10 software, and the corresponding results are presented in Fig. 1. Different circles show a different number of articles and the larger circles are associated with more articles. The lines between circles show the relationships among their articles in terms of their references. Besides, VOSviewer 1.6.10 software clusters different circles into four colored clusters according to their relationships. Figure 2 shows the results according to the year of the published articles.
Figure 1.
Different applications of COVID-19 and expert systems.
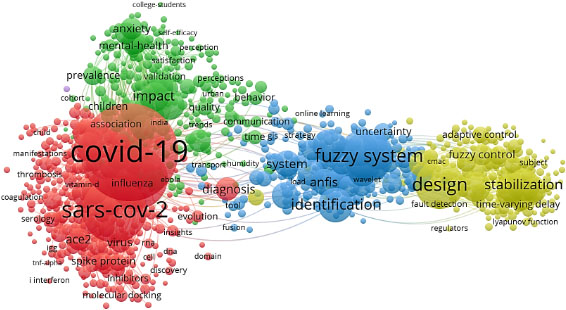
Figure 2.
The year of published articles about COVID-19 and expert systems.
Table 1
A review on the application of fuzzy expert systems in medical fields
| Author (year) | Disease | Technique |
|---|---|---|
| Sotudian et al. (2016) [7] | Hepatitis | Indirect approach for fuzzy system modeling |
| Guzmán et al. (2017) [8] | Blood pressure | Neuro-fuzzy hybrid model |
| Meza-Palacios et al. (2017) [9] | Type-2 diabetes mellitus | Fuzzy expert system based on experts’ guidelines |
| Sadat Asl and Zarandi (2017) [10] | Leukemia | Mamdani-style Type-2 fuzzy expert system |
| Zarandi et al. (2017) [11] | Heart disease | Expert system based on fuzzy bayesian network |
| Motlagh et al. (2018) [12] | Depressive disorder | Web-based fuzzy expert system |
| Caliwag et al. (2018) [13] | Venereal diseases | Mobile expert system based on fuzzy logic |
| Muhammad et al. (2018) [14] | Coronary artery disease | Expert system with developed knowledge acquisition |
| Nazari et al. (2018) [15] | Heart diseases | Fuzzy inference-fuzzy analytic hierarchy process-based |
| Soltani et al. (2018) [16] | Glaucoma | Expert fuzzy logic & image processing methods |
| Tuan et al. (2018) [17] | Dental disorders | Fuzzy computing & image processing methods |
| Terrada et al. (2018) [18] | Cardiovascular diseases | Fuzzy medical system using risk factors based on data |
| Ahmad et al. (2019) [19] | Hepatitis B | Multilayer Mamdani fuzzy inference system |
| Raza et al. (2019) [20] | Erythemato squamous | Expert system based on fuzzy rules |
| Arji et al. (2019) [21] | Infectious disease | Fuzzy inference & rule-based fuzzy logic, ANFIS |
| Kaur and Kakkar (2019) [22] | Neurodevelopmental disorders | Fuzzy based-systems based on co-morbid factors |
| Sadat Asl (2019) [23] | Leukemia | Two-stage expert system based on type-2 fuzzy logic |
| Mirmozaffari (2019) [24] | Liver diseases | Expert system based on the VP-Expert shell |
| Mujawar and Jadhav (2019) [25] | Diabetes | Web-based fuzzy expert system |
| Mutawa and Alzuwawi (2019) [26] | Uveitis | Multilayered rule-based expert system |
| Sajadi et al. (2019) [27] | Hypothyroidism | Fuzzy rule-based expert system |
| Ershadi et al. (2020) [28] | Different diseases and cancers | Multi-classifier based on fuzzy expert system |
| Hamedan et al. (2020) [29] | Chronic kidney disease | Fuzzy expert system with Mamdani inference system |
| Hussain et al. (2020) [30] | Thyroid disease | Multi-layered fuzzy Mamdani inference system |
| Khalil et al. (2020) [31] | Lung cancer | Fuzzy soft expert system |
| Mahanta and Panda (2020) [32] | Prostate cancer | Fuzzy expert system with Mamdani inference system |
| Mirmozaffari (2020) [33] | Gastrointestinal diseases | Fuzzy expert system based on VP-Expert shell |
| Mojrian et al. (2020) [34] | Breast cancer | Multilayer fuzzy expert system based on RBF |
| Naseer et al. (2020) [35] | Heart disease | Mamdani fuzzy inference expert system |
| Siddiqui et al. (2020) [36] | Arthritis | Adaptive hierarchical Mamdani fuzzy expert system |
According to the published research of Web of Science, a search with “COVID-19” or “Coronavirus” or other equivalent terms found more than 3,685,600 results. Besides, “expert systems” is appeared in more than 2,485,000 papers. However, less than 100 paper present a fuzzy expert system for COVID-19 or Coronavirus diagnosis and no paper considers ICU admission in patients with COVID-19 using a fuzzy expert system. These results demonstrate a serious gap due to the importance of the COVID-19 epidemic and the application of expert systems for medical decision support systems. Therefore, in this paper, we are going to fill this gap by designing fuzzy expert systems for the prediction of ICU admission in COVID-19 patients.
Thanks to the importance of expert systems, many researchers have used them in medical fields for the diagnosis of various diseases. For example, Hamedan et al. proposed a fuzzy expert system to predict chronic kidney disease. In their work, first, they identified the diagnostic parameters and risk factors through a literature review and a survey of some nephrologists, then a set of fuzzy rules for the prediction of chronic kidney disease was determined [29]. In another study, Hussain et al. presented a multi-layered fuzzy Mamdani inference system to analyze the prevailing thyroid disease. In their study, the proposed expert system is based on two layers. In layer 1, the presence or absence of thyroid disease is diagnosed. If layer 1 indicates the presence of thyroid disease, then layer 2 is activated by which the type of thyroid disease is determined [30].
Khalil et al. developed a new fuzzy soft expert system to predict lung cancer disease by using weight loss, shortness of breath, chest pain, persistent cough, blood in sputum, and age of patients. In their work, a prediction of the fuzzy soft expert system is composed of four main steps: 1) Transforming real-valued inputs into fuzzy numbers. 2) Converting fuzzy numbers into fuzzy soft sets. 3) Reducing the family of fuzzy soft sets obtained to a new family of fuzzy soft sets. 4) Using the proposed method to get the output data [31]. Mahanta and Panda developed a fuzzy expert system for the prediction of prostate cancer. In their study, age, prostate-specific antigen (PSA), prostate volume (PV), and Free PSA (FPSA) are fed as inputs into the system, and prostate cancer risk (PCR) is obtained as the output [32].
Mirmozaffari et al. presented an expert system for diagnosing the type of gastrointestinal disease and determining the type of tests needed to diagnose the disease [33]. Mojrian et al. presented a method based on a multilayer fuzzy expert system for the detection of breast cancer using an extreme learning machine (ELM) classification model integrated with radial basis function (RBF) kernel called ELM-RBF. In this study, they showed that their proposed method outperforms the linear-SVM model [34].
In another study, Naseer et al. proposed a fuzzy expert system for the diagnosis of heart disease. In their proposed system, the input variables comprised of age, chest pain, electrocardiography, blood pressure systolic, diabetes, and cholesterol are transmitted with the help of fuzzy rules which are framed in the light of low, normal, high, and very high intensity and the output is obtained using the Mamdani Inference method diagnosing the heart disease [35]. Siddiqui et al. developed an adaptive hierarchical Mamdani fuzzy expert system for the detection of arthritis. In their research, the expert system is comprised of two layers. In the first layer, the input variables are rest pain, morning stiffness, body pain, joint infection, swelling, redness, past injury and age that detects output condition of arthritis to be normal, infection and/or other problem, and in the second layer, the type of arthritis is diagnosed [36]. In the above studies, the authors designed various fuzzy expert systems in different medical fields.
However, there are a few studies on coronavirus-related issues, most of which are based on a direct approach where the rules are obtained by experts. Our expert system in this research employs fuzzy modeling using an indirect method, in which the rules are extracted automatically using a clustering approach. We develop an expert system designed specifically for the prediction of ICU admission in COVID-19 patients. Table 1 summarizes the fuzzy expert systems proposed for the diagnosis of various types of diseases.
3.Designing the type-2 fuzzy expert system
Artificial intelligence (AI) has been extensively applied in various fields of science, such as engineering and medical sciences [37, 38, 39, 40]. Expert systems are one of the most commercially successful branches of AI. They are programs with a broad base of knowledge emulating expert problem-solving skills in a certain domain [41]. Besides, fuzzy logic is a suitable modeling method for systems with high uncertainty and complexity by which a framework can be provided for reasoning, inference, control, and decision making [42]. Due to common features and others that complement each other, fuzzy logic and expert system technologies can easily be integrated. Both techniques are well-suited to deal with decision-making and other knowledge-oriented problems. Systems with these techniques have enhanced efficiency, system quality, and speed of execution [43].
As mentioned earlier, the main objective of this paper is to design an expert system to predict ICU needs for COVID-19 patients based on type-2 FL. To this end, there are two common approaches for the selection of the parameters of a type-2 FL system. The first one is the partially dependent approach. In this approach, first, the best possible type-1 FL system is designed. Then, it is used to initialize the parameters of a type-2 FL system. The second one is the totally independent approach where all of the parameters of the type-2 FL system are tuned without using an existing type-1 design [44]. In this paper, we use the partially dependent approach because of its advantages compared with the totally dependent approach. After designing a type 1 fuzzy system, a type-2 rule-based fuzzy system with uncertain standard deviation and interval-valued membership function is implemented. The same rules of the type-1 fuzzy system are used by this system and the only difference is that if-part and then-part are type-2. The designed system is comprised of the following steps:
• Data preprocessing and determining the inputs and output of the system;
• Clustering the output space and determination of the number of rules;
• Projection of membership functions of the output onto the inputs to obtain the membership values of the inputs;
• Tuning the parameters of type-1 membership functions of inputs and output variables;
• Transforming type-1 to interval type-2 membership functions;
• Tuning the parameters of type-2 membership functions.
3.1Data preprocessing
We use a publicly available dataset, containing information of about 566602 patients. The data contains some information about pregnancy, diabetes, chronic obstructive pulmonary disease (COPD), asthma, cardiovascular, obesity, tobacco, etc., and determines whether a patient needs an ICU or not [6]. In this dataset, there are 444814 missing data for ICU. Therefore, the final number of patients used in fuzzy expert systems and other classification techniques is 121788. Besides, a few outliers (e.g., male patient’s pregnancy) were detected and removed from the dataset.
Most precondition features of this dataset are categorical, each of which takes the value yes, no, and unspecified. These categorical features were converted to numerical by ‘one-hot’ encoding. By creating auxiliary variables that help differentiate between various categories of a feature, one-hot encoding transforms the categorical feature into multiple binary variables. Finally, highly correlated variables were eliminated as they provide similar information. Specifically, we calculated pairwise correlations among the variables, and one among any two highly correlated variables with an absolute correlation coefficient higher than 0.85 was removed. After the preparation of the dataset, we reached 27 features and one output determines whether a patient needs to the ICU or not.
3.2Clustering the output space and determination of the number of rules
To determine the number of rules, we use Fukuyama cluster validity index which can be defined as follows [45]:
(1)
where
3.3Projection of membership functions of the output onto the inputs
For the input variables, the appropriate membership grades should be calculated after clustering the output space. One way is to set each input’s membership grade equal to its corresponding output membership grade obtained by the procedure of output data clustering. In this way, for each output data, all the related input variables would then have a similar membership grade. The issue with this approach is that the membership functions are not convex and a further approximation is required to form the convex membership functions. Furthermore, the output membership grade is not always the same as the input membership grades at each sample point [47]. For these reasons, in this paper, Zarandi’s approach is used. According to this approach, first, the ranges in which the membership functions of the input variable adopt value 1 are determined. The data points are then classified using the GK method, by given
3.4Tuning the parameters of type-1 membership functions
There are several parameters in type-1 FL systems that can either be pre-specified or can be tuned during a training phase. An impeccable FL system should have
(2)
3.5Transforming type-1 to interval type-2 membership functions
To transform type-1 to an interval type-2 fuzzy set with uncertain standard deviation, the case of a Gaussian primary membership function with a fixed mean
(3)
where
3.6Tuning the parameters of type-2 membership functions
For tuning the parameters of the interval type-2 FL system, we use the proposed tuning algorithm by Liang and Mendel. In interval type-2 system,
Table 2
The antecedent and consequent parameters of the system
| Parameters | Rule 1 | Rule 2 | Rule 3 | Rule 4 | Rule 5 | |
|---|---|---|---|---|---|---|
| Antecedent-Var 1 |
| 32.562 | 79.019 | 63.131 | 49.029 | 4.849 |
|
| 9.501 | 10.240 | 7.552 | 7.319 | 15.489 | |
|
| 5.700 | 6.144 | 4.531 | 4.391 | 9.294 | |
| Antecedent-Var 2 |
| 1.578 | 1.575 | 1.608 | 1.632 | 1.562 |
|
| 0.362 | 0.357 | 0.444 | 0.440 | 0.253 | |
|
| 0.254 | 0.250 | 0.311 | 0.308 | 0.177 | |
| Antecedent-Var 3 |
| 1.509 | 1.650 | 1.656 | 1.626 | 1.408 |
|
| 0.372 | 0.337 | 0.425 | 0.442 | 0.260 | |
|
| 0.186 | 0.169 | 0.212 | 0.221 | 0.130 | |
| Antecedent-Var 4 |
| 1.004 | 1.005 | 1.005 | 1.006 | 1.002 |
|
| 0.046 | 0.053 | 0.058 | 0.076 | 0.023 | |
|
| 0.041 | 0.047 | 0.052 | 0.068 | 0.021 | |
| Antecedent-Var 5 |
| 1.102 | 1.376 | 1.406 | 1.284 | 1.014 |
|
| 0.186 | 0.337 | 0.44 | 1 0.381 | 0.095 | |
|
| 0.130 | 0.236 | 0.308 | 0.267 | 0.066 | |
| Antecedent-Var 6 |
| 1.004 | 1.005 | 1.004 | 1.005 | 1.002 |
|
| 0.042 | 0.050 | 0.050 | 0.060 | 0.019 | |
|
| 0.034 | 0.040 | 0.040 | 0.048 | 0.015 | |
| Antecedent-Var 7 |
| 1.007 | 1.127 | 1.053 | 1.020 | 1.002 |
|
| 0.023 | 0.139 | 0.089 | 0.045 | 0.015 | |
|
| 0.014 | 0.083 | 0.053 | 0.027 | 0.009 | |
| Antecedent-Var 8 |
| 1.033 | 1.021 | 1.022 | 1.025 | 1.032 |
|
| 0.044 | 0.031 | 0.040 | 0.045 | 0.030 | |
|
| 0.030 | 0.022 | 0.028 | 0.032 | 0.021 | |
| Antecedent-Var 9 |
| 1.005 | 1.006 | 1.005 | 1.006 | 1.004 |
|
| 0.048 | 0.058 | 0.061 | 0.071 | 0.030 | |
|
| 0.038 | 0.046 | 0.049 | 0.057 | 0.024 | |
| Antecedent-Var 10 |
| 1.040 | 1.034 | 1.034 | 1.030 | 1.109 |
|
| 0.056 | 0.049 | 0.062 | 0.057 | 0.083 | |
|
| 0.033 | 0.029 | 0.037 | 0.034 | 0.050 | |
| Antecedent-Var 11 |
| 1.004 | 1.005 | 1.004 | 1.006 | 1.002 |
|
| 0.044 | 0.049 | 0.052 | 0.069 | 0.019 | |
|
| 0.026 | 0.030 | 0.031 | 0.041 | 0.012 | |
| Antecedent-Var 12 |
| 1.111 | 1.552 | 1.443 | 1.277 | 1.014 |
|
| 0.202 | 0.370 | 0.454 | 0.382 | 0.107 | |
|
| 0.141 | 0.259 | 0.318 | 0.267 | 0.075 | |
| Antecedent-Var 13 |
| 1.007 | 1.009 | 1.007 | 1.008 | 1.013 |
|
| 0.076 | 0.085 | 0.094 | 0.104 | 0.083 | |
|
| 0.061 | 0.068 | 0.075 | 0.083 | 0.066 | |
| Antecedent-Var 14 |
| 1.050 | 1.072 | 1.054 | 1.044 | 1.151 |
|
| 0.072 | 0.093 | 0.095 | 0.083 | 0.111 | |
|
| 0.043 | 0.056 | 0.057 | 0.050 | 0.067 | |
| Antecedent-Var 15 |
| 1.016 | 1.116 | 1.058 | 1.028 | 1.046 |
|
| 0.035 | 0.132 | 0.098 | 0.058 | 0.046 | |
|
| 0.024 | 0.092 | 0.068 | 0.041 | 0.032 | |
| Antecedent-Var 16 |
| 1.005 | 1.005 | 1.004 | 1.006 | 1.002 |
|
| 0.048 | 0.049 | 0.058 | 0.074 | 0.019 | |
|
| 0.038 | 0.039 | 0.046 | 0.059 | 0.015 | |
| Antecedent-Var 17 |
| 1.199 | 1.153 | 1.218 | 1.255 | 1.026 |
|
| 0.237 | 0.201 | 0.312 | 0.346 | 0.078 | |
|
| 0.166 | 0.141 | 0.218 | 0.242 | 0.055 | |
| Antecedent-Var 18 |
| 1.004 | 1.005 | 1.004 | 1.005 | 1.002 |
|
| 0.044 | 0.051 | 0.051 | 0.065 | 0.021 | |
|
| 0.026 | 0.030 | 0.030 | 0.039 | 0.012 | |
| Antecedent-Var 19 |
| 1.049 | 1.070 | 1.074 | 1.048 | 1.017 |
|
| 0.071 | 0.091 | 0.121 | 0.088 | 0.029 | |
|
| 0.042 | 0.055 | 0.072 | 0.053 | 0.017 | |
| Antecedent-Var 20 |
| 1.005 | 1.005 | 1.004 | 1.006 | 1.002 |
|
| 0.046 | 0.050 | 0.056 | 0.070 | 0.020 | |
|
| 0.028 | 0.030 | 0.034 | 0.042 | 0.012 |
|
Table 2, continued | ||||||
|---|---|---|---|---|---|---|
| Parameters | Rule 1 | Rule 2 | Rule 3 | Rule 4 | Rule 5 | |
| Antecedent-Var 21 |
| 1.089 | 1.109 | 1.092 | 1.083 | 1.008 |
|
| 0.119 | 0.134 | 0.151 | 0.142 | 0.032 | |
|
| 0.083 | 0.094 | 0.106 | 0.100 | 0.023 | |
| Antecedent-Var 22 |
| 1.456 | 1.572 | 1.545 | 1.497 | 1.404 |
|
| 0.372 | 0.362 | 0.463 | 0.470 | 0.255 | |
|
| 0.297 | 0.289 | 0.370 | 0.376 | 0.204 | |
| Antecedent-Var 23 |
| 1.202 | 1.093 | 1.117 | 1.152 | 1.153 |
|
| 0.228 | 0.135 | 0.196 | 0.237 | 0.129 | |
|
| 0.137 | 0.081 | 0.118 | 0.142 | 0.077 | |
| Antecedent-Var 24 |
| 1.384 | 1.335 | 1.258 | 1.258 | 1.746 |
|
| 0.347 | 0.323 | 0.363 | 0.368 | 0.257 | |
|
| 0.243 | 0.226 | 0.254 | 0.258 | 0.180 | |
| Antecedent-Var 25 |
| 1.504 | 1.539 | 1.619 | 1.627 | 1.152 |
|
| 0.373 | 0.363 | 0.442 | 0.445 | 0.218 | |
|
| 0.335 | 0.327 | 0.398 | 0.400 | 0.196 | |
| Antecedent-Var 26 |
| 1.002 | 1.001 | 1.001 | 1.001 | 1.003 |
|
| 0.021 | 0.013 | 0.012 | 0.019 | 0.019 | |
|
| 0.017 | 0.010 | 0.010 | 0.015 | 0.015 | |
| Antecedent-Var 27 |
| 1.041 | 1.000 | 1.000 | 1.001 | 1.008 |
|
| 0.326 | 0.021 | 0.023 | 0.034 | 0.057 | |
|
| 0.228 | 0.015 | 0.016 | 0.024 | 0.040 | |
| Consequent |
| 1.066 | 1.075 | 1.082 | 1.080 | 1.164 |
|
| 0.095 | 0.102 | 0.138 | 0.136 | 0.121 | |
|
| 0.057 | 0.061 | 0.083 | 0.082 | 0.072 | |
4.Proposed interval type-2 fuzzy expert system
In this paper, we use Mamdani inference system in which the antecedents and consequent are type-2 fuzzy sets that have a fixed mean and an uncertain standard deviation that takes values in an interval. The interval type-2 FL system is created from the type-1 FL system. The proposed system uses singleton fuzzification, product t-norm, product inference, and center-of-sets type-reduction, with the same number of fuzzy sets and rules as the type-1 FL system. Several defuzzification methods have been used, such as centroid, bisector, and Yager. The best results of this system are obtained by Yager defuzzification method. Table 2 shows both consequent and antecedent parameters of the expert system. In this table,
5.Performance evaluation and analysis
In this paper, in addition to developing a type-2 fuzzy expert system for the prediction of ICU admission, we develop the ANFIS model for this prediction task using MATLAB toolbox. Then, we compare the performance of the developed fuzzy expert systems to several well-known classification methods such as NB, CBR, DT, and KNN in terms of accuracy and F-measure. To evaluate the performance of each system, the dataset is divided into training and test sets. In this way, for each system modeling technique, 70% of the dataset has been used for training. Table 3 shows the accuracy and F-measure of different system modeling techniques implemented in this study.
Classification accuracy is the total number of accurate predictions divided by the total number of predictions made for a dataset. As a performance measure, accuracy is not sufficient for imbalanced classification problems. The key explanation is that the vast number of examples from the dominant class or classes would overwhelm the number of minority class examples. Using precision and recall metrics is an alternative to using classification accuracy. F-Measure integrates both precision and recall into a single measure and captures both properties [50]. As can be seen in Table 3, the developed fuzzy expert systems could achieve an accuracy of 91.6% and an F-measure of 95.6%. Comparing to the CBR and KNN methods, the fuzzy expert systems can improve the accuracy and F-measure by about 1.5% to 5% and 1% to 3%, respectively. Furthermore, the developed fuzzy models performed competitively compared to the other classification methods. Overall, the results show that both type-2 fuzzy system and ANFIS model could outperform the well-known classification methods.
Table 3
Accuracy and F-measure of different system modeling techniques
| Methods | Accuracy % | F-measure % |
|---|---|---|
| Type-2 fuzzy system | 91.64 | 95.64 |
| ANFIS | 91.66 | 95.66 |
| NB | 90.79 | 95.15 |
| CBR | 86.26 | 92.54 |
| DT | 90.63 | 95.06 |
| KNN | 90.04 | 94.73 |
Type-2 FL systems usually give better results than their type-1 counterparts as the type-2 fuzzy sets and systems generalize type-1 fuzzy sets and systems so that more uncertainty can be handled. However, in our case, as can be seen, the results of the type-2 fuzzy expert system are very close to the ANFIS model. In the dataset, as most input variables are categorical, the type-2 fuzzy set lost its efficiency. Therefore, in this specific problem, type-2 FL has lost its superiority over the developed ANFIS model.
6.Conclusion
In this study, a type-2 fuzzy expert system and an adaptive neuro-fuzzy inference system are developed for the prediction of ICU admission. Furthermore, to evaluate the performance of these fuzzy systems, several classification methods such as NB, CBR, DT, and KNN are also implemented. All these methods are tested on a publicly available dataset. The results demonstrate the efficacy of the proposed fuzzy expert systems, with an accuracy of 91.6% and an F-measure of 95.6%, which outperform the other conventional classification techniques. When comparing the two developed fuzzy expert systems, we can notice that the results of the type-2 fuzzy expert system are very close to the ANFIS model since, in our problem, most input variables are categorical.
One of the limitations of the present study is a lack of publicly available COVID-19 datasets with detailed symptoms. Most features of the dataset used in this study are categorical which may affect the general superiority of type-2 expert system over the developed ANFIS model. Over time, more COVID-19 datasets will be published because more and more experiments are performed every day for this disease around the world. If the number of continuous input variables in new datasets is higher, the type-2 fuzzy expert system may provide better results due to its higher generalizability. Therefore, for future studies, the proposed fuzzy expert systems can be designed using some other datasets. A prominent feature of type-2 fuzzy logic is its resilience to noise compared to type-1 fuzzy logic. This resilience can be improved by introducing general type-2 fuzzy logic. Thus, an interesting future direction is to extend the proposed model to a general type-2 fuzzy expert system. Finally, we can extend the proposed model to deal with more complex data such as data with missing entries.
Table 4
Summary points:
| What is known? | What this adds? |
|---|---|
| Hospitals have many problems with COVID-19 cases due to limited available medical resources. | Proposed classifiers are designed in this paper to predict ICU admission in COVID-19 patients. |
| There are high uncertainty and complexity to find the proper level of COVID-19 patients. | Fuzzy logic methods are considered in this paper to model related uncertainty and complexity. |
| The number of available data has significant effects on the learning phase of most classifiers. | Different clinical features of 566602 COVID-19 patients are utilized in the learning phase of classifiers. |
| There are different classifiers with special advantages and disadvantages. | We compare the accuracies and F-measures of Naive Bayes (NB), Case-Based Reasoning (CBR), Decision Tree (DT), and K Nearest Neighbor (KNN) to the proposed type-2 fuzzy expert system and ANFIS model. |
References
[1] | Silva PC, Batista PV, Lima HS, Alves MA, Guimarães FG, Silva RC. COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos, Solitons & Fractals. (2020) Oct 1; 139: : 110088. |
[2] | World Health Organization. Coronavirus disease 2019 (COVID-19): situation report, 72. |
[3] | Menni C, Valdes AM, Freidin MB, Sudre CH, Nguyen LH, Drew DA, Ganesh S, Varsavsky T, Cardoso MJ, Moustafa JS, Visconti A. Real-time tracking of self-reported symptoms to predict potential COVID-19. Nature medicine. (2020) May 11; 1–4. |
[4] | Fischer GS, da Rosa Righi R, de Oliveira Ramos G, da Costa CA, Rodrigues JJ. ElHealth: Using Internet of Things and data prediction for elastic management of human resources in smart hospitals. Engineering Applications of Artificial Intelligence. (2020) Jan 1; 87: : 103285. |
[5] | Horvitz E. From data to predictions and decisions: Enabling evidence-based healthcare. Computing Community Consortium. (2010) Sep 18; 6. |
[6] | https://www.kaggle.com/tanmoyx/covid19-patient-precondition-dataset?select=covid.csv. |
[7] | Sotudian S, Fazel Zarandi MH, Turksen IB. From Type-I to Type-II fuzzy system modeling for diagnosis of hepatitis. International Journal of Computer and Information Engineering. (2016) ; 10: (7): 1280–1288. |
[8] | Guzmán JC, Melin P, Prado-Arechiga G. Neuro-fuzzy hybrid model for the diagnosis of blood pressure. In Nature-Inspired Design of Hybrid Intelligent Systems. Springer, Cham. (2017) . pp. 573–582. |
[9] | Meza-Palacios R, Aguilar-Lasserre AA, Ureña-Bogarín EL, Vázquez-Rodríguez CF, Posada-Gómez R, Trujillo-Mata A. Development of a fuzzy expert system for the nephropathy control assessment in patients with type 2 diabetes mellitus. Expert Systems with Applications. (2017) Apr 15; 72: : 335–43. |
[10] | Asl AAS, Mohammad Hossein Fazel Zarandi. A type-2 fuzzy expert system for diagnosis of leukemia. North American Fuzzy Information Processing Society Annual Conference. Springer, Cham, (2017) . |
[11] | Zarandi MH, et al. An expert system based on fuzzy bayesian network for heart disease diagnosis. North American Fuzzy Information Processing Society Annual Conference. Springer, Cham, (2017) . |
[12] | Motlagh HA, Bidgoli BM, Fard AA. Design and implementation of a web-based fuzzy expert system for diagnosing depressive disorder. Applied Intelligence. (2018) May 1; 48: (5): 1302–13. |
[13] | Caliwag JA, Reyes FC, Castro PJ, Castillo RE. A mobile expert system utilizing fuzzy logic for venereal and sexually transmitted diseases. Journal of Advances in Information Technology. (2018) Aug; 9: (3). |
[14] | Muhammad LJ, Garba EJ, Oye ND, Wajiga GM. On the Problems of Knowledge Acquisition and Representation of Expert System for Diagnosis of Coronary Artery Disease (CAD). International Journal of u-and e-Service, Science and Technology. (2018) ; 11: (30): 49–58. |
[15] | Nazari S, Fallah M, Kazemipoor H, Salehipour A. A fuzzy inference-fuzzy analytic hierarchy process-based clinical decision support system for diagnosis of heart diseases. Expert Systems with Applications. (2018) Apr 1; 95: : 261–71. |
[16] | Soltani A, Battikh T, Jabri I, Lakhoua N. A new expert system based on fuzzy logic and image processing algorithms for early glaucoma diagnosis. Biomedical Signal Processing and Control. (2018) Feb 1; 40: : 366–77. |
[17] | Tuan TM, Fujita H, Dey N, Ashour AS, Ngoc VT, Chu DT. Dental diagnosis from X-ray images: An expert system based on fuzzy computing. Biomedical Signal Processing and Control. (2018) Jan 1; 39: : 64–73. |
[18] | Terrada O, Cherradi B, Raihani A, Bouattane O. A fuzzy medical diagnostic support system for cardiovascular diseases diagnosis using risk factors. In 2018 International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS). IEEE. (2018) Dec 5. pp. 1–6. |
[19] | Ahmad G, Khan MA, Abbas S, Athar A, Khan BS, Aslam MS. Automated diagnosis of hepatitis b using multilayer mamdani fuzzy inference system. Journal of healthcare engineering. 2019 Jan 1; 2019. |
[20] | Raza MA, Liaqat MS, Shoaib M. A Fuzzy Expert System Design for Diagnosis of Skin Diseases. In 2019 2nd International Conference on Advancements in Computational Sciences (ICACS). IEEE. (2019) Feb 18. pp. 1–7. |
[21] | Arji G, Ahmadi H, Nilashi M, Rashid TA, Ahmed OH, Aljojo N, Zainol A. Fuzzy logic approach for infectious disease diagnosis: A methodical evaluation, literature and classification. Biocybernetics and Biomedical Engineering. (2019) Oct 1; 39: (4): 937–55. |
[22] | Kaur G, Kakkar D. Fuzzy Based Integrated Diagnostic System for Neurodevelopmental Disorders. In 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN). IEEE. (2019) Mar 7. pp. 132–136. |
[23] | Asl AAS. A Two-Stage Expert System for Diagnosis of Leukemia Based on Type-2 Fuzzy Logic. International Journal of Computer and Information Engineering. (2019) ; 13: (2): 34–41. |
[24] | Mirmozaffari M. Developing an expert system for diagnosing liver diseases. European Journal of Engineering Research and Science. (2019) Mar 2; 4: (3): 1–5. |
[25] | Mujawar IK, Jadhav BT. Web-based Fuzzy Expert System for Diabetes Diagnosis. International Journal of Computer Sciences and Engineering. (2019) ; 7. |
[26] | Mutawa AM, Alzuwawi MA. Multilayered rule-based expert system for diagnosing uveitis. Artificial Intelligence in Medicine. (2019) Aug 1; 99: : 101691. |
[27] | Sajadi NA, Borzouei S, Mahjub H, Farhadian M. Diagnosis of hypothyroidism using a fuzzy rule-based expert system. Clinical Epidemiology and Global Health. (2019) Dec 1; 7: (4): 519–24. |
[28] | Ershadi MM, Seifi A. An efficient multi-classifier method for differential diagnosis. Intelligent Decision Technologies. Intelligent Decision Technologies. (2020) ; 14: (3): 337–347. |
[29] | Hamedan F, Orooji A, Sanadgol H, Sheikhtaheri A. Clinical decision support system to predict chronic kidney disease: A fuzzy expert system approach. International Journal of Medical Informatics. (2020) Mar 30; 104134. |
[30] | Hussain A, Hussnain SA, Fatima A, Siddiqui SY, Saeed A, af Saeed Y, Ahmed A, Khan MA. A Novel Approach for Thyroid Disease Identification Empowered with Fuzzy Logic. IJCSNS. (2020) Jan; 20: (1): 173. |
[31] | Khalil AM, Li SG, Lin Y, Li HX, Ma SG. A new expert system in prediction of lung cancer disease based on fuzzy soft sets. Soft Computing. (2020) Mar 2; 1–29. |
[32] | Mahanta J, Panda S. Fuzzy expert system for prediction of prostate cancer. New Mathematics and Natural Computation. (2020) Mar; 16: (01): 163–76. |
[33] | Mirmozaffari M. Presenting an expert system for early diagnosis of gastrointestinal diseases. International Journal of Gastroenterology Sciences. (2020) ; 1: (1): 21–7. |
[34] | Mojrian S, Pinter G, Joloudari JH, Felde I, Szabo-Gali A, Nadai L, Mosavi A. Hybrid Machine Learning Model of Extreme Learning Machine Radial basis function for Breast Cancer Detection and Diagnosis; a Multilayer Fuzzy Expert System. In 2020 RIVF International Conference on Computing and Communication Technologies (RIVF). IEEE. (2020) Oct 14. pp. 1–7. |
[35] | Naseer I, Khan BS, Saqib S, Tahir SN, Tariq S, Akhter MS. Diagnosis heart disease using mamdani fuzzy inference expert system. EAI Endorsed Transactions on Scalable Information Systems. (2020) ; 7: (26). |
[36] | Siddiqui SY, Hussnain SA, Siddiqui AH, Ghufran R, Khan MS, Irshad MS, Khan AH. Diagnosis of arthritis using adaptive hierarchical Mamdani fuzzy type-1 expert system. EAI Endorsed Transactions on Scalable Information Systems. (2020) ; 7: (26). |
[37] | Sadat Asl AA, et al. A fuzzy capacitated facility location-network design model: A hybrid firefly and invasive weed optimization (FIWO) solution. Iranian Journal of Fuzzy Systems. (2020) ; 17: (2): 79–95. |
[38] | Sotudian S, Mohammad Hossein Fazel Zarandi. Interval Type-2 Enhanced Possibilistic Fuzzy C-Means Clustering for Gene Expression Data Analysis. arXiv preprint arXiv:2101.00304. (2021) . |
[39] | Sadatasl AA, Mohammad Hossein Fazel Zarandi, Abolfazl Sadeghi. A combined facility location and network design model with multi-type of capacitated links and backup facility and non-deterministic demand by fuzzy logic. 2016 Annual Conference of the North American Fuzzy Information Processing Society (NAFIPS). IEEE. (2016) . |
[40] | Zandigohar M, et al. Multimodal Fusion of EMG and Vision for Human Grasp Intent Inference in Prosthetic Hand Control. arXiv preprint arXiv:2104.03893. (2021) . |
[41] | Zarandi MHF, Asl AAS, Sotudian S, Castillo O. A state of the art review of intelligent scheduling. Artificial Intelligence Review. (2020) ; 53: (1): 501–593. |
[42] | Sotudian S, Asl AAS, Zarandi MHF. Fuzzy Gilmore and Gomory algorithm: Application in robotic flow shops with the effects of job-dependent transportation and set-ups. RAIRO-Operations Research. (2021) ; 55: : S1515–S1528. |
[43] | Medsker LR. Fuzzy Logic and Expert Systems. In: Hybrid Intelligent Systems. Springer, Boston, MA. (1995) . doi: 10.1007/978-1-4615-2353-6_6. |
[44] | Wu D, Woei Wan Tan. A type-2 fuzzy logic controller for the liquid-level process. 2004 IEEE International Conference on Fuzzy Systems (IEEE Cat. No. 04CH37542). IEEE. Vol. 2, (2004) . |
[45] | Zarandi MHF, Shahabeddin Sotudian, Oscar Castillo. A New Validity Index for Fuzzy-Possibilistic C-Means Clustering. arXiv preprint arXiv:2005.09162. (2020) . |
[46] | Sugeno M, Yasukawa T. A fuzzy logic based approach to qualitative modeling. IEEE Transactions on Fuzzy Systems. (1993) ; 1: : 7–31. |
[47] | Zarandi MHF, et al. A type-2 fuzzy hybrid expert system for commercial burglary. North American Fuzzy Information Processing Society Annual Conference. Springer, Cham. (2017) . |
[48] | Mendel JM. Uncertainty, fuzzy logic, and signal processing. Signal Processing. (2000) ; 80: (6): 913–933. |
[49] | Liang Q, Mendel JM. Interval type-2 fuzzy logic systems: Theory and design. IEEE Transactions on Fuzzy Systems. (2000) ; 8: (5): 535–550. |
[50] | Brownlee J. How to Calculate Precision, Recall, and F-Measure for Imbalanced Classification. URL: https://machinelearningmastery.com/precisionrecall-and-f-measure-for-imbalanced-classification. (2020) . |



