Enhanced memetic search for reducing energy consumption in fuzzy flexible job shops
Abstract
The flexible job shop is a well-known scheduling problem that has historically attracted much research attention both because of its computational complexity and its importance in manufacturing and engineering processes. Here we consider a variant of the problem where uncertainty in operation processing times is modeled using triangular fuzzy numbers. Our objective is to minimize the total energy consumption, which combines the energy required by resources when they are actively processing an operation and the energy consumed by these resources simply for being switched on. To solve this NP-Hard problem, we propose a memetic algorithm, a hybrid metaheuristic method that combines global search with local search. Our focus has been on obtaining an efficient method, capable of obtaining similar solutions quality-wise to the state of the art using a reduced amount of time. To assess the performance of our algorithm, we present an extensive experimental analysis that compares it with previous proposals and evaluates the effect on the search of its different components.
1.Introduction
Scheduling [1, 2] is a classical manufacturing problem that consists in organizing the execution of a set of tasks or operations to make the best use of the available resources under some constraints in order to fulfill some objectives. Solving scheduling problems is essential not only in industrial applications [3, 4], in particular in Industry 4.0 and 5.0 [5], but also in healthcare [6, 7], computing infrastructures [8] or education [9]. Besides its undeniable applicability, scheduling also poses a computational challenge, since many of its problems are NP-Hard [10].
Due to their complexity, most of these problems are intractable, so exact algorithms cannot be applied except for the smallest instances. In consequence, researchers have been developing approximate search strategies that no longer guarantee optimality but provide instead good enough solutions within a reasonable amount of time [11, 12, 13].
A main source of inspiration for developing new approximate optimization algorithms have been natural phenomena [14, 15, 16, 17, 18, 19, 20, 21, 22, 23]. These methods imitate nature to explore the search space in smart ways that reduce their computational cost and have proved successful in several real-world applications [24, 25, 26, 27]. More recently, the design of solving methods for hard optimization problems has advanced considerably with the development of hyper-heuristics, search or learning methods that either select or generate heuristics [28, 29], and with the growth of hybrid metaheuristics that combine several search strategies to take advantage of their strengths while at the same time reducing their shortcomings [30]. In particular, memetic algorithms are a type of hybrid algorithms which combine population-based algorithms with trajectory-based search methods or other specialized search procedures [31, 32, 33]. They have become popular methods to solve hard combinatorial problems because they provide a very good balance between exploration of the search space and exploitation of the most promising areas [34].
A source of hard optimization problems in the field of scheduling which have been successfully tackled with approximate search algorithms is the family of job shop scheduling problems [35]. The job shop constitutes a thriving area of research, with many of its variants modelling practical engineering and social applications [36]. In particular, the flexible job shop problem has become a popular research topic because it corresponds to many situations arising in industries such as automobile assembly, textile manufacturing, chemical processing or semiconductor manufacturing [37]. This variant of the job shop not only deals with an operation-sequencing problem, but it also incorporates a machine-assignment subproblem. Due to its increased complexity, most of the proposed solving methods fall within the category of metaheuristics [38, 39, 37, 40, 41].
The objective of scheduling problems has continuously evolved since the earliest days of industrialization. Historically, the most common objective was minimizing the time span between the start and the end of the project, known as makespan. While still a relevant objective, it has increasingly been replaced by or combined with other production-related measures such as minimizing tardiness, motivated by inventory management considerations and the growing complexity of supply-chain systems. More recently, energy efficiency and other green objectives have been incorporated, driven by the need to comply with new laws and regulations in industry that seek a reduction in environmental footprint as well as by the surge in energy costs caused not only by these regulations, but also by highly-tensed geopolitical relations. As a result, there has been a steady increase in research devoted to energy efficiency and sustainability within the field of scheduling [42, 43, 44, 45, 46, 47, 33, 3, 8].
Despite being a relatively new topic, it is possible to find in the literature several contributions concerned with reducing energy consumption in job shop scheduling problems [48]. They can be organized into three different non-exclusive high-level approaches.
The first one consists in scheduling operations in such a way that the energy consumed when resources are actively processing operations and when they are kept idle is as low as possible. Following this approach, a multiobjective genetic algorithm based on NSGA-II is proposed in [49] to solve the job shop minimizing the total energy consumption and total weighted tardiness. This work is improved in [50] introducing additional components to help the search. In [47] the model is further extended with the addition of crane transportation between machines.
The second approach consists in allowing to turn on and off the resources during project execution. Thus, if a resource is going to be idle for a long time it can be turned off and the extra energy used in the starting-up process may be compensated with the savings during the off period. This approach is taken in [46], where the model and method from [49] are extended to allow for switching on and off the resources. This is also the energy model in [51], where new job arrivals are considered and a backtracking search algorithm is proposed.
The third approach consists in slowing down resources so that they consume less energy at the cost of taking longer to process the operations. Within this framework, a multi-objective genetic algorithm incorporated with two problem-specific local improvement strategies is used in [52] to reduce total weighted tardiness together with energy consumption in a job shop problem. In [53] the authors consider a job shop with flexibility and they use a shuffled frog-leaping algorithm to reduce total energy consumption and workload.
The choice of one framework over the others depends on the problem under consideration. In [54] all of them are combined in a flexible job shop and a non-dominated sorted genetic algorithm is used to optimize the makespan, the energy consumption and the number of times resources are turned on/off simultaneously.
The majority of research devoted to scheduling in general, and to energy-efficient scheduling in particular, assumes a deterministic setting. However, uncertainty pervades real-life problems and its management poses a challenge in industry 5.0 [5]. Hence the relevance of the subfield of fuzzy shop scheduling [55, 56], where uncertainty is handled using fuzzy numbers. This approach considers a whole range of possible durations during the solving process and thus yields more robust solutions [57]. Triangular fuzzy numbers are probably the most extended model for uncertain durations in scheduling problems (see [55, 58] and references therein). As pointed out in [59], they provide a good balance between expressiveness, computing cost and ease of understanding. Indeed, in most cases there is not enough available knowledge to model uncertain processing times by a probability distribution, but it may be possible to provide an interval that is supposed to contain the eventually observed value of a processing time. Simple intervals have a limited expressive power: if they are too wide, they are not informative enough to be of any use and, if they are too narrow, they may not contain the whole range of possible values for a processing time. An intermediate model is the triangular fuzzy number, which provides an estimate of the processing time using an interval of possible values and the most likely value in it [60].
In the literature, it is possible to find different metaheuristic proposals to optimize production-related objectives in a fuzzy setting [55, 12] and, in particular, in the fuzzy flexible job shop (see [61, 62] for recent and thorough literature reviews). Research in solving problems that combine uncertainty and energy consumption is still incipient, with the proposed solving methods always in the category of metaheuristics and with a majority of memetic algorithms. In [63] the authors propose an evolutionary algorithm to reduce the non-processing energy and the total weighted tardiness in a fuzzy job shop, while two memetic algorithms are proposed in [64] and [41], the former to minimize the non-processing energy and the makespan in a fuzzy job shop and the latter to minimize total energy consumption in a flexible job shop. A multiobjective fuzzy flexible job shop problem is tackled in [65], with the goal of minimising the fuzzy makespan together with the fuzzy total energy consumption as well as maximising flexible due-date satisfaction. The proposed solving method is a bi-population evolutionary algorithm with a feedback mechanism and enhanced local search, thus falling in the category of memetic algorithms. Finally, in a slightly different uncertainty framework, a learning-based memetic algorithm is proposed in [66] to minimize makespan and energy consumption in a bi-objective flexible job shop with type-two fuzzy processing times.
In this work we will tackle a fuzzy flexible job shop problem with the goal of minimizing energy consumption. Specifically, we will consider uncertainty in the processing time of operations modelled as triangular fuzzy numbers and the objective will be to minimize the total energy consumption, a fuzzy quantity defined as the sum of the passive energy, consumed by resources as soon as they are on, whether idle or working, and the active energy, consumed by resources on top of the passive energy when they are processing operations. As solving method, we propose an enhanced memetic algorithm, called ema. Our proposal builds on the simple memetic algorithm (sma) proposed in [41] as a first approach to solving the problem at hand. To improve the performance of sma we will introduce several new components that enhance the method’s search ability. These components pursue a better integration of the exploration provided by the evolutionary component and the exploitation provided by the local search. We claim that by altering the balance along the search between these opposite behaviors the search can be more effective. These new components not only make a difference with the work in [41] but also are novel with respect to those used in other similar methods of the scheduling literature as [38].
The contribution of this work is twofold. On the one hand, we propose an enhanced memetic algorithm ema which improves the state of the art by incorporating new strategies that considerably reduce the computational cost of the search without deteriorating the quality of the obtained solutions. In particular, we propose:
• a new methodology for evolving the population with increased diversity along the search;
• a heuristic seeding mechanism that inserts some expected good traits in the initial population to help in the early stages of the search;
• a new adaptive strategy to control the local search component which translates into an incremental tabu search that strengthens intensification when the search stagnates.
On the other hand, we provide an extensive and thorough computational study to evaluate the proposed method. The experimental results will allow for the following:
• an analysis of the search results in relation to the different features characterizing problem instances;
• a study of the synergies between the two main components of the memetic algorithm: the evolutionary module and the tabu search;
• an analysis of the effects of a filtering mechanism in the local search that discards uninteresting solutions without completely evaluating them to gain efficiency;
• an evaluation of the contribution of the different neighborhood structures used in the local search.
The rest of the paper is organized as follows: Section 2 formally defines the problem, Section 3 describes the proposed algorithm and Section 4 reports and analyzes the experimental results to evaluate the potential of our proposal. Finally, Section 5 presents some conclusions.
2.Problem formulation
The job shop scheduling problem consists in scheduling a set
2.1Fuzzy processing times
We model processing times as triangular fuzzy numbers (TFNs), a particular type of fuzzy numbers [67], with an interval
(1)
For our problem, we need two arithmetic operations between TFNs, the sum and the maximum, as well as the scalar multiplication with a real number
(2)
the scalar multiplication is given by:
(3)
and the maximum is approximated using interpolation on its three defining points as:
(4)
When the result of the actual maximum operation is a TFN, then it coincides with the approximated value from Eq. (4). When this is not the case, the approximation maintains the support and modal value of the non-approximated maximum. Maintaining the support is in fact a very important property in scheduling since a good model of uncertainty should contemplate all possible scenarios. If the support were not maintained under the maximum, the resulting fuzzy schedule might not cover starting or completion times for operations which are actually attainable in a real scenario, resulting in poor and incomplete solutions. The interested reader is referred to [57] and references therein for further arguments supporting the use of this approximation, widely used in fuzzy scheduling.
Another important characteristic to be taken into account when working with TFNs (or fuzzy numbers in general) is that the subtraction is not the inverse of the addition. Indeed, following the Extension Principle, the subtraction of two TFNs
(5)
Clearly
In scheduling, it may be the case that we have two TFNs
(6)
so
Finally, since there exists no natural relation of total order for TFNs, we need to resort to some ranking method. Here, we will use a ranking based on the expected value of TFNs, so
(7)
where
2.2Fuzzy schedules
A schedule is a solution to the problem, a pair
Notice that the starting time assignment
For a given a feasible solution
(8)
where
2.3Total energy objective function
In the fuzzy flexible job shop problem we consider two types of energy: active energy and passive energy. Passive energy
(9)
Active energy consumption
(10)
We adopt an additive model so the total energy consumption
(11)
Given these definitions, the total energy consumption is obtained as the sum of the total energy consumption of each resource:
(12)
This energy model corresponds to the first high-level approach to energy consumption as explained in Section 1. However, it is formulated in a somewhat different way to how it is done in the deterministic setting. In deterministic scheduling, the possible states of the resources are usually disjoint, so they can contribute to either the processing energy cost (the energy consumed when they are executing) or the non-processing energy cost (the energy consumed when they are idle). To compute the latter, it is necessary to calculate the idle time periods for each resource, i.e., the time span between the end of an operation and the start of the following one in the same resource. When durations are real numbers, this is easily done by subtracting the completion time of the first operation from the starting time of the second. However, a direct translation of this approach to the fuzzy job shop means subtracting non-interactive quantities, thus introducing some undesired and artificial uncertainty, as explained above in Section 2.1. For this reason, inspired by energy models used to reduce energy consumption in data centers, we propose instead to make use of overlapping states, resulting in an additive model where the two involved energies are aggregated. Notice that in the deterministic case both approaches, the standard one using disjoint states and the one adopted here using overlapping states are in fact equivalent. In the fuzzy setting, this alternative model has the advantage of avoiding added artificial uncertainty. This is so because it decomposes the total energy calculation in a way that does not imply subtracting interactive fuzzy numbers. The use of overlapping resource states with the goal of avoiding computing the length of idle periods under uncertainty is also underlying the definition of fuzzy total energy proposed in [65], although here the authors assume that resources are turned off individually.
2.4MILP model
In this section we present a MILP model based on [70]. As mentioned in Section 2.2, a solution to the problem is given by a pair
(13)
and for every pair of operations
(14)
It is trivial that the variables
(15)
subject to
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)
Equation (16) ensures that operations are assigned to exactly one resource and Eq. (17) ensures that operations have at most one immediate predecessor in the resource. These two equations conform the two basic constraints of the problem. In order to define the starting time of operations, Eq. (18) ensures that the starting time of an operation is greater or equal than the addition of the starting and processing times of its predecessor in the job, so precedence constraints within jobs hold. Analogously, Eqs (19) and (20) prevents overlapping of operations in the same resource. Finally, Eqs (22)–(26) model the objective function, that is, the total energy consumption.
3.An enhanced memetic algorithm
As solving method we propose a memetic algorithm (see Fig. 1), a hybrid metaheuristic combining an evolutionary algorithm with local search, taking advantage of the synergies between both methods.
Figure 1.
Pseudocode of the memetic algorithm.

3.1Evolutionary algorithm
The evolutionary algorithm maintains a population of solutions so, at each generation, the individuals in the population are combined to obtain a new population that will replace the old one. A solution
3.1.1Heuristic seeding
The first novel component of the memetic algorithm is a heuristic seeding mechanism that inserts some expected good traits in the initial population to help in the early stages of the search. The underlying idea is to add some knowledge about the problem to otherwise random solutions so they can be easily improved without great diversity loss. Here we propose two complementary strategies that either focus on reducing operation processing time or active energy.
The first heuristic strategy consists in generating
(27)
then, the order
The second heuristic strategy consists in assigning an operation
(28)
Then, as in the first heuristic, the order
In general, heuristic rules are designed to generate solutions with interesting or promising features, but there is no guarantee that these features are indeed shared by optimal solutions. Therefore, generating the whole initial population using the proposed heuristic rules may have the undesired effect of leading the evolutionary algorithm away from good areas of the search space. For this reason, we propose to generate 25% of the population using Eq. (27), other 25% of the population using Eq. (28) and the remaining 50% of the population completely at random. This way, although we are slightly reducing diversity with respect to having a fully random initial population, the obtained population is still quite heterogeneous. At the same time, thanks to the heuristic seeding the algorithm is focusing from the start on certain areas of the search space which are expected to contain interesting solutions and which may be left unexplored should we consider only random initial solutions.
3.1.2Immigration Operator
We also propose a new methodology for evolving the population with increased diversity along the search. Diversity is usually achieved by means of a mutation operator, however, in our case, having an intensification operator based on local search causes subtle mutations to have little or no effect. At the same time, stronger mutations seem undesirable, since they annul the crossover operator by removing from the individual promising traits inherited from its parents. For this reason, we use a new immigration operator to introduce diversity.
Immigration operators [72] might be thought of as a means of continually ensuring high diversity in the population by somehow introducing completely new individuals (the “immigrants” bringing progress to the population). Immigration operators usually involve a strategy to remove some individuals from the population to make room for the new ones [73, 74], in order to keep a constant population size. We have opted instead to keep all the existing individuals and allow the population size to grow along the search with the new immigrants. The goal is to keep all the acquired knowledge, without losing any interesting traits. This should increase the diversity in the population and the area of the search space it covers, although it also incurs in a higher computational cost for the search. Therefore, we introduce new individuals only when the search seems to be stagnating and new features might be needed to explore new areas of the search space, which is when ev_im_it generations have passed without improvement. When this happens, ev_im_ind immigrants are generated using the same procedure employed to generate the heuristic initial population (Section 3.1.1) and are added to the existing population. The rationale behind this operator is that, while the population is evolving at a good rate, it should not be disrupted, but when it is starting to stagnate it should be reactivated introducing new individuals with probably new traits.
The two new modifications could be seen as contradictory, since the heuristic seeding reduces diversity in the population while the immigration operator tries to increase it. However, what we are really doing is shifting the stress on diversity to later stages of the search. Without the immigration operator diversity would be only introduced at the start of the search, which does not give the chance to find new interesting traits later.
3.2Tabu search algorithm
Tabu search is a local search algorithm that keeps a memory structure, called tabu list, where it stores a trace of the recently visited search space. In particular, to avoid undoing recently made moves, we store in the tabu list the inverse of the moves performed to obtain the neighbors. Our tabu list has a dynamic size, similar to the one introduced in [75], so the size of the list can vary between a lower bound tb_lst_ubr and an upper bound tb_lst_lbr. When the selected neighbor is worse (resp. better) than the current solution and the upper (resp. lower) bound has not been reached, the list’s size increases (resp. decreases) in one unit. If the selected neighbor is the best solution found so far, the list is cleared; this is similar to restarting the search from this solution. We also incorporate an aspiration criterion, so a tabu move can be executed if it improves the best solution found up to this moment. In the rare situation that all neighbors are tabu, we choose the best one, clear the tabu list and slightly change its bounds by picking a random number within a given range.
3.2.1Neighborhood function
The neighborhood function lies at the core of any local search. To define the function used in this work, we start by introducing some preliminary notation.
Given a solution
(29)
and its tail
(30)
An operation
Since our energy function in Eq. (12) is obtained by adding the passive and the active energy of each resource, we distinguish two types of neighbors.
First, to reduce the passive energy consumption we have to reduce the time the resources are active and this can only happen if we reduce the makespan. Clearly, a neighbor can only improve in terms of makespan (and hence, in passive energy consumption) if there is some change in makespan-critical operations. Also, if a neighbor is obtained by exchanging the position of two consecutive operations, it can be proved that it can only improve in terms of makespan if the operations lie at the extreme of a makespan-critical block. This motivates the definition of a neighborhood function for passive energy that is the union of two smaller ones, one that acts on the resource assignment (
Neighbors in
Definition 1. Makespan-critical operation resource reassignment neighborhood (
(31)
Neighbors in
Definition 2. Makespan-critical end transpose neighborhood (
(32)
Second, active energy consumption can only be reduced by moving operations to a more efficient resource. This motivates the definition of neighborhood
Definition 3. Operation power-efficient resource reassignment neighborhood (
(33)
The complete neighborhood is obtained as the union of the two neighborhoods aiming at reducing passive energy and the neighborhood aimed at reducing active energy:
(34)
It is worth mentioning that, although we have designed
3.2.2Neighbor filtering mechanism
As neighbor evaluation is the most time-consuming part of the local search, we make use of a filtering mechanism to discard uninteresting solutions and make this process faster. This mechanism assumes that for a neighbor it is possible to compute a lower bound of the objective function value. Then, the filtering consists in evaluating the neighbors following the order defined by the lower bound, stopping as soon as the lower bound of a neighbor is greater than the exact value of any of the already evaluated solutions.
In the case of active energy, the new exact value of a neighbor can be easily calculated as follows. For the active energy to change, the neighbor must have been obtained by moving an operation from one resource to another. Then, we only need to remove the operation’s energy consumption in the old resource from the current active energy value and then add the operation’s energy consumption in the new resource. Notice that here we are making use of the inverse of the sum
This mechanism allows to discard many non-improving neighbors without getting to evaluate them while keeping the same neighbor selection that we would obtain using the expensive exact value calculation for all neighbors. This is because a neighbor is discarded only if its real energy value is worse than that of the selected individual, since the energy’s lower bound is also worse. Notice that, since the neighbor selection is the same as using the exact evaluation, the results of every run of the tabu search will be the same as using the exact evaluation, so the filtering mechanism does not alter in any way the course of the algorithm even if it substantially reduces its execution time.
3.2.3Adaptive stopping criterion
The intensification phase is by far the most computationally demanding one in the hybrid method. For this reason, we propose to introduce a new mechanism to make a better use of the running time given to the tabu search. We propose a new adaptive strategy to control the number of iterations and, in consequence, the running time used by the local search component which translates into an incremental tabu search that strengthens intensification when the search stagnates. The point here is that tabu search in the job shop problem is quite dependent on the starting point, as we shall see in Section 4. For this reason, it seems reasonable not to spend too long on local search in the earlier iterations of the memetic algorithm, when the quality of individuals in the population, that is, the starting points of the tabu search, is not that high. In the earlier stages of the evolution, short runs of the local search will produce considerable improvements. But as the search progresses and our population improves, we will increase the depth of the intensification. We do this by allowing the tabu search to run for more iterations. Specifically, the tabu search will have a dynamic stopping criterion, so it stops after a given number of iterations without improving. When the search starts, this maximum number of iterations will take a value ls_st_it, but after ls_st_incr_it non-improving generations of the memetic algorithm, this value will be incremented in ls_st_incr units. In this way, the intensification power slowly increases.
4.Experimental results
The purpose of this experimental study is twofold. On the one hand, we intend to assess the performance of our proposal. Therefore, in the first set of experiments we shall evaluate if the algorithm described in Section 3.1, referred to as ema hereafter, is comparable to the state of the art in terms of solution quality while significantly reducing its runtime. Also, we analyze the results in relation to the different features characterizing problem instances. On the other hand, we want to assess the inner workings of the algorithm. With this objective, we present a second set of experiments to study the synergies between the two search paradigms (evolutionary and local search) hybridized in ema, analyze the effect of the filtering mechanism that discards uninteresting solutions in the local search and evaluate the contribution of the different neighborhoods to the search.
Table 1
Instance parameters
| Instance |
|
|
|
|
| RP |
|---|---|---|---|---|---|---|
| 07a | 15 | 8 | [15,25] | [10,100] | 0 | 0.1 |
| 08a | 15 | 8 | [15,25] | [10,100] | 0 | 0.3 |
| 09a | 15 | 8 | [15,25] | [10,100] | 0 | 0.5 |
| 10a | 15 | 8 | [15,25] | [10,100] | 5 | 0.1 |
| 11a | 15 | 8 | [15,25] | [10,100] | 5 | 0.3 |
| 12a | 15 | 8 | [15,25] | [10,100] | 5 | 0.5 |
| 13a | 20 | 10 | [20,25] | [10,100] | 0 | 0.1 |
| 14a | 20 | 10 | [20,25] | [10,100] | 0 | 0.3 |
| 15a | 20 | 10 | [20,25] | [10,100] | 0 | 0.5 |
| 16a | 20 | 10 | [20,25] | [10,100] | 5 | 0.1 |
| 17a | 20 | 10 | [20,25] | [10,100] | 5 | 0.3 |
| 18a | 20 | 10 | [20,25] | [10,100] | 5 | 0.5 |
Throughout these experiments we will use the 12 instances from [41]. These instances are based on the ones introduced in [38] for a fuzzy flexible job shop, which in turn are fuzzyfied versions of the ones in [78]. In order to understand how the algorithm performs on these instances, we will concisely explain how they have been generated. The parameters for instance generation are shown in Table 1; when an interval is given, this means that the actual values were randomly generated using a uniform distribution. The first three columns correspond to the name of the instance, the number of jobs
The values of these parameters allow us to organize instances in different groups, as depicted in Fig. 2. Depending on their size, we have a group of instances with 15 jobs and 8 resources:
and a group of instances with 20 jobs and 15 resources:
There is another difference between those instances and it is the ratio
Also, we have instances where the processing time of an operation is the same across resources:
and instances where it is resource-dependent:
The
Table 2
Parameters of the memetic algorithm
| ev_pop_sz | ev_st_it | ev_im_ind | ev_im_it | tb_lst_ubr | tb_lst_lbr | ls_st_it | ls_st_incr | ls_st_incr_it |
|---|---|---|---|---|---|---|---|---|
| 48 | 20 | 4 | 5 | [20,30] | [50,60] | 50 | 1 | 1 |
Table 3
Comparison with state of the art (SMA [41])
| Mean(E) | Best(E) | CPU time(s) | |||||
|---|---|---|---|---|---|---|---|
| Instance | Value | RE(%) | Value | RE(%) | Value | RE(%) | Real time (s) |
| 07a | 5370576.83 | 5320420.50 | -0.71 | 691.84 | 14.79 | 42.26 | |
| 08a | 4443247.07 | 0.09 | 4407688.00 | 0.33 | 584.21 | 51.06 | 37.24 |
| 09a | 4716263.95 | 0.87 | 4677323.50 | 0.83 | 1451.29 | 46.03 | 83.43 |
| 10a | 5169338.85 | 5101404.25 | 746.35 | 44.50 | |||
| 11a | 4804433.73 | 0.20 | 4754363.75 | 0.55 | 783.77 | 36.14 | 47.49 |
| 12a | 4357380.39 | 0.87 | 4329576.25 | 0.69 | 968.65 | 56.17 | 57.96 |
| 13a | 7015100.06 | 6966566.75 | 1759.01 | 268.55 | |||
| 14a | 6668717.56 | 0.71 | 6612014.75 | 0.87 | 2117.42 | 19.81 | 279.26 |
| 15a | 5933030.70 | 1.67 | 5887458.75 | 1.53 | 3387.64 | 36.71 | 338.82 |
| 16a | 6603274.18 | 6561246.25 | 2017.21 | 302.09 | |||
| 17a | 5971996.66 | 0.55 | 5911686.50 | 0.89 | 2160.72 | 12.70 | 284.75 |
| 18a | 5967547.58 | 1.65 | 5924213.75 | 1.48 | 3096.41 | 33.04 | 325.58 |
| Mean | 0.29 | 0.48 | 17.87 | ||||
Instances can be further classified depending on their flexibility into three groups:
To represent this third dimension in Fig. 2, instance names are included in circles with a radius proportional to their flexibility.
This instance taxonomy is important because, as we shall see in the following, we can appreciate certain patterns in the results depending on these features.
Figure 2.
Results and instance parameters.

The parameters used for ema in this experimental study can be seen in Table 2. It includes the population size (ev_pop_sz); the number of generations without improvement used for the evolutionary algorithm stopping criterion (ev_st_it); the immigration operator rate, that is, the number of individuals inserted (ev_im_ind) after a number of iterations without improving (ev_im_it); the tabu list size lower and upper bound ranges (tb_lst_ubr and tb_lst_lbr) and the parameters for the adaptive stopping criterion, i.e., the initial value for the number of iterations without improvement (ls_st_it) and the number of iterations to be added when updating this value (ls_st_incr) after a number of iterations without improvement (ls_st_incr_it).
All results have been obtained in a Linux machine with two Intel Xeon Gold 6132 processors without Hyper-Threading (14 cores/14 threads) and 128GB RAM using a parallelized implementation of the algorithm in Rust. The source code together with detailed results and benchmark instances can be found at https://pablogarciagomez.com/research.
4.1Comparison with state of the art
In Table 3 we can see the results obtained with 30 runs of our metaheuristic ema including a comparison with the state-of-the-art method which, to the best of our knowledge, is sma. Each row except the last one corresponds to an instance. The instance name constitutes the first column. The next columns report for each instance the best and mean expected value of the total energy consumption together with the average runtime obtained with ema. Next to each energy and runtime value we find its relative difference with respect to the same value for sma. The last row contains the average relative differences across all instances.
We can see that, overall, the mean and best energy values obtained by ema improve 0.29% and 0.48% respectively with a reduction in CPU time of 17.87%. We can conclude, supported by running a Wilcoxon signed rank test (after rejecting normality with a Shapiro–Wilk test), that our proposal ema is significantly faster than sma while obtaining comparable results quality-wise.
A more detailed look at the results shows that for those instances with the lowest flexibility ema performs worse both in quality and in time. This can be explained because instances with low flexibility are closer to the traditional job shop, i.e., there exists little variation for executing operations in different resources, and thus their search space is smaller. Compared to the parameter setting for sma presented at [41] we have decreased the initial size of the population ev_pop_size, since the immigration operator in ema introduces new individuals during the search to increase diversity. Less flexible instances do not seem to need the extra diversity we are seeking to obtain with the immigration operator and instead benefit from a larger initial population that is intensified from the start of the search. However, for instances with higher flexibility, sma improves both in quality and in time. Besides, for larger instances that also have a higher ratio
In [41] it is shown that it is precisely in those instances with large size and high flexibility where exact methods (in particular, a constraint programming solver) struggle to find a solution and metaheuristics become more relevant. In consequence, the improvements obtained with ema are very significant. Moreover, we have compared instances in terms of relative error, but it is important to keep in mind that a little relative worsening in a small quantity is not as significant as a big improvement in a large quantity.
4.2Synergies study
To check the synergies between the evolutionary and local search components of ema, we run individually each component for the same CPU time as the hybridized version. Finding a fair way of doing this experiment is not easy because each algorithm has different requirements and we have to find a set of parameters that make good use of the total CPU time.
Although we could have stopped the execution of each component after the average running time of ema, by doing this the search could be stopped in an improvement phase or be unnecessarily extended when it is trapped in an unpromising one. For this reason, each algorithm has been individually configured in such a way that the average execution time is similar to that of ema but giving each run independence to last longer or shorter, as necessary. To do this, in the evolutionary component we have increased the initial population size to 30000, we add 50 individuals every 5 iterations without improving and we stop the search after 50 iterations without an improvement. In the case of the tabu search, we make 15000 restarts and stop each one after 500 iterations without an improvement. All other parameters are kept as in the main experiment.
Table 4 reports the relative difference between the results obtained with each component of ema separately and the results obtained with the complete algorithm, already shown in Table 3. These relative difference values are also depicted as a bar chart in Fig. 3. Only relative differences are shown because neither the evolutionary algorithm nor the tabu search on their own can match the results obtained by ema and relative differences provide a better insight into how much the results have been altered by using only one of the search strategies.
Table 4
Results of the synergy study
| Tabu search | Evolutionary algorithm | |||
|---|---|---|---|---|
| Instance | Mean RE(%) | Best RE(%) | Mean RE(%) | Best RE(%) |
| 07a | ||||
| 08a | ||||
| 09a | ||||
| 10a | ||||
| 11a | ||||
| 12a | ||||
| 13a | ||||
| 14a | ||||
| 15a | ||||
| 16a | ||||
| 17a | ||||
| 18a | ||||
| Mean | ||||
Figure 3.
Synergy study.
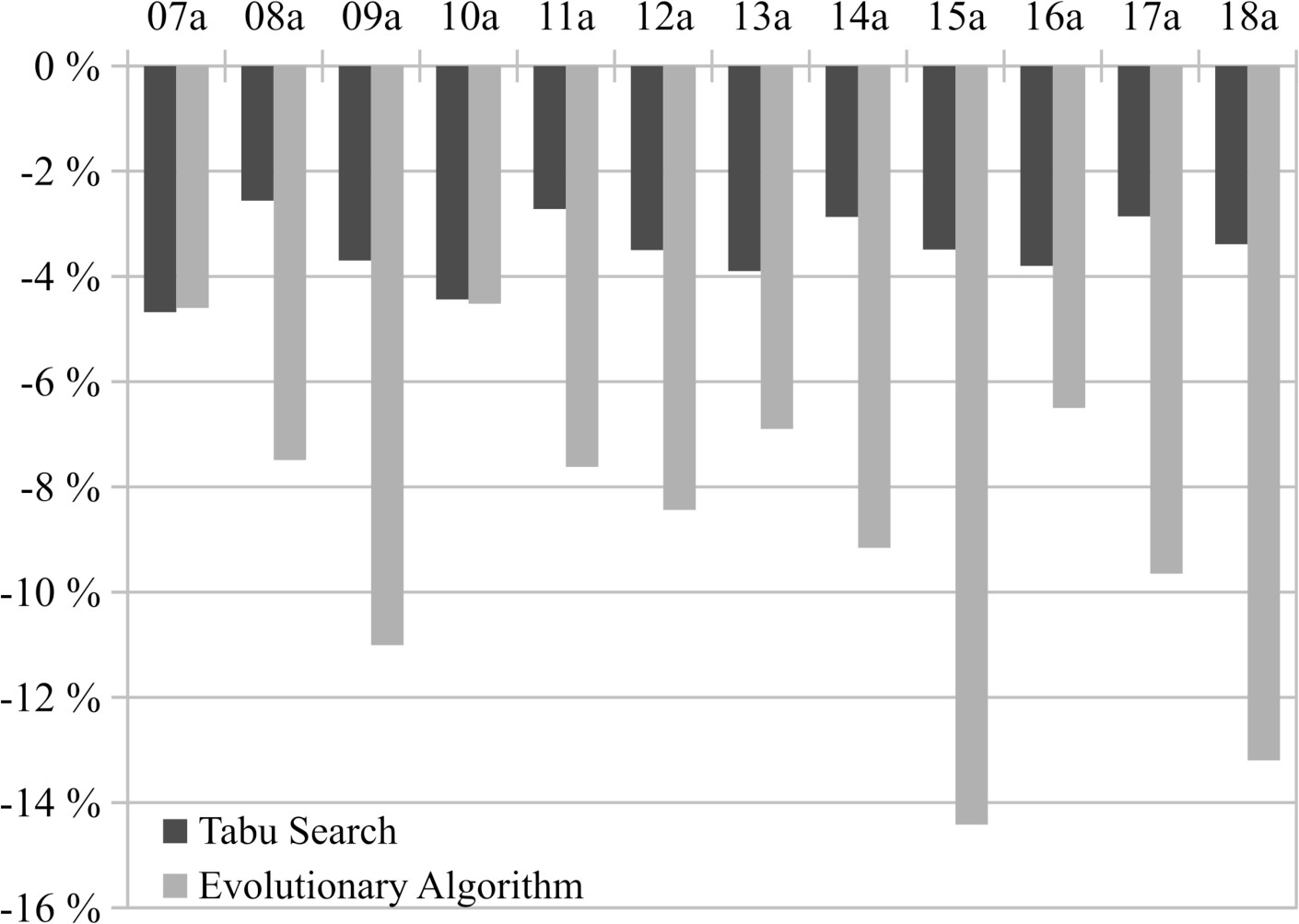
In the case of the tabu search, it gives worse results because local search is very dependent on the starting point, so it is crucial to provide it with a good initial solution. Choosing these initial solutions at random, even with thousands of runs, there is a very low probability of finding a good one. In ema the evolutionary component is not so much responsible for finding good solutions, but for finding good starting points for the tabu search. This is something evolutionary algorithms excel at because they explore different areas of the search space. On the other hand, the evolutionary algorithm lacks a proper intensification mechanism, so even if it is able to explore different areas, it fails at performing a deeper search in the most promising ones. This can be clearly seen as in smaller instances with little flexibility 07a and 10a the pure evolutionary algorithm can compete with the tabu search, but as instances get harder differences become bigger. In smaller search spaces a shallow exploration yields acceptable results but as the search space increases, the need of a proper intensification becomes evident. We can also conclude that the tabu search clearly dominates the evolutionary module and its relative difference with respect to the memetic ema is pretty constant across instances.
Table 5
Effects of the filtering mechanism
| Instance | Generated | Evaluated | Discarted (%) |
|---|---|---|---|
| 07a | 45.22 | 2.01 | 95.56 |
| 08a | 209.46 | 4.17 | 98.01 |
| 09a | 437.91 | 7.35 | 98.32 |
| 10a | 47.07 | 2.08 | 95.59 |
| 11a | 213.00 | 4.40 | 97.94 |
| 12a | 439.49 | 8.40 | 98.09 |
| 13a | 73.12 | 2.81 | 96.15 |
| 14a | 335.66 | 6.27 | 98.13 |
| 15a | 743.24 | 18.07 | 97.57 |
| 16a | 73.01 | 2.60 | 96.44 |
| 17a | 337.39 | 6.35 | 98.12 |
| 18a | 702.05 | 12.47 | 98.22 |
| Mean | 97.34 |
Figure 4.
Effect of the filter.
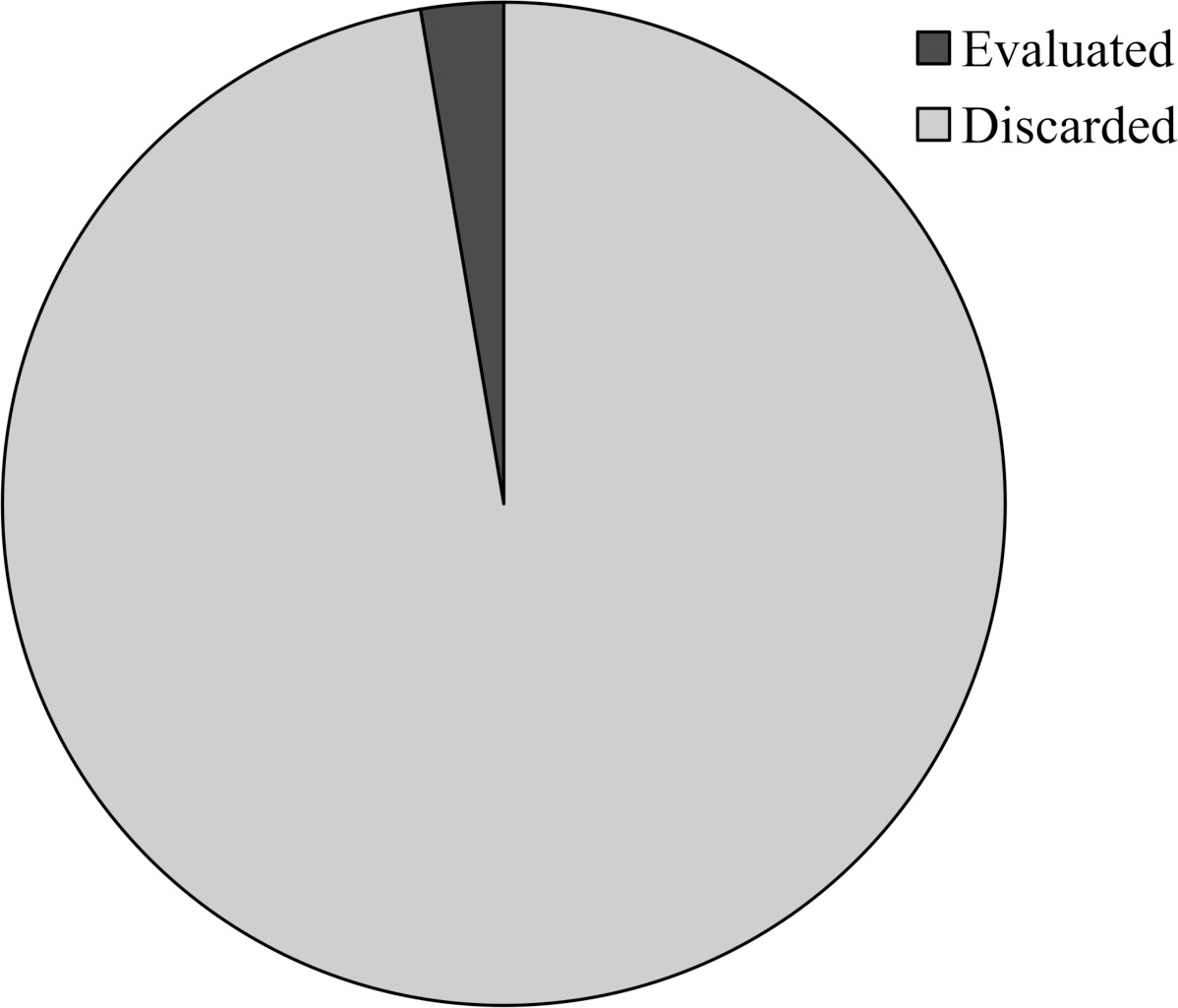
Figure 5.
Comparison between neighborhood functions.
4.3Filtering mechanism
In our next experiment we evaluate empirically how many neighbors are filtered using the mechanism described in Section 3.2.2. First of all, it is important to note that the used lower bound is interesting because it is very fast to calculate, as we do not need to propagate the changes made by the neighbors. It is also important to remember that this mechanism leads to the same selection as using the exact value, so there is not any difference as far as the search process is concerned, only in the time taken by the method. In other words, neither the diversification nor the intensification in the algorithm are altered, even if neighbor selection becomes more efficient. In Table 5 we can see for each instance the total number of generated neighbors (column 2) together with the number of neighbors exactly evaluated by ema to obtain their real energy value (column 3) and the percentage of discarded neighbors with respect to the total (column 3). The last row provides the average across all instances of this percentage of neighbors discarded by the filtering mechanism, which is also illustrated in Fig. 4.
The results clearly show that the filtering mechanism has a strong effect, since it enables ema to discard over 95% of the neighbors. This plays a crucial role in the speed of the algorithm. It is also interesting to notice that the effect is greater as flexibility increases. Larger flexibility means a larger search space and therefore ema generates more neighbors, corresponding to alternative resource assignments. However, many of these reassignments are likely to be bad because they correspond either with slow resources with high execution time or inefficient resources with high energy consumption or even both. In any case, these alternatives must be checked and discarded and this is what the filtering mechanism achieves with undoubted speed and effectiveness.
In the light of these results, one may wonder if some of the neighborhoods are considering numerous bad-quality movements, thus increasing the number of generated neighbors without a real effect on the search, and if similar results could be achieved without using them. This leads to our last experiment.
4.4Neighborhoods comparison
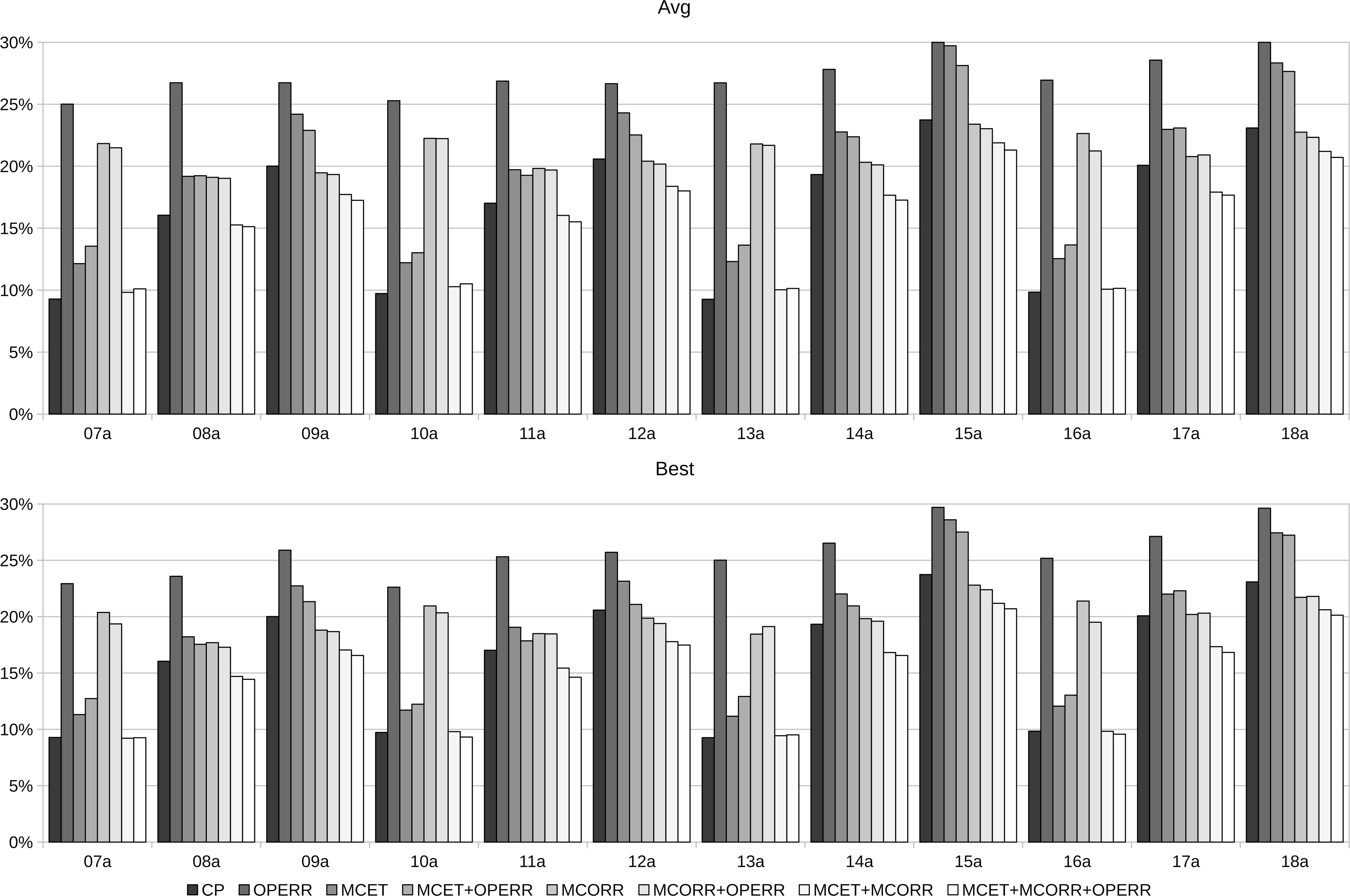
The goal of this last experiment is to assess the performance of the different neighborhoods defined in Section 3.2.1. To this end, we compare the results of running ema with the tabu search using any possible combination of
To evaluate the results obtained with the different neighborhood combinations, we take as reference a lower bound of the optimal energy for each instance obtained with a constraint programming solver in [41]. Figure 5 depicts the relative difference between this lower bound and the average and best energy value obtained by ema with the different combinations of neighborhoods. If we pay attention to the average results,
5.Conclusions
We have tackled the problem of minimizing energy consumption in a flexible job shop scheduling problem with uncertain processing times modeled as triangular fuzzy numbers. This is a relevant problem in manufacturing engineering and incorporating uncertainty helps to improve its applicability. Based on a state-of-the-art solving method from the literature, we have proposed an enhanced memetic algorithm (ema), with a balance between intensification and diversification in the search.
We have carried out an experimental analysis comparing our proposal with the state of the art, showing ema to be competitive in terms of solution quality while it achieves a significant reduction in computation cost. The experimental results have also served to assess the performance of some of the components integrated in ema. In particular, we have confirmed the existence of a synergy effect between the evolutionary algorithm and the tabu search, which cooperate to find better solutions. We have also ascertained how the filtering mechanism used by the tabu search is able to discard numerous unpromising neighbors without fully evaluating them, thus contributing to the algorithm’s efficiency. Finally, having defined the neighborhood function as a union of three different neighborhoods, we have analysed the influence of these components of the neighborhood in the search. We have ascertained that, despite some neighborhoods being undoubtedly more powerful than others, our algorithm can reach better solutions when the three of them are jointly used.
To conclude, we would like to highlight that research into energy efficiency, already relevant due to climate change, has unfortunately gained a sudden and unexpected importance due to the energetic crisis caused by the Ukraine war. It is now fundamental for industry to cut down their energy consumption and make an efficient use of their resources.
Acknowledgments
Supported by the Spanish Government under research grants PID2019-106263RB-I00 and TED2021-131938B-I00 and by Universidad de Cantabria and the Government of Cantabria under Grant Concepción Arenal UC-20-20.
References
[1] | Pinedo ML. Scheduling. Theory, Algorithms, and Systems. 5th ed. Springer; (2016) . |
[2] | Błazewicz J, Ecker KH, Pesch E, Schmidt G, Sterna M, Wȩglarz J. Handbook on Scheduling: From Theory to Practice. Second edition ed. International Handbooks on Information Systems. Springer; (2019) . |
[3] | Han Z, Zhang X, Zhang H, Zhao J, Wang W. A hybrid granular-evolutionary computing method for cooperative scheduling optimization on integrated energy system in steel industry. Swarm and Evolutionary Computation. (2022) ; 73: : 101123. |
[4] | Iannino V, Colla V, Maddaloni A, Brandenburger J, Rajabi A, Wolff A, et al. A hybrid approach for improving the flexibility of production scheduling in flat steel industry. Integrated Computer-Aided Engineering. (2022) ; 29: (4): 367-87. |
[5] | Bakon K, Holczinger T, Sule Z, Jasko S. Scheduling Under Uncertainty for Industry 4.0 and 5.0. IEEE Access. (2022) ; 10: : 74977-5017. |
[6] | Razali MKM, Abd Rahman AH, Ayob M, Jarmin R, Qamar F, Kendall G. Research Trends in the Optimization of the Master Surgery Scheduling Problem. IEEE Access. (2022) ; 10: : 91466-80. |
[7] | Luo H, Dridi M, Grunder O. A Green Routing and Scheduling Problem in Home Health Care. IFAC PapersOnLine. (2020) ; 52: (2): 11119-24. |
[8] | Mansouri N, Ghafari R. Cost Efficient Task Scheduling Algorithm for Reducing Energy Consumption and Makespan of Cloud Computing. Journal of Computer and Knowledge Engineering. (2022) ; 5: (1): 1-10. |
[9] | Imaran Hossain S, Akhand MAH, Bhuvo MIR, Sidiqque N, Adeli H. Optimization of University Course Scheduling Problem using Particle Swarm Optimization with Selective Search. Expert Systems with Applications. (2019) ; 127: : 9-24. |
[10] | Lenstra JK, Kan AHGR, Brucker P. Complexity of Machine Scheduling Problems. In: Studies in Integer Programming. Elsevier; (1977) . pp. 343-62. |
[11] | Gendreau M, Potvin JY, editors. Handbook of Metaheuristics. vol. 272 of International Series in Operations Research & Management Science. 3rd ed. Springer; (2019) . |
[12] | Palacios JJ, González-Rodríguez I, Vela CR, Puente J. Satisfying flexible due dates in fuzzy job shop by means of hybrid evolutionary algorithms. Integrated Computer-Aided Engineering. (2019) ; 26: : 65-84. |
[13] | Gil Gala F, Mencia C, Sierra MR, Varela R. Learning Ensembles of Priority Rules for Online Scheduling by Hybrid Evolutionary Algorithms. Integrated Computer-Aided Engineering. (2021) ; 28: (1): 65-80. |
[14] | Siddique NH, Adeli H. Nature Inspired Computing: An Overview and Some Future Directions. Cognitive Computation. (2015) ; 7: (6): 706-14. |
[15] | Siddique NH, Adeli H. Spiral Dynamics Algorithm. International Journal on Artificial Intelligence Tools. (2014) ; 23: (6): 1430001. |
[16] | Siddique NH, Adeli H. Physicsâ€based search and optimization: Inspirations from nature. Expert Systems. (2016) ; 33: (6): 607-23. |
[17] | Siddique NH, Adeli H. Gravitational Search Algorithm and Its Variants. International Journal of Pattern Recognition and Artificial Intelligence. (2016) ; 30: (8): 1639001. |
[18] | Siqueira H, Santana C, Macedo M, Figueiredo E, Gokhale A, Bastos-Filho C. Simplified binary cat swarm optimization. Integrated Computer-Aided Engineering. (2020) ; 28: (1): 35-50. |
[19] | Zhu M, Yang Q, Dong J, Zhang G, Gou X, Rong H, et al. An Adaptive Optimization Spiking Neural P System for Binary Problems. International Journal of Neural Systems. (2020) ; 31: (1): 2050054. |
[20] | Siddique NH, Adeli H. Harmony Search Algorithm and its Variants. International Journal of Pattern Recognition and Artificial Intelligence. (2015) ; 29: (8): 1539001. |
[21] | Siddique NH, Adeli H. Water Drop Algorithms. International Journal on Artificial Intelligence Tools. (2014) ; 23: (6): 1430002. |
[22] | Siddique NH, Adeli H. Nature-Inspired Chemical Reaction Optimisation Algorithms. Cognitive Computation. (2017) ; 9: : 411-22. |
[23] | Siddique NH, Adeli H. Simulated Annealing, Its Variants and Engineering Applications. International Journal on Artificial Intelligence Tools. (2016) ; 25: (6): 1630001. |
[24] | Judt D, Lawson C, van Heerden ASJ. Rapid design of aircraft fuel quantity indication systems via multi-objective evolutionary algorithms. Integrated Computer-Aided Engineering. (2021) ; 28: (2): 141-58. |
[25] | Park HS, Adeli H. Distributed Neural Dynamics Algorithms for Optimization of Large Steel Structures. Journal of Structural Engineering. (1997) ; 123: (7): 880-8. |
[26] | Akhand MAH, Ayon SI, Shahriyar SA, Siddique N, Adeli H. Discrete Spider Monkey Optimization for Travelling Salesman Problem. Applied Soft Computing. (2020) ; 86: : 105887. |
[27] | Liang Y, He F, Zeng X, Luo J. An improved loop subdivision to coordinate the smoothness and the number of faces via multi-objective optimization. Integrated Computer-Aided Engineering. (2022) Dec; 29: (1): 23-41. |
[28] | Burke EK, Gendreau M, Hyde M, Kendall G, Ochoa G, Özkan E, et al. Hyper-heuristics: A survey of the state of the art. Journal of the Operational Research Society. (2013) ; 64: (12): 1695-724. |
[29] | Duflo G, Danoy G, Talbi EG, Bouvry P. A Generative Hyper-Heuristic based on Multi-Objective Reinforcement Learning: the UAV Swarm Use Case. In: 2022 IEEE Congress on Evolutionary Computation (CEC). (2022) . pp. 1-8. |
[30] | Talbi EG. Hybrid Metaheuristics. vol. 434 of Studies in Computational Intelligence. Springer-Verlag; 2013. |
[31] | Neri F, Cotta C. Memetic algorithms and memetic computing optimization: A literature review. Swarm and Evolutionary Computation. (2012) ; 2: : 1-14. Available from: https://www.sciencedirect.com/science/article/pii/S2210650211000691. |
[32] | Chen X, Ong YS, Lim MH, Tan KC. A Multi-Facet Survey on Memetic Computation. IEEE Transactions on Evolutionary Computation. (2011) ; 15: (5): 591-607. |
[33] | Gong G, Chiong R, Deng Q, Luo Q. A memetic algorithm for multi-objective distributed production scheduling: minimizing the makespan and total energy consumption. Journal of Intelligent Manufacturing. (2020) Jan; 31: (6): 1443-66. |
[34] | Osaba E, Ser JD, Cotta C, Moscato P. Memetic Computing: Accelerating optimization heuristics with problem-dependent local search methods (Editorial). Swarm and Evolutionary Computation. (2022) ; 70: : 101047. |
[35] | Çalis B, Bulkan S. A research survey: review of AI solution strategies of job shop scheduling problem. Journal of Intelligent Manufacturing. (2015) ; 26: (5): 961-73. |
[36] | Xiong H, Shi S, Ren D, Hu J. A survey of job shop scheduling problem: The types and models. Computers & Operations Research. (2022) ; 142: : 105731. |
[37] | Gao K, Cao Z, Zhang L, Chen Z, Han Y, Pan Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA Journal of Automatica Sinica. (2019) ; 6: (4): 904-16. |
[38] | Palacios JJ, González MA, Vela CR, González-Rodríguez I, Puente J. Genetic tabu search for the fuzzy flexible job shop problem. Computers & Operations Research. (2015) ; 54: : 74-89. |
[39] | Chaudhry IA, Khan AA. A research survey: review of flexible job shop scheduling techniques. International Transactions in Operational Research. (2016) ; 23: (3): 551-91. |
[40] | Gen M, Lin L, Ohwada H. Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey. In: Proceedings of the 13th International Conference on Agents and Artificial Intelligence, ICAART 2021. vol. 1; (2021) . pp. 562-73. |
[41] | García Gómez P, González-Rodríguez I, Vela CR. Reducing Energy Consumption in Fuzzy Flexible Job Shops Using Memetic Search. In: Proceedings of the 9th International Work-Conference on the Interplay Between Natural and Artificial Computation, IWINAC 2022. Puerto de la Cruz, Spain: vol. 13259 of Lecture Notes in Computer Science; (2022) . pp. 140-50. |
[42] | Li M, Wang GG. A Review of Green Shop Scheduling Problem. Information Sciences. (2022) ; 589: : 478-96. |
[43] | Li XX, Li WD, Cai XT, He FZ. A Hybrid Optimization Approach for Sustainable Process Planning and Scheduling. Integrated Computer-Aided Engineering. (2015) ; 22: (4): 311-26. |
[44] | Villar JR, de la Cal E, Sedano J. A Fuzzy Logic Based Efficient Energy Saving Approach for Domestic Heating Systems. Integrated Computer-Aided Engineering. (2008) ; 15: : 1-9. |
[45] | Ahn S, Lee S, Bahn H. A smart elevator scheduler that considers dynamic changes of energy cost and user traffic. Integrated Computer-Aided Engineering. (2017) ; 24: : 187-202. |
[46] | Liu Y, Dong H, Lohse N, Petrovic S. A multi-objective genetic algorithm for optimisation of energy consumption and shop floor production performance. International Journal of Production Economics. (2016) ; 179: : 259-72. |
[47] | Liu Z, Guo S, Wang L. Integrated green scheduling optimization of flexible job shop and crane transportation considering comprehensive energy consumption. Journal of Cleaner Production. (2019) ; 211: : 765-86. |
[48] | Fernandes JMRC, Homayouni SM, Fontes DBMM. Energy-Efficient Scheduling in Job Shop Manufacturing Systems: A Literature Review. Sustainability. (2022) ; 14: : 6264. |
[49] | Liu Y, Dong H, Lohse N, Petrovic S, Gindy N. An investigation into minimising total energy consumption and total weighted tardiness in job shops. Journal of Cleaner Production. (2014) ; 65: : 87-96. |
[50] | González MÁ, Oddi A, Rasconi R. Multi-Objective Optimization in a Job Shop with Energy Costs through Hybrid Evolutionary Techniques. In: Proceedings of the Twenty-Seventh International Conference on Automated Planning and Scheduling (ICAPS 2017). Pittsburgh, Pennsylvania, USA: AAAI Press; June 18–23, (2017) . pp. 140-8. |
[51] | Caldeira RH, Gnanavelbabu A, Vaidyanathan T. An effective backtracking search algorithm for multi-objective flexible job shop scheduling considering new job arrivals and energy consumption. Computers & Industrial Engineering. (2020) ; 149: : 106863. |
[52] | Zhang R, Chiong R. Solving the energy-efficient job shop scheduling problem: a multi-objective genetic algorithm with enhanced local search for minimizing the total weighted tardiness and total energy consumption. Journal of Cleaner Production. (2016) ; 112: : 3361-75. |
[53] | Lei D, Zheng Y, Guo X. A shuffled frog-leaping algorithm for flexible job shop scheduling with the consideration of energy consumption. International Journal of Production Research. (2017) ; 55: (11): 3126-40. |
[54] | Wu X, Sun Y. A green scheduling algorithm for flexible job shop with energy-saving measures. Journal of Cleaner Production. (2018) ; 172: : 3249-64. |
[55] | Abdullah S, Abdolrazzagh-Nezhad M. Fuzzy Job-Shop Scheduling Problems: A Review. Information Sciences. (2014) ; 278: : 380-407. |
[56] | Behnamian J. Survey on fuzzy shop scheduling. Fuzzy Optimization and Decision Making. (2016) ; 15: : 331-66. |
[57] | Palacios JJ, González-Rodríguez I, Vela CR, Puente J. Coevolutionary makespan optimisation through different ranking methods for the fuzzy flexible job shop. Fuzzy Sets and Systems. (2015) ; 278: : 81-97. |
[58] | Palacios JJ, Puente J, Vela CR, González-Rodríguez I. Benchmarks for fuzzy job shop problems. Information Sciences. (2016) ; 329: : 736-52. |
[59] | Dubois D, Fargier H, Fortemps P. Fuzzy Scheduling: Modelling flexible constraints vs. coping with incomplete knowledge. European Journal of Operational Research. (2003) ; 147: : 231-52. |
[60] | McCahon CS, Lee ES. Job sequencing with fuzzy processing times. Computers & Mathematics with Applications. (1990) ; 19: (7): 31-41. |
[61] | Sun L, Lin L, Gen M, Li H. A Hybrid Cooperative Coevolution Algorithm for Fuzzy Flexible Job Shop Scheduling. IEEE Transactions on Fuzzy Systems. (2019) ; 27: (5): 1008-22. |
[62] | Li R, Gong W, Lu C. Self-adaptive multi-objective evolutionary algorithm for flexible job shop scheduling with fuzzy processing time. Computers & Industrial Engineering. (2022) ; 168: : 108099. |
[63] | González-Rodríguez I, Puente J, Palacios JJ, Vela CR. Multi-objective evolutionary algorithm for solving energy-aware fuzzy job shop problems. Soft Computing. (2020) ; 24: (21): 16291-302. |
[64] | Afsar S, Palacios JJ, Puente J, Vela CR, González-Rodríguez I. Multi-objective enhanced memetic algorithm for green job shop scheduling with uncertain times. Swarm and Evolutionary Computation. (2022) ; 68: : 101016. |
[65] | Pan Z, Lei D, Wang L. A Bi-Population Evolutionary Algorithm With Feedback for Energy-Efficient Fuzzy Flexible Job Shop Scheduling. IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2022) ; 52: (8): 5295-307. |
[66] | Li R, Gong W, Lu C, Wang L. A Learning-based Memetic Algorithm for Energy-Efficient Flexible Job Shop Scheduling With Type-2 Fuzzy Processing Time. IEEE Transactions on Evolutionary Computation. (2022) . Early access. |
[67] | Dubois D, Prade H. Fuzzy numbers: An overview. In: Readings in Fuzzy Sets for Intelligent Systems. Elsevier; (1993) . pp. 112-48. |
[68] | Hapke M, Slowinski R. Fuzzy priority heuristics for project scheduling. Fuzzy Sets and Systems. (1996) ; 83: (3): 291-9. |
[69] | Heilpern S. The expected value of a fuzzy number. Fuzzy Sets and Systems. (1992) ; 47: : 81-6. |
[70] | Shen L, Dauzère-Pérés S, Neufeld JS. Solving the flexible job shop scheduling problem with sequence-dependent setup times. European Journal of Operational Research. (2018) ; 265: (2): 503-16. |
[71] | García Gómez P, Vela CR, González-Rodríguez I. A memetic algorithm to minimize the total weighted tardiness in the fuzzy flexible job shop. In: Proceedings of the 19th Conference of the Spanish Association for Artificial Intelligence, CAEPIA 2020/2021. Málaga, Spain: September 22-24, 2021. |
[72] | Cobb H, Grefenstette J. Genetic Algorithms for trakcing changing environments. In: Forrest S, editor. Proceedings of the Fifth International Conference on Genetic Algorithms. Morgan Kaufmann Publishers; (1993) . p. 523-9. |
[73] | Yang WX. An improved genetic algorithm adopting immigration operator. Intelligent Data Analysis. (2004) ; 8: (4): 385-401. Available from: http://content.iospress.com/articles/intelligent-data-analysis/ida00176. |
[74] | Xing LN, Chen YW, Yang KW, Hou F, Shen XS, Cai HP. A hybrid approach combining an improved genetic algorithm and optimization strategies for the asymmetric traveling salesman problem. Engineering Applications of Artificial Intelligence. (2008) ; 21: (8): 1370-80. |
[75] | Dell’Amico M, Trubian M. Applying tabu search to the job-shop scheduling problem. Annals of Operations Research. (1993) ; 41: (3): 231-52. |
[76] | González MA, Vela CR, Varela R. An Efficient Memetic Algorithm for the Flexible Job Shop with Setup Times. In: Proceedings of the Twenty-Third International Conference on Automated Planning and Scheduling, ICAPS 2013. Rome, Italy: AAAI; June 10–14, (2013) . |
[77] | Nowicki E, Smutnicki C. A Fast Taboo Search Algorithm for the Job Shop Problem. Management Science. (1996) ; 42: (6): 797-813. |
[78] | Dauzère-Pérès S, Paulli J. An integrated approach for modeling and solving the general multiprocessor job-shop scheduling problem using tabu search. Annals of Operations Research. (1997) ; 70: : 281-306. |
[79] | Strassl S, Musliu N. Instance space analysis and algorithm selection for the job shop scheduling problem. Computers & Operations Research. (2022) ; 141: : 105661. |
[80] | Streeter MJ, Smith SF. How the landscape of random job shop scheduling instances depends on the ratio of jobs to machines. Journal of Artificial Intelligence Research. (2006) ; 26: : 247-87. |




