A fitting algorithm based on multi-touch gesture for rapid generation of railway line

1.Introduction

Line location as an overall work plays a decisive role in the safety, economy, comfort, and environmental protection of railway construction and operation, and even impacts all aspects of the railway [1]. To determine a satisfactory location scheme, professional engineers need to comprehensively analyze the specific conditions in detail and optimize iteratively [2, 3, 4]. More importantly, a large number of scheme discussions are required with repeated human-computer interaction (HCI) from an initial line to the final determination. For instance, designers need to conveniently generate a quick line scheme at the field site or meeting room according to experts’ suggestions or comments for further discussion [5]. However, the traditional HCI with mouse+keyboard cannot well meet the increasing requirements of rapid generation of the railway line location during scheme discussion. Therefore, more efficient HCI technologies, especially natural and intuitive HCI, were quite necessary. Historically, the HCI technology gradually transforms from the traditional computer-centered interaction mode with the mouse+keyboard to a new human-centered interaction mode – the natural HCI mode [6].

For nearly half a century, HCI technology has undergone tremendous changes. Since the 1950s, Command-Line Interface (CLI) has begun to appear [7]. The computer completed the interaction process by feeding the results received from the command line back to the monitor [8]. Massachusetts Institute of Technology (MIT) first made significant contributions to computer-aided alignment design [9]. The Xerox Palo research center developed a graphical user interface (GUI) based on Windows, Icons, Menu, and Pointing (WIMP) Devices in the late 1970s. GUI is an interface display format for communication between humans and computers. GUI allows users to manipulate icons or menu options on the screen with input devices such as a mouse+keyboard to select commands, invoke files, start programs or perform other daily tasks [10, 11]. Currently, the third generation of natural user interaction (NUI) interface only needs users to communicate with the computer in the most natural ways, such as by voice, facial expression, hand gestures, moving body, and a rotating head, to get rid of the mouse+keyboard [12]. Several developed countries, such as the United States, United Kingdom, Germany, and Canada, early conducted intensive research on the design of computer-aided alignment systems. The functions of horizontal and vertical alignment design, earthwork calculation, numerical simulation system, and 3D alignment visualization were integrated and developed collaboratively. This set of sophisticated alignment design systems has fundamentally changed the interaction mode [13], making methods of computer-aided design (CAD) alignment evolve ultimately. The CAD alignment technology started late in China. However, the current independent CAD alignment system developed rapidly, which integrates functions such as horizontal and vertical alignment control, engineering cost calculation, 3D visualization, and even intelligent optimization [14, 15, 16, 17]. With the development of computer science, various new interactive technologies, such as multi-touch, voice input, and retina formation, appeared successively. For example, a novel computer system integrated vision with haptics (touch) and sound as Multi-Sensory Information System (MSIS) has been developed and efficiently applied for planning the location (the alignment) of a new road [18, 19]. In addition, Kinect, the interactive control device of the Xbox 360 game host released by Microsoft in November 2010, realized dynamic HCI by capturing the action of the human body and transforming it into the operation signal of the machine [20, 21]. Meanwhile, research on hand gesture definition and algorithm of multi-touch and pen-touch interaction in human-computer interaction expands the thinking for developers and users by using the pen-touch interface [22, 23]. Jan Derboven discussed the universal hand gesture of multi-touch, some simple gestures are proved by experimental comparison, but it is pretty challenging to deal with some complex gestures [24]. Hand gestures are divided into contact, natural, and pointing gestures, according to the differences in finger movement modes, the number of contacts, arrangement order, and other factors. Contact and natural gestures can be divided into static and dynamic gestures in terms of the specific movement of fingers [25]. The subject is the fingers, and the connection form of the primary receptor is gesture recognition. The interaction is carried out in a natural, intuitive, convenient, and fast manner [26, 27]. Multi-touch interaction technology is often used in the tactile analysis [28]. Uthpala Samarakoon analyzed gesture performance and requirements in early childhood education’s multi-touch applications, providing theoretical support for multi-touch hand gesture design principles [29]. Therefore, how to improve the work efficiency of HCI is still a focus of conducting railway alignment design. Currently, multi-touch technology has been widely applied in various fields, such as the military, classroom teaching, and business meetings. However, the application in alignment exploration and design is still in the primary stage. The high efficiency of railway alignment design and the modernization of interaction mode urgently need development. This paper proposes an approach to the rapid generation of railway lines by using a multi-touch gesture algorithm. An example verification is conducted for the location design of the Sichuan-Tibet railway. Expressly, three aspects are contained, (1) The natural interaction method of multi-touch hand gesture for railway alignment is proposed; (2) The rapid fitting method of alignment design based on hand gesture (or hand-drawing) recognition is given; (3) An example study for the realization and verification of the railway alignment design based on multi-touch interaction is conducted. Accordingly, this paper is organized into five parts. Following Section 1 as this Introduction, Section 2 presents the multi-touch gesture definition. Section 3 describes the fitting algorithm of alignment design based on hand gesture recognition. Section 4 presents an example verification of the approach to rapid generation of railway line location by employing a multi-touch gesture algorithm before the conclusions in Section 5.

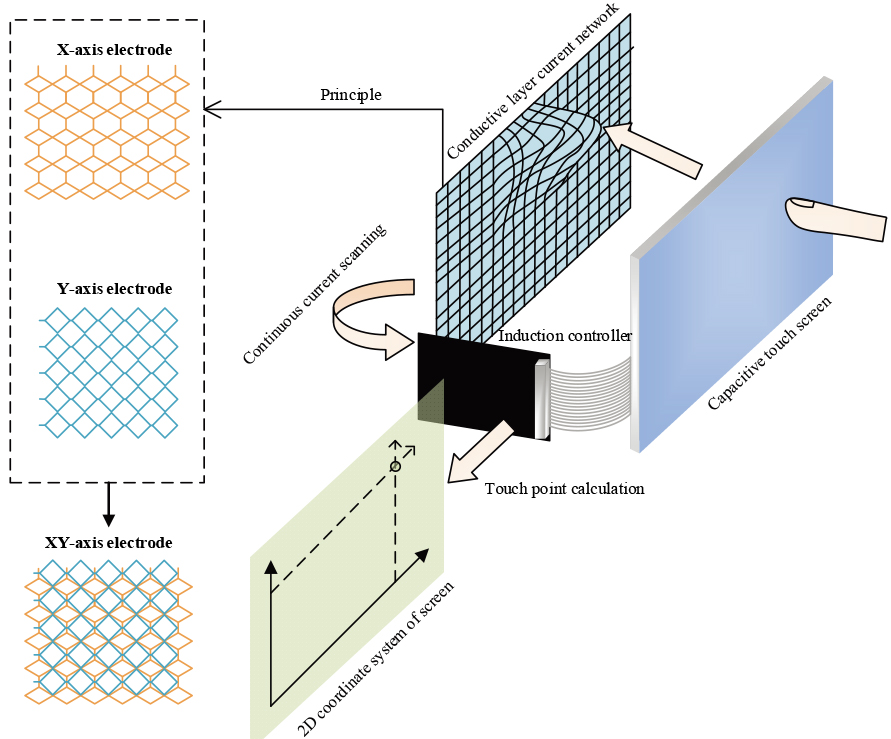
Figure 1.

The principle of capacitive touch screen.

2.Multi-touch interactive hand gesture definition

Multi-touch technology refers to how users interact with the computer system through multiple fingers moving and controlling the dynamic change of the graphical interface with different hand gestures. Users use multiple fingers for human-computer interaction to control the dynamic change of the graphical interface to achieve natural operation and flexible cooperation. The receptor of multi-touch gesture interaction is the multi-touch screen. According to the previous study [30, 31], touch screens can be divided into resistance, capacitance, infrared, and surface acoustic type. The principle of the capacitive touch screen applied in this research is shown in Fig. 1.

The hand gesture semantic diversity classification effect is achieved by setting the horizontal, and vertical two-way expansion, and accumulation. Interactive gestures are defined as listed in Table 1, covering the following three operation modes. (i) Geographical environment browsing manipulation gestures. Long strips usually characterize the terrain of the alignment system. It is necessary to overview the overall trend of the terrain belt, browse the geographical environment characteristics of each part according to the block, and accurately view the geographical environment details of the block position. Browse operations are divided into terrain translation, scaling, rotation, initialization viewpoint, line roaming, and perspective and orthographic switching to the overall scene. (ii) Alignment design operating gestures. To meet the alignment entity operating tasks and detail information inspection, the gestures include line drawing, erasing, marking the control point, and highlighting displays. Users can operate control points (intersection or gradient change point) to complete the relative position change and deletion to realize the curve section angle, direction, or vertical section gradient value change. Users also can query geographic information, and line entity interactive editing to change the curve element information. (iii) Mode switching gestures. To avoid the action conflict between two patterns of geographical environment and interactive alignment design, different types of gestures are placed in different modules, serially connecting model switch gestures to realize rapid and straightforward switching between the two modes.

Table 1

Interactive hand gesture definition

Model type	Hand gesture	Action	Action description	Semantic connotation
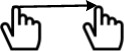
The operation mode of geographical environment browsing	Slip		Holding a single finger drag along any direction	Model movement
	Amplification		Drag two fingers on opposite sides	Model amplification
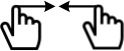
	Reduction		Hold double fingers and merge to the middle	Model reduction
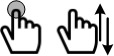
The operation mode of alignment design	Rotation		One finger hold and the other move	Rotation around y-axis
			Double fingers hold rotating	Rotation around z-axis
	Double click		Quickly double-click the same position at the blank	Back to the initial view
	Move		Single finger stroke on terrain	Generate hand-drawing line
	Remove		Single finger stroke on a hand-drawing line	Delete hand-drawing line
	Press + drag		Press the mark to drag	Control point operation
	Long press		Single finger press	Sensitive point labeling
Mode switching	Long press		Three fingers press	Mode switching

3.Fitting algorithm for railway alignment

Research on the fitting method focuses on inflection point detection of hand-drawing line points. Many valuable studies have been on image inflection point detection algorithms, including Moravec inflection point detection technology, Harris inflection point detection technology, SUSAN inflection point detection technology [32], and FAST inflection point detection technology in the gray value detection method [33]. Moreover, the image edge contour curve detection algorithm is based on methods of Freeman chain code (FCC), Euclidean distance (ED) [34], curvature scale space (CSS), and chord-to-point distance accumulation and inflection point detection method based on contour curve [35]. The above inflection detection algorithms have specific graphic geometry characteristics. Inflection detection algorithms can be divided into two categories. One is to detect the inflection by changing the multi-direction grey value of image elements. The other is to judge the inflection by changing the curvature, position, and geometric shape of image edge contour points [36]. According to the distribution law and elements of hand-drawing and the requirements of railway alignment design, this section adopts the Euclidean distance and chord-to-point distance accumulation for the inflection point detection algorithm on a plane and vertical sections, which improves the algorithm kernel to make it better in fitting the railway central line.

3.1Fitting algorithm for a horizontal design

3.1.1Inflection detection algorithm based on Euclidean distance

The fitting method focuses on the inflection detection of hand-drawing points on hand-drawing lines. After hand-drawing, data points intersecting with the terrain in the plane will be generated. Trend distribution is along the terrain belt with the inevitable trend and geometric law, which provides the initial data basis for line fitting of subsequent alignment design. The ultimate goal of graphic alignment fitting is to extract data points at critical positions of planar hand-drawing and convert them into control points of the designed lines, composed of straight lines – curves – straight lines after algorithmic processing and calculation. Based on the Euclidean distance for the inflection detection algorithm of planar hand-drawing lines, the curvature element d is defined to describe the sum of squares of Euclidean distances between k point pairs centered on each discrete point. Euclidean distance and straight line distance from inflection point d to the before and after of point k are shown in Fig. 2.

Figure 2.

Euclidean distance and straight line distance.

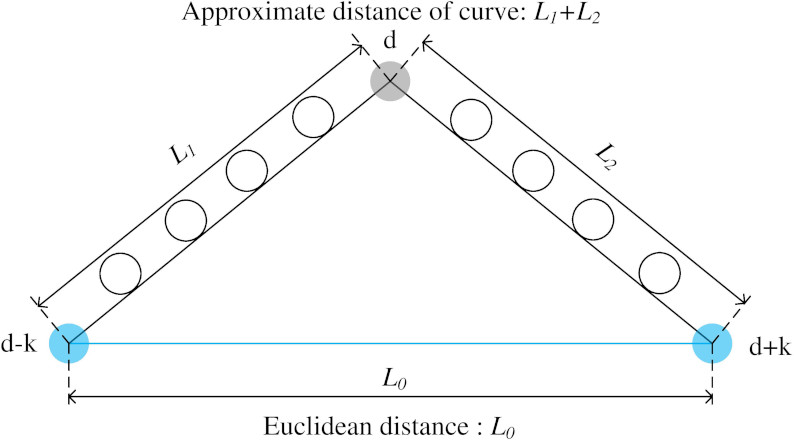
Curvature element calculation is shown as Eq. (1),

(1)

di⁢(k)=∑j=1k(pi-j⁢pi+j¯)2

where di – the curvature element of point Pi. pi-j⁢pi+j¯ – the Euclidean distance between point Pi-j and point Pi+j. k – the number of points.

Since the density of discrete points on the curve is not fixed, it is necessary to normalize the curvature element of each point when calculating it. The curve normalization is seen as Eq. (2),

(2)

dj⁢(k)=∑j=1k(pi-j⁢pi+j¯)2∑j=1k(pi-j⁢pi¯+pi⁢pi+j¯)2

where, pi-j⁢pi¯ – the approximate curve distance between point Pi-j and point Pi. pi⁢pi+j¯ – the approximate curve distance between point Pi and point Pi+j.

The curvature element is used to determine the trend of curvature at any inflection point on the curve, which ranges from 0 to 1. According to the definition of curvature element, when the discrete point is close to the curve inflection point, the curvature element of the point will begin to decrease. When the discrete point is far away from the curve inflection point, the curvature element of the point will begin to increase; the curvature element of a straight line is maximum and close to 1.

A parameter threshold t is defined, which is used to determine the steering interval of the sample curve. When ds<t and ds-1>t, the ps is the starting point of the discrete curve. When de>t and de-1<t, the pe is the end turning point of the discrete curve. From point ps to point pe is the turning part of the discrete curve, and the inflection point of the curve is also included in this part. The inflection detection algorithm based on Euclidean distance is to find out the point with the smallest curvature element in this point set, namely, the inflection point.

The curvature meta-container data are calculated by the data of each point in the hand-drawing point container. The pseudo-code of the program is written below,

Begin For i= 0 to hand-drawing points. size ()  Calculation of hand-drawing point curvature  element by Euclidean distance normalization [i]  Curvature [i] stored in curvature element  container End For End

3.1.2Horizontal curve fitting based on the inflection detection algorithm

In the design and construction of railway lines, the circular curve needs to be measured in detail. When the curve is set in detail, the middle pile spacing on the curve should be 20 m to meet the accuracy requirements of the fitting. If the terrain is flat and the curve radius is greater than 800 m, the middle pile spacing in the circular curve can be 40 m [37]. Therefore, when selecting the points of the curve, the minimum distance between the two points is less than 20 m to meet the accuracy requirements.

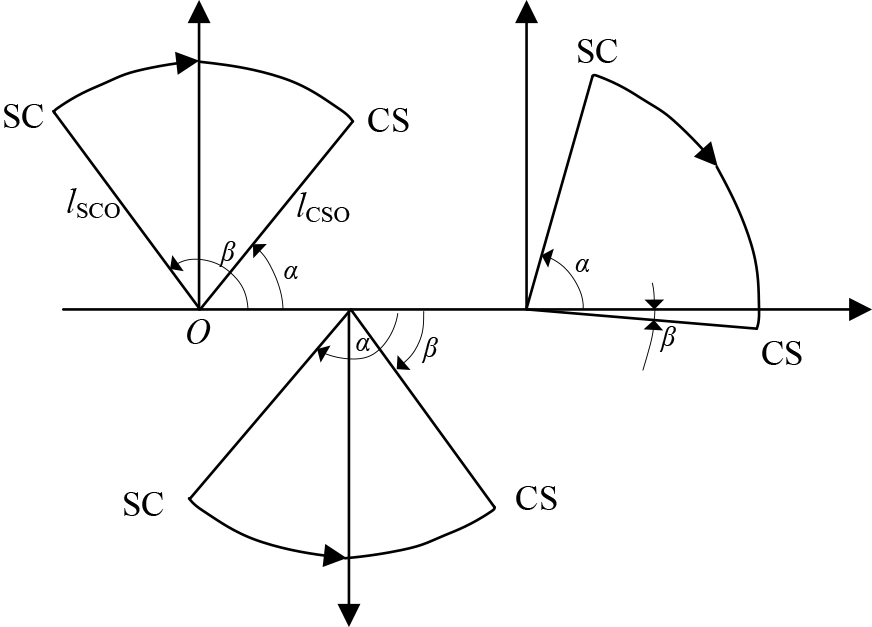
When designed by regulation, it is necessary to add a transition curve to the steering section of the circular curve. The elements of the curve section of the transition curve include angle α, radius R, transition curve length l0, tangent length T, curve length L, and outer sagittal distance E. Meanwhile, the critical control points include tangent-spiral point (TS), spiral-circle point (SC), curve-midpoint (CM), circle-spiral point (CS), and spiral-tangent point (ST). According to the curve elements of the alignment without setting a circular curve, the curve elements of the setting transition curve are calculated.

The normalized value of the curvature element of each point is calculated, and a fixed constraint threshold t less than one is set to identify the inflection position. Meanwhile, for eliminating noise points in the straight line segment, the constraint is realized by the double-loop and judgment method. The algorithm process is that when di<t, point i is set as the center, the mean curvature of the first k points is greater than the threshold t, and the mean curvature of the last k points is less than the threshold, which could be determined that the random point i is the point SC. On the contrary, when dj<t, point j is set as the center, the mean curvature of the first k points is less than the threshold t, and the mean curvature of the last k points is greater than the threshold t, which obtained that the random point j was a point CS. Each adjacent point starting with point SC formed a complete turning interval between i and j. Using the data in the curvature element container, the initial inflection point position of the line is determined. The pseudo-code of the program is written below,

Begin  For i= 10 to Curvature. size() - 10   sum_behind = curvature [i+ 1] to curvature   [i+ 11] summation   sum_front = curvature [i- 1] to curvature   [i- 11] summation   average_behind = sum_behind/10   average_front = sum_front/10   IF curvature[i] <t && average_behind <t   && average_front >t    Point i stored in steering interval control    points   ELSE IF curvature[i] >t && average_behind   >t && average_front <t    Point i stored in steering interval control    points   End If  End For End

First, determine the length of the transition curve l0, the actual super-high value h, the maximum driving speed V𝑚𝑎𝑥, and V𝑅𝑀𝑆 (root mean square).

Based on the calculation results of RMS speed, superelevation, and under elevation, the minimum transition curve l0 is obtained,

(3)

l0=max⁡{l01,l02,l03}=max⁡{hi0,h×Vmax3.6⁢f,hq×Vmax3.6⁢b}

where l0 – the length of the transition curve (m). l01 – the length of the transition curve at the maximum slope (m). l02 – the length of the transition curve (m) that is super high and not exceeding the limit. l03 – the length of the transition curve (m) with under-high and non-over-limit. i0 – the maximum slope of the transition curve. f – the rate of change (mm/s) for passengers at super high comfort levels. b – the rate of change (mm/s) for under-high comfort levels.

Finally, the transition curve corresponding to the typical radius is calculated. If the radius is the intermediate value, the interpolation method is used to calculate the radius of the curve segment after setting the corresponding transition curve. The program pseudo-code is written as below,

Begin  For i= 1 to steering interval standing point.  size() - 1  Using TS, ST as the tangent point of the curve  intersects at the center of the circle, the center  O(x0, y0), radius R.  The radius R and the recommended radius  corresponding to the relaxation curve length, the  actual transition curve length l0 should be set by  interpolation method.  R is stored in a radius container, l0 in a buffer  curve container.  End For End

The radius R of the circular curve and the length l0 of the transition curve are brought into the transition curve calculation.

The curve element information of the transition curve can be obtained. It is necessary to calculate the world coordinates of points on the transition curve to fit the horizontal curve. The inner shift distance is generated by adding the internal shift of the transition curve segment. Intersection point (JD) position coordinates are related to the approximate alignment position coordinates. The coordinates of point TS and ST can be calculated by JD coordinate, and tangent length T. Calculation equation of angle θ between JD and horizontal coordinate and coordinates of TS (x𝑇𝑆,y𝑇𝑆) and ST (x𝑆𝑇,y𝑆𝑇) are shown as follows,

The radius R of the circular curve and the length l0 of the transition curve are brought into the transition curve calculation.

The curve element information of the transition curve can be obtained. It is necessary to calculate the world coordinates of points on the transition curve to fit the horizontal curve. The inner shift distance is generated by adding the internal shift of the transition curve segment. JD position coordinates are related to the approximate alignment position coordinates. The coordinates of point TS and ST can be calculated by JD coordinate and tangent length T. Calculation equation of angle θ between JD and horizontal coordinate and coordinates of TS (xTS,yTS) and ST (xST,yST) are shown as follows,

(4)

θ=arctan⁡(k)

(5)

{xTS=xJD-T⁢cos⁡θyTS=yJD-T⁢sin⁡θ

(6)

{xST=xJD+T⁢cos⁡θyST=yJD+T⁢sin⁡θ

where θ – the angle between JD and horizontal coordinate. k – the slope of the straight line before and after JD. (xJD, yJD), (xTS, yTS) and (xST, yST) – the world coordinate of JD, TS, and ST, respectively.

The distance of points SC and CS is calculated by points TS, ST, and the length of transition curve l0. The endpoint of the transition curve segment is point SC, and the starting point of the opposite transition curve is point CS. The parameter equation and the equation of the rectangular coordinate equation of a cubic parabolic curve are described below,

(7)

x≈l-l540⁢R2⁢l02

(8)

y≈x36⁢R⁢l0

where x, y – the horizontal and vertical coordinates of any point on the curve, respectively; l – the distance (m) between any point of the transition and TS (ST) points. R – the radius of the circular curve(m). l0 is the length of the transition curve(m).

Figure 3.

Calculation chart of each point of the transition curve.

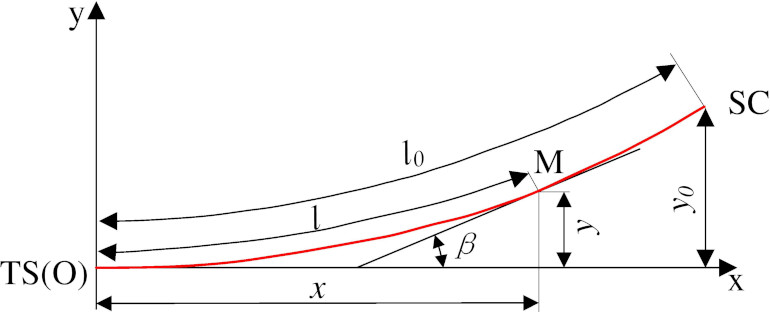
Figure 4.

Transformation diagram from local coordinate to the world coordinate.

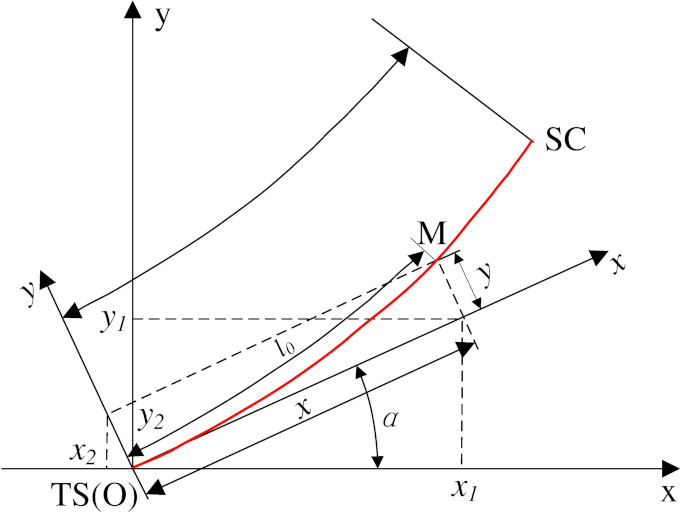
Bringing the length of transition curve l0 into Eq. (7), getting the coordinate values (l0, l0/6R) in the relative coordinate system with TS as the origin, the curve is shown in Fig. 3. The curve segment for adding a transition curve is from TS to SC. Each appropriate point in this section is located in the relative coordinate system with the point TS as the origin. Before drawing, it is necessary to convert the local coordinate system to the world coordinate system, as shown in Fig. 4.

The triangular transformation transforms the relative coordinates of each point [38]. Then, the X and Y directions components are added respectively to get them xr and yr transformed world coordinates. Ultimately, the natural-world coordinates of the point TS are added to obtain the world coordinates of any point in the transition curve. The calculations for xr and yr are as follows,

(9)

xr=l0⁢cos⁡θ-l026⁢R⁢sin⁡θ

(10)

yr=l0⁢sin⁡θ-l026⁢R⁢cos⁡θ

where (xα, yα) – the angle between the relative coordinate X-axis and the world coordinate X-axis.

The coordinate of any point on the transition curve is calculated below,

(11)

(xα,yα)=(xTS,yTS)+(xr,yr)

where (xα, yα) – the absolute coordinates of a point in the world coordinate system, (xTS, yTS) – the absolute coordinates of point TS in the world coordinate system. (xr, yr) – a point coordinate in the relative coordinate system with TS point as origin.

The point between SC and CS is on a circular curve. Given the center coordinates of point O, the line lSCO is obtained by connecting point SC with O, and the angle between lSCO and X-axis is β, the line lSCO is obtained by connecting point CS with O, and the angle between lSCO and X-axis is α. If β>α, the arc is drawn clockwise. Supposing β<α, the arc is drawn counterclockwise. The detailed location is shown in Fig. 5.

Figure 5.

Coordinate calculation of circular curve.

By connecting the points, TS and SC, CS, and ST, smoothly by cubic parabola curve fitting method, as well as connecting points SC and CS by arc corresponding to curve angle, then four relative coordinate systems with TS, ST, SC, and CS as the origin are established, respectively. With an equal step increment in the x-direction, all curve increment points are connected in sequence from the origin. Finally, the fitting curve is drawn by adding the world coordinates of the origin in each coordinate system. The program pseudo-code is as below,

Figure 6.

Fitting point of vertical section.

Begin  For i= 1 to JD.size() - 1   For ZHD_i = 0 to ZHD_i * 0.2 <l0   The tangent angle of the slope of the front clip   line at the intersection is θ1, starting with ZHD,   relative coordinate.   The variation of x-direction Δ⁢x= 0.2 i,   the variation of y-direction Δ⁢y= (0.2i)2/6R   The absolute coordinate system in right devia-   tion   Δ⁢x0=Δ⁢x⁢cos⁡θ1+Δ⁢y⁢sin⁡θ1   Δ⁢y0=Δ⁢x⁢sin⁡θ1+Δ⁢y⁢cos⁡θ1   END For   For fabs(αSC) > fabs(αCS)   Starting from the CS point, the angular step   reduces 0.02 radians every time, right   deviation α-= 0.02, Each time the   angle step increases 0.02 radian, left deviation   α+= 0.02   END For   For ZHD_i= 0 to ZHD_i* 0.2 <l0   The tangent angle of the slope of the behind   clip line at the intersection is θ2, starting with   HZD, relative coordinate.   The variation of x-direction Δ⁢x= 0.2 i,   The variation of y-direction Δ⁢y= (0.2i)2/6R   The absolute coordinate system in right devia-   tion:   Δ⁢x0=Δ⁢x⁢cos⁡θ2-Δ⁢y⁢sin⁡θ2   Δ⁢y0=Δ⁢x⁢sin⁡θ2+Δ⁢y⁢cos⁡θ2   The absolute coordinate system in left devia-   tion:   Δ⁢x0=Δ⁢x⁢cos⁡θ2+Δ⁢y⁢sin⁡θ2   Δ⁢y0=Δ⁢x⁢sin⁡θ2-Δ⁢y⁢cos⁡θ2   End For  End For End

3.2Vertical curve fitting based on extreme point-to-point (EPP) and chord-to-point distance accumulation (CPDA)

Horizontal design line fitting only aims at the x, and y-direction of the space dimension of the hand-drawing point. Vertical ground line elevation points are generally interpolated from the horizontal line digital terrain model. In the three-dimensional terrain environment, the vertical intersection of space rays with infinite extension. It is obtained that each point on the plane design line corresponds to clear space or a buried depth and actual elevation value projected onto the terrain surface. Take two ends (x, y, +∞), (x, y, -∞) of enough z to form a straight line parallel to the normal vector of the terrain array.

Using hand-drawing lines to increase the line mileage, the ground line elevation data of the vertical section can be obtained. Take the points as shown in Fig. 6, where x represents mileage and y represents elevation.

Vertical alignment design is to find the elevation projection of points on horizontal alignment in 3D terrain. Obtaining elevation data from the ground line in the vertical section provides essential support for the following vertical design and fitting method. The inflection detection algorithm of the hand-drawing line on the vertical section applies the chord-to-point distance accumulation method. The inflection point position is determined by accumulating the distance between the point on the profile curve and the tangent at a fixed position. The inflection detection method based on the relative distance difference between the chord and point has obvious pertinency, which is suitable for the inflection detection set of vertical curve drawings. However, due to the poor inhibition effect on noise points, this method may be affected readily. Therefore, it is necessary to de-duplicate and de-noise hand-drawing data points in advance. Vertical curve radius, slight slope, slope length, and gradient difference between adjacent slopes are considered when the hand-drawing lines of the vertical section are fitted to the designed alignment.

Figure 7.

Initial gradient change point calculation.

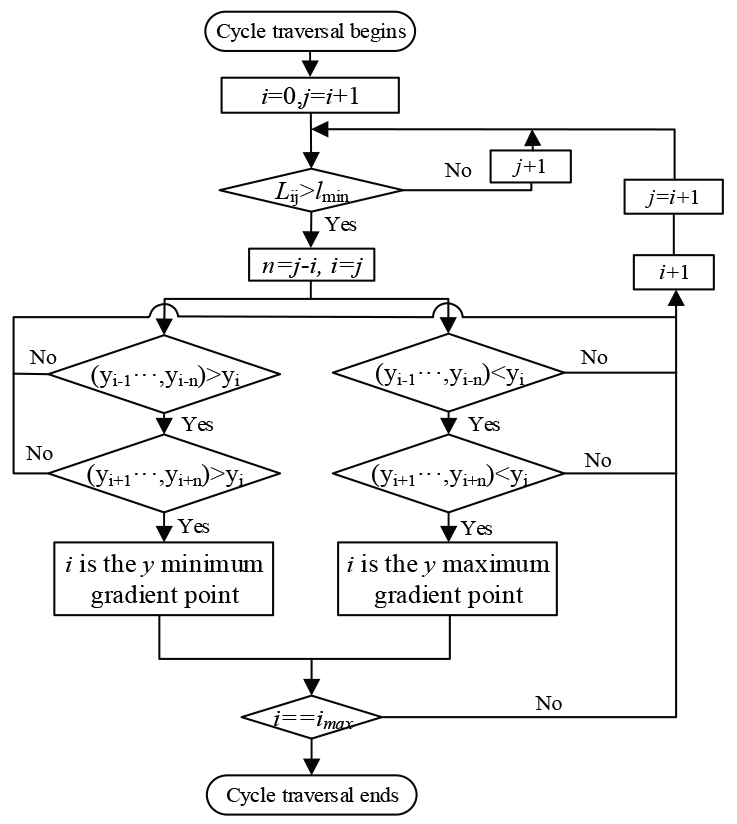
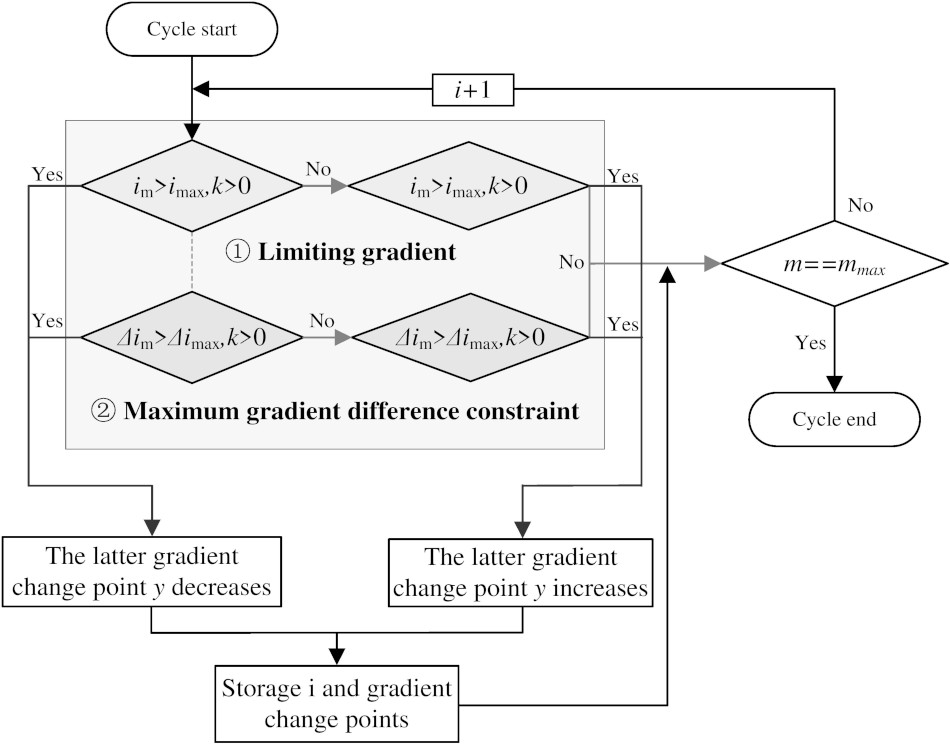
Figure 8.

Resetting gradient change points with limiting gradient and maximum gradient difference constraint.

After de-noising and de-duplication, the initial data is input into the fitting program to calculate the positions of the gradient change points. The process is shown in Fig. 7. The calculation process is described in the following steps. (1) Use the starting hand-drawing point P0 as the first gradient change point. The one-way cycle traverses the point behind P0 and calculates the distance between Pi and P0 each time. If li>l𝑚𝑖𝑛, the distance between Pi and P0 satisfies the constraint of minimum slope length. Meanwhile, the fitting points n between Pi and P0 is calculated and saved, and whether there is a gradient change point can be judged from the Pi point. (2) If there is a relationship ∑j=1nyi-j<yi between all points of Pi and Pi+n, that is, the y coordinates of all points between Pi and Pi-n are less than the y coordinates of Pi. Moreover, if there is a relationship ∑j=1nyi+j<yi between all points of Pi and Pi+n, that is, the y coordinates of all points between Pi and Pi+n are less than the y coordinates of Pi. Then we can determine that point Pi is a maximum gradient change point in the y-direction and save the gradient change point. (3) Similarly, if there is a relationship ∑k=1nyi-k>yi between Pi and Pi-n, and a relationship ∑k=1nyi+k>yi between Pi and Pi+n. Then the point Pi is a minimum gradient change point in the y-direction. Save the gradient change point. (4) If the point Pi does not meet the conditions described in (2) and (3), it proves that the current point is not a gradient change point. Please continue to traverse downwards.

Then, the direction of all hand-drawing points with the current vertical section has been preliminarily found. And the position information of gradient change points satisfies the minimum slope length constraint. It is also necessary to determine whether the restricted gradient (imax) and the adjacent gradient difference (Δ⁢ilim) meet the constraints. For the slope sections that do not meet the requirements of the slight gradient and the maximum gradient difference between adjacent slope sections, the position of the connected gradient change points is automatically optimized and adjusted by algorithm control. To meet the required gradient constraints and the maximum gradient difference constraint between adjacent slope sections, the information of gradient change points that violate the constraints is changed, as seen in Fig. 8.

The former calculation process is described in the following steps: (1) The first gradient change point (the line’s starting point) begins, and the slope sections connecting the two adjacent gradient change points are calculated sequentially. The gradient i of each section is stored in the vector container varied by order. (2) Traverse all gradients i in the gradient container; if i>imax, k> 0, reduce the y value of the last gradient change point. Conversely, when |i|>imax, k< 0, increase the y value of the last gradient change point. The partial allowance shall be reserved for reduction or increase, and the absolute value of the gradient after resetting shall be less than the limit gradient. (3) Store the reset gradient i in the vector container’s mth position and store the reset gradient change point in the vector container.

The latter calculation process is shown in the following steps (1) Starting from the first slope section, the absolute value Δ⁢i of gradient difference between adjacent slope sections is calculated successively. The gradient value i is stored in the vector container variation. (2) If Δ⁢im>Δ⁢i𝑙𝑖𝑚, k> 0, the point value of the ith slope will decrease. If Δ⁢im<Δ⁢i𝑙𝑖𝑚, k< 0, the y value of the ith slope point will increase. To reduce the number of slope sections with maximum gradient difference, there is a remaining amount. The equation is y=|i-56⁢imax|. (3) Store the reset gradient value iin theith position of the vector container variable, gradient change point replacement stored in a vector.

4.Case verification

This paper selects a section of the Sichuan-Tibet Railway from Xierong to Zhaqi (STR-XZ) and verifies the design and implementation of railway alignment based on multi-touch control. The design speed is 160 km/h with a minimum curve radius of 1600 m. The primary design requirements are listed in Table 2.

This research selects a projective capacitance induction touch screen (PCITS), which can support multiple points (up to ten points) with user-friendly consideration, and applies the Windows system for multi-touch interactive alignment design and development. As a realization method of terrain entity translation, the corresponding operation is single finger pressing and dragging in geographical environment browsing mode. For single finger operations, the only movement of single contact mode is involved. Through the distance change between two frames, the corresponding matrix (Δ⁢xΔ⁢y 0)T is transformed. In a line-drawing way, the corresponding operation is double fingers pressing and dragging. The distance between two frames is the average distance between two fingers.

The operations of single fingers and double fingers are taken as examples for calculating essential limiting conditions when touch events occur. The point positions of the double fingers in the previous frame are P𝑙𝑎𝑠𝑡0, P𝑙𝑎𝑠𝑡1. The distance between the two fingers is Δ⁢x0=P𝑙𝑎𝑠𝑡1⋅l-P𝑙𝑎𝑠𝑡0⋅l. The point positions of two fingers in the current frame are P𝑛𝑜𝑤0, P𝑛𝑜𝑤1, the distance is Δ⁢x0=P𝑛𝑜𝑤1⋅l-P𝑛𝑜𝑤0⋅l. In adjacent frames, finger 0 moving distance is η0=P𝑛𝑜𝑤0-P𝑙𝑎𝑠𝑡0, and finger 1 is η1=P𝑛𝑜𝑤1-P𝑙𝑎𝑠𝑡1. The main finger distance classification process is shown in Fig. 9.

Figure 9.

Primary finger distance classification process.

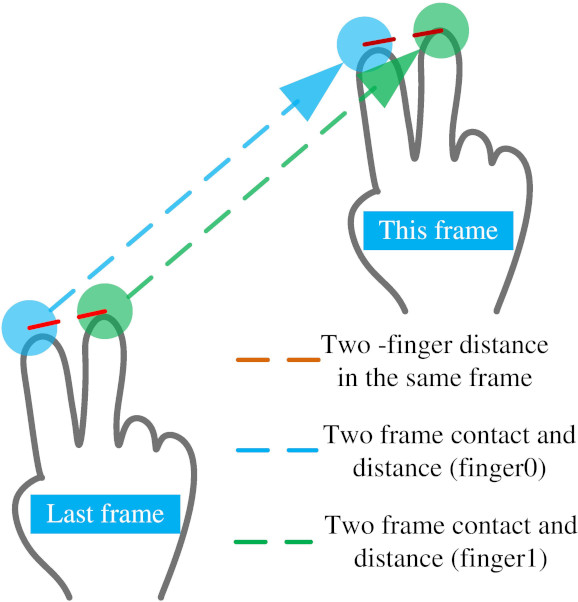
The center point matrix of the camera observation position is (x⁢y 0)T. According to the equation, the change of camera observation position is obtained, and the final display effect is the synchronous movement of solid terrain and finger contact points:

where the center is the camera center position matrix, and M is the camera rotation matrix.

Figure 10.

Projection from a plane to a trackball.

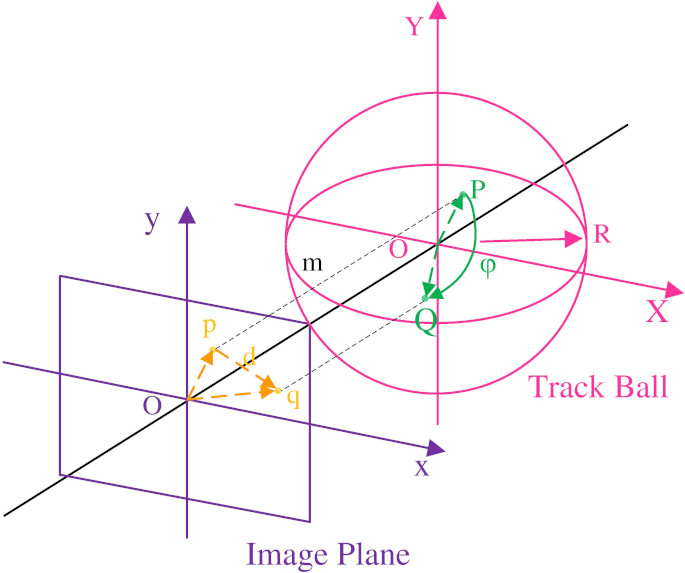
Figure 11.

Alignment deletion processing.

The implementation method of terrain entity scaling is as follows: distance change rate r=(Δ⁢x0-Δ⁢x1)/Δ⁢x0 between two fingers of adjacent frames can be obtained by holding two fingers away or near simultaneously. When r> 0, the principle is that the viewpoint position is far from the terrain, manifested as the reduction of terrain entity shape. When r< 0, the principle is that the viewpoint is close to the terrain, and the terrain is enlarged. To prevent the gesture misjudgment of double finger movement and the ‘drift’ phenomenon of the picture, the distance change rate control α is added. When the distance change rate is greater than the threshold α, the scaling event occurs.

The realization of terrain entity rotation is that entity rotation control is set up according to OpenGL standard trackball principle to ensure a smooth and stable image during finger rotation [39]. The tracking ball is a virtual spherical tool used to simulate and control the rotation of objects in 3D space on a 2D screen. The rotation center is located in the entity’s center on the visual interface, and the radius is adapted to the object’s size, as seen in Fig. 10.

The rotation radian and rotation axis vector in 3D space are calculated when the entity rotates by determining the amount of finger movement. After that, the implementation of terrain browsing state initialization is as follows. The terrain beyond the scope of view cannot be seen caused by the excessive translation. So the single finger fast double-click screen at the same position, the viewpoint, viewport, and sight distance are re-initialized as _homeEye= (x0, y0-y, z0), _homeCenter= (x0, y0-y, z0), _homeUp= (x0, y0-y, z0) respectively. The three variables are set to initial values, and the camera observation position and perspective are returned to the initial state.

The finger moves along the hand-drawing line in deletion mode and erases along the hand-drawing line. The deletion algorithm is based on Open Source Graphic (OSG) node traversal and deletion and the computer hand-drawing deletion principle [40]. The single finger is imaged as an eraser with both length and width at a threshold t. The alignment deletion process and its algorithm flow chart are shown in Fig. 11.

Figure 12.

Flow chart of mode switching.

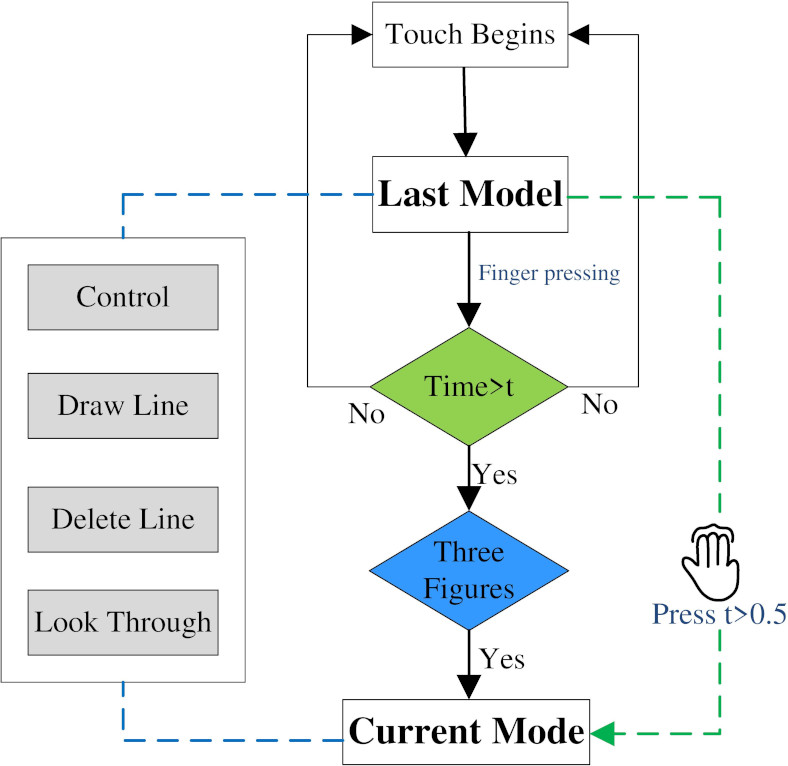
The operation mode switching process is described in Fig. 12. If the three-finger screen time exceeds t (0.5 s), the current mode will switch. The overall switching process sequence is illustrated.

Figure 13.

Initial effect diagram of orthographic projection.

Figure 14.

Horizontal hand-drawing line and the fitted line.

The Virtual Planet Builder (VPB) was loaded into the 3D terrain of OSG. VPB + osgdem tool combines Digital Elevation Model (DEM) elevation and texture data in the same projection coordinate system to generate 3D terrain with elevation information. After reading and generating entity terrain, it is imported into the OSG program and converted into a .ive file format to improve the speed of terrain import. The initial effect of the orthographic projection of terrain after the import is shown in Fig. 13.

The horizontal design based on multi-touch refers to the final formation of a complete horizontal alignment scheme for the railway, including drawing the initial hand-drawing scheme, the processing of the hand-drawing data, and the automatic fitting of the hand-drawing points to the horizontal design scheme. The line drawn by hand gestures should conform to the fundamental law of alignment design. The smooth curve should be drawn in the curve section to avoid excessive turning angle at the turning point or too close to the two turning points, resulting in the calculation results being unable to meet the requirements of the minimum curve radius and the length of the intermediate straight line.

Figure 15.

Vertical section fitting diagram.

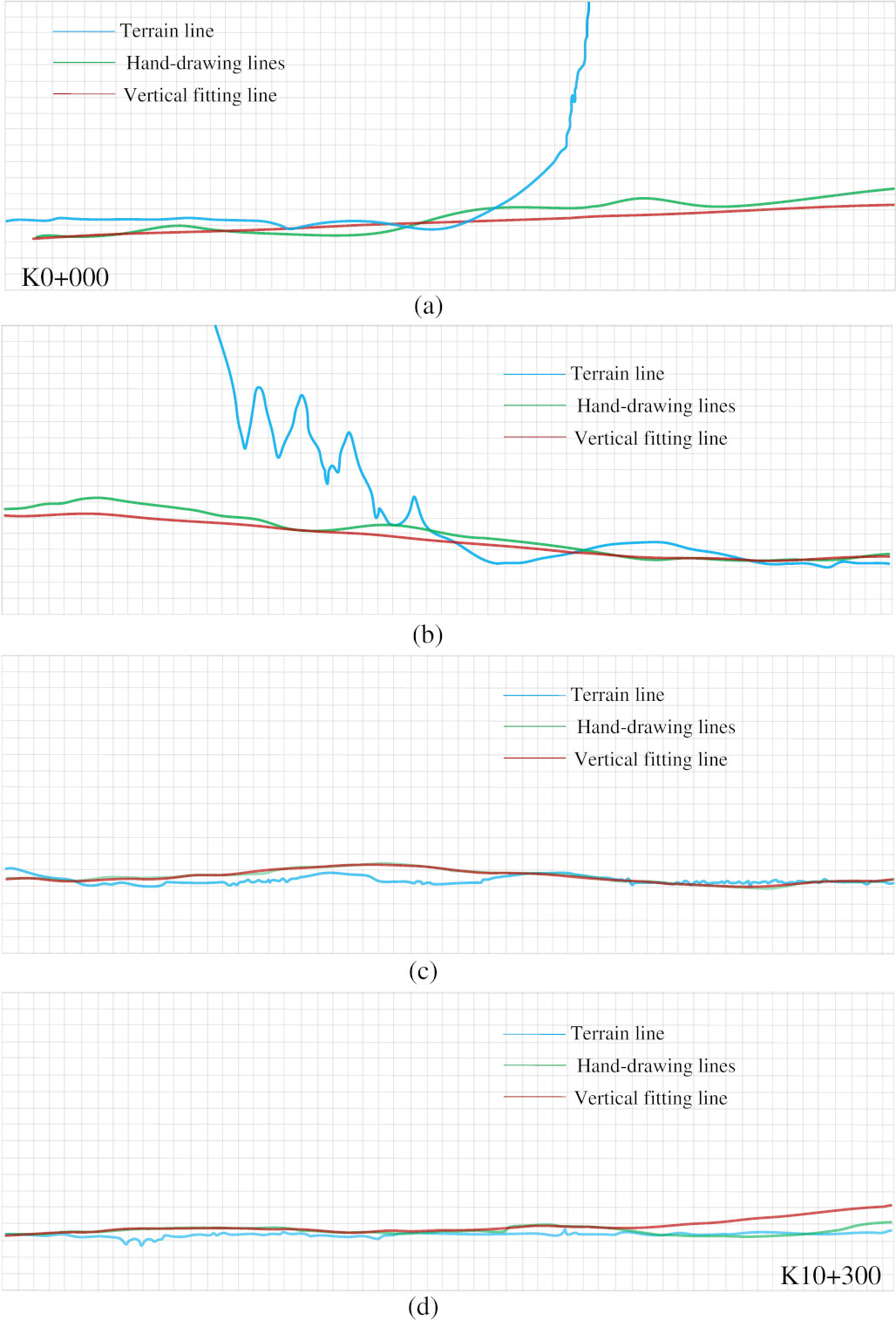
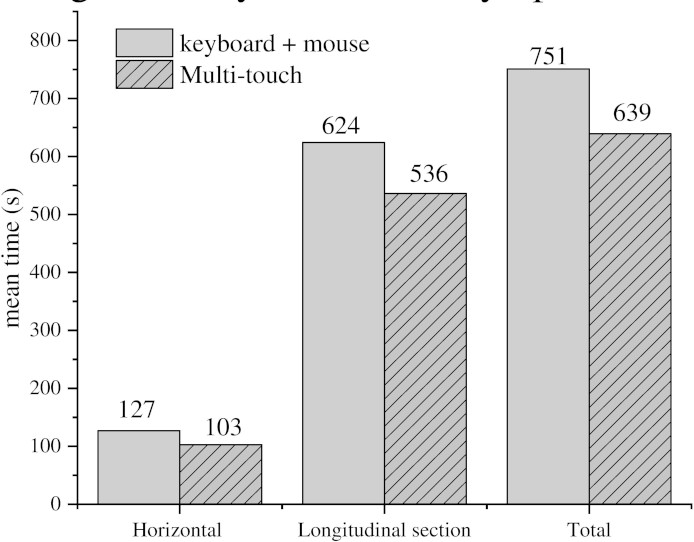
Figure 16.

Time-consuming comparison between traditional interaction and multi-touch.

After completing the basic drawing process, the data container in the program is set to store the necessary line information for the drawing process, including hand-drawing points, curvature elements, the control points of the turning interval starting point and endpoint, as well as an intermediate straight line, intersection points, slope and intercept, left or right deviation judgment, control points TS, SC, CS, ST. Meanwhile, the curve segment elements of the label information storage container are set, including radius R, transition curve length l0, curve length L, tangent length T, and rotation angle α.

Firstly, the line is drawn by hand gesture on a multi-touch screen. Then, the line data are stored, and the line is automatically fitted after running the plane fitting program. The red line is the direct line drawn by hand, which is the horizontal curve. The blue line is the fitting line with the plane curve element. The hand-drawing curve and the effect of the fitting by-hand gesture interaction are shown in Fig. 14. According to China’s Code for Design of Railway Lines [41], it can be seen that the fitting line coincides with the red hand-drawing line based on conforming to the railway design specification.

Railway vertical alignment design is to fit the hand-drawing lines of the vertical section to the alignment design and then form the complete process of the vertical design scheme. According to the vertical curve fitting method of the vertical section described above, the selected points of the initial fitting procedure of the design alignment are collected, and the data information is automatically processed and calculated by the program algorithm. The hand-drawing points are fitted to the vertical section scheme in line with the design specification of railway alignment. The relevant results and necessary annotations are written in the program. Finally, the railway vertical alignment design based on multi-touch interaction is realized.

This example in the real world selects the vertical terrain section where the horizontal is located. The limiting gradient is 12‰, the length of the vertical curve is 15,000 m, the maximum gradient difference is 15‰, and the total length of the railway line is 10.3 km from K0+000 to K10+300. Ultimately, the 17 gradient change points in the vertical section, with the synthetic results of terrain line, hand-drawing line, and vertical fitting line, are shown in Fig. 15. The fitted length and gradient of each slope segment are listed in Table 3.

The results indicate that in the design process based on multi-touch interaction, the position elements of each gradient change point are automatically calculated by an integrated multi-touch gestures algorithm to output the alignment autonomously. The comparison contrasted the scheme based on the mouse+ keyboard and multi-touch is shown in Fig. 16. The user test is carried out with all the time-consuming of the design process as the judgment result. Without considering the advantages and disadvantages of the scheme, the alignment efficiency between the traditional interaction model and the multi-touch interaction mode is carried out in the same design zone. The hand-drawing lines can be directly and rapidly converted to the design alignment in the arbitrary scene, which notably saves the consumption time of railway alignment design up to 18.9% and 14.1% for horizontal and vertical alignment, respectively. The total working time may be reduced by up about 15%.

5.Conclusions

This paper presents an approach to the rapid generation of railway lines using a multi-touch gesture algorithm for natural, intuitive, flexible, and efficient implementation, including the multi-touch interactive hand gesture definition, horizontal and vertical fitting algorithm from gesture recognition, and a real-world example verification. The conclusions can be drawn as follows,