Transportation Mode Selection for Organ Transplant Networks by a New Multi-Criteria Group Decision Model Under Interval-Valued Intuitionistic Fuzzy Uncertainty
Abstract
This study introduces a new multi-criteria group decision-making model in organ transplant transportation networks under uncertain situations. A new combined weighting approach is presented to obtain expert weights with various kinds of opinions by integrating similarity measure and subjective judgments of experts. Also, the CRITIC approach is given to obtain transportation criteria weights. Finally, a novel integrated ranking approach is proposed to calculate the rank of each alternative based on ideal point solution and relative preference relation (RPR) methods. This study regards an interval-valued intuitionistic fuzzy set to cope with the vagueness of uncertain conditions in a real case study.
1Introduction
The first organ transplant surgery in 1954 showed the important status of transplantation in the therapy of various diseases. Solid organs can be categorized into kidneys, livers, intestines, hearts, lungs, and heart-lung integrations. In this respect, the demand for organs is a significant issue that outmatched the supply. Therefore, the proper allocation of organs can be considered for an optimization condition. Furthermore, organ allocation is one of the first statements of medical optimization, which is related to transportation requirements (Alagoz et al., 2009). The different transportation modes are used to transfer organs among echelons of the network. In general, the transplant supply chain network is created based on three sections: donor hospitals, transplant centres, and recipient zones. Nevertheless, after taking the confirmation of the organs’ health, organs are separated from a brain-dead patient or volunteer and are transferred from the removal department of the donor hospital to the transplant centre (Zahiri et al., 2014; Salimian and Mousavi, 2022b, 2022c). In this network, the first phase is related to facility locations, the second phase concerns assigning the collected organs after making demands, and the quantities of different transportation modes constitute the third phase. Transportation selections contain several modes available, either by purchasing or leasing transport fleets or by engaging with outside providers (Haddadsisakht and Ryan, 2018).
In this regard, two types of ground and air transport modes are utilized to connect the various echelons of the supply chain. The selection of an appropriate transportation mode with a suitable vehicle is an important decision that needs a proper decision technique. The vehicle selection in an organ transplant network is related to the quality of the organs by considering the proper speed of vehicles in a risky environment. Hence, the change of the weather condition is one of the network risks that influences choosing the vehicle in different conditions (Kengpol et al., 2014; Wang et al., 2019). Consequently, combining climate change with transportation evaluation authority to assess the risk of transplant destruction due to climate change becomes decisive (Chang et al., 2021).
The multi-criteria group decision-making (MCGDM) approach is one of the appropriate ways to solve complex management and engineering problems (Zavadskas et al., 2019, 2021; Mohammadian et al., 2021; Kaya et al., 2022; Krishankumar et al., 2022), e.g. the selection of a suitable transportation mode. Qu and Chen (2008) proposed a hybrid multi-criteria decision-making (MCDM) approach to select a route in multi-modal transportation networks. Farkas (2009) introduced the selection method to evaluate a route or site in urban transportation. This paper utilized the combination of MCDM and GIS method to assess the transportation system. Tuzkaya (2009) generated a combined MCDM approach based on the preference ranking organization method for enrichment evaluation (PROMETHEE) approach to evaluate a suitable transportation mode that reduced the environmental impacts in the network. Fierek and Zak (2012) regard an integrated MCDM and simulation-based technique to evaluate the urban transportation system in Tehran. Kundu et al. (2014) presented a fuzzy MCDM method to assess the solid transportation mode with an experimental application. Żak and Węgliński (2014) proposed an MCDM technique to select the logistic centre location for four transportation modes: rail, water, air, and road. Kumru and Kumru (2014) applied an analytic hierarchy process (AHP) method to assess transportation modes in a logistic company. Zheng (2015) suggested a fuzzy technique for order of preference by similarity to ideal solution (TOPSIS) method to assess the transportation with an experience of Suburban university. Nassereddine and Eskandari (2017) introduced an integrated Delphi-GAHP-PROMETHEE method to evaluate the public transportation system in Tehran. Galińska (2019) utilized an MCDM technique with an intelligent way to select a suitable transportation mode. Zhang et al. (2021) proposed a hybrid MCDM approach to locate a logistic hub in China under the belt and route initiative. Görçün (2021) proposed a hybrid approach with respecting the criteria importance through intercriteria correlation (CRITIC) approach to calculate the weights of criteria in the metro and tram choice in the urban transportation system. Simic et al. (2021) analysed the combination of CRITIC and MACBAC methods to select the suitable price of an urban transportation system under type-2 fuzzy environments. Salimian et al. (2022) proposed a combination approach based on integrating an extended VIKOR method and MARCOS approach under interval-valued intuitionistic fuzzy (IVIF) conditions to evaluate the organ transplantation network problem. Salimian and Mousavi (2022a) introduced a hybrid MCDM method under IVIF situations to evaluate the digital technology to handle COVID-19 pandemic conditions.
Transportation selection processes with uncertain situations can be added as a new study region to explain difficult evaluation and selection problems. However, the available methods have had additions to select transportation modes under vagueness conditions by employing a traditional fuzzy set; most of the relevant studies represented the specific efficiency of alternatives. Because of the complicated and unknown character and circumstances of many real-world transportation mode assessment problems, display details of options regularly have to be represented by the usage of more difficult uncertain modelling media. Lately, multiple kinds of research have begun to suggest new techniques for the selection of high uncertainty, which can represent uncertain transportation condition information more accurately and effectively. However, there are few types of studies that can be observed in the recent papers regarding the selection by employing interval-valued intuitionistic fuzzy sets (IVIFSs). The IVIFS theory was proposed by Atanassov and Gargov (1989) to cope with the vagueness in the knowledge and the opinion of the decision-makers (DMs) in effective decision-making problems. Its primary characteristic is that both membership and non-membership values of a factor to a provided stage are recognized and used as interval values rather than exact quantities, with remarkable applications in management and engineering (Hashemi et al., 2018; Davoudabadi et al., 2019, 2020, 2021). So, there is an especially critical requirement to examine additional efficient and proper mathematical techniques by using the IVIFSs in order to properly control selection issues of increased vagueness and indecision (Atanassov, 1999). The main advantage of IVIFSs is the capability of mitigating membership and non-membership degrees together with respecting fuzzy numbers that is a strong point over traditional fuzzy sets (Davoudabadi et al., 2020). Furthermore, the IVIFS examines the interval matters to determine the degrees rather than applying a crisp value. Also, uncertain values can be considered sufficiently by using IVIFSs in comparison with other fuzzy kinds of approaches. Moreover, by examining the membership and non-membership values, IVIFs are introduced as ranges instead of exact degrees (Davoudabadi et al., 2021).
In relation to the previous issues, this study objects to developing a new account of the integrated soft computing approach by considering the decision-making methods under IVIFs for controlling transportation evaluation system problems. The presented transportation system choice model has the capability to handle both subjective opinions and objective data in naturalistic usage with the IVIF requirements. The proposed method utilizes the combination form of subjective judgments and similarity measures to obtain the DMs weights. Moreover, the criteria weights are obtained with the CRITIC method, and the alternative rank is done with an integrated approach based on positive and negative distance from ideal solutions and the relative preference relation (RPR) method. Eventually, an application example is reported for the transportation system selection in organ transplant networks to determine the IVIF operation-integrated model. The outcomes determine that the introduced model can help the DMs and managers become well-organized to solve complex decisions of transportation systems and uncertain choice problems. The main innovations of this study are described below:
• Introducing integrated subjective judgment weights and objective similarity measure weights of DMs under IVIF conditions to choose the transportation modes in an organ transplantation chain problem.
• Applying the CRITIC method to compute the criteria weights in an organ transplant network for transportation modes selection.
• Introducing a novel combination approach according to the ideal solutions and RPR method under IVIF situations to rank the alternatives of transportation modes in an organ transplant network.
The rest of the paper is organized as follows. Section 2 briefly represents some primary descriptions of IVIFSs. Section 3 presents the introduced integrating soft computing model. Section 4 applies an application example and Section 5 provides a sensitivity analysis. Eventually, the paper is discussed in Section 6.
2Basic Definitions
This sector provides the basic definitions and equations of the IVIFS to make a suitable decision with vague information. These are presented with the following definitions:
Definition 1
Definition 1(Atanassov and Gargov, 1989).
Let
(1)
(2)
(3)
Definition 2
Definition 2(Liu and Jiang, 2020).
Hamming distance is computed with Eq. (4):
(4)
3Proposed Soft Computing Model
This section introduces a novel methodology to compute the experts’ weights, the indicators’ weights, and ranking the candidate alternatives of transportation selection mode problem in an organ transplant network. The integrated DMs’ weighting approach is obtained based on similarity measures and subjective weights that are gathered from experts. According to the CRITIC approach, the weights of the indicators are calculated. Furthermore, based on integrating the positive ideal degree distance and negative ideal distance values from ideal solutions and RPR approach, alternative ranking is obtained. Eventually, this model is introduced under IVIFSs to cope with an uncertain condition. The framework of the proposed model is depicted in Fig. 1.
Fig. 1
Framework of the suggested model.
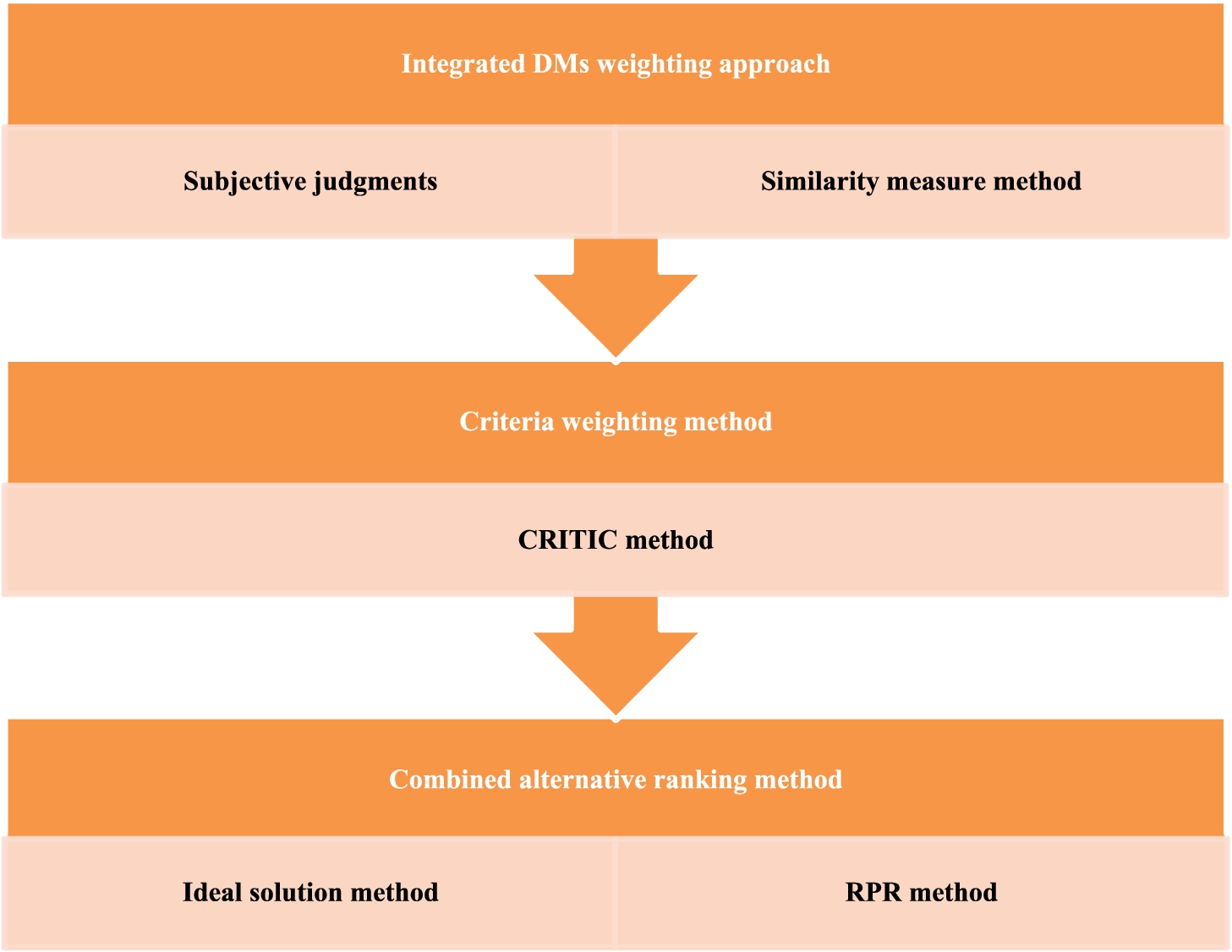
Also, the introduced approach stages are presented in the following:
Stage 1. Collecting the experts’ opinions to create a decision matrix
(8)
Stage 2. Computing the DMs’ weights with a new integrated approach.
Sub-stage 2.1 (Liu and Qiu, 1998). Calculating the normalized decision
(9)
(10)
(11)
Sub-stage 2.2 (Yue, 2011; Zhang and Xu, 2015). Computing the ideal normalized decision matrix based on normalized decision matrix
(12)
(13)
(14)
(15)
(16)
Sub-stage 2.3. Obtaining a similarity measure (Sim) by Eq. (17):
(17)
(18)
(19)
Sub-stage 2.4. Computing the weights of DMs from Eq. (20):
(20)
Sub-stage 2.5. Gathering the subjective weights
Sub-stage 2.6. Obtaining the final weights of DMs from Eq. (21):
(21)
Stage 3 (Peng and Garg, 2022; Qi, 2021). Computing the weights of indicators with the CRITIC approach.
Sub-stage 3.1. Obtaining the score function of normalized decision matrix
(22)
Sub-stage 3.2. Computing the standard deviation of indicators with Eq. (23):
(23)
(24)
Sub-stage 3.3. Calculating the correlation degree among pairs of criteria by Eq. (25):
(25)
Sub-stage 3.4. Computing the criteria’s information numbers with Eq. (26):
(26)
Sub-stage 3.5. Obtaining the weights of indicators with Eq. (27):
(27)
Stage 4. Computing the alternatives’ ranks.
Sub-stage 4.1. Aggregating the normalized decision matrix with Eq. (28):
(28)
Sub-stage 4.2. Calculating the weighting normalized decision matrix with Eq. (29):
(29)
Sub-stage 4.3. Obtaining the positive and negative ideal solutions with Eqs. (30)–(33), respectively.
(30)
(31)
(32)
(33)
Sub-stage 4.4. Computing the distance from positive and negative ideal solutions with Eqs. (34) and (37):
(34)
(35)
(36)
(37)
Sub-stage 4.5. Calculating collective index with Eqs. (38)–(41):
(38)
(39)
(40)
(41)
Sub-stage 4.6. Calculating a border approximation area vector from Eqs. (42) and (43):
(42)
(43)
Sub-stage 4.7. Computing a border approximation area decision matrix with Eqs. (44) and (45):
(44)
(45)
Sub-stage 4.8. Computing the IVIF-RPR for alternatives ranks with Eqs. (46)–(57).
In this respect,
(46)
(47)
(48)
(49)
(50)
(51)
(52)
(53)
Sub-stage 4.9. Computing the alternatives’ value with Eq. (54):
(54)
Sub-stage 4.10. Computing the distance between
(55)
(56)
Sub-stage 4.11. Obtaining the alternatives rank with Eq. (57):
(57)
Stage 5. Computing the final ranking value of alternatives with Eq. (58):
(58)
Eventually, the options are organized in descending order.
4An Application of Introduced Soft Computing Approach
This sector provides an empirical example from the recent literature studies to illustrate and validate the introduced approach (Kundu et al., 2014). This example extended to three types of vehicles that consist of ground vehicle, aircraft, and helicopter. Furthermore, in regards to the transportation criteria, experts want to evaluate the three types based on several further indicators that are very significant for transportation policy. In this regard, three DMs
Table 1
Linguistic terms.
| Linguistic terms | IVIF rates |
| Very high (VH) | ( |
| High (H) | ( |
| Medium high (MH) | ( |
| Medium (M) | ( |
| Medium low (ML) | ( |
| Low (L) | ( |
| Very low (VL) | ( |
Table 2
DMs judgments-based decision matrix.
| Criteria | DMs | Alternatives | ||
| VH | VH | H | ||
| H | H | MH | ||
| VH | H | H | ||
| VH | H | VH | ||
| MH | MH | H | ||
| H | H | VH | ||
| H | VH | H | ||
| MH | H | MH | ||
| MH | H | MH | ||
| ML | L | L | ||
| H | VH | H | ||
| MH | MH | L | ||
| H | H | VH | ||
| MH | MH | H | ||
| VH | H | H | ||
Firstly, the weights of the DMs are obtained according to similarity measure approach with Eq. (20). Afterward, the subjective weights are gathered from experts, and the final weights are calculated with Eq. (21). The final values show that the first DM has greater importance than others. Also, the second and third DMs have the next priorities, respectively. The final outcomes are determined in Table 3.
Table 3
DMs weights.
| Decision makers | Similarity measure weights | Subjective weights | Final weights |
| 0.35822 | 0.40000 | 0.37911 | |
| 0.33095 | 0.35000 | 0.34047 | |
| 0.31083 | 0.25000 | 0.28042 |
Furthermore, the standard deviation (
Table 4
Criteria weights.
| Criteria | Criteria weights | ||
| 6.67083 | 20.95322 | 0.19526 | |
| 8.12664 | 25.52592 | 0.23787 | |
| 4.79583 | 15.06380 | 0.14038 | |
| 8.32150 | 26.13801 | 0.24358 | |
| 6.24901 | 19.62827 | 0.18291 |
Moreover, the alternative rank technique is one of the new concepts of this study that is constructed based on an integrating approach. This method is made based on ideal point solutions and RPR method. In the first part, the
Table 5
Ideal point solutions result.
| Alternatives | |||
| 0.84754 | 0.15814 | 1.33802 | |
| 0.98244 | 0.12609 | 1.14397 | |
| 1.04327 | 0.10525 | 1.06378 |
Table 6
Final ranking of the alternatives.
| Alternatives | Final ranking values | Final rank | ||
| 15.53462 | 2.15116 | 1.74459 | 3 | |
| 9.25518 | 3.61067 | 2.37732 | 2 | |
| 8.62759 | 3.87332 | 2.46855 | 1 |
Afterward, the distance
5Discussion of Results
In this section, sensitivity analysis and comparative analysis were performed in order to get proper outcomes. The purpose of sensitivity analysis is to change every indicator’s weight with another indicator’s weight; therefore, 10 various computations are developed. This part seeks to find C* values for each consideration, and several names are given for each calculation. For example, C13 means criterion 1’s and criterion 3’s weights have been exchanged and C45 means criterion 4’s and criterion 5’s weights have been exchanged. Fig. 2 describes new C* values of the alternatives on the graph. Therefore, Table 7 displays new C* values. As can be seen from Fig. 2 and Table 7,
Fig. 2
Alternatives values with different amounts of criteria weights.

Table 7
Sensitivity analysis on criteria weights impact on alternatives values.
| C*12 | 1.65918 | 2.47090 | 2.77099 |
| C*13 | 1.75996 | 2.32668 | 2.43819 |
| C*14 | 1.75398 | 2.35522 | 2.48002 |
| C*15 | 1.71523 | 2.42158 | 2.49601 |
| C*23 | 1.80446 | 2.22123 | 2.50660 |
| C*24 | 1.74331 | 2.37501 | 2.47114 |
| C*25 | 1.74511 | 2.37639 | 2.43773 |
| C*34 | 1.78851 | 2.21040 | 2.49010 |
| C*35 | 1.62815 | 2.56905 | 2.78734 |
| C*45 | 1.72775 | 2.36588 | 2.46150 |
Furthermore, the impact of variable (θ) is discussed in the final ranking results. This value is changed from 0.1 to 0.9, and the final outcomes are shown in Fig. 3. All of them determined that the RPR method has a high effect on the ultimate ranking outcomes, and only the final result is similar to the ideal point solution approach in
Fig. 3
Impact of θ on final ranking results.
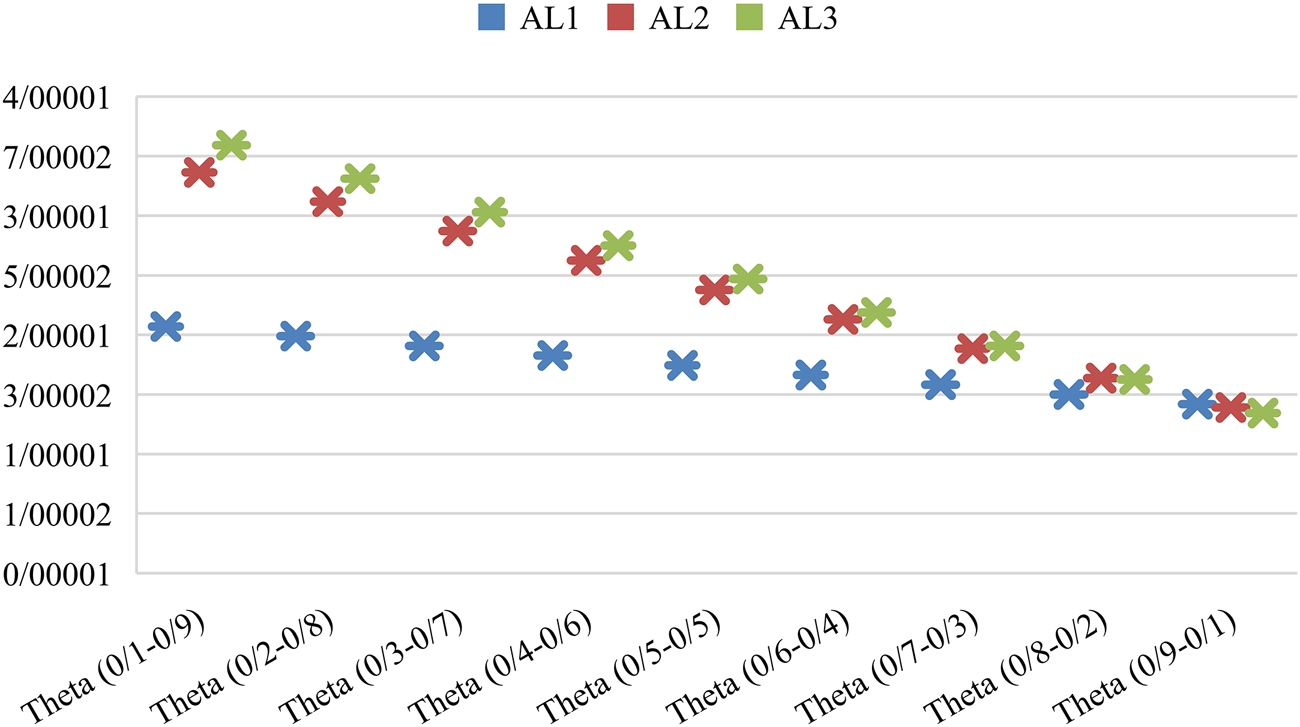
Table 8
Comparing proposed model with IVIF-RPR method.
| Alternatives | IVIF-RPR values | IVIF-RPR ranking based on Dorfeshan and Mousavi (2019)’ study | Proposed approach values | Final ranking of proposed approach |
| 2.15116 | 3 | 1.74459 | 3 | |
| 3.61067 | 2 | 2.37732 | 2 | |
| 3.87332 | 1 | 2.46855 | 1 |
Finally, the introduced methodology is compared with the IVIF-RPR approach based on Dorfeshan and Mousavi (2019)’ study to validate the final outcomes and shows the performance of using this approach to rank the main alternatives of the transportation systems in the organ transplantation network. The final result shows that the ultimate ranking of the introduced approach is similar to the IVIF-RPR approach. This point is indicated in Table 8, which determines the validity of the introduced model in real-world application problems. Also, helicopter is selected to be utilized in the network due to suitable speed and appropriate safety to maintain organ quality unaffected in various situations.
6Conclusion and Future Suggestions
The choice of a proper transportation mode is one of the most crucial decision problems in the transportation system of an organ transplant network with a perishable product. This paper proposed a multi-criteria group decision-making (MCGDM) approach to obtain the most ideal transportation mode among possible modes concerning some assessment criteria for a transportation problem. Besides, there is uncertainty in realistic conditions. In this respect, uncertainty exists throughout the possible experience. So here, the study made an attempt to employ an interval-valued intuitionistic fuzzy set (IVIFS) to describe the vague information, so all the parameters are estimated as IVIFS values. Moreover, a multi-item organ was inscribed using the transportation mode. The models utilized in this paper are general and computationally practical. This model was made based on the computation of the weights of decision-makers (DMs) with an integrated approach that consisted of a similarity measure method and subjective weights. Afterward, the criteria weights were computed with the CRITIC approach, and the ranking method was constructed based on combining an ideal point solution method and relative preference relation (RPR) approach. After that, an application example was represented from previous studies to determine the validity and efficiency of the introduced approach, and some sensitivity analyses were suggested to demonstrate the performance of the introduced methodology. The introduced approach has potential purposes, and it can be introduced to some industry-based MCDM problems in the future. Also, the presented organ transportation network problem can be developed into various kinds of realistic healthcare transportation problems with perishable items. Furthermore, the presented soft computing model is able to solve various kinds of the research areas, such as maintenance strategy selection, material selection, infrastructure project evaluation, warehouse location selection, supplier selection, product design and selection, energy technology assessment, low-carbon port evaluation, etc. Moreover, the proposed model can be combined with an interval-valued Pythagorean fuzzy set, which is similar to the IVIFS in the main procedure; they can be compared with each other to determine the way that improves the soft computing model. Another direction for future research is to handle mixed uncertainties, including intuitionistic fuzzy and stochastic, in the decision problems for organ transplantation networks.
Acknowledgements
The authors express their gratitude to reviewers for their valuable comments and suggestions on the study.
References
1 | Alagoz, O., Schaefer, A.J., Roberts, M.S. ((2009) ). Optimizing organ allocation and acceptance. In: Handbook of Optimization in Medicine. Springer, Boston, MA, pp. 1–24. |
2 | Atanassov, K.T. ((1999) ). Interval valued intuitionistic fuzzy sets. In: Intuitionistic Fuzzy Sets. Physica, Heidelberg, pp. 139–177. |
3 | Atanassov, K., Gargov, G. ((1989) ). Interval-valued intuitionistic fuzzy sets. Fuzzy Sets and Systems, 31: (3), 343–349. |
4 | Chang, C.M., Ortega, O., Weidner, J. ((2021) ). Integrating the risk of climate change into transportation asset management to support bridge network-level decision-making. Journal of Infrastructure Systems, 27: (1), 04020044. |
5 | Davoudabadi, R., Mousavi, S.M., Mohagheghi, V., Vahdani, B. ((2019) ). Resilient supplier selection through introducing a new interval-valued intuitionistic fuzzy evaluation and decision-making framework. Arabian Journal for Science and Engineering, 44: , 7351–7360. |
6 | Davoudabadi, R., Mousavi, S.M., Mohagheghi, V. ((2020) ). A new last aggregation method of multi-attributes group decision making based on concepts of TODIM, WASPAS and TOPSIS under interval-valued intuitionistic fuzzy uncertainty. Knowledge and Information Systems, 62: (4), 1371–1391. |
7 | Davoudabadi, R., Mousavi, S.M., Mohagheghi, V. ((2021) ). A new decision model based on DEA and simulation to evaluate renewable energy projects under interval-valued intuitionistic fuzzy uncertainty. Renewable Energy, 164: , 1588–1601. |
8 | Dorfeshan, Y., Mousavi, S.M. ((2019) ). A new interval type-2 fuzzy decision method with an extended relative preference relation and entropy to project critical path selection. International Journal of Fuzzy System Applications (IJFSA), 8: (1), 19–47. |
9 | Farkas, A. ((2009) ). Route site selection of urban transportation facilities: an integrated GIS.MCDM approach. In: 7th International Conference on Management, Enterprise and Benchmarking, pp. 5–6. |
10 | Fierek, S., Zak, J. ((2012) ). Planning of an integrated urban transportation system based on macro-simulation and MCDM/A methods. Procedia-Social and Behavioral Sciences, 54: , 567–579. |
11 | Galińska, B. ((2019) ). MCDM as the tool of intelligent decision making in transport. Case study analysis. In: Scientific And Technical Conference Transport Systems Theory And Practice. Springer, Cham, pp. 67–79. |
12 | Görçün, Ö.F. ((2021) ). Evaluation of the selection of proper metro and tram vehicle for urban transportation by using a novel integrated MCDM approach. Science Progress, 104: (1), 0036850420950120. |
13 | Haddadsisakht, A., Ryan, S.M. ((2018) ). Closed-loop supply chain network design with multiple transportation modes under stochastic demand and uncertain carbon tax. International Journal of Production Economics, 195: , 118–131. |
14 | Hashemi, H., Mousavi, S.M., Zavadskas, E.K., Chalekaee, A., Turskis, Z. ((2018) ). A new group decision model based on grey-intuitionistic fuzzy-ELECTRE and VIKOR for contractor assessment problem. Sustainability, 10: , 1635–1653. |
15 | Jia, F., Liu, Y., Wang, X. ((2019) ). An extended MABAC method for multi-criteria group decision making based on intuitionistic fuzzy rough numbers. Expert Systems with Applications, 127: , 241–255. |
16 | Kaya, S.K., Pamucar, D., Aycin, E. ((2022) ). A new hybrid fuzzy multi-criteria decision methodology for prioritizing the antivirus mask over COVID-19 pandemic. Informatica, 33: (3), 545–572. |
17 | Kengpol, A., Tuammee, S., Tuominen, M. ((2014) ). The development of a framework for route selection in multimodal transportation. The International Journal of Logistics Management, 25: (3), 581–610. |
18 | Krishankumar, R., Mishra, A.R., Cavallaro, F., Zavadskas, E.K., Antuchevičienė, J., Ravichandran, K.S. ((2022) ). A new approach to the viable ranking of zero-carbon construction materials with generalized fuzzy information. Sustainability, 14: (13), 7691. |
19 | Kumru, M., Kumru, P.Y. ((2014) ). Analytic hierarchy process application in selecting the mode of transport for a logistics company. Journal of Advanced Transportation, 48: (8), 974–999. |
20 | Kundu, P., Kar, S., Maiti, M. ((2014) ). A fuzzy MCDM method and an application to solid transportation problem with mode preference. Soft Computing, 18: (9), 1853–1864. |
21 | Liu, S.L., Qiu, W.H. ((1998) ). Studies on the basic theories for MADM. Systems Engineering-Theory and Practice, 18: (1), 38–43. |
22 | Liu, Y., Jiang, W. ((2020) ). A new distance measure of interval-valued intuitionistic fuzzy sets and its application in decision making. Soft Computing, 24: (9), 6987–7003. |
23 | Mohammadian, A., Heidary Dahooie, J., Qorbani, A.R., Zavadskas, E.K., Turskis, Z. ((2021) ). A new multi-attribute decision-making framework for policy-makers by using interval-valued triangular fuzzy numbers. Informatica, 32: (3), 583–618. |
24 | Nassereddine, M., Eskandari, H. ((2017) ). An integrated MCDM approach to evaluate public transportation systems in Tehran. Transportation Research Part A: Policy and Practice, 106: , 427–439. |
25 | Peng, X., Garg, H. ((2022) ). Intuitionistic fuzzy soft decision making method based on CoCoSo and CRITIC for CCN cache placement strategy selection. Artificial Intelligence Review, 55: , 1567–1604. |
26 | Qi, Q.S. (2021). GRA and CRITIC method for intuitionistic fuzzy multiattribute group decision making and application to development potentiality evaluation of cultural and creative garden. Mathematical Problems in Engineering, 2021, 9957505. https://doi.org/10.1155/2021/9957505. |
27 | Qu, L., Chen, Y. ((2008) ). A hybrid MCDM method for route selection of multimodal transportation network. In: International Symposium on Neural Networks. Springer, Berlin, Heidelberg, pp. 374–383. |
28 | Rouyendegh, B.D., Yildizbasi, A., Üstünyer, P. ((2020) ). Intuitionistic fuzzy TOPSIS method for green supplier selection problem. Soft Computing, 24: (3), 2215–2228. |
29 | Salimian, S., Mousavi, S.M. ((2022) a). A multi-criteria decision-making model with interval-valued intuitionistic fuzzy sets for evaluating digital technology strategies in COVID-19 pandemic under uncertainty. Arabian Journal for Science and Engineering. https://doi.org/10.1007/s13369-022-07168-8. |
30 | Salimian, S., Mousavi, S.M. ((2022) b). A new scenario-based robust optimization approach for organ transplantation network design with queue condition and blood compatibility under climate change. Journal of Computational Science, 62: , 101742. |
31 | Salimian, S., Mousavi, S.M. (2022c). A robust possibilistic optimization model for organ transplantation network design considering climate change and organ quality. Journal of Ambient Intelligence and Humanized Computing, 1(24). https://doi.org/10.1007/s12652-022-03863-4. Article in Press. |
32 | Salimian, S., Mousavi, S.M., Antucheviciene, J. ((2022) ). An interval-valued intuitionistic fuzzy model based on extended VIKOR and MARCOS for sustainable supplier selection in organ transplantation networks for healthcare devices. Sustainability, 14: (7), 3795. |
33 | Simic, V., Gokasar, I., Deveci, M., Karakurt, A. (2021). An integrated CRITIC and MABAC based Type-2 neutrosophic model for public transportation pricing system selection. Socio-Economic Planning Sciences, 80, 101157. |
34 | Tuzkaya, U.R. ((2009) ). Evaluating the environmental effects of transportation modes using an integrated methodology and an application. International Journal of Environmental Science & Technology, 6: (2), 277–290. |
35 | Wang, T., Qu, Z., Yang, Z., Nichol, T., Dimitriu, D., Clarke, G., Bowden, D. ((2019) ). How can the UK road system be adapted to the impacts posed by climate change? By creating a climate adaptation framework. Transportation Research Part D: Transport and Environment, 77: , 403–424. |
36 | Yue, Z. ((2011) ). An extended TOPSIS for determining weights of decision makers with interval numbers. Knowledge-Based Systems, 24: (1), 146–153. |
37 | Zahiri, B., Tavakkoli-Moghaddam, R., Pishvaee, M.S. ((2014) ). A robust possibilistic programming approach to multi-period location-allocation of organ transplant centers under uncertainty. Computers & Industrial Engineering, 74: , 139–148. |
38 | Żak, J., Węgliński, S. ((2014) ). The selection of the logistics center location based on MCDM/A methodology. Transportation Research Procedia, 3: , 555–564. |
39 | Zavadskas, E.K., Stević, Ž., Turskis, Z., Tomašević, M. ((2019) ). A novel extended EDAS in Minkowski Space (EDAS-M) method for evaluating autonomous vehicles. Studies in Informatics and Control, 28: (3), 255–264. |
40 | Zavadskas, E.K., Antucheviciene, J., Turskis, Z. ((2021) ). Symmetric and asymmetric data in solution models. Symmetry, 13: (6), 1045. |
41 | Zhang, X., Xu, Z. ((2015) ). Soft computing based on maximizing consensus and fuzzy TOPSIS approach to interval-valued intuitionistic fuzzy group decision making. Applied Soft Computing, 26: , 42–56. |
42 | Zhang, X., Lu, J., Peng, Y. ((2021) ). Hybrid MCDM model for location of logistics hub: a case in China under the belt and road initiative. IEEE Access, 9: , 41227–41245. |
43 | Zheng, J.H. (2015). A fuzzy TOPSIS approach based to evaluate the transportation mode selection: an experience in a suburban university. Advances in Transportation Studies. http://www.atsinternationaljournal.com/index.php/2015-issues/special-issue-2015-vol1/770-a-fuzzy-topsis-approach-based-to-evaluate-the-transportation-mode-selection-an-experience-in-a-suburban-university. |




