Interval-Valued and Circular Intuitionistic Fuzzy Present Worth Analyses

1Introduction

Engineering economics is a collection of mathematical techniques which easify the comparison of investment alternatives. The main investment analysis techniques of engineering economics are benefit/cost ratio analysis (B/C), rate of return analysis (ROR), present worth analysis (PW), annual cash flow analysis (ACF) and payback period analysis (PPA). PW analysis is the major technique of engineering economics which finds the equivalent present worth of the future cash flows based on these parameters: first cost (FC), salvage value (SV), interest rate (i), annual benefits (AB), annual cost (AC), and life (n).

Fuzzy sets theory was developed by Zadeh (1965) in 1965 and the extensions of these ordinary fuzzy sets (OFSs) have been developed by numerous fuzzy set researchers. These fuzzy set extensions have been used in estimating, decision making, engineering economics, and controlling together with other intelligent systems. The extensions of ordinary fuzzy sets can be given as type-2 fuzzy sets in Zadeh (1975), intuitionistic fuzzy sets (IFSs) in Atanassov (1986), fuzzy multisets in Yager (1986), intuitionistic fuzzy sets of second type in Atanassov (1989), neutrosophic sets (NSs) in Smarandache (1999), nonstationary fuzzy sets in Garibaldi and Ozen (2007), hesitant fuzzy sets (HFSs) in Torra (2010), Pythagorean fuzzy sets (PFSs) in Yager (2013), picture fuzzy sets in Cuong (2014), q-rung orthopair fuzzy sets (q-ROFs) in Yager (2017), fermatean fuzzy sets (FFSs) in Senapati and Yager (2020), spherical fuzzy sets (SFSs) in Kutlu Gündoğdu and Kahraman (2019) and circular intuitionistic fuzzy sets (C-IFSs) in Atanassov (2020). In Fig. 1, the historical progress of the fuzzy set theory is given.

Fig. 1

Fuzzy set extensions.

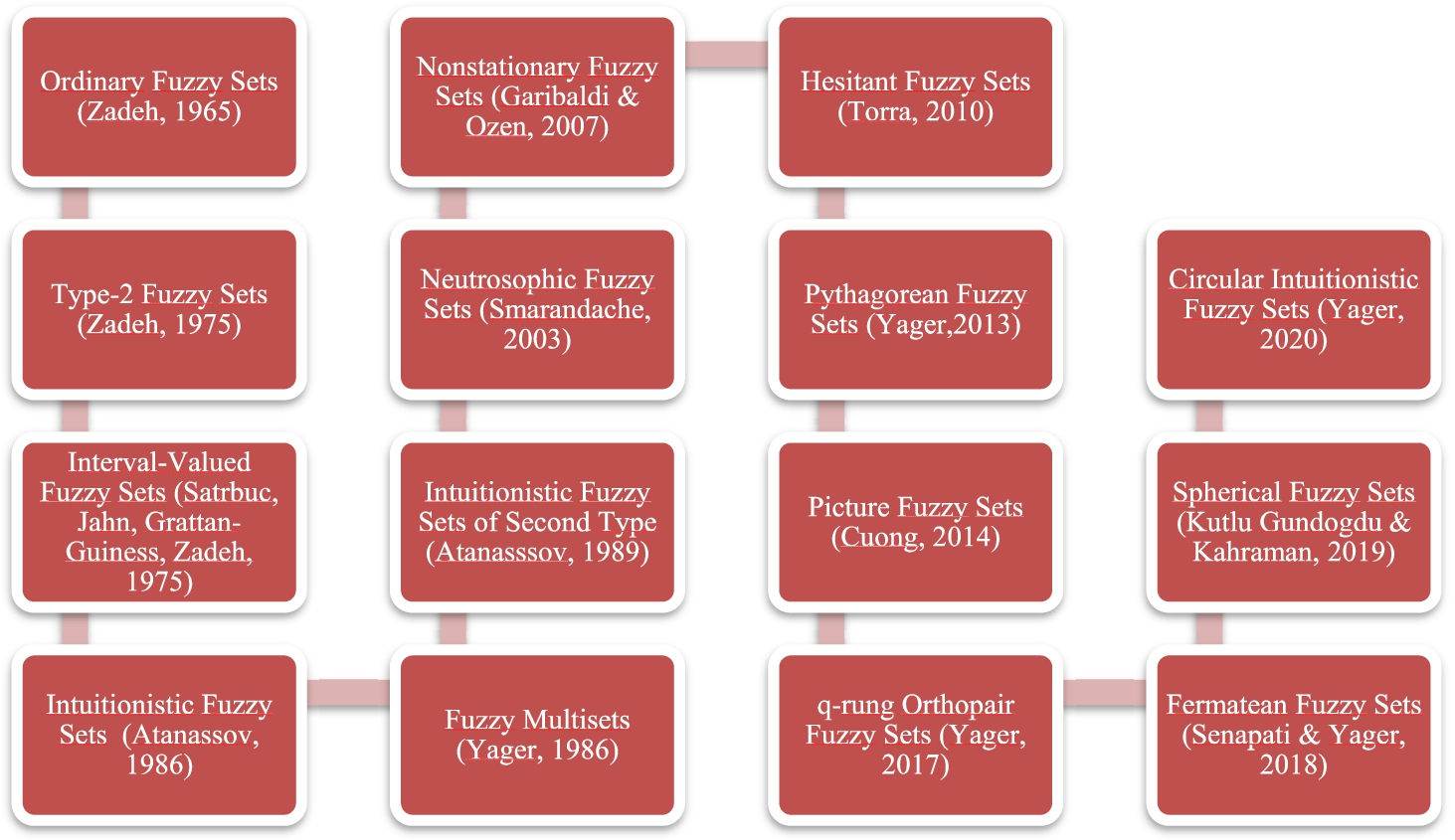
Consideration of vagueness in the definition of membership functions is an old issue first time handled by Zadeh (1975). Type-2 fuzzy sets, interval-valued fuzzy sets and hesitant fuzzy sets try to incorporate this vagueness into their models. Similarly, Atanassov (2020) developed C-IFSs as an extension of IFSs in order to handle this issue. A circle around the single valued intuitionistic fuzzy number is defined by a radius r. In this study, the main aim and contribution is to introduce a new extension of PW analysis with interval-valued intuitionistic fuzzy sets (IVIF) and C-IFSs.

The estimation of investment parameters generally involves uncertainty and vagueness. This uncertainty is best handled by the fuzzy set theory in the literature. Most of the publications on fuzzy engineering economics employ ordinary fuzzy sets. However, there are some papers employing intuitionistic fuzzy sets, Pythagorean fuzzy sets, neutrosophic sets, hesitant fuzzy sets, type-2 fuzzy sets, and fermatean fuzzy sets in the investment analysis techniques. In the following, we present the review results on fuzzy PW analysis. Kahraman et al. (1995) presented financial models based on some discounting techniques such as fuzzy equivalent uniform annual worth and fuzzy PW analyses. Iliev and Fustik (2003) used fuzzy net present analysis in evaluating hydroelectric projects based on fuzzy profitability index. This model was created by using triangular fuzzy numbers. Omitaomu et al. (2004) used present value model with triangular fuzzy numbers in the evaluation of information system projects. Kahraman et al. (2004) proposed fuzzy present worth based fuzzy models for quantifying manufacturing flexibility. The fuzzy model included uncertain cash flows and discount rates that were handled as triangular fuzzy numbers. Kahraman and Kaya (2008) studied equivalent fuzzy annual worth analysis in investment assessment. Matos and Dimitrovski (2008) introduced studies using equivalent uniform annual worth analysis with trapezoidal fuzzy numbers. Kuchta (2008) presented fuzzy PW analysis applications in optimization. Dimitrovski and Matos (2008) introduced uncorrelated and correlated cash flows in fuzzy PW analysis with arithmetic operations. Shahriari (2011) proposed a fuzzy net present value methodology that uses triangular fuzzy numbers in investment analysis. Kahraman et al. (2015) presented hesitant and intuitionistic fuzzy present and annual worth analyses. These developed methods use triangular hesitant fuzzy data, triangular intuitionistic fuzzy data, interval-valued hesitant data, and interval-valued intuitionistic fuzzy data in engineering economic problems for better forecasting. Kahraman et al. (2018a) introduced Pythagorean PW analysis for investment decision problems. Sarı and Kahraman (2017) applied net PW analysis with type-2 fuzzy sets. One of the PW analysis papers which uses neutrosophic sets belongs to Aydin et al. (2018). They introduced simplified neutrosophic PW analysis. The investment parameters’ membership functions were defined by neutrosophic sets. The method was compared with classical and intuitionistic fuzzy PW analysis. Kahraman et al. (2018b) proposed ordinary fuzzy PW analysis, type-2 fuzzy PW analysis, intuitionistic fuzzy PW analysis, and hesitant fuzzy PW analysis in wind energy investment analysis. Aydin and Kabak (2020) developed future and present worth techniques in investment analysis with neutrosophic sets. Sergi and Sari (2021) extended PW analysis with fermatean fuzzy sets. The literature review is summarized in Table 1.

This paper is organized as follows: In Section 2, preliminaries of IVIF and C-IFSs are given. In Section 3, interval-valued intuitionistic fuzzy PW analysis extension is given. In Section 4, circular intuitionistic fuzzy PW analysis extension is given. In Section 5, a real life problem is solved with these proposed extensions in order to show the applicability of these proposed methods with a sensitivity analysis. Finally, conclusion is given in Section 6 with future suggestions.

2Preliminaries

In this section, the preliminaries of interval-valued intuitionistic fuzzy sets and C-IFSs are given with definitions.

2.2Circular Intuitionistic Fuzzy Sets

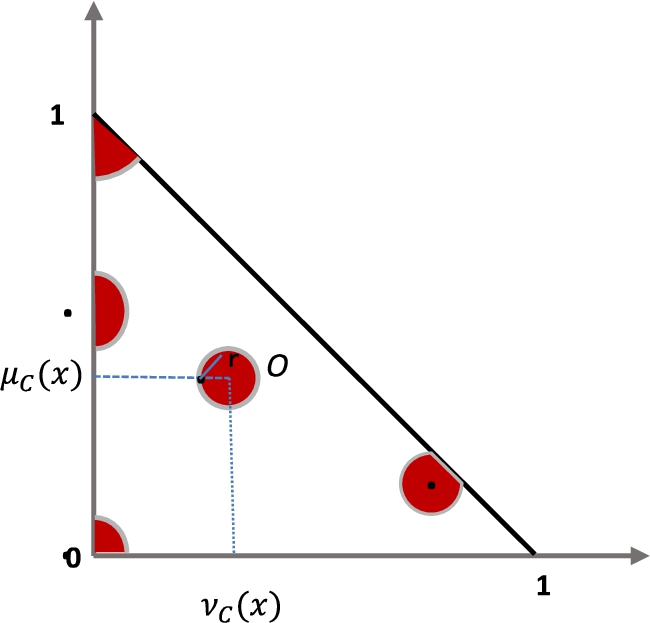
C-IFSs are introduced by Atanassov (2020) as an extension of the IFSs which each element is represented by a circle with radius r. C-IFSs is defined in Definition 8.

Definition 8.

Let E be a fixed universe. A C-IFS Cr in E is an object having the form as in Eq. (9).

(9)

Cr={⟨x,μC(x),νC(x);r⟩|x∈E},

where

(10)

0⩽μC(x)+νC(x)⩽1

and r∈[0,1] is a radius of the circle around each element x∈E, is called Circular-IFS and the functions μC:E→[0,1] and υC:E→[0,1] represent the degree of membership and the degree of non-membership of the element x∈E to the set C⊆E, respectively.

The degree of indeterminacy is calculated as in Eq. (11):

(11)

πC(x)=1−μC(x)−νC(x).

In contrast with the standard IFSs, where each element is represented by a point in the intuitionistic fuzzy interpretation triplet, each element in C-IFSs is represented by a circle with centre ⟨μC(x),νC(x)⟩ and radius r.

Definition 9.

In an IFS Cj, let intuitionistic fuzzy pairs have the form {⟨mj,1,nj,1⟩,⟨mj,2,nj,2⟩,…}. j is the number of IFSs Cj, each including kj IF pairs. Then, C-IFSs is calculated as follows. The arithmetic average of the IF pairs is given as in Eq. (12):

(12)

⟨μ(Ci),ν(Ci)⟩=⟨∑s=1kjmi,jkj,∑s=1kjni,jkj⟩,

where kj is the number of intuitionistic fuzzy pairs in Cj.

Then, the radius of the ⟨μ(Cj),ν(Cj)⟩ is the maximum of the Euclidean distances given as in Eq. (13):

(13)

rj=max1⩽j⩽kj(μ(Cj)−mi,j)2+(ν(Cj)−ni,j)2.

For universe W={C1,C2,…}, the C-IFS can be built as in Eq. (14):

(14)

Ar={⟨Cj,μ(Cj),ν(Cj);r⟩|Cj∈W}={⟨Cj,Or(μ(Cj),ν(Cj))⟩|Cj∈W}.

Definition 10.

Let’s have five circle forms as it is shown in Fig. 2, where the basic geometric interpretation of C-IFS is given.

(15)

L∗={⟨a,b⟩|a,b∈[0,1]&a+b⩽1}.

Therefore, Cr can be rewritten in the form

(16)

Cr∗={⟨x,O(μC(x),νC(x));r⟩|x∈E},

where O is a function representing a circle, whose radius is r and whose centre is (μC(x),νC(x)).

O(μC(x),νC(x))=⟨a,b⟩|a,b∈[0,1],(μC(x)−a)2+(νC(x)−b)2⩽r∩L∗=⟨a,b⟩|a,b∈[0,1],(μC(x)−a)2+(νC(x)−b)2⩽r,a+b⩽1.

C-IFSs is an extension of the standard IFSs and each standard IFS has the form C=C0={⟨x,O(μC(x),νC(x));0⟩∣x∈E}, therefore, C-IFS with r>0 can’t be represented by a standard IFS.

Fig. 2

C-IFS geometrical representation.

Definition 11.

Let C1=⟨μC1(x),νC1(x);r1⟩ and C2=⟨μC2(x),νC2(x);r2⟩ be two circular intuitionistic fuzzy numbers. The operations given here are based on the minimum and maximum of the radiuses separately since they give the results with minimum and maximum level of uncertainty, respectively. Smaller radius represents smaller vagueness whereas larger radius represents larger vagueness for IF pairs. Their operations can be described in Eqs. (17)–(24):

(17)

C1∩minC2={⟨x,min(μC1(x),μC2(x)),max(νC1(x),νC2(x));min(r1,r2)⟩|x∈E},

(18)

C1∩maxC2={⟨x,min(μC1(x),μC2(x)),max(νC1(x),νC2(x));max(r1,r2)⟩|x∈E},

(19)

C1∪minC2={⟨x,max(μC1(x),μC2(x)),min(νC1(x),νC2(x));min(r1,r2)⟩|x∈E},

(20)

C1∪maxC2={⟨x,max(μC1(x),μC2(x)),min(νC1(x),νC2(x));max(r1,r2)⟩|x∈E},

(21)

C1⊕minC2={⟨x,μC1(x)+μC2(x)−μC1(x)∗μC2(x),νC1(x)∗νC2(x);min(r1,r2)⟩|x∈E},

(22)

C1⊕maxC2={⟨x,μC1(x)+μC2(x)−μC1(x)∗μC2(x),νC1(x)∗νC2(x);max(r1,r2)⟩|x∈E},

(23)

C1⊗minC2={⟨x,μC1(x)∗μC2(x),νC1(x)+νC2(x)−νC1(x)∗νC2(x);min(r1,r2)⟩|x∈E},

(24)

C1⊗maxC2={⟨x,μC1(x)∗μC2(x),νC1(x)+νC2(x)−νC1(x)∗νC2(x);max(r1,r2)⟩|x∈E}.

Aggregation of the intuitionistic fuzzy numbers is realized by using Definition 12.

Definition 12.

Let A˜i=(μA˜i,νA˜i) (i=1,2,…,n) be a set of IFNs and w=(w1,w2,…,wn)T be weight vector of A˜i with ∑i=1nwi=1, then an intuitionistic fuzzy weighted geometric (IFWG) operator is given in Eq. (25) (Xu and Yager, 2006):

(25)

IFWG(A˜1,A˜2,…,A˜n)=(∏i=1nμA˜iwi,(1−∏i=1n(1−υA˜i)wi)).

3Interval-Valued Intuitionistic Fuzzy PW Analysis

The parameters of FC, SV, AB, AC, i, and n are given with interval-valued intuitionistic fuzzy values which are expressed by circular intuitionistic fuzzy numbers (IVFN) in Eqs. (26)–(31):

Aggregation of IVIF numbers is performed by Eq. (25). Later, parameter values can be computed by multiplying the defuzzified values of membership functions with parameter values. The score function and defuzzification function of memberships are used for obtaining crisp values for each parameter. After defuzzification process the present worth is obtained by Eq. (32):

4Circular Intuitionistic Fuzzy PW Analysis

The parameters of FC, SV, AB, AC, i, and n are given by circular intuitionistic fuzzy numbers (CIFN) as in Eqs. (33)–(38):

In this method, aggregation of IFSs is performed by Eq. (25).

Later, parameter values can be computed by multiplying the defuzzified values of membership functions with parameter values. The score function and defuzzification function of memberships are used for obtaining crisp values for each parameter. After defuzzification process the present worth is obtained by Eq. (39):

5Application

A water treatment device will be purchased by a local municipality. The interval-valued intuitionistic fuzzy data of this device are given in Table 2. Three experts having different experiences assign three different intervals for each of investment parameters and determine their interval-valued intuitionistic fuzzy membership and non-membership degrees. w values in Table 2 represent the weights of experts based on their experience levels.

We apply two levels of aggregation: Aggregation within each parameter and aggregation between parameters. In Table 3, the aggregated membership functions and expected weighted interval-values within each parameter are given. Then, aggregation between parameters is applied. For both of aggregation levels, Eq. (4) is used.

Expected value calculations are given in Table 4. For instance, the value [218,650;259,325] is calculated as follows: