A New Hybrid Fuzzy Multi-Criteria Decision Methodology for Prioritizing the Antivirus Mask Over COVID-19 Pandemic
Abstract
During the COVID-19 pandemic, masks have become essential items for all people to protect themselves from the virus. Because of considering multiple factors when selecting an antivirus mask, the decision-making process has become more complicated. This paper proposes an integrated approach that uses F-BWM-RAFSI methods for antivirus mask selection process with respect to the COVID-19 pandemic. Finally, sensitivity analysis was demonstrated by evaluating the effects of changing the weight coefficients of the criterion on the ranking results, simulating changes in Heronian operator parameters, and comparing the obtained solution to other MCDM approaches to ensure its robustness.
1Introduction
The COVID-19 pandemic, which is the result of the SARS-CoV-2 virus, has spread around the world in a short time since its emergence in Wuhan, China, mobilized international health authorities and its effect continues to be serious. The studies and reports published by the World Health Organization on the pandemic are followed with interest and concern by the whole world.
Studies examining the effects of the virus on China’s and the world’s economy have revealed that the virus caused a loss of approximately 62 billion dollars to the Chinese economy and more than 280 billion dollars to the world economy in the first quarter (Ayittey et al., 2020).
In line with the instructions of the World Health Organization (WHO) against this pandemic that threatens international public health, national administrations also take various measures to protect public health and to get rid of the epidemic with the least damage. However, despite the strictness of the measures, the continuous increase in death cases due to the impact of the epidemic and the epidemic itself causes serious concerns at the international level.
When the reports and scientific studies published by the WHO were examined, it was determined that the demand for healthcare materials such as protective masks and gloves has increased worldwide since the outbreak occurred and that the prices of related healthcare materials also increased significantly due to the increase in demand (Mahase, 2020).
Fuzzy multi criteria decision-making (MCDM) methods are commonly used for decision-making in medical and healthcare fields (Kumar et al., 2020; Omrani et al., 2018; Otay et al., 2017; Reddy et al., 2014; Rouyendegh et al., 2019; Stević et al., 2020; Sumrit, 2020; Thakur and Ramesh, 2017; Zare et al., 2019). Yucesan and Gul (2020) proposed an integrated fuzzy MCDM framework using the Pythagorean fuzzy-AHP and TOPSIS methods to evaluate hospital service quality. Lee et al. (2017) aimed to explore a hybrid evaluation model based on fuzzy AHP and fuzzy TOPSIS methods for Taiwan’s medical device manufacturers. Nilashi et al. (2019) proposed a hybrid fuzzy MCDM method based on the Decision-Making Trial and Evaluation Laboratory (DEMATEL) and fuzzy Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) to reveal the interrelationships among the factors influencing the development of medical tourism in Malaysia and to find the relative importance of these factors. Abdel-Basset et al. (2019) offer a group decision-making approach for estimating the Smart Medical Devices (SMDs) selection process using the TOPSIS method. Gao et al. (2020) developed a group decision-making method based on q-rung interval-valued orthopair fuzzy VIse KriterijumsaOptimizacija I Kompromisno Resenje (VIKOR) model for selecting the supplier of medical consumption products. Yang et al. (2020) developed the MCDM method based on SpNoF Bonferroni mean operator and the weighted Bonferroni mean operator for selecting an antivirus mask during the COVID-19 pandemic. Torkayesh et al. (2021) proposed a combination model based on best-worst method (BWM) and level based weight assessment (LBWA) to estimate the rating of healthcare parameters and integrated compromise solution (CoCoSo) method for selecting the optimal healthcare sector of eastern European countries. Ecer and Pamucar (2021) suggested a Measurement of Alternatives and Ranking according to the Compromise Solution (MARCOS) approach using intuitionistic fuzzy sets to score healthcare insurance organizations in the COVID-19 period. Ozsahin et al. (2021) examined 24 various migraine medicines that help to regulate productive migraine drugs in overall using TOPSIS method.
It can be clearly seen that the integrated MCDM methods based on fuzzy set theory are widely used in the fields of medical and healthcare. However, there are limited studies about the selection of personal protective equipment, especially antivirus masks, during the COVID-19 pandemic.
This paper proposes an integrated approach that uses fuzzy BWM and Ranking of Alternatives through Functional mapping of criterion sub-intervals into a Single Interval (F-BWM-RAFSI) methods for antivirus mask selection process with respect to the COVID-19 pandemic. Due to the vagueness of data and the ambiguity of decision-maker, the involvement of the fuzzy concept into MCDM can obtain much more reliable results in real-life applications. The F-BWM approach which combines the fuzzy set theory and BWM can provide more consistent comparisons. It has been demonstrated that the BWM method performs significantly better than other MCDM methods such as AHP in terms of consistency index, minimum violation, total deviation and conformity (Rezaei, 2015). These advantages are indicated below (Stević et al., 2018; Zolfani et al., 2019; Ecer and Pamucar, 2020; Luo et al., 2020): (i) AHP requires
The rest of the paper is presented as follows: Section 2 presents the contribution and novelty of this study. Section 3 introduces the detailed algorithm for hybrid F-BWM-RAFSI methodology. Section 4 gives an illustrative example of antivirus medical mask selection. The sensitivity analysis and the validation of the proposed model are given in Section 5. Finally, Section 6 summarizes the conclusion, limitation and directions for future study.
2Contribution and Novelty of the Paper
The primary transmission route of COVID-19 is respiratory droplets and contact. During the COVID-19 pandemic, personal protective equipment like antivirus masks has become essential items for medical staff and people to work and travel. Therefore, selection of the personal protective equipment such as antivirus masks are especially important. This paper focuses on the selection process of the antivirus masks under the COVID-19 pandemic situation and aims to address the following research questions (RQs):
RQ1: Which criterion is more important for selecting an antivirus mask?
RQ2: How to effectively evaluate the antivirus masks through the subjective judgment of group experts in medicine sector?
RQ3: How to build a decision-making approach that evaluates the antivirus mask alternatives?
To answer these RQ’s, this study proposes a new hybrid MCDM method that will be addressed here for the first time in order to be applied to a medical mask selection problem. One of the novel MCDM methods, called RAFSI method under a fuzzy environment, can be easily used for solving complex problems. The novelties found in the methodological application of this study are as follows: 1) A new extension of the BWM and RAFSI MCDM model using fuzzy sets is introduced in this paper. The model provides a more objective experts’ evaluation of the criteria and alternatives in a subjective environment. The present methodology enables the evaluation of alternative solutions despite dilemmas in the decision-making process and a lack of quantitative information. 2) Using fuzzy sets in the RAFSI methodology instead of using a crisp value, the structure of the given data is exclusively used. In this way, the uncertainties present in the data are used, thus improving the objectivity of the decision process. According to the authors, the application of fuzzy numbers for the purpose of exploiting the uncertainty that occurs during criteria and alternatives group evaluation using the BWM-RAFSI method has not been considered in the literature so far. Fuzzy numbers allow for the transformation of the uncertainties and inaccuracies present during the evaluation of alternatives and criteria pairwise comparisons.
In sum, the contributions of this paper can be highlighted as follows:
• It presents a framework that helps the selection of personal protective equipment such as antivirus masks during COVID-19 pandemic.
• It performs a comprehensive evaluation of the antivirus mask selection process through a new MCDM method F-BWM-RAFSI.
• Although the RAFSI technique is a powerful decision-making tool, it cannot express fuzziness and ambiguity information. Combined with the fuzzy sets, we posit the fuzzy RAFSI model, which can better describe decision-makers’ evaluation information.
• We extend assessments of decision-makers to the fuzzy sets to extract criteria weights and rank the alternatives.
• F-BWM-RAFSI approach is suggested to apply to multiple criteria group decision making (MCGDM) problems. It presents a real case study with respect to the evaluation of the antivirus mask alternatives; and
• It performs a sensitivity analysis to validate the proposed quantitative evaluation process.
3Preliminaries
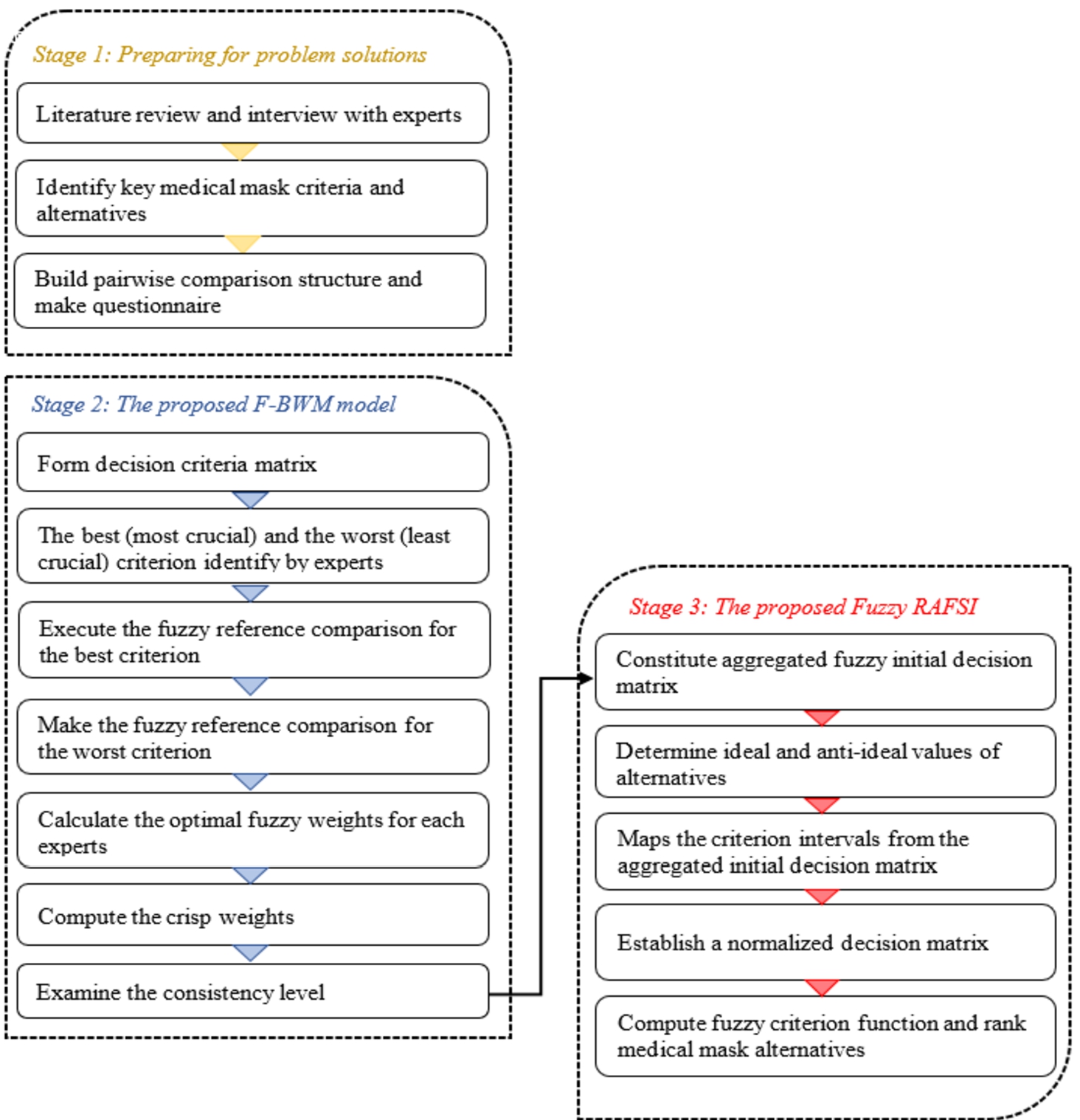
This study proposes a new hybrid MCDM method that will be addressed here for the first time in order to be applied to a medical mask selection problem. Rezaei (2015) proposed BWM, a newly developed MCDM approach for weighting criteria and alternatives based on pairwise comparisons. The fuzzy logic extension of BWM method proposed by Rezaei (2015), a newly developed MCDM approach for weighting criteria and alternatives based on pairwise comparisons, can handle uncertainties and vagueness of decision-makers’ opinions in the comparison matrix better. Consequently, this feature of F-BWM which makes the linguistic evaluations of decision-makers more effective and more flexible, makes it superior to other similar methods. RAFSI (Pamučar and Savin, 2020; Žižović et al., 2020) is a novel method, which can significantly eliminate rank reversal problems with a simple mathematical formulation. RAFSI in an uncertain environment (RAFSI-F) has been improved and adapted to deal with inaccuracy and uncertainty into antivirus mask selection problem. Consequently, a combined method of F-BWM-RAFSI seems to be an applicable hybrid MCDM model that can increase the validity of the model in the real-life problem. The general framework of the integrated model is demonstrated in Fig. 1.
Fig. 1
Systematic steps of the integrated methodology.
3.1Triangular Fuzzy Numbers
The fuzzy set theory was introduced by Zadeh in 1965 for better reflecting on human judgments and assessment in the decision-making process. Real case decision-making problems include fuzziness and uncertainty, as decision, goals, constraints, decision-maker opinions are not completely known. For that reason, group decision maker problems practically have used fuzzy numbers (Zadeh, 1965). In this study, we prefer to use a triangular fuzzy number that can be defined as
Definition 1.
Let
Fig. 2
Triangular fuzzy numbers.
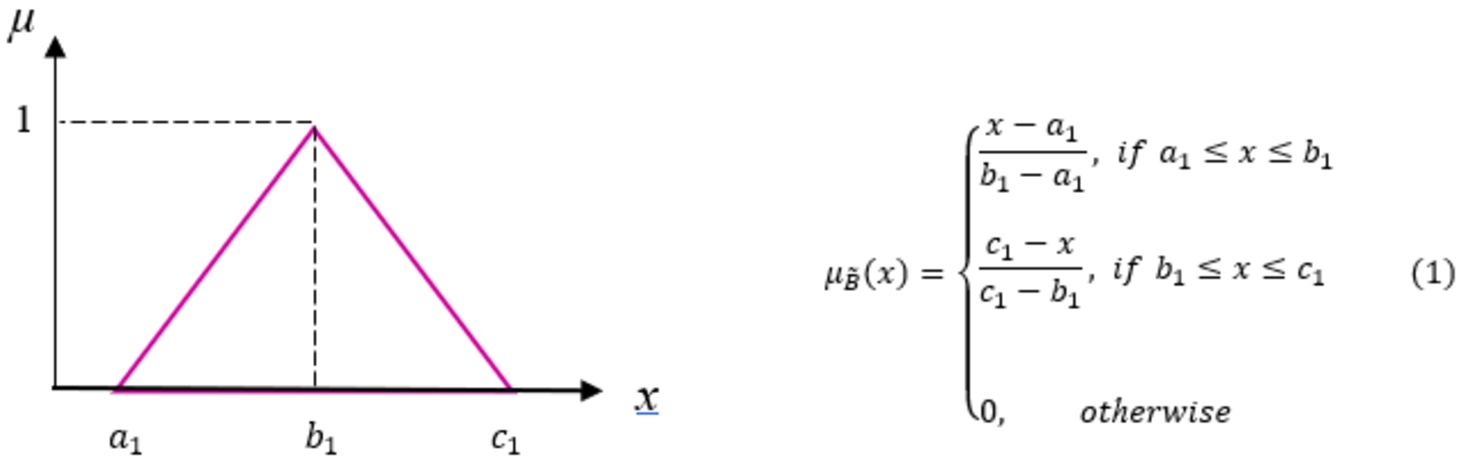
Table 1
Some triangular fuzzy operations (Carlsson and Fullér, 2001).
| Summing operation |
(2) |
| Subtracting operation |
(3) |
| Multiplication operation |
(4) |
| Division operation |
(5) |
Also, the mathematical operations of the triangular fuzzy number are formulated in Table 1.
Assume
3.2Fuzzy Best Worst Method
Fuzzy BWM method have been applied successfully in various areas such as evaluating the sustainable supplier selection criteria (Ecer and Pamucar, 2020; Pamučar and Savin, 2020; Amiri et al., 2021), identifying challenges and barriers for development of solar energy (Mostafaeipour et al., 2021), evaluating driver behaviour factors (Muravev and Mijic, 2020; Malakoutikhah et al., 2021), weighting the risk parameters of FMEA (Tian et al., 2018) plant site selection process (Luo et al., 2020), environmental performance evaluation (Liu et al., 2021; Dwivedi et al., 2021), evaluating the green supplier selection criteria (Wu et al., 2019), evaluating traffic parameters (Subotić et al., 2020) and hospital performance evaluation (Liao et al., 2019).
In addition, BWM has been incorporated with a different type of fuzzy sets such as interval type-2 fuzzy number (Wu et al., 2019; Qin and Liu, 2019), intuitionistic fuzzy sets (Tian et al., 2018; Mou et al., 2017), triangular fuzzy numbers (Guo and Zhao, 2017; Hafezalkotob and Hafezalkotob, 2017; Ecer and Pamucar, 2020), Z-numbers (Aboutorab et al., 2018), hesitant fuzzy numbers (Mi and Liao, 2019; Yazdani et al., 2021; Liao et al., 2019), rough-fuzzy approach (Chen and Ming, 2020), Pythagorean hesitant fuzzy sets (Liu et al., 2019).
The fuzzy pairwise comparisons are applied based on the linguistic terms given in Table 1. Then, the linguistic evaluations are transformed into triangular fuzzy numbers. The fuzzy comparison matrix (
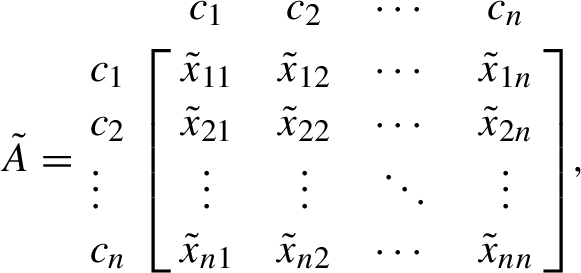
Step 1. Build the decision criteria system. The decision criteria system consists of a set of decision criteria. n decision criteria set is presented as follows:
Step 2. Decide the best and the worst criterion. In this step, the best and the worst criterion is decided by experts based on the constructed criteria set in Step 1. The best and the worst criterion are denoted as
Step 3. Implement the fuzzy reference comparisons for the best criterion
Step 4. Do the fuzzy reference comparisons for the worst criterion
Step 5. Determine the optimal fuzzy weights
(6)
(7)
Considering
(8)
The GMIR formula is as follows:
(9)
(10)
Table 2
Consistency index values for F-BWM (Guo and Zhao, 2017).
| Linguistic terms | Equally important (EI) | Weakly important (WI) | Fairly important (EI) | Very important (VI) | Absolutely important (AI) |
| CI | 3 | 3.8 | 5.29 | 6.69 | 8.04 |
3.3Fuzzy RAFSI Evaluation Method
Ranking of Alternatives through Functional mapping of criterion subintervals Into a Single Interval (RAFSI) method (Žižović et al., 2020) is based on defining ideal and anti-ideal reference points and defining the relationship between alternatives concerning defined reference points. The relationships between criterion values and reference points are defined using criterion functions that map criterion sub-intervals into a single criterion interval. This achieves two key advantages of the RAFSI method (Alosta et al., 2021; Božanić et al., 2021): i) A data standardization algorithm that allows the translation of data from the initial decision matrix into an interval that is suitable for rational decision making; and ii) The mathematical formulation of the RAFSI method eliminates the rank reversal problem, as one of the significant shortcomings of many traditional MCDM methods. The following section shows the extension of the RAFSI method to a fuzzy environment (RAFSI-F). By applying fuzzy sets, the RAFSI algorithm has been improved and adapted to handle the inaccuracies and uncertainties that arise when solving real-world problems. The algorithm of the RAFSI-F method is realized through four steps:
Step 1: Formation of an aggregated fuzzy initial decision matrix. Suppose that the evaluation of alternatives from the set
(11)
Since we have a group decision-making model, we obtain k experts’ initial decision-making matrices
(12)
Step 2: Mapping the elements of the initial decision matrix into criterion intervals. For each criterion
(13)
Thus, we obtain a standardized decision matrix
Step 3: Formation of a normalized decision matrix
(14)
Step 4: Calculation of fuzzy criterion functions of alternatives
(15)
4Case Study of Antivirus Mask Selection
COVID-19 is an infectious disease that primarily spreads out between humans through direct contact with an infected person or their respiratory droplets. Respiratory droplets are generated by breathing, speaking, coughing, and sneezing. Droplet nuclei are respiratory droplets that dry quickly after expiration and shrink to a diameter of less than 5 m. Droplet nuclei remain suspended in air and can travel over long distances. Goggles and respiratory protection are recommended for airborne prevention; a medical mask is needed to avoid COVID-19 infection from spreading via the air (Azap and Erdi˙nç, 2020). To prevent the transmission of COVID-19 infection, wearing masks is one of the most protective measures in order to limit the spread of airborne particles containing the virus (Bir and Widmar, 2021).
This study presents integrated methods that use fuzzy BWM and RAFSI-F approach-based framework for mask selection with respect to COVID-19 disease. We have five experts who are caring for coronavirus patients in the hospital in Istanbul and Bursa which are two cities with the highest population density in Turkey. The details of experts are indicated in Table 3.
Table 3
Expert information.
| Experts | Profession | Experience | Department | Location |
| EX1 | Doctor | 5 years | Public Health | Istanbul |
| EX2 | Doctor | 3 years | Internal Medical | Istanbul |
| EX3 | Doctor | More than 10 years | Infectious diseases and clinical microbiology | Istanbul |
| EX4 | Doctor | More than 15 years | Infectious diseases and clinical microbiology | Bursa |
| EX5 | Doctor | More than 15 years | Infectious diseases and clinical microbiology | Bursa |
The F-BWM was applied to determine the relative weight scores of the antivirus mask selection criteria and then, the most favoured mask is selected by the RAFSI-F approach using the evaluated weights. For this purpose, the criteria determined in the selection of medical masks and short description were obtained from expert opinions and literature review, mask selection criteria are identified in Table 4.
Table 4
Mask selection criteria.
| Code | Criteria | Brief description |
| C1 | Leak age rate (fitting rate for face) | Covers the face perfectly, does not stretch or sag |
| C2 | Quality of raw material | Manufactured using non-woven fabric material, its pores should be small and it should be made in accordance with health procedure |
| C3 | Reusability | Has two or more layer washable |
| C4 | Breathability | Allows comfortable breathing |
| C5 | Use of hypo-allergenic materials | Contains non-harmful particles and carcinogen substance |
| C6 | Easy to wear and take off | Conformity to the face |
| C7 | Filtration rate | Preserves the respiratory system against the viruses |
| C8 | Tear and deformation resistant | Has a durable and undeformed material |
Six different types of medical masks including basic cloth face mask, surgical face mask, single use face mask, particulate respirators (N95 and above), full face respirator and full-length face shield and their descriptions are also shown in Table 5 (Health, 2021).
Table 5
Medical mask alternatives.
| Code | Figure | Name | Statement |
 | Basic cloth mask | This is a typical face mask recommended for public to avoid spreading coronavirus, everyday version of a face mask. | |
 | Surgical face mask | A variation of this face mask is worn by medical professionals who are presently doing COVID-19 drive-thru testing. It’s a mask that doctors and nurses use. The safety factor is pretty high, and it has good antibacterial and antiviral resistance. | |
 | Single use face mask | This is a disposable mask that prevent leaks from nose and mouth. However, it not intended for medical use. It is made of a single-use plastic product. | |
 | Particulate respirators (N95 and above) | This kind of face mask is essential for medical staff and first responders. When the user inhales, it filters out both large and micro particulates, providing better protection than a medical mask. | |
 | Full face respirator | A full-face respirator is a type of mask that is commonly used in home basic repairs and be a good choice for providing coronavirus assistance. However, it can cause some breathing problems or respiratory issues. | |
 | Full-length face shield | This is a flimsier, plastic variant of the glass masks used on welders. It has a padded headband that covers the full face from brow to chin. |
4.1Application of Fuzzy BWM Model
Step 1: Eight criteria for medical selection are shown in Table 3.
Step 2: According to F-BWM, evaluations of experts in linguistic terms are used to obtain the importance weights of antivirus mask criteria, the best criteria, the worst criteria, the best to other comparison matrix, and the other to worst comparison matrix of each expert (EX) are given in Table 6 and Table 7 by using linguistic terms, respectively.
Table 6
Best criteria and Best to Other (BO) vectors identified by experts.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | ||
| EX 1 | C7 | WI | AI | FI | VI | AI | AI | EI | VI |
| EX 2 | C7 | WI | FI | VI | WI | WI | AI | EI | VI |
| EX 3 | C7 | EI | VI | FI | FI | VI | FI | EI | FI |
| EX 4 | C7 | WI | WI | WI | WI | FI | AI | EI | WI |
| EX 5 | C7 | FI | FI | AI | VI | VI | FI | EI | VI |
Step 3: To take evaluations of Expert 1, as an example, the fuzzy preferences of the best criterion over all the criteria can be obtained with respect to Table 3.
Table 7
Worst criteria and Other to Worst (OW) vectors identified by experts.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | ||
| EX 1 | C6 | FI | WI | FI | WI | WI | EI | AI | WI |
| EX 2 | C6 | VI | FI | WI | VI | WI | EI | AI | WI |
| EX 3 | C5 | AI | FI | FI | VI | EI | FI | VI | FI |
| EX 4 | C6 | FI | FI | FI | FI | WI | EI | AI | FI |
| EX 5 | C3 | WI | WI | EI | FI | WI | WI | AI | WI |
Step 4: The fuzzy preferences of all the criteria over the worst criterion can be presented in Table 4.
Step 5: Then, for obtaining the optimal fuzzy weights of all the criteria, the nonlinearly constrained model is established as follows in Eq. (7).
Step 6: The following nonlinearly constrained optimization problem is obtained using represented by crisp numbers as in Eq. (8).
(16)
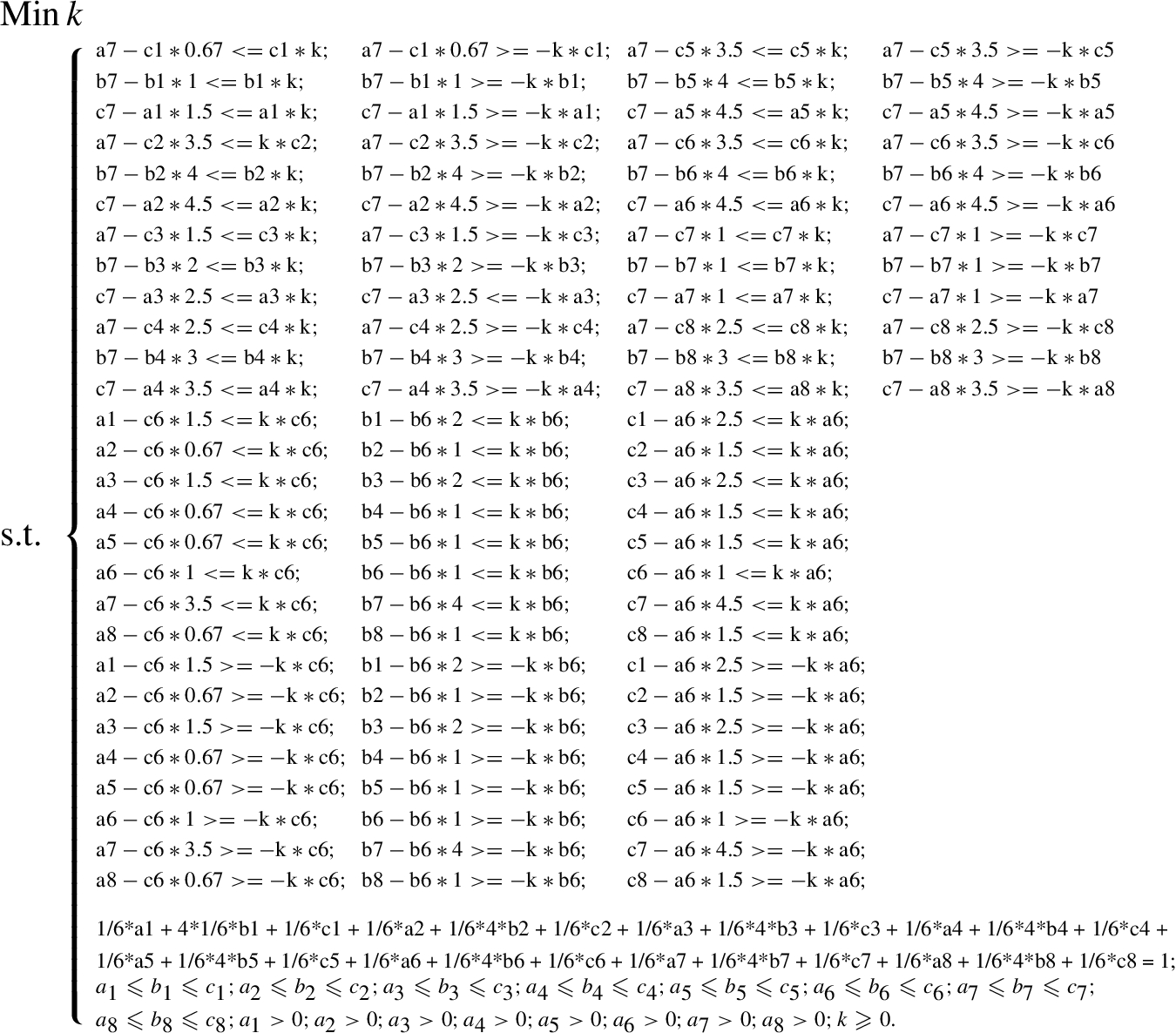
Solving above model by using LINGO 18.0 software, the optimal fuzzy weights with regards to EX1 can be calculated, which are:
Then, all F-BWM steps have been implemented for each expert. Results of all optimal fuzzy weights and average optimal fuzzy weights (AOFW) of eight criteria are given in Table 8. The average crisp weights of eight criteria are illustrated in Fig. 3, respectively. Heronian function, Eq. (12) was used for aggregation of fuzzy weight coefficients.
Table 8
Optimal fuzzy weights for five experts.
| EX1 | EX2 | EX3 | EX4 | EX5 | AOFW | |
According to the results of the F-BWM model, among the antivirus mask criteria, “Filtration rate (
Step 7: The consistency ratio is an important indicator for calculating the consistency of pairwise comparisons for all experts’ opinions. Its closeness to zero indicates its higher consistency. The consistency ratio is computed for pairwise comparisons that indicate high consistency in paired comparisons, as shown in Table 9. The consistency ratio for each expert is close to zero. Therefore, the weights obtained for the criteria are confirmed.
Fig. 3
Average crisp weight for each criterion.
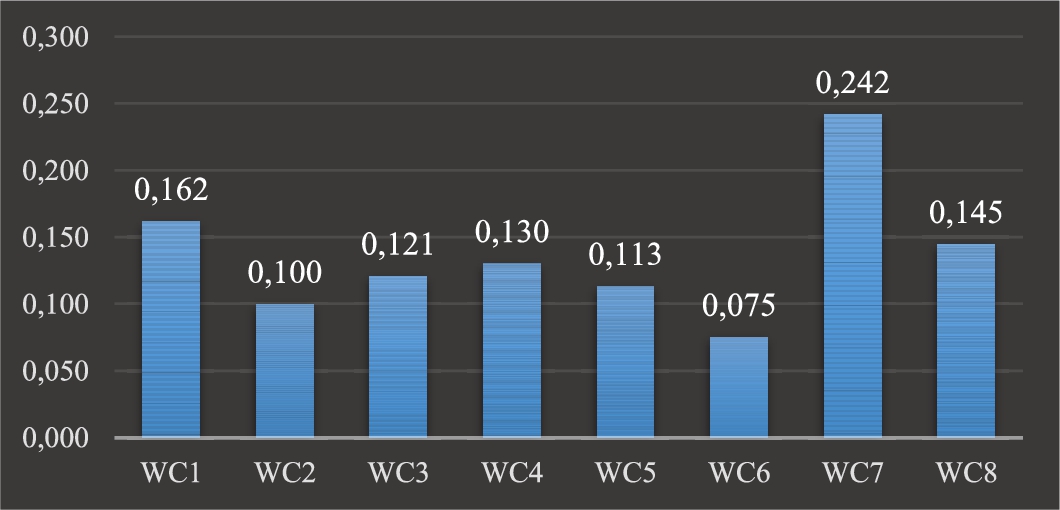
Table 9
Consistency ratio.
| CI | CR | ||
| EX1 | 0.4494 | 8.040 | 0.055 |
| EX2 | 0.7912 | 8.040 | 0.098 |
| EX3 | 0.6093 | 6.690 | 0.091 |
| EX4 | 0.6232 | 8.040 | 0.077 |
| EX5 | 0.5000 | 8.040 | 0.062 |
4.2Application of Fuzzy RAFSI Model
After defining the weight coefficients of the criteria, five experts evaluated the alternatives
Table 10
Fuzzy linguistic scale.
| Linguistic terms | Membership function |
| Very Poor (VP) | (1, 1, 1) |
| Poor (P) | (1, 2, 3) |
| Medium Poor (MP) | (2, 3, 4) |
| Medium (M) | (3, 4, 5) |
| Medium High (MH) | (4, 5, 6) |
| High (H) | (5, 6, 7) |
| Very High (VH) | (6, 7, 8) |
| Extremely High (EH) | (7, 8, 9) |
| Absolutely High (AH) | (8, 9, 9) |
After evaluating the alternatives, the experts’ correspondence matrices were obtained and are shown in Table 11.
Table 11
The experts’ correspondence matrices.
| Criteria | |||
| VP; P; M; P; MH | VP; P; MP; MH; M | VP; P; M; H; M | |
| MH; MH; MP; MP; P | H; M; M; MH; VH | MP; MP; MP; MP; VH | |
| H; MH; VP; AH; EH | VP; VP; VP; VP; VP | VP; VP; VP; VP; VP | |
| H; MH; VH; MH; EH | M; M; VH; MP; VH | MH; MH; VH; MP; VH | |
| M; MH; MH; M; M | VH; M; EH; VH; EH | MH; M; EH; MP; EH | |
| EH; VH; EH; EH; VH | VH; M; EH; EH; AH | H; M; MH; VH; AH | |
| MP; MP; P; P; MP | EH; M; MP; MH; VH | VP; P; P; MH; VH | |
| H; M; P; H; EH | MP; MP; P; MP; MH | MP; MP; VP; MP; MH |
| Criteria | |||
| VP; VP; VP; P; P | VP; P; VP; P; P | VP; MP; P; VH; MH | |
| MH; M; EH; EH; EH | H; MH; EH; AH; EH | VP; VP; H; MP; EH | |
| M; M; M; MH; VP | EH; VH; EH; AH; VH | VP; M; VH; MP; VH | |
| M; M; H; MP; M | P; VP; MH; P; MH | VP; M; H; M; AH | |
| MH; MH; EH; VH; EH | MH; P; H; VH; EH | VP; VP; H; H; EH | |
| MP; M; H; P; VH | MP; VP; MP; P; VH | VP; MH; M; MP; AH | |
| EH; H; VH; EH; AH | EH; EH; VH; EH; EH | VP; VP; M; P; VH | |
| MH; M; H; MH; VH | EH; H; EH; EH; EH | VP; P; H; MP; VP |
By applying expression (12) we get an aggregated initial decision matrix, Table 12. When calculating the initial rank of alternatives, it is recommended that decision-makers choose the values
Table 12
The aggregated initial decision matrix.
| Criteria | ||||||
The element at position
Step 2: The experts defined the ideal and anti-ideal points,
Table 13
The standardized initial decision matrix.
| Criteria | ||||||
By substituting the values from the aggregated initial decision matrix into the function
Step 3: By applying expression (14), the normalization of the matrix element of the standardized initial decision matrix is performed. As shown in expression (14), the arithmetic mean
Step 4: By applying expression (15), the criterion functions of alternatives are calculated. Based on the
Table 14
Normalized initial decision matrix.
| Criteria | ||||||
Table 15
The ranking of alternatives.
| Alt. | Fuzzy value ( | Crisp value ( | Rank |
| 0.3930 | 4 | ||
| 0.4255 | 3 | ||
| 0.3569 | 6 | ||
| 0.5477 | 2 | ||
| 0.5726 | 1 | ||
| 0.3611 | 5 |
Based on the obtained results, we can single out the antivirus mask A5 as the dominant solution, i.e. the following ranking of alternatives is proposed:
5Validation and Discussion of Results
To verify the proposed solution, the sensitivity analysis of the fuzzy BWM-RAFSI model is presented in the following section. After obtaining the initial results in the MCDM framework, the question arises as to how subjectively defined input parameters influence decision making and what solutions are obtained by applying other multi-criteria techniques (Muhammad et al., 2021). Therefore, in the next section of the paper, the robustness check and sensitivity analysis of the obtained results to the change of the input parameters of the MCDM model were performed. The input parameters of the MCDM model mean the parameters that are defined based on the subjective preferences of the decision-maker (Biswas, 2020). In the following section, sensitivity analysis and validation of results were performed through four sections. In the first section, the analysis of the influence of the change of the weight coefficients of the criteria on the ranking results was performed. In the second and third sections, the analysis of the influence of the change of the parameters p and q in the Heronian operator on the ranking results was performed. In the fourth section, the robustness of the obtained solution was checked by comparison with other MCDM techniques.
5.1Influence of Change of Criterion Weight Coefficients on Ranking Results
It is indisputable that the results of multi-criteria models largely depend on the values of the weight coefficients of the criteria. In this study, experts’ preferences were used to determine the weight coefficients of the criteria, which were processed using fuzzy BWM. Since this is a subjective model for determining the weights of the criteria, the question arises as to how these subjective assessments affect the final results of the research. Since the greatest influence on the final decision has the criterion that has the highest value of the criteria weight
Fig. 4
Influence of change of criteria weights on change of criterion functions of alternatives
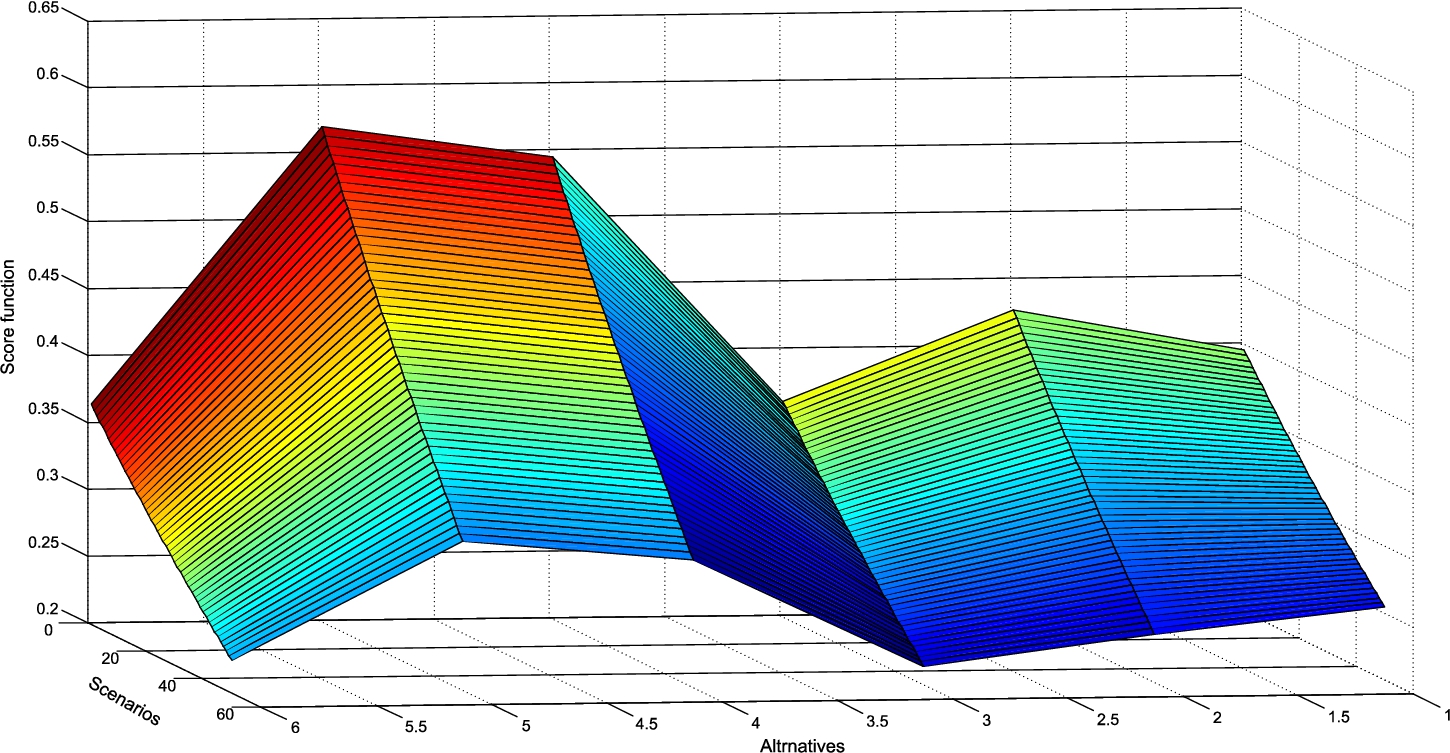
The analysis shown in Fig. 4 shows that the new vectors of the weight coefficients of the criteria affect the change in the values of the criterion functions of the alternative, which shows that the model is sensitive to changes in the input parameters. Also, it was shown that through the first 31 scenarios, the initial rank
5.2Influence of Change of Values of Parameters p and q on Change of Weight Coefficients of Criteria
By changing the values of the parameters p and q in the Heronian function, the calculation of the aggregate values of the criteria weights becomes more complicated, since a larger number of mutual relations between the attributes is considered at the same time. Therefore, it is necessary to perform an analysis of the influence of changes in the parameters p and q on the change of the criteria weights, and indirectly on the change in the ranks of the alternative. The change of the parameters p and q was performed through three experiments: Experiment I: The influence of the change of the parameter
Fig. 5
Influence of parameters p and q on change of weight coefficients and change of criterion functions of alternatives.
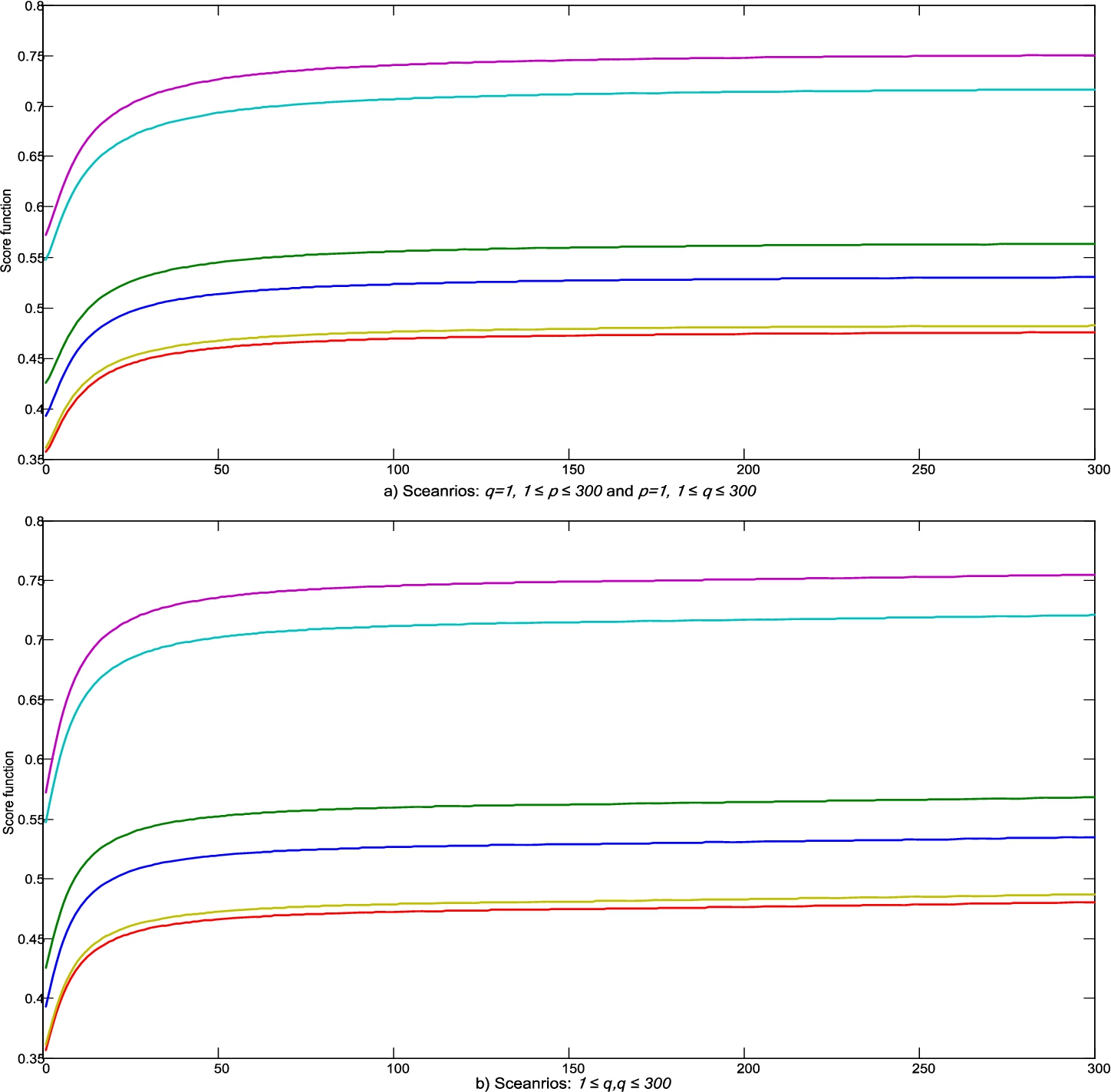
The presented experiments showed that changes in the values of the parameters p and q affect the change in the values of the weight coefficients of the criteria and the change in the criterion functions of the alternative. Through 900 scenarios that were divided into three experiments, there were no changes in the ranks of the alternative, despite changes in the values of the criterion functions. Through all scenarios, the initial rank
5.3Influence of Change of the Value of Parameters p and q on Change of Value in the Initial Decision Matrix
Since the Heronian function was used to aggregate values from experts’ initial decision matrices into an aggregated initial decision matrix, this section analyses the impact of changing the p and q parameters on the change in the value of the aggregated initial decision matrix. As in the previous section, three experiments were performed here during which the influence of the change of the parameters p and q in the interval
Fig. 6
Influence of parameters p and q on the change of aggregate values in the initial decision matrix.

The values of the criterion functions of the alternatives (Fig. 6) show that changes in the values of the parameters p and q lead to changes in the aggregate initial decision matrix. In the presented simulation, it is noticed that there is a change only in the ranks of the worst-ranked alternatives, i.e. alternatives
5.4Comparison with Fuzzy MCDM Methodologies
Since fuzzy sets were used for uncertainty processing in this paper, four fuzzy multicriteria techniques were chosen to compare the results: fuzzy COPRAS (Complex Proportional Assessment) technique (Fouladgar et al., 2012) method, fuzzy MABAC (Multi-Attributive Border Approximation area Comparison) method (Božanić et al., 2021), fuzzy MAIRCA (Multi-Attributive Ideal-Real Comparative Analysis) method (Gul and Ak, 2020) and fuzzy MARCOS (Measurement Alternatives and Ranking according to the Compromise Solution) method (Stanković et al., 2020; Arsu and Ayçin, 2021).
A comparative overview of the application of these fuzzy MCMD methodologies is shown in Fig. 7.
Fig. 7
Ranks of the alternatives based on the different fuzzy methodology.
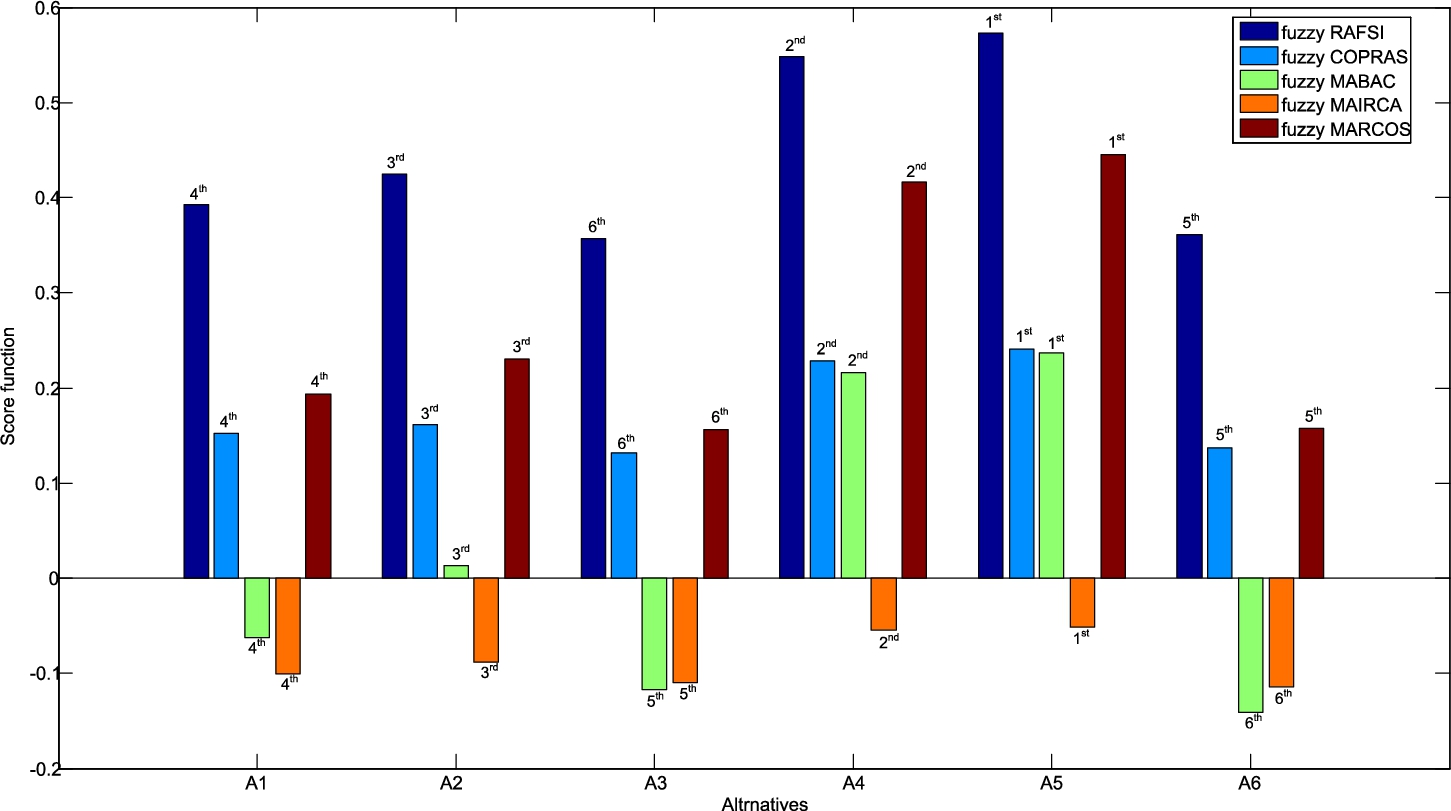
Based on the obtained results, it was confirmed that alternative
6Conclusion
COVID-19 has spread more like most other common respiratory diseases, mainly through respiratory droplet transmission without physical contact. Therefore, wearing a face mask is one of the most effective ways to prevent the spread of the virus. Especially, health workers are the most likely to be exposed to COVID-19 because they are in close contact with patients with suspected, probable or confirmed COVID-19. During the COVID-19 epidemic, face masks have become a highly effective item for health care staff and ordinary people. Different types of masks have been suggested throughout the COVID-19 pandemic. However, some masks are more effective than others. In order to determine what types of face mask work best to prevent the spread of COVID-19, this paper proposes a combined approach that uses F-BWM and fuzzy RAFSI methods for the mask selection process for healthcare personnel with respect to the COVID-19 pandemic to fill the gap in the literature.
There are two main advantages of the proposed fuzzy BWM-RAFSI methodology: 1) fuzzy BWM-RAFSI method has a new mathematical treatment for data normalization that enables transferring data from the initial decision making matrix into any interval which is adequate for making rational decisions and 2) resistance of fuzzy BWM-RAFSI method to rank reversal problem (Žižović et al., 2020). This paper offers some important contributions to the literature: (i) A novel integrated MCDM approach was used to select an appropriate medical face mask for preventing COVID-19 in healthcare workers, (ii) Antivirus mask selection criteria were considered under the fuzzy environment to make a more accurate decision, (iii) The proposed MCDM methodology can evaluate alternatives, although it is inaccurate and lacks quantitative information, (vi) The combination of two model BWM-RAFSI under fuzzy environment enables a more flexible decision-making process in the healthcare sector during COVID-19 pandemic, (v) This proposed model was compared with other MCDM methods with sensitivity analysis and validation of this model was demonstrated.
One of the possible limitations of the fuzzy BWM-RAFSI multi-criteria methodology is the mathematical complexity that requires the knowledge of nonlinear mathematical programming and fuzzy theory. This feature may be a limiting factor for a broader application in the multi-criteria decision-making field. To overcome this limitation, it is recommended that future research be directed towards developing a decision support system based on the application of the fuzzy BWM-RAFSI methodology. Also, a major source of limitation is that due to the over-intensity and high workload during the pandemic process, the opinions of healthcare workers such as nurses, medical technicians, dentists and etc. were not considered in this evaluation process.
Further research can benefit from the perspectives of healthcare workers from other professions and occupations. Furthermore, this proposed model can be performed for the same problem under newly released fuzzy extensions such as Pythagorean fuzzy sets, cubic picture fuzzy sets and spherical fuzzy sets for the future work. By doing this way, the validity of this hybrid model can be tested with the results obtained from several fuzzy sets. Finally, this new integrated model may be used in a variety of healthcare domains, including the development of an optimum COVID-19 diagnostic system, wearable health devices, and treatment techniques.
Compliance with ethical standards
Conflict of interest: The authors declare that they have no conflict of interest.
Ethical approval: This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent: N/A.
References
1 | Abdel-Basset, M., Manogaran, G., Gamal, A., Smarandache, F. ((2019) ). A group decision making framework based on neutrosophic TOPSIS approach for smart medical device selection. Journal of Medical Systems, 43: , 38. |
2 | Aboutorab, H., Saberi, M., Asadabadi, M.R., Hussain, O., Chang, E. ((2018) ). ZBWM: the Z-number extension of Best Worst Method and its application for supplier development. Expert Systems with Applications, 107: , 115–125. |
3 | Alosta, A., Elmansuri, O., Badi, I. ((2021) ). Resolving a location selection problem by means of an integrated AHP-RAFSI approach. Reports in Mechanical Engineering, 2: , 135–142. |
4 | Amiri, M., Hashemi-Tabatabaei, M., Ghahremanloo, M., Keshavarz-Ghorabaee, M., Zavadskas, E.K., Banaitis, A. ((2021) ). A new fuzzy BWM approach for evaluating and selecting a sustainable supplier in supply chain management. International Journal of Sustainable Development & World Ecology, 28: , 125–142. |
5 | Arsu, T., Ayçin, E. ((2021) ). Evaluation of OECD countries with multi-criteria decision-making methods in terms of economic, social and environmental aspects. Operational Research in Engineering Sciences: Theory and Applications, 4: , 55–78. |
6 | Ayittey, F.K., Ayittey, M.K., Chiwero, N.B., Kamasah, J.S., Dzuvor, C. ((2020) ). Economic impacts of Wuhan 2019-nCoV on China and the world. Journal of Medical Virology, 92: , 473–475. |
7 | Azap, A., Erdi˙nç, F.Ş. ((2020) ). Medical mask or N95 respirator: when and how to use? Turkish Journal of Medical Sciences, 50: , 633–637. |
8 | Bir, C., Widmar, N.O. ((2021) ). Societal values and mask usage for COVID-19 control in the US. Preventive Medicine, 153: , 106784. https://doi.org/10.1016/j.ypmed.2021.106784. |
9 | Biswas, S. ((2020) ). Measuring performance of healthcare supply chains in India: a comparative analysis of multi-criteria decision making methods. Decision Making: Applications in Management and Engineering, 3: , 162–189. |
10 | Božanić, D., Milić, A., Tešić, D., Salabun, W., Pamučar, D. ((2021) ). D numbers – fucom – fuzzy rafsi model for selecting the group of construction machines for enabling mobility. Facta Universitatis, Series: Mechanical Engineering, 19: (6), 447–471. |
11 | Carlsson, C., Fullér, R. ((2001) ). On possibilistic mean value and variance of fuzzy numbers. Fuzzy sets and systems, 122: , 315–326. |
12 | Chen, Z., Ming, X. ((2020) ). A rough–fuzzy approach integrating best–worst method and data envelopment analysis to multi-criteria selection of smart product service module. Applied Soft Computing, 94: , 106479. |
13 | Dwivedi, R., Prasad, K., Mandal, N., Singh, S., Vardhan, M., Pamucar, D. ((2021) ). Performance evaluation of an insurance company using an integrated Balanced Scorecard (BSC) and Best-Worst Method (BWM). Decision Making. Applications in Management and Engineering, 4: , 33–50. |
14 | Ecer, F., Pamucar, D. ((2020) ). Sustainable supplier selection: a novel integrated fuzzy best worst method (F-BWM) and fuzzy CoCoSo with Bonferroni (CoCoSo’B) multi-criteria model. Journal of Cleaner Production, 266: , 121981. |
15 | Ecer, F., Pamucar, D. ((2021) ). MARCOS technique under intuitionistic fuzzy environment for determining the COVID-19 pandemic performance of insurance companies in terms of healthcare services. Applied Soft Computing, 104: , 107199. |
16 | Fouladgar, M.M., Yazdani-Chamzini, A., Lashgari, A., Zavadskas, E.K., Turskis, Z. ((2012) ). Maintenance strategy selection using AHP and COPRAS under fuzzy environment. International Journal of Strategic Property Management, 16: , 85–104. |
17 | Gao, H., Ran, L., Wei, G., Wei, C., Wu, J. ((2020) ). VIKOR method for MAGDM based on q-rung interval-valued orthopair fuzzy information and its application to supplier selection of medical consumption products. International Journal of Environmental Research and Public Health, 17: , 525. |
18 | Gul, M., Ak, M.F. ((2020) ). Assessment of occupational risks from human health and environmental perspectives: a new integrated approach and its application using fuzzy BWM and fuzzy MAIRCA. Stochastic Environmental Research and Risk Assessment, 34: , 1231–1262. |
19 | Guo, S., Zhao, H. ((2017) ). Fuzzy best-worst multi-criteria decision-making method and its applications. Knowledge-Based Systems, 121: , 23–31. |
20 | Hafezalkotob, A., Hafezalkotob, A. ((2017) ). A novel approach for combination of individual and group decisions based on fuzzy best-worst method. Applied Soft Computing, 59: , 316–325. |
21 | Health, C. for D. and R (2021). Face Masks, Barrier Face Coverings, Surgical Masks, and Respirators for COVID-19. FDA. |
22 | Kumar, R., Pandey, A.K., Baz, A., Alhakami, H., Alhakami, W., Agrawal, A., Khan, R.A. ((2020) ). Fuzzy-based symmetrical multi-criteria decision-making procedure for evaluating the impact of harmful factors of healthcare information security. Symmetry, 12: , 664. |
23 | Lee, Y.C., Chung, P.-H., Shyu, J.Z. ((2017) ). Performance evaluation of medical device manufacturers using a hybrid fuzzy MCDM. Journal of Scientific & Industrial Research, 76: , 28–31. |
24 | Liao, H., Mi, X., Yu, Q., Luo, L. ((2019) ). Hospital performance evaluation by a hesitant fuzzy linguistic best worst method with inconsistency repairing. Journal of Cleaner Production, 232: , 657–671. |
25 | Liu, A., Ji, X., Lu, H., Liu, H. ((2019) ). The selection of 3PRLs on self-service mobile recycling machine: Interval-valued pythagorean hesitant fuzzy best-worst multi-criteria group decision-making. Journal of Cleaner Production, 230: , 734–750. |
26 | Liu, P., Zhu, B., Wang, P. ((2021) ). A weighting model based on best-worst method and its application for environmental performance evaluation. Applied Soft Computing, 103: , 107168. |
27 | Luo, C., Ju, Y., Gonzalez, E.D.S., Dong, P., Wang, A. ((2020) ). The waste-to-energy incineration plant site selection based on hesitant fuzzy linguistic best-worst method ANP and double parameters TOPSIS approach: a case study in China. Energy, 211: , 118564. |
28 | Mahase, E. (2020). Coronavirus: global stocks of protective gear are depleted, with demand at “100 times” normal level, WHO warns. British Medical Journal Publishing Group. |
29 | Malakoutikhah, M., Alimohammadlou, M., Jahangiri, M., Rabiei, H., Faghihi, S.A., Kamalinia, M. ((2021) ). Modeling the factors affecting unsafe behaviors using the fuzzy best-worst method and fuzzy cognitive map. Applied Soft Computing, 114: , 108119. |
30 | Mi, X., Liao, H. ((2019) ). An integrated approach to multiple criteria decision making based on the average solution and normalized weights of criteria deduced by the hesitant fuzzy best worst method. Computers & Industrial Engineering, 133: , 83–94. |
31 | Mostafaeipour, A., Alvandimanesh, M., Najafi, F., Issakhov, A. ((2021) ). Identifying challenges and barriers for development of solar energy by using fuzzy best-worst method: a case study. Energy, 226: , 120355. |
32 | Mou, Q., Xu, Z., Liao, H. ((2017) ). A graph based group decision making approach with intuitionistic fuzzy preference relations. Computers & Industrial Engineering, 110: , 138–150. |
33 | Muhammad, L.J., Badi, I., Haruna, A.A., Mohammed, I.A. ((2021) ). Selecting the best municipal solid waste management techniques in Nigeria using multi criteria decision making techniques. Reports in Mechanical Engineering, 2: , 180–189. |
34 | Muravev, D., Mijic, N. ((2020) ). A novel integrated provider selection multicriteria model: the BWM-MABAC model. Decision Making: Applications in Management and Engineering, 3: , 60–78. |
35 | Nilashi, M., Samad, S., Manaf, A.A., Ahmadi, H., Rashid, T.A., Munshi, A., Almukadi, W., Ibrahim, O., Ahmed, O.H. ((2019) ). Factors influencing medical tourism adoption in Malaysia: a DEMA-fuzzy TOPSIS approach. Computers & Industrial Engineering, 137: , 106005. |
36 | Omrani, H., Alizadeh, A., Emrouznejad, A. ((2018) ). Finding the optimal combination of power plants alternatives: A multi response Taguchi-neural network using TOPSIS and fuzzy best-worst method. Journal of Cleaner Production, 203: , 210–223. https://doi.org/10.1016/j.jclepro.2018.08.238. |
37 | Otay, İ., Oztaysi, B., Onar, S.C., Kahraman, C. ((2017) ). Multi-expert performance evaluation of healthcare institutions using an integrated intuitionistic fuzzy AHP&DEA methodology. Knowledge-Based Systems, 133: , 90–106. |
38 | Ozsahin, D.U., Hamidat, L., Alimi, F.D., Uzun, B., Ozsahin, I. ((2021) ). Evaluation of migraine drugs using MCDM methods. In: Applications of Multi-Criteria Decision-Making Theories in Healthcare and Biomedical Engineering. Elsevier, pp. 261–275. |
39 | Pamučar, D.S., Savin, L.M. ((2020) ). Multiple-criteria model for optimal off-road vehicle selection for passenger transportation: BWM-COPRAS model. Vojnotehnički Glasnik, 68: , 28–64. |
40 | Qin, J., Liu, X. ((2019) ). Interval Type-2 Fuzzy Group Decision Making by Integrating Improved Best Worst Method with COPRAS for Emergency Material Supplier Selection. In: Type-2 Fuzzy Decision-Making Theories, Methodologies and Applications. Springer, pp. 249–271. |
41 | Reddy, B.P., Kelly, M.P., Thokala, P., Walters, S.J., Duenas, A. ((2014) ). Prioritising public health guidance topics in the National Institute for Health and Care Excellence using the analytic hierarchy process. Public Health, 128: , 896–903. |
42 | Rezaei, J. ((2015) ). Best-worst multi-criteria decision-making method. Omega, 53: , 49–57. |
43 | Rouyendegh, B.D., Oztekin, A., Ekong, J., Dag, A. ((2019) ). Measuring the efficiency of hospitals: a fully-ranking DEA–FAHP approach. Annals of Operations Research, 278: , 361–378. |
44 | Stanković, M., Stević, Ž., Das, D.K., Subotić, M., Pamučar, D. ((2020) ). A new fuzzy MARCOS method for road traffic risk analysis. Mathematics, 8: , 457. |
45 | Stević, Ž., Pamučar, D., Subotić, M., Antuchevičiene, J., Zavadskas, E.K. ((2018) ). The location selection for roundabout construction using rough BWM-rough WASPAS approach based on a new rough hamy aggregator. Sustainability, 10: , 2817. https://doi.org/10.3390/su10082817. |
46 | Stević, Ž., Pamučar, D., Puška, A., Chatterjee, P. ((2020) ). Sustainable supplier selection in healthcare industries using a new MCDM method: measurement of alternatives and ranking according to Compromise solution (MARCOS). Computers & Industrial Engineering, 140: , 106231. |
47 | Subotić, M., Stević, B., Ristić, B., Simić, S. ((2020) ). The selection of a location for potential roundabout construction–a case study of Doboj. Operational Research in Engineering Sciences: Theory and Applications, 3: , 41–56. |
48 | Sumrit, D. ((2020) ). Supplier selection for vendor-managed inventory in healthcare using fuzzy multi-criteria decision-making approach. Decision Science Letters, 9: , 233–256. |
49 | Thakur, V., Ramesh, A. ((2017) ). Healthcare waste disposal strategy selection using grey-AHP approach. Benchmarking: An International Journal, 24: (3), 735–749. |
50 | Tian, Z.-P., Zhang, H.-Y., Wang, J.-Q., Wang, T.-L. ((2018) ). Green supplier selection using improved TOPSIS and best-worst method under intuitionistic fuzzy environment. Informatica, 29: , 773–800. |
51 | Torkayesh, A.E., Pamucar, D., Ecer, F., Chatterjee, P. ((2021) ). An integrated BWM-LBWA-CoCoSo framework for evaluation of healthcare sectors in Eastern Europe. Socio-Economic Planning Sciences, 78: , 101052. |
52 | Wu, Q., Zhou, L., Chen, Y., Chen, H. ((2019) ). An integrated approach to green supplier selection based on the interval type-2 fuzzy best-worst and extended VIKOR methods. Information Sciences, 502: , 394–417. |
53 | Yang, Z., Li, X., Garg, H., Qi, M. ((2020) ). Decision support algorithm for selecting an antivirus mask over COVID-19 pandemic under spherical normal fuzzy environment. International Journal of Environmental Research and Public Health, 17: , 3407. |
54 | Yazdani, M., Mohammed, A., Bai, C., Labib, A. ((2021) ). A novel hesitant-fuzzy-based group decision approach for outsourcing risk. Expert Systems with Applications, 184: , 115517. |
55 | Yu, D. ((2013) ). Intuitionistic fuzzy geometric Heronian mean aggregation operators. Applied Soft Computing, 13: , 1235–1246. |
56 | Yucesan, M., Gul, M. ((2020) ). Hospital service quality evaluation: an integrated model based on Pythagorean fuzzy AHP and fuzzy TOPSIS. Soft Computing, 24: , 3237–3255. |
57 | Zadeh, L.A. ((1965) ). Fuzzy sets. Information and Control, 8: , 338–353. |
58 | Zare, H., Tavana, M., Mardani, A., Masoudian, S., Saraji, M.K. ((2019) ). A hybrid data envelopment analysis and game theory model for performance measurement in healthcare. Health Care Management Science, 22: , 475–488. |
59 | Žižović, M., Pamučar, D., Albijanić, M., Chatterjee, P., Pribićević, I. ((2020) ). Eliminating rank reversal problem using a new multi-attribute model—the RAFSI method. Mathematics, 8: , 1015. |
60 | Zolfani, S.H., Chatterjee, P., Yazdani, M. ((2019) ). A structured framework for sustainable supplier selection using a combined BWM-CoCoSo model. In: International Scientific Conference in Business, Management and Economics Engineering, Vilnius, Lithuania, pp. 797–804. |




