A Comprehensive Solution Approach for CNC Machine Tool Selection Problem
Abstract
A proper CNC machine selection problem is an important issue for manufacturing companies under competitive market conditions. The selection of an improper machine tool can cause many problems such as production capabilities and productivity indicators considering time and money industrially and practically. In this paper, a comprehensive solution approach is presented for the CNC machine tool selection problem according to the determined criteria. Seven main and thirteen sub-criteria were determined for the evaluation of the seven alternatives. To purify the selection process from subjectivity, instead of a single decision-maker, the opinions of six different experts on the importance of the criteria were taken and evaluated using the Best-Worst method. According to the evaluations, the order of importance of the main criteria has been determined as cost, productivity, flexibility, and dimensions. After the weighting of the criteria, three different ranking methods (GRA, COPRAS, and MULTIMOORA) were preferred due to the high investment costs of the selected alternatives. The findings obtained by solving the problem of selection of the CNC machine are close to those obtained by past researchers. As a result, using the suggested methodology, effective alternative decision-making solutions are obtained.
1Introduction
Companies need to have many plans related to marketing, financing, and production in today’s competitive markets. On the other hand, companies, based on these strategies, have to take a series of decisions, especially at the stage of establishment and when making growth decisions. One of these decisions is the selection of machines and equipment to be used in manufacturing. Identifying the appropriate machine or equipment from among the alternatives available is also a very important decision which, in the long run, affects the efficiency of the production system. The use of suitable machinery improves the manufacturing process, ensures the effective use of manpower, increases productivity, and enhances the versatility of the system (Dağdeviren, 2008). Also, the characteristics of the chosen machine have a considerable effect on prices, efficiency, and performance numbers, which are the key objectives of the production strategy.
Generally, computer numerical control (CNC) machines, which can be used with high precision to perform repetitive, challenging, and unsafe production jobs, are considered cost-effective equipment (Athawale and Chakraborty, 2010). CNC machines are regarded as cost-effective instruments that can be used to perform routine, demanding, and dangerous manufacturing tasks by offering a high degree of precision to eliminate human errors. CNC machines are also used in innovative fields such as the production of molds for phase change material (PCM) (Lim et al., 2018). A very complex decision problem is the purchase of such a technological machine tool, as it requires a large investment and has many alternative and selection criteria. There is a large amount of data to be analysed by the decision-maker and many features to consider for an appropriate and effective evaluation of the selection of machine tools. To choose the most suitable one, the decision-maker must be an expert or be familiar with the technical specifications of the machines (Rao, 2006).
The scope of this paper, which is based on these needs, is to select a proper machine tool using Best-Worst weighted GRA, COPRAS, and MULTIMOORA methods. These methods are used to determine the order of priority with managerial insights and implications. However, this paper tries to answer the following questions:
(1) What are the criteria of the most used features in the CNC machine tool selection process?
(2) Which alternative CNC machine tool may be more suitable under variable weighted uncertainties?
(3) How different weights of expert opinions will affect this selection problem on the Best-Worst methodology?
The rest of this study is organized as follows: a related literature review is given in Section 2. In Section 3, at first, the problem definition is given and then, Best-Worst, Grey Relational Analysis (GRA), COPRAS, and MULTIMOORA methodologies are explained. The proposed solution approach and its implementation are placed in Section 4 with the numerical case study. In Section 5, the conclusion and discussions are presented for considering future studies.
2Literature Review
For several years, machine tool selection has been an important decision problem for manufacturing firms. The primary explanation for this is that there are several issues with the selection of an inappropriate machine that affects overall efficiency and production capabilities in the long run (Taha and Rostam, 2012). A detailed literature review is given in Table 1 and some selected studies are summarized in the following.
Since there is more than one criterion, Multi-Criteria Decision Making (MCDM) methods are widely used in the solution of the Machine Tool Selection (MTS) problem. Several options and criteria are evaluated in these studies to decide the best alternative. It is considered as the most suitable option for the decision-maker who, after rating the alternatives, gets the highest score (Ayağ and Özdemir, 2006). The researchers have used various approaches to solve the MTS problem until today. The Analytical Hierarchy Process (AHP) and TOPSIS Method are the most commonly used methods among these techniques.
Due to uncertainties in the decision-maker’s decisions, a fuzzy AHP instead of traditional AHP was used for the evaluation and justification of an advanced production system (Ayag and Ozdemir, 2006) with developing a software (Durán and Aguilo, 2008). To analyse the structure of the equipment selection problem and evaluate the weights of the parameters, Dağdeviren (2008) suggested an integrated approach using AHP and the PROMETHEE approach for obtaining the final rating and conducting sensitivity analysis by adjusting weights. Önüt et al. (2008) suggested a fuzzy TOPSIS based approach for the evaluation and selection of vertical CNC machining centres, where weights were determined by fuzzy AHP.
Moreover, in order to measure the level of benefit provided by using fuzzy numbers in multi-criteria decision models, Yurdakul and Ic (2009) solved the problem of MTS and compared the solutions of TOPSIS and Fuzzy TOPSIS techniques. The TOPSIS method was used by Athawale and Chakraborty (2010) to evaluate CNC machines in terms of system features and costs. Then, as the consecutive studies, fuzzy numbers were used for pairwise comparison with an Analytic Network Process (ANP) which was proposed to improve the imprecise ranking of the company’s requirements which is based on the conventional ANP for machine tool selection problem. The proposed methodology was developed to eliminate the effects of vagueness and uncertainty on the judgments of a decision-maker (Ayağ and Özdemir, 2011). The next one is TOPSIS and ANP methods which are commonly used MCDM methods for performance analysis on the machine tool selection problem (Ayağ and Özdemir, 2012). Similarly, Fuzzy ANP and Fuzzy PROMETHEE-II techniques were integrated by Samanlioglu and Ayağ (2016) to solve the problem of machine tool selection. Chen et al. (2021) proposed an approach consisting of DEMANTEL, ULOWA, and PROMETHEE methods for mechanical product optimization design based on meta-action reliability. An example of the application and feasibility of their proposed method is demonstrated with an automatic pallet changer (APC) of a CNC machine tool.
Table 1
Detailed literature review.
| Application area | Method | Uncertainty | ||||||
| Source | Machine selection | Tool selection | Technology selection | MCDM Method | Integrated method | Others | Crisp | Fuzzy |
| Arslan et al. (2004) | ||||||||
| Yurdakul (2004) | ||||||||
| Kulak et al. (2005) | ||||||||
| Ayağ and Özdemir (2006) | ||||||||
| Ayağ (2007) | ||||||||
| Çimren et al. (2007) | ||||||||
| Dağdeviren (2008) | ||||||||
| Önüt et al. (2008) | ||||||||
| Durán and Aguilo (2008) | ||||||||
| Yurdakul and Ic (2009) | ||||||||
| Rao and Parnichkun (2009) | ||||||||
| Athawale and Chakraborty (2010) | ||||||||
| Qi (2010) | ||||||||
| Özgen et al. (2011) | ||||||||
| Paramasivam et al. (2011) | ||||||||
| Ayağ and Özdemir (2011) | ||||||||
| İç et al. (2012) | ||||||||
| Ayağ and Özdemir (2012) | ||||||||
| Taha and Rostam (2012) | ||||||||
| İç (2012) | ||||||||
| Samvedi et al. (2012) | ||||||||
| Ilangkumaran et al. (2012) | ||||||||
| Aghdaie et al. (2013) | ||||||||
| Perçin and Min (2013) | ||||||||
| Tho et al. (2013) | ||||||||
| Sahu et al. (2014) | ||||||||
| Vatansever and Kazancoglu (2014) | ||||||||
| Prasad and Chakraborty (2015) | ||||||||
| Izadikhah (2015) | ||||||||
| Nguyen et al. (2015) | ||||||||
| Sahu et al. (2015a) | ||||||||
| Sahu et al. (2015b) | ||||||||
| Sarkar et al. (2015) | ||||||||
| Jing et al. (2015) | ||||||||
| Kumar et al. (2015) | ||||||||
| Kumru and Kumru (2015) | ||||||||
| Samanlioglu and Ayağ (2016) | ||||||||
| Özceylan et al. (2016) | ||||||||
| Wu et al. (2016) | ||||||||
| Karim and Karmaker (2016) | ||||||||
| Chakraborty and Boral (2017) | ||||||||
| Özdağoğlu et al. (2017) | ||||||||
| Cakir (2018) | ||||||||
| Liu et al. (2018) | ||||||||
| Zaied et al. (2019) | ||||||||
| Li et al. (2020) | ||||||||
| Chen et al. (2021) | ||||||||
| Villa Silva et al. (2021) | ||||||||
Methods such as SAW (Patel et al., 2012; Özdağoğlu et al., 2017), Multi-Moora-Interval Value Grey Number Sets (IVGN) (Sahu et al., 2014), MOORA-MOOSRA (Sarkar et al., 2015), VIKOR (Jing et al., 2015), Fuzzy ANP-Promethee (Özceylan et al., 2016), QFD (Perçin and Min, 2013; Prasad and Chakraborty, 2015), Axiomatic Design (Kulak et al., 2005; Cakir, 2018), a neutrosophic MOORA method (Zaied et al., 2019) and entropy weighted fuzzy DEMATEL with VIKOR defuzzification (Li et al., 2020) were used for the selection problem in the literature in addition to these studies. In addition to the studies with details, the studies in the literature regarding machine selection, tool selection, and technology selection are shown in Table 1.
In this study, a new solution approach is proposed where criteria weights are determined by the Best-Worst method, and rankings are determined by considering with GRA, COPRAS, and MULTIMOORA methods. Within the scope of the study, a new solution approach in which weighting and ranking methods are used together has been tried to be put forward. The methods used are powerful methods that have not been used before in the machine tool selection problem and their effectiveness has been shown in previous studies in the literature and this study.
3Material and Methods
3.1Problem Definition (CNC Machine Selection Process)
In the machine tool market, there are hundreds of CNC machine alternatives. In the first step, machine tool alternatives that can satisfy the company’s needs should be identified. In the second stage, the defined alternatives are evaluated using any decision model. When comparing various machine tools, decision-makers use a set of criteria. These criteria are generally related to the technological features of the machine, but they also include criteria such as productivity, flexibility, cost, maintenance, and service. Ayağ and Özdemir (2006), as well as Ayağ (2007), defined 8 key criteria and 19 sub-criteria for machine tool selection. Productivity, flexibility, space adaptability, precision, reliability, safety and environment, and maintenance and service are the main criteria used in these studies. Taha and Rostam (2012) used literature information and expert opinion to develop 5 key and 27 sub-criteria that represent the technological characteristics of a machine tool. In their fuzzy-based decision-support system, Özceylan et al. (2016) used “cost”, “quality”, “flexibility”, and “performance” as the main criteria. These four criteria are subdivided into 15 sub-criteria. Due to differences in manufacturing facilities and decision makers’ viewpoints, different criteria have been used in machine tool selection in previous research. As shown by the examples in this section, technological features and cost elements are commonly used in machine selection.
3.2Methods
In this paper, the Best-Worst method is applied for determining the criteria weights using the mean of the expert opinions via taking advantage of pairwise comparison from best to worst. This method has been preferred for reasons such as making less and more consistent comparisons, being able to be used with other methods to be used for sorting, and not having to deal with fractional numbers. On the other hand, the choice of CNC machine tool is one of the decision problems that require a very high investment. For this reason, alternatives and decisions can be compared by using more than one method rather than a single method for ranking the alternatives. As for the choice of alternatives, GRA is selected with reference series, COPRAS is also selected to evaluate the performance of each alternative, taking into account the contradictory situations, and MULTIMOORA is preferred to apply dominance solution in terms of the subordinate ranking methods for this study. These alternative selection methods are used with the determined criteria weights from the Best-Worst method. Consequently, the whole solution procedure is designed for the proper decision-making process on the CNC selection research problem.
3.2.1Best-Worst Method
The method proposed by Rezaei (2015) is a multi-criteria decision-making method based on pairwise comparison. In areas such as supplier selection (Rezaei et al., 2016), assessment of the social sustainability of supply chains (Ahmadi et al., 2017), evaluation of service quality in the aviation industry (Gupta, 2018), and evaluation of companies’ RandD performance (Salimi and Rezaei, 2018) applications have been made. The steps of the method are presented below (Kheybari et al., 2019).
Step 1: Evaluation criteria
Step 2: The best (most important) and the worst (least important) criteria are determined.
Step 3: A pairwise comparison is made between the best criterion and other criteria using a scale of 1-9 and the BO vector
Step 4: A binary comparison is made between the other criteria and the worst criterion, again using the scale 1–9, and the OW vector (
Step 5: Optimal weights (
Here, the status
(1)
(2)
Then the expressions here are converted into the mathematical model shown below:
(3)
(4)
(5)
(6)
With the solving of the model, the value of the optimal weights is obtained that is the criterion that shows how consistent the evaluations are. If this value is close to zero, it means that a consistent evaluation has been made.
3.2.2Grey Relational Analysis (GRA)
An essential approach of the grey system theory (GST) used in the decision-making process and measuring the changes of similarities and differences between its factors over time is called Grey Relational Analysis (GRA) (Feng and Wang, 2000; Aydemir et al., 2013). This method is used in the elimination and analysis of ambiguous relationships between criteria and options, examination of integrated circuit marking process (Jiang et al., 2002), restoration planning of power distribution systems (Chen et al., 2005), recruitment decisions (Olson and Wu, 2006), damage assessment (He and Hwang, 2007), a causal decision-making model (Tseng, 2009), determination of critical path through a network (Zhongmin and Xizu, 2009), supplier selection (Yang and Chen, 2006; Özdemir and Deste, 2009; Zavadskas et al., 2010; Hashemi et al., 2015; Cakir and Akel, 2017), stock market forecasts and portfolio selection (Huang and Jane, 2009), optimization of turning parameters (Yilmaz and Gungor, 2010; Ramesh et al., 2016; Prakash et al., 2020; Lakshmanan et al., 2021), evaluation of e-commerce system security (Liu, 2011), ergonomics (Akay, 2011), evaluation of the performance of enterprises (Tayyar et al., 2014; Aydemir and Sahin, 2019), risk and quality analysis (Baynal et al., 2018; Yazdani et al., 2019), product analysis (Chan and Tong, 2007; Sahin and Aydemir, 2019), and social networks (Weng et al., 2021).
In the method, when the decision-maker has no information, that is, when the information is black, the greyness of a process is done. In most decision problems with insufficient and/or incomplete information, the GRA method is used to select, rank, and evaluate (Chan and Tong, 2007; Yildirim, 2014; Aydemir, 2020). In the solution process, logical and numerical measurements between two decision series are called grey relational degrees, and values are assigned between 0–1. The method consists of three steps: normalization, grey relational coefficient calculation, and grey relational degree calculation. In the first step, the data of the alternatives are transformed into comparison sequences by the normalization process. In the GRA method, the normalization process is performed using Eqs. (7)–(9), respectively, according to benefit, cost, and optimality (Feng and Wang, 2000; Yildirim, 2014; Sahin and Aydemir, 2019):
(7)
(8)
(9)
After the normalization process, all values take values between 0–1. A decision alternative (i) getting a value close to 1, and 1 for a criterion (j) means that the alternative is one of the best alternatives for that criteria. It is uncommon in practice that any decision alternative provides the best value for all criteria. Therefore, the closest alternative to a reference series should be determined (Kuo et al., 2008). For this process, the absolute differences between the reference series values and the normalized benchmark value are calculated using Eq. (10) and thus the absolute difference matrix is created (Yildirim, 2014).
(10)
In the following step, the relationship between the desired and actual experimental data is determined by calculating the grey relational coefficient from the absolute difference matrix. Grey coefficients (
(11)
In the last step, the grey relational degree is calculated by taking the average of the grey relational coefficients and the ranking is performed according to this value. Grey relational degrees (
(12)
(13)
3.2.3COPRAS Method
The COPRAS method developed by Zavadskas et al. (1994) applies a stepwise ranking procedure to evaluate the performance of each alternative, taking into account the contradictory situations. It is a frequently preferred method especially for ranking processes in subjects such as evaluation of road design solutions (Zavadskas et al., 2007), supplier selection (Keshavarz Ghorabaee et al., 2014; Yildirim and Timor, 2019), investment project selection (Popović et al., 2012), and analysis of the basic factors of sustainable architecture (Amoozad Mahdiraji et al., 2018).
The COPRAS method assumes a direct and proportional dependence of the degree of importance and utility of decision options on a system of criteria that adequately defines the alternatives and the values and weights of the criteria. Determining the importance, priority order, and degree of use of alternatives is carried out in five stages (Kaklauskas et al., 2005, 2006):
Step 1: The weighted normalized decision matrix
(14)
The sum of the dimensionless weighted index values is equal to “
(15)
Step 2: The sum of the weighted normalized indices defining the alternative j is calculated. The index of the criteria trying to be minimized is shown as “
(16)
Step 3: The degree of importance of comparative alternatives (
(17)
The larger the value of
Step 4: The utility degree of the alternative j (
(18)
Step 5: The order of the alternatives is determined according to the degree of use (
3.2.4MULTIMOORA Method
The Multi-Objective Optimization Based on Ratio Analysis (MOORA) method proposed by Brauers and Zavadskas (2006) was later developed as MULTIMOORA by Brauers and Zavadskas (2010) with the addition of the “Full Multiplicative Form of Multiple Objectives” method. MOORA plus the full Multiplicative form, which consists of three subordinate methods: full multiplicative, reference point, and full multiplicative.
MULTIMOORA is mostly used as a multi-criteria decision-making technique in fields such as industry, economy, environment, health services, and information technologies as practical applications. In this section, we first explain the MULTIMOORA method in terms of the subordinate ranking methods. The first step also involves generating a decision matrix and weight vector, as seen below, with

Also, on the MCDM problems, the ratings of alternatives may have different dimensions generally, so, the normalized ratings should be required and for this, Van Delft and Nijkamp normalization approach is used in MULTIMOORA application considering the most robust choice and proving by Brauers et al. (2008) for the denominator in the ratio system:
(20)
In certain cases, the triple subordinate methods are also known as the ratio, complete multiplicative, and reference point forms, and they are used to solve the exits problem. The ratio method should be used as a completely compensatory model if the problem has any independent criteria. The ratio system is computed by Eq. (21), where g is the number of useful criteria and
(21)
(22)
The reference point approach, on the other hand, is a conservative method for measuring and comparing the ratio system and complete multiplicative form with Eqs. (23)–(25). Initially, the maximal objective reference point (MORP) vector is defined as Eq. (23), where
(23)
Eq. (24) defines the distance between the weighted value of the vector members and the weighted alternative rating, and the efficiency of the Reference Point Approach is obtained by maximizing the distance introduced in Eq. (25):
(24)
(25)
The best alternative found by the Reference Point Approach has the least benefit (
(26)
Although Brauers and Zavadskas (2012) demonstrated that using weights as multipliers in the full multiplicative form is meaningless, it is mentioned that the weights determined in the developed MULTIMOORA method proposed by Hafezalkotob and Hafezalkotob (2016) can be calculated as shown in Eq. (27):
(27)
The maximum utility alternative is the best alternative based on the Full Multiplicative Form, and the sequence of this technique is obtained by equation (28) in descending order:
(28)
Using these subordinate ranks, we also should decide the final ranking of the alternatives in the final phase. The aggregating multiple subordinate rankings are presented by Brauers and Zavadskas (2012) to obtain a final ranking list that is more robust than each ranking list of the subordinate methods. Dominance-based principles, mathematical operators, MCDM methods, and programming approaches are examples of these approaches. Using the principle of dominance, the original MULTIMOORA incorporates MOORA with the exact multiplicative form. At this point, it is obvious that Dominance Theory (Brauers and Zavadskas, 2011) is the most widely applied method; but, in recent years, other tools with potential success have been used instead of this theory (Brauers and Zavadskas, 2006; Hafezalkotob et al., 2019). As a result, the dominance theory is used in this analysis to produce a unified final ranking list.
Fig. 1
The basic framework of the proposed method.

4Results
One of the most important decisions in the design and construction of a competitive manufacturing environment is the selection of the appropriate machine tools. This chapter contains the application of the proposed method to solve the machine tool selection problem. The basic framework of the methods proposed within the scope of the study and detailed in Section 3.2 is shown in Fig. 1. The method starts with determining the criteria to be used. After the literature review and the determination of the criteria by taking the expert opinion, the criteria weights were determined with the BWM, details of which are specified in Section 3.2.1. The determined weighted criteria are used as inputs to the GRA, COPRAS, and MULTIMOORA methods used in the ranking of machine alternatives. Final rankings were obtained as a result of the calculations made separately with these methods.
4.1Determination of Criteria and Weighting
According to the consumer specifications, the appropriate machine should be selected from the existing database. At the beginning of the research, 4 main and 13 sub-criteria were determined to be used in the solution of the problem, taking into account the literature research and expert opinions. Dimensions (C1), Flexibility (C2), Productivity (C3), and Cost (C4) criteria, whose sub-criteria are shown in Table 2, were determined as the main criteria.
The determined weights can be used with equal weight or they can be weighted differently according to the needs of the company. The importance of the criteria was determined by using the Best-Worst method, details of which are given in Section 3.2.1, as a result of the interviews with six experts. BWM is a method based on testing the importance level of criteria. Also, BWM emerges as a method that is being used frequently in scientific and industrial situations. The criterion weights determined as a result of the calculations made with the BO and OW vectors created as a result of expert opinions are shown in Tables 3, 4 and 5, respectively.
Table 2
The mainand sub-criteria.
| Main criteria | Sub-criteria | Objective | Unit |
| Dimensions (C1) | Table load (C11) | Max | kg s |
| Main travel (C12) | Max | mm | |
| Table size (C13) | Max | m2 | |
| Machine weight (C14) | Min | kg s | |
| Flexibility (C2) | Spindle rate (C21) | Max | rpm |
| Spindle power (C22) | Max | kw | |
| Max. tool weight (C23) | Max | kg s | |
| Productivity (C3) | Feed rate (axis x, y and z) (C31) | Max | mm/min s |
| Tool magazine capacity (C32) | Max | set | |
| Cutting feed rate (C33) | Max | mm/min s | |
| Cost (C4) | Procurement price (C41) | Min | $ |
| Operation cost (C42) | Min | $ | |
| Maintenance cost (C43) | Min | $ |
Table 3
BO vectors for main criteria.
| Experts no. | Best | Dimensions (C1) | Flexibility (C2) | Productivity (C3) | Cost (C4) |
| Experts 1 | Cost (C4) | 6 | 4 | 2 | 1 |
| Experts 2 | Cost (C4) | 5 | 3 | 2 | 1 |
| Experts 3 | Cost (C4) | 7 | 4 | 2 | 1 |
| Experts 4 | Cost (C4) | 6 | 5 | 3 | 1 |
| Experts 5 | Cost (C4) | 6 | 2 | 4 | 1 |
| Experts 6 | Cost (C4) | 6 | 2 | 4 | 1 |
Table 4
OW vectors for main criteria.
| Experts No. | Worst | Dimensions (C1) | Flexibility (C2) | Productivity (C3) | Cost (C4) |
| Experts 1 | Dimensions (C1) | 1 | 2 | 4 | 6 |
| Experts 2 | Dimensions (C1) | 1 | 2 | 3 | 5 |
| Experts 3 | Dimensions (C1) | 1 | 2 | 3 | 7 |
| Experts 4 | Dimensions (C1) | 1 | 2 | 2 | 6 |
| Experts 5 | Dimensions (C1) | 1 | 3 | 2 | 6 |
| Experts 6 | Dimensions (C1) | 1 | 4 | 2 | 6 |
The weights of all the main and sub-criteria are shown in Table 6, and the values taken by the alternatives for these criteria (decision matrix) are shown in Table 7. The weight calculations of the sub-criteria are presented in Appendix A.
After determining the decision alternatives and criteria weights, the ranking process was started with the GRA, COPRAS, and MULTIMOORA methods. The following section explains the details of the sorting process with the aforementioned methods.
Table 5
The weights of the main criteria.
| Criteria | Weights of criteria | Mean | |||||
| Exp. 1 | Exp. 2 | Exp. 3 | Exp. 4 | Exp. 5 | Exp. 6 | ||
| Dimensions (C1) | 0.0784 | 0.0923 | 0.0784 | 0.0879 | 0.0811 | 0.0709 | 0.0815 |
| Flexibility (C2) | 0.1373 | 0.1692 | 0.1373 | 0.1255 | 0.2703 | 0.2196 | 0.1765 |
| Productivity (C3) | 0.2745 | 0.2538 | 0.2549 | 0.2092 | 0.1351 | 0.1318 | 0.2099 |
| Cost (C4) | 0.5098 | 0.4846 | 0.5294 | 0.5774 | 0.5135 | 0.5777 | 0.5321 |
| Ksi | 0.0392 | 0.0231 | 0.0196 | 0.0502 | 0.0270 | 0.0811 | 0.0400 |
Table 6
The final weights of criteria.
| Main criteria | The weight of main criteria | Sub-criteria | The weight of sub-criteria | Final weights |
| Dimensions (C1) | 0.0815 | Table load (C11) | 0.197 | 0.016 |
| Main travel (C12) | 0.558 | 0.046 | ||
| Table size (C13) | 0.153 | 0.012 | ||
| Machine weight (C14) | 0.092 | 0.007 | ||
| Flexibility (C2) | 0.1765 | Spindle rate (C21) | 0.222 | 0.039 |
| Spindle power (C22) | 0.591 | 0.104 | ||
| Max. tool weight (C23) | 0.187 | 0.033 | ||
| Productivity (C3) | 0.2099 | Feed rate (C31) | 0.159 | 0.033 |
| Tool magazine capacity (C32) | 0.581 | 0.122 | ||
| Cutting feed rate (C33) | 0.261 | 0.055 | ||
| Cost (C4) | 0.5321 | Procurement price (C41) | 0.719 | 0.382 |
| Operation cost (C42) | 0.169 | 0.090 | ||
| Maintanance cost (C43) | 0.113 | 0.060 |
Table 7
The data of the alternatives (decision matrix).
| C1 | C2 | C3 | C4 | ||||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |
| Units | kg s | mm | m2 | kg s | rpm | kw | kg s | mm/min s | set | mm/min s | $ | $ | $ |
| Goal | Max | Max | Max | Min | Max | Max | Max | Max | Max | Max | Min | Min | Min |
| Alt.∖Weights | 0.016 | 0.046 | 0.012 | 0.007 | 0.039 | 0.104 | 0.033 | 0.033 | 0.122 | 0.055 | 0.382 | 0.090 | 0.060 |
| 400 | 687 | 0.465 | 5800 | 8000 | 7.5 | 7 | 28.0 | 24 | 10.0 | 206250 | 25800 | 5150 | |
| 400 | 720 | 0.500 | 6000 | 8000 | 5.5 | 6 | 26.7 | 24 | 12.0 | 262500 | 32000 | 5800 | |
| 800 | 710 | 0.720 | 8000 | 15000 | 7.5 | 10 | 27.9 | 32 | 1.2 | 318750 | 39800 | 7000 | |
| 300 | 600 | 0.550 | 3300 | 10000 | 10.1 | 3 | 52.0 | 21 | 30.0 | 335750 | 41000 | 8000 | |
| 1600 | 953 | 0.975 | 11000 | 8000 | 11 | 6 | 18.3 | 24 | 5.0 | 412500 | 51500 | 10300 | |
| 250 | 567 | 0.336 | 3800 | 12000 | 5.5 | 6 | 48.0 | 25 | 15.0 | 262500 | 31250 | 5470 | |
| 3000 | 980 | 1.000 | 12500 | 8000 | 11 | 15 | 19.3 | 20 | 10.0 | 487500 | 58000 | 11000 | |
| Min | 250 | 566.67 | 0.336 | 3300 | 8000 | 5.5 | 3 | 18.333 | 20 | 1.2 | 206250 | 25800 | 5150 |
| Max | 3000 | 980 | 1.000 | 12500 | 15000 | 11 | 15 | 52 | 32 | 30 | 487500 | 58000 | 11000 |
4.2Sorting the Alternatives Using GRA
The method consists of three basic steps: normalization, grey relational coefficient calculation, and grey relational degree calculation. In the first step, the data of the alternatives are transformed into comparison sequences by normalizing the criteria according to the benefits, cost, and optimality of the criteria. Normalized versions of the data presented in Table 7 are shown in Table 8.
Table 8
The normalized decision matrix.
| C1 | C2 | C3 | C4 | ||||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |
| Alt.∖Ref. serie | 1.000 | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| A1 | 0.055 | 0.290 | 0.194 | 0.728 | 0.000 | 0.364 | 0.333 | 0.287 | 0.333 | 0.306 | 1.000 | 1.000 | 1.000 |
| 0.055 | 0.371 | 0.247 | 0.707 | 0.000 | 0.000 | 0.250 | 0.248 | 0.333 | 0.375 | 0.800 | 0.807 | 0.889 | |
| 0.200 | 0.347 | 0.578 | 0.489 | 1.000 | 0.364 | 0.583 | 0.284 | 1.000 | 0.000 | 0.600 | 0.565 | 0.684 | |
| 0.018 | 0.081 | 0.322 | 1.000 | 0.286 | 0.836 | 0.000 | 1.000 | 0.083 | 1.000 | 0.540 | 0.528 | 0.513 | |
| 0.491 | 0.935 | 0.962 | 0.163 | 0.000 | 1.000 | 0.250 | 0.000 | 0.333 | 0.132 | 0.267 | 0.202 | 0.120 | |
| 0.000 | 0.000 | 0.000 | 0.946 | 0.571 | 0.000 | 0.250 | 0.881 | 0.417 | 0.479 | 0.800 | 0.831 | 0.945 | |
| 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | 1.000 | 1.000 | 0.030 | 0.000 | 0.306 | 0.000 | 0.000 | 0.000 | |
After the normalization process, the absolute value table is created by using the equation shown in equation (10). The values in the absolute value table correspond to the absolute value of the difference between the reference series and the criteria value. The absolute values calculated are shown in Table 9.
Table 9
The absolute value table.
| C1 | C2 | C3 | C4 | ||||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |
| Alt.∖Goal | Max | Max | Max | Min | Max | Max | Max | Max | Max | Max | Min | Min | Min |
| 0.945 | 0.710 | 0.806 | 0.728 | 1.000 | 0.636 | 0.667 | 0.713 | 0.667 | 0.694 | 1.000 | 1.000 | 1.000 | |
| 0.945 | 0.629 | 0.753 | 0.707 | 1.000 | 1.000 | 0.750 | 0.752 | 0.667 | 0.625 | 0.800 | 0.807 | 0.889 | |
| 0.800 | 0.653 | 0.422 | 0.489 | 0.000 | 0.636 | 0.417 | 0.716 | 0.000 | 1.000 | 0.600 | 0.565 | 0.684 | |
| 0.982 | 0.919 | 0.678 | 1.000 | 0.714 | 0.164 | 1.000 | 0.000 | 0.917 | 0.000 | 0.540 | 0.528 | 0.513 | |
| 0.509 | 0.065 | 0.038 | 0.163 | 1.000 | 0.000 | 0.750 | 1.000 | 0.667 | 0.868 | 0.267 | 0.202 | 0.120 | |
| 1.000 | 1.000 | 1.000 | 0.946 | 0.429 | 1.000 | 0.750 | 0.119 | 0.583 | 0.521 | 0.800 | 0.831 | 0.945 | |
| 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.970 | 1.000 | 0.694 | 0.000 | 0.000 | 0.000 | |
Grey coefficients (
Table 10
The absolute value table.
| C1 | C2 | C3 | C4 | Weighted rank | |||||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |||
| Goal | Max | Max | Max | Min | Max | Max | Max | Max | Max | Max | Min | Min | Min | ||
| Weights | 0.016 | 0.046 | 0.012 | 0.007 | 0.039 | 0.104 | 0.033 | 0.033 | 0.122 | 0.055 | 0.382 | 0.090 | 0.060 | ||
| 0.346 | 0.413 | 0.383 | 0.407 | 0.333 | 0.440 | 0.429 | 0.412 | 0.429 | 0.419 | 0.333 | 0.333 | 0.333 | 0.0286 | 7 | |
| 0.346 | 0.443 | 0.399 | 0.414 | 0.333 | 0.333 | 0.400 | 0.399 | 0.429 | 0.444 | 0.385 | 0.382 | 0.360 | 0.0298 | 6 | |
| 0.385 | 0.434 | 0.542 | 0.505 | 1.000 | 0.440 | 0.545 | 0.411 | 1.000 | 0.333 | 0.455 | 0.469 | 0.422 | 0.0411 | 3 | |
| 0.337 | 0.352 | 0.425 | 0.333 | 0.412 | 0.753 | 0.333 | 1.000 | 0.353 | 1.000 | 0.481 | 0.486 | 0.494 | 0.0402 | 4 | |
| 0.495 | 0.886 | 0.930 | 0.754 | 0.333 | 1.000 | 0.400 | 0.333 | 0.429 | 0.365 | 0.652 | 0.712 | 0.807 | 0.0493 | 2 | |
| 0.333 | 0.333 | 0.333 | 0.346 | 0.538 | 0.333 | 0.400 | 0.808 | 0.462 | 0.490 | 0.385 | 0.376 | 0.346 | 0.0314 | 5 | |
| 1.000 | 1.000 | 1.000 | 1.000 | 0.333 | 1.000 | 1.000 | 0.340 | 0.333 | 0.419 | 1.000 | 1.000 | 1.000 | 0.0645 | 1 | |
4.3Sorting the Alternatives Using COPRAS
The second method used to sort the alternatives is the COPRAS method. This method starts with the formation of the weighted decision matrix with the help of Eq. (14). The matrix obtained with this equation is shown in Table 11.
Table 11
The weighted normalized decision matrix for the COPRAS method.
| C1 | C2 | C3 | C4 | ||||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |
| Alt.∖Goal | Max | Max | Max | Min | Max | Max | Max | Max | Max | Max | Min | Min | Min |
| 0.0010 | 0.0060 | 0.0013 | 0.0009 | 0.0046 | 0.0135 | 0.0044 | 0.0042 | 0.0172 | 0.0066 | 0.0345 | 0.0083 | 0.0059 | |
| 0.0010 | 0.0063 | 0.0014 | 0.0009 | 0.0046 | 0.0099 | 0.0037 | 0.0040 | 0.0172 | 0.0079 | 0.0439 | 0.0103 | 0.0066 | |
| 0.0019 | 0.0062 | 0.0020 | 0.0012 | 0.0085 | 0.0135 | 0.0062 | 0.0042 | 0.0229 | 0.0008 | 0.0533 | 0.0128 | 0.0080 | |
| 0.0007 | 0.0052 | 0.0015 | 0.0005 | 0.0057 | 0.0181 | 0.0019 | 0.0079 | 0.0151 | 0.0197 | 0.0562 | 0.0132 | 0.0091 | |
| 0.0038 | 0.0083 | 0.0027 | 0.0016 | 0.0046 | 0.0197 | 0.0037 | 0.0028 | 0.0172 | 0.0033 | 0.0690 | 0.0165 | 0.0117 | |
| 0.0006 | 0.0049 | 0.0009 | 0.0006 | 0.0068 | 0.0099 | 0.0037 | 0.0073 | 0.0179 | 0.0099 | 0.0439 | 0.0100 | 0.0062 | |
| 0.0071 | 0.0086 | 0.0027 | 0.0019 | 0.0046 | 0.0197 | 0.0094 | 0.0029 | 0.0143 | 0.0066 | 0.0816 | 0.0186 | 0.0125 | |
After calculating the normalized decision matrix, the sum of the criteria values to be minimized for each alternative (
Table 12
Calculations of the COPRAS method.
| Alternatives | Order of alternatives | ||||||||
| 1.059 | 0.395 | 0.395 | 4.000 | 1.000 | 5.258 | 1.8195 | 86 | 4 | |
| 1.038 | 0.458 | 0.862 | 1.6936 | 80 | 7 | ||||
| 1.278 | 0.573 | 0.689 | 1.8020 | 85 | 5 | ||||
| 1.376 | 0.511 | 0.774 | 1.9647 | 93 | 2 | ||||
| 1.337 | 0.778 | 0.508 | 1.7236 | 82 | 6 | ||||
| 1.147 | 0.406 | 0.974 | 1.8877 | 90 | 3 | ||||
| 1.766 | 0.878 | 0.451 | 2.1089 | 100 | 1 |
4.4Sorting the Alternatives Using MULTIMOORA
The first step of the MULTIMOORA method also includes creating a decision matrix and weight vector with
Table 13
Normalized decision matrix.
| Alternatives | C1 | C2 | C3 | C4 | |||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |
| Goal | Max | Max | Max | Min | Max | Max | Max | Max | Max | Max | Min | Min | Min |
| Weights | 0.0160 | 0.0455 | 0.0125 | 0.0075 | 0.0393 | 0.1042 | 0.0330 | 0.0333 | 0.1219 | 0.0547 | 0.3825 | 0.0897 | 0.0599 |
| 0.1120 | 0.3410 | 0.2540 | 0.2780 | 0.2970 | 0.3300 | 0.3160 | 0.3130 | 0.3700 | 0.2590 | 0.2300 | 0.2360 | 0.2480 | |
| 0.1120 | 0.3580 | 0.2730 | 0.2870 | 0.2970 | 0.2420 | 0.2710 | 0.2980 | 0.3700 | 0.3100 | 0.2930 | 0.2930 | 0.2800 | |
| 0.2250 | 0.3530 | 0.3930 | 0.3830 | 0.5570 | 0.3300 | 0.4510 | 0.3120 | 0.4930 | 0.0310 | 0.3560 | 0.3640 | 0.3380 | |
| 0.0840 | 0.2980 | 0.3000 | 0.1580 | 0.3710 | 0.4440 | 0.1350 | 0.5820 | 0.3230 | 0.7760 | 0.3750 | 0.3750 | 0.3860 | |
| 0.4490 | 0.4740 | 0.5330 | 0.5270 | 0.2970 | 0.4840 | 0.2710 | 0.2050 | 0.3700 | 0.1290 | 0.4600 | 0.4710 | 0.4970 | |
| 0.0700 | 0.2820 | 0.1840 | 0.1820 | 0.4460 | 0.2420 | 0.2710 | 0.5370 | 0.3850 | 0.3880 | 0.2930 | 0.2860 | 0.2640 | |
| 0.8430 | 0.4870 | 0.5460 | 0.5980 | 0.2970 | 0.4840 | 0.6770 | 0.2160 | 0.3080 | 0.2590 | 0.5440 | 0.5310 | 0.5300 | |
After the normalized decision matrix is created, the alternative ranking is determined according to the decreasing order of the calculated
Table 14
Calculations of the ratio system.
| C1 | C2 | C3 | C4 | Order | |||||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |||
| Alt.∖Goal | Max | Max | Max | Min | Max | Max | Max | Max | Max | Max | Min | Min | Min | ||
| 0.002 | 0.016 | 0.003 | 0.002 | 0.012 | 0.034 | 0.010 | 0.010 | 0.045 | 0.014 | 0.088 | 0.021 | 0.015 | 0.020 | 1 | |
| 0.002 | 0.016 | 0.003 | 0.002 | 0.012 | 0.025 | 0.009 | 0.010 | 0.045 | 0.017 | 0.112 | 0.026 | 0.017 | −0.018 | 4 | |
| 0.004 | 0.016 | 0.005 | 0.003 | 0.022 | 0.034 | 0.015 | 0.010 | 0.060 | 0.002 | 0.136 | 0.033 | 0.020 | −0.024 | 5 | |
| 0.001 | 0.014 | 0.004 | 0.001 | 0.015 | 0.046 | 0.004 | 0.019 | 0.039 | 0.042 | 0.143 | 0.034 | 0.023 | −0.016 | 3 | |
| 0.007 | 0.022 | 0.007 | 0.004 | 0.012 | 0.050 | 0.009 | 0.007 | 0.045 | 0.007 | 0.176 | 0.042 | 0.030 | −0.087 | 6 | |
| 0.001 | 0.013 | 0.002 | 0.001 | 0.017 | 0.025 | 0.009 | 0.018 | 0.047 | 0.021 | 0.112 | 0.026 | 0.016 | −0.001 | ||
| 0.014 | 0.022 | 0.007 | 0.004 | 0.012 | 0.050 | 0.022 | 0.007 | 0.038 | 0.014 | 0.208 | 0.048 | 0.032 | −0.106 | ||
In the Reference Point Approach (RPA), which is a conservative method, first of all, the absolute difference (distance) between the
In the Full Multiplicative Form (FMF), the multiplication values of the criteria in the normalized decision matrix, which are in the direction of maximization, are divided by the multiplication value of the criteria to be minimized, and “
At the last stage, the rankings found as a result of the calculations above have been converted into a single line with the theory of dominance. The final ranks were determined by taking the average of the rankings. The final rankings determined by applying the theory of dominance in the MULTIMOORA method are given in Table 17. The order obtained in the last step is “
Table 15
Calculations of the reference point approach.
| C1 | C2 | C3 | C4 | Order | |||||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |||
| Alt.∖Goal | Max | Max | Max | Min | Max | Max | Max | Max | Max | Max | Min | Min | Min | ||
| 0.012 | 0.007 | 0.004 | 0.002 | 0.010 | 0.016 | 0.012 | 0.009 | 0.015 | 0.028 | 0.120 | 0.026 | 0.017 | 0.1201 | 7 | |
| 0.012 | 0.006 | 0.003 | 0.002 | 0.010 | 0.025 | 0.013 | 0.009 | 0.015 | 0.025 | 0.096 | 0.021 | 0.015 | 0.0961 | 5-6 | |
| 0.010 | 0.006 | 0.002 | 0.002 | 0.000 | 0.016 | 0.007 | 0.009 | 0.000 | 0.041 | 0.072 | 0.015 | 0.012 | 0.0720 | 4 | |
| 0.012 | 0.009 | 0.003 | 0.003 | 0.007 | 0.004 | 0.018 | 0.000 | 0.021 | 0.000 | 0.065 | 0.014 | 0.009 | 0.0648 | 3 | |
| 0.006 | 0.001 | 0.000 | 0.001 | 0.010 | 0.000 | 0.013 | 0.013 | 0.015 | 0.035 | 0.032 | 0.005 | 0.002 | 0.0353 | 2 | |
| 0.012 | 0.009 | 0.005 | 0.003 | 0.004 | 0.025 | 0.013 | 0.001 | 0.013 | 0.021 | 0.096 | 0.022 | 0.016 | 0.0961 | 5-6 | |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.010 | 0.000 | 0.000 | 0.012 | 0.023 | 0.028 | 0.000 | 0.000 | 0.000 | 0.0283 | 1 | |
| 0.014 | 0.022 | 0.007 | 0.004 | 0.022 | 0.050 | 0.022 | 0.019 | 0.060 | 0.042 | 0.208 | 0.048 | 0.032 | |||
Table 16
Calculations of the full multiplicative form.
| C1 | C2 | C3 | C4 | Order | |||||||||||
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | |||
| Alt.∖Goal | Max | Max | Max | Min | Max | Max | Max | Max | Max | Max | Min | Min | Min | ||
| 0.966 | 0.952 | 0.983 | 0.990 | 0.953 | 0.891 | 0.963 | 0.962 | 0.886 | 0.929 | 0.570 | 0.879 | 0.920 | 1.28132 | 1 | |
| 0.966 | 0.954 | 0.984 | 0.991 | 0.953 | 0.862 | 0.958 | 0.961 | 0.886 | 0.938 | 0.625 | 0.896 | 0.927 | 1.10843 | 3 | |
| 0.976 | 0.954 | 0.988 | 0.993 | 0.977 | 0.891 | 0.974 | 0.962 | 0.917 | 0.827 | 0.674 | 0.913 | 0.937 | 0.99529 | 5 | |
| 0.961 | 0.946 | 0.985 | 0.986 | 0.962 | 0.919 | 0.936 | 0.982 | 0.871 | 0.986 | 0.687 | 0.916 | 0.945 | 1.06753 | 4 | |
| 0.987 | 0.967 | 0.992 | 0.995 | 0.953 | 0.927 | 0.958 | 0.949 | 0.886 | 0.894 | 0.743 | 0.935 | 0.959 | 0.90819 | 6 | |
| 0.958 | 0.944 | 0.979 | 0.987 | 0.969 | 0.862 | 0.958 | 0.979 | 0.890 | 0.950 | 0.625 | 0.894 | 0.923 | 1.15174 | 2 | |
| 0.997 | 0.968 | 0.992 | 0.996 | 0.953 | 0.927 | 0.987 | 0.950 | 0.866 | 0.929 | 0.792 | 0.945 | 0.963 | 0.89015 | 7 | |
Table 17
Calculations of the full multiplicative form.
| Alternatives | RS | RPA | FMF | Mean | Final order |
| A1 | 1 | 7 | 1 | 3.00 | 1 |
| A2 | 4 | 6 | 3 | 4.33 | 4 |
| A3 | 5 | 4 | 5 | 4.67 | 5 |
| A4 | 3 | 3 | 4 | 3.33 | 3 |
| A5 | 6 | 2 | 6 | 4.67 | 6 |
| A6 | 2 | 5 | 2 | 3.00 | 2 |
| A7 | 7 | 1 | 7 | 5.00 | 7 |
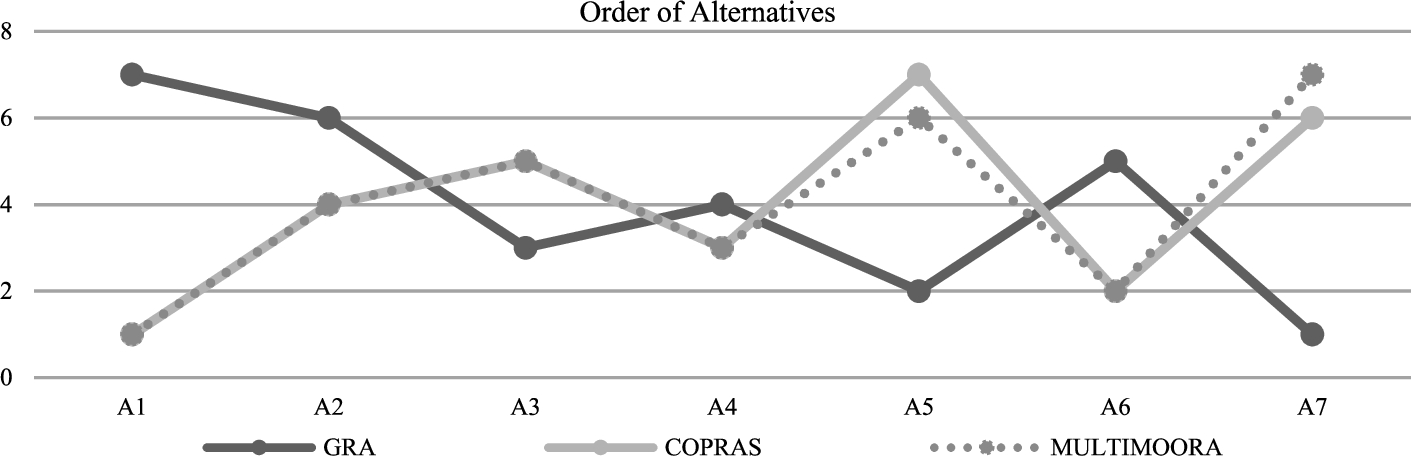
As a result, the different sequences shown in Table 18 and Fig. 2 were determined. The sequences obtained with the COPRAS and MULTIMOORA methods are similar. The rankings obtained by grey relational analysis differ from the other two methods. Due to the dominant ranking, decision-makers may consider Alternative 1 as the best option.
Table 18
Rankings obtained by different methods.
| Alternatives | GRA | COPRAS | MULTIMOORA |
| A1 | 7 | 1 | 1 |
| A2 | 6 | 4 | 4 |
| A3 | 3 | 5 | 5 |
| A4 | 4 | 3 | 3 |
| A5 | 2 | 7 | 6 |
| A6 | 5 | 2 | 2 |
| A7 | 1 | 6 | 7 |
Fig. 2
The final rankings obtained by different methods.
5Discussion and Conclusions
The abundance of machine alternatives, the difficulty in accessing reliable information, and the lack of experts in evaluating machine features make machine tool selection a difficult and important problem. In addition, it is known that an unsuitable machine selection adversely affects the efficiency, sensitivity, and flexibility of the entire production system. When all these situations are taken into consideration, it is seen that the right information should be made by the right people and using the appropriate methods for the selection of a proper machine tool. When the studies in the literature are examined, many different methods provide different solutions. In this context, many studies have been conducted in which the uncertainty situation, as well as deterministic methods, are taken into account. The important thing here is to make the right decision by evaluating the opinions of more than one expert working in the production environment with different methods, rather than a single method and a single expert’s opinion.
In this paper, a new framework is proposed to examine the performance of different methods using the same criteria weights for a suitable machine tool (CNC machine) selection problem. Weights of the criteria determined by BWM were used for weighting decision matrices for the sorting methods in this new framework. Using seven alternatives, four main, and thirteen sub-criteria in the problem, machine alternatives were evaluated with GRA, COPRAS, and MULTIMOORA methods. To create a reliable final ranking in the MULTIMOORA method, the theory of dominance was used and the final rankings were determined by averaging the different rank values. As a result, it is aimed to increase the reliability of the final solution with this new approach including BWM as the criteria weighting method. In the evaluations made for the main criteria, it has been seen that the cost of the machine tool is the most important criterion, as in the studies of similar criteria in the literature (Arslan et al., 2004; Önüt et al., 2008), followed by the productivity, flexibility and dimensions criteria, respectively. In the ranking made using the criterion weights obtained, it is seen that COPRAS and MULTIMOORA methods give similar rankings, but the gray relational analysis method offers a different ranking.
The proposed solution procedure is well-designed for the research problem. The CNC machine selection problem is also studied in many pieces of research. In this way, the selected seven alternatives, four main, and thirteen sub-criteria can also be accepted as the main research limitation. On the other hand, the obtained results are shown effective and robust decisions for the problem using comprehensive methods as the main advantage. In future studies, it may be considered that fuzzy logic-based methods can be used for the solution in cases where decision-makers express the importance levels of the criteria with linguistic variables. The evaluation of the expert opinions can be considered by intuitionistic approaches on MCDM methodologies.
Appendices
A
AAppendix. The Weights of Sub-Criteria
The weight calculation of sub-criteria of dimensions (C1) main criteria.
| BO vectors for sub-criteria | Experts No. | Best | Table load (C11) | Main travel (C12) | Table size (C13) | Machine weight (C14) |
| Experts 1 | Main travel (C12) | 4 | 1 | 2 | 6 | |
| Experts 2 | Main travel (C12) | 3 | 1 | 4 | 7 | |
| Experts 3 | Main travel (C12) | 4 | 1 | 5 | 8 | |
| Experts 4 | Main travel (C12) | 3 | 1 | 5 | 7 | |
| Experts 5 | Main travel (C12) | 2 | 1 | 6 | 4 | |
| Experts 6 | Main travel (C12) | 3 | 1 | 5 | 8 | |
| OW vectors for sub-criteria | Experts No. | Worst | Table load (C11) | Main travel (C12) | Table size (C13) | Machine weight (C14) |
| Experts 1 | Machine weight (C14) | 2 | 6 | 3 | 1 | |
| Experts 2 | Machine weight (C14) | 2 | 3 | 2 | 1 | |
| Experts 3 | Machine weight (C14) | 2 | 8 | 2 | 1 | |
| Experts 4 | Machine weight (C14) | 3 | 1 | 5 | 7 | |
| Experts 5 | Table size (C13) | 2 | 6 | 1 | 2 | |
| Experts 6 | Machine weight (C14) | 3 | 8 | 2 | 1 | |
| The weights of sub-criteria | Sub-criteria | Exp. 1 | Exp. 2 | Exp. 3 | Exp. 4 | Exp. 5 | Exp. 6 | Mean |
| Table load (C11) | 0.135 | 0.231 | 0.163 | 0.208 | 0.238 | 0.206 | 0.197 | |
| Main travel (C12) | 0.514 | 0.496 | 0.630 | 0.589 | 0.524 | 0.598 | 0.558 | |
| Table size (C13) | 0.270 | 0.174 | 0.130 | 0.125 | 0.095 | 0.124 | 0.153 | |
| Machine weight (C14) | 0.081 | 0.099 | 0.076 | 0.079 | 0.143 | 0.072 | 0.092 | |
| Ksi | 0.027 | 0.198 | 0.022 | 0.034 | 0.048 | 0.021 | 0.058 | |
The weight calculation of sub-criteria of flexibility (C2) main criteria.
| BO vectors for sub-criteria | Experts No. | Best | Spindle rate (C21) | Spindle power (C22) | Max. tool weight (C23) |
| Experts 1 | Spindle power (C22) | 2 | 1 | 4 | |
| Experts 2 | Spindle power (C22) | 3 | 1 | 5 | |
| Experts 3 | Spindle power (C22) | 3 | 1 | 2 | |
| Experts 4 | Spindle power (C22) | 4 | 1 | 2 | |
| Experts 5 | Spindle power (C22) | 3 | 1 | 2 | |
| Experts 6 | Spindle power (C22) | 3 | 1 | 6 | |
| OW vectors for sub-criteria | Experts No. | Worst | Spindle rate (C21) | Spindle power (C22) | Max. Tool Weight (C23) |
| Experts 1 | Max. tool weight (C23) | 2 | 4 | 1 | |
| Experts 2 | Max. tool weight (C23) | 2 | 5 | 1 | |
| Experts 3 | Spindle rate (C21) | 1 | 3 | 2 | |
| Experts 4 | Spindle rate (C21) | 1 | 4 | 2 | |
| Experts 5 | Spindle rate (C21) | 1 | 3 | 2 | |
| Experts 6 | Max. tool weight (C23) | 2 | 6 | 1 | |
| The weights of sub-criteria | Sub-criteria | Exp. 1 | Exp. 2 | Exp. 3 | Exp. 4 | Exp. 5 | Exp. 6 | Mean |
| Spindle rate (C21) | 0.286 | 0.225 | 0.167 | 0.143 | 0.292 | 0.222 | 0.222 | |
| Spindle power (C22) | 0.571 | 0.650 | 0.542 | 0.571 | 0.542 | 0.667 | 0.591 | |
| Max. tool weight (C23) | 0.143 | 0.125 | 0.292 | 0.286 | 0.167 | 0.111 | 0.187 | |
| Ksi | 0.000 | 0.025 | 0.042 | 0.000 | 0.042 | 0.000 | 0.0181 | |
The weight calculation of sub-criteria of productivity (C
| BO vectors for sub-criteria | Experts No. | Best | Feed rate (C31) | Tool magazine capacity (C23) | Cutting feed rate (C33) |
| Experts 1 | Tool magazine capacity (C23) | 5 | 1 | 3 | |
| Experts 2 | Tool magazine capacity (C23) | 4 | 1 | 2 | |
| Experts 3 | Tool magazine capacity (C23) | 2 | 1 | 3 | |
| Experts 4 | Tool magazine capacity (C23) | 2 | 1 | 2 | |
| Experts 5 | Tool magazine capacity (C23) | 5 | 1 | 3 | |
| Experts 6 | Tool magazine capacity (C23) | 4 | 1 | 2 | |
| OW vectors for sub-criteria | Experts No. | Worst | Feed rate (C31) | Tool magazine capacity (C23) | Cutting feed rate (C33) |
| Experts 1 | Feed rate (C31) | 1 | 5 | 2 | |
| Experts 2 | Feed rate (C31) | 1 | 4 | 2 | |
| Experts 3 | Cutting feed rate (C33) | 2 | 3 | 1 | |
| Experts 4 | Feed (C31) | 1 | 2 | 1 | |
| Experts 5 | Feed rate (C31) | 1 | 5 | 2 | |
| Experts 6 | Feed rate (C31) | 1 | 4 | 2 | |
| The weights of sub-criteria | Sub-criteria | Exp. 1 | Exp. 2 | Exp. 3 | Exp. 4 | Exp. 5 | Exp. 6 | Mean |
| Feed rate (C31) | 0.125 | 0.143 | 0.167 | 0.250 | 0.125 | 0.143 | 0.159 | |
| Tool magazine capacity (C32) | 0.650 | 0.571 | 0.542 | 0.500 | 0.650 | 0.571 | 0.581 | |
| Cutting feed rate (C33) | 0.225 | 0.286 | 0.292 | 0.250 | 0.225 | 0.286 | 0.261 | |
| Ksi | 0.025 | 0.000 | 0.042 | 0.000 | 0.025 | 0.000 | 0.015 | |
The weight calculation of sub-criteria of cost (C
| BO vectors for sub-criteria | Experts No. | Best | Procurement price (C41) | Operation cost (C42) | Maintenance cost (C43) |
| Experts 1 | Procurement price (C41) | 1 | 5 | 8 | |
| Experts 2 | Procurement price (C41) | 1 | 4 | 7 | |
| Experts 3 | Procurement price (C41) | 1 | 6 | 4 | |
| Experts 4 | Procurement price (C41) | 1 | 3 | 5 | |
| Experts 5 | Procurement price (C41) | 1 | 4 | 9 | |
| Experts 6 | Procurement price (C41) | 1 | 5 | 8 | |
| OW vectors for sub-criteria | Experts No. | Worst | Procurement price (C41) | Operation cost (C42) | Maintenance cost (C43) |
| Experts 1 | Maintenance cost (C43) | 8 | 2 | 1 | |
| Experts 2 | Maintenance cost (C43) | 7 | 2 | 1 | |
| Experts 3 | Operation cost (C42) | 6 | 1 | 2 | |
| Experts 4 | Maintenance cost (C43) | 5 | 2 | 1 | |
| Experts 5 | Maintenance cost (C43) | 9 | 2 | 1 | |
| Experts 6 | Maintenance cost (C43) | 8 | 2 | 1 | |
| The weights of sub-criteria | Sub-criteria | Exp. 1 | Exp. 2 | Exp. 3 | Exp. 4 | Exp. 5 | Exp. 6 | Mean |
| Procurement price (C41) | 0.753 | 0.717 | 0.704 | 0.650 | 0.736 | 0.753 | 0.719 | |
| Operation cost (C42) | 0.156 | 0.183 | 0.111 | 0.225 | 0.181 | 0.156 | 0.169 | |
| Maintanance cost (C43) | 0.091 | 0.100 | 0.185 | 0.125 | 0.083 | 0.091 | 0.113 | |
| Ksi | 0.026 | 0.017 | 0.037 | 0.025 | 0.014 | 0.026 | 0.024 | |
References
1 | Aghdaie, M.H., Zolfani, S.H., Zavadskas, E.K. ((2013) ). Decision making in machine tool selection: an integrated approach with SWARA and COPRAS-G methods. Inzinerine Ekonomika-Engineering Economics, 24: (1), 5–17. |
2 | Ahmadi, H.B., Kusi-Sarpong, S., Rezaei, J. ((2017) ). Assessing the social sustainability of supply chains using Best Worst Method. Resources, Conservation and Recycling, 129: , 99–106. |
3 | Akay, D. ((2011) ). Grey relational analysis based on instance based learning approach for classification of risks of occupational low back disorders. Safety Science, 49: (8–9), 1277–1282. |
4 | Amoozad Mahdiraji, H., Arzaghi, S., Stauskis, G., Zavadskas, E.K. ((2018) ). A hybrid fuzzy BWM-COPRAS method for analyzing key factors of sustainable architecture. Sustainability, 10: (5), 1626. |
5 | Arslan, M.C., Çatay, B., Budak, E. ((2004) ). A decision support system for machine tool selection. Journal of Manufacturing Technology Management, 15: (1), 101–109. |
6 | Athawale, V.M., Chakraborty, S. ((2010) ). A TOPSIS method-based approach to machine tool selection. In: Proceedings of the 2010 International Conference on Industrial Engineering and Operations Management Dhaka, Bangladesh, Vol. 2: , pp. 83–94. |
7 | Ayağ, Z. ((2007) ). A hybrid approach to machine-tool selection through AHP and simulation. International Journal of Production Research, 45: (9), 2029–2050. |
8 | Ayağ, Z., Özdemir, R. ((2006) ). A fuzzy AHP approach to evaluating machine tool alternatives. Journal of Intelligent Manufacturing, 17: (2), 179–190. |
9 | Ayağ, Z., Özdemir, R. ((2011) ). An intelligent approach to machine tool selection through fuzzy analytic network process. Journal of Intelligent Manufacturing, 22: , 163–177. |
10 | Ayağ, Z., Özdemir, R. ((2012) ). Evaluating machine tool alternatives through modified TOPSIS and alpha-cut based fuzzy ANP. International Journal of Production Economics, 140: (2), 630–636. |
11 | Aydemir, E. ((2020) ). A new approach for interval grey numbers: n-th order degree of greyness. Journal of Grey System, 32: (2), 89–103. |
12 | Aydemir, E., Sahin, Y. ((2019) ). Evaluation of healthcare service quality factors using grey relational analysis in a dialysis center. Grey Systems: Theory and Application, 9: (4), 432–448. |
13 | Aydemir, E., Bedir, F., Özdemir, G. ((2013) ). Grey system theory and applications: a literature review. Suleyman Demirel University The Journal of Faculty of Economics and Administrative Sciences, 18: (3), 187–200. |
14 | Baynal, K., Sarı, T., nar B, A. ((2018) ). Risk management in automotive manufacturing process based on FMEA and grey relational analysis: a case study. Advances in Production Engineering Management, 13: (1), 69–80. |
15 | Brauers, W.K.M., Zavadskas, E.K. ((2006) ). The MOORA method and its application to privatization in a transition economy. Control and Cybernetics, 35: , 445–469. |
16 | Brauers, W.K.M., Zavadskas, E.K., Peldschus, F., Turskis, Z. ((2008) ). Multi-objective decision-making for road design. Transport, 23: (3), 183–193. |
17 | Brauers, W.K.M., Zavadskas, E.K. ((2010) ). Project management by MULTIMOORA as an instrument for transition economies. Technological and economic development of economy, 16: (1), 5–24. |
18 | Brauers, W.K.M., Zavadskas, E.K. ((2011) ). MULTIMOORA optimization used to decide on a bank loan to buy property. Technological and economic development of economy, 17: (1), 174–188. |
19 | Brauers, W.K.M., Zavadskas, E.K. ((2012) ). Robustness of MULTIMOORA: a method for multi-objective optimization. Informatica, 23: (1), 1–25. |
20 | Cakir, E., Akel, G. ((2017) ). Evaluation of service quality of hotel and holiday reservation web sites in Turkey by Integrated Swara-Gray relationship analysis method. Press Academia Procedia, 31: (1), 81–95. |
21 | Cakir, S. ((2018) ). An integrated approach to machine selection problem using fuzzy SMART-fuzzy weighted axiomatic design. Journal of Intelligent Manufacturing, 29: (7), 1433–1445. |
22 | Chakraborty, S., Boral, S. ((2017) ). A developed case-based reasoning system for machine tool selection. Benchmarking: An International Journal, 24: (5), 1364–1385. |
23 | Chan, J.W., Tong, T.K. ((2007) ). Multi-criteria material selections and end-of-life product strategy: grey relational analysis approach. Materials Design, 28: (5), 1539–1546. |
24 | Chen, W.H., Tsai, M.S., Kuo, H.L. ((2005) ). Distribution system restoration using the hybrid fuzzy-grey method. IEEE Transactions on Power Systems, 20: (1), 199–205. |
25 | Chen, Y., Ran, Y., Wang, Z., Li, X., Yang, X., Zhang, G. ((2021) ). Meta-action reliability-based mechanical product optimization design under uncertainty environment. Engineering Applications of Artificial Intelligence, 100: , 104174. |
26 | Çimren, E., Çatay, B., Budak, E. ((2007) ). Development of a machine tool selection system using AHP. The International Journal of Advanced Manufacturing Technology, 35: (3–4), 363–376. |
27 | Dağdeviren, M. ((2008) ). Decision making in equipment selection: an integrated approach with AHP and PROMETHEE. Journal of Intelligent Manufacturing, 19: (4), 397–406. |
28 | Durán, O., Aguilo, J. ((2008) ). Computer-aided machine-tool selection based on a fuzzy-AHP approach. Expert Systems with Applications, 34: (3), 1787–1794. |
29 | Feng, C.M., Wang, R.T. ((2000) ). Performance evaluation for airlines including the consideration of financial ratios. Journal of Air Transport Management, 6: (3), 133–142. |
30 | Gupta, H. ((2018) ). Evaluating service quality of airline industry using hybrid best worst method and VIKOR. Journal of Air Transport Management, 68: , 35–47. |
31 | Hafezalkotob, A., Hafezalkotob, A. ((2016) ). Extended MULTIMOORA method based on Shannon entropy weight for materials selection. Journal of Industrial Engineering International, 12: (1), 1–13. |
32 | Hafezalkotob, A., Hafezalkotob, A., Liao, H., Herrera, F. ((2019) ). An overview of MULTIMOORA for multi-criteria decision-making: theory, developments, applications, and challenges. Information Fusion, 51: , 145–177. |
33 | Hashemi, S.H., Karimi, A., Tavana, M. ((2015) ). An integrated green supplier selection approach with analytic network process and improved Grey relational analysis. International Journal of Production Economics, 159: , 178–191. |
34 | He, R.S., Hwang, S.F. ((2007) ). Damage detection by a hybrid real-parameter genetic algorithm under the assistance of grey relation analysis. Engineering Applications of Artificial Intelligence, 20: (7), 980–992. |
35 | Ho, C.Y., Lin, Z.C. ((2003) ). Analysis and application of grey relation and ANOVA in chemical–mechanical polishing process parameters. The International Journal of Advanced Manufacturing Technology, 21: (1), 10–14. |
36 | Huang, K.Y., Jane, C.J. ((2009) ). A hybrid model for stock market forecasting and portfolio selection based on ARX, grey system and RS theories. Expert Systems with Applications, 36: (3), 5387–5392. |
37 | İç, Y.T. ((2012) ). An experimental design approach using TOPSIS method for the selection of computer-integrated manufacturing technologies. Robotics and Computer-Integrated Manufacturing, 28: (2), 245–256. |
38 | İç, Y.T., Yurdakul, M., Eraslan, E. ((2012) ). Development of a component-based machining centre selection model using AHP. International Journal of Production Research, 50: (22), 6489–6498. |
39 | Ilangkumaran, M., Sasirekha, V., Anojkumar, L., Boopathi Raja, M. ((2012) ). Machine tool selection using AHP and VIKOR methodologies under fuzzy environment. International Journal of Modelling in Operations Management, 2: (4), 409–436. |
40 | Izadikhah, M. ((2015) ). A fuzzy goal programming based procedure for machine tool selection. Journal of Intelligent Fuzzy Systems, 28: (1), 361–372. |
41 | Jiang, B.C., Tasi, S.L., Wang, C.C. ((2002) ). Machine vision-based gray relational theory applied to IC marking inspection. IEEE Transactions on Semiconductor Manufacturing, 15: (4), 531–539. |
42 | Jing, S., Niu, Z., Chang, P. ((2015) ). The application of VIKOR for the tool selection in lean management. Journal of Intelligent Manufacturing, 30: , 2901–2912. |
43 | Kaklauskas, A., Zavadskas, E.K., Raslanas, S. ((2005) ). Multivariant design and multiple criteria analysis of building refurbishments. Energy and Buildings, 37: (4), 361–372. |
44 | Kaklauskas, A., Zavadskas, E.K., Raslanas, S., Ginevicius, R., Komka, A., Malinauskas, P. ((2006) ). Selection of low-e windows in retrofit of public buildings by applying multiple criteria method COPRAS: a Lithuanian case. Energy and Buildings, 38: (5), 454–462. |
45 | Karim, R., Karmaker, C.L. ((2016) ). Machine selection by AHP and TOPSIS methods. American Journal of Industrial Engineering, 4: (1), 7–13. |
46 | Keshavarz Ghorabaee, M., Amiri, M., Sadaghiani, J.S., Goodarzi, G.H. ((2014) ). Multiple criteria group decision-making for supplier selection based on COPRAS method with interval type-2 fuzzy sets. The International Journal of Advanced Manufacturing Technology, 75: (5–8), 1115–1130. |
47 | Kheybari, S., Kazemi, M., Rezaei, J. ((2019) ). Bioethanol facility location selection using best-worst method. Applied Energy, 242: , 612–623., 242, 612-623. |
48 | Kulak, O., Durmuşoğlu, M.B., Kahraman, C. ((2005) ). Fuzzy multi-attribute equipment selection based on information axiom. Journal of Materials Processing Technology, 169: (3), 337–345. |
49 | Kumar, J., Soota, T., Singh, G.S. ((2015) ). TOPSIS and VIKOR approaches to machine tool selection. Journal of Scientific Research and Advances, 2: (3), 125–130. |
50 | Kumru, M., Kumru, P. ((2015) ). A fuzzy ANP model for the selection of 3D coordinate-measuring machine. Journal of Intelligent Manufacturing, 26: , 999–1010. |
51 | Kuo, Y., Yang, T., Huang, G.W. ((2008) ). The use of grey relational analysis in solving multiple attribute decision-making problems. Computers Industrial Engineering, 55: (1), 80–93. |
52 | Lakshmanan, M., Rajadurai, J.S., Rajakarunakaran, S. ((2021) ). Machining studies of Al7075 in CNC turning using grey relational analysis. Materials Today: Proceedings, 39: , 1625–1628. |
53 | Li, H., Wang, W., Fan, L., Li, Q., Chen, X. ((2020) ). A novel hybrid MCDM model for machine tool selection using fuzzy DEMATEL, entropy weighting and later defuzzification VIKOR. Applied Soft Computing, 91: , 106207. |
54 | Lim, J., Kim, D.Y., Kim, S. ((2018) ). An experimental study for quality assurance of free-form concrete panels produced by CNC machine. Journal of Civil Engineering and Management, 24: (2), 145–154. |
55 | Lin, C.L., Lin, J.L., Ko, T.C. ((2002) ). Optimisation of the EDM process based on the orthogonal array with fuzzy logic and grey relational analysis method. The International Journal of Advanced Manufacturing Technology, 19: (4), 271–277. |
56 | Liu, D. ((2011) ). E-commerce system security assessment based on grey relational analysis comprehensive evaluation. International Journal of Digital Content Technology and Its Applications, 5: (10), 279–284. |
57 | Liu, P., Tuo, J., Liu, F., Li, C., Zhang, X. ((2018) ). A novel method for energy efficiency evaluation to support efficient machine tool selection. Journal of Cleaner Production, 191: , 57–66 |
58 | Nguyen, H.T., Dawal, S.Z., Nukman, Y., Aoyama, H., Case, K. ((2015) ). An integrated approach of fuzzy linguistic preference based AHP and fuzzy COPRAS for machine tool evaluation. PloS One, 10: (9), e0133599. |
59 | Olson, D.L., Wu, D. ((2006) ). Simulation of fuzzy multiattribute models for grey relationships. European Journal of Operational Research, 175: (1), 111–120. |
60 | Önüt, S., Soner Kara, S., Efendigil, T. ((2008) ). A hybrid fuzzy MCDM approach to machine tool selection. Journal of Intelligent Manufacturing, 19: (4), 443–453. |
61 | Özceylan, E., Kabak, M., Dağdeviren, M. ((2016) ). A fuzzy-based decision making procedure for machine selection problem. Journal of Intelligent Fuzzy Systems, 30: (3), 1841–1856. |
62 | Özdağoğlu, A., Yakut, E., Bahar, S. ((2017) ). Machine selection in a dairy product company with entropy and SAW methods integration. Dokuz Eylül University Faculty of Economics and Administrative Science Journal, 32: (1), 341–359. |
63 | Özdemir, A.I., Deste, M. ((2009) ). Multicriteria supplier selection by gray relational analysis: a case study in automotive industry. Istanbul University Journal of the School of Business Administration, 38: (2), 147–156. |
64 | Özgen, A., Tuzkaya, G., Tuzkaya, U.R., Özgen, D. ((2011) ). A multi-criteria decision-making approach for machine tool selection problem in a fuzzy environment. International Journal of Computational Intelligence Systems, 4: (4), 431–445. |
65 | Paramasivam, V., Senthil, V., Ramasamy, N.R. ((2011) ). Decision making in equipment selection: an integrated approach with digraph and matrix approach, AHP and ANP. The International Journal of Advanced Manufacturing Technology, 54: (9–12), 1233–1244. |
66 | Patel, N., Patel, R., Patel, U., Patel, B. ((2012) ). A novel approach for selection of tool insert in CNC turning process using MADM methods. International Journal of Engineering and Advanced Technology, 1: (5), 2249–2258. |
67 | Perçin, S., Min, H. ((2013) ). Optimal machine tools selection using quality function deployment and fuzzy multiple objective decision making approach. Journal of Intelligent Fuzzy Systems, 24: (1), 163–174. |
68 | Popović, G., Stanujkić, D., Stojanović, S. ((2012) ). Investment project selection by applying copras method and imprecise data. Serbian Journal of Management, 7: (2), 257–269. |
69 | Prakash, K.S., Gopal, P.M., Karthik, S. ((2020) ). Multi-objective optimization using Taguchi based grey relational analysis in turning of Rock dust reinforced Aluminum MMC. Measurement, 157: , 107664. |
70 | Prasad, K., Chakraborty, S. ((2015) ). Development of a QFD-based expert system for CNC turning centre selection. Journal of Industrial Engineering International, 11: (4), 575–594. |
71 | Qi, J. ((2010) ). Machine tool selection model based on fuzzy MCDM approach. In: International Conference on Intelligent Control and Information Processing. IEEE, pp. 282–285. |
72 | Ramesh, S., Viswanathan, R., Ambika, S. ((2016) ). Measurement and optimization of surface roughness and tool wear via grey relational analysis, TOPSIS and RSA techniques. Measurement, 78: , 63–72. |
73 | Rao, R.V. ((2006) ). A decision-making framework model for evaluating flexible manufacturing systems using digraph and matrix methods. The International Journal of Advanced Manufacturing Technology, 30: (11–12), 1101–1110. |
74 | Rao, R.V., Parnichkun, M. ((2009) ). Flexible manufacturing system selection using a combinatorial mathematics-based decision-making method. International Journal of Production Research, 47: (24), 6981–6998. |
75 | Rezaei, J. ((2015) ). Best-worst multi-criteria decision-making method. Omega, 53: , 49–57. |
76 | Rezaei, J., Nispeling, T., Sarkis, J., Tavasszy, L. ((2016) ). A supplier selection life cycle approach integrating traditional and environmental criteria using the best worst method. Journal of Cleaner Production, 135: , 577–588. |
77 | Sahin, Y., Aydemir, E. ((2019) ). An AHP-weighted grey relational analysis method to determine the technical characteristics’ importance levels of the smartphone. Eskisehir Osmangazi University Journal of Economics and Administrative Sciences, 14: (1), 225–238. |
78 | Sahu, A.K., Datta, S., Mahapatra, S.S. ((2015) b). GDMP for CNC machine tool selection with a compromise ranking method using generalised fuzzy circumstances. International Journal of Computer Aided Engineering and Technology, 7: (1), 92–108. |
79 | Sahu, A.K., Sahu, N.K., Sahu, A.K. ((2015) a). Benchmarking CNC machine tool using hybrid-fuzzy methodology: a multi-indices decision making (MCDM) approach. International Journal of Fuzzy System Applications, 4: (2), 28–46. |
80 | Sahu, A., Sahu, N., Sahu, A. ((2014) ). Appraisal of CNC machine tool by integrated MULTI-MOORA-IVGN circumferences: an empirical study. Grey Systems: Theory and Application, 4: (1), 104–123. |
81 | Salimi, N., Rezaei, J. ((2018) ). Evaluating firms’ RD performance using best worst method. Evaluation and Program Planning, 66: , 147–155. |
82 | Samanlioglu, F., Ayağ, Z. ((2016) ). Fuzzy ANP-based PROMETHEE II approach for evaluation of machine tool alternatives. Journal of Intelligent Fuzzy Systems, 30: (4), 2223–2235. |
83 | Samvedi, A.J., Jain, V. Chan, F.T. ((2012) ). An integrated approach for machine tool selection using fuzzy analytical hierarchy process and grey relational analysis. International Journal of Production Research, 50: (12), 3211–3221. |
84 | Sarkar, A.P., Das, D., Sarkar, B. ((2015) ). Developing an efficient decision support system for non-traditional machine selection: an application of MOORA and MOOSRA. Production Manufacturing Research, 3: (1), 324–342. |
85 | Taha, Z., Rostam, S. ((2012) ). A hybrid fuzzy AHP-PROMETHEE decision support system for machine tool selection in flexible manufacturing cell. Journal of Intelligent Manufacturing, 23: (6), 2137–2149. |
86 | Tayyar, N., Akcanlı, F., Genç, E., Erem, I. ((2014) ). Financial performance evaluation of technology companies quoted in BIST with Analytic Hierarchy Process (AHP) and Grey Relational Analysis (GRA). The Journal of Accounting and Finance, 61: , 19–40. |
87 | Tho, N.H., Md Dawal, S.Z., Yusoff N, b., Tahriri, F., Aoyama, H. ((2013) ). Selecting a CNC machine tool using the intuitionistic fuzzy TOPSIS approach for FMC. Applied Mechanics and Materials, 315: , 199–205. |
88 | Tseng, M.L. ((2009) ). A causal and effect decision making model of service quality expectation using grey-fuzzy DEMATEL approach. Expert Systems with Applications, 36: (4), 7738–7748. |
89 | Vatansever, K., Kazancoglu, Y. ((2014) ). Integrated usage of fuzzy multi criteria decision making techniques for machine selection problems and an application. International Journal of Business and Social Science, 5: (9), 12–24. |
90 | Villa Silva, A.J., Pérez-Domínguez, L., Martínez Gómez, E., Luviano-Cruz, D., Valles-Rosales, D. ((2021) ). Dimensional analysis under linguistic Pythagorean fuzzy set. Symmetry, 13: (3), 440. |
91 | Weng, L., Zhang, Q., Lin, Z., Wu, L. ((2021) ). Harnessing heterogeneous social networks for better recommendations: A grey relational analysis approach. Expert Systems with Applications, 174: , 114771. |
92 | Wu, Z., Ahmad, J., Xu, J. ((2016) ). A group decision making framework based on fuzzy VIKOR approach for machine tool selection with linguistic information. Applied Soft Computing, 2: (3), 314–324. |
93 | Yang, C.C., Chen, B.S. ((2006) ). Supplier selection using combined analytical hierarchy process and grey relational analysis. Journal of Manufacturing Technology Management, 17: (7), 926–941. |
94 | Yazdani, M., Kahraman, C., Zarate, P., Onar, S.C. ((2019) ). A fuzzy multi attribute decision framework with integration of QFD and grey relational analysis. Expert Systems with Applications, 115: , 474–485. |
95 | Yildirim, B.F. ((2014) ). Gri iliskisel analiz. In: Yildirim, F.B., Onder, E. (Eds.), Cok Kriterli Karar Verme Yöntemleri, pp. 227–242 |
96 | Yildirim, B.F., Timor, M. ((2019) ). Development of a supplier selection model using fuzzy and grey COPRAS methods. Optimum Journal of Economics and Management Sciences, 6: (2), 283–310. |
97 | Yilmaz, E., Gungor, F. ((2010) ). Gri iliskisel analiz yontemine gore farklı sertliklerde optimum takim tutucusunun belirlenmesi. In: 2. Ulusal Tasarım Imalat ve Analiz Kongresi, pp. 11–12. |
98 | Yurdakul, M. ((2004) ). AHP as a strategic decision-making tool to justify machine tool selection. Journal of Materials Processing Technology, 146: (3), 365–376. |
99 | Yurdakul, M., Ic, Y. ((2009) ). Analysis of the benefit generated by using fuzzy numbers in a TOPSIS model developed for machine tool selection problems. Journal of Materials Processing Technology, 209(1): , 310–317. |
100 | Zaied, A.N., Ismail, M., Gamal, A., Mostafa, N. ((2019) ). An integrated neutrosophic and MOORA for selecting machine tool. Neutrosophic Sets and Systems, 28: (1), 23–33. |
101 | Zavadskas, E.K., Kaklauskas, A., Sarka, V. ((1994) ). The new method of multicriteria complex proportional assessment of projects. Technological and Economic Development of Economy, 1: (3), 131–139. |
102 | Zavadskas, E.K., Kaklauskas, A., Peldschus, F., Turskis, Z. ((2007) ). Multi-attribute assessment of road design solutions by using the COPRAS method. The Baltic Journal of Road and Bridge Engineering, 2: (4), 195–203. |
103 | Zavadskas, E.K., Turskis, Z., Tamošaitiene, J. ((2010) ). Risk assessment of construction projects. Journal of Civil Engineering and Management, 16: (1), 33–46. |
104 | Zhongmin, S., Xizu, Y. ((2009) ). Critical path for a grey interval project network. In: International Conference on Grey Systems and Intelligent Services. IEEE, pp. 697–701. |




