Developing of a Novel Integrated MCDM MULTIMOOSRAL Approach for Supplier Selection
Abstract
The main aim of the article is to propose a new multiple criteria decision-making approach for selecting alternatives, the newly-developed MULTIMOOSRAL approach, which integrates advantages of the three well-known and prominent multiple-criteria decision-making methods: MOOSRA, MOORA, and MULTIMOORA. More specifically, the MULTIMOOSRAL method has been further upgraded with an approach that can be clearly seen in the well-known WASPAS and CoCoSo methods, which rely on the integration of weighted sum and weighted product approaches. In addition to the above approaches, the MULTIMOOSRAL method also integrates a logarithmic approximation approach. The expectation from the development of this method is that the integration of several approaches can provide a much more reliable selection of the most appropriate alternative, which can be very important in cases where the performance of alternatives obtained by using some other method does not differ much. Finally, the ranking of alternatives based on the dominance theory, used in the MOORA and MULTIMOORA methods, is replaced by a new original approach that should allow a much simpler final ranking of alternatives in order to reach a stronger result with five different techniques. The suitability and efficacy of the proposed MULTIMOOSRAL approach are presented through an illustrative case study of the supplier selection.
1Introduction
The increasing competitiveness and complexity of the market, the accelerated development of information and communication technologies have caused the decision-making process in many organizations to become of crucial and decisive importance. Decision-making involves human judgments and logic. Therefore, increasingly complex business conditions require a multi-criteria approach to solving business problems, which allows an objective comparison of several alternatives evaluated in a system of multiple heterogeneous and different criteria with other extremization requirements and different relative importance. Consequently, multi-criteria decision-making (MCDM) methods are useful for facilitation of decision-making process in situations when there are a number of often conflicting criteria (Karamaşa et al., 2020; Stanujkic et al., 2019). Hafezalkotob et al. (2019a) emphasizes three categories of the MCDM techniques, such as: Value Measurement Methods (the SAW method; the WASPAS method etc.); Goal or Reference Level Models (the VIKOR method, the TOPSIS method etc.); and Outranking Techniques (the ELECTRE method; the PROMETHEE method etc.).
Accelerated growth and the existence of numerous methods of multi-criteria decision-making can improve the decision-making process in all areas of life. Solving problems by utilizing MCDM is based on quantitative analyses and represent elegant solutions when making decisions between multiple alternatives based on multiple-criteria. Therefore, in due course of time, there are prominent and most common developed MCDM methods, among the dozens of approaches proposed over time for solving complex-decision making problems, such as the Maxmax method, the Maxmin method, the SAW method, the AHP method, the ELECTRE method, the PROMETHEE method, the TOPSIS method, the VIKOR method, the COPRAS method, the MACBETH method, the ANP method, the MOORA method, the MULTIMOORA method, and so forth (Zavadskas et al., 2020; Ulutaş et al., 2020; Jauković-Jocić et al., 2020).
The need to solve as wide a range of real-world problems has led to the creation of a new generation of MCDM methods and approaches, such as: the HEBIN method (Zavadskas et al., 2021); the MARCOS method (Stević et al., 2020); the CoCoSo method (Yazdani et al., 2019); the SECA method (Keshavarz-Ghorabaee et al., 2018); the FUCOM method (Pamučar et al., 2018); the ARCAS (Stanujkic et al., 2017a); the PIPRECIA method (Stanujkić et al., 2017b); the MABAC method (Pamučar and Ćirović, 2015); the EDAS method (Keshavarz Ghorabaee et al., 2015), and so forth. Some of the aforementioned methods were used for ranking of alternatives whereas some of them for the purpose of weight determination.
The MOOSRA method (Multi-Objective Optimization on the basis of Simple Ratio Analysis) belongs to the group of multi-objective optimization methods and is developed by Brauers (2004). The main difference between the MOOSRA method and the MOORA method is reflected in the negative performance scores that do not appear in the MOOSRA method, unlike the MOORA method. Besides, the MOOSRA method is less sensitive to the large variation in the values of the criteria (Adalı and Işık, 2017). So far, the MOOSRA method has been applied for solving of a various complex decision-making problems, such as: the laptop selection problem (Adalı and Işık, 2017); project-critical path selection (Dorfeshan et al., 2018); bio-medical waste disposal assessment (Narayanamoorthy et al., 2020); machine selection (Sarkar et al., 2015), and so forth. The simplicity of the calculation procedure of the MOOSRA method, which is based on the ratio between weighted ratings of beneficial and non-beneficial criteria, can be mentioned as an important characteristic of this method.
Brauers (2004) also developed the MOORA method (Multi-Objective on the basis of Ratio Analysis). Somewhat later, based on the ideas of the MOORA method, Brauers and Zavadskas (2010) have proposed the MULTIMOORA method (Multi-Objective Optimization by Ratio Analysis plus Full Multiplicative Form). Both methods have been proposed to cope with subjectivity problems. The usability of the MOORA method has been demonstrated in numerous cases, such as: credit evaluation model using MOORA method (İç, 2020); evaluation of the work performance (Fadli and Imtihan, 2019); decision-making in the production system (Attri and Grover, 2014); supplier selection (Karande and Chakraborty, 2012); decision-making in a manufacturing environment (Chakraborty, 2011); privatization in a transition economy (Brauers and Zavadskas, 2006), and so on. When it comes to the MULTIMOORA method, the same has also been applied in various and numerous cases, such as: personnel selection (Karabasevic et al., 2015; Baležentis et al., 2012); risk assessment (Liu et al., 2014); project management (Brauers and Zavadskas, 2010); strategy assessment (Fedajev et al., 2020); ranking of the renewable energy sources (Alkan and Albayrak, 2020); site selection (Rahimi et al., 2020); hybrid vehicle engine selection (Hafezalkotob et al., 2019b), and so on. Integration of several proven multicriteria approaches for ranking alternatives and the use of dominance theory for the final ranking of alternatives can be mentioned as an important characteristic of these methods, which is also proven in the above-mentioned articles.
The main motivation of this research is to develop a new simpler and much more reliable MCDM approach for selecting alternatives. Accordingly, the paper aims to propose a new MCDM-based technique that is based in some segments on previous well-known MCDM techniques (MOOSRA, MOORA, MULTIMOORA), and as a novelty also includes the logarithmic approximation (LA) approach. Therefore, it is also important to state that there are four arithmetic operations in the proposed MULTIMOOSRAL method. These are as follows: addition, subtraction, multiplication, and division. In addition to these arithmetic operations, a fifth evaluation technique, which is the logarithmic approach has been added to the MULTIMOOSRAL method. Thus, unlike other methods (MULTIMOORA, MOORA, and MOOSRA), the MULTIMOOSRAL method was tried to reach a stronger result with five different techniques. For example, MULTIMOORA method uses only three arithmetic operations, which are subtraction, division, and multiplication. On the other hand, MOORA and MOOSRA use only two arithmetic operations. However, the MULTIMOOSRAL method uses all arithmetic operations and a logarithmic approach to reach much more valid and rigorous results.
Further, highlights of the logarithmic normalization are emphasized by Zavadskas and Turskis (2008). Therefore, the newly-developed, so-called MULTIMOOSRAL method integrates five approaches for ranking alternatives. In order to apply and test the new approach, an illustrative case study of the supplier selection is conducted. Accordingly, the paper is structured as follows: in Section 1, the introductory consideration are given. In Section 2, the MOOSRA method, the MOORA method and the MULTIMOORA method are presented. The new MULTIMOOSRAL approach is presented in Section 3, whereas in Section 4, a conducted case study is demonstrated. Finally, at the end of the article, conclusions are given.
2Methodology
2.1The MOOSRA Method
The overall performance score of each alternative
(1)
The MOOSRA method uses vector normalization procedure for normalization as follows:
(2)
In the MOOSRA method, the alternatives are ranked on the basis of values of
2.2The MOORA Method
The MOORA method combines two approaches to ranking alternatives. The first approach, named the Ratio System (RS) approach, calculates the difference between the ratings of beneficial and non-beneficial criteria as follows:
(3)
The alternative with a higher value of
The second approach, named the Reference Point (RP) approach, is based on Tchebycheff Min–Max metric. A maximal distance between alternative and the reference point
(4)
(5)
The alternative with the lowest value of
The final ranking of the alternatives in the MOORA method is based on the dominance theory, i.e. the alternative with the highest number of appearances in the first positions on two ranking lists is the most appropriate alternative.
2.3The MULTIMOORA Method
The MULTIMOORA method combines three approaches, where two are adopted from the MOORA method, as shown in Fig. 1. The third approach, named Full Multiplicative Form (FMF), calculates the ratio between ratings of beneficial and non-beneficial criteria as follows:
(6)
The alternative with a higher value of
Fig. 1
Computational procedure of the MULTIMOORA method.
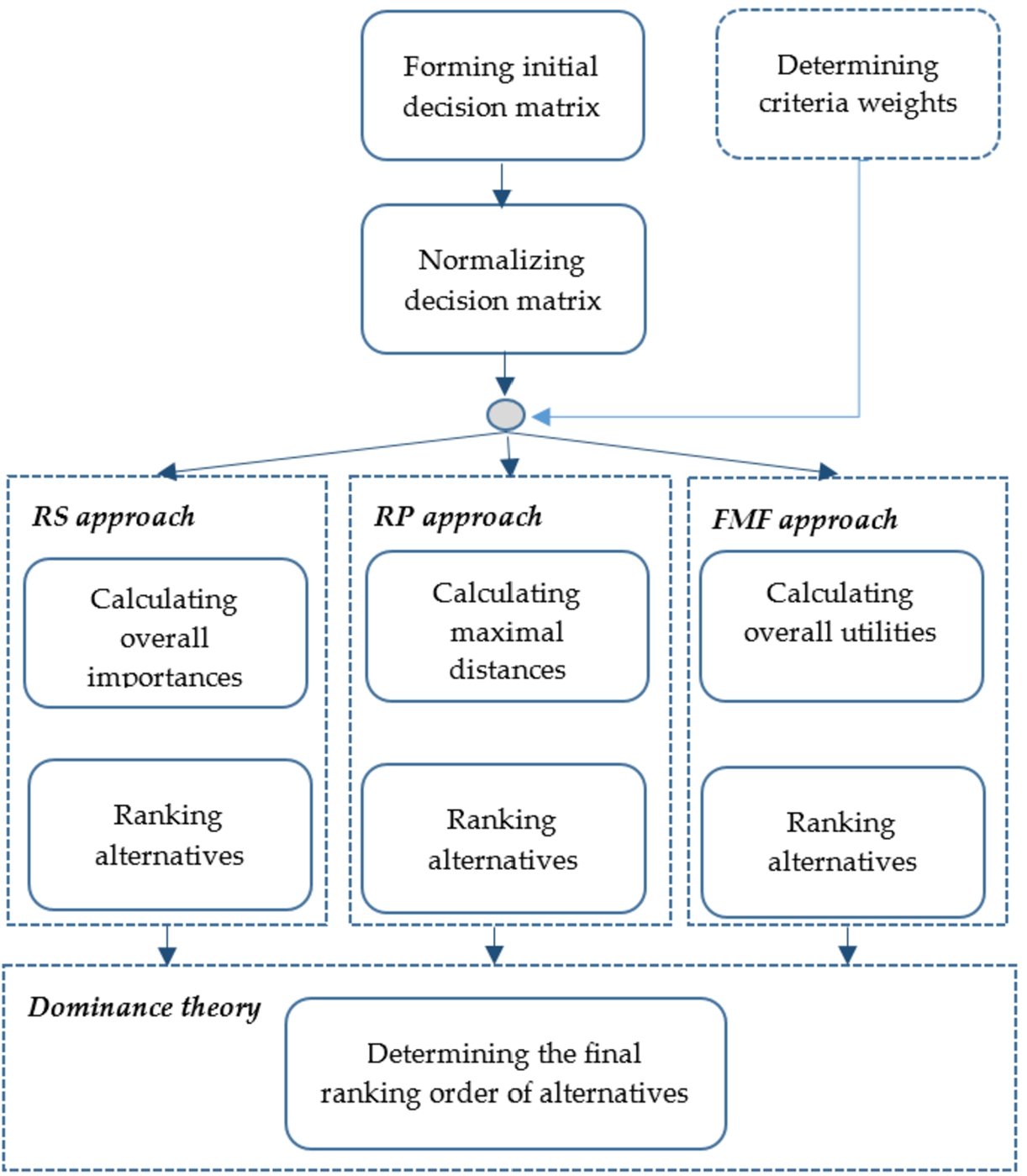
Similarly as in the MOORA method, as a result of the evaluation of the alternatives using the MULTIMOORA method, three ranking orders of alternatives are formed, obtained using three approaches, and the final ranking order, as well as the selection of the most suitable alternative, is made based on the dominance theory.
However, it should be noted that Dahooie et al. (2019) considered an approach for ranking alternatives that is not based on the dominance theory.
3The MULTIMOOSRAL Method
The newly proposed MULTIMOOSRAL method integrates five approaches for ranking alternatives. In addition to the previously discussed approaches, applied in MOOSRA, MOORA and MULTIMOORA methods, the MULTIMOOSRAL method also includes the LA approach. In addition, an important characteristic of MULTIMOOSRAL method can be mentioned, that is, it uses a new approach for determining the final ranking order of alternatives, which is not based on the dominance theory.
The computational procedure of the MULTIMOOSRAL method, presented in Fig. 2, can be precisely presented using the following steps:
Step 1. Forming the initial decision matrix and determining criteria weights.
Fig. 2
Computational procedure of the MULTIMOOSRAL method.
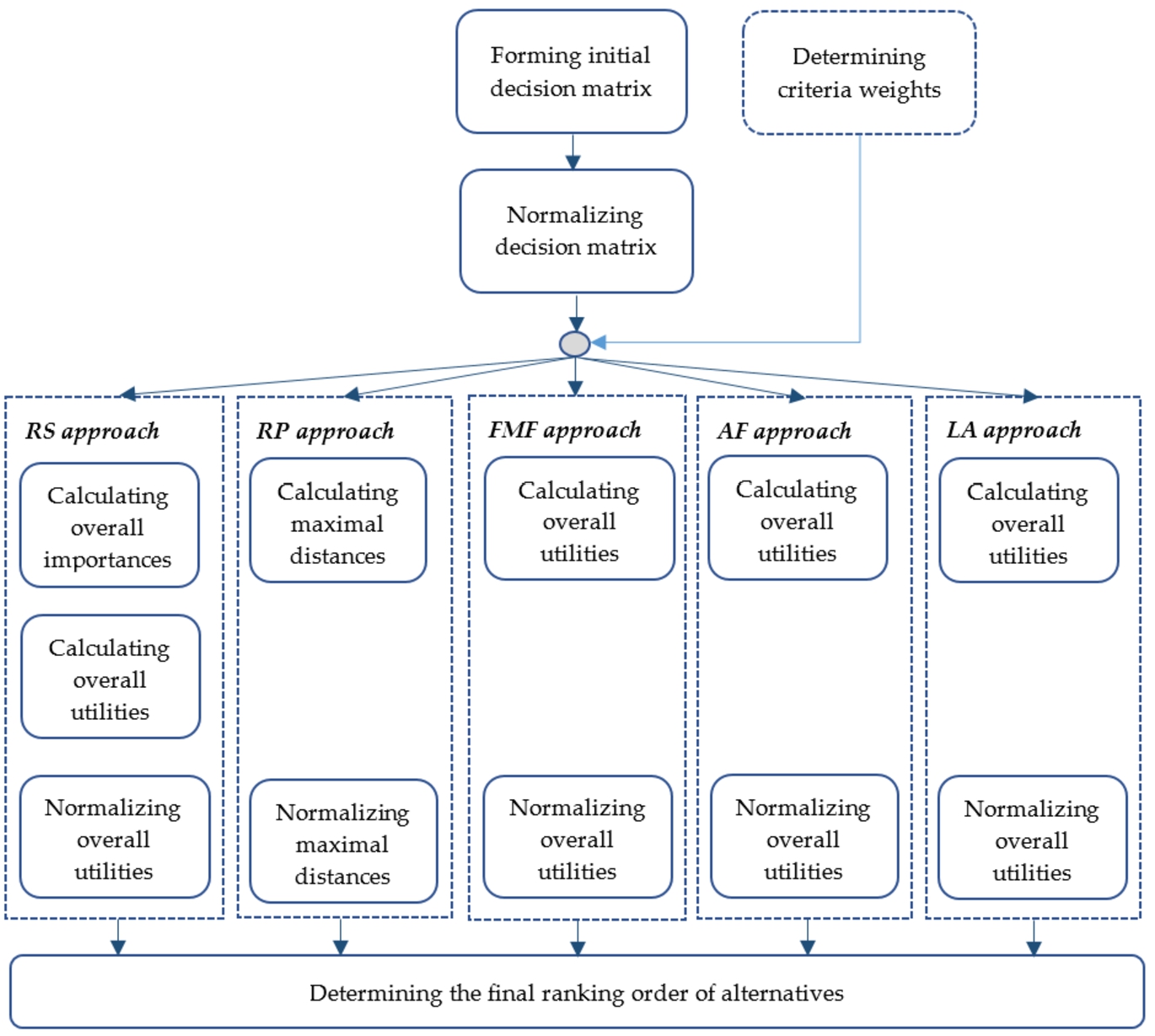
Step 2. Forming the normalized decision matrix. The normalized decision matrix is formed using Eq. (7), which is:
(7)
Step 3. Calculating the normalized overall utilities of alternatives based on the five approaches included in the MULTIMOOSRAL method, as follows:
Step 3.1. Determining the utility of alternatives based on the RS approach by applying the following substeps:
Substep 3.1.1. Calculating the overall importance of considered alternatives is performed using Eq. (8), which is:
(8)
Substep 3.1.2. Calculating the overall utility of considered alternatives as follows:
(9)
Substep 3.1.3. Normalizing the overall utilities obtained on the basis of RS approach as follows:
(10)
Step 3.2. Determining the utility of alternatives based on the RP approach by applying the following substeps:
Substep 3.2.1. Determining reference point
(11)
Substep 3.2.2. Calculating the maximal distance between each alternative and the reference point using Eq. (12), which is:
(12)
Substep 3.2.3. Normalizing maximal distances as follows as follows:
(13)
Step 3.3. Determining the utility of alternatives based on the FMF approach by applying the following substeps:
Substep 3.3.1. Calculating the overall utility of the alternatives using Eq. (14), which is:
(14)
Substep 3.3.2. Normalizing the overall utilities obtained on the basis of FMF approach as follows:
(15)
Step 3.4. Determining the utility of alternatives based on an addition form (AF) approach by applying the following substeps:
Substep 3.4.1. Calculating the overall utility of each alternative using Eq. (16), which is:
(16)
Substep 3.3.2. Normalizing the overall utilities obtained on the basis of AF approach as follows:
(17)
Step 3.5. Determining the utility of alternatives based on the LA approach by applying the following substeps:
Substep 3.5.1. Calculating the overall utility of alternatives based on the LA approach
(18)
Substep 3.5.2. Normalizing the overall utilities obtained on the basis of AF approach as follows:
(19)
Step 4. Determining the final ranking orders of alternatives. The final ranking of alternatives is determined based on their total utility
(20)
After that, the alternatives are ranked on the basis of values of
4An Illustrative Case Study
In this study the usability of the MULTIMOOSRAL method was demonstrated on supplier selection problem for a textile company. All data were collected from three managers of the company and the actual data of company. Managers of the company evaluated the criteria (indicated in Table 1) to obtain criteria weights. The evaluation criteria, as well as their weights (obtained by using the SWARA method, Keršuliene et al., 2010), are shown in Table 1.
Table 1
Evaluation criteria and their weights.
| Criterion | Abbreviation | Weight | Type |
| Reject ratio | RjR | 0.163 | Non-beneficial |
| Purchasing cost | PCo | 0.166 | Non-beneficial |
| Late delivery ratio | LDT | 0.161 | Non-beneficial |
| Discount opportunity | DO | 0.130 | Beneficial |
| Technical assistance | TA | 0.139 | Beneficial |
| Technological capability | TecC | 0.123 | Beneficial |
| Supplier reputation | SRe | 0.117 | Beneficial |
The data of the first three criteria are actual data and the data of the other criteria are obtained from managers of the company. The ratings of suppliers and normalized decision matrix are shown in Table 2 and Table 3.
Table 2
Initial decision matrix.
| Criteria suppliers | RjR | PCo | LDT | DO | TA | TecC | SRe |
| Supplier 1 | 0.02 | 2.64 | 0.02 | 6.3 | 7.7 | 7.3 | 8.3 |
| Supplier 2 | 0.04 | 2.45 | 0.03 | 7 | 6.3 | 5 | 6.7 |
| Supplier 3 | 0.04 | 2.40 | 0.04 | 6.7 | 6.3 | 5 | 6.7 |
| Supplier 4 | 0.03 | 2.64 | 0.01 | 4.7 | 8.3 | 7.7 | 8 |
| Supplier 5 | 0.04 | 2.26 | 0.04 | 7.7 | 5.7 | 7 | 7 |
Table 3
Normalized decision matrix.
| Criterian suppliers | RjR | PCo | LDT | DO | TA | TecC | SRe |
| Supplier 1 | 0.256 | 0.476 | 0.294 | 0.430 | 0.497 | 0.502 | 0.504 |
| Supplier 2 | 0.513 | 0.441 | 0.441 | 0.477 | 0.407 | 0.344 | 0.407 |
| Supplier 3 | 0.513 | 0.432 | 0.588 | 0.457 | 0.407 | 0.344 | 0.407 |
| Supplier 4 | 0.385 | 0.476 | 0.147 | 0.321 | 0.536 | 0.529 | 0.485 |
| Supplier 5 | 0.513 | 0.407 | 0.588 | 0.525 | 0.368 | 0.481 | 0.425 |
The overall importance of alternatives, overall utilities and normalized overall utilities obtained on the basis of RS approach, calculated by Eqs. (8), (9) and (10), are shown in Table 4.
Table 4
Computational details obtained on the basis of RS approach.
| Suppliers | Overall importance | Overall utility | Normalized overall utility |
| Supplier 1 | 0.078 | 0.078 | 1.000 |
| Supplier 2 | −0.019 | −0.019 | 0.211 |
| Supplier 3 | −0.045 | −0.045 | 0.000 |
| Supplier 4 | 0.073 | 0.073 | 0.959 |
| Supplier 5 | −0.019 | −0.019 | 0.211 |
The reference point, obtained using Eq. (11) and data from Table 3, is shown in Table 5.
Table 5
The reference point.
| RjR | PCo | LDT | DO | TA | TecC | SRe | |
|
| 0.256 | 0.407 | 0.147 | 0.525 | 0.536 | 0.529 | 0.504 |
After that, the maximal distances and normalized maximal distances are calculated, using Eq. (12) and Eq. (13), as shown in Table 6.
Table 6
Computational details obtained on the basis of RP approach.
| Suppliers | Maximal distance | Normalized maximal distance |
| Supplier 1 | 0.024 | 1.000 |
| Supplier 2 | 0.047 | 0.511 |
| Supplier 3 | 0.071 | 0.000 |
| Supplier 4 | 0.027 | 0.936 |
| Supplier 5 | 0.071 | 0.000 |
The overall utility and normalized overall utility of alternatives obtained on the basis of FMF approach, using Eqs. (14) and (15), are shown in Table 7.
Table 7
Computational details obtained on the basis of FMF approach.
| Suppliers | Overall utility | Normalized overall utility |
| Supplier 1 | 0.0906 | 0.918 |
| Supplier 2 | 0.0164 | 0.053 |
| Supplier 3 | 0.0118 | 0.000 |
| Supplier 4 | 0.0977 | 1.000 |
| Supplier 5 | 0.0189 | 0.082 |
The overall utility and normalized overall utility of alternatives obtained on the basis of AF approach, using Eqs. (16) and (17), are shown in Table 8.
Table 8
Computational details obtained on the basis of AF approach.
| Suppliers | Overall utility | Normalized overall utility |
| Supplier 1 | 1.4643 | 1.000 |
| Supplier 2 | 0.9167 | 0.149 |
| Supplier 3 | 0.8207 | 0.000 |
| Supplier 4 | 1.4398 | 0.962 |
| Supplier 5 | 0.9231 | 0.159 |
The overall utility and normalized overall utility of alternatives obtained on the basis of LA approach, using Eqs. (18) and (19), are shown in Table 9.
Table 9
Computational details obtained on the basis of LA approach.
| Suppliers | Overall utility | Normalized overall utility |
| Supplier 1 | 6.3697 | 0.962 |
| Supplier 2 | 4.7551 | 0.193 |
| Supplier 3 | 4.3512 | 0.000 |
| Supplier 4 | 6.4490 | 1.000 |
| Supplier 5 | 4.4375 | 0.041 |
Finally, in Table 10 results obtained using five approaches integrated in MULTIMOOSRAL method, overall utility of considered alternatives, calculated using Eq. (20), and ranking order of alternatives are presented.
Table 10
Computational details obtained using the MULTIMOOSRAL method.
| Suppliers |
|
|
|
|
|
| Rank |
| Supplier 1 | 1.000 | 1.000 | 0.918 | 1.000 | 0.962 | 4.880 | 1 |
| Supplier 2 | 0.211 | 0.511 | 0.053 | 0.149 | 0.193 | 1.117 | 3 |
| Supplier 3 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 5 |
| Supplier 4 | 0.959 | 0.936 | 1.000 | 0.962 | 1.000 | 4.857 | 2 |
| Supplier 5 | 0.211 | 0.000 | 0.082 | 0.159 | 0.041 | 0.494 | 4 |
As it can be seen from Table 10, the best supplier selected using the MULTIMOOSRAL method is supplier denoted as “Supplier 1”.
In order to further verify the obtained results, a comparison with the results obtained using the MOOSRA, MOORA and MULTIMOORA methods was performed below. The results obtained using the above methods are shown in Tables 11, 12 and 13.
Table 11
Rankingof alternatives using the MOOSRA method.
| Suppliers |
| Rank |
| Supplier 1 | 1.4643 | 1 |
| Supplier 2 | 0.9167 | 4 |
| Supplier 3 | 0.8207 | 5 |
| Supplier 4 | 1.4398 | 2 |
| Supplier 5 | 0.9231 | 3 |
Table 12
Rankingof alternatives using the MOORA method.
| Suppliers | RS | RS Rank | RP | RP Rank | Rank |
| Supplier 1 | 0.078 | 1 | 0.024 | 1 | 1 |
| Supplier 2 | −0.019 | 3 | 0.047 | 3 | 3 |
| Supplier 3 | −0.045 | 5 | 0.071 | 4 | 4–5 |
| Supplier 4 | 0.073 | 2 | 0.027 | 2 | 2 |
| Supplier 5 | −0.019 | 4 | 0.071 | 4 | 4 |
Table 13
Rankingof alternatives using the MULTIMOORA method.
| Suppliers | RS | RS Rank | RP | RP Rank | FMF | FMF Rank | Rank |
| Supplier 1 | 0.078 | 1 | 0.024 | 1 | 0,0906 | 2 | 1 |
| Supplier 2 | −0.019 | 3 | 0.047 | 3 | 0,0164 | 4 | 3 |
| Supplier 3 | −0.045 | 5 | 0.071 | 4 | 0,0118 | 5 | 5 |
| Supplier 4 | 0.073 | 2 | 0.027 | 2 | 0,0977 | 1 | 2 |
| Supplier 5 | −0.019 | 4 | 0.071 | 4 | 0,0189 | 3 | 4 |
From Tables 11, 12 and 13 it can be seen that the ranking results obtained using the MULTIMOOSRAL method are identical to the results obtained using the MOOSRA, MOORA and MULTIMOORA methods.
In order to finally verify the results obtained using the MULTIMOOSRAL method, a comparative analysis was performed with several well-known MCDM methods, such as TOPSIS, MULTIMOORA, and CoCoSo methods, as shown in Table 14.
Table 14
Comparative analysis of ranking orders obtained using different MCDM methods.
| Suppliers | MULTIMOOSRAL | TOPSIS | MULTIMOORA | CoCoSo |
| Supplier 1 | 1 | 1 | 1 | 1 |
| Supplier 2 | 3 | 3 | 3 | 3 |
| Supplier 3 | 5 | 5 | 5 | 4 |
| Supplier 4 | 2 | 2 | 2 | 2 |
| Supplier 5 | 4 | 4 | 4 | 5 |
It can be observed from Table 14, that the MULTIMOOSRAL method gives the same ranking orders as the TOPSIS and MULTIMOORA methods. Some discrepancy in the rank of the alternative can be observed in the case of the use of the CoCoSo method, which refers to the fourth and fifth-ranked alternatives. However, such phenomena are expected because the newly proposed MULTIMOOSRAL method integrates more ranking approaches and because of that, it should allow a more accurate ranking of the alternatives.
5Conclusions
This paper proposes a new MCDM technique called MULTIMOOSRAL that is based on the approaches in MOOSRA, MOORA, and MULTIMOORA methods and LA approach for the facilitation of a decision-making process. The main incentive for proposing the new method reflects the desire to develop such an approach that will contribute to the increasing of the credibility of the obtained results. In this case, by involving five approaches (RS, RP, FMF, AF, and LA) the reliability of the final ranking order as well as its stability is raised to a higher level.
In order to demonstrate the applicability and usefulness of the proposed method, the illustrative case study pointed to the selection of the adequate supplier of the textile company is presented. The evaluation process, entrusted to 3 managers, is based on the 7 criteria and 5 alternatives. The gained result revealed that supplier 1 is the most suitable to work within the present conditions, while supplier 3 is the worst choice according to the given performances.
To acknowledge the reliability of the obtained ranking order, the MOOSRA, MOORA, and MULTIMOORA methods are applied. The results from all three used techniques confirmed that one was obtained by using the newly proposed MULTIMOOSRAL method. Namely, in all three observations, supplier 1 is ranked as the best alternative, while supplier 3 is ranked as the last and worst option. In this way, the stability of the proposed MCDM method is verified as well as its suitability for applying in the decision-making process.
Although this novel method contributes to the reliability of the performed decision process by involving more approaches, the same thing could be considered as its main deficiency, too. Namely, the computational procedure could be considered as complex for application by the users that are not familiar with the MCDM field. Additionally, in order to better incorporate the uncertainty, this model could be extended by involving the fuzzy, grey, or neutrosophic numbers. But, despite the mentioned imperfections, the MULTIMOOSRAL method proved its efficiency in enhancing the decision-making process and its possibilities should be further examined.
References
1 | Adalı, E.A., Işık, A.T. ((2017) ). The multi-objective decision making methods based on MULTIMOORA and MOOSRA for the laptop selection problem. Journal of Industrial Engineering International, 13: (2), 229–237. |
2 | Alkan, Ö., Albayrak, Ö.K. ((2020) ). Ranking of renewable energy sources for regions in Turkey by fuzzy entropy based fuzzy COPRAS and fuzzy MULTIMOORA. Renewable Energy, 162: , 712–726. |
3 | Attri, R., Grover, S. ((2014) ). Decision making over the production system life cycle: MOORA method. International Journal of System Assurance Engineering and Management, 5: (3), 320–328. |
4 | Baležentis, A., Baležentis, T., Brauers, W.K. ((2012) ). Personnel selection based on computing with words and fuzzy MULTIMOORA. Expert Systems with Applications, 39: (9), 7961–7967. |
5 | Brauers, W.K.M. ((2004) ). Optimization Methods for a Stakeholder Society. A Revolution in Economic Thinking by Multiobjective Optimization. Kluwer, Boston, MA. |
6 | Brauers, W.K., Zavadskas, E.K. ((2006) ). The MOORA method and its application to privatization in a transition economy. Control and Cybernetics, 35: , 445–469. |
7 | Brauers, W.K.M., Zavadskas, E.K. ((2010) ). Project management by MULTIMOORA as an instrument for transition economies. Technological and Economic Development of Economy, 16: (1), 5–24. |
8 | Chakraborty, S. ((2011) ). Applications of the MOORA method for decision making in manufacturing environment. The International Journal of Advanced Manufacturing Technology, 54: (9–12), 1155–1166. |
9 | Dahooie, J.H., Zavadskas, E.K., Firoozfar, H.R., Vanaki, A.S., Mohammadi, N., Brauers, W.K.M. ((2019) ). An improved fuzzy MULTIMOORA approach for multi-criteria decision making based on objective weighting method (CCSD) and its application to technological forecasting method selection. Engineering Applications of Artificial Intelligence, 79: , 114–128. |
10 | Dorfeshan, Y., Mousavi, S.M., Mohagheghi, V., Vahdani, B. ((2018) ). Selecting project-critical path by a new interval type-2 fuzzy decision methodology based on MULTIMOORA, MOOSRA and TPOP methods. Computers & Industrial Engineering, 120: , 160–178. |
11 | Fadli, S., Imtihan, K. ((2019) ). Implementation of MOORA method in evaluating work performance of honorary teachers. SinkrOn, 4: (1), 128–135. |
12 | Fedajev, A., Stanujkic, D., Karabašević, D., Brauers, W.K., Zavadskas, E.K. ((2020) ). Assessment of progress towards “Europe 2020” strategy targets by using the MULTIMOORA method and the Shannon Entropy Index. Journal of Cleaner Production, 244: , 118895. |
13 | Hafezalkotob, A., Hafezalkotob, A., Liao, H., Herrera, F. ((2019) a). Interval MULTIMOORA method integrating interval Borda rule and interval best–worst-method-based weighting model: case study on hybrid vehicle engine selection. IEEE Transactions on Cybernetics, 50: (3), 1157–1169. |
14 | Hafezalkotob, A., Hafezalkotob, A., Liao, H., Herrera, F. ((2019) b). An overview of MULTIMOORA for multi-criteria decision-making: theory, developments, applications, and challenges. Information Fusion, 51: , 145–177. |
15 | İç, Y.T. ((2020) ). A multi-objective credit evaluation model using MOORA method and goal programming. Arabian Journal for Science and Engineering, 45: (3), 2035–2048. |
16 | Jauković-Jocić, K., Karabašević, D., Jocić, G. ((2020) ). The use of the PIPRECIA method for assessing the quality of e-learning materials. Ekonomika, 66: (3), 37–45. |
17 | Karabasevic, D., Stanujkic, D., Urosevic, S., Maksimovic, M. ((2015) ). Selection of candidates in the mining industry based on the application of the SWARA and the MULTIMOORA methods. Acta Montanistica Slovaca, 20: (2), 116–124. |
18 | Karamaşa, Ç., Demir, E., Memiş, S., Korucuk, S. ((2020) ). Weighting the factors affecting logistics outsourcing. Decision Making: Applications in Management and Engineering, 4: (1), 19–32. |
19 | Karande, P., Chakraborty, S. ((2012) ). Decision making for supplier selection using the MOORA method. IUP Journal of Operations Management, 11: (2), 6–18. |
20 | Keršuliene, V., Zavadskas, E.K., Turskis, Z. ((2010) ). Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). Journal of Business Economics and Management, 11: (2), 243–258. |
21 | Keshavarz Ghorabaee, M., Zavadskas, E.K., Olfat, L., Turskis, Z. ((2015) ). Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica, 26: (3), 435–451. |
22 | Keshavarz-Ghorabaee, M., Amiri, M., Zavadskas, E.K., Turskis, Z., Antucheviciene, J. ((2018) ). Simultaneous evaluation of criteria and alternatives (SECA) for multi-criteria decision-making. Informatica, 29: (2), 265–280. |
23 | Kumar, R., Ray, A. ((2015) ). Selection of material under conflicting situation using simple ratio optimization technique. In: Proceedings of Fourth International Conference on Soft Computing for Problem Solving. Springer, New Delhi, pp. 513–519. |
24 | Liu, H.C., Fan, X.J., Li, P., Chen, Y.Z. ((2014) ). Evaluating the risk of failure modes with extended MULTIMOORA method under fuzzy environment. Engineering Applications of Artificial Intelligence, 34: , 168–177. |
25 | Narayanamoorthy, S., Annapoorani, V., Kang, D., Baleanu, D., Jeon, J., Kureethara, J.V., Ramya, L. ((2020) ). A novel assessment of bio-medical waste disposal methods using integrating weighting approach and hesitant fuzzy MOOSRA. Journal of Cleaner Production, 275: , 122587. |
26 | Pamučar, D., Ćirović, G. ((2015) ). The selection of transport and handling resources in logistics centers using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Systems with Applications, 42: (6), 3016–3028. |
27 | Pamučar, D., Stević, Ž., Sremac, S. ((2018) ). A new model for determining weight coefficients of criteria in MCDM models: full consistency method (FUCOM). Symmetry, 10: (9), 393. |
28 | Rahimi, S., Hafezalkotob, A., Monavari, S.M., Hafezalkotob, A., Rahimi, R. ((2020) ). Sustainable landfill site selection for municipal solid waste based on a hybrid decision-making approach: fuzzy group BWM-MULTIMOORA-GIS. Journal of Cleaner Production, 248: , 119186. |
29 | Sarkar, A., Panja, S.C., Das, D., Sarkar, B. ((2015) ). Developing an efficient decision support system for non-traditional machine selection: an application of MOORA and MOOSRA. Production & Manufacturing Research, 3: (1), 324–342. |
30 | Stanujkic, D., Zavadskas, E.K., Karabasevic, D., Turskis, Z., Keršulienė, V. ((2017) a). New group decision-making ARCAS approach based on the integration of the SWARA and the ARAS methods adapted for negotiations. Journal of Business Economics and Management, 18: (4), 599–618. |
31 | Stanujkić, D., Zavadskas, E.K., Karabašević, D., Smarandache, F., Turskis, Z. ((2017) b). The use of Pivot Pair-wise Relative Criteria Importance Assessment method for determining weights of criteria. Romanian Journal of Economic Forecasting, 20: (4), 116–133. |
32 | Stanujkic, D., Karabasevic, D., Zavadskas, E.K., Smarandache, F., Brauers, W.K. ((2019) ). A bipolar fuzzy extension of the MULTIMOORA method. Informatica, 30: (1), 135–152. |
33 | Stević, Ž., Pamučar, D., Puška, A., Chatterjee, P. ((2020) ). Sustainable supplier selection in healthcare industries using a new MCDM method: measurement of alternatives and ranking according to compromise solution (MARCOS). Computers & Industrial Engineering, 140: , 106231. |
34 | Ulutaş, A., Popovic, G., Stanujkic, D., Karabasevic, D., Zavadskas, E.K., Turskis, Z. ((2020) ). A new hybrid MCDM model for personnel selection based on a novel grey PIPRECIA and grey OCRA methods. Mathematics, 8: (10), 1698. |
35 | Yazdani, M., Zarate, P., Zavadskas, E.K., Turskis, Z. ((2019) ). A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Management Decision, 57: , 2501–2519. |
36 | Zavadskas, E.K., Turskis, Z. ((2008) ). A new logarithmic normalization method in games theory. Informatica, 19: (2), 303–314. |
37 | Zavadskas, E.K., Turskis, Z., Stević, Ž., Mardani, A. ((2020) ). Modelling procedure for the selection of steel pipes supplier by applying fuzzy AHP method. Operational Research in Engineering Sciences: Theory and Applications, 3: (2), 39–53. |
38 | Zavadskas, E.K., Bausys, R., Lescauskiene, I., Usovaite, A. ((2021) ). MULTIMOORA under interval-valued neutrosophic sets as the basis for the quantitative heuristic evaluation methodology HEBIN. Mathematics, 9: (1), 66. |




