An Extended Intuitionistic Fuzzy Multi-Attributive Border Approximation Area Comparison Approach for Smartphone Selection Using Discrimination Measures
Abstract
The objective of the paper is to introduce a novel approach using the multi-attribute border approximation area comparison (MABAC) approach under intuitionistic fuzzy sets (IFSs) to solve the smartphone selection problem with incomplete weights or completely unknown weights. A novel discrimination measure of IFSs is proposed to calculate criteria weights. In view of the fact that the ambiguity is an unavoidable feature of multiple-criteria decision-making (MCDM) problems, the proposed approach is an innovative process in the decision-making under uncertain settings. To express the utility and strength of the developed approach for solving problems in the area of MCDM, a smartphone selection problem is demonstrated. To validate the IF-MABAC approach, a comparative discussion is made between the outcomes of the developed and those of the existing methods. The outcomes of analysis demonstrate that the introduced method is well-ordered and effective with the existing ones.
1Introduction
Until now, users’ attentiveness in mobile communication is increasing and is analogous to this concern; Smartphone developers have manufactured various latest models. As per the survey report of the International Telecommunication Union (ITU) (ITU, 2017), the utilization of communication technologies is increased, while communication costs are reduced. Due to quick evolution in Smartphone models, the subscribers have faced decision making complexity when acquiring the most desirable Smartphone. Moreover, the young generations are using Smartphones not only for phone calls, but also for numerous functions, viz., internet access, camera, music, and video players, and so on. For that reason, the customers desire to select the Smartphone by considering different qualitative and quantitative criteria. Quantitative criteria contain camera quality, RAM size, battery capacity, built-in memory, screen dimension, processor type, and cost, while qualitative criteria contain durability, user-friendliness, and brand.
Nowadays, MCDM approaches are extensively applied to elucidate the problems, namely Smartphone selection problem. However, MCDM problems differ according to the solution status and the approaches’ implementation. Up until now various MCDM approaches have been proposed in the literature, like the TOPSIS (Akyene, 2012; Mishra, 2016; Mishra et al., 2017a; Büyüközkan and Güleryüz, 2016), VIKOR (Vls Kriteriju miska Optimizacija I Kompromisno Resenje) (Hu et al., 2014; Mishra and Rani, 2019; Rani and Mishra, 2020a; Rani et al., 2019b), ELECTRE (ELimination and Choice Expressing REality) (Chen et al., 2018; Mishra et al., 2020a), WASPAS (Weighted Aggregates Sum Product Assessment) (Mishra et al., 2019a; Rani and Mishra, 2020b), PROMETHEE (Rani and Jain, 2017; Liao et al., 2018), MULTIMOORA (Wu et al., 2018) and GLDS (Wu and Liao, 2019) methods. From the literature, various MCDM approaches have been applied to identify the most desirable Smartphone (Hu et al., 2014; Akyene, 2012; Büyüközkan and Güleryüz, 2016; Wu et al., 2018). Hu et al. (2018) proposed a procedure that can promote mobile-commerce improvement towards attaining the aspiration level in a fuzzy setting. They developed fusion model to conduct the feedback-effect and dependency among criteria, and it combined the DEMATEL, DANP, and GRA methods.
The MABAC is an original MCDM approach pioneered by Pamučar and Ćirović (2015). MABAC has an easy computational process, organized procedure, and an innovative direction that determines the foundation of real-world decision-making problems. Peng and Yang (2016) utilized MABAC method to solve R&D project assessment with Pythagorean fuzzy sets (PFSs). Under IVIFSs (interval-valued intuitionistic fuzzy sets) environment, the MABAC approach is implemented for material evaluation (Xue et al., 2016) and programming language selection (Mishra et al., 2020d). Therefore, it is an attractive explorative way to implement the MABAC in the Smartphone selection. Atanassov (1986) developed the notion of IFSs which extends the fuzzy sets doctrine by accumulating the non-membership degree. As IFSs doctrine has widely been implemented by the researchers in various disciplines for handling uncertainties in the MCDM (Liu and Liao, 2017; Mishra and Rani, 2019), their analogous analysis is significant.
Discrimination and entropy and measures are prominent tools for tackling the ambiguous information in the various fields. Entropy measures, measurement of the degree of fuzziness for FSs and IFSs have gained huge concentration from scholars in various disciplines (Liao et al., 2014; Tang and Liao, 2019). To evaluate the discrimination information between IFSs, first, Vlachos and Sergiadis (2007) proposed IF-discrimination measure, established relation between them and implemented it in various disciplines. Consequently, various prominent discrimination measures have been introduced for FSs and IFSs (Mishra et al., 2017b; Ansari et al., 2018; Rani et al., 2019a; Jiang et al., 2019; Liang et al., 2019b; Rani et al., 2020; Mishra et al., 2020b, 2020c; Kumari and Mishra, 2020).
Nevertheless, from the literature, it is examined that all the measures do not incorporate the decision expert opinion of the preferences into the measure. In addition, the existing measure is in linear order and does not show the accurate behaviour of alternatives. As a result, by concentrating the standards of flexibility and proficiency of IFSs, this study proposes novel parametric discrimination measures. It has been observed from the literature that the existing discrimination measures are the special cases of the developed one. Next, to estimate the weights criteria, the developed IF-discrimination measures have been applied. Using this procedure for weighting criteria, an intuitionistic fuzzy MABAC (IF-MABAC) approach is developed to deal with MCDM problems. Now, we implement only subjective considerations of options; however, developed method is appropriate for ordinary MCDM circumstances with objective and/or subjective evaluations. Further, a Smartphone selection problem is considered to elucidate the procedure and interpret the performance of IF-MABAC approach in real case decision-making issues. To illustrate the reliability of the results, a comparative discussion between our developed approach and the other current approaches is performed to determine the validity of the results.
However, according to the above motivations, the main contributions of the paper are pointed out as
i. New IF-discrimination measures using the characteristics of IFSs are proposed and compared with other current discrimination measures under IFSs.
ii. Considering the discrimination between alternatives, a procedure to assess the criteria weights is carried out.
iii. After defining the border approximation area (BAA) matrix using the proposed discrimination measure, an integrated MCDM method, IF-MABAC, is developed for MCDM problems under intuitionistic fuzzy environment.
iv. Considering a real-life smartphone selection problem, the IF-MABAC approach is implemented to choose the desirable smartphone. The usefulness of the introduced approach is examined by comparing it with existing approaches.
The organization of this paper is as follows. In Section 2, we discuss the review of the MABAC method and existing discriminations measures for IFSs. Section 3 illustrates the research method based on the basic information of IFSs, and the recent related works about IF-discrimination measures. In Section 4, the novel IF-discrimination measures are presented, and some attractive properties of proposed measures are conferred. Section 5 presents the IF-MABAC approach for MCDM problem. In Section 6, we discuss the application of smartphone selection of IF-MABAC approach and compare it with currents works. In the last section, the conclusion of this paper is provided.
2Literature Review
2.1An Overview of MABAC Method
For the first time, Pamučar and Ćirović (2015) proposed the MABAC as an original MCDM approach. This approach provided an easy computational process, organized procedure, and an innovative direction that determines the foundation of practical MCDM problems. Over the past years, the MABAC approach is used by many scholars in different application areas. Peng and Yang (2016) extended a MABAC procedure with Pythagorean fuzzy Choquet integral. Liang et al. (2019a) introduced MABAC technique to assess rockburst risks under triangular fuzzy numbers (TFNs). Xue et al. (2016) proposed IVIF-MABAC approach to assess the material selection. Gigović et al. (2017) presented a combined method with DEMATEL, MABAC, Geographic Information Systems (GIS) and ANP to select the location for the wind farms. Peng and Dai (2018) established a new model on single-valued neutrosophic (SVN) and similarity measure and distance measure to solve MADM problem based on MABAC and TOPSIS procedures. Yu et al. (2017) proposed a method based on MABAC under interval type-2 fuzzy numbers (IT2FNs) for selecting the best hotel on a tourism website. Sun et al. (2018) established a projection-based MABAC approach under hesitant fuzzy linguistic term sets (HFLTSs) to select and evaluate patients. The summary of other related papers is presented in Table 1.
Table 1
Summary of the related works of MABAC method.
| Authors | Method | Fuzzy and conventional environment | Application area |
| Roy et al. (2016) | MABAC | Type-2 trapezoidal fuzzy sets environment | System analysis engineer selection |
| Peng and Dai (2017) | MABAC, COPRAS, WASPAS, | HFSSs | Software development project |
| Peng et al. (2017) | MABAC, EDAS | IVIFSs | Investment company |
| Ji et al. (2018) | ELECTRE, MABAC | SVN linguistic sets | Outsourcing provider selection |
| Nunić (2018) | MABAC, WASPAS, ARAS, FUCOM | Conventional MCDM | Manufacturer PVC carpentry |
| Vesković et al. (2018) | Delphi, MABAC SWARA | Conventional MCDM | Railway management |
| Bozanic et al. (2018) | Fuzzy MABAC, fuzzy Analytic Hierarchy Process (AHP) | Saaty’s fuzzy sets | Deep wading location selection |
| Bojanic et al. (2018) | Fuzzy AHP, MABAC | Interval of fuzzy numbers | Military decision-making process |
| Hu et al. (2019) | MABAC | Interval type-2 fuzzy numbers (IT2FNs) | Patient care assessment |
| Jia et al. (2019) | MABAC | Intuitionistic fuzzy rough numbers | Medical devices supplier selection |
| Božanić et al. (2019) | Full Consistency Method. (FUCOM), fuzzy MABAC | Triangular fuzzy number | Location selection for bridge construction |
| Biswas and Das (2019) | MABAC, fuzzy AHP | Fuzzy sets | Commercially available electric vehicle |
| Majchrzycka and Poniszewska-Maranda (2018) | MABAC | Conventional MCDM | Mobile access control |
| Biswas and Das (2018) | MABAC | Conventional MCDM | Hybrid vehicle selection |
| Luo and Liang (2019) | MABAC | Linguistic neutrosophic numbers | Roadway support schemes |
| Liu (2019) | MABAC | IVIFSs | Radiation therapy assessment |
| Božanić et al. (2016) | MABAC | Conventional MCDM | Defensive operation |
| Pamučar and Božanić (2019) | MABAC | SVNSs | Logistics center selection |
| Liang et al. (2019a) | MABAC | IFSs | Human resource management problem |
| Shen et al. (2020) | MABAC | Z-number | Circular economy development selection |
| Dorfeshan and Mousavi (2020) | MABAC, WASPAS | IT2FSs | Aircraft maintenance planning |
| Mishra et al. (2020c) | MABAC | IVIFSs | Programming language assessment |
| Wang et al. (2020) | MABAC | Q-rung orthopair fuzzy sets | Construction projects selection |
| Wei et al. (2020) | MABAC | Uncertain probabilistic linguistic sets (UPLTSs) | Green supplier selection |
2.2Review of Discrimination Measures of IFSs
In the current decade, the applications of IFSs and information measures, namely, discrimination, entropy, and similarity, have been investigated by various scholars in different regions (Deng et al., 2015; Bao et al., 2017; Cavallaro et al., 2018, 2019; Kong et al., 2018; Lohrmann et al., 2018; Luo and Zhao, 2018; Ngan et al., 2018; Shen et al., 2018). Jia et al. (2019) introduced a new IF-similarity measure of pattern recognition problem based on isosceles triangles. Bao et al. (2017) presented a new approach according to evidential reasoning and prospect theory and extended new measures for IF-entropy and discrimination measure in the field of international shipping market. Shen et al. (2018) generalized the IF-TOPSIS approach derived from similarity and distance measures for handling the risk assessment of MCDM issue. Luo and Zhao (2018) developed an IF-distance measure-based on a strictly increasing binary function and matrix norm for evaluating the medical diagnosis. Deng et al. (2015) investigated monotonic similarity and geometrical relation measures under IFSs based on inclusion and entropy measures. Cavallaro et al. (2018) and Cavallaro et al. (2019) extended an IFs based on fuzzy Shannon entropy measure and extended IF-TOPSIS based on circular entropy weights vector for evaluating of the concentrated solar power (CSP).
3Intuitionistic Fuzzy Sets and Existing Discrimination Measures
This part of the paper presents some basic information of IFSs and the IF-discrimination measures.
3.1The Concepts Related to IFSs
Atanassov (1986) developed the view of the fuzzy sets (FSs) to IFSs by distinguishing belongingness and the non-belongingness functions where the sum of both degrees is equal to one or less than one.
Definition 1
Definition 1(Intutionistic fuzzy sets, see Atanassov, 1986).
An IFS E on universe set
(1)
(2)
The hesitancy degree of an element
For effortlessness, an intuitionistic fuzzy number (IFN) is characterized by
(3)
(4)
Let
(5)
The discrimination measure is a recognized device to measure the discrimination degree in IFSs. Later on, Montes et al. (2015) demonstrated the discrimination measure is the more restrictive way when the comparison is performed with other measures and necessary for avoiding counter-intuitive situations.
Definition 2
Definition 2(Discrimination measure, see Montes et al., 2015).
A mapping
3.2Existing Discrimination Measures for IFSs
Various existing IF-discrimination measures are analysed from the literature. The details of recent discrimination measures are listed as follows:
Maheshwari and Srivastava (2015):
Verma and Sharma (2014):
Garg (2016):
Srivastava and Maheshwari (2016):
Ohlan (2016):
Mishra et al. (2019b):
Mishra et al. (2020d):
From the above discussions, it has been examined that all measures do not incorporate decision experts’ preferences into the measure. Keeping in mind the flexibility and efficiency of criteria for IFSs, this paper develops generalized discrimination measure to evaluate the fuzziness degree of a set.
4New IF-Discrimination Measure and Comparison
In the following sub-section, to evade the drawbacks of current discrimination measures, novel IF-discrimination measures are developed.
4.1New Discrimination Measure for IFSs
Here, we have proposed some flexible and generalized parametric IF-discrimination measures. Various attractive properties of developed ones are being studied.
Let
Definition 3.
Let
(6)
(7)
Definition 4.
A parametric symmetric IF-discrimination measure between IFSs E and F with
(8)
Theorem 1.
The functions
(P1).
(
(P3).
(P4).
(P5).
(P6).
(P7).
(P8).
(P9).
4.2Comparison with the Existing IF-Discrimination Measures
To indicate the superiority of the developed IF-discrimination measures, we compared the developed IF-discrimination and the current discrimination measures. A comparison is employed based on the extensively utilized counter-intuitive cases. Table 2 demonstrates the result of the proposed and existing IF-discrimination measures.
Table 2
Comparison of IF-discrimination measures (counter-intuitive cases are in bold type).
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0.0000 | 0.0050 | 0.0000 | 0.0000 | 0.0013 |
|
| 0.0226 | 0.0072 | NaN | 0.0233 | 0.0063 |
|
| 0.0078 | 0.0026 | NaN | 0.0081 | 0.0023 |
|
| 0.8385 | 0.7852 | NaN | 0.8052 | 0.7882 |
|
| 0.4122 | 0.3581 | 1.0000 | 0.4122 | 0.3581 |
|
| 0.0000 | 0.0050 | 0.0000 | 0.0000 |
|
|
| 0.0000 | 0.0017 | 0.0000 | 0.0000 | 0.0005 |
|
| 0.0025 | 0.0025 | 0.2402 | 0.0027 | 0.0010 |
|
| 0.0555 | 0.0173 | 0.9353 | 0.0565 | 0.0157 |
From Table 2,
5The IF-MABAC Approach for MCDM Problem
Here, the MABAC method is explored for solving the MCDM issues under IFSs.
5.1The Extended IF-MABAC Method-Based on the Discrimination Measures
Let
Stage 1: Determine weights of decision experts’ (DEs)
Fig. 1
A graphical presentation of the proposed IF-MABAC algorithm.

Construct a group ℓ DEs to include decision making concerning various perspectives. Suppose the rating specified for each DE through experts is
(9)
Stage 2: Construct IF-aggregation decision matrix (IF-ADM) over DEs weights
Aggregate the individual DEs assessment matrices
Stage 3: Evaluate the criteria weights based on the IF-discrimination measures
Let
(10)
Stage 4: Build the normalized IF-ADM
The normalized IF-ADM
(11)
Stage 5: Evaluate the weighted IF-ADM
When the weight
(12)
Stage 6: Compute the border approximation area (BAA) matrix
The matrix for BAA
(13)
Stage 7: Compute the discrimination values from the BAA
With the proposed IF-discrimination measure, the degree of discriminations of the alternative from the BAA are determined by
(14)
Stage 8: Derive the ranking order
The degrees of performance function for an alternative are determined to add the discriminations from the BAA for each alternative and are specified by
(15)
Next, the preference order of their degree of performance function for the alternative is evaluated and the desirable Smartphone for the given SPS problem can be demonstrated.
6Application of Smartphone Selection of IF-MABAC Method
In the present section, the developed IF-MABAC approach is implemented to solve SPS problem. Seven Smartphones as alternatives are considered as follows: Apple
Fig. 2
Hierarchical configuration of Smartphone selection problem.
Here, Table 3 and Table 4 describe the linguistic terms (LTs) in the forms of IFNs for the criteria and DEs importance. According to these two tables and Eq. (9), the DEs’ weights are calculated and presented in Table 5. The linguistic values illustrated in Table 6 by three DEs under the criteria parameters of specified SPSs.
Table 3
The LTs to rate the significant criteria and DEs.
| LTs | IFNs |
| Very Significant (VS) | (0.90, 0.10) |
| Significant (S) | (0.80, 0.15) |
| Moderate (M) | (0.65, 0.30) |
| Insignificant (IS) | (0.45, 0.50) |
| Very Insignificant (VI) | (0.20, 0.70) |
Table 4
The LTs to rate the Smartphones selection.
| LTs | IFNs |
| Extremely High (EH) |
|
| Very High (VH) |
|
| High (H) |
|
| Average (A) |
|
| Low (L) |
|
| Very Low (VL) |
|
| Extremely Low (EL) |
|
Table 5
The significance of the weights by experts.
|
|
|
| |
| LTs | Very significant | Significant | Moderate |
| IFNs |
|
|
|
| Weight | 0.3709 | 0.3470 | 0.2821 |
Table 6
The linguistic variable for Smartphones rating.
| Parameters | Smartphone | Experts | ||
|
|
|
| ||
| Price
|
| H | H | H |
|
| L | L | A | |
|
| H | H | H | |
|
| H | VH | H | |
|
| VL | H | H | |
|
| VL | A | VH | |
|
| H | VH | H | |
| Battery power
|
| H | VH | VH |
|
| A | VH | H | |
|
| VH | VH | A | |
|
| VH | H | H | |
|
| A | VH | H | |
|
| H | A | VH | |
|
| H | VH | VH | |
| Camera
|
| A | VH | VH |
|
| H | A | A | |
|
| A | A | H | |
|
| A | VH | VH | |
|
| L | VH | H | |
|
| L | VH | H | |
|
| A | VH | VH | |
| Storage capacity and RAM
|
| L | A | VH |
|
| VH | A | VH | |
|
| L | H | VH | |
|
| L | H | H | |
|
| L | H | VH | |
|
| H | L | H | |
|
| VH | A | VH | |
| Processor type
|
| A | H | H |
|
| A | H | H | |
|
| H | H | A | |
|
| H | H | A | |
|
| A | H | A | |
|
| H | H | A | |
|
| VH | VH | VH | |
| Screen size
|
| VH | VH | H |
|
| H | VH | A | |
|
| H | H | VH | |
|
| H | H | VH | |
|
| H | VH | A | |
|
| VH | VH | H | |
|
| VH | VH | H | |
| Ease of use
|
| A | H | VH |
|
| A | H | VH | |
|
| H | L | A | |
|
| H | L | A | |
|
| L | H | H | |
|
| L | VH | H | |
|
| VH | H | VH | |
| Operating system
|
| A | A | H |
|
| H | A | H | |
|
| A | A | H | |
|
| A | VH | A | |
|
| A | VH | A | |
|
| H | A | H | |
|
| A | A | VH | |
According to DEs weights obtained by Eq. (9), and Eq. (5), IF-ADM regarding SPSs is constructed and shown in Table 7. Since one criterion is non-benefit type and the remaining are benefit type, by Eq. (11), Table 8 depicts the normalized decision matrix for SPSs.
Table 7
The IF-ADM for Smartphones.
|
|
|
|
|
|
|
| |
|
| (0.7000, 0.2000) | (0.4648, 0.4329) | (0.7000, 0.2000) | (0.7951, 0.1572) | (0.5684, 0.3183) | (0.6502, 0.3013) | (0.7951, 0.1572) |
|
| (0.8493, 0.1293) | (0.7720, 0.1828) | (0.8521, 0.1363) | (0.8004, 0.1547) | (0.7720, 0.1828) | (0.7568, 0.1893) | (0.8493, 0.1293) |
|
| (0.8328, 0.1503) | (0.6405, 0.2581) | (0.6312, 0.2676) | (0.8328, 0.1503) | (0.7350, 0.2209) | (0.7350, 0.2209) | (0.8328, 0.1503) |
|
| (0.6856, 0.2660) | (0.8382, 0.1464) | (0.7154, 0.2310) | (0.6121, 0.2809) | (0.7154, 0.2310) | (0.6184, 0.2749) | (0.8382, 0.1464) |
|
| (0.6662, 0.2325) | (0.6662, 0.2325) | (0.6746, 0.2242) | (0.6746, 0.2242) | (0.6380, 0.2606) | (0.6746, 0.2242) | (0.9000, 0.1000) |
|
| (0.8637, 0.1216) | (0.7778, 0.1763) | (0.7799, 0.1645) | (0.7799, 0.1645) | (0.7778, 0.1763) | (0.8637, 0.1216) | (0.8637, 0.1216) |
|
| (0.7552, 0.1912) | (0.7552, 0.1912) | (0.5862, 0.3082) | (0.5862, 0.3082) | (0.6121, 0.2000) | (0.7350, 0.2209) | (0.8536, 0.1272) |
|
| (0.6312, 0.2676) | (0.6685, 0.2302) | (0.6312, 0.2676) | (0.7527, 0.2049) | (0.7527, 0.2049) | (0.6685, 0.2302) | (0.7295, 0.2201) |
Table 8
The normalized IF-ADM for Smartphones.
|
|
|
|
|
|
|
| |
|
| (0.2000, 0.7000) | (0.4329, 0.4648) | (0.2000, 0.7000) | (0.1572, 0.7951) | (0.3183, 0.5684) | (0.3103, 0.6502) | (0.1572, 0.7951) |
|
| (0.8493, 0.1293) | (0.7720, 0.1828) | (0.8521, 0.1363) | (0.8004, 0.1547) | (0.7720, 0.1828) | (0.7568, 0.1893) | (0.8493, 0.1293) |
|
| (0.8328, 0.1503) | (0.6405, 0.2581) | (0.6312, 0.2676) | (0.8328, 0.1503) | (0.7350, 0.2209) | (0.7350, 0.2209) | (0.8328, 0.1503) |
|
| (0.6856, 0.2660) | (0.8382, 0.1464) | (0.7154, 0.2310) | (0.6121, 0.2809) | (0.7154, 0.2310) | (0.6184, 0.2749) | (0.8382, 0.1464) |
|
| (0.6662, 0.2325) | (0.6662, 0.2325) | (0.6746, 0.2242) | (0.6746, 0.2242) | (0.6380, 0.2606) | (0.6746, 0.2242) | (0.9000, 0.1000) |
|
| (0.8637, 0.1216) | (0.7778, 0.1763) | (0.7799, 0.1645) | (0.7799, 0.1645) | (0.7778, 0.1763) | (0.8637, 0.1216) | (0.8637, 0.1216) |
|
| (0.7552, 0.1912) | (0.7552, 0.1912) | (0.5862, 0.3082) | (0.5862, 0.3082) | (0.6121, 0.2000) | (0.7350, 0.2209) | (0.8536, 0.1272) |
|
| (0.6312, 0.2676) | (0.6685, 0.2302) | (0.6312, 0.2676) | (0.7527, 0.2049) | (0.7527, 0.2049) | (0.6685, 0.2302) | (0.7295, 0.2201) |
Using Eqs. (7) and (10), the objective weights of the criteria is computed as:
Table 9
The weighted IF-ADM for Smartphone selection.
|
|
|
|
|
|
|
| |
|
| (0.0590, 0.9073) | (0.1433, 0.8115) | (0.0590, 0.9073) | (0.0456, 0.9394) | (0.0992, 0.8573) | (0.0963, 0.8893) | (0.0456, 0.9394) |
|
| (0.0708, 0.9237) | (0.0557, 0.9362) | (0.0715, 0.9256) | (0.0606, 0.9301) | (0.0557, 0.9362) | (0.0534, 0.9375) | (0.0709, 0.9237) |
|
| (0.1963, 0.7933) | (0.1175, 0.8475) | (0.1148, 0.8512) | (0.1963, 0.7933) | (0.1498, 0.8315) | (0.1498, 0.8315) | (0.1963, 0.7933) |
|
| (0.1573, 0.8221) | (0.2362, 0.7526) | (0.1696, 0.8052) | (0.1307, 0.8288) | (0.1696, 0.8052) | (0.1328, 0.8261) | (0.2362, 0.7526) |
|
| (0.1645, 0.7874) | (0.1645, 0.7874) | (0.1680, 0.7828) | (0.1680, 0.7828) | (0.1533, 0.8023) | (0.1680, 0.7828) | (0.3142, 0.6858) |
|
| (0.0850, 0.9103) | (0.0649, 0.9255) | (0.0653, 0.9227) | (0.0653, 0.9227) | (0.0649, 0.9255) | (0.0850, 0.9103) | (0.0850, 0.9103) |
|
| (0.2148, 0.7526) | (0.2148, 0.7526) | (0.1407, 0.8169) | (0.1407, 0.8169) | (0.1502, 0.7584) | (0.2040, 0.7715) | (0.2811, 0.7017) |
|
| (0.0375, 0.9508) | (0.0414, 0.9453) | (0.0375, 0.9508) | (0.0521, 0.9411) | (0.0521, 0.9411) | (0.0414, 0.9453) | (0.0488, 0.9437) |
The BAA
Next, the discrimination matrix of SPSs option from BAA is evaluated by Eq. (7) and Eq. (15). The corresponding discrimination matrix is established and revealed in Table 10. The closeness degree of the BAA for each Smartphone is computed by Eq. (15) and shown in Table 10. Finally, all Smartphones ranks are shown based on the values which are depicted in Table 10. As a result, Smartphone
Table 10
The discrimination matrix of all alternatives from the BAA for Smartphones.
|
|
|
|
|
|
|
|
|
| Rank | |
|
| −0.0001 | 0.00004 | 0.00033 | −0.00009 | −0.00005 | 0.0039 | 0.0004 | −0.0003 | 0.00413 | 2 |
|
| 0.0026 | 0.00002 | 0.0003 | 0.0008 | 0.00005 | 0.00003 | 0.0001 | 0.0001 | 0.00400 | 3 |
|
| 0.00005 | 0.00003 | 0.0004 | 0.000003 | 0.00002 | 0.00002 | 0.0006 | 0.0003 | 0.001423 | 5 |
|
| 0.0007 | 0.0000 | 0.0003 | 0.0003 | 0.00002 | 0.00002 | 0.0006 | 0.00004 | 0.00198 | 4 |
|
| 0.0005 | 0.00002 | 0.00002 | 0.00002 | 0.0002 | 0.00003 | 0.00005 | 0.00004 | 0.00088 | 6 |
|
| 0.0001 | 0.00004 | 0.00002 | 0.0003 | 0.00002 | 0.00005 | 0.00001 | 0.0001 | 0.00064 | 7 |
|
| 0.0007 | 0.00004 | 0.0003 | 0.0008 | 0.0028 | 0.00005 | 0.0014 | 0.00008 | 0.00617 | 1 |
6.1Comparison with Other Works
Here, we illustrate a comparative evaluation with the existing method to show the validity and usefulness of the IF-MABAC approach based on IF-discrimination measures. We have implemented the same numerical example applying the developed approach for comparing with the existing approaches.
The above Smartphone selection problem is also solved by the ANP-Generalized Choquet integral method (Yildiz and Ergul, 2015), the fuzzy ELECTRE method (Belbag et al., 2016) and the Shapley discrimination measure VIKOR method (Mishra and Rani, 2019). Outcomes of the different approaches were obtained to certify the outcomes of the developed IF-MABAC method. Moreover, we implement the given case study to investigate the above methods and to show the effectiveness of the proposed approach. Figure 3 and Table 11 demonstrate the preference orders of the SPSs alternatives as achieved by applying the existing methods.
Fig. 3
Rankings order comparison of Smartphones with different methods.
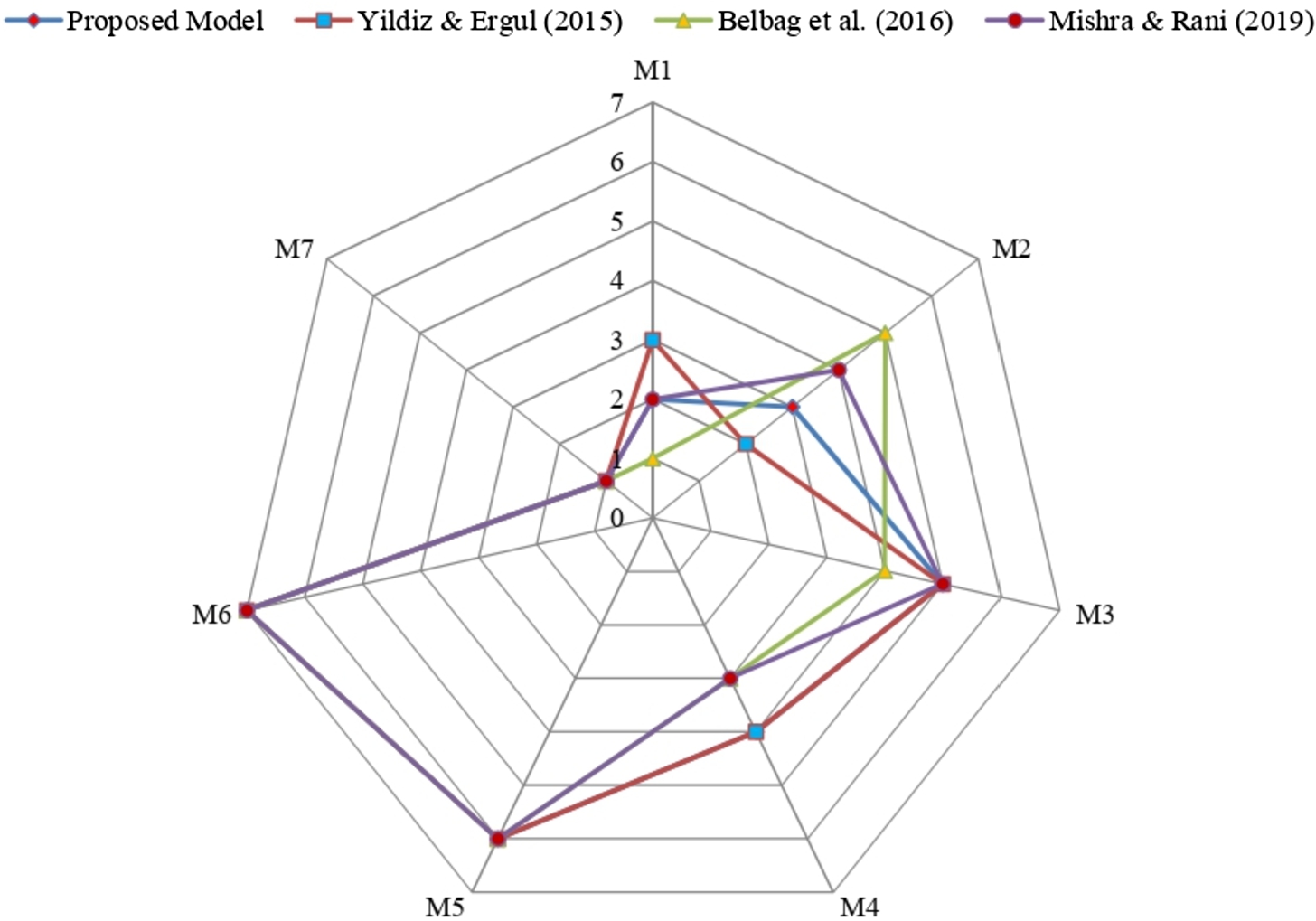
Table 11
Discussion of the developed method with current methods.
| Methods | Discipline | Benchmark | Criterion weights | Expert weights | Ranking order | Best Smartphone |
| Yildiz and Ergul (2015) | FSs | ANP – Generalized choquet integral | ANP | Assumed |
|
|
| Belbag et al. (2016) | FSs | Fuzzy ELECTRE | TFNs | Assumed |
|
|
| Mishra and Rani (2019) | IFSs | IF-VIKOR | Shapley function with entropy method | Not considered |
|
|
| Proposed method | IFSs | IF-MABAC | Discrimination measure | Computed |
|
|
The outcomes show that the optimal preference of SPSs is the same, i.e.
The key distinctive outcomes of the developed IF-MABAC framework are as follows:
i. To tackle with uncertainty in MCDM problems, all the facets, namely, the alternative on the assessments criteria by various DEs, the DEs weights, and the criteria weights are taken in the form of IFNs.
ii. The developed approach utilizes IFSs to develop the procedure, different from the methods in Yildiz and Ergul (2015) and Belbag et al. (2016), wherein the FSs are implemented.
iii. The criteria weights of proposed IF-MABAC approach are obtained through the proposed IF-discrimination measure, which gives more precise weights, different from the randomly assumed criteria weights in Belbag et al. (2016).
iv. Multiple DEs have been selected in the developed method whose weights are given in terms of IFNs, while the methodology proposed in Yildiz and Ergul (2015), Belbag et al. (2016) and Mishra and Rani (2019) did not incorporate the group decision making (GDM) procedure.
v. Criteria weights in the developed IF-MABAC method are provided as IFNs, whereas in Belbag et al. (2016) and Mishra and Rani (2019), the crisp weights are assumed, leaving no space to handle the uncertainty.
7Conclusions
With the use of technology, human life becomes more comfortable, and therefore it becomes a requisite for users. Several brands or products materialize on the business world with fast-growing technology and Smartphones are one of these products. A desirable Smartphone selection from the available options is a complex problem since it has different types of processors, RAM in GB, screens with HD resolution, O/S, etc. Several interesting criteria affect the SPS, as similar to various products. Hence, MCDM approaches can facilitate to evaluate SPS problem. Here, an integrated approach based on MABAC under IFSs was developed to assess the SPS problem. To compute the weight of the vector, new IF-discrimination measures were developed, and some useful properties were presented. The novel developed discrimination measure based on IFSs is verified, it would solve the problem of some current distance measures. The assessment of each SPSs alternative over different criteria was assessed on IFSs, and a new IF-MABAC framework was applied to prefer the most desirable Smartphone. To investigate the usefulness of the IF-MABAC method, comparative analyses with existing approaches were presented. The computational findings found that the ranking outcomes achieved based on the IF-MABAC method were reliable with existing ones; and hence, the developed method was sound to the SPSs under uncertainty. By employing the integrated IF-MABAC approach, a more consistent and best ranking findings of SPS case would be obtained, which help to make the accurate decision for selection of smartphone.
Further, we will integrate the MABAC framework with various other procedures, viz., CRITIC, AHP and SWARA, in the MCDM process. Also, the introduced approach would be employed for deciphering the several real-world problems, namely, supplier or material selection, and electric vehicles charging station selection to elucidate its strength and usefulness.
References
1 | Akyene, T. ((2012) ). Cell phone evaluation base on entropy and TOPSIS. Interdisciplinary Journal of Research in Business, 1: , 9–15. 2012. |
2 | Ansari, M.D., Mishra, A.R., Ansari, F.T. ((2018) ). New discrimination and entropy measures for intuitionistic fuzzy sets on edge detection. International Journal of Fuzzy Systems, 20: , 474–487. |
3 | Atanassov, K.T. ((1986) ). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20: , 87–96. |
4 | Bao, T., Xie, X., Long, P., Wei, Z. ((2017) ). MADM method based on prospect theory and evidential reasoning approach with unknown attribute weights under intuitionistic fuzzy environment. Expert Systems with Applications, 88: , 305–317. |
5 | Belbag, S., Gungordu, A., Yumusak, T., Yilmaz, K.G. ((2016) ). The evaluation of smartphone brand choice: an application with the fuzzy ELECTRE I method. International Journal of Business and Management Invention, 5: , 55–63. |
6 | Biswas, T.K., Das, M.K. ((2018) ). Selection of hybrid vehicle for green environment using multi-attributive border approximation area comparison method. Management Science Letters, 8: , 121–130. |
7 | Biswas, T.K., Das, M.K. ((2019) ). Selection of commercially available electric vehicle using fuzzy AHP-MABAC. Journal of the Institution of Engineers (India): Series C, 100: , 531–537. |
8 | Bojanic, D., Kovač, M., Bojanic, M., Ristic, V. ((2018) ). Multi-criteria decision-making in A defensive operation of the guided anti-tank missile battery: an example of the hybrid model fuzzy AHP-MABAC. Decision Making: Applications in Management and Engineering, 1: , 51–66. |
9 | Boran, F.E., Genc, S., Kurt, M., Akay, D. ((2009) ). A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Systems with Applications, 36: , 11363–11368. |
10 | Božanić, D., Pamučar, D., Karović, S.M. ((2016) ). Application the MABAC method in support of decision-making on the use of force in a defensive operation. Tehnika, 7: , 129–136. |
11 | Bozanic, D., Tešić, D., Milićević, J. ((2018) ). A hybrid fuzzy AHP-MABAC model: application in the Serbian Army – the selection of the location for deep wading as a technique of crossing the river by tanks. Decision Making: Applications in Management and Engineering, 1: , 143–164. |
12 | Božanić, D., Tešić, D., Kočić, J. ((2019) ). Multi-criteria FUCOM – fuzzy MABAC model for the selection of location for construction of single-span Bailey bridge. Decision Making: Applications in Management and Engineering, 2: , 132–146. |
13 | Büyüközkan, G., Güleryüz, S. ((2016) ). Multi criteria group decision making approach for smart phone selection using intuitionistic fuzzy TOPSIS. International Journal of Computational Intelligence Systems, 9: , 709–725. |
14 | Cavallaro, F., Zavadskas, E.K., Streimikiene, D. ((2018) ). Concentrated solar power (CSP) hybridized systems. Ranking based on an intuitionistic fuzzy multi-criteria algorithm. Journal of Cleaner Production, 179: , 407–416. |
15 | Cavallaro, F., Zavadskas, E.K., Streimikiene, D., Mardani, A. ((2019) ). Assessment of concentrated solar power (CSP) technologies based on a modified intuitionistic fuzzy TOPSIS and trigonometric entropy weights. Technological Forecasting and Social Change, 140: , 258–270. |
16 | Chen, I.F., Tsaur, R.C., Chen, P.Y. ((2018) ). Selection of Best Smartphone using revised ELECTRE-III method. International Journal of Information Technology & Decision Making, 17: , 1915–1936. |
17 | Deng, G., Jiang, Y., Fu, J. ((2015) ). Monotonic similarity measures between intuitionistic fuzzy sets and their relationship with entropy and inclusion measure. Information Sciences, 316: , 348–369. |
18 | Dorfeshan, Y., Mousavi, S.M. ((2020) ). A novel interval type-2 fuzzy decision model based on two new versions of relative preference relation-based MABAC and WASPAS methods (with an application in aircraft maintenance planning). Neural Computing and Applications, 32: , 3367–3385. |
19 | Garg, H. ((2016) ). Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making. Computers & Industrial Engineering, 101: , 53–69. |
20 | Gigović, L., Pamučar, D., Božanić, D., Ljubojević, S. ((2017) ). Application of the GIS-DANP-MABAC multi-criteria model for selecting the location of wind farms: a case study of Vojvodina, Serbia. Renewable Energy, 103: , 501–521. |
21 | Hu, J.H., Chen, P.P., Yang, Y. ((2019) ). An interval type-2 fuzzy similarity-based MABAC approach for patient-centered care. Mathematics, 7(2), 140: , 140. https://doi.org/10.3390/math7020140. |
22 | Hu, S.K., Lu, M.T., Tzeng, G.H. ((2014) ). Exploring smart phone improvements based on a hybrid MCDM model. Expert Systems with Applications, 41: , 4401–4413. |
23 | Hu, S.K., Liou, J., Chuang, Y.C., Tzeng, G.H. ((2018) ). New hybrid FMADM model for mobile commerce improvement. Technological and Economic Development of Economy, 24: (5), 1801–1828. https://doi.org/10.3846/20294913.2017.1318311. |
24 | Ji, P., Zhang, H.Y., Wang, J.Q. ((2018) ). Selecting an outsourcing provider based on the combined MABAC–ELECTRE method using single-valued neutrosophic linguistic sets. Computers & Industrial Engineering, 120: , 429–441. |
25 | Jia, F., Liu, Y., Wang, X. ((2019) ). An extended MABAC method for multi-criteria group decision making based on intuitionistic fuzzy rough numbers. Expert Systems with Applications, 127: , 241–255. |
26 | Jiang, Q., Jin, X., Lee, S.J., Yao, S. ((2019) ). A new similarity/distance measure between intuitionistic fuzzy sets based on the transformed isosceles triangles and its applications to pattern recognition. Expert Systems with Applications, 116: , 439–453. |
27 | Kong, D., Chang, T., Wang, Q., Sun, H., Dai, W. ((2018) ). A threat assessment method of group targets based on interval-valued intuitionistic fuzzy multi-attribute group decision-making. Applied Soft Computing, 67: , 350–369. |
28 | Kumari, R., Mishra, A.R. ((2020) ). Multi-criteria COPRAS method based on parametric measures for intuitionistic fuzzy sets: application of green supplier selection. Iranian Journal of Science and Technology, Transactions of Electrical Engineering https://doi.org/10.1007/s40998-020-00312-w. |
29 | Liang, R.X., He, S.S., Wang, J.Q., Chen, K., Li, L. ((2019) a). An extended MABAC method for multi-criteria group decision-making problems based on correlative inputs of intuitionistic fuzzy information. Computational and Applied Mathematics, 38: , 112. |
30 | Liang, W., Zhao, G., Wu, H., Dai, B. ((2019) b). Risk assessment of rockburst via an extended MABAC method under fuzzy environment. Tunnelling and Underground Space Technology, 83: , 533–544. |
31 | Liao, H.C., Xu, Z.S., Zeng, X.J. ((2014) ). Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making. Information Sciences, 271: , 125–142. |
32 | Liao, H.C., Wu, D., Huang, Y.L., Ren, P.J., Xu, Z.S., Verma, M. ((2018) ). Green logistic provider selection with a hesitant fuzzy linguistic thermodynamic method integrating cumulative prospect theory and PROMETHEE. Sustainability, 10: , 1291. https://doi.org/10.3390/su10041291. |
33 | Liu, H.C. ((2019) ). FMEA using IVIFSs and MABAC method and its application to radiation therapy. In: Liu, H.-C. (Ed.), Improved FMEA Methods for Proactive Healthcare Risk Analysis. Springer Singapore, Singapore, pp. 125–150. |
34 | Liu, W.S., Liao, H.C. ((2017) ). A bibliometric analysis of fuzzy decision research during 1970–2015. International Journal of Fuzzy Systems., 19: (1), 1–14. |
35 | Lohrmann, C., Luukka, P., Jablonska-Sabuka, M., Kauranne, T. ((2018) ). A combination of fuzzy similarity measures and fuzzy entropy measures for supervised feature selection. Expert Systems with Applications, 110: , 216–236. |
36 | Luo, M., Zhao, R. ((2018) ). A distance measure between intuitionistic fuzzy sets and its application in medical diagnosis. Artificial Intelligence in Medicine, 89: , 34–39. |
37 | Luo, S.Z., Liang, W.Z. ((2019) ). Optimization of roadway support schemes with likelihood-based MABAC method. Applied Soft Computing, 80: , 80–92. |
38 | Maheshwari, S., Srivastava, P. ((2015) ). Application of intuitionistic fuzzy cross entropy measure in decision making for medical diagnosis. International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, 9: , 254–258. |
39 | Majchrzycka, A., Poniszewska-Maranda, A. ((2018) ). Control operation flow for mobile access control with the use of MABAC model. In: Kosiuczenko, P., Madeyski, L. (Eds.), Towards a Synergistic Combination of Research and Practice in Software Engineering. Springer International Publishing, Cham, pp. 179–192. |
40 | Mishra, A.R. ((2016) ). Intuitionistic fuzzy information with application in rating of township development. Iranian Journal of Fuzzy Systems, 13: , 49–70. |
41 | Mishra, A.R., Rani, P. ((2019) ). Shapley discrimination measures with VIKOR method for multi-attribute decision-making problems. Neural Computing and Applications, 31: , 1299–1316. https://doi.org/10.1007/s00521-017-3101-x. |
42 | Mishra, A.R., Rani, P., Jain, D. ((2017) a). Information measures based TOPSIS method for multicriteria decision making problem in intuitionistic fuzzy environment. Iranian Journal of Fuzzy Systems, 14: (6), 41–63. |
43 | Mishra, A.R., Jain, D., Hooda, D. ((2017) b). Exponential intuitionistic fuzzy information measure with assessment of service quality. International Journal of Fuzzy Systems, 19: , 788–798. |
44 | Mishra, A.R., Singh, R.K., Motwani, D. ((2019) a). Multi-criteria assessment of cellular mobile telephone service providers using intuitionistic fuzzy WASPAS method with similarity measures. Granular Computing, 4: , 511–529. https://doi.org/10.1007/s41066-018-0114-5. |
45 | Mishra, A.R., Kumari, R., Sharma, D.K. ((2019) b). Intuitionistic fuzzy divergence measure-based multi-criteria decision-making method. Neural Computing & Applications, 31: , 2279–2294. https://doi.org/10.1007/s00521-017-3187-1. |
46 | Mishra, A.R., Singh, R.K., Motwani, D. ((2020) a). Intuitionistic fuzzy discrimination measure-based ELECTRE method for performance of cellular mobile telephone service providers. Neural Computing and Applications, 32: , 3901–3921. https://doi.org/10.1007/s00521-018-3716-6. |
47 | Mishra, A.R., Sisodia, G., Pardasani, K.R., Sharma, K. ((2020) b). Multi-criteria IT personnel selection on intuitionistic fuzzy information measures and ARAS methodology. Iranian Journal of Fuzzy Systems, 17: (4), 5–68. https://doi.org/10.22111/ijfs.2019.27737.4871. |
48 | Mishra, A.R., Chandel, A., Motwani, D. ((2020) c). Extended MABAC method based on discrimination measures for multi-criteria assessment of programming language with interval-valued intuitionistic fuzzy sets. Granular Computing, 5: (1), 97–117. |
49 | Mishra, A.R., Mardani, A., Rani, P., Zavadskas, E.K. ((2020) d). A novel EDAS approach on intuitionistic fuzzy set for assessment of health-care waste disposal technology using new parametric divergence measures. Journal of Cleaner Production, 272: , 122807. https://doi.org/10.1016/j.jclepro.2020.122807. |
50 | Montes, I., Pal, N.R., Janis, V., Montes, S. ((2015) ). Discrimination measures for intuitionistic fuzzy sets. IEEE Transaction on Fuzzy Systems, 23: , 444–456. |
51 | Ngan, R.T., Son, L.H., Cuong, B.C., Ali, M. ((2018) ). H-max distance measure of intuitionistic fuzzy sets in decision making. Applied Soft Computing, 69: , 393–425. |
52 | Nunić, Z. ((2018) ). Evaluation and selection of manufacturer PVC carpentry using FUCOM-MABAC model. Operational Research in Engineering Sciences: Theory and Applications, 1: , 13–28. |
53 | Ohlan, A. ((2016) ). Intuitionistic fuzzy exponential discrimination: application in multi-attribute decision making. Journal of Intelligent & Fuzzy Systems, 30: , 1519–1530. |
54 | Pamučar, D., Ćirović, G. ((2015) ). The selection of transport and handling resources in logistics centers using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Systems with Applications, 42: , 3016–3028. |
55 | Pamučar, D., Božanić, D. ((2019) ). Selection of a location for the development of multimodal logistics center: application of single-valued neutrosophic MABAC model. Operational Research in Engineering Sciences: Theory and Applications, 2: , 55–71. |
56 | Parkash, O., Kumar, R. ((2017) ). Modified fuzzy discrimination measure and its applications to medical diagnosis and MCDM. Risk and Decision Analysis, 6: , 231–237. |
57 | Peng, X., Dai, J. ((2017) ). Hesitant fuzzy soft decision making methods based on WASPAS, MABAC and COPRAS with combined weights. Journal of Intelligent & Fuzzy Systems, 33: , 1313–1325. |
58 | Peng, X., Dai, J. ((2018) ). Approaches to single-valued neutrosophic MADM based on MABAC, TOPSIS and new similarity measure with score function. Neural Computing and Applications, 29: , 939–954. |
59 | Peng, X., Yang, Y. ((2016) ). Pythagorean fuzzy Choquet integral based MABAC method for multiple attribute group decision making. International Journal of Intelligent Systems, 31: , 989–1020. |
60 | Peng, X., Dai, J., Yuan, H. ((2017) ). Interval-valued fuzzy soft decision making methods based on MABAC, similarity measure and EDAS. Fundamenta Informaticae, 152: , 373–396. |
61 | Rani, P., Jain, D. ((2017) ). Intuitionistic fuzzy PROMETHEE technique for multi-criteria decision making problems based on entropy measure. In: Proceedings of Communications in Computer and Information Science (CCIS), Vol. 721: . Springer pp. 290–301. |
62 | Rani, P., Mishra, A.R. ((2020) a). Single-valued neutrosophic SWARA-VIKOR framework for performance assessment of eco-industrial thermal power plants. ICSES Transactions on Neural and Fuzzy Computing, 3: , 1–9. |
63 | Rani, P., Mishra, A.R. ((2020) b). Multi-criteria weighted aggregated sum product assessment framework for fuel technology selection using q-rung orthopair fuzzy sets. Sustainable Production and Consumption, 24: , 90–104. https://doi.org/10.1016/j.spc.2020.06.015. |
64 | Rani, P., Jain, D., Hooda, D. ((2019) a). Extension of intuitionistic fuzzy TODIM technique for multi-criteria decision making method based on shapley weighted discrimination measure. Granular Computing, 4: , 407–420. |
65 | Rani, P., Mishra, A.R., Pardasani, K.R., Mardani, A., Liao, H.C., Streimikiene, D. ((2019) b). A novel VIKOR approach based on entropy and discrimination measures of Pythagorean fuzzy sets to evaluate renewable energy technologies in India. Journal of Cleaner Production, 238: , 117936. https://doi.org/10.1016/j.jclepro.2019.117936. |
66 | Rani, P., Mishra, A.R., Mardani, A., Cavallaro, F., Alrasheedi, M., Alrashidi, A. ((2020) ). A novel approach to extended fuzzy TOPSIS based on new divergence measures for renewable energy sources selection. Journal of Cleaner Production, 257: , 120352. https://doi.org/10.1016/j.jclepro.2020.120352. doi. |
67 | Roy, J., Ranjan, A., Debnath, A., Kar, S. (2016). An extended MABAC for multi-attribute decision making using trapezoidal interval type-2 fuzzy numbers arXiv:1607.01254 [cs.AI]. |
68 | Shen, F., Ma, X., Li, Z., Xu, Z.S., Cai, D. ((2018) ). An extended intuitionistic fuzzy TOPSIS method based on a new distance measure with an application to credit risk evaluation. Information Sciences, 428: , 105–119. |
69 | Shen, K., Wang, X., Qiao, D., Wang, J. ((2020) ). Extended Z-MABAC method based on regret theory and directed distance for regional circular economy development program selection with Z-information. IEEE Transactions on Fuzzy Systems, 28: (8), 1851–1863. |
70 | Srivastava, P., Maheshwari, S. ((2016) ). Decision making in medical investigations using new discrimination measures for intuitionistic fuzzy sets. Iranian Journal of Fuzzy Systems, 13: , 25–44. |
71 | Sun, R., Hu, J., Zhou, J., Chen, X. ((2018) ). A hesitant fuzzy linguistic projection-based MABAC method for patients’ prioritization. International Journal of Fuzzy Systems, 20: , 2144–2160. |
72 | Tang, M., Liao, H.C. ((2019) ). Managing information measures for hesitant fuzzy linguistic term sets and their applications in designing clustering algorithms. Information Fusion, 50: , 30–42. |
73 | Verma, R., Sharma, B.D. ((2014) ). A new measure of inaccuracy with its application to multi-criteria decision making under intuitionistic fuzzy environment. Journal of Intelligent & Fuzzy Systems, 27: , 1811–1824. |
74 | Vesković, S., Stević, Ž., Stojić, G., Vasiljević, M., Milinković, S. ((2018) ). Evaluation of the railway management model by using a new integrated model DELPHI-SWARA-MABAC. Decision Making: Applications in Management and Engineering, 1: , 34–50. |
75 | Vlachos, I.K., Sergiadis, G.D. ((2007) ). Intuitionistic fuzzy information – applications to pattern recognition. Pattern Recognition Letters, 28: , 197–206. |
76 | Wang, J., Wei, G., Wei, C., Wei, Y. ((2020) ). MABAC method for multiple attribute group decision making under q-rung orthopair fuzzy environment. Defence Technology, 16: (2), 208–216. |
77 | Wei, G., He, Y., Lei, F., Wu, J., Wei, C., Guo, Y. (2020). Green supplier selection with an uncertain probabilistic linguistic MABAC method. Journal of Intelligent & Fuzzy Systems, 1–12. https://doi.org/10.3233/jifs-191584. |
78 | Wu, X., Liao, H.C. ((2019) ). A consensus based probabilistic linguistic gained and lost dominance sore method. European Journal of Operational Research, 272: (3), 1017–1027. |
79 | Wu, X., Liao, H.C., Xu, Z.S., Hafezalkotob, A., Herrera, F. ((2018) ). Probabilistic linguistic MULTIMOORA: a multi-criteria decision making method based on the probabilistic linguistic expectation function and the improved Borda rule. IEEE Transactions on Fuzzy Systems, 26: (6), 3688–3702. |
80 | Xu, Z.S. ((2007) ). Intuitionistic fuzzy aggregation operators. IEEE Trans Fuzzy Syst, 15: (6), 1179–1187. |
81 | Xu, G.L., Wan, S.P., Xie, X.L. ((2015) ). A selection method based on MAGDM with interval-valued intuitionistic fuzzy sets. Mathematical Problems in Engineering, 2015: , 1–13. (Article ID 791204). |
82 | Xue, Y.X., You, J.X., Lai, X.D., Liu, H.C. ((2016) ). An interval-valued intuitionistic fuzzy MABAC approach for material selection with incomplete weight information. Applied Soft Computing, 38: , 703–713. |
83 | Yildiz, A., Ergul, E. ((2015) ). A two-phased multi-criteria decision-making approach for selecting the best smartphone. South African Journal of Industrial Engineering, 26: , 194–215. |
84 | Yu, S.M., Wang, J., Wang, J.Q. ((2017) ). An interval type-2 fuzzy likelihood-based mabac approach and its application in selecting hotels on a tourism website. International Journal of Fuzzy Systems, 19: , 47–61. |




