Efficient Image Encryption Scheme Based on 4-Dimensional Chaotic Maps
Abstract
This paper proposes a new family of 4-dimensional chaotic cat maps. This family is then used in the design of a novel block-based image encryption scheme. This scheme is composed of two independent phases, a robust light shuffling phase and a masking phase which operate on image-blocks. It utilizes measures of central tendency to mix blocks of the image at hand to enhance security against a number of cryptanalytic attacks. The mixing is designed so that while encryption is highly sensitive to the secret key and the input image, decryption is robust against noise and cropping of the cipher-image. Empirical results show high performance of the suggested scheme and its robustness against well-known cryptanalytic attacks. Furthermore, comparisons with existing image encryption methods are presented which demonstrate the superiority of the proposed scheme.
1Introduction
The rapid growth in multimedia applications has led to the vast spread of multimedia information across public networks. As a consequence, such information has become vulnerable to eavesdropping. Therefore, the need for safeguarding algorithms has become of major concern. Digital images are amongst the most popular digital media, they are found in a number of applications including military, medical and geographical applications. Due to this wide range of applications, research for developing efficient safeguarding algorithms has grasped the attention of scientists and engineers more than ever.
Cryptography is a field of mathematics and computer science that provide many security services including encryption and data hiding. Data hiding is a process that intends to hide secret information within cover media in such a way that an eavesdropper is incapable to detect the presence of such information within the carrier. On the contrary, encryption is a process that transforms secret information into scrambled data which is totally meaningless to an eavesdropper (Katz et al., 1996; Rijmen and Daemen, 2001; Rivest et al., 1978). Both techniques require a secret key that entitles the recipient to recover back the secret information. One disadvantage of data hiding techniques is that most schemes hide the raw data within the cover media (Cheddad et al., 2010; Mao and Qin, 2013; Ghebleh and Kanso, 2014; Tang et al., 2014). Furthermore, secret images of large sizes require quite large carriers. Due to some inherent characteristics of digital images such as bulk data capacity, high redundancy and correlation between adjacent pixels, conventional encryption schemes such as the Data Encryption Standard (DES) (Katz et al., 1996), the Advanced Encryption Standard (AES) (Rijmen and Daemen, 2001), the Rivest, Shamir and Adleman’s scheme (RSA) (Rivest et al., 1978) are unsuitable for the encryption of digital images.
Chaotic systems have a number of important characteristics such as high sensitive dependence on initial conditions and control parameters, large keyspace, unpredictability, ergodicity, and mixing property. Furthermore, with suitable control parameters and initial conditions, they can generate random looking sequences indistinguishable from random sequences. Confusion and diffusion are two important properties of any suitable encryption scheme (Shannon, 1949). In image encryption, confusion makes the relationship between the cipher-image and the secret key as complex as possible. That is, the impact of a tiny change to the secret key results in a major change in the cipher-image. On the other hand, diffusion makes the statistical relationship between the plain-image and the cipher-image as complex as possible. That is, the impact of a tiny change in the plain-image results in a major change in the cipher-image. This complexity can be obtained by a number of permutations and substitutions. Owing to the strong relationship between the properties of chaotic systems and Shannon’s principles of confusion and diffusion (Shannon, 1949), which are ideal properties in the design of a strong image encryption scheme, chaotic systems have become promising building blocks in the construction of such schemes. In 1998, Fridrich (1998) presented an elegant chaos-based image encryption scheme that consists of two phases: a shuffling phase to confuse the relationship between the cipher-image and the plain-image, and a masking phase to spread a small change in the plain-image throughout the whole cipher-image. Despite the fact that Fridrich’s scheme is shown to suffer from security issues under chosen cipher-image scenario (Solak et al., 2010; Xie et al., 2017), Fridrich’s approach has been adopted in the designs of most proposed chaos-based image encryption schemes. Throughout the last two decades, a number of chaos-based image encryption schemes have been developed (Chen et al., 2004; Guan et al., 2005; Behnia et al., 2008; Zhang et al., 2010; Liu Y. et al., 2016; Hua et al., 2015; Kanso and Ghebleh, 2012, 2015a; Khan et al., 2017; Fu et al., 2018; Khan and Shah, 2015). Chen et al. (2004) proposed an image encryption scheme that employs a 3-dimensional (3D) cat map. However, Chen et al.’s scheme (Chen et al., 2004) is shown to be vulnerable to differential attacks (Li and Chen, 2008; Wang et al., 2005). Guan et al. (2005) proposed an image encryption scheme based on Arnold cat map and Chen’s chaotic system. Cokal and Solak (2009) proved that this scheme suffers from security weaknesses under chosen plain-image and known plain-image scenarios. Behnia et al. (2008) proposed a new kind of image encryption scheme based on composition of trigonometric chaotic maps. However, this scheme is shown to suffer from security issues under chosen plain-image scenario and differential attacks (Li et al., 2010). Zhang et al. (2010) proposed an image encryption scheme based on DNA addition in conjunction with two chaotic logistic maps. Hermassi et al. (2014) revealed a number of flaws including non-invertibility of Zhang et al.’s scheme (Zhang et al., 2010). In Zhu (2012), Zhu proposed an image encryption scheme based on improved hyper-chaotic sequences. Li et al. (2013) showed that Zhu’s scheme can be broken with only one known plain-image. In Liu Y. et al. (2016), a hyper-chaos-based image encryption algorithm with linear feedback shift registers is proposed. Zhang et al. (2017) showed that this scheme has some flaws due to weak security of the diffusion process and it is vulnerable to differential attacks. Hua et al. (2015) introduced a new 2D sine logistic modulation map and proposed a chaotic magic transform image encryption scheme. Kanso and Ghebleh (2012) proposed an image encryption scheme based on 3D cat map. In Kanso and Ghebleh (2015a), a new family of 4D cat maps is proposed together with an image encryption scheme for medical applications. Khan et al. (2017) proposed a chaos-based image encryption scheme that utilizes a non-linear chaotic algorithm for destroying correlation and diffusion in plain-image. In Fu et al. (2018), Fu et al. proposed an algorithm based on a 4D hyper-chaotic system in conjunction with the hash function SHA-224. In addition to the aforementioned schemes, the research committee has proposed a number of schemes such as those presented in Wang et al. (2015), Zhou et al. (2014), Xu et al. (2016), Liu et al. (2016), Hua and Zhou (2017), Zhou et al. (2013), Wu et al. (2014), Cao et al. (2018), Hua et al. (2019), Khan et al. (2017), Fu et al. (2018), Liu et al. (2019), Sun et al. (2020), Hemdan et al. (2019) and references therein.
Among the large number of image encryption schemes that have appeared in the literature, security flaws in some of these schemes have been revealed by the cryptographic community. Furthermore, the rapid advancement of digital media technology demands the attention of researchers to develop fast and efficient image encryption schemes. Arnold’s cat map (Arnol’d and Avez, 1968) is one of the most studied 2D chaotic maps. Due to its characteristics, it has been widely used in a number of cryptographic applications (Guan et al., 2005; Xiao et al., 2009; Fu et al., 2011; Ghebleh et al., 2014b; Soleymani et al., 2014; Kanso and Ghebleh, 2015a,b). Furthermore, a number of generalizations of the 2D cat map have appeared in the literature (Chen et al., 2004; Kanso and Ghebleh, 2013). In this paper, we propose a new family of 4D chaotic cat maps that is an extension of the generalization suggested in Kanso and Ghebleh (2013) for use in cryptographic applications. The objective of this proposal is to increase the number of control parameters in the coefficient matrix defining the 4D cat map which in turn increases the size of the keyspace of any cryptographic scheme adopting the generalization. We then propose an image encryption scheme based on members of this family. The proposed scheme follows Fridrich’s approach. It is composed of a light shuffling phase and a masking phase, which operate on image-blocks. The shuffling phase preforms a circular shift on the rows and columns of the image at hand in conjunction with a zigzag ordering algorithm. The masking phase uses pseudorandom sequences generated by the proposed 4D cat map for diffusion of the resulting shuffle-image. Furthermore, the masking phase applies measures of central tendency to enhance security against a number of cryptanalytic attacks such as differential attacks. The mixing is designed so that while encryption is highly sensitive to the secret key and the input image, decryption is robust against noise and cropping of the cipher-image. Simulation results are presented to demonstrate the high performance of the proposed scheme and its high security level.
The main contributions of this work are as follows:
• The method is simple and efficient.
• The encryption scheme is highly sensitive to its key and input image, while the decryption scheme is robust against various alternations such as noise and cropping of cipher-image.
• The method is block-based. Based on the block size, there is a tradeoff between the security and the speed of the proposed scheme. However, simulations show that the chosen block size makes the scheme robust to existing attacks, insensitive to cipher-image attacks, and faster than existing schemes.
The paper is organized as follows: Section 2 presents the proposed family of 4D cat maps. In Section 3, we give a detailed description of the proposed image encryption scheme. We also demonstrate the randomness of matrices generated by successive iterations of the proposed 4D cat map. Section 4 showcases the efficiency of the proposed scheme. It also presents simulation results that demonstrate the robustness of the proposed scheme against statistical attacks. In Section 5, we further analyse the security of the proposed scheme. In Section 6, we showcase the superiority of the proposed scheme over some of the existing schemes. Finally, we end the paper with some concluding remarks.
2The 4-Dimensional Cat Map
Arnold’s cat map (Arnol’d and Avez, 1968) is a chaotic map defined on the torus
(1)
We consider the following path to define a new
(2)
(3)
It is easy to see that each matrix
For all the experimental results presented in this work, we use the values
(4)
3Description of the Proposed Scheme Pr-IES
In this work, we propose an image encryption scheme that follows Fridrich’s approach. The proposed scheme consists of three phases (i) a preprocessing phase for reshaping the input image, (ii) a shuffling phase for destroying any correlation between adjacent intensity values, and (iii) a masking phase that acts on the shuffle-image to change its intensity values in such a way that a tiny change in one intensity value spreads out to almost all intensity values in the cipher-image. Algorithm 1 depicts the phases of the proposed image encryption scheme.
Algorithm 1
The proposed image encryption scheme Pr-IES

3.1The Preprocessing Phase
The size of the input image plays an important role in the performance of the proposed scheme. In the preprocessing phase, the input image J, typically a 2D (for grayscale images) or 3D (for colour images) array of bytes, is reshaped into an almost square 2D matrix
3.2The Shuffling Phase
This phase aims to destroy correlations between adjacent pixels in the input image. It performs an
Algorithm 2
The shuffling of the matrix

To illustrate the shuffling phase, we present a one round toy example on the
Traverse
This gives the 1D array
3.3The Masking Phase
The masking phase acts on the shuffled matrix
Algorithm 3
Generation of the scrambled matrix

3.4Randomness of the Masking Matrices
In Bassham et al. (2010), the National Institute of Standards and Technology (NIST) proposes a Statistical Test Suite (STS) which is one of the most popular tools for validation of random number generators and pseudorandom number generators for cryptographic applications. To assess randomness of their entries, we subject the matrices
Table 1
Statistical Test Suite results for a matrix
| Statistical test | Set of matrices | |
| P-value | Result | |
| Frequency | 0.455937 |
|
| Block-frequency | 0.983453 |
|
| Cumulative-sums (forward) | 0.350485 |
|
| Cumulative-sums (reverse) | 0.383827 |
|
| Runs | 0.779188 |
|
| Longest-runs | 0.191687 |
|
| Rank | 0.616305 |
|
| FFT | 0.494392 |
|
| Non-overlapping-templates | 0.616305 |
|
| Overlapping-templates | 0.289667 |
|
| Universal | 0.494392 |
|
| Approximate entropy | 0.657933 |
|
| Random-excursions | 0.324180 |
|
| Random-excursions variant | 0.706149 |
|
| Serial 1 | 0.383827 |
|
| Serial 2 | 0.816537 |
|
| Linear-complexity | 0.213309 |
|
4Statistical Analysis of Cipher-Images
In this section, we showcase the efficiency of the proposed scheme. We then evaluate the randomness of cipher-images corresponding to standard test images. Furthermore, we consider cipher-images corresponding to bank of test plain-images.
4.1Test Images and Parameters
This section shows the efficiency of the proposed image encryption scheme Pr-IES. Figure 1 depicts standard grayscale test images Barbara of size
Fig. 1
Test plain-images Barbara of size

Figure 2 presents the shuffle-images corresponding to the test images Barbara, Lena and Elaine for
Fig. 2
The shuffle-images corresponding to the test images Barbara, Lena and Elaine.

Figure 3 depicts the shuffle-images and cipher-images corresponding to the test plain-images Barbara, Lena and Elaine, with
Fig. 3
The shuffle-images (top) and cipher-images (bottom) for

4.2Histogram Analysis
Histogram analysis is an important test which shows the distribution of the intensity values of the pixels within an image. A secure image encryption scheme produces cipher-images whose pixel intensity values are uniformly distributed in the interval
Table 2
The chi-square test results for the cipher-images corresponding to the test images Barbara, Lena and Elaine. This table also reports the chi-square value for a random image.
| Cipher-image |
|
| Cipher-Barbara | 262.5859 |
| Cipher-Lena | 248.8477 |
| Cipher-Elaine | 222.1147 |
| Random image | 235.4453 |
Fig. 4
Histograms of the test images Barbara, Lena and Elaine (top) and their corresponding cipher-images (bottom).
4.3Correlation Analysis of Adjacent Pixels
A secure image encryption scheme generates cipher-images almost free of any correlation. The correlation coefficients
Table 3 reports the correlation coefficients for cipher-images corresponding to the test plain-images Barbara, Lena and Elaine. Furthermore, the table presents the correlation coefficients of the shuffle-images corresponding to the test images. It is evident from this table that the correlation coefficients of the cipher-images and the shuffle-images are almost zero. Hence, the cipher-images are almost free of any correlation.
Table 3
Correlation coefficients of the test plain-images, shuffle-images and cipher-images for
| Image | Adjacency | Plain-image | Shuffle-image | Cipher-image |
| Barbara | Horizontal | 0.956279 |
|
|
| Vertical | 0.971464 | 0.003786 | 0.007816 | |
| Diagonal | 0.935520 |
|
| |
| Lena | Horizontal | 0.972826 | 0.006197 | 0.001692 |
| Vertical | 0.986398 |
| 0.020036 | |
| Diagonal | 0.962357 |
|
| |
| Elaine | Horizontal | 0.994613 | 0.015765 |
|
| Vertical | 0.993920 |
| 0.008746 | |
| Diagonal | 0.989842 | 0.003508 |
|
Figure 5 depicts a plot of the points
Fig. 5
Point plots of the intensity values of randomly chosen pairs of horizontally, vertically and diagonally adjacent pixels in the plain-image Lena (top), its corresponding shuffle-image (middle) and cipher-image (bottom).
4.4Information entropy analysis
Information entropy (Shannon, 1948) is an important measure for evaluating the strength of an image encryption scheme. It measures the distribution of gray-values in an image. The entropy
Table 4
Entropy measures for the test plain-images Barbara, Lena, Elaine and their corresponding cipher-images.
| Image | Entropy | |
| Plain-image | Cipher-image | |
| Barbara | 7.6019 | 7.9971 |
| Lena | 7.4455 | 7.9993 |
| Elaine | 7.5029 | 7.9998 |
To further showcase the randomness of the proposed image encryption scheme we measure the entropy over local cipher-images blocks (Wu et al., 2013). Table 5 reports the mean of entropy measures over local cipher-images blocks, where the block sizes are
Table 5
Average entropy of image blocks.
| Image | Plain-image | Cipher-image | ||||
|
|
|
|
|
|
| |
| Barbara | 5.7160 | 6.5322 | 7.0868 | 7.1766 | 7.8076 | 7.9549 |
| Lena | 4.9910 | 5.6328 | 6.2260 | 7.1763 | 7.8098 | 7.9550 |
| Elaine | 4.7618 | 5.3754 | 5.9626 | 7.1759 | 7.8095 | 7.9546 |
| Random | 7.1750 | 7.8097 | 7.9542 | 7.1738 | 7.8090 | 7.9542 |
4.5Randomness Analysis
In this section, we evaluate the randomness of cipher-images generated by the proposed scheme Pr-IES using the STS proposed by the National Institute for Standards and Technology (NIST) (Bassham et al., 2010). For this regard, we consider the first 100 images from the test bank of images in BOWS2 (2019). We encrypt each
Table 6
Statistical Test Suite results for 100 cipher-images, each of length 2097152 bits.
| Statistical test | Cipher-images | |
| P-value | Result | |
| Frequency | 0.911413 |
|
| Block-frequency | 0.366918 |
|
| Cumulative-sums (forward) | 0.924076 |
|
| Cumulative-sums (reverse) | 0.851383 |
|
| Runs | 0.334538 |
|
| Longest-runs | 0.419021 |
|
| Rank | 0.816537 |
|
| FFT | 0.108791 |
|
| Non-overlapping-templates | 0.897763 |
|
| Overlapping-templates | 0.739918 |
|
| Universal | 0.994250 |
|
| Approximate entropy | 0.657933 |
|
| Random-excursions | 0.534146 |
|
| Random-excursions variant | 0.846579 |
|
| Serial 1 | 0.719747 |
|
| Serial 2 | 0.191687 |
|
| Linear-complexity | 0.289667 |
|
4.6Speed Analysis
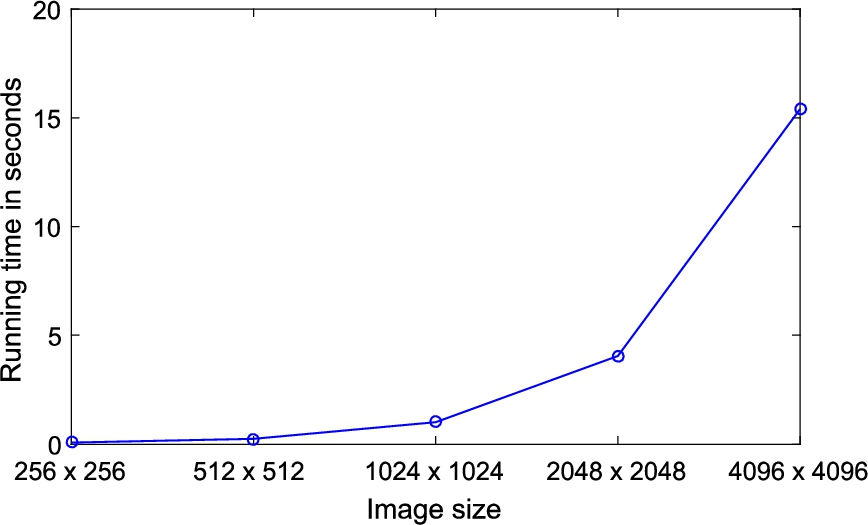
In this section, we report the running speed of the proposed image encryption scheme Pr-IES in MATLAB on a desktop machine with an Intel® Core™ i7-4770 processor and 8GB of memory, running Windows 10. Table 7 reports the running time for encrypting the test images by the proposed scheme. Furthermore, Fig. 6 shows a sample of the running times for encrypting grayscale images of different sizes by the proposed image encryption scheme with
Table 7
Running time of the proposed encryption scheme.
| Size | Encryption time in seconds |
|
| 0.0644554 |
|
| 0.2422222 |
|
| 1.0021399 |
Fig. 6
Encryption time versus image size.
5Security Analysis
In this section, we evaluate the security level of the proposed scheme. We show that the proposed scheme Pr-IES is highly sensitive to a slight modification in the plain-image. We further show that the scheme has a large keyspace, and it is highly sensitive to its secret key and control parameters. Moreover, we analyse the security of the proposed scheme under cipher-image scenario and chosen plain-image scenario. In addition to that, we demonstrate the robustness of its decryption to various alterations in the cipher-image.
5.1Differential analysis
Differential analysis of an image encryption scheme investigates the affect of a slight modification in the plain-image on the corresponding cipher-image. In this section, we measure the sensitivity of the proposed image encryption against slight modification in the plain-image. The Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) are two measures used to evaluate the strength of image encryption schemes against differential attacks (Wu et al., 2011). Suppose
According to Wu et al. (2011), the theoretical ideal NPCR and UACI measures for
Table 8
Acceptance intervals for the null hypothesis with different levels of significance (Wu et al., 2011).
| Parameter | Size | 0.05-level | 0.01-level | 0.001-level |
| NPCR |
|
|
|
|
|
|
|
|
| |
|
|
|
|
| |
| UACI |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
We evaluate the robustness of the proposed image encryption scheme by considering two plain-images
Table 9
NPCR and UACI measures between cipher-images
| Measures | Cipher-images of Barbara | Cipher-images of Lena | Cipher-images of Elaine | ||||||
| Min | Mean | Max | Min | Mean | Max | Min | Mean | Max | |
| NPCR | 99.5483 | 99.6093 | 99.6796 | 99.5819 | 99.6110 | 99.6399 | 99.5972 | 99.6089 | 99.6252 |
| UACI | 33.2820 | 33.4913 | 33.6932 | 33.3231 | 33.4388 | 33.5638 | 33.4136 | 33.4649 | 33.5160 |
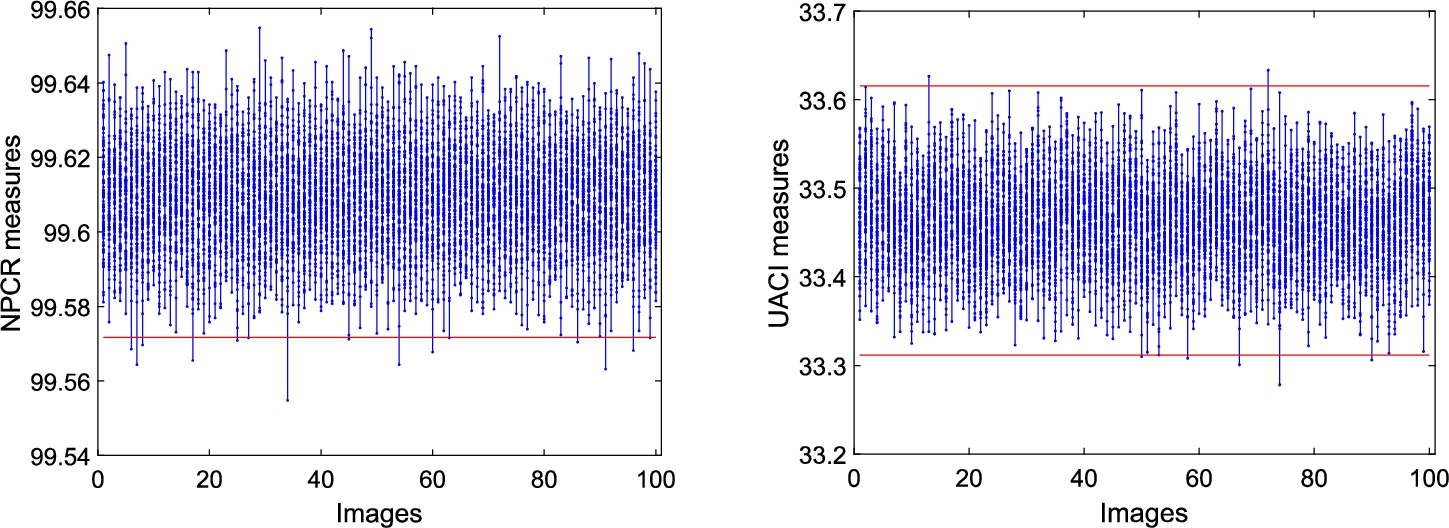
We further evaluate the robustness of the proposed scheme by subjecting each of the first 100 test images from (BOWS2) to the plain-image sensitivity test. For each plain-image we repeat the test 100 times, where each time we make a change to the least significant bit of a randomly chosen intensity value of the original plain-image. It turns out that the pass rate for the NPCR is
Fig. 7
NPCR (left) and UACI (right) measures for plain-image sensitivity of the proposed scheme. Each point represent an NPCR/UACI measure resulting from repeating the test 100 for each test image in (BOWS2).
5.2Keyspace
The secret key
Figure 8 depicts the bitwise xor (exclusive or) of two cipher-images
The experimental results presented in Fig. 8, Fig. 9, and Table 10 demonstrate high sensitivity of the proposed scheme to its secret key, hence its robustness against key search attacks.
Fig. 8
Bitwise xor between cipher-images

5.3Cipher-Image and Plain-Image Analysis
In this section, we show that the proposed scheme is robust against cipher-image and plain-image analysis. In a cipher-image attack, the intruder has only access to the cipher-image. Since the above tests show that no useful information about the plain-image can be gained from the corresponding cipher-image, we conclude that the proposed scheme is robust against this type of attack. In a plain-image attack, the intruder can choose any part of the plain-image and request its corresponding cipher-image part. The aim of this attack is to reconstruct some other plain-image parts. The fact that the chaotic map possesses the one-way property due to floating point errors makes the inverse computation very difficult. Furthermore, since the proposed scheme is highly dependent on its secret key, one cannot predict further outputs of the 4D cat map. Thus, the scheme is robust against this type of attacks.
Table 10
NPCR and UACI measures between cipher-images
| Measures | Cipher-images of Barbara | Cipher-images of Lena | Cipher-images of Elaine | |||
| NPCR | 99.6338 | 99.6124 | 99.6002 | 99.6101 | 99.6215 | 99.6066 |
| UACI | 33.6906 | 33.4831 | 33.3946 | 33.4988 | 33.4807 | 33.4435 |
5.4Robustness to Noise and Data Loss
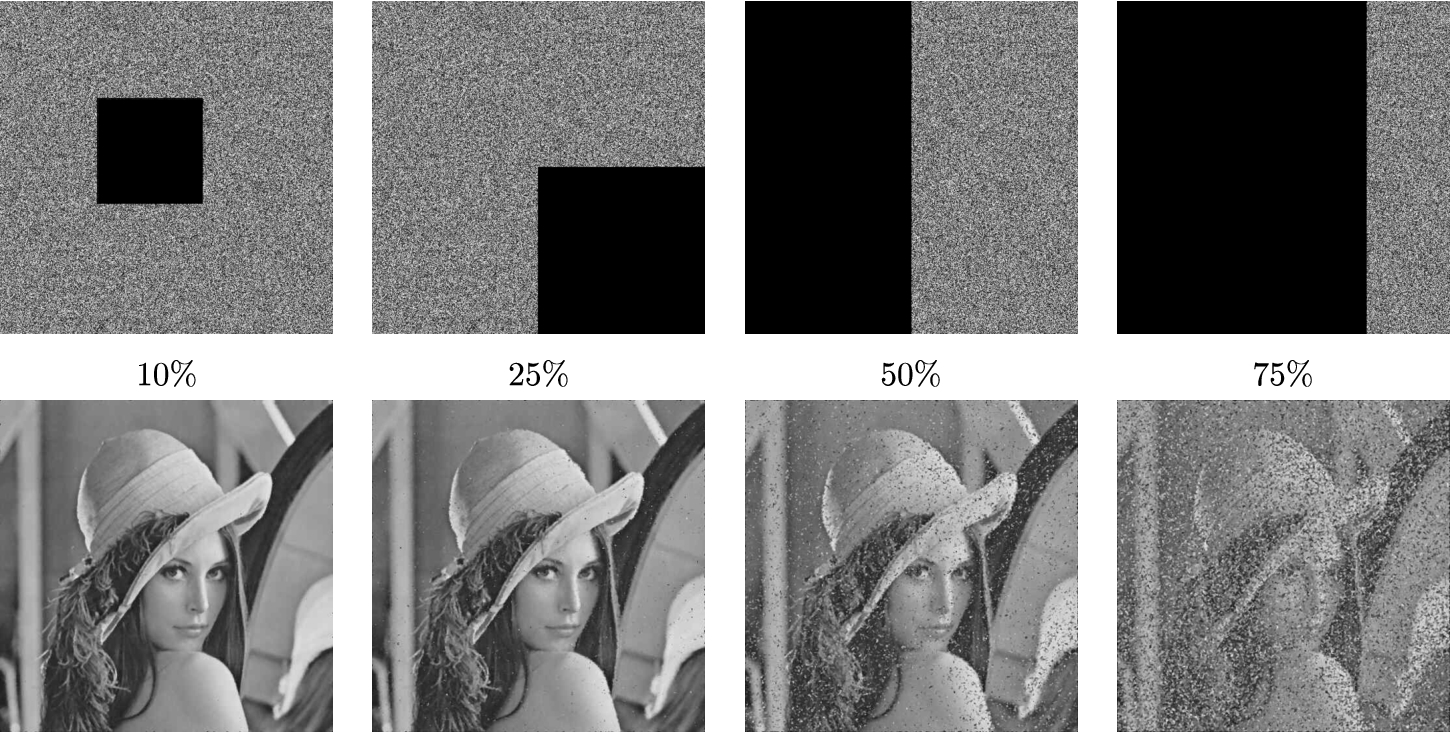
Earlier, we have shown that the proposed scheme is highly sensitive to its secret key, and it is also highly sensitive to a tiny change in its input plain-image. That is, a change in a plain-image intensity value spreads over all intensity values in the corresponding cipher-image. In this section, we show that a change in intensity values in the cipher-image affects only few intensity values in the corresponding plain-image. The importance of this feature is that with distortion of cipher-images due to salt and pepper noise or data loss one can still successfully recover the corresponding plain-image. Figure 10 depicts median filtered recovered plain-image Lena resulting from subjecting its corresponding cipher-image to salt and pepper noise for different levels of added noise. Figure 11 depicts the median filtered recovered plain-image Lena resulting from subjecting its corresponding cipher-image to data loss for different sizes of data loss.
Fig. 10
The reconstructed plain-image Lena resulting from subjecting its corresponding cipher-image to a

Fig. 11
The reconstructed plain-image Lena (bottom) resulting from subjecting its corresponding cipher-image to a
6Comparison with Existing Work
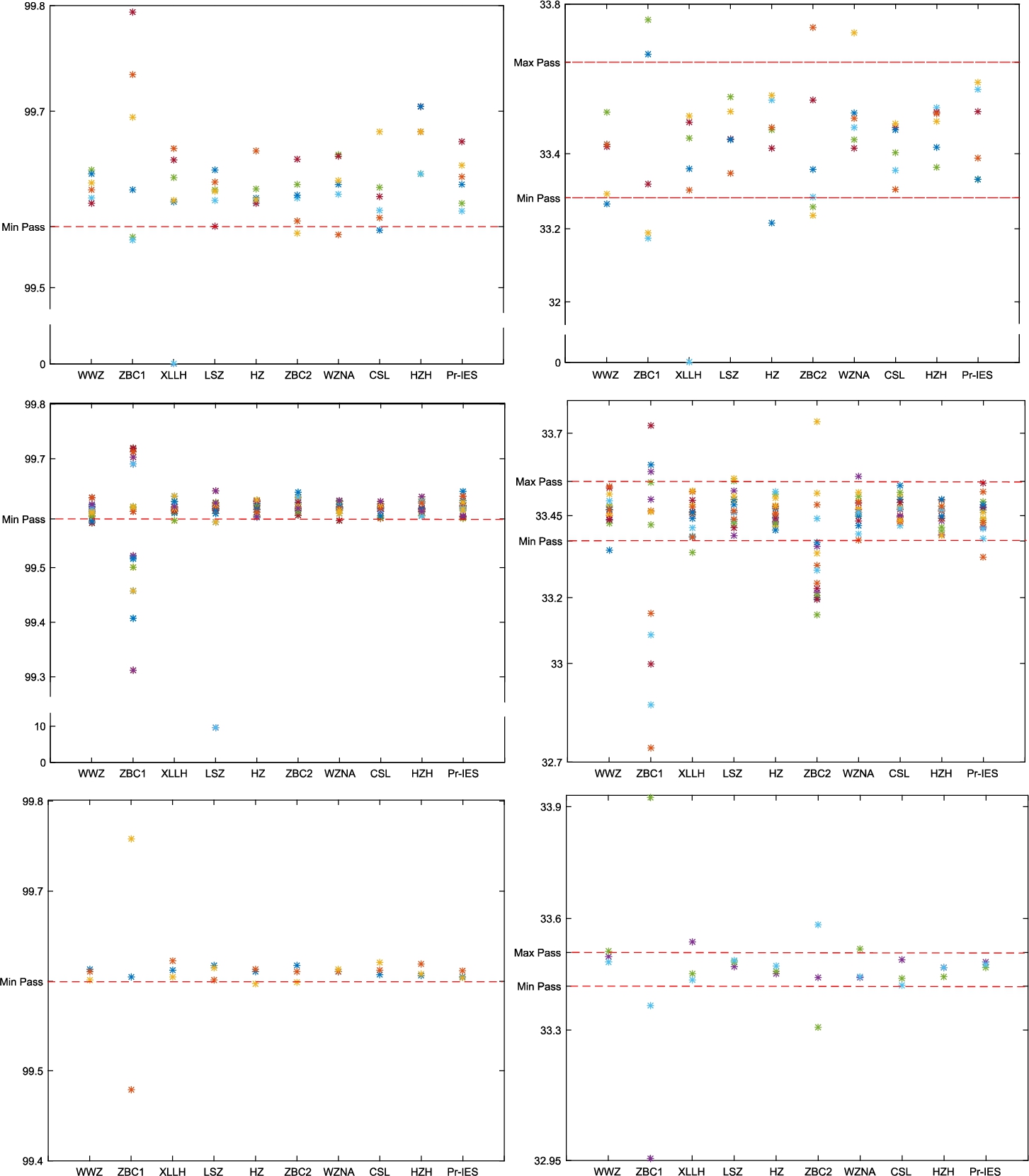
In this section, we compare the performance of the proposed scheme Pr-IES with existing ones. Figure 12 presents NPCR and UACI measures for cipher-images corresponding to 25 test images in Test-images (2019) for a number of existing schemes. There are 7 test images of size
Table 11
The NPCR and UACI pass rates of the proposed scheme and some existing schemes. The pass rates for the schemes under comparison are quoted from Hua et al. (2019).
| Scheme | Pass rate | |
| NPCR | UACI | |
| WWZ (Wang et al., 2015) |
|
|
| ZBC1 (Zhou et al., 2014) |
|
|
| XLLH (Xu et al., 2016) |
|
|
| LSZ (Liu et al., 2016) |
|
|
| HZ (Hua and Zhou, 2017) |
|
|
| ZBC2 (Zhou et al., 2013) |
|
|
| WZNA (Wu et al., 2014) |
|
|
| CSL (Cao et al., 2018) |
|
|
| HZH (Hua et al., 2019) |
|
|
| Pr-IES |
|
|
Fig. 12
NPCR (left) and UACI (right) measures for cipher-images generated by existing image encryption schemes and the proposed scheme. The measures for existing schemes are obtained from Hua et al. (2019).
We further compare the correlation coefficients between adjacent pixels of the proposed scheme and existing ones. Figure 13 depicts the correlation coefficients between adjacent intensity values in the horizontal, vertical and diagonal directions for the test image Lena and its corresponding cipher-images generated by the proposed scheme and existing schemes. Note the schemes proposed in Fu et al. (2011) and Liao et al. (2010) are referred to by FLMLC and LLZ, respectively.
Fig. 13
Adjacent intensity values correlation coefficients for the test image Lena and corresponding cipher-images generated by existing schemes and the proposed scheme. The values for existing schemes are obtained from Hua et al. (2019).
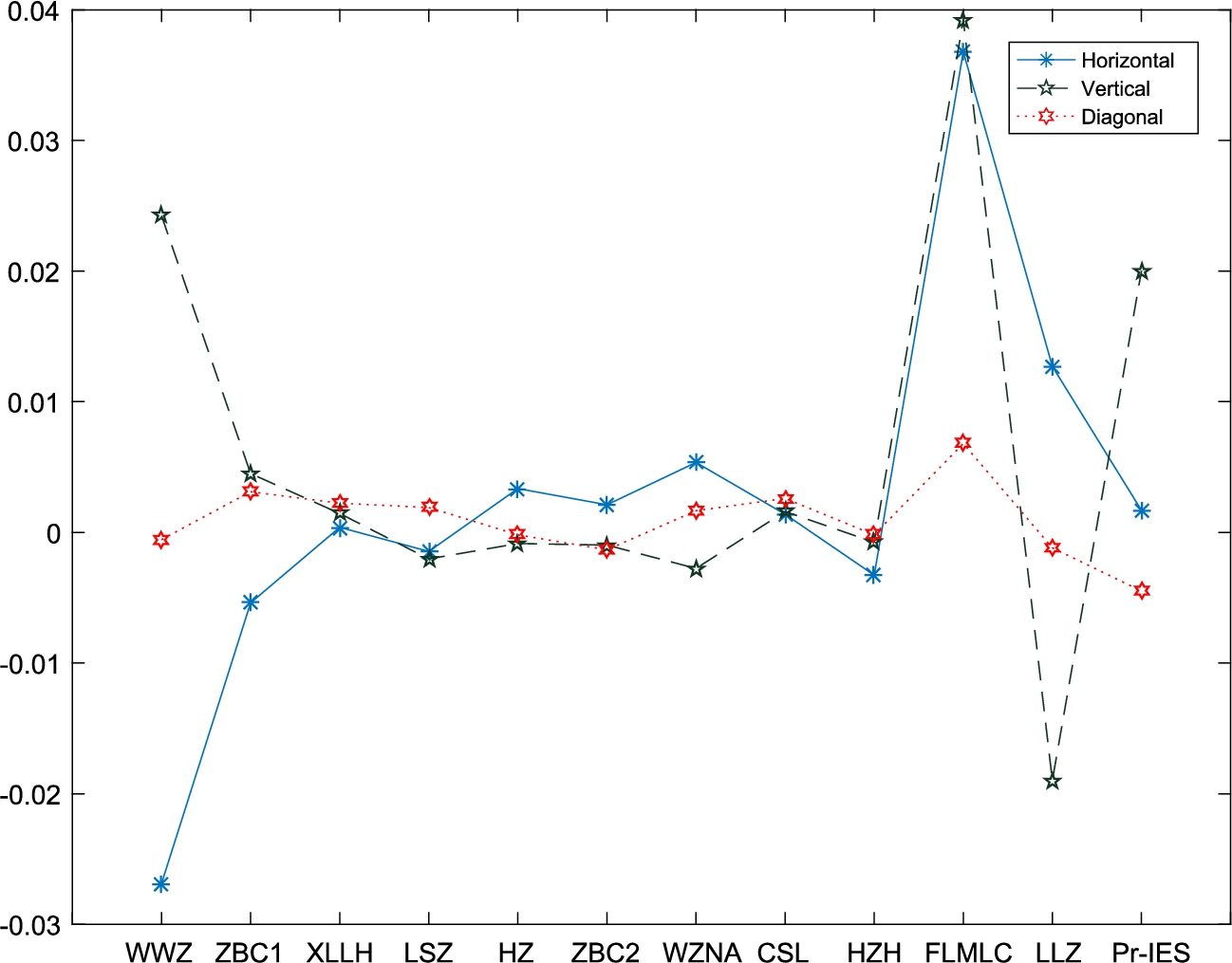
Table 12 reports the running time in seconds for encrypting a single image with some existing schemes and the proposed scheme. The reported running times for the schemes under comparison are quoted from Hua et al. (2019). According to Hua et al. (2019), the reported running times for existing schemes are obtained on a computer under the following environments: Intel® Core™ i7-7700 CPU @3.60 GHz and 8 GB of memory, running Windows 10 operating system. While the reported running times for the proposed scheme Pr-IES are obtained on a desktop machine with an Intel® Core™ i7-4770 processor @3.40 GHz and 8GB of memory, running Windows 10 operating system.
Table 12
Running time in seconds for encrypting a single image by existing schemes and the proposed encryption scheme Pr-IES. The running times for the schemes under comparison are quoted from Hua et al. (2019) used under license CC BY-NC-ND 4.0 (License, 2020).
| Image size |
|
|
|
|
| (Diaconu, 2016) | 0.0579 | 0.2224 | 0.9731 | 3.8377 |
| (Ping et al., 2018) | 0.0902 | 0.3440 | 1.3357 | 5.3223 |
| (Chai et al., 2017) | 0.2757 | 0.9810 | 3.8539 | 15.4565 |
| (Hua and Zhou, 2017) | 0.1531 | 0.6347 | 2.4913 | 9.9185 |
| (Xu et al., 2016) | 0.0247 | 0.1164 | 0.4924 | 20.144 |
| (Zhou et al., 2014) | 0.0933 | 0.3843 | 1.4824 | 5.8175 |
| (Liao et al., 2010) | 0.0323 | 0.1440 | 0.5510 | 2.0864 |
| (Hua et al., 2019) | 0.0244 | 0.0949 | 0.4010 | 1.9857 |
| Pr-IES | 0.0217 | 0.0645 | 0.2422 | 1.0021 |
It is evident from the obtained results that the proposed scheme has superiority over existing schemes and competitive with others.
7Conclusion
We propose a new family of 4D chaotic cat maps. As an application of these maps, we present a novel block-based image encryption scheme utilizing them. This scheme consists of a light shuffling phase and a masking phase which uses measures of central tendency for mixing the image blocks. While encryption is highly sensitive to the secret key and the input image, decryption is robust against noise and cropping of the cipher-image. Simulations show that the proposed scheme generates cipher-images possessing high randomness properties. Furthermore, the scheme is shown to be robust against differential cryptanalysis. With respect to existing works, the proposed scheme is shown to have superior performance over existing image encryption algorithms and to be competitive with others.
Acknowledgements
The authors are grateful to the anonymous referees whose remarks helped improve the presentation of this work.
References
1 | Alvarez, G., Li, S. ((2006) ). Some basic cryptographic requirements for chaos-based cryptosystems. International Journal of Bifurcation and Chaos, 16: (08), 2129–2151. |
2 | Arnol’d, V.I., Avez, A. ((1968) ). Ergodic Problems of Classical Mechanics. WA Benjamin. |
3 | Bassham, L.E. III., Rukhin, A.L., Soto, J., Nechvatal, J.R., Smid, M.E., Barker, E.B., Leigh, S.D., Levenson, M., Vangel, M., Banks, D.L. (2010). Sp 800-22 rev. 1a. A statistical test suite for random and pseudorandom number generators for cryptographic applications. |
4 | Behnia, S., Akhshani, A., Mahmodi, H., Akhavan, A. ((2008) ). Chaotic cryptographic scheme based on composition maps. International Journal of Bifurcation and Chaos, 18: (01), 251–261. |
5 | Cao, C., Sun, K., Liu, W. ((2018) ). A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map. Signal Processing, 143: , 122–133. |
6 | Chai, X., Chen, Y., Broyde, L. ((2017) ). A novel chaos-based image encryption algorithm using DNA sequence operations. Optics and Lasers in Engineering, 88: , 197–213. |
7 | Cheddad, A., Condell, J., Curran, K., Mc Kevitt, P. ((2010) ). Digital image steganography: survey and analysis of current methods. Signal Processing, 90: (3), 727–752. |
8 | Chen, G., Mao, Y., Chui, C.K. ((2004) ). A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos, Solitons & Fractals, 21: (3), 749–761. |
9 | Cokal, C., Solak, E. ((2009) ). Cryptanalysis of a chaos-based image encryption algorithm. Physics Letters A, 373: (15), 1357–1360. |
10 | Diaconu, A.-V. ((2016) ). Circular inter-intra pixels bit-level permutation and chaos-based image encryption. Information Sciences, 355: , 314–327. |
11 | Fridrich, J. ((1998) ). Symmetric ciphers based on two-dimensional chaotic maps. International Journal of Bifurcation and Chaos, 8: (06), 1259–1284. |
12 | Fu, C., Lin, B-b., Miao, Y-s., Liu, X., Chen, J-j. ((2011) ). A novel chaos-based bit-level permutation scheme for digital image encryption. Optics Communications, 284: (23), 5415–5423. |
13 | Fu, C., Zhang, G.-Y., Zhu, M., Chen, J.-X., Lei, W.-M. ((2018) ). A fast chaos-based colour image encryption algorithm using a hash function. Informatica, 29: (4), 651–673. |
14 | Ghebleh, M., Kanso, A. ((2014) ). A robust chaotic algorithm for digital image steganography. Communications in Nonlinear Science and Numerical Simulation, 19: (6), 1898–1907. |
15 | Ghebleh, M., Kanso, A., Noura, H. ((2014) a). An image encryption scheme based on irregularly decimated chaotic maps. Signal Processing: Image Communication, 29: (5), 618–627. |
16 | Ghebleh, M., Kanso, A., Own, H.S. ((2014) b). A blind chaos-based watermarking technique. Security and Communication Networks, 7: (4), 800–811. |
17 | Guan, Z.-H., Huang, F., Guan, W. ((2005) ). Chaos-based image encryption algorithm. Physics Letters A, 346: (1–3), 153–157. |
18 | Hemdan, A.M., Faragallah, O.S., Elshakankiry, O., Elmhalaway, A. ((2019) ). A fast hybrid image cryptosystem based on random generator and modified logistic map. Multimedia Tools and Applications, 78: (12), 16177–16193. |
19 | Hermassi, H., Belazi, A., Rhouma, R., Belghith, S.M. ((2014) ). Security analysis of an image encryption algorithm based on a DNA addition combining with chaotic maps. Multimedia Tools and Applications, 72: (3), 2211–2224. |
20 | Hua, Z., Zhou, Y. ((2017) ). Design of image cipher using block-based scrambling and image filtering. Information Sciences, 396: , 97–113. |
21 | Hua, Z., Zhou, Y., Pun, C.-M., Chen, C.P. ((2015) ). 2D Sine Logistic modulation map for image encryption. Information Sciences, 297: , 80–94. |
22 | Hua, Z., Yi, S., Zhou, Y., Li, C., Wu, Y. ((2017) ). Designing hyperchaotic cat maps with any desired number of positive Lyapunov exponents. IEEE Transactions on Cybernetics, 48: (2), 463–473. |
23 | Hua, Z., Zhou, Y., Huang, H. ((2019) ). Cosine-transform-based chaotic system for image encryption. Information Sciences, 480: , 403–419. |
24 | Kanso, A., Ghebleh, M. ((2012) ). A novel image encryption algorithm based on a 3D chaotic map. Communications in Nonlinear Science and Numerical Simulation, 17: (7), 2943–2959. |
25 | Kanso, A., Ghebleh, M. ((2013) ). A fast and efficient chaos-based keyed hash function. Communications in Nonlinear Science and Numerical Simulation, 18: (1), 109–123. |
26 | Kanso, A., Ghebleh, M. ((2015) a). An efficient and robust image encryption scheme for medical applications. Communications in Nonlinear Science and Numerical Simulation, 24: (1–3), 98–116. |
27 | Kanso, A., Ghebleh, M. ((2015) b). A structure-based chaotic hashing scheme. Nonlinear Dynamics, 81: (1–2), 27–40. |
28 | Katz, J., Menezes, A.J., Van Oorschot, P.C., Vanstone, S.A. ((1996) ). Handbook of Applied Cryptography. CRC Press. |
29 | Khan, M., Shah, T. ((2015) ). An efficient chaotic image encryption scheme. Neural Computing and Applications, 26: (5), 1137–1148. |
30 | Khan, J.S., Khan, M.A., Ahmad, J., Hwang, S.O., Ahmed, W. ((2017) ). An improved image encryption scheme based on a non-linear chaotic algorithm and substitution boxes. Informatica, 28: (4), 629–649. |
31 | Kwok, H., Tang, W.K. ((2007) ). A fast image encryption system based on chaotic maps with finite precision representation. Chaos, Solitons & Fractals, 32: (4), 1518–1529. |
32 | Li, C., Chen, G. ((2008) ). On the security of a class of image encryption schemes. In: 2008 IEEE International Symposium on Circuits and Systems. IEEE, pp. 3290–3293. |
33 | Li, C., Arroyo, D., Lo, K.-T. ((2010) ). Breaking a chaotic cryptographic scheme based on composition maps. International Journal of Bifurcation and Chaos, 20: (08), 2561–2568. |
34 | Li, C., Liu, Y., Xie, T., Chen, M.Z. ((2013) ). Breaking a novel image encryption scheme based on improved hyperchaotic sequences. Nonlinear Dynamics, 73: (3), 2083–2089. |
35 | Liao, X., Lai, S., Zhou, Q. ((2010) ). A novel image encryption algorithm based on self-adaptive wave transmission. Signal Processing, 90: (9), 2714–2722. |
36 | Liu, H., Zhang, Y., Kadir, A., Xu, Y. ((2019) ). Image encryption using complex hyper chaotic system by injecting impulse into parameters. Applied Mathematics and Computation, 360: , 83–93. |
37 | Liu, W., Sun, K., Zhu, C. ((2016) ). A fast image encryption algorithm based on chaotic map. Optics and Lasers in Engineering, 84: , 26–36. |
38 | Liu, Y., Tong, X., Ma, J. ((2016) ). Image encryption algorithm based on hyper-chaotic system and dynamic S-box. Multimedia Tools and Applications, 75: (13), 7739–7759. |
39 | Mao, Q., Qin, C. ((2013) ). A novel turbo unequal error protection scheme for image steganography. Informatica, 24: (4), 561–576. |
40 | Ott, E. ((2002) ). Chaos in Dynamical Systems. Cambridge University Press. |
41 | Ping, P., Xu, F., Mao, Y., Wang, Z. ((2018) ). Designing permutation–substitution image encryption networks with Henon map. Neurocomputing, 283: , 53–63. |
42 | Rijmen, V., Daemen, J. ((2001) ). Advanced encryption standard. In: Proceedings of Federal Information Processing Standards Publications, National Institute of Standards and Technology, pp. 19–22 |
43 | Rivest, R.L., Shamir, A., Adleman, L. ((1978) ). A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21: (2), 120–126. |
44 | Shannon, C.E. ((1948) ). A mathematical theory of communication. Bell System Technical Journal, 27: (3), 379–423. |
45 | Shannon, C.E. ((1949) ). Communication theory of secrecy systems. Bell System Technical Journal, 28: (4), 656–715. |
46 | Solak, E., Çokal, C., Yildiz, O.T., Biyikoğlu, T. ((2010) ). Cryptanalysis of Fridrich’s chaotic image encryption. International Journal of Bifurcation and Chaos, 20: (05), 1405–1413. |
47 | Soleymani, A., Nordin, M.J., Sundararajan, E. (2014). A chaotic cryptosystem for images based on henon and arnold cat map. The Scientific World Journal, 2014. |
48 | Sun, Y-J., Zhang, H., Wang, X-Y., Wang, X-Q., Yan, P-F. ((2020) ). 2D non-adjacent coupled map lattice with q and its applications in image encryption. Applied Mathematics and Computation, 373: , 125039. |
49 | Tang, M., Hu, J., Song, W. ((2014) ). A high capacity image steganography using multi-layer embedding. Optik-International Journal for Light and Electron Optics, 125: (15), 3972–3976. |
50 | Wang, C., Fan, C., Ding, Q. ((2018) ). Constructing discrete chaotic systems with positive Lyapunov exponents. International Journal of Bifurcation and Chaos, 28: (07), 1850084. |
51 | Wang, K., Pei, Zou, L., Song, A., He, Z. ((2005) ). On the security of 3D cat map based symmetric image encryption scheme. Physics Letters A, 343: (6), 432–439. |
52 | Wang, X., Wang, Q., Zhang, Y. ((2015) ). A fast image algorithm based on rows and columns switch. Nonlinear Dynamics, 79: (2), 1141–1149. |
53 | Wu, Y., Noonan, J.P., Agaian, S. ((2011) ). NPCR and UACI randomness tests for image encryption. Cyber Journals: Multidisciplinary Journals in Science and Technology, Journal of Selected Areas in Telecommunications (JSAT), 1: (2), 31–38. |
54 | Wu, Y., Zhou, Y., Saveriades, G., Agaian, S., Noonan, J.P., Natarajan, P. ((2013) ). Local shannon entropy measure with statistical tests for image randomness. Information Sciences, 222: , 323–342. |
55 | Wu, Y., Zhou, Y., Noonan, J.P., Agaian, S. ((2014) ). Design of image cipher using latin squares. Information Sciences, 264: , 317–339. |
56 | Xiao, D., Liao, X., Wei, P. ((2009) ). Analysis and improvement of a chaos-based image encryption algorithm. Chaos, Solitons & Fractals, 40: (5), 2191–2199. |
57 | Xie, E.Y., Li, C., Yu, S., Lü, J. ((2017) ). On the cryptanalysis of Fridrich’s chaotic image encryption scheme. Signal Processing, 132: , 150–154. |
58 | Xu, L., Li, Z., Li, J., Hua, W. ((2016) ). A novel bit-level image encryption algorithm based on chaotic maps. Optics and Lasers in Engineering, 78: , 17–25. |
59 | Zhang, Q., Guo, L., Wei, X. ((2010) ). Image encryption using DNA addition combining with chaotic maps. Mathematical and Computer Modelling, 52: (11–12), 2028–2035. |
60 | Zhang, X., Nie, W., Ma, Y., Tian, Q. ((2017) ). Cryptanalysis and improvement of an image encryption algorithm based on hyper-chaotic system and dynamic S-box. Multimedia Tools and Applications, 76: (14), 15641–15659. |
61 | Zhou, Y., Bao, L., Chen, C.P. ((2013) ). Image encryption using a new parametric switching chaotic system. Signal Processing, 93: (11), 3039–3052. |
62 | Zhou, Y., Bao, L., Chen, C.P. ((2014) ). A new 1D chaotic system for image encryption. Signal Processing, 97: , 172–182. |
63 | Zhu, C. ((2012) ). A novel image encryption scheme based on improved hyperchaotic sequences. Optics Communications, 285: (1), 29–37. |
64 | The 2nd BOWS contest. http://bows2.ec-lille.fr. Accessed: 2019-12-14. |
65 | Attribution-noncommercial-noderivatives 4.0 international (CC BY-NC-ND 4.0). https://creativecommons.org/licenses/by-nc-nd/4.0/. Accessed: 2020-02-20. |
66 | Signal and Image Processing Institute: Miscellaneous volume. http://sipi.usc.edu/database/database.php?volume=misc, Accessed: 2019-12-14. |