MACONT: Mixed Aggregation by Comprehensive Normalization Technique for Multi-Criteria Analysis
Abstract
Normalization and aggregation are two most important issues in multi-criteria analysis. Although various multi-criteria decision-making (MCDM) methods have been developed over the past several decades, few of them integrate multiple normalization techniques and mixed aggregation approaches at the same time to reduce the deviations of evaluation values and enhance the reliability of the final decision result. This study is dedicated to introducing a new MCDM method called Mixed Aggregation by COmprehensive Normalization Technique (MACONT) to tackle complicate MCDM problems. This method introduces a comprehensive normalization technique based on criterion types, and then uses two mixed aggregation operators to aggregate the distance values between each alternative and the reference alternative on different criteria from the perspectives of compensation and non-compensation. An illustrative example is given to show the applicability of the proposed method, and the advantages of the proposed method are highlighted through sensitivity analyses and comparative analyses.
1Introduction
Decision making is a frequent activity in management. It is a process of analysis and judgment in which an optimal alternative is selected from several alternatives to achieve a certain target. For a decision-making problem, alternatives and criteria used to evaluate the performance of alternatives are two essential elements. However, in many practical decision-making problems, it is difficult or unrealistic for decision-makers to establish a criterion to cover all aspects of the problem and capture the best alternative by evaluating alternatives under the criterion. It is common to portray the performance of alternatives in complex environments by multiple criteria with different dimensions and potentially conflicting to rank alternatives and then select the optimal alternative. This enables various multi-criteria decision-making (MCDM) methods being developed to solve complicated decision-making problems (Alinezhad and Khalili, 2019; Liao et al., 2020, 2018; Zavadskas et al., 2014). For example, Kou et al. (2012) employed the TOPSIS, ELECTRE, GRA, VIKOR, and PROMETHEE methods (the explanations of all abbreviations used in this paper can be found in Table A.1 in Appendix A) for classification algorithm selection; Liao et al. (2019) integrated the BWM and ARAS methods for digital supply chain finance supplier selection; Kou et al. (2020) applied the TOPSIS, VIKOR, GRA, WSM, and PROMETHEE methods to evaluate feature selection methods for text classification with small datasets.
From the perspective of obtaining the final ranking of alternatives, the existing MCDM methods can be divided into two categories: one is based on the pairwise comparisons between alternatives, such as the AHP, ANP, TODIM, PROMETHEE, EXPROM, ELECTRE, and GLDS methods (Wu and Liao, 2019); the other is based on the utility values of alternatives, such as the TOPSIS, VIKOR, ARAS, WASPAS, MULTIMOORA methods (Wu and Liao, 2019). For the latter category of MCDM methods, the following stages are included: 1) establishing a decision matrix, 2) normalizing the decision matrix, 3) aggregating the performance of alternatives under all criteria, and 4) determining the ranking of alternatives and the optimal alternative. In this sense, the main reason why different methods may produce different decision-making results lies in the differences of normalization techniques and aggregation functions used in these methods.
Generally, the performance of alternatives under different criteria are measured by different units, and all elements in a decision matrix must be dimensionless to make an effective comparison. Linear normalization, as a normalization technique widely used in MCDM methods, has three main forms, i.e. the linear sum-based normalization, linear ratio-based normalization, and linear max-min normalization (Jahan and Edwards, 2015). Each of these normalization techniques has its own emphasis: the linear sum-based normalization technique emphasizes the proportion of the performance of an alternative in the sum of the performance of all alternatives under a criterion; the linear ratio-based normalization technique emphasizes the ratio between the performance of an alternative and the best one under a criterion; the linear max-min normalization technique emphasizes the ratio of the difference between the performance of an alternative and the worst one and the difference between the best alternative and the worst alternative under a criterion. As we can see, most MCDM methods only use a single normalization technique, which easily makes faulty results because it cannot fully reflect the original information. In this regard, this study presents a comprehensive normalization technique which combines the aforementioned three normalization techniques to make the normalized data reflect the original data synthetically. It is worth noting that the hybrid/mixed normalization approaches used in many MCDM methods emphasize the single normalization technique of different types of criteria, while the comprehensive normalization technique proposed in this study emphasizes the integration of multiple normalization techniques of the same type of criteria. To some extent, the comprehensive normalization technique can reduce the error caused by single normalization technique to the collective results (it is illustrated by the example in Section 3). In addition, to fuse the normalized data derived by the three normalization techniques, we introduce two parameters to represent the weights of different normalized date according to the preferences of experts.
Almost all MCDM problems depend on the aggregation functions to aggregate the performance of alternatives under different criteria, and the selection of aggregation function may directly affect the decision-making results (Aggarwal, 2017). The arithmetic weighted aggregation operator and geometric weighted aggregation operator has been universally applied in many MCDM methods, such as the VIKOR, WASPAS, ARAS, and MULTIMOORA. The arithmetic weighted aggregation operator has also been used to aggregate the group opinions of decision-making problems (Zhang et al., 2019). However, these two aggregation operators lead to compensation effects among criteria. An alternative that performs well under few criteria with high weights and performs poorly under most criteria may be selected as the optimal alternative because of the compensation effect among these criteria, but due to the poor performance of this alternative under most criteria, it is not the optimal alternative expected. In response to this problem, this study fuses the performance of alternatives under different criteria by two mixed aggregation operators from the perspectives of compensation and non-compensation among criteria.
In addition, setting a reference alternative in the decision-making process can reduce the impact of the loss-aversion bias (Lahtinen et al., 2020). The reference alternative in many methods, such as the TOPSIS, VIKOR and ARAS, consists of the best performance of alternatives under each criterion, and the optimal alternative is determined according to the principle of the closest distance from the reference alternative (the TOPSIS method not only sets this reference alternative, but also sets the worst reference alternative which consists of the worst performance of alternatives under each criterion, and the optimal alternative is determined according to the principle of farthest distance from the reference alternative). However, there are few methods using the average performance of alternatives under each criterion as the reference alternative, which determines the optimal alternative according to the principle of the longest positive distance from the reference alternative and the shortest negative distance from the reference alternative. Inspired by this idea, before the aggregation process, we set a virtual reference alternative which consists of the average performance of alternatives under each criterion. Such a reference alternative can comprehensively consider the good performance and bad performance of an alternative compared with other alternatives.
To sum up, this study is devoted to the following innovations:
1. Present a comprehensive normalization method which combines three linear normalization techniques based on the criterion types to reduce the deviations produced in the normalization process.
2. Set a virtual reference alternative which consists of the average performance of alternatives on each criterion to simultaneously consider the good performance and bad performance of an alternative compared with other alternatives.
3. Introduce two mixed aggregation operators from the perspectives of compensation and non-compensation among criteria to aggregate the distance value between each alternative and the reference alternative under each criterion, which can obtain multi-aspect and reliable ranking results of alternatives.
4. Propose the detailed operational procedure of the MACONT method, and apply this method to solve a selection problem of sustainable third-party reverse logistics providers.
The framework of this study is divided into the following parts: Section 2 reviews the normalization techniques and aggregation functions used in various MCDM methods. Section 3 proposes the mixed aggregation by comprehensive normalization technique (MACONT) method. Section 4 gives an illustrative example to demonstrate the applicability of the proposed method. Section 5 provides some sensitivity analyses and comparative analyses to highlight the advantages of the proposed method. The conclusion is drawn in Section 6.
2Literature Review
In the section, we review the normalization techniques and aggregation approaches used in various MCDM methods.
2.1Review of Normalization Techniques
In many MCDM problems, different criteria usually differ in dimension and magnitude (Chen, 2019). To compare alternatives effectively, the original data under different evaluation criteria need to be transformed into dimensionless form by various normalization techniques (Jahan and Edwards, 2015). The vector normalization technique and linear normalization technique are two commonly used normalization techniques in many MCDM methods.
The MCDM methods using the vector normalization technique include TOPSIS (Hwang and Yoon, 1981), MOORA (Brauers and Zavadskas, 2009), MULTIMOORA (Brauers and Zavadskas, 2010) and ELECTRE (Roy, 1991; Govindan and Jepsen, 2016). Opricovic and Tzeng (2004) pointed out that the normalized data computed by the vector normalization technique relies on the evaluation unit of a criterion, and the normalized data of different evaluation units for a criterion may be different. Regarding the MCDM methods using the linear normalization technique, the COPRAS (Zolfani and Bahrami, 2014), ARAS (Zavadskas and Turskis, 2010), ANP (Jharkharia and Shankar, 2007), IDOCRIW (Zavadskas and Podvezko, 2016) and TODIM (Gomes, 2009) methods apply the linear sum-based normalization technique, the WASPAS (Zavadskas et al., 2012) and EDAS (Keshavarz Ghorabaee et al., 2015) methods exploit the linear ratio-based normalization technique, and the VIKOR (Opricovic and Tzeng, 2007), MABAC (Pamucar and Cirovic, 2015), MACBETH (Bana e Costa and Chagas, 2004), MAUT (Emovon et al., 2016), CRITIC (Diakoulaki et al., 1995), KEMIRA (Krylovas et al., 2014) and CoCoSo (Yazdani et al., 2019) methods employ the linear max-min normalization technique. However, these methods only use a single normalization technique, which easily leads to deviations between the normalized data and original data. To ameliorate this problem, Liao and Wu (2020) present the DNMA method which is an MCDM method combining the target-based vector normalization technique and target-based linear normalization technique. Nevertheless, such a double normalization technique does not normalize the original data in accordance with the different types of criteria. Hence, this study proposes a comprehensive normalization technique based on the criterion types to reduce the deviations produced in the normalization process.
2.2Review of Aggregation Functions
Table 1
The normalization technique and aggregation operator in various MCDM methods.
| MCDM method | Normalization technique | Aggregation operator | ||||||
| Vector | Linear sum-based | Linear ratio-based | Linear max-min | Arithmetic weighted | Geometric weighted | Weighted maximum | Weighted minimum | |
| TOPSIS | ✓ | ✓ | ||||||
| ARAS | ✓ | ✓ | ||||||
| COPRAS | ✓ | ✓ | ||||||
| MACBETH | ✓ | ✓ | ||||||
| MAUT | ✓ | ✓ | ||||||
| EDAS | ✓ | ✓ | ||||||
| VIKOR | ✓ | ✓ | ✓ | |||||
| MULTIMOORA | ✓ | ✓ | ✓ | ✓ | ||||
| WASPAS | ✓ | ✓ | ✓ | |||||
| CoCoSo | ✓ | ✓ | ✓ | |||||
| The proposed method | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
Aggregation operators are the basis of information fusion, which are used to combine multiple values into a collective one (Blanco-Mesa et al., 2019; Mi et al., 2020). In many MCDM methods, the arithmetic weighted aggregation operator has been frequently used. The TOPSIS method (Hwang and Yoon, 1981) uses the arithmetic weighted aggregation operator to calculate the distances of alternatives from the positive ideal solution and negative ideal solution. The ARAS method (Zavadskas and Turskis, 2010) attains the optimality function value by the arithmetic weighted aggregation operator. In the COPRAS method (Zolfani and Bahrami, 2014), the arithmetic weighted aggregation operator is used to obtain the maximizing and minimizing indexes separately according to different types of criteria. The MACBETH method (Bana e Costa and Chagas, 2004) employs the arithmetic weighted aggregation operator to calculate the overall score. The MAUT method (Emovon et al., 2016) applies the arithmetic weighted aggregation operator to compute the final utility score. The EDAS method (Keshavarz Ghorabaee et al., 2015) exploits the arithmetic weighted aggregation operator to respectively aggregate the positive distances from average and negative distances from average. The VIKOR method (Opricovic and Tzeng, 2007) fuses the arithmetic weighted aggregation operator and weighted maximum formula to derive a “group utility” value and an “individual regret” value. Based on different criterion types, the MULTIMOORA method (Brauers and Zavadskas, 2010) synthesizes the arithmetic weighted aggregation operator, weighted maximum formula and geometric weighted aggregation operator to get three subordinate utility values. The WASPAS method (Zavadskas et al., 2012) combines the arithmetic weighted aggregation operator and geometric weighted aggregation operator to deduce the joint generalized criterion value. The CoCoSo method (Yazdani et al., 2019) performs the aggregation process according to the attitudes of additive and multiplicative aggregations in the WASPAS method.
From Table 1, we can find that many of the above methods aggregate the performance values of alternatives, but few of them aggregate the distance values between each alternative and the reference alternative by multiple aggregation operators. Hence, this study introduces two mixed aggregation operators to aggregate the distance value between each alternative and the reference alternative under each criterion.
3The Mixed Aggregation by Comprehensive Normalization Technique (MACONT) Method
In this section, a new MCDM method called the Mixed Aggregation by COmprehensive Normalization Technique (MACONT) is presented. The main idea of this method is as follows: 1) normalize the performance values of alternatives over criteria by three normalization techniques; 2) synthesize the three normalized performance values; 3) set a virtual reference alternative; 4) combining the weights of criteria, use two mixed aggregation operators to integrate the distances between each alternative and the reference alternative; 5) based on integration of the subordinate comprehensive scores derived by two mixed aggregation operators, calculate the final comprehensive scores of alternatives, and then rank the alternatives according to the final comprehensive scores.
The specific implementation minds of this method in solving MCDM problems are as follows:
Firstly, for an MCDM problem, it is essential to establish a series of alternatives (
Then, normalize the decision matrix respectively by three normalization techniques. The first normalization technique is the linear sum-based normalization technique, as shown in Eq. (1), and the normalized value is represented by
(1)
(2)
(3)
After the three kinds of normalized performance values of alternatives over criteria are obtained, to make the decision-making process flexible, two balance parameters, λ and μ, are introduced to integrate these normalized performance values, and the integration equation is as follows:
(4)
To illustrate the function of the comprehensive normalization technique in reducing deviations, we give an example here.
Example 1.
Suppose that there are three alternatives (
By Eqs. (1)–(3), we can get three normalized matrices as:
If the weights of all criteria are the same, then, based on the arithmetic weighted aggregation operator, we can obtain the ranking results of the alternatives derived from the above three decision matrices as
Let
After obtaining a normalized decision matrix, we calculate the average performance values
(5)
(6)
In Eq. (5),
Afterwards, the final comprehensive score
(7)
It is noted that, for the accuracy and reliability of results, we need to use a normalization technique to ensure that the dimensions of the values of
In summary, the procedure of the proposed MACONT method can be summarized as below:
Step 1. Give the evaluation information of alternatives and the criteria weights, and form a decision matrix based on the evaluation information.
Step 2. Normalize the decision matrix by Eqs. (1)–(3), and use Eq. (4) to integrate the three normalized decision matrices.
Step 3. Set a virtual reference alternative by the average performance values of alternatives on each criterion, and calculate the subordinate comprehensive scores of alternatives by Eqs. (5) and (6).
Step 4. Obtain the final comprehensive scores of alternatives by Eq. (7), and determine the ranking of alternatives and the optimal alternative.
4An Illustration Example: Sustainable Third-Party Reverse Logistics Provider Selection
Recently, the selection problem of sustainable third-party reverse logistics provider has become a hot research topic (Govindan et al., 2018; Bai and Sarkis, 2019; Zarbakhshnia et al., 2018, 2019). Company R is a multi-national professional paint manufacturing enterprise. To reduce the cost of recycling logistics and enhance the sustainable development, company R needs to choose a suitable supplier. First of all, company R selected 8 providers
• Economic dimension, such as quality, lead time, cost, delivery and services, relationship, and innovativeness;
• Environment dimension, such as pollution controls, resource consumption, remanufacture and reuse, green technology capability, and environmental management system;
• Social dimension, such as health and safety, employment stability, customer satisfaction, reputation, respect for the policy, and contractual stakeholders influence.
The details of the evaluation criteria are shown in Table 2. The weights of these criteria are determined by the experts as (0.048, 0.067, 0.085, 0.026, 0.017, 0.034, 0.098, 0.087, 0.065, 0.113, 0.046, 0.079, 0.047, 0.025, 0.072, 0.080, 0.011).
Table 2
The evaluation criteria of sustainable third-party reverse logistics providers.
| Dimensions | Criteria | Type | References |
| Economic |
| Benefit | Govindan et al. (2018), Bai and Sarkis (2019), Zarbakhshnia et al. (2018, 2019) |
|
| Cost | Bai and Sarkis (2019); Zarbakhshnia et al. (2018, 2019) | |
|
| Cost | Govindan et al. (2018), Bai and Sarkis (2019), Zarbakhshnia et al. (2018, 2019) | |
|
| Benefit | Zarbakhshnia et al. (2018, 2019) | |
|
| Benefit | Govindan et al. (2018) | |
|
| Benefit | Bai and Sarkis (2019) | |
| Environment |
| Benefit | Bai and Sarkis (2019) |
|
| Cost | Bai and Sarkis (2019) | |
|
| Benefit | Zarbakhshnia et al. (2018, 2019) | |
|
| Benefit | Zarbakhshnia et al. (2018) | |
|
| Benefit | Govindan et al. (2018) | |
| Social |
| Benefit | Bai and Sarkis (2019), Zarbakhshnia et al. (2018, 2019) |
|
| Benefit | Zarbakhshnia et al. (2018) | |
|
| Benefit | Govindan et al. (2018), Zarbakhshnia et al. (2018, 2019) | |
|
| Benefit | Zarbakhshnia et al. (2019) | |
|
| Benefit | Zarbakhshnia et al. (2019) | |
|
| Benefit | Bai and Sarkis (2019) |
Below we use the proposed MACONT method to solve this problem.
Step 1. The experts evaluated the providers’ performance under each criterion and established a decision matrix: 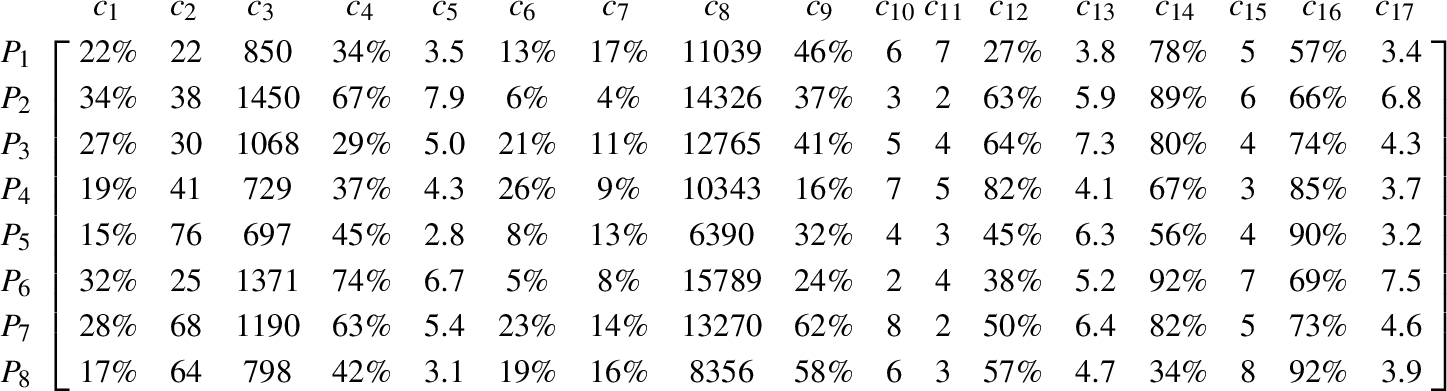
Step 2. We utilize Eqs. (1)–(3) to calculate three normalized decision matrices:
Integrate the above three normalized decision matrices by Eq. (4) to obtain a comprehensive decision matrix (here the two balance parameters are set as
Step 3. Compute the average performance values of the providers on each criterion to form a virtual reference provider
Step 4. Calculate the final comprehensive values of providers by Eq. (7), and rank the providers according to the descending order of the final comprehensive values. The ranking results of the providers are listed in Table 3. We can determine that the optimal provider is
Table 3
The ranking results of the providers derived by the proposed method.
| Providers |
|
|
|
|
| Rank |
|
| 0.0207 | 1.6741 | 0.3074 | 0.0017 | 0.2029 | 4 |
|
| −0.0729 | 0.8401 | −0.1595 | 0.0103 | −0.3740 | 8 |
|
| 0.0114 | 0.4684 | 0.1071 | 0.0011 | 0.0836 | 6 |
|
| 0.0210 | 1.7719 | 0.3222 | 0.0018 | 0.2116 | 3 |
|
| −0.0141 | 0.6037 | 0.0297 | 0.0043 | 0.1382 | 5 |
|
| −0.0711 | 0.5186 | −0.1968 | 0.0096 | −0.3708 | 7 |
|
| 0.0362 | 0.5762 | 0.2154 | 0.0082 | 0.3422 | 2 |
|
| 0.0688 | 2.3379 | 0.5797 | 0.0040 | 0.4047 | 1 |
5Sensitivity Analyses and Comparative Analyses
In this section, based on the data in Section 4, sensitivity analyses of the parameters set in the proposed method are carried out to explore the impact of the changes of parameters and criterion weights on the final ranking results of the alternatives. Moreover, other MCDM methods are applied to derive the ranking results of the alternatives, and the advantages of the proposed method are highlighted by comparing these results with that of the proposed method.
5.1Sensitivity Analyses
(1) Sensitivity analyses on the balance parameters λ and μ.
Table 4
The ranking results derived by different values of the parameters λ and μ.
| λ | μ |
| Ranks | |
| Value | 0 | 0 |
| (5, 7, 4, 3, 6, 8, 2, 1) |
| 0 | 0.5 |
| (4, 7, 6, 3, 5, 8, 2, 1) | |
| 0 | 1 |
| (3, 8, 6, 5, 4, 7, 2, 1) | |
| 0.2 | 0.2 |
| (4, 7, 6, 3, 5, 8, 2, 1) | |
| 0.2 | 0.6 |
| (5, 8, 6, 4, 3, 7, 2, 1) | |
| 0.5 | 0 |
| (4, 7, 6, 3, 5, 8, 2, 1) | |
| 0.5 | 0.5 |
| (3, 8, 6, 5, 4, 7, 2, 1) | |
| 0.6 | 0.2 |
| (4, 8, 6, 3, 5, 7, 2, 1) | |
| 1 | 0 |
| (3, 8, 6, 5, 4, 7, 2, 1) |
In the process of integrating three normalized matrices, the two balance parameters λ and μ are introduced. It can be seen from Table 4 that the rankings of providers derived by different parameter values are different, which shows that experts need to determine parameter values according to actual conditions to ensure the accuracy of the results. Moreover, in the proposed method, if only one of the three normalization techniques is used, i.e.
(2) Sensitivity analysis of the preference parameter δ.
In the first mixed aggregation operator of the proposed method (i.e. Eq. (5)), the preference parameter δ is set to reasonably aggregate the comprehensive performance and individual performance of alternatives. From Table 5, it can be found that the change of this preference parameter value has little effect on the final ranking result. With the increase of the parameter value, the rank of
(3) Sensitivity analysis of the preference parameter ϑ.
Table 5
The ranking results derived by different values of the preference parameter δ.
| δ |
| Ranks | |
| Value | 0 |
| (4, 7, 6, 3, 5, 8, 2, 1) |
| 0.1 |
| (4, 7, 6, 3, 5, 8, 2, 1) | |
| 0.2 |
| (4, 7, 6, 3, 5, 8, 2, 1) | |
| 0.3 |
| (4, 7, 6, 3, 5, 8, 2, 1) | |
| 0.4 |
| (4, 7, 6, 3, 5, 8, 2, 1) | |
| 0.5 |
| (4, 8, 6, 3, 5, 7, 2, 1) | |
| 0.6 |
| (4, 8, 6, 3, 5, 7, 2, 1) | |
| 0.7 |
| (4, 8, 6, 3, 5, 7, 2, 1) | |
| 0.8 |
| (4, 8, 6, 3, 5, 7, 2, 1) | |
| 0.9 |
| (4, 8, 6, 3, 5, 7, 2, 1) | |
| 1 |
| (4, 8, 6, 3, 5, 7, 2, 1) |
In the second mixed aggregation operator of the proposed method, the preference parameter ϑ is set to reasonably aggregate the best performance and the worst performance of alternatives. From Table 6, we can find that the change of this preference parameter value has a significant influence on the final ranking result. With the increase of the parameter value, the ranks of
Table 6
The ranking results derived by different values of the preference parameter ϑ.
| ϑ |
| Ranks | |
| Value | 0 |
| (3, 7, 5, 2, 6, 8, 4, 1) |
| 0.1 |
| (4, 7, 5, 2, 6, 8, 3, 1) | |
| 0.2 |
| (4, 7, 5, 3, 6, 8, 2, 1) | |
| 0.3 |
| (4, 7, 5, 3, 6, 8, 2, 1) | |
| 0.4 |
| (4, 7, 5, 3, 6, 8, 2, 1) | |
| 0.5 |
| (4, 8, 6, 3, 5, 7, 2, 1) | |
| 0.6 |
| (4, 8, 6, 3, 5, 7, 2, 1) | |
| 0.7 |
| (3, 8, 6, 4, 5, 7, 2, 1) | |
| 0.8 |
| (3, 8, 6, 4, 5, 7, 2, 1) | |
| 0.9 |
| (3, 8, 6, 4, 5, 7, 2, 1) | |
| 1 |
| (3, 8, 6, 4, 5, 7, 2, 1) |
5.2Comparative Analyses
In this subsection, we compare the proposed method with various MCDM methods, including the TOPSIS, VIKOR, WASPAS, ARAS, and MULTIMOORA. The reason for comparison with the TOPSIS method is that both methods use the idea of reference points. The reason for comparison with the VIKOR method is that both methods use the linear max-min normalization. The reason for comparison with the WASPAS method is that both methods use the linear ratio-based normalization technique and the combination of arithmetic weighted aggregation operator and geometric weighted aggregation operator. The reason for comparison with the ARAS method is that both methods use the sum-based normalization technique and arithmetic weighted aggregation operator. The reason for comparison with the MULTIMOORA method is that both methods take into account the compensation and non-compensation effects among criteria.
5.2.1Comparative Analysis Between the Proposed Method and the TOPSIS Method
TOPSIS method, introduced by Hwang and Yoon in 1981, deduces the optimal alternative with the shortest distance from the positive ideal solution and the farthest distance from the negative ideal solution (Opricovic and Tzeng, 2004). The procedure of the TOPSIS method is as follows. First, normalize the decision matrix by the vector normalization technique (Eq. (8)). Second, determine two ideal solutions
(8)
(9)
(10)
(11)
(12)
(13)
Table 7
The results obtained by the TOPSIS method.
| Providers |
|
|
| Ranks |
|
| 0.0439 | 0.0645 | 0.5951 | 2 |
|
| 0.0686 | 0.0374 | 0.3526 | 8 |
|
| 0.0451 | 0.0503 | 0.5274 | 5 |
|
| 0.0476 | 0.0608 | 0.5609 | 4 |
|
| 0.0574 | 0.0483 | 0.4571 | 6 |
|
| 0.0704 | 0.0388 | 0.3550 | 7 |
|
| 0.0449 | 0.0641 | 0.5877 | 3 |
|
| 0.0376 | 0.0659 | 0.6368 | 1 |
Comparing the ranking result of the proposed MACONT method and that of the TOPSIS method, except for
5.2.2Comparative Analysis Between the Proposed Method and the VIKOR Method
VIKOR method, proposed by Opricovic in 1998, aims to find a compromise solution between maximum “group utility” of the “majority” and minimum “individual regret” of the “opponent” (Opricovic and Tzeng, 2007). The VIKOR method firstly normalizes each element in the decision matrix by Eq. (14), and then computes the group utility value
(14)
(15)
(16)
(17)
Table 8
The results obtained by the VIKOR method.
| Providers |
| Rank |
| Rank |
| Ranks |
|
| 0.4754 | 5 | 0.0800 | 6 | 0.4391 | 5 |
|
| 0.6256 | 7 | 0.0980 | 7 | 0.8680 | 7 |
|
| 0.4692 | 4 | 0.0590 | 2 | 0.2551 | 3 |
|
| 0.4491 | 3 | 0.0720 | 4 | 0.3240 | 4 |
|
| 0.5178 | 6 | 0.0753 | 5 | 0.4801 | 6 |
|
| 0.6304 | 8 | 0.1130 | 8 | 1.0000 | 8 |
|
| 0.4361 | 2 | 0.0637 | 3 | 0.2316 | 2 |
|
| 0.3632 | 1 | 0.0521 | 1 | 0.0000 | 1 |
Comparing the ranking result deduced by the proposed MACONT method and that obtained by the VIKOR method, except for
5.2.3Comparative Analysis Between the Proposed Method and the WASPAS Method
WASPAS method, introduced by Zavadskas et al. (2012), firstly normalizes each element in the decision matrix by the linear ratio-based normalization technique (Eq. (2)), and then the normalized performance values of alternatives on all criteria are aggregated by the arithmetic weighted aggregation operator (Eq. (18)) and the geometric weighted aggregation operator (Eq. (19)). Afterwards, a parameter β (here
(18)
(19)
(20)
Table 9
The results obtained by the WASPAS method.
| Providers |
|
|
| Ranks |
|
| 0.7028 | 0.6715 | 0.6871 | 3 |
|
| 0.5764 | 0.5245 | 0.5504 | 8 |
|
| 0.6750 | 0.6619 | 0.6685 | 4 |
|
| 0.6844 | 0.6412 | 0.6628 | 5 |
|
| 0.6477 | 0.6021 | 0.6249 | 6 |
|
| 0.5844 | 0.5306 | 0.5575 | 7 |
|
| 0.7155 | 0.6762 | 0.6958 | 2 |
|
| 0.7437 | 0.7088 | 0.7262 | 1 |
Comparing the ranking result of the proposed MACONT method and that of the WASPAS method, the ranks of
5.2.4Comparative Analysis Between the Proposed Method and the ARAS Method
ARAS method, presented by Zavadskas and Turskis (2010), firstly sets the optimal alternative
(21)
(22)
(23)
Table 10
The results obtained by the ARAS method.
| Providers |
|
| Ranks |
|
| 0.1593 | 1.0000 | – |
|
| 0.1123 | 0.7054 | 3 |
|
| 0.0904 | 0.5678 | 8 |
|
| 0.1066 | 0.6694 | 5 |
|
| 0.1083 | 0.6798 | 4 |
|
| 0.1012 | 0.6356 | 6 |
|
| 0.0921 | 0.5781 | 7 |
|
| 0.1126 | 0.7070 | 2 |
|
| 0.1172 | 0.7358 | 1 |
Comparing the ranking result of the proposed MACONT method and that of the ARAS method, the ranks of
5.2.5Comparative Analysis Between the Proposed Method and the MULTIMOORA Method
MULTIMOORA method, proposed by Brauers and Zavadskas (2010), exploits three subordinate ranking methods to obtain three ranking lists based on the decision matrix which is normalized by the vector normalization technique (Eq. (8)). The first subordinate ranking method is the Ratio System, and the utility values of alternatives can be calculated by Eq. (24). The second subordinate ranking method is the Reference Point Approach, and the utility values of alternatives can be calculated by Eq. (25). The third subordinate ranking method is the Full Multiplicative Form, and the utility values of alternatives can be calculated by Eq. (26). Afterwards, this method aggregates the three subordinate ranking results based on the dominance theory (Brauers and Zavadskas, 2011) to determine the final ranking of alternatives. The results derived by the MULTIMOORA method based on the data in Section 4 are shown in Table 11.
(24)
(25)
(26)
Table 11
The results obtained by the MULTIMOORA method.
| Providers |
| Ranks |
| Ranks |
| Ranks | Final ranks |
|
| 0.1973 | 3 | 0.0276 | 5 | 0.5883 | 3 | 4 |
|
| 0.1309 | 7 | 0.0369 | 7 | 0.4595 | 8 | 7 |
|
| 0.1853 | 5 | 0.0219 | 1 | 0.5799 | 4 | 3 |
|
| 0.1909 | 4 | 0.0232 | 3 | 0.5617 | 5 | 5 |
|
| 0.1524 | 6 | 0.0292 | 6 | 0.5275 | 6 | 6 |
|
| 0.1303 | 8 | 0.0439 | 8 | 0.4648 | 7 | 8 |
|
| 0.1999 | 2 | 0.0251 | 4 | 0.5924 | 2 | 2 |
|
| 0.2150 | 1 | 0.0229 | 2 | 0.6210 | 1 | 1 |
Comparing the ranking result of the proposed MACONT method and that of the MULTIMOORA method, we can find that the ranks of other providers are different except for
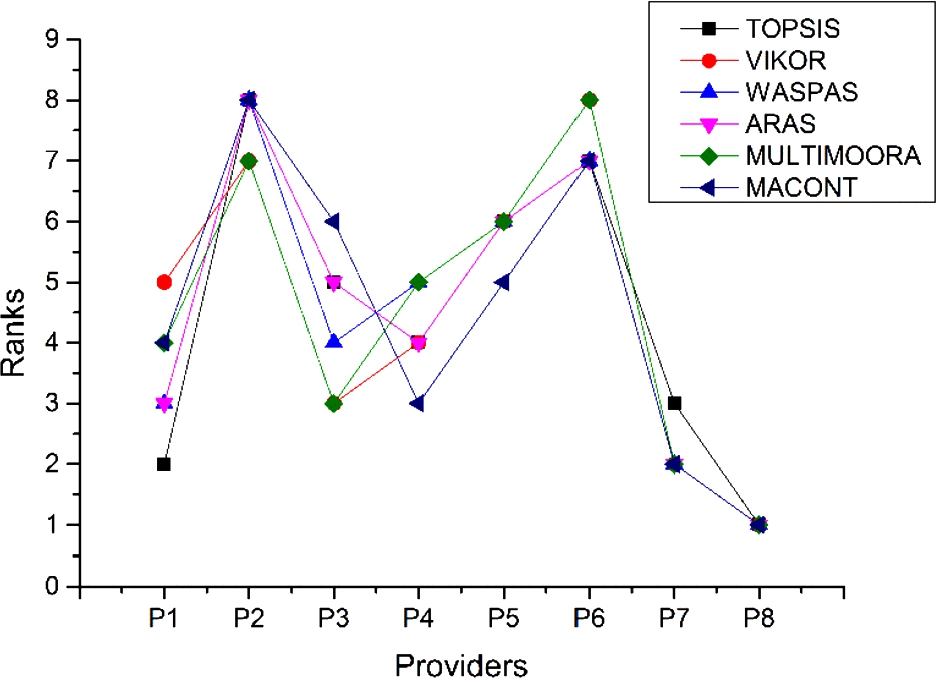
The ranks of providers obtained by the proposed MACONT method and the aforementioned methods are displayed in Fig. 1. From this figure, we can find that the ranking results derived by each MCDM method are different, and the ranks result of the providers derived by the proposed MACONT method is a comprehensive solution.
Fig. 1
Comparison of the MACONT method and the other MCDM methods.
6Conclusion
This study mainly proposed an MACONT method which involves a comprehensive normalization technique based on criterion types and two mixed aggregation operators to aggregate the distance values between each alternative and the reference alternative on different criteria from the perspectives of compensation and non-compensation. To testify the applicability of the proposed method, an illustration example regarding the selection of sustainable third-party reverse logistics providers was given. Through the sensitivity analyses and comparative analyses, we highlight that the proposed MACONT method has the following advantages:
1) It integrates three linear normalization techniques with respect to criterion types to make the normalized values reflect the original values synthetically, which is beneficial to reduce the deviations produced by single normalization techniques;
2) It measures the good performance and bad performance of one alternative compared with other alternatives by only one reference alternative. It is easy to operate and makes the results convincing;
3) It applies two mix aggregation operators to get a multi-aspect and reliable result from the perspectives of compensation and non-compensation among criteria;
4) It sets some parameters, enhances the application scope of the method, and enables experts to assign values to the parameters according to actual situations of decision-making problems, and thus the results are reasonable and reliable.
In this study, there is a deficiency that we did not analyse the impact of the change of criterion weights on the final result derived by the proposed method, because the number of criteria in the illustration example is large, and it is not easy to grasp the influence of the change of criterion weights on the ranking results. In the future, we will analyse this problem. In addition, we will consider to combine the proposed method with the fuzzy set theory, extending the proposed method to intuitionistic fuzzy environment, hesitant fuzzy linguistic environment and probabilistic linguistic environment to solve complex decision-making problems in various fields.
Appendices
A
AAppendix
Table A.1
Full names of abbreviations about MCDM methods.
| Abbreviation | Explanation |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| ELECTRE | ELimination Et Choix Traduisant la REalite, in French, ELimination and Choice Expressing the Reality |
| GRA | Grey relational analysis |
| VIKOR | VlseKriterijumska Optimizacija I Kompromisno Resenje |
| PROMETHEE | Preference Ranking Organization METHod for Enrichment of Evaluations |
| DEA | Data Envelopment Analysis |
| BWM | Best Worst Method |
| ARAS | Additive Ratio ASsessment |
| WSM | Weighted Sum Method |
| AHP | Analytical Hierarchy Process |
| ANP | Analytic Network Process |
| TODIM | an acronym in Portuguese of interactive and multicriteria decision making |
| EXPROM | EXtension of the PROMethee |
| MULTIMOORA | Multi-Objective Optimization on the basis of a Ratio Analysis plus the full MULTIplicative form |
| MOORA | Multi-Objective Optimization Ratio Analysis |
| COPRAS | COmplex PRoportional ASsessment |
| IDOCRIW | Integrated Determination of Objective CRIteria Weights |
| EDAS | Evaluation based on Distance from Average Solution |
| MABAC | Multi-Attributive Border Approximation area Comparison |
| MACBETH | Measuring Attractiveness by a Categorical Based Evaluation THchnique |
| MAUT | Multi-Attribute Utility Theory |
| CRITIC | CRiteria Importance Through Intercriteria Correlation |
| KEMIRA | KEmeny Median Indicator Ranks Accordance |
| CoCoSo | Combined Compromise Solution |
| DNMA | Double Normalization-based Multiple Aggregation |
| WASPAS | Weighted Aggregated Sum Product ASsessment |
| GLDS | Gained and Lost Dominance Score |
References
1 | Aggarwal, M. ((2017) ). Discriminative aggregation operators for multi criteria decision making. Applied Soft Computing, 52: , 1058–1069. https://doi.org/10.1016/j.asoc.2016.09.025. |
2 | Alinezhad, A., Khalili, J. ((2019) ). New Methods and Applications in Multiple Attribute Decision Making (MADM). International Series in Operations Research & Management Science, Vol. 277: . Springer, Switzerland. https://doi.org/10.1007/978-3-030-15009-9. |
3 | Bai, C., Sarkis, J. ((2019) ). Integrating and extending data and decision tools for sustainable third-party reverse logistics provider selection. Computers & Operations Research, 110: , 188–207. https://doi.org/10.1016/j.cor.2018.06.005. |
4 | Bana e Costa, C.A., Chagas, M.P. ((2004) ). A career choice problem: an example of how to use MACBETH to build a quantitative value model based on qualitative value judgments. European Journal of Operational Research, 153: (2), 323–331. https://doi.org/10.1016/s0377-2217(03)00155-3. |
5 | Blanco-Mesa, F., León-Castro, E., Merigó, J.M. ((2019) ). A bibliometric analysis of aggregation operators. Applied Soft Computing, 81: , 105488. https://doi.org/10.1016/j.asoc.2019.105488. |
6 | Brauers, W.K.M., Zavadskas, E.K. ((2009) ). Robustness of the multi-objective MOORA method with a test for the facilities sector. Technological and Economic Development of Economy, 15: (2), 352–375. https://doi.org/10.3846/1392-8619.2009.15.352-375. |
7 | Brauers, W.K.M., Zavadskas, E.K. ((2010) ). Project management by MULTIMOORA as an instrument for transition economies. Technological and Economic Development of Economy, 16: (1), 5–24. https://doi.org/10.3846/tede.2010.01. |
8 | Brauers, W.K.M., Zavadskas, E.K. ((2011) ). MULTIMOORA optimization used to decide on a bank loan to buy property. Technological and Economic Development of Economy, 17: (1), 174–188. https://doi.org/10.3846/13928619.2011.560632. |
9 | Chen, P. ((2019) ). Effects of normalization on the entropy-based TOPSIS method. Expert Systems with Applications, 136: , 33–41. https://doi.org/10.1016/j.eswa.2019.06.035. |
10 | Diakoulaki, D., Mavrotas, G., Papayannakis, L. ((1995) ). Determining objective weights in multiple criteria problems: the CRITIC method. Computers & Operations Research, 22: (7), 763–770. https://doi.org/10.1016/0305-0548(94)00059-h. |
11 | Emovon, I., Norman, R.A., Murphy, A.J. ((2016) ). Methodology of using an integrated averaging technique and MAUT method for failure mode and effects analysis. Journal of Engineering and Technology, 7: (1), 140–155. http://journal.utem.edu.my/index.php/jet/article/view/777. |
12 | Gomes, L.F.A.M. ((2009) ). An application of the TODIM method to the multicriteria rental evaluation of residential properties. European Journal of Operational Research, 193(1): , 204–211. https://doi.org/10.1016/j.ejor.2007.10.046. |
13 | Govindan, K., Jepsen, M.B. ((2016) ). ELECTRE: a comprehensive literature review on methodologies and applications. European Journal of Operational Research, 250: (1), 1–29. https://doi.org/10.1016/j.ejor.2015.07.019. |
14 | Govindan, K., Kadziński, M., Ehling, R., Miebs, G. ((2018) ). Selection of a sustainable third-party reverse logistics provider based on the robustness analysis of an outranking graph kernel conducted with ELECTRE I and SMAA. Omega, 85: , 1–15. https://doi.org/10.1016/j.omega.2018.05.007. |
15 | Hwang, C.L., Yoon, K. ((1981) ). Multiple Attribute Decision Making-Methods and Applications: A State-of-the-Art Survey. Lecture Notes in Economics and Mathematical Systems, Vol. 186: . Springer-Verlag, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-48318-9. |
16 | Jahan, A., Edwards, K.L. ((2015) ). A state-of-the-art survey on the influence of normalization techniques in ranking: improving the materials selection process in engineering design. Materials & Design, (1980–2015), 65: , 335–342. https://doi.org/10.1016/j.matdes.2014.09.022. |
17 | Jharkharia, S., Shankar, R. ((2007) ). Selection of logistics service provider: an analytic network process (ANP) approach. Omega, 35: (3), 274–289. https://doi.org/10.1016/j.omega.2005.06.005. |
18 | Keshavarz Ghorabaee, M., Zavadskas, E.K., Olfat, L., Turskis, Z. ((2015) ). Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica, 26: , 435–451. https://doi.org/10.15388/Informatica.2015.57. |
19 | Kou, G., Lu, Y., Peng, Y., Shi, Y. ((2012) ). Evaluation of classification algorithms using MCDM and rank correlation. International Journal of Information Technology & Decision Making, 11: (01), 197–225. https://doi.org/10.1142/s0219622012500095. |
20 | Kou, G., Yang, P., Peng, Y., Xiao, F., Chen, Y., Alsaadi, F.E. ((2020) ). Evaluation of feature selection methods for text classification with small datasets using multiple criteria decision-making methods. Applied Soft Computing, 86: , 105836. https://doi.org/10.1016/j.asoc.2019.105836. |
21 | Krylovas, A., Zavadskas, E.K., Kosareva, N., Dadelo, S. ((2014) ). New KEMIRA method for determining criteria priority and weights in solving MCDM problem. International Journal of Information Technology & Decision Making, 13: (06), 1119–1133. https://doi.org/10.1142/s0219622014500825. |
22 | Lahtinen, T.J., Hämäläinen, R.P., Jenytin, C. ((2020) ). On preference elicitation processes which mitigate the accumulation of biases in multi-criteria decision analysis. European Journal of Operational Research, 282: (1), 201–210. https://doi.org/10.1016/j.ejor.2019.09.004. |
23 | Liao, H.C., Wu, X.L. ((2020) ). DNMA: a double normalization-based multiple aggregation method for multi-expert multi-criteria decision making. Omega, 94: , 102058. https://doi.org/10.1016/j.omega.2019.04.001. |
24 | Liao, H.C., Xu, Z.S., Herrera-Viedma, E., Herrera, F. ((2018) ). Hesitant fuzzy linguistic term set and its application in decision making: a state-of-the art survey. International Journal of Fuzzy Systems, 20: (7), 2084–2110. https://doi.org/10.1007/s40815-017-0432-9. |
25 | Liao, H.C., Wen, Z., Liu, L.L. ((2019) ). Integrating BWM and ARAS under hesitant linguistic environment for digital supply chain finance supplier section. Technological and Economic Development of Economy, 25: (6), 1188–1212. https://doi.org/10.3846/tede.2019.10716. |
26 | Liao, H.C., Mi, X.M., Xu, Z.S. ((2020) ). A survey of decision-making methods with probabilistic linguistic information: bibliometrics, preliminaries, methodologies, applications and future directions. Fuzzy Optimization and Decision Making, 19: (1), 81–134. https://doi.org/10.1007/s10700-019-09309-5. |
27 | Mi, X.M., Liao, H.C., Wu, X.L., Xu, Z.S. ((2020) ). Probabilistic linguistic information fusion: a survey on aggregation operators in terms of principles, definitions, classifications, applications and challenges. International Journal of Intelligent Systems, 35: (3), 529–556. https://doi.org/10.1002/int.22216. |
28 | Opricovic, S., Tzeng, G.H. ((2004) ). Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. European Journal of Operational Research, 156: (2), 445–455. https://doi.org/10.1016/S0377-2217(03)00020-1. |
29 | Opricovic, S., Tzeng, G.H. ((2007) ). Extended VIKOR method in comparison with outranking methods. European Journal of Operational Research, 178: (2), 514–529. https://doi.org/10.1016/j.ejor.2006.01.020. |
30 | Pamucar, D., Cirovic, G. ((2015) ). The selection of transport and handling resources in logistics centers using multi-attributive border approximation area comparison (MABAC). Expert Systems with Applications, 42: (6), 3016–3028. https://doi.org/10.1016/j.eswa.2014.11.057. |
31 | Roy, B. ((1991) ). The outranking approach and the foundations of ELECTRE methods. Theory and Decision, 31: (1), 49–73. https://doi.org/10.1007/bf00134132. |
32 | Wu, X.L., Liao, H.C. ((2019) ). A consensus-based probabilistic linguistic gained and lost dominance score method. European Journal of Operational Research, 272: (3), 1017–1027. https://doi.org/10.1016/j.ejor.2018.07.044. |
33 | Yazdani, M., Zarate, P., Zavadskas, E.K., Turskis, Z. ((2019) ). A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Management Decision, 57: (9), 2501–2519. https://doi.org/10.1108/MD-05-2017-0458. |
34 | Zarbakhshnia, N., Soleimani, H., Ghaderi, H. ((2018) ). Sustainable third-party reverse logistics provider evaluation and selection using fuzzy SWARA and developed fuzzy COPRAS in the presence of risk criteria. Applied Soft Computing, 65: , 307–319. https://doi.org/10.1016/j.asoc.2018.01.023. |
35 | Zarbakhshnia, N., Wu, Y., Govindan, K., Soleimani, H. ((2019) ). A novel hybrid multiple attribute decision-making approach for outsourcing sustainable reverse logistics. Journal of Cleaner Production, 242: , 118461. https://doi.org/10.1016/j.jclepro.2019.118461. |
36 | Zavadskas, E.K., Turskis, Z. ((2010) ). A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technological and Economic Development of Economy, 16: , 159–172. https://doi.org/10.3846/tede.2010.10. |
37 | Zavadskas, E.K., Podvezko, V. ((2016) ). Integrated determination of objective criteria weights in MCDM. International Journal of Information Technology & Decision Making, 15: (02), 267–283. https://doi.org/10.1142/s0219622016500036. |
38 | Zavadskas, E.K., Turskis, Z., Antucheviciene, J., Zakarevicius, A. ((2012) ). Optimization of weighted aggregated sum product assessment. Elektronika ir elektrotechnika, 122: (6), 3–6. https://doi.org/10.5755/j01.eee.122.6.1810. |
39 | Zavadskas, E.K., Turskis, Z., Kildienė, S. ((2014) ). State of art surveys of overviews on MCDM/MADM methods. Technological and Economic Development of Economy, 20: (1), 165–179. https://doi.org/10.3846/20294913.2014.892037. |
40 | Zhang, H., Kou, G., Peng, Y. ((2019) ). Soft consensus cost models for group decision making and economic interpretations. European Journal of Operational Research, 277: , 964–980. https://doi.org/10.1016/j.ejor.2019.03.009. |
41 | Zolfani, S.H., Bahrami, M. ((2014) ). Investment prioritizing in high tech industries based on SWARA-COPRAS approach. Technological and Economic Development of Economy, 20: (3), 534–533. https://doi.org/10.3846/20294913.2014.881435. |




