CLAP_CDC wins Chinese dark chess tournament
The 2022 Computer Olympiad was held online during July 23–29, 2022. The computer Chinese dark chess tournament took place on July 24. Five teams from Taiwan, Japan, and China participated in the tournament, as listed in Table 1. Detailed rules of Chinese dark chess can be found in Chen et al. (2010) and Yen et al. (2015)’s articles. The rules to judge draws in Chinese dark chess tournaments are slightly different from those in the articles. In the tournaments, a game ends with a draw when both players do not capture or flip any piece within 180 plies, or when both players play the same position three times.
In the 2022 Computer Olympiad Chinese dark chess tournament, double round-robin system was applied. Namely, each program played two games against each of the other programs. Among the two games, each program alternatively played as the first player. The time constraint for each program was 15 minutes per game without any extension. A program lost immediately when it used up its time. All the games were played on a game-playing platform implemented by Jr-Chang Chen’s team (Zhong, 2020; Chen et al.). The server was convenient in that each program only needed to connect to the server at the beginning and the server did the rest. The server arranged the matches in each round, randomized unrevealed pieces, communicated between programs, served as the time keeper, judged the game results, and collected the game records.
Table 1
The participants
| Program | Abbr. | Author(s) | Operator | Country |
| Yahari | Yah | Jr-Chang Chen, You-Cheng Syu, Gang-Yu Fan, Ting-Yu Lin, Tsan-sheng Hsu, Hsuan-Yu Wang, Jun-Ping Chen | Jun-Ping Chen | Taiwan |
| Poyo | Poyo | Ping-Chun Chen, Hsuan-Yu Yaung | Ping-Chun Chen | Taiwan |
| DarkKnight | Dkn | Chu-Hsuan Hsueh, Wen-Jie Tseng, I-Chen Wu | Chu-Hsuan Hsueh | Japan & Taiwan |
| CLAP_CDC | Clap | Chu-Hsuan Hsueh, Yuan-Hao Chen, Wen-Jie Tseng, I-Chen Wu | Chu-Hsuan Hsueh | Japan & Taiwan |
| alphacat | ACat | Jin Liu | Jin Liu | China |
For each game, a program obtained 1 point for a win, 0 for a loss, and 0.5 for a draw. Table 2 lists the detailed scores and the final ranks. CLAP_CDC obtained 6 points with 5 wins, 2 draws, and 1 loss, winning the gold medal. alphacat obtained 5 points with 5 wins and 3 losses, winning the silver medal. Poyo obtained 3.5 points with 3 wins, 1 draw, and 4 losses, winning the bronze medal.
CLAP_CDC was based on the CLAP framework (Chen, 2020), an AlphaZero framework developed by I-Chen Wu’s team (Wu). alphacat was based on the alpha-beta algorithm with incorporating neural networks in the evaluation function. DarkKnight was based on Monte-Carlo tree search with incorporating techniques of early playout terminations, implicit minimax backups, and progressive bias (Hsueh et al., 2016; Hsueh, 2019). Yahari was based on the alpha-beta algorithm with a heuristic evaluation function (Chang et al., 2019).
Table 2
The detailed scores and the final ranks
| ID | Yah | Poyo | Dkn | Clap | ACat | Total Score | Rank |
| Yah | – | 0.5 | 0.5 | 0.5 | 1 | 2.5 | 5 |
| Poyo | 1.5 | – | 2 | 0 | 0 | 3.5 | 3 |
| Dkn | 1.5 | 0 | – | 0.5 | 1 | 3 | 4 |
| Clap | 1.5 | 2 | 1.5 | – | 1 | 6 | 1 |
| ACat | 1 | 2 | 1 | 1 | – | 5 | 2 |
1.Selected games
This report comments on two games, one between CLAP_CDC (the gold) and alphacat (the silver), and the other between CLAP_CDC and DarkKnight (the fourth). In game records, P(T) denotes an action of flipping a piece with type T at position P, and S-D denotes an action of moving a piece from position S to D. The pieces are denoted as follows: uppercase and lowercase letters represent red and black pieces, respectively, and the pieces king, guard, minister, rook, knight, cannon, and pawn are abbreviated as K/k, G/g, M/m, R/r, N/n, C/c, and P/p, respectively.
Game 1: CLAP_CDC (Black) vs. alphacat (Red) 1-0
1. d1(g) d3(k) 2. c1(P) b3(g) 3. b4(P) d5(G) 4. d4(M) d6(r) 5. d3-d4 d5-d6 6. d4-d5 c4(C) 7. b3-b4 c4-d4 8. d5-d4 d7(M) 9. d4-d5 c7(p) 10. d5-d6 d7-c7 11. b4-c4 c8(P) 12. d1-c1 a1(p) 13. b5(c) a5(n) 14. d6-d5 b6(P) 15. d5-d4 a8(n) 16. d2(N) c7-d7 17. b8(m) a6(G) 18. b8-c8 a6-a5 19. c4-b4 c6(N) 20. b2(p) c5(C) 21. d4-d5 c5-c8 22. a8-b8 c6-c5 23. b8-c8 c5-b5 24. d5-c5 d8(c) 25. d8-d2 d7-c7 26. d2-d1 a4(p) 27. c8-b8 c3(R) 28. c5-c4 c3-d3 29. a3(P) d3-d2 30. a4-a3 a2(m) 31. c4-c5 d2-d1 32. c1-d1 b1(R) 33. b2-b3 b6-c6 34. c5-b5 a5-a4 35. b4-a4 c6-c5 36. b5-b6 c5-c6 37. b6-b5 c6-c5 38. b5-a5 c5-b5 39. a5-a6 b5-b6 40. a6-a5 b6-b5 41. a5-a6 b5-b6 42. d1-c1 b6-a6 43. c1-b1 b7(K) 44. a4-a5 a6-b6 45. a7(r) b7-a7 46. a5-b5 a7-b7 47. a3-a4 c7-c8 48. a4-a5 b6-c6 49. a5-a6 c8-b8 50. b3-b4 c6-d6 51. b1-b2 b7-c7 52. a6-b6 b8-b7 53. b6-a6 c7-c8 54. b5-b6 b7-a7 55. a6-a5 c8-c7 56. b6-a6 a7-b7 57. b2-b3 d6-d5 58. b3-c3 c2(p) 59. c2-d2 d5-d6 60. d2-d3 b7-b8 61. b4-b5 c7-b7 62. b5-b6 b7-a7 63. c3-c4 b8-b7 64. b6-b5 a7-a8 65. a6-b6 b7-a7 66. c4-c5 d6-d7 67. b6-b7 a7-a6 68. b7-b6 a6-a5 69. b6-a6 a5-b5 70. c5-b5 a8-b8 71. b5-c5 b8-b7 72. c5-c4 b7-b6 73. d3-d4 d7-d6 74. a6-a5 b6-b7 75. a5-b5 d6-d7 76. b5-c5 d7-d6 77. c5-d5 d6-c6 78. d5-d6 c6-b6 79. d6-c6 b6-a6 80. c4-b4 b7-c7 81. c6-b6 a6-a7 82. b6-a6 a7-b7 83. a6-a7 b7-b6 84. d4-d5 b6-c6 85. b4-c4 c7-b7 86. a7-a6 b7-a7 87. a6-b6 c6-c7 88. b6-c6 c7-c8 89. c6-c7 c8-b8 90. d5-d6 a7-b7 91. d6-c6 b8-a8 92. c7-d7 a8-a7 93. c6-c7 b7-b6 94. d7-d8 b6-b5 95. c7-c6 b5-b4 96. c6-c5 a7-a6 97. c4-d4 a6-b6 98. a1-b1 b4-b3 99. b1-b2 b3-a3 100. a2-a1 a3-a4 101. b2-b3 a4-a5 102. d8-d7 a5-a6 103. d4-d5 a6-a7 104. d5-d6 a7-b7 105. d6-c6 b6-a6 106. c5-b5 a6-a7 107. b5-b6 b7-c7 108. c6-c5 a7-a8 109. b6-b7 c7-c6 110. c5-c4 c6-c5 111. b3-b4 c5-d5 112. d7-c7 d5-d6 113. c7-c8 d6-d5 114. c8-b8 a8-a7 115. b7-a7 d5-d4 116. c4-c5 d4-d5 117. b4-c4 d5-d6 118. a7-b7 d6-d5 119. c5-b5 d5-d6 120. c4-c5 d6-d7 121. b7-c7 d7-d6 122. c5-d5 d6-c6 123. c7-c6
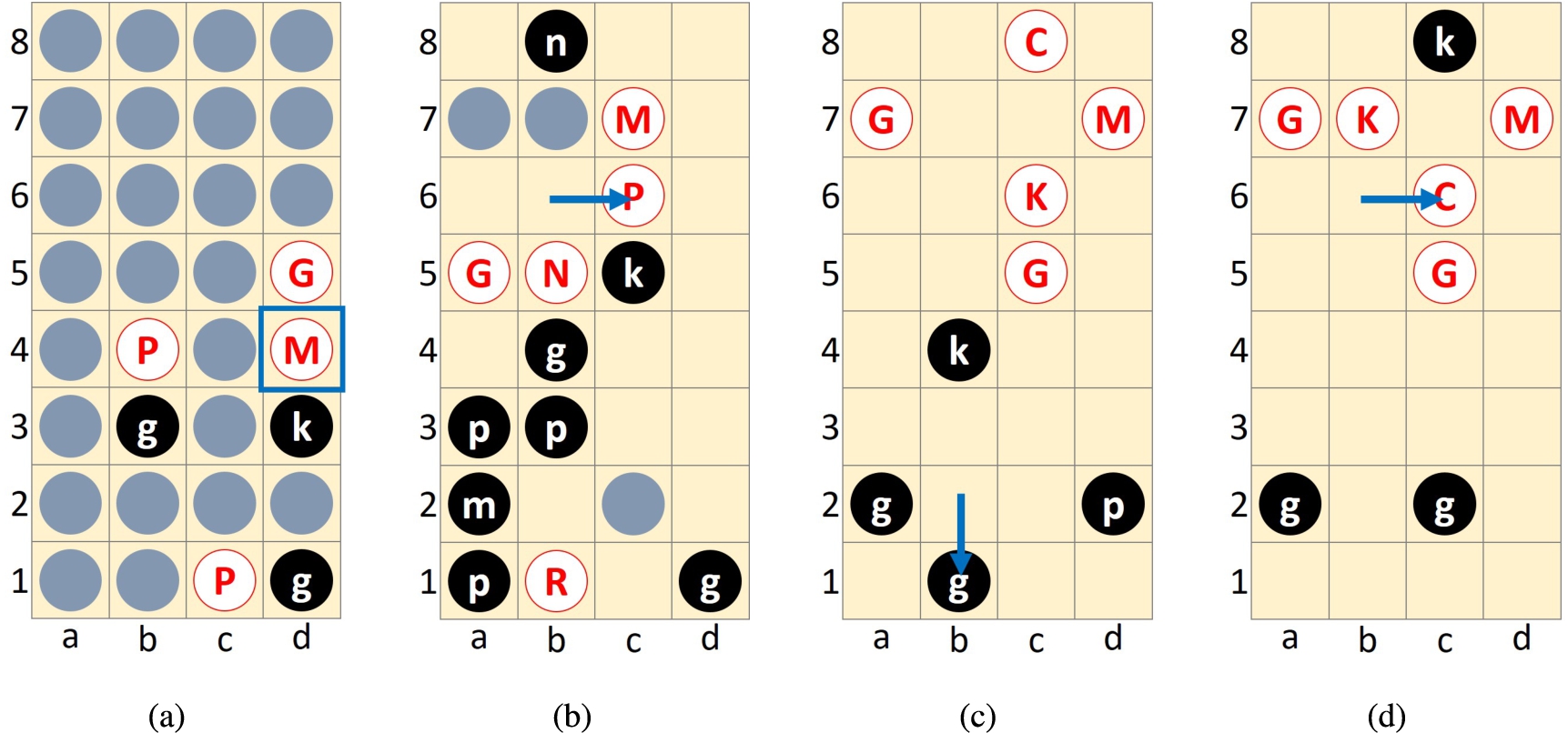
Both CLAP_CDC and alphacat had good senses in the opening. Figure 1(a) shows the 7th ply, where CLAP_CDC flipped d4. This action may look risky at the first glance because the k will be captured if the piece is K or P (a probability of 4/26). CLAP_CDC’s policy network also preferred d1-c1 (0.24) or b3-b4 (0.20) rather than d4(?) (0.02). However, considering the expected values, it was indeed worth giving a try to flip d4 because CLAP_CDC will be in a big advantage if the piece is G, M, R, N, or C (a probability of 9/26). The piece turned out to be M, making CLAP_CDC advantageous.
As the game proceeded, neither did CLAP_CDC make fatal mistakes nor did the flipping outcomes make CLAP_CDC extremely disadvantageous; thus, CLAP_CDC kept leading in the game. At the 65th ply, CLAP_CDC estimated its win rate to be 92%. Figure 1(b) (the unrevealed pieces were K, r, and p) shows the 66th ply, where alphacat moved the P at b6 to c6. CLAP_CDC then used the k at c5 to capture the N at b5, of course. At the 68th ply, alphacat moved the G at a5 to a4, which were captured by the g at b4 immediately. For this action (the 69th ply), CLAP_CDC estimated its win rate to be 97%. Although alphacat had almost no chances to win from the 66th ply, the 66th ply (b6-c6) and the 68th ply (a5-a4) were considered as bad actions since they made alphacat lose more quickly.
Fig. 1.
Game 1 (a) 7th ply d4(M) and (b) 66th ply b6-c6 and Game 2 (c) 281st ply b2-b1 and (d) 380th ply b6-c6.
Game 2: DarkKnight (Black) vs. CLAP_CDC (Red) 0.5-0.5
1. b2(m) a4(n) 2. a5(R) c1(p) 3. a7(P) a5-a4 4. a2(k) b4(c) 5. b3(c) a4-b4 6. b1(P) b1-c1 7. b2-b1 b4-b3 8. a2-b2 b3-b4 9. b1-c1 b5(p) 10. b5-a5 b4-a4 11. a5-b5 a4-a5 12. b5-b4 b6(p) 13. b7(P) b7-b6 14. b4-b3 a5-a4 15. b2-b1 a4-b4 16. b3-b2 b4-b3 17. b2-a2 b3-b2 18. b1-b2 b6-b5 19. b2-b1 c6(N) 20. c2(p) a6(m) 21. c2-b2 b5-b4 22. a6-a7 c5(N) 23. c1-c2 c4(C) 24. b1-c1 c7(G) 25. d4(n) c4-c2 26. c1-c2 d6(K) 27. a7-a6 c6-b6 28. a6-b6 d6-c6 29. b6-b5 b4-a4 30. b5-a5 a4-b4 31. a5-b5 b4-a4 32. b5-a5 c7-b7 33. a5-a4 b7-b6 34. b2-b1 b6-b5 35. c2-b2 b5-b4 36. a4-a5 c6-b6 37. d3(R) b4-a4 38. a5-a6 a4-a5 39. d2(g) d3-d4 40. d1(P) a5-a6 41. d2-d1 b8(r) 42. d1-d2 d4-c4 43. b2-b3 a1(M) 44. b3-b4 a1-b1 45. b4-c4 b1-b2 46. d2-c2 b2-a2 47. c4-c5 a3(g) 48. d8(M) a2-a1 49. a3-b3 d7(C) 50. b8-b7 c8(P) 51. b7-c7 c8-b8 52. b3-b2 d7-d6 53. c7-c6 d6-d7 54. c6-c7 d7-d6 55. c7-c6 d8-d7 56. b2-a2 b8-b7 57. a2-a1 b7-c7 58. c6-c7 d7-c7 59. d5(r) d6-d7 60. c5-c4 d7-d8 61. c4-b4 d8-c8 62. a8(G) a8-a7 63. b4-a4 c7-d7 64. c2-b2 d7-d6 65. d5-c5 a7-b7 66. a4-b4 b7-c7 67. b2-c2 c8-b8 68. b4-c4 b8-c8 69. c4-b4 c7-c6 70. c5-b5 d6-d7 71. c2-d2 c6-c5 72. d2-d1 c5-b5 73. b4-c4 d7-c7 74. c4-b4 c7-d7 75. b4-a4 b5-c5 76. a4-b4 c5-c6 77. a1-a2 c8-b8 78. b4-c4 b8-c8 79. c4-b4 c3(p) 80. a2-a1 c8-b8 81. b4-c4 b8-c8 82. c4-b4 a6-a7 83. c3-b3 c8-b8 84. b4-c4 b8-c8 85. c4-b4 d7-d8 86. a1-a2 c8-b8 87. b4-c4 a7-a6 88. b3-c3 b8-c8 89. c4-b4 c8-b8 90. b4-c4 b8-c8 91. c4-b4 a6-a5 92. a2-a1 c8-b8 93. b4-c4 b8-c8 94. c4-b4 c8-b8 95. b4-c4 d8-d7 96. c4-d4 b6-b7 97. d4-d5 c6-b6 98. d5-c5 a5-a4 99. a1-a2 b7-c7 100. c5-c4 b6-b7 101. c3-d3 d7-d6 102. d1-c1 c7-c6 103. c1-c2 a4-a5 104. d3-c3 b8-c8 105. c4-b4 c8-b8 106. b4-c4 a5-a4 107. c3-d3 b8-c8 108. c4-b4 a4-a5 109. c2-b2 c8-b8 110. b4-c4 b7-b6 111. d3-c3 a5-a6 112. a2-a1 b8-c8 113. c4-b4 c8-b8 114. b4-c4 a6-a5 115. a1-a2 a5-a4 116. c3-d3 a4-b4 117. d3-c3 b4-a4 118. c3-d3 d6-d7 119. b2-b3 b6-b7 120. d3-c3 d7-d6 121. b3-b2 b8-c8 122. c4-b4 a4-a5 123. c3-d3 c8-b8 124. b4-c4 a5-a6 125. d3-d2 b7-b6 126. d2-d1 d6-d7 127. c4-c3 b8-c8 128. c3-b3 c8-b8 129. b3-c3 b8-c8 130. c3-b3 d7-d6 131. b3-a3 c8-b8 132. d1-d2 b8-a8 133. a3-b3 a8-b8 134. b3-a3 a6-a7 135. d2-c2 b8-a8 136. a3-b3 a8-b8 137. b3-a3 b8-c8 138. c2-d2 d6-d7 139. a3-a4 b6-b5 140. a4-b4 b5-c5 141. b2-b1 c5-c4 142. b1-c1 c4-c3 143. c1-d1 c3-c2 144. b4-b5 c2-d2 145. d1-c1 d2-d3 146. b5-b4 c8-b8 147. b4-c4 b8-c8 148. c4-b4 c8-b8 149. b4-c4 d3-d2 150. c4-c3 b8-c8 151. c3-b3 a7-b7 152. b3-a3 c8-b8 153. a3-a4 d7-d6 154. a2-a1 d2-d3 155. a4-a3 d3-d2 156. a3-a4 d2-d3 157. a4-a3 b7-a7 158. a3-b3 b8-c8 159. c1-d1 d3-d4 160. a1-a2 c8-b8 161. b3-c3 b8-c8 162. c3-b3 d4-d3 163. a2-a1 c6-c7 164. b3-b4 d6-d7 165. a1-b1 a7-b7 166. b1-a1 c8-b8 167. b4-c4 b8-c8 168. c4-b4 c8-b8 169. b4-c4 b7-a7 170. c4-c5 b8-c8 171. c5-b5 c8-b8 172. b5-c5 b8-c8 173. c5-b5 d3-d4 174. b5-b6 c8-b8 175. d1-d2 a7-b7 176. b6-a6 c7-c6 177. a6-a7 c6-b6 178. a7-a8 b8-c8 179. a8-b8 c8-c7 180. d2-d1 c7-c6 181. d1-c1 b7-a7 182. b8-c8 b6-b7 183. c1-c2 d4-c4 184. c2-b2 c4-c5 185. a1-a2 c6-b6 186. b2-c2 b6-c6 187. c2-b2 c6-b6 188. b2-c2 b6-c6 189. c2-b2 c6-b6 190. b2-c2 b6-c6 191. c2-b2
Until the endgame (say the time point that all the pieces were revealed), there was no clear and continuous advantage between DarkKnight and CLAP_CDC. Interestingly, both programs made mistakes in the endgame phase. For DarkKnight, the mistake happened at the 281st ply, as shown in Fig. 1(c). DarkKnight moved the g at b2 to b1, while moving the k at b4 to c4 seemed better. After then, CLAP_CDC cleverly utilized the C at c8 so that it could move the G at c5 toward the p at d2. CLAP_CDC captured the p at the 288th ply, removing a big threat of K. DarkKnight’s mistake made it almost lose the game.
CLAP_CDC’s mistake happened at the 380th ply, as shown in Fig. 1(d). CLAP_CDC moved the C at b6 to c6 to chase the g at c2. The two pieces have been chasing/escaping since the 371st ply. At the 381st ply, DarkKnight moved the g at c2 to b2 to draw the game. CLAP_CDC’s mistake made it lose the chance to win.
References
1 | Chang, H.-J., Chen, J.-C., Fan, G.-Y., Hsueh, C.-W. & Hsu, T. ((2019) ). Using Chinese dark chess endgame databases to validate and fine-tune game evaluation functions. ICGA Journal, 40: (2), 45–60. doi:10.3233/icg-180048. |
2 | Chen, B.-N., Shen, B.-J. & Hsu, T. ((2010) ). Chinese dark chess. ICGA Journal, 33: (2), 93–106. doi:10.3233/ICG-2010-33204. |
3 | Chen, J.-C., et al. GamePlatform. http://120.126.195.84/index.php. Last accessed: Jul. 28, 2022. |
4 | Chen, Y.-H. (2020). A high-performance, distributed AlphaZero framework. Master’s thesis, National Chiao Tung University, Hsinchu, Taiwan. https://hdl.handle.net/11296/64c8e8. |
5 | Hsueh, C.-H. (2019). On strength analyses of computer programs for stochastic games with perfect information. PhD thesis, National Chiao Tung University, Hsinchu, Taiwan. https://hdl.handle.net/11296/ku48z7. |
6 | Hsueh, C.-H., Wu, I., Tseng, W.-J., Yen, S.-J. & Chen, J.-C. ((2016) ). An analysis for strength improvement of an MCTS-based program playing Chinese dark chess. Theoretical Computer Science, 644: , 63–75. doi:10.1016/j.tcs.2016.06.025. |
7 | Wu, I. I-Chen Wu, Ph.D. https://cgilab.nctu.edu.tw/~icwu/. Last accessed: Jul. 28, 2022. |
8 | Yen, S.-J., Chou, C.-W., Chen, J.-C., Wu, I. & Kao, K.-Y. ((2015) ). Design and implementation of Chinese dark chess programs. IEEE Transactions on Computational Intelligence and AI in Games, 7: (1), 66–74. doi:10.1109/TCIAIG.2014.2329034. |
9 | Zhong, Y.-X. (2020). Design of a web-based client for Chinese dark chess. Master’s thesis, National Taipei University. https://hdl.handle.net/11296/j69k4q. |



