You are viewing a javascript disabled version of the site. Please enable Javascript for this site to function properly.
Go to headerGo to navigationGo to searchGo to contentsGo to footer
In content section. Select this link to jump to navigation

Monte_Alpha Wins the EinStein Würfelt Nicht Tournament

Article type: Other

Authors: Chen, Chih-Hunga; * | Chiu, Sin-Yia; * | Lin, Shun-Shiia; *; ** | Chen, Jr-Changb; ***

Affiliations: [a] National Taiwan Normal University, Taiwan, R.O.C. | [b] National Taipei University, Taiwan, R.O.C.

Correspondence: [**] Corresponding author. E-mail: [email protected].

Note: [*] Department of Computer Science and Information Engineering, National Taiwan Normal University, Taipei, Taiwan, R.O.C.

Note: [***] Department of Computer Science and Information Engineering, National Taipei University, New Taipei, Taiwan, R.O.C.

DOI: 10.3233/ICG-230219

Journal: ICGA Journal, vol. 44, no. 3, pp. 111-113, 2022

Published: 3 February 2023
Get PDF

The 25th Computer Olympiad, an event of ICGA 2022, was held online from July 23rd (Saturday) to July 29th (Friday). In recent years, the EinStein Würfelt Nicht (Althöfer, 2011; Althöfer and Voigt, 2014) tournament is part of the Computer Olympiad. This year, three programs participated the EinStein Würfelt Nicht tournament. Their descriptions are introduced as follows.

  • Reinstein (Hsu, 2022), written in C/C++, is created by Tzu-Yang Hsu from National Taipei University. This program is based on Monte-Carlo Tree Search (MCTS) (Browne et al., 2012; Oster, 2015) and uses the bitboard data structure (Browne, 2014) to improve its overall efficiency. Moreover, it uses 9-tuple and 6-tuple networks (Chu et al., 2017) to extract the features for training in Red and Blue players separately. Finally, the pre-trained networks are used in MCTS to improve the accuracy of tree search.

  • Monte_Alpha, written in C++, is created by Sin-Yi Chiu and Shun-Shii Lin from National Taiwan Normal University. This program is based on Upper Confidence bounds applied to Trees (UCT) (Bradberry, 2015) and uses a one-dimensional array with 256 elements (Gambiter, 2008-2022) to maintain the whole game state. Although this array wastes more memory space and performs worse than bitboard, it is easy to understand and debug. In addition, Monte_Alpha builds a table in advance to store the dice roll probabilities of each situation that greatly improves the performance of tree search.

  • YJ_EinStein, written in Python, is created by Yun-Jie Ho and Shun-Shii Lin from National Taiwan Normal University. This program is based on alpha-beta search (Hsu et al., 2017) and uses the bitboard data structure to improve the performance.

The EinStein Würfelt Nicht tournament was conducted on a double round-robin tournament. Each pair of programs played 12 games, i.e. each program played against every other program in 6 games as the first player, and vice versa. Programs got 1 point for a win and 0 for a loss. The time limit was 30 seconds for each move. If it took more than 30 seconds, the player lost the game. All games were played through the ECUI platform (Hsieh and Lin, 2016a,b), in which the AI programs can be executed automatically. Among these three participants this year, YJ_EinStein and Monte_Alpha can be mounted on ECUI, but Reinstein cannot. So, the operator of Reinstein played all matches manually. The competition rules (ICGA, 2022) and the platform (Hsieh and Lin, 2016b) can be found on the ICGA website.

The first round matchup started in the afternoon on July 23rd. Monte_Alpha and YJ_EinStein faced off in this match, and Monte_Alpha has been leading the way in this series. Finally, this match was 9-3 to Monte_Alpha.

It then went on to the second round, which was Monte_Alpha versus Reinstein. Reinstein got off to a hot start to lead the series 3-0, but Monte_Alpha soon caught up to make it 3-all. Afterward, Reinstein scored two goals successively, but Monte_Alpha caught up to tie again. After that, Reinstein was leading Monte_Alpha 6-5, and Reinstein’s piece number 2 (the Red player in Fig. 1) was just one step away from the goal. At this moment, Monte_Alpha rolled number 3 continuously and won this game. They finally drew 6-all. This matchup turned out to be the most exciting series of the tournament so far.

The matchup between Reinstein and YJ_EinStein was the last round in the regular contests. The status of this matchup was similar to the first round, Reinstein always kept one jump ahead of YJ_EinStein. Finally, Reinstein led by 6 points.

At the end of the regular contests, Monte_Alpha and Reinstein both scored 15 points. Both teams were equally good, and therefore Monte_Alpha and Reinstein went into a playoff. They played 6 extra games for determining the winner of the tournament. In this playoff, the lead seesawed back and forth between Monte_Alpha and Reinstein. After the tense playoff, the matchup also ended in a draw. So, Monte_Alpha and Reinstein went into another playoff. This time Monte_Alpha had taken the lead in the matchup and won by 5-1 finally. After the playoff games, Monte_Alpha led by 4 points. It was a tremendous matchup, and the winner of the EinStein Würfelt Nicht tournament was Monte_Alpha. The final results of the tournament are shown in Table 1.

Fig. 1.

Number 2 of the Red player (Reinstein) was just one step away from the goal.

Number 2 of the Red player (Reinstein) was just one step away from the goal.
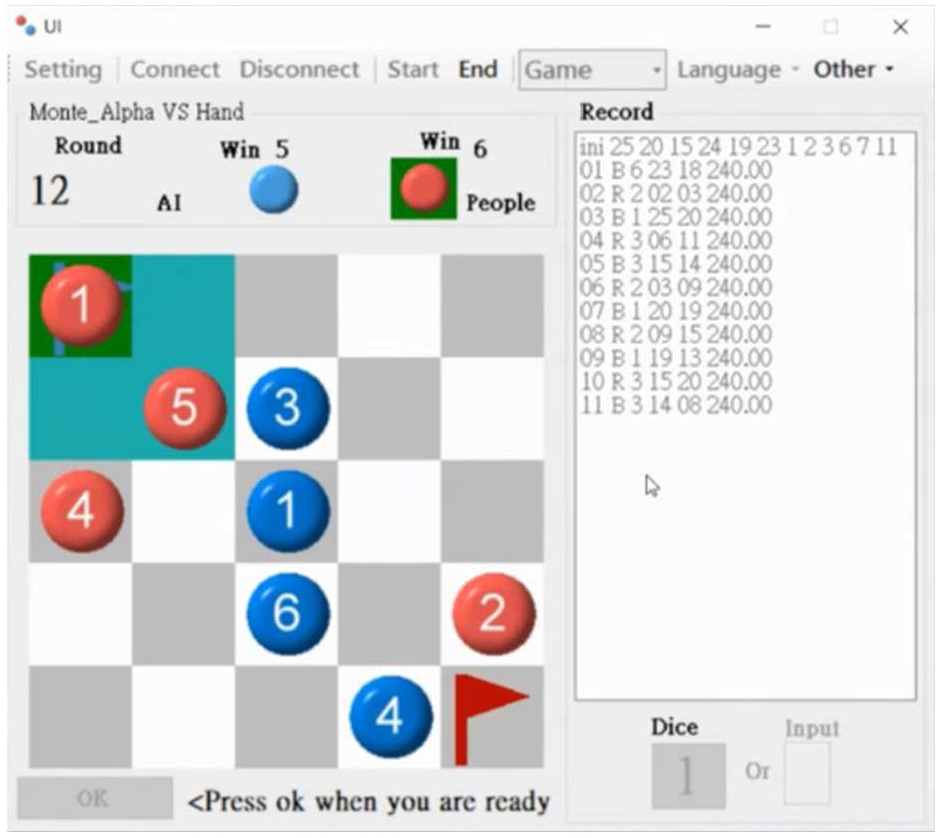
Table 1

The results of the EinStein Würfelt Nicht tournament

ProgramMonte_AlphaReinsteinYJ_EinSteinTotalPlayoff IPlayoff IIFinalRank
Monte_AlphaX69153581
Reinstein6X9153142
YJ_EinStein33X63

References

1 

Althöfer, I. ((2011) ). On the Origins of “EinStein würfelt nicht!”. Available at: https://althofer.de/origins-of-ewn.html.

2 

Althöfer, I. & Voigt, R. ((2014) ). EinStein würfelt nicht. In: Spiele, Rätsel, Zahlen. Springer. (In German). doi:10.1007/978-3-642-55301-1_4.

3 

Bradberry, J. ((2015) ). Introduction to Monte Carlo Tree Search. Available at: http://jeffbradberry.com/posts/2015/09/intro-to-monte-carlo-tree-search/.

4 

Browne, C.B. ((2014) ). Bitboard Methods for Games. ICGA Journal, 37: (2), 67–84. doi:10.3233/ICG-2014-37202.

5 

Browne, C.B., Powley, E., Whitehouse, D., Lucas, S.M., Cowling, P.I., Rohlfshagen, P., Tavener, S., Perez, D., Samothrakis, S. & Colton, S. ((2012) ). A survey of Monte Carlo tree search methods. IEEE Transactions on Computational Intelligence and AI in Games, 4: (1), 1–43. doi:10.1109/TCIAIG.2012.2186810.

6 

Chu, Y.-J., Chen, Y.-H., Hsueh, C.-H. & Wu, I-C. ((2017) , Dec. 1-3). An Agent for EinStein Würfelt Nicht! Using N-Tuple Networks. 2017 Conference on Technologies and Applications of Artificial Intelligence, Taipei, Taiwan (pp. 184–189). doi:10.1109/TAAI.2017.32.

7 

Gambiter (2008–2022). Board representation in chess. Available at: https://gambiter.com/chess/computer/Board_representation_chess.html.

8 

Hsieh, C.-L. & Lin, S.-S. (2016a, Jun. 4-5). The Design and Implementation of the EinStein Würfelt Nicht Gaming Platform. 2016 TCGA Computer Game Workshop, Taichung, Taiwan. (In Chinese).

9 

Hsieh, C.-L. & Lin, S.-S. (2016b). ECUI Platform. Available at https://tcga.tw/icga-computer-olympiad-2022/attachment/rules/EinStein_Wurfelt_Nicht/EinStein_w%C3%BCrfelt_nicht_platform.rar.

10 

Hsu, T.-s., Hsu, S.-C., Chen, J.-C., Chiang, Y.-T., Chen, B.-N., Liu, Y.-C., Chang, H.-J., Tsai, S.-C., Lin, T.-Y. & Fan, G.-Y. ((2017) , Jun.). Computers and Classical Board Games: An Introduction. National Taiwan University Press. (In Chinese).

11 

Hsu, T.-Y. (2022, Jul.). Applying Bitboard and N-Tuple Networks to EinStein Würfelt Nicht! [Master thesis]. National Taipei University, New Taipei City, Taiwan. (In Chinese).

12 

ICGA (2022). Competition Rules of EinStein würfelt nicht!. Available at: https://tcga.tw/icga-computer-olympiad-2022/attachment/rules/EinStein_Wurfelt_Nicht/Rules%20of%20EinStein%20w%C3%BCrfelt%20nicht%21.pdf.

13 

Oster, E. ((2015) , Jul.). An MCTS Agent for EinStein Würfelt Nicht! [Master Thesis]. Maastricht University, Maastricht, The Netherlands.

Show more