FinalGen revisited: new discoveries

1.Key concepts and notation

Notation is needed to refer to various position depth metrics, expressible in moves or plies. Strategies for choosing moves should defend the theoretical value of the position and this is assumed. Here it should be noted that FinalGen’s ‘win or draw’ verdict introduces a notional value of ¾ points! In a decisive position, and sometimes in a drawn position, move-optimality may further be determined by a strategy successively minimising (or maximising) depth using a set of depth metrics. Moves may be the only legal move or the only value-preserving move. In the context of a defined strategy, moves may be uniquely optimal, equi-optimal or sub-optimal. The amount by which a move is optimal (sub-optimal) indicates the positional-strength preserved (lost). It should be noted that depth-optimisation is not the only fruit. In chess studies and in games, the defender should be making the move that makes it hardest for the attacker to find the winning move. This is not necessarily the depth-maximising move which, in any case, can vary with metric and sometimes makes no chessic sense at all. Further, a winning strategy will be easier to understand if it does not take advantage of every helpful fortuity.

Depth metric notation:

 DTF: ‘Depth according to FinalGen’, usually to a conversion before a clear win,

 DTM, DTC: ‘Depth to Mate’, ‘Depth to Conversion’ (i.e., to capture, conversion and/or mate),

 DTZ: ‘Depth to Zeroing (of the ply count)’, i.e., to pawn-push, capture and/or mate,

 DTZ₅₀′: ‘Depth to Zeroing of ply count in the context of the FIDE 50-move draw-claim rule,

 dtc/f/m/z/z₅₀′ 9p(m): an actual position DTC/F/M/Z/Z₅₀′-depth of 9 plies (moves).

Strategies for choosing optimal moves:

 S(FMZ)−≡SF−M−Z−: a strategy preserving value11 and minimising dtf, dtm and dtz in that order,

 S(F&M)+≡S(F+&M+): a strategy preserving value and maximising both dtf and dtm,

 Sω/Sβ: defined strategies Sω for White and Sβ for Black,

 S(FMZ)∓≡S(FMZ)−/S(FMZ)+, and similarly, S(FMZ)±≡S(FMZ)+/S(FMZ)−.

Move optimality, sub-optimality and evaluation:

 ′≡ a value-preserving, equi-optimal move (not noted in our pgn files),

 ″≡ a value-preserving, uniquely-optimal move (‘!’ in our pgn files),

 ″″≡ a uniquely value-preserving move (‘!!’ in our pgn files),

 [±4pF]≡ move conceding 4 ply in terms of the DTF metric, ‘+(-)’ for attacker (defender),

 ∘≡ the only legal move,

 ?≡ a move ‘dropping ¼ point’, e.g., FinalGen finesses ‘win’ ↔ ‘win or draw’,

 ??≡ a move dropping ½ point, i.e., ‘win’ ↔ ‘draw’ or ‘draw’ ↔ ‘loss’, and

 Eds+0.97 ≡ an engine (here, Fritz14) evaluation of +0.97 at nominal search-depth of s plies.

Further, it is worth noting that our use of ‘!’ and ‘!!’ in the pgn files is unusual, and in particular, that these symbols are not emoticons marking notably perceptive and/or surprising moves as is the custom. Indeed, many of the moves denoted in this way are entirely obvious.

2.Positions 01-10b: Romero’s original FinalGen demonstrations

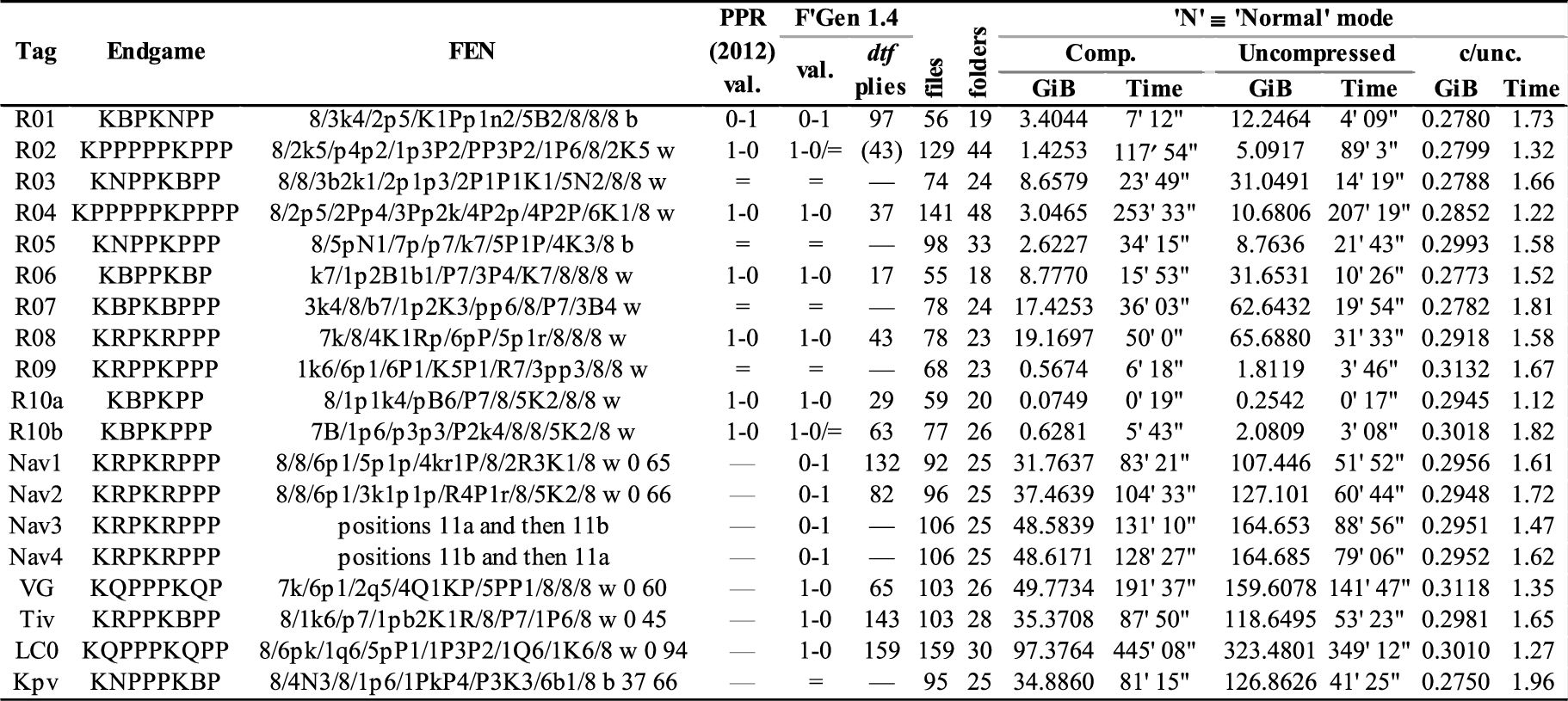
Romero (2012) provides eleven endgame positions. Four of these – R01/06/10a/10b – are admittedly directly evaluable using online ‘EGT’ endgame tables (de Man et al., 2018; Guo, 2018; Lomonosov, 2012). However, these examples are a convenient introduction to FinalGen and show where SF/M/Z strategies diverge. A further five – R03/05/07/08/09 – feature eight men and are arguably in range for albeit fallible, deep-searching, multi-threaded chess engines with 7- or 6-man EGTs.

Finalgen creates EGTs in two modes, ‘Normal’ (‘N’ below) and ‘Search for Draw’ (‘SfD’). ‘SfD’ is more efficient in both space and time than ‘N’ and only returns a ‘Draw’ verdict if this is the case.

The second author reproduced all the Romero (2012) results apart from those for R02 and R10b where the currently downloadable FinalGen v1.4 gives an indecisive ‘win or draw’ evaluation. Rusz (2018) confirms that a previous version created the results on the website. The supplementary document investigates why FinalGen does not see the win in these two examples.

EGT creation was done on two computers22^,33 in both ‘N’ and ‘SfD’ modes and with EGT files NTFS-compressed or not. The computational experiments were not run under strict benchmark conditions, e.g., with defined clock-rate and controlled temperatures. The space figures are accurate to five figures44 but the time figures are reasonably indicative rather than exactly reproducible. Space and time constraints did not allow all eight options to be pursued for every position of interest.

Fig. 2 includes Romero’s 2012 evaluations of the positions with Finalgen v1. The appendix notes some detailed logistics but the headlines are:

Fig. 1.

Romero’s examples, all wtm: (a) R02 1-0, (b) R03 =, (c) R04 1-0, (d) R07 = and (e) R08 1-0.

Fig. 2.

Positions analysed here with FinalGen on PC B.

3.Positions 11a-11b: Navrotescu–Shah, Pays de Charleroi Open, 2017, round 4

This game featured in the Chessbase (2018) Endgame Magic 110 as the finale of a rich and fascinating discussion between the first author and IM Sagar Shah. Navrotescu lost in Fig. 3a with 56. Rd3?? as 56. Bc4!! draws. Even so, the win was not simple and White need not have resigned on move 65: the endgame is a big fish which still has to be landed. The position after 64. . . . Rxf4 attracted the sharp minds and serious attention of GMs Tigran Gharamian, Sandipan Chanda and Jacob Aagaard. For months, the win was not at all clear until Jacob attacked it with FinalGen. It was then clear why the win was not clear: it is exceptionally deep. Sandipan then commented on the themes that emerged, noting that Black must prevent White from establishing its king on f4 and its rook on a4. Perhaps, looking past the sometimes-distracting detail of the computer’s lines, there is perhaps a principle here that, given a choice of taking the f- or h-pawn, one should take the h-pawn.

After 56. Rd3?? [Ed24-3.54], the play was 56. . . . Rxa7 57. f3+ Ke5 58. Bd1 Ra3 59. f4+ Ke4 60. Bc2 Ne3 61. Rxc3+ Nxc2+ 62. Rxc2 Rxg3 63. Kf2 Rf3+ (63. . . . Rg4 64. Rc4+ Kd5 65. Ra4 Rxh4, Fig. 3d) 64. Kg2 Rxf4, Fig. 3b. Our FinalGen computations ran from figures 3b and 3d. 65. . . . Rxh4 would have left a win with dtf = 44 moves and a first phase of nine moves leading to Fig. 3e. However, the chosen 64. . . . Rxf4 left a much more difficult win with dtf = 66 moves and a first phase of 37 moves in the line we followed leading to Fig. 3c. In both cases and particularly as played, White could have fought on for a while, hoping to be defending the usually drawn KRKRP(f)P(h) endgame (Müller and Konoval, 2016; Müller and Lamprecht, 2001) and/or hoping for the 50-move-draw.

Fig. 3.

Navrotescu–Shah: as played (a) 56w and (b) 65w, hypothetically leading with SF± to (c) 103w after f4; the easier win (d) 66w after Rxh4 leading with SF± to (e) 75w after h4.

4.Position 12: Vidit Gujrathi–L’Ami, NED–IND, 43^rd Olympiad r10, Batumi 2018

Fig. 4.

Vidit Gujrathi–L’Ami: as played, (a) ‘won’ 60w, (b) drawn 61b and (c) 7m-draw 69b. In the chosen winning line by FinalGen, (d) 66. g5 and (e) 76. f5 are wiser and later advances than the played line.

At position 60w of Fig. 4a, FinalGen says White has a win in 33 moves. However, Vidit Gujrathi played 60. f5?? and the position is now drawn, a fact which totally escaped top engine Stockfish, kibitzing at the time (Chessbomb, 2018). Position 61b of Fig. 4b required 61. . . . Qd2″″ but 61. . . . Qc1? was played, and now FinalGen says ‘win or draw’. In fact, all lines seem to lead to a draw with pawns and evaluations stalled at 0.00, or with a 7-man draw as at position 69b as played, see Fig. 4c. An analysis engine recognising position-repetition and interfaced to Finalgen and 7-man EGTs would speed searching here. The winning SF∓ optimal line from Fig. 4a is a lesson in festina lente, showing much later advances of the g-pawn as in Fig. 4d and the f-pawn as in Fig. 4e. Both had been providing some shelter from a rainstorm of Black checks until it abated.

We are not dependant on FinalGen for the next observations but it is worth noting how difficult this 6-man endgame is. On thirteen occasions, the most challenging play leaves value preserved by a unique move. The half-point separating Vidit Gujrathi’s win from L’Ami’s draw in fact transferred six times, with moves 71. . . . Kh8, 72. Qe5+, 76. . . . Qa3+, 82. Qe3, 85. . . . Kh8 and 87. h6. After 89. g5 and another 50 moves, the draw was claimed by L’Ami under FIDE Article 9.3.1.

5.Position 13: Tiviakov–Korsunsky, Frunze Open, 1989, 45w

The position of Fig. 5a was long thought to be a fortress, with the bishop on the a7-g1 diagonal blocking Kc6. Nevertheless, Hawkins (2012) first analysed this as a win with the help of 6-man EGTs. FinalGen provided confirmation and a clear, benchmark analysis (Müller and Haworth, 2013), fully considered in the first author’s latest work (Müller and Schaeffer, 2018). Here, we merely supply the played line and, for comparison, an SFMZ∓ line which assumes pawn-promotion is the main objective and minimaxes DTF, DTM and DTZ in that order.

As played, partially annotated relative to move-filtering strategy S(FMZ)∓: {Fig. 5a, dtf = 143p} 45. Ke4″ Bf2 46. Rf5 (46. a4″ bxa4″) Bg1 47. Rf1 Bc5′ 48. Kd5″ Be3″ 49. Rf7+ Kb6″ 50. Rf3 Bg1 51. Rf1′ Be3′ 52. Ke4 Bg5′ 53. Rf5 Bc1″ 54. Rf2″ Bg5′ 55. Kd4 Bc1 [−96pF, dtf = 47p] 56. Re2″ Ka5″ 57. Kc3″ Kb6″ 58. Kd4 Ka5″ 59. Rc2 Bh6″ 60. Rg2″ Bc1″ 61. Rc2 Bh6″ Fig. 5b 62. Rc7 Kb6″ 63. Re7″ Bc1″ 64. Re6+ Kb7″ 65. Re2 [+40pF] Kb6 [−46pF] 66. Kd5″ Bg5 [−10pF] 67. Re6+″ Kb7″ 68. Kc5″ Bd8 69. b3 Bh4 70. Rb6+″″ Ka7″ 71. Kc6, Fig. 5c. White’s king has reached the key square c6 and it is over. Bf2″ 72. Rb7+″″ Ka8∘ 73. Rf7 Bg1 74. Rf4 Ka7″ 75. a4′ bxa4 [−14pF] 76. Rxa4″ {KRPKBP, dtc/f/m/z55 = 14/28/24/2p} Bf2 77. b4″ Be3 78. b5″ Kb8″ 79. Rxa6″ Fig. 5d, 1-0.

The ‘computer line’ below highlights the intrinsic difficulty of this endgame. Certainly, Tiviakov would have found it hard to win this if Korsunsky had somehow found the best defence on each move. The surprisingly early pawn-offer, which cannot reasonably be refused, takes us into a dual between rook and bishop with the rook ultimately the victor.

Fig. 5.

Tiviakov–Korsunsky: positions in the played line, (a) 45w, (b) 62w, (c) 71b and (d) 79b. The SF∓ FinalGen line chosen converts to KRPKBP at (e) position 51b.

An S(FMZ)∓ line: 45. Ke4″ Kc6″ 46. Rh6+′ Kb7″ 47. Kd5′ Bf2′ 48. Re6′ Bg1′ 49. Re4″ Kb6′ 50. a4″ bxa4″ 51. Rxa4″ {Fig. 5e, KRPKBP, dtf/m/z = 130/146/82p} Be3′ 52. Ra1″ Kb7′ 53. Re1′ Bf2″ 54. Rf1″ Be3″ 55. Rf3″ Bg1″ 56. Kd6″ Bh2+″ 57. Ke6″ Kc6″ 58. Rf1″ Bg3″ 59. Kf5″ Bd6″ 60. Rc1′+ Kb6″ 61. Ke4″ Bc5″ 62. Kd3″ Kb5″ 63. Ra1″ Kb6″ 64. Kc4″ Be3″ 65. Re1′ Bf2″ 66. Rf1″ Be3″ 67. Rf3″ Bg1″ 68. Kb4″ Bd4″ 69. Rb3″ Be5″ 70. Ka4+″ Ka7″ 71. Ka5″ Bf6″ 72. Kb4″ Kb6″ 73. Ka4+″ Ka7″ 74. Rb4″ Be5″ 75. Kb3″ Bd6″ 76. Rg4″ Be5″ 77. Rg2″ Kb7″ 78. Kc4″ Bf4″ 79. Rg7+″ Kb6″ 80. Rg4″ Bb8″ 81. Rg6+″ Kb7″ 82. Kd5″ Bf4″ 83. Rg4″ Bb8″ 84. Kc5″ Ba7+″ 85. Kd6″ Bb8+″ 86. Kd7″ a5″ 87. Rg8′ Bf4′ 88. Rf8″ Bd2″ 89. Rc8″ Bb4′ 90. Rc6″ Bf8″ 91. Rc2′ Kb6″ 92. Rc8″ Bg7″ 93. Kd6″ a4″ 94. Rb8+″ Ka7″ 95. Rb5″ a3″ 96. bxa3″″ {KRPKB, dtf/m/z = 40/62/4p} 1-0.

6.Position 14: Leela Chess Zero–Ethereal, TCEC Cup 1, game 14, pos. 90b

The radical ‘neural network’ and rapidly improving chess engine ‘LC0’ was of major interest to the inaugural TCEC Cup audience (Haworth and Hernandez, 2019). Ethereal was also a dark horse, newly risen to the Premier Division of the TCEC league. The ‘best of eight’ rapid tempo match between them passed 4-4 en route to ‘best of two’ and featured unusually long contests, largely because LC0’s evaluations frustrated the TCEC adjudication rules. Game 14 was no exception.

This theoretically reached FinalGen territory at position 74w which requires 11TB for workspace so we quickly advance to position 94w of Fig. 6a. Removing the f- or g-pawns leaves a win with dtf = 29m/57p or 28m/55p respectively. Removing the four pawns leaves a draw. This suggests but does not guarantee that the 9-man position 94w is decisive. FinalGen proves that White did in fact have a win: dtf = 159 plies: the FIDE 50-move rule, with the advancing pawn on b4 and pawns to advance or capture, appears not to be an issue. Figs 6(b–d) mark successive phases of the endgame. The actual game was adjudicated by the ‘TCEC draw rule’ at move 175b, Fig. 6e.

Fig. 6.

LC0-Et: (a) 94w; FinalGen-optimal line (b) 105w before b6″″, (c) 7m 116w and (d) 6m 128b; (e) drawn 175b.

7.Position 15: Karpov–Kasparov, World Chess Ch. 1984, game 9, 66b

This is the ‘Fermat’s Last Theorem’ of endgame quests, a position that has inspired more incorrect arguments than any other, so many that the analysis of those arguments would be a separate and interesting thesis of its own. Fortunately, this saga is now at an end as we can definitively assess both the ‘ground truth’ and the false proofs with FinalGen.

The game is no less significant than the endgame. It saw Karpov go 4-0 up and preceded 17 draws in the controversial championship match eventually abandoned at 5-3 after five months and 48 games. The position of Fig. 7a has been an enduring mystery, visited many times over the years (Dvoretsky, 2008; Karolyi and Aplin, 2007; Marin, 2006; Müller, 2003, 2005; Müller and Konoval, 2018; Timman, 2007). Was the draw missed (Kasparov, 2007) with the move 66. . . . Bb7?

Fig. 7.

Karpov–Kasparov: (a) pos. 66b; drawing line (b) 73b and (c) 77w; in a better defence (d) 69w and (e) 74b.

FinalGen shows not only that the amazing defence 66. . . . Bh1 draws but that it is the only drawing move. Figs. 7b–c are taken from the drawing line. It also shows that the path to the winning line after 66. . . . Bb7?? is long and narrow with six ‘only’ moves for White. Figs. 7d–e are from a ‘best defence’ albeit losing line. After we had run this FinalGen computation in 2017, Jan Kominek pointed out that Roman Jiganchine (2015), whom we salute, had already got the same result. It is intriguing to think that there must be many other famous game and study positions (van der Heijden, 2017) whose FinalGen analyses have not been widely promulgated or even done.

8.Summary

FinalGen works beyond today’s endgame table limit of seven men, bringing definitive knowledge to the table, providing benchmark standards of play and resolving questions that have remained unanswered for as long as thirty years. In the context of current technology, it has untapped potential both as a working program and as a concept.

It is currently single-threaded but the principles of concurrent programming are well known and cpu chips continue to offer more cores and processing threads. PC B’s 4-lane PCIe v3.0 interface to its SSD provides over 1GB/s but PCIe v5.0 (PCI-SIG, 2019) in 16-lane mode promises to offer 16 times the bandwidth, effectively reducing disc-latency to zero. Romero (2012) provides code libraries to interface chess engines to FinalGen EGTs: we do not believe these have been used yet. FinalGen does not create value-only EGTs as de Man et al. (2018) do. Nor does it use two ideas exploited in Bleicher’s Freezer (Müller, 2005), namely trial-constraints on the chessmen and interfacing to precomputed EGTs. The full analyses (Müller and Haworth, 2019) show how truncated FinalGen’s searches would be if 7-man EGTs could be consulted. These considerations suggest that the efficient creation of FinalGen-type EGTs could be a part of chess engines’ runtime calculations.

More immediately, a growing FinalGen community, centred around the forum (Romero, 2012) could evolve and share future results. Endgame tables now give instant answers for 7-man positions but FinalGen can address many positions with eight men or more. The examples here will hopefully inspire others to show what is possible in creating further unarguable insights into the game of chess.