A formalisation and prototype implementation of argumentation for statistical model selection
Abstract
The task of data collection is becoming routine in many disciplines and this results in increased availability of data. This routinely collected data provides a valuable opportunity for analysis with a view to support evidence based decision making. In order to confidently leverage the data in support of decision making the most appropriate statistical method needs to be selected, and this can be difficult for an end user not trained in statistics. This paper outlines an application of argumentation to support the analysis of clinical data, that uses Extended Argumentation Frameworks in order to reason with the meta-level arguments derived from preference contexts relevant to the data and the analysis objective of the end user. We outline a formalisation of the argument scheme for statistical model selection, its critical questions and the structure of the knowledge base required to support the instantiation of the arguments and meta-level arguments through the use of Z notation. This paper also describes the prototype implementation of argumentation for statistical model selection based on the Z specification outlined herein.
1.Introduction
The increased availability of data, in particular data collected routinely, provides a valuable opportunity for analysis with a view to supporting evidence based decision making. Analysing available data in support of a research question or hypothesis necessitates some statistical approach to ascertain whether any effect observed in the data is due to chance or not. In a simple example one may have access to data on the number of patients admitted or the number of students passing a test, and one may wish to answer the question: “Is there an increase between last year and this year?” Simply comparing the number of patients admitted each year or comparing the pass percentage of students on its own does not provide an answer to the question asked. A difference in the values, however large or small, may be due to random variations and as such provides no confident evidence that there is indeed a difference between the years.
It is at this point that the statistical model selection problem arises. Each of these situations can be supported through the use of an appropriate statistical model or approach. In some cases there will be more than one possible approach to statistically test the research question or hypothesis. A human statistician is trained and experienced at considering all the factors relevant to a specific research question and data in order to recommended an analysis model or approach.
As there is an ever increasing amount of data available to test hypotheses on, coupled with easily usable statistical functionality being offered in standard (off-the-shelf) spreadsheet products there is a need to offer a method to guide, support and justify the selection of one statistical approach over another. This can be done by consulting a statistician, but this involves additional effort and time. An automated recommendation and justification shortens the time required.
The choice of model in support of a research question involves knowledge on what model approaches achieve the type of objective specified by the research question and by the available data. Additionally, statistical theory dictates conditions under which models cannot be used and conditions under which models may not perform at their best. The former are known as critical assumptions and the latter are context domains. The extent to which these conditions are met can be tested either by querying the data or by eliciting information about the data from the domain expert. Utilising a model when its critical assumptions don’t hold can lead to erroneous conclusions being drawn, or effects being missed.
In previous work [23,24] we proposed an argumentation-based approach to providing decision support to a user when deciding which statistical model or approach is best suited to their research question and data. In this paper we build on our previous work by articulating a formalisation of the argumentation schemes, critical questions and knowledge base required to support the instantiation of an Extended Argumentation Framework (EAF) [20]. The application of EAFs and their instantiation in the context of statistical model selection is a novel approach. We also outline Z notation schemes [26] to describe this formalisation and outline the prototype development that was based on these Z schemes. To the best of our knowledge this approach, although used in Multi Agent Systems has not previously been applied to argumentation.
An initial step towards evaluating the contributions outlined in this paper has been achieved through the use of case studies, one of which is included herein. The next step in evaluation will involve user studies aimed both at ensuring the reasoning and recommendations made by implementing our approach is consistent with the recommendations a statistician would make, and to asses the end user experience.
The paper is structured as follows: Section 2 provides relevant background and introduces a motivating example. Section 3 formalises the argument schemes, knowledge base and critical questions. It illustrates the formalisms through the use of an example and also provides Z notation schemas. Section 4 describes the prototype implemented. Section 5 discusses related work. Section 6 provides a summary of the work proposed and articulates our plans for further research.
2.Background
In order to illustrate the process of selecting an appropriate statistical model we will be introducing an example based on a freely available data set. The data set is called ovarian and it contains the data for 26 patients collected in a randomised trial comparing two treatments for ovarian cancer [8]. The data includes the follow up time (futime), an indication of whether the patient is censored i.e. lost to follow up (fustat), the patient’s treatment (rx) and additional demographics. The end user (likely to be a clinician in this case) may be interested in testing the following hypothesis on the ovarian data:
Hypothesis 1.
There is a difference in patient survival (fustat) between treatments.
In order to test Hypothesis 1 there is a need to select and apply a statistical model. The target attribute for the hypothesis is survival time contained in futime and the censoring status is in the column fustat which determines if the event of interest has occurred. This type of analysis of this research question is survival analysis and therefore the analysis objective is survival.
The presence of a significant difference in survival times between different groups of patients can be formally tested using Kaplan–Meier (KM) [15]. This compares the observed number of events occurring at each particular time point for each separate group to the number expected if the survival curve is the same in each group.
Prior to applying the KM model to test Hypothesis 1 its assumptions should be tested to ensure that they hold. The first assumption relates to the lack of independence in censoring and requires that the clinician confirm whether censoring is informative or not. In this case there is no evidence of censoring patterns being different between the two treatment groups. As the assumption holds, it is appropriate to apply the KM model to the ovarian data to test Hypothesis 1. This results in a p-value of 0.303 which makes the difference between the survival curves for different treatments not significant at α=0.05.
The other common Survival Analysis method is Proportional Hazards (PH) and it models the Hazard function [5]. Proportional hazards model is a semi-parametric method that also allows the introduction of numerical continuous covariates within the model.
There are some assumptions that must be met prior to the use of PH. The first assumption is on lack of independence in censoring, and this is an assumption shared with KM. The second assumption is that the hazards are proportional. The hazard functions of any two patients are assumed to be constant multiples of each other. As this is the same data as the one used to apply KM then there is no need to test the first assumption. The second assumption, one of proportional hazards will need to be tested. The proportional hazards assumption for the ovarian data is tested and it holds. This means there are no significant time dependent covariates. When the PH model is applied to test Hypothesis 1, no significant difference between treatment groups is discovered either. This confirms the findings of the KM model.
A third approach to consider is Weibull [29]. This shares the same first assumption as KM and PH. However the second assumption for the Weibull model does not hold for the ovarian data, as such the Weibull model is not one to consider or use in this case.
There are many additional models for survival analysis but for the purpose of this example we only chose to consider three. Of the three models considered in this example there were two models that were possible (KM, PH), and in this case both confirmed that there is no significant difference in survival times between treatments (Hypothesis 1).
It is also possible to assess whether one model is more suitable that the other one by taking into account some additional conditions. A statistician may assess the situation by discussing the objective of the analysis with the clinician. If the objective of the analysis extends beyond testing Hypothesis 1 but also looks to produce a benchmark to be used to estimate survival time for future patients then the recommendation would be to use PH as it facilitates predictions. Another consideration relates to the different models’ resilience to censoring. In the ovarian data set there are 14 patients who are still alive at the last follow up, resulting in a censoring rate of 1426=0.54 which is considered light and most models considered are not affected by this level of censoring. Light censoring in this case has no impact on which model is more suitable.
2.1.Z notation
Z notation [26] is a formalism created to represent interacting computational systems and it is based on elementary components such as set theory and first order predicate logic. There are examples of the use of Z notation to formalise multi agent systems ([6,17,19]). Luck et al. [17] use Z to provide an accessible and formal account of agent systems. The authors use Z as it is sufficiently expressive to allow a consistent unified structured account of a system and its associated operations and it is deemed suitable to facilitate implementation. Z notation was also used by Miller et al. [19] as a basis for an extension of Z aimed at modeling software agents in a multi agent environment.
An additional implementation in a multi agent setting that makes use of Z is provided by D’inverno et al. [6]. The authors use Z to provide an abstract formal model of an idealised dMARS (distributed Multi Agent Reasoning System). The authors justify the use of Z as it enables designs of systems to be formally developed, whilst allowing for the systematic reduction of these specifications to implementation. The authors also describe Z as having the desirable property of being accessible and extremely expressive allowing for consistent unified and structured accounts of systems. Furthermore the large array of books and cases studies (academic and industry) is also cited.
We have expressed our argumentation-based method in a formal language in order to make the specification precise, and to aid its implementation. The expressiveness and accessibility of Z notation coupled with the need to facilitate a prototype implementation justified our use of it to formalise the contributions in this paper.
3.Method
In this section we articulate the elements that comprise our method to support statistical model selection through the use of Extended Argumentation Frameworks (EAF). We also provide the Z notation schemes representation of the elements introduced.
3.1.The statistical knowledge base
Our method relies on a statistical knowledge base (SKB) which includes all of the relations between the objectives of the research question or hypothesis (O), the models (M) and the assumptions (A). The SKB holds facts linking O, M, A in a way that supports the queries from the argumentation scheme and its critical questions. The SKB holds multiple research question types and each is linked to the objectives O that can fulfil that research question R, models M are defined and linked to the respective objectives they are suitable for, and for each model the critical assumptions are defined. The objective O of a research question or hypothesis (such as Hypothesis 1) is derived from the attribute type of the target. For example in the ovarian data the target attribute was futime which is of type “time to event” and this equates to an objective os.
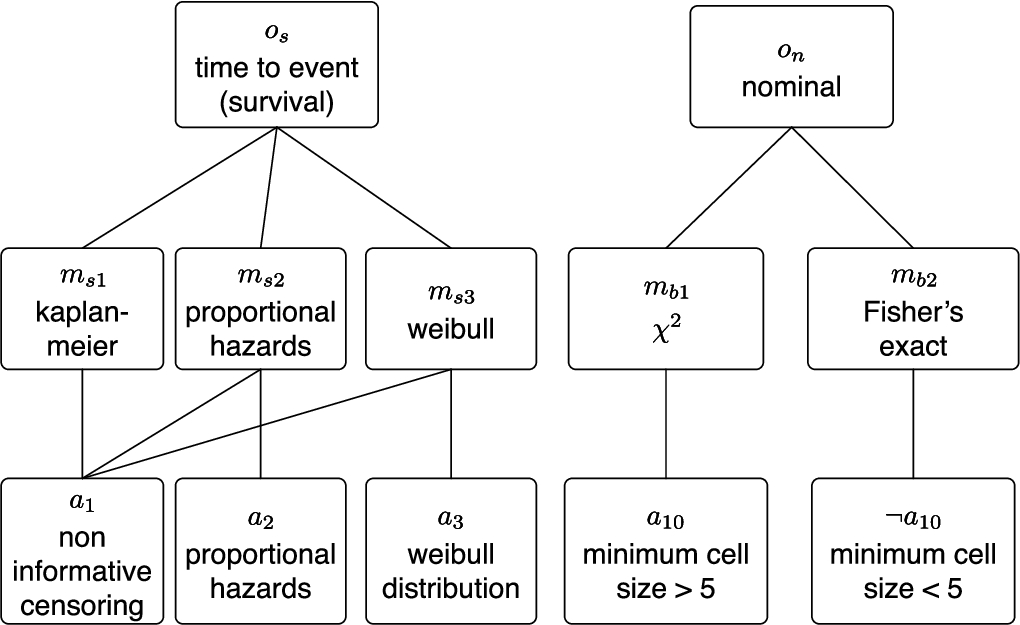
The relations and contents of the SKB are derived from statistical theory and best practice, these relations are defined by an expert, not the end user. An example of the elements of the SKB is illustrated in Fig. 1, this is pertinent to the ovarian example. Figure 1 illustrates the contents of the SKB for the objectives of time to event (or survival) analysis and nominal analysis (or table analysis). From Fig. 1 it can be seen that there are three models suitable for an objective of type os and for each of these three models (ms1,ms2,ms3) there are different critical assumptions, for example model ms2 relies on two critical assumptions a1, a2 the former a1 also being an assumption to both ms1 and ms3. The elements of the SKB are denoted as follows:
Fig. 1.
The knowledge base contents relevant to the example.
Definition 1
Definition 1(Elements in the statistical knowledge base).
The set of models: M={m1,…,mK} where k=1,…,K
The set of assumptions: A={a1,…,mP} where p=1,…,P
The set of objectives: O={o1,…,oQ} where q=1,…,Q
The following relationships are defined in the SKB:
Definition 2
Definition 2(Relations in the statistical knowledge base).
F⊆M×O where if mk fulfils objective oq then (mk,oq)∈F
C⊆M×A where if ap is a critical assumption for mk then (ap,mk)∈C
OBJ⊆O×O where if or is an alternative objective to oq then (or,oq)∈OBJ
The Z notation basic types required to define the elements of the SKB (Definition 1) are:
[MODEL] – the set of all possible models
[OBJECTIVE] – the set of all possible objectives
[ASSUMPTION] – the set of all possible assumptions
There is also a need to strengthen the specification by setting up variables to account for potential input errors. Z schemas can be implemented (such as REPORT) so that when used in conjunction with the other schemas errors can be flagged. The state space for the SKB is:

The SKB contents relevant to the example introduced are in Fig. 1 and the relations as per Definitions 1 and 2 are:
The SKB contents in Z notation are:
3.2.Argument schemes and critical questions
When the AS for model to consider on the grounds of achieving the objective (AS1) is instantiated it leverages the additional argumentation schemes as part of the critical questions in order to identify potential under-cutters, rebuttals or undermines.
Definition 3
Definition 3((AS1): Argument Scheme for model to consider on grounds of achieving the objective – PM(R,O,M)).
| Premise – | O is the objective of the research question R |
| Premise – | M is a model able to analyse O |
| ∴ M is suitable to answer R |
The premises for this AS1 (Definition 3) are statements that are verified against the SKB, given the specific oq and r that the end user is interested in. The instantiation of AS1 (Definition 3) given an objective is in the form of the following Z enquiry schema. A schema denoted by Ξ in Z is a schema that does not change a state.

where the type REPORT will be defined to flag situations where the objective stated is not known.
AS1 (Definition 3) is subject to critical questions. These are used to test the assumptions of the scheme (such as CQ2) for potential undercuts or to highlight exceptions (CQ1) or rebuttals. The CQs identified and their respective argument schemes are:
CQ1: Are there alternative ways of answering R? This leads to using another objective as this would support the same analysis through a different set of models. The Argument Scheme for alternative objective (AO) – this instantiates rebuttal arguments (Definition 4).
CQ2: Do any of the critical assumptions for M fail to hold? Argument Scheme for failed assumptions (CA) – this instantiates arguments against the use of a model if any of its critical assumptions fail. This undercuts the arguments generated by the argument scheme for models to consider on the grounds of achieving the objective (Definition 5).
Definition 4
Definition 4((AS2): CQ1: Argument for alternative objective: AO(R,O,Oalt)).
| – | O is the objective of research question R |
| – | Oalt is an alternative objective to O to answer R |
| – | M is a model able to analyse Oalt |
| ∴ | M is suitable to answer R |
Definition 5
Definition 5((AS3): CQ2: Argument against the use of a Model for failed critical assumptions: CA(M)).
| – | Model M is suitable to achieve O |
| – | A is a critical assumption for M |
| – | A does not hold |
| ∴ | ¬M (M is not suitable to achieve O) |
The premises for CQ1 (Definition 4) are statements extracted from the SKB once the initial research objective O is known. The first two premises for CQ2 (Definition 5) are statements from the SKB for a given model to be considered mi, and the last premise is validated either by performing an analysis on the data or by querying the end user (clinician or equivalent domain expert).
Given the list of models, the critical questions need to be instantiated. CQ1: Are there alternative ways of answering the research question? In order to model this critical question an additional relation is to be introduced to the [StatisticalKnowledgeBase]. This will be a relation between OBJECTIVES:

In order to set this relation up the schema is initialised:

The schema [AddAlternativeObjective] is used to populate the relationship between alternative objectives. A Z schema denoted by Δ is one that describes a state change.

The [AddAlternativeObjective] schema adds a relation between one objective (o1) and another (o2) that can be used as an alternative analysis approach to it. The schema will only allow a relation to be added if both o1 and o2 are defined in the Statistical Knowledge Base [StatisticalKnowledgeBase].
Now the argument scheme AS2 in support of CQ1 (Definition 4) is instantiated through the following schema:

The aim of CQ2 (Definition 5) is to validate the critical assumptions for each of the models returned as part of [FindModels] (note that the latter will be instantiated for both the original objective and any additional alternative objectives resulting from [FindAlternativeObjective])

The resulting list of assumptions contain elements of the type: {a1,a2,…,an} and these can each then be validated against either the data or by querying the clinician.
3.3.Instantiation of the argument scheme and critical questions for the example
In order to illustrate the application of the ASs and CQs the example introduced in Section 2 is used. The objective of the research question is os. As illustrated in Fig. 1 the objectives and models in the SKB are:
Survival Analysis os which includes the following models:
ms1
Kaplan-meier,
ms2
Proportional Hazards and
ms3
Weibull
Table Analysis on which includes the following models:
mb1
χ2 (Chi squared),
mb2
Fisher’s Exact
a1 | non informative censoring |
a2 | proportional hazards |
a3 | Weibull distribution |
a10 | table cell minimum >5 |
Instantiating AS1 (Definition 3) in this example leads to the following:
Arg1 Argument Scheme for model to consider on grounds of achieving the objective os: PM(os,r,ms1)
| Premise – | os is the objective of the research question r |
| Premise – | ms1 is able to analyse os |
| ∴ – | ms1 is suitable to answer r |
| Premise – | os is the objective of the research question r |
| Premise – | ms2 is able to analyse os |
| ∴ – | ms2 is suitable to answer r |
| Premise – | os is the objective of the research question r |
| Premise – | ms3 is able to analyse os |
| ∴ – | ms3 is suitable to answer r |
Three arguments have been instantiated, these now need to be subject to the two critical questions. Instantiating CQ1 using AS2 (Definition 4) generates the following argument:
Arg′4 Argument for alternative objective: AO(os,r)
| – | os is the objective of research question r |
| – | on is an alternative objective to os to answer r |
| – | mb1 is able to analyse on calling AS1: PM(on,r,mb1) |
| ∴ – | mb1 is suitable to answer r |
| – | os is the objective of research question r |
| – | on is an alternative objective to os to answer r |
| – | mb2 is able to analyse on calling PM(on,r,mb2) |
| ∴ – | mb2 is suitable to answer r |
This results in the following set of arguments: {Arg1: PM(os,r,ms1): ms1, Arg2: PM(os,r,ms2): ms2, Arg3: PM(os,r,ms3): ms3, Arg′4: AO(os,r): mb1, Arg4: AO(os,r): mb2}.
Instantiating CQ2 using AS3 (Definition 5):
Arg7 Argument against the use of a Model for failed critical assumption: CA(ms3)
| – | Model ms3 achieves objective os |
| – | a3 is a critical assumption for ms3 |
| – | a3 does not hold |
| ∴ – | ms3 is not suitable to answer os |
| – | Model mb2 achieves objective os |
| – | a10 is a critical assumption for mb2 |
| – | a10 does not hold |
| ∴ – | mb1 is not suitable to answer os |
The instantiation of AS3 (Definition 5) generates two undercuts to two of the arguments in favour of the use of the respective models.
Arg1: | PM(os,r,ms1): ms1 |
Arg2: | PM(os,r,ms2): ms2 |
Arg3: | PM(os,r,ms3): ms3 |
Arg′4: | AO(os,r): mb1 |
Arg4: | AO(os,r): mb2 |
Arg7: | CA(ms3): ¬ms3 |
Arg8: | CA(mb2): ¬mb1 |
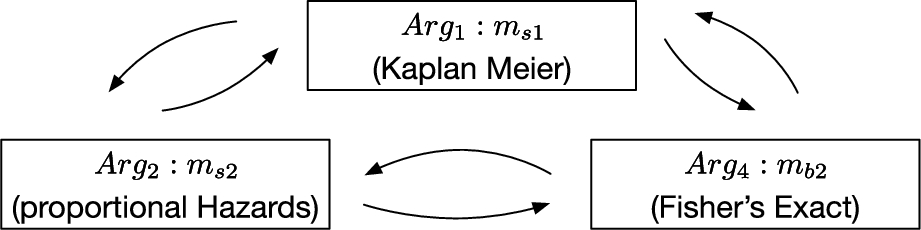
AS3 (Definition 5) can generate an undercut to AS1 (Definition 3) thereby undercutting some arguments in support of models from the set of ones that could be applied in this example. The resulting AF is illustrated in Fig. 2 and its arguments are Arg1: PM(os,r,ms1): ms1, Arg2: PM(os,r,ms2): ms2 and Arg4: PM(on,r,mb2): mb2.
Fig. 2.
Argumentation Framework for the ovarian example with symmetrical attacks.
The instantiation of all of these argument schemes (Definitions: 3, 4, 5) will produce a set of arguments in support of or against the use of a specific model. This set of arguments make up the argumentation framework (AF) of relevant arguments to the research question and data at hand. The attack relations within this AF are relevant and derived from the desire to run only the most appropriate models, implying that a decision to use one model (with arguments in support of its use) negates the use of other models with arguments supporting their use in the AF.
If it is acceptable to run all the models that have an argument supporting their use then the AF contains no attack relations per se. If it is desirable to run only the most suitable models the relative strength or preference of each argument in support of the use of a model should be considered. In order to pick the most suitable of the models, this approach is extended with a means to express and reason with preferences.
3.4.Preferences
We identified three different sources of preferences in the context of statistical model selection and we formalise these preferences through an extended SKB and EAFs. Feature based preferences arise from the statistical theory underpinning each model and dictating which models perform better when certain conditions are present in the data or the research question. An example of such a preference is one model being preferred given a data set with missing data as it is more resilient to it. Intent based preferences relate to the intent or purpose of the analysis as the definition of a good model will depend on the specific analysis objective. The different model purposes and implications on model selection are explored in [18,25]. Finally there may be preferences derived from the end users themselves, domain based preferences. For example users may prefer to use a model that has been used in related analyses or publications.
A preference expressed in the context of statistical model selection refers to an order of priority between models. If we have a set of models {m1,…,mn} then a preference order Pref⊆M×M where prefj on these models would be of the form: prefj={m1≻mi,…,mi≻mn} where i∈{1,…,n} and j=1,…,J. For example if we consider a set of only three models {m1,m2,m3} then m1≻m2 indicates that m1 is preferred to m2. Preference orders can be empty, in which case all models would be equally preferred, and not all models need to be included in each preference order.
The source of the preference orders are mapped to a priority or importance when leveraging the preferences to find the model most suitable to the situation. Feature based preferences are generally more important in determining a model’s relative suitability than intent based preferences or domain based preferences. Furthermore the intent based preferences are more important than domain based preferences. This can be represented as an order of importance over the different preference orders that are relevant to each type of preference source.
To incorporate preferences into the approach, the SKB introduced in Definition 1 is extended:
Definition 6
Definition 6(Extended statistical knowledge base).
A set of context domains CD={CD1,…,CDH}.
A set of totally ordered sets of performance measures P={P1,…,PH}. Each Ph contains a set of measures ph1≺…≺phj by means of which a model’s performance is assessed in a specific context.
A set of performance functions PF={PF1,…,PFH}, such that each PFi:CDi×M↦Pi.
The mapping of the model to the performance measure PFi is dependent on the context domain CDh. Optionally an order of importance for the context domains can be defined where I is the ordered set of context domains. The order determines the relative importance of the context domain.
In order to extend the SKB as per (Definition 6) context domain and performance measure are added to the specification.The state space for the extension of the SKB is defined as follows:

In order to populate this extended knowledge base, firstly the context domains are defined:

For each given context domain (defined with the previous two schemas) the models relevant to it can be added and mapped onto the existing defined performance measures. The schema to map a model to a context domain and performance measure is defined as follows:

The [AddModelToContext] schema takes a model and context domain as inputs and maps the model to the measure level defined for the specific context domain in question. For example if we have a context domain for censoring cd12 as defined in Table 1(a) then the values could be: domain={cd12}, measures={p1,p2,p3} where p1=unaffected, p2=mildly affected and p3=strongly affected.
The AddContextDomain schema is used to define this context domain (assuming it has not been already defined). Once the context domain is defined the AddModelToContext schema is employed to map all the relevant models to the appropriate measures. In this example using context domain cd12 from Table 1(a) results in effect={ms1↦p2,ms2↦p1,mb2↦p3}. Which results in the following preference between models resulting from cd12: {ms2≻ms1,ms2≻mb2,ms1≻mb2}.
Table 1
Context Domains Performance Measure Mapping for (a) cd12 light censoring and (b) cd22 model intent explain
| CD | model m | performance measure p | CD | model m | performance measure p |
| (a) cd12 light censoring | (b) cd22 model intent is explain | ||||
| cd12 | ms1 KM | p2 mildly affected | cd22 | ms1 KM | p1 suitable |
| ms2 PH | p1 unaffected | ms2 PH | p1 suitable | ||
| ms3 Weibull | p1 unaffected | ms3 Weibull | p1 suitable | ||
| mb1 χ2 | p3 strongly affected | mb1 χ2 | p2 neutral | ||
| mb2 Fisher’s | p3 strongly affected | mb2 Fisher’s | p2 neutral | ||
The definition of the context domain that is derived from clinician preference is also mapped using the Z schemas [AddContextDomain] and [AddModelToContext]. An example of such a context domain where there are only two performance measure p1 and p2 where p1≻p2 would lead the following mapping if the clinician prefers the use of model ms2: effect={ms1↦p2,ms2↦p1,mb2↦p2}. Which results in the following preference between models resulting from the specified clinician preferences: {ms2≻ms1,ms2≻mb2}.
3.5.Extended argumentation framework
To construct an EAF based on the extended SKB, first the set of contexts ˆCD⊆CD1∪⋯∪CDH for the problem at hand must be established. ˆCD contains the subset of contexts taken from all the context domains in CD. Whether a context is relevant to a problem is derived by applying a test on the data, elicited from the domain expert/clinician or elicited from the research question. Where identification of the context is not straightforward, the contexts in CD provide hooks (conclusions) for further arguments about the appropriate statistical model.
Let ⟨Arg,R⟩ be an AF generated by instantiating AS1 (Definition 3) and CQs (Definitions 4 & 5). Such an AF is extended to an EAF ⟨Arg,R,D⟩ as follows:
Definition 7
Definition 7(Generating the EAF using the extended statistical knowledge base).
Intuitively, an attack relationship PAcdhxy↠(mx⇀my) is added for each attack of a model mx by a model my where a context (CDh) justifies a preference of my over mx. The notation used in Definition 7 PAcdhxy↠(mx⇀my) denotes (PAcdhxy,(mx,my))∈D and was used in [20]. Optionally there may be a preference order I over the context domains, CDM⊆CD×CD.
Within an EAF that includes the preference arguments from one context domain the acceptable arguments supporting the use of a model to the preferred extension semantics provide justification to the suitability of the model. These preferred or more suitable models are the ones supported by an argument that is acceptable with respect to the set of preference arguments from the context domain in question. If the arguments in support of the use of more than one model are acceptable to the set of preference arguments generated by one context domain, another context domain (the next one in order of importance) can be introduced.
3.6.Instantiating the extended argumentation framework for the example
Table 1(a) contains a subset of the feature based preferences context domains related to light censoring. These are mapped for absent and heavy censoring in a similar fashion. Table 1(b) contains the mappings related to intent based preferences cd22 where the intent is to explore (not predict). The mapping is determined by statistical theory and is performed by an expert, not the end user.
In this situation we have an AF containing three arguments each supporting the use of a different model, this is illustrated in Fig. 2. If the overall aim is to recommend one model or aim to refine the list of models to apply then the AF is extended to include and account for the information that can assist in arguing what contexts are relevant to the situation and leverage them in order to recommend the most suitable model(s).
The AF from the ovarian example is ⟨Arg,R⟩ where:
In order to generate the EAF for this scenario then the following additional inputs are required in order to generate the preference meta level arguments D:
ˆCD={cd12,cd22,cd3} where cd12 in this case corresponds to light censoring, cd22 is model intent and cd3 is clinician preference.
I={cd12≻cd22≻cd3}
The ovarian data is light censored (the proportion of censored patients is 54%). The preference meta level arguments related to models which have an argument in their support in the AF (Fig. 2) are instantiated by applying Definition 7:
The second context domain of relevance in this example is cd22 as the intent of the analysis is to explore the hypothesis (to explain not to predict) therefore an additional set of meta level preference arguments are generated from Table 1(b) for cd22. By applying Definition 7 the following set of meta level preference arguments are generated:
Finally there is a clinician expressed preference, this will be cd3 and the clinician has expressed a preference for ms1 such that:
There are now seven meta level arguments derived from the preferences in D. Figure 3 illustrates the EAF that includes the preference arguments PAs from each of the three context domains.
Fig. 3.
EAF for ovarian including preference arguments (in light grey) from all the contexts.
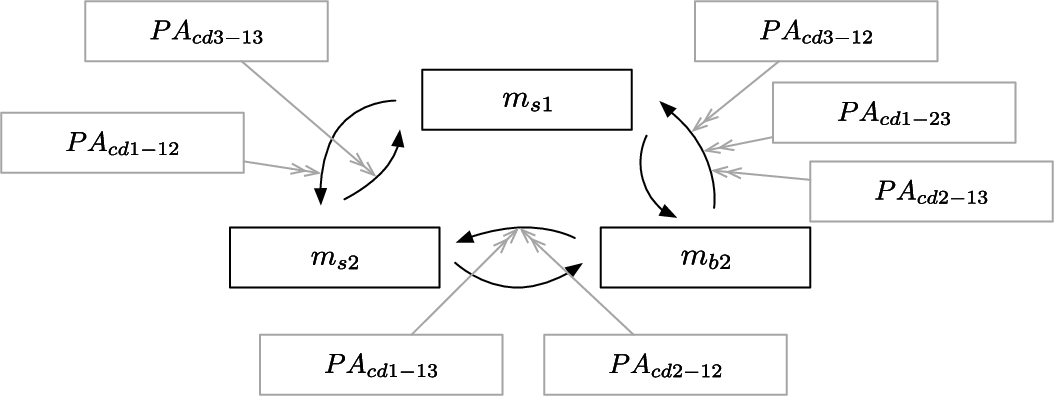
Fig. 4.
EAF for ovarian including preference arguments from cd12 only. The preference arguments from other contexts are in grey.
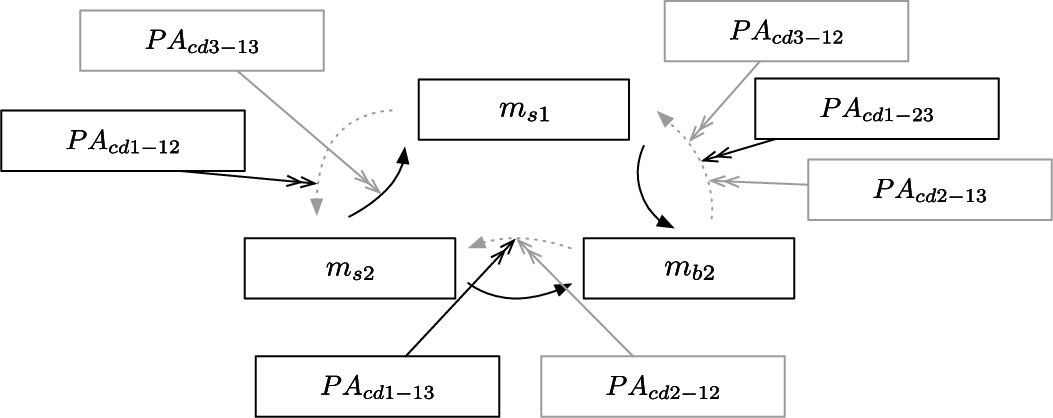
The most important context domain in this example is derived from censoring (cd12). When only the meta-level arguments from cd12 are considered in the EAF then only ms2 is acceptable with respect to S′cd12={PAcd1−12,PAcd1−13,PAcd1−23} under the preferred extension semantics in Fig. 4. ms2 is the recommended model to be used when cd12 is considered and the justification to its choice over ms1 and mb2 is given by the context domain used. In this case the recommendation of ms2 over the other models is explained by it being preferred under conditions of mild censoring.
If we assume that the order over the context domains in ˆCD for the same example is not given, then the preferred extensions for the EAF can be computed for each cdi in turn. The resulting extensions would be: S1={ms2}, S2={ms2}, S3={ms1} for cd12, cd22 and cd3 respectively. In other words model ms1 would only be selected in a situation where the preferences of the clinician (cd3) are prioritised over all other contexts.
4.The prototype
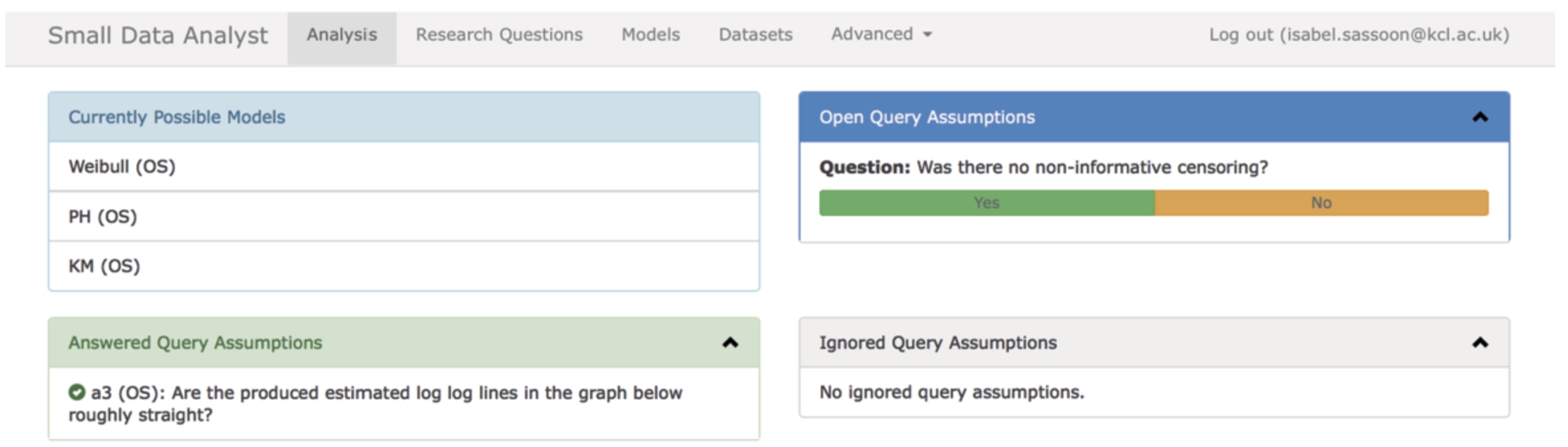
The formalisation and the Z notation schemes presented in this paper formed the basis for the development of the Small Data Analyst prototype [30]. This was developed and deployed on heroku in Ruby.11 The prototype was designed with two different user types in mind: an end user (in this case a clinician) and an administrator. Different options are available in the app depending on the user type. Initially a welcome and instructions screen is displayed to the end user. The user then selects a research question for their data. Figure 5 shows how the user is prompted to confirm assumptions (that cannot be tested from the data). In this case there is a need to confirm that censoring is non informative. The data being used in these screenshots is the ovarian data and Hypothesis 1.
Fig. 5.
The user interaction to confirm an assumption for a model.
Once all the assumptions are tested, and the context domains identified the model recommendations are presented both in a list and as an EAF. In Fig. 6 the models considered are Kaplan–Meier and Proportional Hazards, the recommended model is Proportional Hazards. The visual EAF format in Fig. 7 confirms the recommendation.
Fig. 6.
The model recommendation made in case of the ovarian.
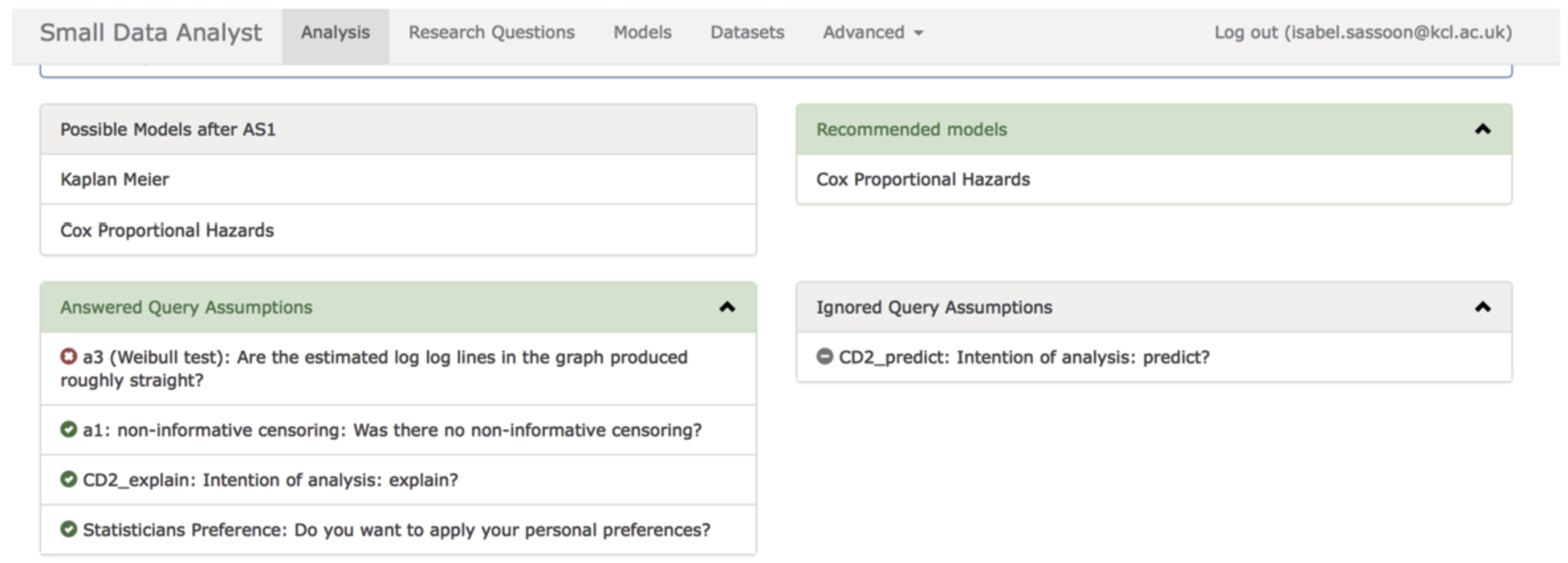
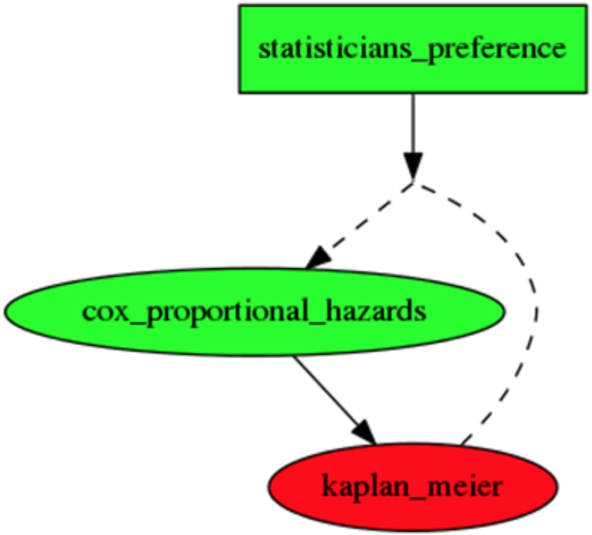
Fig. 7.
Graphical display of the resulting EAF to user (optional view for end user).
The administrator has access to functionality to populate the Extended SKB (Fig. 8(a)) and to modify the model definitions, such as assumptions required for a model (Fig. 8(b)).
Fig. 8.
Administrator screens for editing the Extended SKB.

5.Related work
Outside the context of statistical model selection there are examples of the application of argumentation to decision support, Fox et al. [9,10] provide a medical perspective on the application of argumentation in the domain. Although none of these applications tackle statistical model selection, there are parallels to be drawn with this situation. Studies have shown marked similarities in the way statisticians decide which model to use and how clinicians diagnose a patient [13], as such applications of argumentation for clinical decision support are of particular relevance to our work.
EIRA (Explaining, Inferencing, and Reasoning about Anomalies) is an argumentation-based clinical decision support system designed to flag anomalies in patients’ reactions to medication within the Intensive Care Unit [11,12]. Grando et al. describe EIRA as a hypothesis generation tool that leverages Argumentation Schemes and Dung’s argumentation frameworks. Similarly to our preference for a methodology that was extensible, EIRA also separates domain and process knowledge. Furthermore Grando et al. emphasize the importance of providing feedback to the end user, this has also been a consideration for our work. EIRA differs from the approach proposed herein with regards to the use of critical questions. Our approach relies on critical questions, and it also differs from EIRA is our use of EAF [20] to reason with and consider preferences.
A further example of the use of argumentation schemes and knowledge bases in support of clinical decision support is provided by Atkinson et al. The DRAMA agent (Deliberative Reasoning with Arguments about Actions) is the system that is proposed by Atkinson et al. [3] to decide the best treatment for a patient, through the use of Argumentation Schemes and multiple knowledge bases. The DRAMA agent makes use of a value in order to resolve the argumentation framework and decide on the recommended treatment. The use of value within the context of statistical model selection is not a suitable approach, as there is no measure of value that would promote the most suitable model in all cases. The DRAMA agent reasons with the arguments instantiated using the argument schemes and knowledge bases in an Argumentation Framework [7] and reason with values promoted by employing Value Based Argumentation Frameworks [4] whilst in our case we employ EAFs.
Another decision support system that leverages argumentation is in organ transplant allocation mechanisms. There is a known shortage of viable organs, therefore the allocation process needs to be as efficient as possible. In their papers [27,28] Tolchinsky et al. describe the CARREL and CARREL+ systems. In CARREL+ argumentation involves multiple agents; a parallel can be made with statistical model selection where the argumentation schemes are instantiated by involving both the end user and the data. Similarly one of the objectives of CARREL is to ensure that all options are explored; within statistical model selection this is also a relevant aspect, as there is a need to ensure all possible modeling approaches are considered. In the methodology proposed herein this is achieved through the appropriate critical question. In contrast to the system proposed herein, CARREL+ involves the deliberation and point of view of multiple agents.
A related challenge in the clinical domain is reasoning with all the available evidence on treatment outcomes. In [14] Hunter et al. propose an approach that uses argumentation, specifically Preference Argumentation Frameworks (PAF) [1] to reason with the evidence and use preferences to take into account the relative benefits of the treatments being considered. Similarly to our approach [14] deals with representing knowledge on treatment outcomes and benefits into argumentation, whilst in our case the knowledge is from statistical theory. Our approach leverages EAFs whilst [14] use PAFs.
Automation of model selection has recently been central to the “Automatic Statistician” project [16] where a different approach to automation of model selection is proposed, compared to the work articulated herein. The approach and type of analysis tackled by the “Automatic Statistician” is different from the one this paper is focusing on. Lloyd et al. [16] focus on time series data and on analysis that is totally independent of any end user interaction, as the approach taken is to explore all the possible model options before selecting the model that best fits the data. The approach proposed in this paper assumes that transparency and interaction with the end user will provide confidence in the model recommendations made. Our approach focuses on recommending the most suitable models in a given situation and as such the end user will not need to apply all the models that could be applicable to their analysis and data.
The evaluation of methodologies and prototypes leveraging argumentation for clinical decision support has been through case studies and user studies. ArguEIRA [12] was evaluated by clinicians assessing the tool’s output, CARREL [28] was similarly evaluated on a set of examples as well as DRAMA [2,3] where examples were also used to ensure the proposed argument scheme and knowledge base were comprehensive enough. The initial evaluation approach we took is similar in nature as it is initially case study based.
6.Conclusion and future work
This paper reports on an application of argumentation theory to the analysis of clinical data. Our contributions presented in this paper are a formalisation of the argument scheme and its associated critical questions for this domain, and an extended knowledge base containing preference orders for the models that enable the instantiation of an Extended Argumentation Framework (EAF). We also present an implementation of these formalisations in Z notation. These elements offer a novel approach to supporting the automation of the process of statistical model selection. The application of the method we have proposed herein supports an end user by suggesting the recommended statistical model to use given their specific research question and the data available.
Our application of EAFs as well as the formalisation of the argument schemes in Z notation sets this work apart from all the work cited. Our approach provides an example of an application of argumentation and preferences with a prototype application in the clinical domain. The use of Z notation to bridge the gap between the definitions and the implementation has enabled all of the specifications required of the system to be articulated, furthermore the strength of Z notation as a step between definitions and implementation has enabled the introduction of variables to account for potential errors. The advantage of using EAFs is their support for reasoning that leverages different sets of preferences through their representation as meta level arguments. This enables the reasoning to argue at the preference as well as the argument level. In future work we will investigate the benefit of exploring a meta-level argumentation representation [21].
The initial steps in evaluation of the method proposed herein were achieved through the use of case studies from the clinical domain, one of which is articulated in this paper. There is a requirement for further evaluation through user studies. The first of which will assess whether the outlined method will provide the same recommended model and justification when compared to what a statistician would recommend based on the same data, research question and available models. This will then be followed up by a user study where the prototype will be used by clinicians. The latter would enable us to ascertain whether this is usable and acceptable to the end user. A further aspect we will be researching is how to best present the results of the EAF to the end user. These evaluation steps are ongoing work to be reported in future publications, more detailed plans are outlined in [22].
Acknowledgements
The authors would like to thank Professor Mark McGurk for supporting this research. The research is also partially supported by CONSULT EPSRC grant no. EP-P010105-1.
References
[1] | L. Amgoud and C. Cayrol, A reasoning model based on the production of acceptable arguments, Annals of Mathematics and Artificial Intelligence 34: (1–3) ((2002) ), 197–215. |
[2] | K. Atkinson, What should we do?: Computational representation of persuasive argument in practical reasoning, PhD Thesis, University of Liverpool, 2005. |
[3] | K. Atkinson, T.J.M. Bench-Capon and S. Modgil, Argumentation for decision support, in: DEXA, S. Bressan, J. Küng and R. Wagner, eds, Lecture Notes in Computer Science, Vol. 4080: , Springer, (2006) , pp. 822–831. |
[4] | T. Bench Capon, Persuasion on practical argument using value based argumentation frameworks, Journal of Logic and Computation 13: (3) ((2003) ), 429–448. doi:10.1093/logcom/13.3.429. |
[5] | D.R. Cox, Regression models and life-tables, Journal of the Royal Statistics Society, Series B 34: ((1972) ), 187–220. |
[6] | M. d’Inverno, M. Luck, M. Georgeff, D. Kinny and M. Wooldridge, The dMARS architecture: A specification of the distributed multi-agent reasoning system, Autonomous Agents and Multi-Agent Systems 9: (1–2) ((2004) ), 5–53. doi:10.1023/B:AGNT.0000019688.11109.19. |
[7] | P.M. Dung, On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games, Artificial Intelligence 77: (2) ((1995) ), 321–358. doi:10.1016/0004-3702(94)00041-X. |
[8] | J.H. Edmonson, T.R. Fleming, D. Decker, G. Malkasian, E. Jorgensen, J. Jefferies, M. Webb and L. Kvols, Different chemotherapeutic sensitivities and host factors affecting prognosis in advanced ovarian carcinoma versus minimal residual disease, Cancer treatment reports 63: (2) ((1979) ), 241–247. |
[9] | J. Fox, D. Glasspool, D. Grecu, S. Modgil, M. South and V. Patkar, Argumentation-based inference and decision making—A medical perspective, IEEE intelligent systems 22: (6) ((2007) ). doi:10.1109/MIS.2007.102. |
[10] | J. Fox, N. Johns, C. Lyons, A. Rahmanzadeh, R. Thomson and P. Wilson, Proforma: A general technology for clinical decision support systems, Computer methods and programs in biomedicine 54: (1) ((1997) ), 59–67. doi:10.1016/S0169-2607(97)00034-5. |
[11] | M.A. Grando, L. Moss, D. Glasspool, D.H. Sleeman, M. Sim, C.J. Gilhooly and J. Kinsella, Argumentation-logic for explaining anomalous patient responses to treatments, in: Artificial Intelligence in Medicine, M. Peleg, N. Lavrac and C. Combi, eds, Lecture Notes in Computer Science, Vol. 6747: , Springer, (2011) , pp. 35–44. doi:10.1007/978-3-642-22218-4_5. |
[12] | M.A. Grando, L. Moss, D.H. Sleeman and J. Kinsella, Argumentation-logic for creating and explaining medical hypotheses, Artificial Intelligence in Medicine 58: (1) ((2013) ), 1–13. doi:10.1016/j.artmed.2013.02.003. |
[13] | D.J. Hand, Statistical expert systems: Design, The Statistician ((1984) ), 351–369. doi:10.2307/2987739. |
[14] | A. Hunter and M. Williams, Aggregating evidence about the positive and negative effects of treatments, Artificial intelligence in medicine 56: (3) ((2012) ), 173–190. doi:10.1016/j.artmed.2012.09.004. |
[15] | E.L. Kaplan and P. Meier, Nonparametric estimation from incomplete observations, Journal of the American Statistical Association 53: (282) ((1958) ), 457–481. doi:10.1080/01621459.1958.10501452. |
[16] | J.R. Lloyd, D.K. Duvenaud, R.B. Grosse, J.B. Tenenbaum and Z. Ghahramani, Automatic construction and natural-language description of nonparametric regression models, CoRR (2014), abs/1402.4304. |
[17] | M. Luck and M. d’Inverno, A conceptual framework for agent definition and development, The Computer Journal 44: (1) ((2001) ), 1–20. doi:10.1093/comjnl/44.1.1. |
[18] | P. McBurney, What are models for? in: Proceedings of the 9th European Conference on Multi-Agent Systems, EUMAS’11, Springer-Verlag, Berlin, Heidelberg, (2012) , pp. 175–188. doi:10.1007/978-3-642-34799-3_12. |
[19] | T. Miller and P. McBurney, Multi-agent system specification using TCOZ, in: German Conference on Multiagent System Technologies, Springer, (2005) , pp. 216–221. doi:10.1007/11550648_20. |
[20] | S. Modgil, Reasoning about preferences in argumentation frameworks, Artificial Intelligence 173: (9–10) ((2009) ), 901–934. doi:10.1016/j.artint.2009.02.001. |
[21] | S. Modgil and T. Bench-Capon, Metalevel argumentation, Journal of Logic and Computation 2010: ((2010) ). |
[22] | I. Sassoon, Argumentation for statistical model selection, PhD Thesis, King’s College London, 2017. |
[23] | I. Sassoon, J. Keppens and P. McBurney, Towards argumentation for statistical model selection, in: Fifth International Conference on Computational Models of Argument, IOS Press, (2014) , pp. 67–74. |
[24] | I. Sassoon, J. Keppens and P. McBurney, Preferences in argumentation for statistical model selection, in: Sixth International Conference on Computational Models of Argument, IOS Press, (2016) , pp. 53–60. |
[25] | G. Shmueli, To explain or to predict?, Statistical Science 25: (3) ((2010) ), 289–310. doi:10.1214/10-STS330. |
[26] | J.M. Spivey and J. Abrial, The Z Notation, Prentice Hall, Hemel Hempstead, (1992) . |
[27] | P. Tolchinsky, U. Cortés, S. Modgil, F. Caballero and A. López-Navidad, Increasing human-organ transplant availability: Argumentation-based agent deliberation, IEEE Intelligent Systems 21: (6) ((2006) ), 30–37. doi:10.1109/MIS.2006.116. |
[28] | P. Tolchinsky, S. Modgil, K. Atkinson, P. McBurney and U. Cortés, Deliberation dialogues for reasoning about safety critical actions, Autonomous Agents and Multi-Agent Systems 25: (2) ((2012) ), 209–259. doi:10.1007/s10458-011-9174-5. |
[29] | W. Weibull, Wide applicability, Journal of Applied Mechanics ((1951) ). |
[30] | S. Zillessen, Small data analyst, MSc Thesis, King’s College, London, 2016. |



