Comparing decoding mechanisms for parsing argumentative structures
Abstract
Parsing of argumentative structures has become a very active line of research in recent years. Like discourse parsing or any other natural language task that requires prediction of linguistic structures, most approaches choose to learn a local model and then perform global decoding over the local probability distributions, often imposing constraints that are specific to the task at hand. Specifically for argumentation parsing, two decoding approaches have been recently proposed: Minimum Spanning Trees (MST) and Integer Linear Programming (ILP), following similar trends in discourse parsing. In contrast to discourse parsing though, where trees are not always used as underlying annotation schemes, argumentation structures so far have always been represented with trees. Using the ‘argumentative microtext corpus’ [in: Argumentation and Reasoned Action: Proceedings of the 1st European Conference on Argumentation, Lisbon 2015 / Vol. 2, College Publications, London, 2016, pp. 801–815] as underlying data and replicating three different decoding mechanisms, in this paper we propose a novel ILP decoder and an extension to our earlier MST work, and then thoroughly compare the approaches. The result is that our new decoder outperforms related work in important respects, and that in general, ILP and MST yield very similar performance.
1.Introduction
In recent years, automatic argumentation mining in natural language text has become a very active line of research in natural language processing (NLP). For a long time, finding opinions was a very popular task, which primarily involves detecting the target and the polarity of opinions, for instance in product reviews. Example: “We highly enjoyed [opinion: positive] this book [target].” Being able to extract this information from review web sites or from social media contributions turned out both commercially relevant and interesting from the research perspective. Now, one extension of this idea is to also look for the reasons that customers provide for their opinions, as in: “We highly enjoyed this book. It is so awfully well-written.” This extension of opinion mining is one prominent application of argumentation mining, but there are various others, such as identifying justifications in legal documents, or uncovering the structure of argumentative essays for the purpose of providing feedback to students.
In its full-fledged form, the argumentation mining problem involves the following subtasks:
identifying argumentative (portions of) text,
detecting central claims (theses),
detecting supporting and objecting (attacking) statements, and
establishing relations among all those statements.
Most of the work in argumentation mining, however, so far addresses only some of those subtasks, for instance the identification of claims and supporting statements, which for many practical applications is already sufficient. Consider our example of product reviews, where it is already quite valuable if the opinionated statement (i.e., the claim) and the reasons (i.e., the supporting statements) can be identified.
On the other hand, for more ambitious purposes it is necessary to target the more comprehensive problem of actually constructing a structural representation of the full argument. To achieve this, early computational approaches opted for implementing a pipeline architecture [6,17, inter alia] that uses a series of modules, with each being responsible for one subtask and passing their intermediate result onward to the next module. For instance, one module early in the pipeline might try to classify the stance taken in the text: is the attitude toward the topical issue positive or negative? Using this information, the subsequent claim detection module might look specifically for a pro or con claim statement in the text; and so forth.
This approach, while conceptually simple and straightforward to implement, suffers from two problems: First, errors made by an early module are propagated to the subsequent ones, and can essentially not be corrected anymore, which can lead to overall low performance. Second, in a pipeline of autonomous modules, it is quite difficult to coordinate the individual analysis decisions in such a way that global structural constraints on the overall result (such as well-formedness conditions on a tree or graph representing the argumentation) are being met.
In response, more recent approaches adopted the computational perspective of global optimization, where subtasks are not solved individually and sequentially but can inform each other about potential output variants. A popular approach is a so-called global decoding over local probability distributions: The probabilities for certain local decisions (what is the argumentative role of a text segment, what is the probability that two argumentative units are connected, and so on) are computed by individual modules, and then an optimization step finds the overall best (i.e., most probable) well-formed solution. This move to more structured output prediction naturally responds to the error propagation problems, and it mirrors activities in related NLP tasks such as discourse parsing,11 an area that argumentation parsing shares many commonalities with. Technically, most current approaches follow what [26] categorizes under polytope decoding, and more specifically Integer Linear Programming (ILP) [25,28]; or decoding using specialized graph algorithms, in particular Minimum Spanning Trees (MST) [22]. More sophisticated approaches involving structured output prediction with a logistic or hinge loss have not been proposed for argumentation yet, mainly due to the lack of an appropriate cost function,22 although recently [19] have used the AD3 algorithm from [15] in order to predict argumentation structures that are directed acyclic graphs (henceforth DAGs) and not trees. This lack of more structured output prediction approaches is also due to the fact that the community lacks a common relational modeling of argumentation as well as adequate amounts of annotated data.
MST and ILP decoding mechanisms both have been proposed in discourse parsing, too [1,13,24], where ILP has been used as decoder only for DAG structures [24] while MST has only been used for tree structures [13]. In argumentation mining, both approaches have been employed for predicting tree structures.
So far, no conclusive results have been obtained as to which of the two decoding approaches is better-suited for the (full) argumentation mining task. In this paper, we report on experiments that show that ILP does not have any per se advantage over the MST approach. Hence, for predicting tree structures, employing ILP as decoding should essentially emulate a minimum spanning tree approach, unless constraints that are not limited to structural properties of the output object are coded into the ILP constraints. In order to show this, we use for both approaches the same local model learned from a dataset that has commonly been used in the community. For a fair comparison of the optimization approaches, we first replicate the MST decoder from [22] and the ILP decoders from [25] and from [28], which all are known to produce competitive results for the tree prediction task on this dataset. Furthermore, as additional contributions of this paper, we provide an improved version of the MST-decoding ‘evidence graph’ model of [22], as well as a new ILP decoder, which for most configurations outperforms earlier approaches using ILP. Accordingly, our results in almost all respects improve on the earlier ones and thus can be considered state of the art for these types of approaches.
The paper is structured as follows: In Section 2, we present the schema that forms the basis for our annotation of argumentation structure, and we introduce the corresponding dataset. Section 3 explains how we have transformed our data into dependency structures, and describes our local models for the various argumentation mining subtasks. These models provide the local common input to all the decoders, which are presented in Section 4. Experiments and results are presented in Section 5. Finally, Section 6 discusses related work, and Section 7 concludes the paper.
2.Argumentative structures and data
Our annotation of argumentation structure follows the scheme outlined in [21], which in turn is based on the work of [7]. The building blocks of such an analysis are Argumentative Discourse Units (ADUs): text segments that play an argumentative role.33 Hence the initial step of an analysis is to demarcate ADU boundaries in the text; for the purposes of this paper, we do not implement this step but assume it as already given (and our various parsers will all start from the same segmentation).
The annotation scheme posits that every ADU be labeled with a “voice”, which is either the “proponent” of the argument or the imaginary “opponent”. Each text is supposed to have a central claim (henceforth: CC), which the author can back up with statements that are in a Support relation to it. This relation can be used recursively, which leads to “serial support” in Freeman’s terms. A statement can also have multiple immediate Supports; these can be independent (each Support works on its own) or linked (only the combination of two statements provides the Support). The CC as well as all the Support statements bear the “proponent’s” voice: The author of the text is putting forward his or her position.
When the text mentions a potential objection, this segment is labeled as bearing the role of “opponent’s voice”; this goes back to Freeman’s insight that any argumentation contrasts the author’s view with that of an imagined opponent. The segment will be in an Attack relation to another one of the proponent’s voice; the scheme distinguishes between “rebut” (attack the validity of a statement) and “undercut” (attack the relevance of a premise for a conclusion). In turn, the proponent can then use a segment to counter-attack the proponent’s objection.
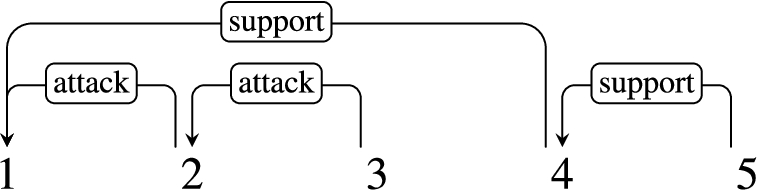
For illustration, below we give a sample text from the corpus we use (see next Section), and its analysis is shown in Fig. 1. Proponent ADUs are in circle nodes, the opponent’s ADU 2 appears in a box. An arrowhead denotes Support, a bullet or square-head denotes Attack. In our example the CC presented in ADU 1 is attacked by ADU 2, an instance of Rebut. This relation is then undercut by ADU 3. Finally, ADUs 4 and 5 provide a linked Support for the CC 1.
Fig. 1.
Argumentation structure of the example text.
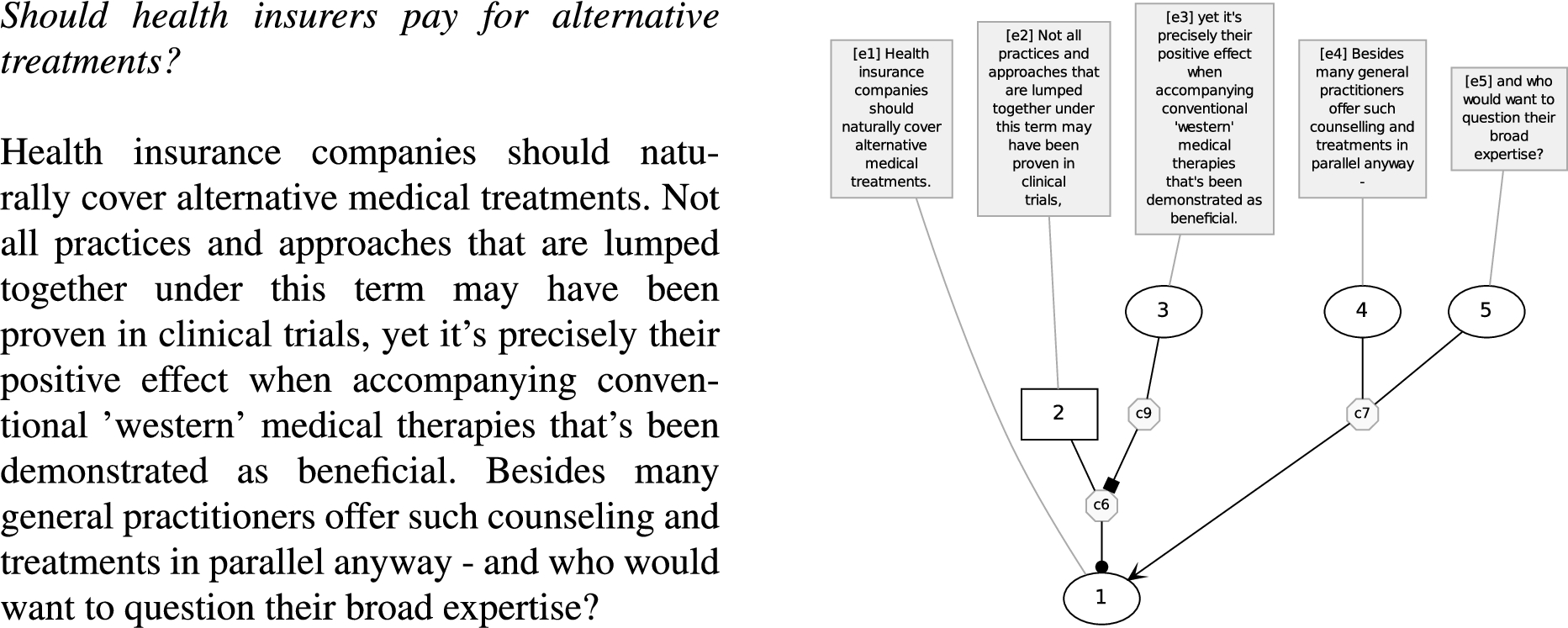
The dataset we are targeting is the ‘Argumentative Microtext Corpus’ [23]. It consists of 112 short texts originally written in German by students in response to a trigger question. These questions concern issues of public debate, such as whether all citizens should pay fees for public broadcasting, or whether health insurance should cover alternative medical treatments. The texts consist of five to six sentences; writers have been asked to state their position, back it up with arguments, and if possible also mention a potential objection to the position. All texts have been professionally translated to English, and have been annotated according to the scheme previously explained (cf. the example in Fig. 1).
The annotation process (described in detail in [23]) was based on written guidelines, which are available from the corpus website.44 The process began with experiments on inter-annotator agreement, to verify that the scheme is used consistently by different annotators. It has been found that on the basis of brief guidelines (eight pages), three trained annotators achieved an agreement of Fleiss
In automatic argumentation mining, fine-grained distinctions such as those between linked support/normal support and between rebut/undercut are usually not accounted for. In order to facilitate comparison to the related work, for the experiments reported below we thus use a “coarse-grained” version of the annotations, which reduces the aformentioned pairs to just Support and Attack, respectively.
Notice that in the dataset, the argumentation covers the text completely; i.e., there are no text segments that do not belong to an ADU. For the parser this implies that each text segment has to be mapped to a node in the graph. In the 112 texts, there are 579 argumentative units, of which 454 (78%) are in the “proponent’s voice”, and 125 (22%) in the “opponent’s voice”. Of the 464 relations, 286 (62%) are Support, and 178 (38%) are Attack.
3.Underlying model
Assigning the argumentation structure to a microtext involves the tasks of segmentation into ADUs, assigning voice to each ADU, and determining its relation to other ADUs. For our present purposes, we leave out the segmentation task and thus assume pre-segmented texts. In order to perform structured output prediction for this problem, ideally one would like to learn a model
Note that we do not directly make a classifier out of this model. In other words, we do not try to directly extract relations from the above model by searching for a threshold that will have optimal local results. Had we done so, we might have had good enough local results, but the global structure resulting from simply concatenating the relations predicted by a local classifier would not necessarily be well-formed: There is no guarantee that the resulting structure would be a cycle-free single connected component, as required by our data. Instead, we thus use the probability distribution that this model yields as input to a decoder that tries to globally optimize the argumentation structure.
3.1.Local models
For our experiments and in line with those of [22], we use the dependency conversion of the microtext corpus with the coarse-grained relations of Support and Attack: The graphs have first been converted to dependency trees by serializing more complex configurations such as Undercuts or linked relations, a proceedure which is reversible for our graphs. The set of relations is then reduced to Support and Attack, a lossy transformation. For more details and a motivation for this conversion, we refer the interested reader to [22,30]. Figure 2 illustrates the dependency graph for the argumentation structure of the example text shown in Fig. 1.
[22] proposed the following four subtasks for predicting the argumentation structures:
attachment (at): Given a pair of ADUs, are they connected? [yes, no]
central claim (cc): Given an ADU, is it the central claim of the text? [yes, no]
role (ro): Given an ADU, is it in the [proponent]’s or the [opponent]’s voice?
function (fu): Given an ADU, what is its argumentative function? [support, attack or none]
We reproduced this approach and trained a log-loss SGD classifier for each of these tasks. Note that relation labels are classified using only the source segment. We also reimplemented their feature set, which consists of lemma uni- and bigrams, the first three lemmata of each segment, POS-tags, lemma- and POS-tag-based dependency parse triples, discourse connectives, main verb of the sentence, and all verbs in the segments, absolute and relative segment position, length and punctuation counts, linear order and distance between segment pairs. Note that most of these features are also applied to the left and right context of the segment of interest.
For the syntactic analysis, we use the spacy parser [9] (instead of the Mate parser [3] that was originally employed by [22]). Both parsers provide pre-trained models for English and German. The spacy parser comes with Brown-clusters and vector-space representations, which we want to test in addition to the features proposed in the earlier work. We also extended the underlying list of English discourse connectives with the connectives collected in the EDUCE project.55
New features. In addition to the reimplemented feature set, we test the impact of the following new features: We add Brown cluster unigrams (BC) and bigrams (BC2) of words occurring in the segment. We completed the discourse relations features (DR): While the lexicon of discourse connectives for German used in experiments of [22] was annotated with potentially signaled discourse relations, their English lexicon was lacking this information. We extended the English connective lexicon by those collected by EDUCE which also have been annotated with signaled discourse relations. Also, a feature representing the main verb of the segment was added (VS); the already existing verb features either focused on the verb of the whole sentence which might be too restrictive, or on all possible verbal forms in the segment which might not be restrictive enough. Furthermore, we added features for better capturing the inter-sentential structure, i.e. for relations with subordinate clauses: One feature representing that the source and target segments are part of the same sentence (SS) and one representing that the target is the matrix clause of the source (MC).
In order to investigate the impact of word embeddings for this task, we add the 300-dimensional word-vector representations provided by the spacy parser, averaged over all content words of the segment, as a feature for segment wise classifiers (VEC). Moreover, we derive scores of semantic distance between two segments using these vectors: We measure the cosine distance between the average word vector representations of the segment and its left and right antecedents (VLR). Also, for the attachment classifier, we measure the cosine distance between the average word vectors of the source and target segment (VST). Table 1 provides a summary of the all aforementioned features.
Table 1
Summary of the features. The last column provides a short reference for each feature. Those marked with (base) are our reimplementation of the features of [22] and serve as a baseline. For all other features a short acronym is given. These will be tested separately in a feature study, see Section 5.2.
| Category | Description | Reference |
| Positional | absolute and relative segment position | (base) |
| linear order and distance between segment pairs | (base) | |
| source and target are in same sentence | (SS) | |
| Lexical | lemma uni- and bigrams | (base) |
| first three lemmata of each segment | (base) | |
| POS-tags | (base) | |
| length and punctuation counts | (base) | |
| Syntactic | lemma- and POS-tag-based dependency parse triples | (base) |
| main verb of the sentence | (base) | |
| all verbs in the segment | (base) | |
| main verb in the segment | (VS) | |
| target is the matrix clause of the source | (MC) | |
| Semantic | Brown cluster unigrams | (BC) |
| Brown cluster bigrams | (BC2) | |
| vector-space representation of the segment (averaged word embeddings) | (VEC) | |
| vector-space distance between left and right antecedents | (VLR) | |
| vector-space distance between source and target | (VST) | |
| Discourse | discourse connectives | (base) |
| discourse relations signalled by connectives | (DR) |
4.Decoders
4.1.MST decoder
In a classic MST decoding scenario, one uses a matrix
4.2.ILP decoders
Integer Linear Programming (ILP) can also be used as another decoder. In ILP one needs to provide an objective function which needs to be maximized under specific constraints. The objective function is a combination of linear equations of n variables each of which should take integer values. In the general case solving an ILP problem is NP-hard but efficient implementations are capable of producing very good approximations of the solution in an amount of time provided by the user.
4.2.1.Novel ILP decoder
Objective function. Using as input the same local model as before, we try to construct a DAG
We define different sets of constraints and will investigate different combinations, in order to evaluate the individual impact of each set.
Tree constraints on the attachment predictions (tree). The predicted graphs are trees: All nodes have one or no outgoing arc (1) and as many arcs as nodes, except for the root node (2). Also, to rule out cycles, we introduce an auxiliary set of integer variables
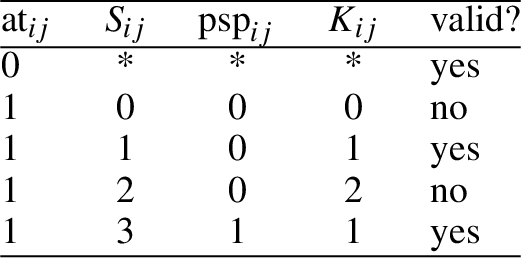
Relation labelling through function predictions (label). The constraints above only yield an unlabelled tree. We want to use the prediction of the function classifier and assign one argumentative function to every node (5). Furthermore, we only want to predict Support or Attack as relation label, since the central claim function is not a relation label, and the decoded tree might have another root than the segment predicted to have the function central claim (6).
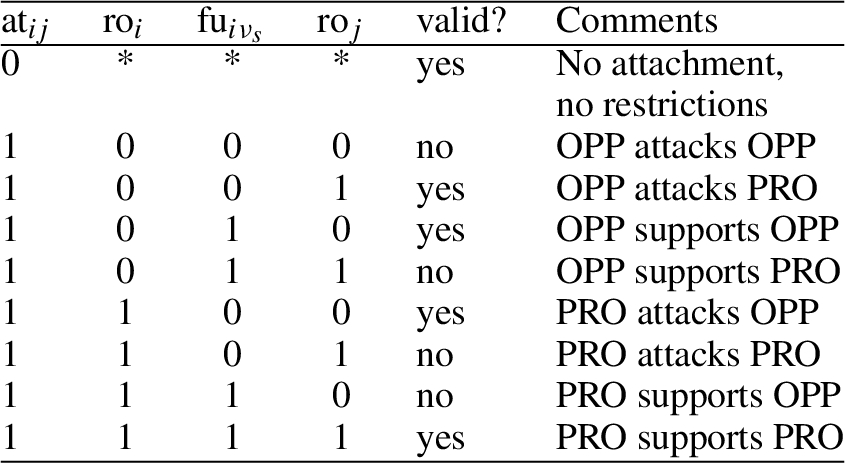
Interaction between central claim and attachment (cc-at). Turning to the predictions on the other levels, we first integrate the predictions of the designated CC classifier, and describe the relation between the identified CC and the root of the attachment tree. Only one central claim may be chosen (7). Secondly, all vertices have exactly one outgoing edge with the exception of the central claim, which is a sink node (8): If
Interaction between central claim and role (ro-cc). Integrating the predictions of the role classifier gives the requirement that the central claim must be a proponent node (9). This bans the case
Interaction between role and function (ro-fu). The following constraint represents the intuition that every argumentative role (proponent or opponent) will only support itself, not the other; and only attack the other, not itself. Hence, supporting relations are role-preserving, and attacking relations are role inverting. Consider an edge from
We now define

We introduce a set of auxiliary variables
If
If
4.2.2.ILP approach by Stab/Gurevych [28]
Stab and Gurevych [28] primarily work on a corpus of persuasive essays but also report results on the argumentative microtext corpus mentioned above, also using ILP. They strip the original argumentative graphs from their roles supporting only central claims, claims and premises and build local classifiers for argumentative relations and detection of argument components. They do not use structured output prediction but create matrices representing the local classification results. These matrices are linearly combined with another matrix derived from a combination of incoming and outgoing links on the non-decoded graph, thus providing a new matrix which is used to maximize their objective function. Constraints guarantee a rooted tree without cycles. We replicated their work using probability distributions from our local models as input; below, we refer to this decoder as repl. ILP S&G.
4.2.3.ILP approach by Persing/Ng [25]
Persing and Ng [25] work on the corpus by [27], which contains 90 essays, essentially using the same annotation scheme as the data that we use here. In contrast to our ILP approach, Persing/Ng [25] use an objective function that maximizes the average score over two probability distributions representing the types of argumentative components (major claim, claim, premise or none) as well as the relation type between two argumentative components (Support, Attack or no relation). They achieve that by estimating the expected values of TP, FP and FN values from the results of the two classifiers. Their constraints pertain to major claims (exactly one, in the first paragraph, no parents), premises (at least one parent from the same paragraph), claims (at most one parent which should be a major claim). Other constraints ask for at most two argumentative components per sentence, etc. We replicated their objective function and constraints using probability distributions from our local models as input. In a variant, we used their objective function but our own set of constraints. The results are shown in Table 3 as repl. ILP P&N and new ILP objective 2, respectively.
5.Experiments and results
5.1.Evaluation procedure
In our experiments, we follow the setup of [22]. We use the same train-test splits, resulting from 10 iterations of 5-fold cross validation, and adopt their evaluation procedure, where the correctness of predicted structures is assessed separately for the four subtasks, reported as macro averaged F1.
While these four scores cover important aspects of the structures, it would be nice to have a unified, summarizing metric for evaluating the decoded argumentation structures. To our knowledge, no such metric has yet been proposed, prior work just averaged over the different evaluation levels. Here, we will additionally report labelled attachment score (LAS) as a measure that combines attachment and the argumentative function labelling, as it is commonly used in dependency parsing. Note however, that this metric is not specifically sensitive for the importance of selecting the right central claim and also not sensitive for the dialectical dimension (choosing just one incorrect argumentative function might render the argumentative role assignment for the whole argumentative thread wrong).
For significance testing, we apply the Wilcoxon signed-rank test on the series of scores from the 50 train-test splits and assume a significance level of
5.2.Local models
Table 2
Evaluation scores for the local models, the base classifiers, reported as macro avg. F1. The first two rows report on earlier results. Against this we compare the new classifiers using the new linguistic pipeline (base), followed by a feature study showing the impact of adding the new features (described in Section 3.1). Finally, we show the results of the final classifiers combining these features.
| English | German | |||||||
| model | cc | ro | fu | at | cc | ro | fu | at |
| [22] | 0.817 | 0.750 | 0.671 | 0.663 | 0.849 | 0.755 | 0.703 | 0.679 |
| [28] | 0.830 | 0.745 | 0.650 | |||||
| base | 0.832 | 0.762 | 0.710 | 0.690 | 0.827 | 0.757 | 0.709 | 0.696 |
| base + BC | +0.008 | −0.005 | +0.001 | +0.004 | +0.008 | +0.005 | −0.001 | −0.003 |
| base + BC2 | −0.003 | −0.002 | +0.001 | −0.001 | +0.003 | −0.001 | ||
| base + DR | +0.005 | +0.018 | +0.019 | +0.003 | +0.002 | −0.002 | −0.001 | |
| base + VS | −0.001 | −0.002 | −0.001 | +0.002 | +0.001 | +0.001 | −0.001 | |
| base + VEC | −0.002 | −0.002 | −0.002 | +0.001 | +0.004 | −0.003 | +0.002 | +0.002 |
| base + VLR | −0.002 | +0.001 | −0.001 | +0.001 | −0.002 | |||
| base + VST | −0.001 | |||||||
| base + SS | +0.009 | +0.009 | ||||||
| base + MC | +0.012 | +0.016 | ||||||
| all − VEC | 0.840 | 0.782 | 0.723 | 0.711 | 0.837 | 0.765 | 0.709 | 0.711 |
| all | 0.840 | 0.780 | 0.724 | 0.710 | 0.836 | 0.762 | 0.712 | 0.711 |
The results of the experiment with the local models are shown in Table 2. We first repeat the reported results of [22] and [28] for comparison. Below is our re-implementation of the classifiers of [22] (base), followed a feature analysis where we report on the impact of adding each new feature to the replicated baseline, reported as the delta.
Our replication of the baseline features (base) already provides a substantial improvement on all levels for the English version of the dataset. We attribute this mainly to the better performance of spacy in parsing English. For German, the results are competitive. Only for central claim identification our replicated local models do not fully match the original model, which might be due to the fact that the spacy parser does not offer a morphological analysis as deep as the mate parser and thus does not derive predictions for sentence mood.
Investigating the impact of the new features, the highest gain is achieved by adding the features for subordinate clauses (SS and MC) to the attachment classifier. Brown cluster unigrams give a moderate boost for central claim identification. Interestingly, the word-vector representation did not have a significant impact. The averaged word embeddings themselves (VEC) lowered the scores minimally for English and improved the results minimally for German, but increased the training time considerably.66 The distance measures based on word vectors (VST and VLR) yielded no improvement likewise.
Taking all features together, excluding only the time-costly word embeddings (all − VEC), provides us with local models that achieve state of the art performance on all levels but fu for English and cc for German. We use this set of classifiers as the local models in all decoding experiments.
Table 3
Evaluation scores for the global models, the decoders, reported as macro avg. F1 for the cc, ro, fu, and at levels, and as labelled attachment score (LAS). The first two rows report on earlier results. In the following block of rows, we present the novel ILP decoder model with different sets of constraints used: The first only produces labelled trees without exploiting interactions. We then report on the impact of adding the interaction constraints. In the final row block, we report on our replication of related approaches and on the evidence graph model serving as a baseline.
| English | German | |||||||||
| model | cc | ro | fu | at | LAS | cc | ro | fu | at | LAS |
| [22] (EG-equal) | 0.860 | 0.721 | 0.707 | 0.692 | 0.481 | 0.879 | 0.737 | 0.735 | 0.712 | 0.508 |
| [28] | 0.857 | 0.745 | 0.683 | |||||||
| new ILP (no interaction, just labelled trees) | 0.844 | 0.689 | 0.733 | 0.715 | 0.494 | 0.858 | 0.656 | 0.719 | 0.722 | 0.490 |
| new ILP (cc-at) | 0.870 | 0.699 | 0.752 | 0.716 | 0.502 | 0.865 | 0.651 | 0.725 | 0.722 | 0.493 |
| new ILP (ro-cc) | 0.844 | 0.689 | 0.733 | 0.715 | 0.494 | 0.858 | 0.656 | 0.719 | 0.722 | 0.490 |
| new ILP (ro-fu) | 0.846 | 0.770 | 0.742 | 0.718 | 0.516 | 0.852 | 0.745 | 0.726 | 0.729 | 0.517 |
| new ILP (cc-at + ro-cc) | 0.870 | 0.701 | 0.752 | 0.716 | 0.503 | 0.872 | 0.654 | 0.730 | 0.724 | 0.497 |
| new ILP (cc-at + ro-cc + ro-fu) | 0.862 | 0.783 | 0.750 | 0.720 | 0.524 | 0.870 | 0.753 | 0.740 | 0.733 | 0.528 |
| new ILP (cc-at + ro-cc + ro-fu) objective 2 | 0.866 | 0.782 | 0.753 | 0.722 | 0.526 | 0.867 | 0.756 | 0.739 | 0.733 | 0.529 |
| repl. ILP S&G | 0.837 | 0.673 | 0.727 | 0.687 | 0.456 | 0.834 | 0.654 | 0.704 | 0.690 | 0.451 |
| repl. ILP P&N | 0.869 | 0.699 | 0.751 | 0.716 | 0.502 | 0.866 | 0.653 | 0.726 | 0.723 | 0.494 |
| new EG equal | 0.876 | 0.766 | 0.757 | 0.722 | 0.529 | 0.861 | 0.730 | 0.725 | 0.731 | 0.523 |
5.3.Global model
The results of the experiments with the decoders are shown in Table 3. Consider first the novel ILP decoder and the impact of adding the different constraint sets to the baseline, which just predicts labelled trees without exploiting any interaction. Adding the cc-at interaction constraints yields an improvement on the CC and function level. The ro-cc interaction does not increase the scores on its own, but it helps a little when combined with the cc-at interaction constraint set. A strong improvement in role classification and a smaller one in function classification is achieved by adding the ro-fu interaction. The full constraint set with all three interactions yields the best novel ILP decoder model. Changing our objective function against that of [25] (objective 2) does not significantly affect the results.
When we compare the replicated decoders (repl ILP S&G) and (repl ILP P&N) against our novel ILP decoder, we observe that they perform worse by nearly 10 points F1 in role classification. This is to some degree expected, as these approaches do not involve a role classifier and thus cannot exploit interactions involving that level. The novel ILP decoder, however, also yields better results in attachment and (for German) in function classification. The results of (repl ILP P&N) are nearly equal to that of new ILP (cc-at): This is expected, as their constraints are very similar, and the special objective function of P& N has been shown to not have a significant effect here. To our surprise, the (repl ILP S&G) performs worse than the labelled tree baseline, although it adds a variant of the cc-at interaction, that the labelled tree baseline does not have.77
While the novel ILP decoder gives the best result of all ILP decoders, the EG model and the new ILP decoder are generally on par, but have different strengths: The EG model is better at CC identification; the new ILP decoder is better at role classification. Both perform equally for attachment. Function classification, on the other hand, varies depending on the language. This is also shown by the LAS metric, where new-EG-equal scores best for English, and the new ILP decoder for German. The differences in cc, ro & fu between both models are all statistically significant. However, they are spread across different levels and partly depend on the modeled language. We therefore cannot conclude that one approach is superior to the other.
Finally, it is worth pointing out that our replication of the MST-based model of [22] for English and the novel ILP decoder for German represent the new state of the art for automatically recognising the argumentation structure in the microtext corpus.
6.Related work
Our work on globally optimizing an argumentation graph started out with the previous results of [22] who learned local models that yield local probability distributions over ADUs, and then perform global decoding using Minimum Spanning Trees (MST). In contrast to this work, we have developed an improved local model which outperforms their local model in every aspect but role identification, and we also built an improved decoding mechanism that employs Integer Linear Programming (ILP) and yields better results for role identification. Two other works that use ILP decoding are that of [28] and [25], which have been re-implemented in this paper.
While these approaches try to globally optimize an argumentation structure via decoding, others have focused more on local elements of argumentation. We mention here [17], who experimented with the classification of sentences into non-/argumentative by using a variety of input documents such as newspapers, parliamentary records and online discussions. Binary classification of sentences into having an argumentative role or not was also the focus of [6]. [12] used boosting in order to classify sentences into non-/argumentative and to further separate argumentative sentence into Support, Oppose and Propose categories. Finally, [16] worked on documents describing legal decisions and used SVMs in order to classify decisions as claims or premises.
7.Conclusions
We presented a comparative study of various structured prediction methods for the extraction of argumentation graphs. The methods we compared are all based on the decoding paradigm [26] where a local model is learned from input data but final decisions are taken upon decoding which imposes structural constraints on the output. We have used two different decoding mechanisms. The first is the classic MST, which has been extensively used in discourse parsing as well [1,8,18], while the second falls under the polytope decoding paradigm and employs ILP in order to impose constraints while maximizing a given objective function. This approach has also been used in discourse parsing in the past [1].
In order to be able to meaningfully compare the various decoding mechanisms, we used the same underlying corpus [23] and the same local model. Specifically, we constructed a new and improved version of the base model presented in [22], which is our first contribution of this paper. We reimplemented three different recent approaches and also presented a novel ILP approach with two variations on the objective function (our second contribution). It turned out that both our novel ILP decoder and the replicated MST decoder yield the best results in comparison to previous approaches, as they exploit all structural interactions. The differences between our ILP and the MST approach are, however, not decisive. They appear to have individual strengths on different levels, but we found no evidence in our experiments to consider one approach to be generally superior to the other, as long as the goal is to predict tree structures.
Both decoding approaches are general enough in order to be able to be used with other corpora. As far as the underlying local model is concerned, if the data are i.i.d., then the local model can be used as is; otherwise a training corpus should be provided in order to be able to have appropriate probability distributions. Regarding the decoders, the only assumption that they make is that the structures that we want to predict are trees, so as long as this is the case there is nothing to change.
In the future we plan to extend these experiments to discourse parsing, using two different theories, namely RST (Rhetorical Structure Theory, [14]) and SDRT (Segmented Discourse Representation Theory, [2]). The first uses tree structures for the representation of discourse while the second uses directed acyclic graphs when converted into dependency structures. Moreover we plan to use other structured prediction methods combining deep neural architectures with structured prediction [11]. Finally we plan to study the interplay between discourse and argumentation, trying to jointly learn both structures using the corpus presented in [30] which contains annotations for both discourse structure and argumentation.
Notes
1 The goal of discourse parsing is to produce a representation of text structure by means of coherence relations holding between spans of text; see [29, ch. 3].
2 A cost function
3 Typically, most of these units are sentences. They can sometimes consist of more than one “elementary discourse unit” (EDU) as they are used in discourse parsing.
6 One explanation for the missing impact of the raw word embeddings could be that we used pre-trained word embeddings and did not learn representations specific for our task, as advised by [10] in the context of discourse parsing.
7 Keep in mind, though, that our replications only amount to characteristic features of their decoders and constraints that are applicable on the microtext corpus. The result we obtained here do not represent what their whole system (including their local models and domain-specific constraints) might predict.
References
[1] | S. Afantenos, E. Kow, N. Asher and J. Perret, Discourse parsing for multi-party chat dialogues, in: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, (2015) , pp. 928–937. http://aclweb.org/anthology/D15-1109. doi:10.18653/v1/D15-1109. |
[2] | N. Asher and A. Lascarides, Logics of Conversation, Studies in Natural Language Processing, Cambridge University Press, Cambridge, UK, (2003) . |
[3] | B. Bohnet, Very high accuracy and fast dependency parsing is not a contradiction, in: Proceedings of the 23rd International Conference on Computational Linguistics (COLING), Beijing, (2010) , pp. 89–97. |
[4] | Y.J. Chu and T.H. Liu, On the shortest arborescence of a directed graph, Science Sinica 14: ((1965) ), 1396–1400. |
[5] | J. Edmonds, Optimum branchings, Journal of Research of the National Bureau of Standards 71B: ((1967) ), 233–240. |
[6] | E. Florou, S. Konstantopoulos, A. Koukourikos and P. Karampiperis, Argument extraction for supporting public policy formulation, in: Proceedings of the 7th Workshop on Language Technology for Cultural Heritage, Social Sciences, and Humanities, Sofia, Bulgaria, (2013) , pp. 49–54. http://www.aclweb.org/anthology/W13-2707. |
[7] | J.B. Freeman, Dialectics and the Macrostructure of Argument, Foris, Berlin, (1991) . doi:10.1515/9783110875843. |
[8] | K. Hayashi, T. Hirao and M. Nagata, Empirical comparison of dependency conversions for RST discourse trees, in: Proceedings of SIGDIAL 2016, (2016) . |
[9] | M. Honnibal and M. Johnson, An improved non-monotonic transition system for dependency parsing, in: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, (2015) , pp. 1373–1378. http://aclweb.org/anthology/D15-1162. doi:10.18653/v1/D15-1162. |
[10] | Y. Ji and J. Eisenstein, Representation learning for text-level discourse parsing, in: Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Association for Computational Linguistics, Baltimore, Maryland, (2014) , pp. 13–24. http://www.aclweb.org/anthology/P14-1002. doi:10.3115/v1/P14-1002. |
[11] | A. Kuncoro, M. Ballesteros, L. Kong, C. Dyer and N.A. Smith, Distilling an ensemble of Greedy dependency parsers into one MST parser, in: Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, Association for Computational Linguistics, Austin, Texas, (2016) , pp. 1744–1753. https://aclweb.org/anthology/D16-1180. doi:10.18653/v1/D16-1180. |
[12] | N. Kwon, L. Zhou, E. Hovy and S.W. Shulman, Identifying and classifying subjective claims, in: Proceedings of the 8th Annual International Conference on Digital Government Research: Bridging Disciplines & Domains, (2007) , pp. 76–81. |
[13] | S. Li, L. Wang, Z. Cao and W. Li, Text-level discourse dependency parsing, in: Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, Baltimore, Maryland, (2014) , pp. 25–35. http://www.aclweb.org/anthology/P14-1003. doi:10.3115/v1/P14-6. |
[14] | W. Mann and S. Thompson, Rhetorical structure theory: Towards a functional theory of text organization, TEXT 8: ((1988) ), 243–281. |
[15] | A.F.T. Martins, M.A.T. Figueiredo, P.M.Q. Aguiar, N.A. Smith and E.P. Xing, AD3: Alternating directions dual decomposition for MAP inference in graphical models, Journal of Machine Learning Research 16: ((2015) ), 495–545. http://jmlr.org/papers/v16/martins15a.html. |
[16] | R. Mochales and M.-F. Moens, Argumentation mining, Artificial Intelligence and Law 19: (1) ((2011) ), 1–22. doi:10.1007/s10506-010-9104-x. |
[17] | M.-F. Moens, E. Boiy, R.M. Palau and C. Reed, Automatic detection of arguments in legal texts, in: Proceedings of the 11th International Conference on Artificial Intelligence and Law, (2007) , pp. 225–230. |
[18] | P. Muller, S. Afantenos, P. Denis and N. Asher, Constrained decoding for text-level discourse parsing, in: Proceedings of COLING 2012, Mumbai, India, (2012) , pp. 1883–1900. http://www.aclweb.org/anthology/C12-1115. |
[19] | V. Niculae, J. Park and C. Cardie, Argument Mining with Structured SVMs and RNNs, CoRR abs/1704.06869 (2017). http://arxiv.org/abs/1704.06869. |
[20] | A. Peldszus, Towards segment-based recognition of argumentation structure in short texts, in: Proceedings of the First Workshop on Argumentation Mining, Association for Computational Linguistics, Baltimore, Maryland, (2014) , pp. 88–97. http://www.aclweb.org/anthology/W14-2112. doi:10.3115/v1/W14-2112. |
[21] | A. Peldszus and M. Stede, From argument diagrams to automatic argument mining: A survey, International Journal of Cognitive Informatics and Natural Intelligence (IJCINI) 7: (1) ((2013) ), 1–31. doi:10.4018/jcini.2013010101. |
[22] | A. Peldszus and M. Stede, Joint prediction in MST-style discourse parsing for argumentation mining, in: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, (2015) , pp. 938–948. http://aclweb.org/anthology/D15-1110. doi:10.18653/v1/D15-1110. |
[23] | A. Peldszus and M. Stede, An annotated corpus of argumentative microtexts, in: Argumentation and Reasoned Action: Proceedings of the 1st European Conference on Argumentation, Lisbon 2015 / Vol. 2, College Publications, London, (2016) , pp. 801–815. |
[24] | J. Perret, S. Afantenos, N. Asher and M. Morey, Integer linear programming for discourse parsing, in: Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics, San Diego, California, (2016) , pp. 99–109. http://www.aclweb.org/anthology/N16-1013. |
[25] | I. Persing and V. Ng, End-to-end argumentation mining in student essays, in: Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics, San Diego, California, (2016) , pp. 1384–1394. http://www.aclweb.org/anthology/N16-1164. |
[26] | N.A. Smith, Linguistic Structure Prediction, Synthesis Lectures on Human Language Technologies, Morgan and Claypool, (2011) . |
[27] | C. Stab and I. Gurevych, Annotating argument components and relations in persuasive essays, in: Proceedings of COLING 2014, Dublin, Ireland, (2014) , pp. 1501–1510. http://www.aclweb.org/anthology/C14-1142. |
[28] | C. Stab and I. Gurevych, Parsing Argumentation Structures in Persuasive Essays, ArXiv e-prints (2016), https://arxiv.org/abs/1604.07370. |
[29] | M. Stede, Discourse Processing, Morgan and Claypool, (2011) . |
[30] | M. Stede, S. Afantenos, A. Peldszus, N. Asher and J. Perret, Parallel discourse annotations on a corpus of short texts, in: Proc. of the Ninth International Conference on Language Resources and Evaluation (LREC 2016), Portoroz, Slovenia, (2016) . |