Hierarchical Bayesian models as formal models of causal reasoning

1.Introduction

Causal reasoning is arguably one of our central cognitive competencies. By means of causal reasoning, we are able to explain events, to diagnose causes, to make predictions about future events, to choose effective actions and to envision hypothetical and counterfactual scenarios. Causal induction allows us to infer the causal structure of the world from a limited set of observations, to revise existing causal assumptions and to categorise causes and effects. All of these forms of causal learning and reasoning can be found in many scientific and everyday domains. For example, in medicine diagnoses are made to explain observable symptoms and interventions are chosen to eliminate the respective disease's causes or at least relieve its symptoms. Diseases themselves are categorised according to their pathology and aetiology. Hence, categories are based on the underlying causal processes.

A number of theoretical accounts have been proposed in the literature to model these inferences (see, Waldmann, Cheng, Hagmayer, and Blaisdell, 2008; Waldmann and Hagmayer, in press). Some try to reduce causal reasoning to associative learning, while others view causal learning and reasoning as a form of logical or probabilistic inference. However, neither associative nor logical accounts capture critical aspects of causality. For example, causal relations have an inherent directionality. Associations and covariations, by contrast, are symmetric. Logical implications can be constructed for predictive and diagnostic causal relations as well as mere statistical relations (e.g. if cause C, then effect E; if effect E, then cause C, if event A, then event B). This is why associative or logical accounts cannot differentiate between causal relations and spurious relations. This distinction, however, is crucial, because only causal relations, but not spurious relations support interventions. A manipulation of a cause changes its effect, but an intervention on the effect has no bearing on the cause. In addition, neither account represents the causal structure of a domain, but only the observable correlations due to the underlying causal mechanisms.

Over the past decade, an alternative theoretical account has been developed that views causal reasoning as based on representations of causal structure: Causal Bayes nets. These models originate in philosophy and computer sciences (cf. Pearl 2000; Spirtes, Glymour, and Scheines 2000) and are the formal variant of causal model theories used in psychology (e.g. Waldmann 1996; Sloman 2005). When combined with hierarchical Bayesian models (HBMs), they provide a powerful formal model of causal induction and inference (see, Griffiths and Tenenbaum 2009).

The aim of this paper is to outline HBMs, present respective empirical evidence and discuss their strengths and limitations. First, a brief introduction is given. It will be shown how HBMs can account for the induction of causal models by considering abstract theoretical assumptions. Then it will be described how HBMs can explain the induction of causal laws (i.e. the induction of causal relations among types of events from observations of relations among particular token events). In the last section, limitations of HBMs will be pointed out, and the relation of this formal, computational account to cognitive process models will be discussed.

2.HBMs of causal induction

HBMs assume that learners induce causal models of a particular problem or domain by taking into account abstract theoretical knowledge and the observable evidence (Griffiths and Tenenbaum 2005, 2009). Figure 1 illustrates a hierarchical Bayesian model of causal reasoning. The graph shown on the left-hand side of Figure 1 specifies the relation between abstract theories, causal models and observable data. It states that causal model hypotheses are probabilistically dependent on theoretical assumptions, and that causal models entail observations (i.e. specific patterns of data that should be observed if the respective hypothesis was true). More precisely, the HBM specifies probability distributions over theoretical assumptions, causal models and data. The probability distributions over causal models and data are conditional distributions. Conditional on the theoretical assumptions, causal model hypotheses have different likelihoods. Crucially, some causal model hypotheses will be ruled out by the theoretical assumptions, thereby constraining the set of causal model hypotheses.

Figure 1.

Hierarchical Bayesian model representing the relations between abstract theoretical knowledge, causal models of a particular domain, problem or situation, and observable data. The graph entails conditional and unconditional probability distributions over theories, causal models, and data. On the right-hand side, an example from the medical domain is shown (see text for explanations).

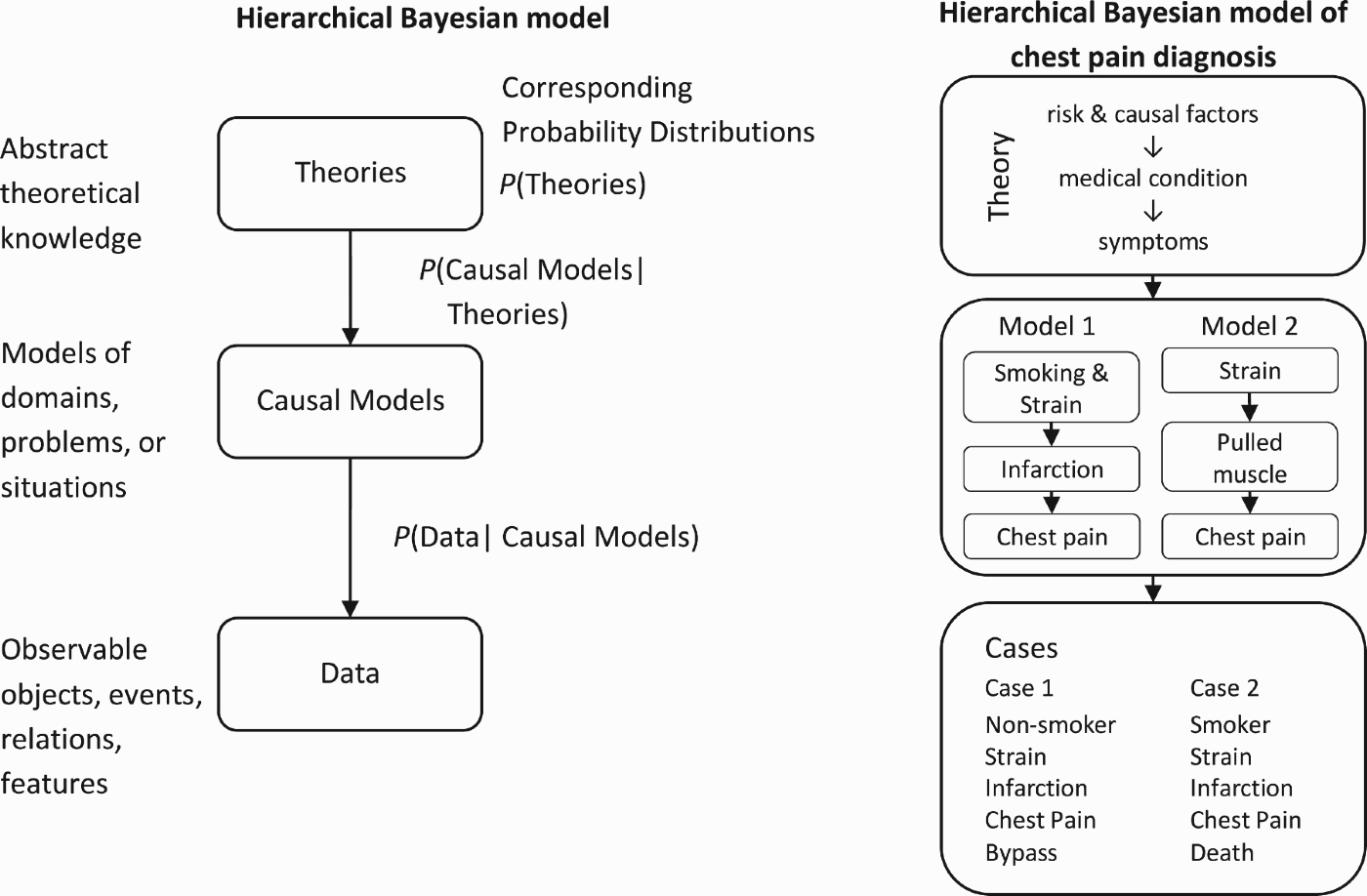
Causal Models within a HBM specify hypotheses about the possible structures of the underlying causal mechanisms (Figure 1). They are represented as causal Bayes nets using directed acyclic graphs with nodes representing causal variables (e.g. events, objects or states) and arrows representing causal mechanisms (Pearl 2000). The causal models in turn specify conditional and unconditional probability distributions over the variables within the causal system. Probability distributions over the system's exogenous variables (i.e. variables not being caused by other variables) represent their base rates. Conditional probability distributions over the endogenous variables represent the strength of the causal relations. These probability distributions in turn entail the likelihoods of all possible observations.

On the right-hand side of Figure 1, a more concrete example from the medical domain is given. According to general medical knowledge, risk and causal factors contribute to the presence of medical conditions (i.e. diseases), which in turn cause the presence of symptoms. This knowledge constrains the number of possible causal models explaining the presence of chest pain. Two possible models are shown. Model 1 assumes that chest pain is caused by cardiac infarction, whose likelihood is increased by smoking and physical exertion. Model 2 explains chest pain by a musculoskeletal diagnosis (a pulled muscle), which is due to physical strain. Of course, many more causal models of chest pain are possible. Each of these models entails a certain probability distribution over observable risk factors and symptoms. For example, assuming Model 1, an observation of a patient being a smoker and complaining of chest pain is more likely than an observation of a non-smoker reporting the same complaints.

HBM model the induction of causal models by means of Bayesian inference. More precisely, the posterior probability of a causal model hypothesis M given data d and theoretical knowledge T can be computed as

Equation (1) shows how the theoretical assumptions constrain the set of causal model hypotheses by specifying the probabilities of the target hypothesis and all its competitors. Given no previous theoretical assumptions, a vast number of causal model hypotheses are possible and equally likely. In this case, causal induction becomes intractable if the system includes more than few variables and only limited data are available. Given theoretical assumptions, a vast majority of causal models hypotheses can be ruled out (i.e. P(M|T)=0). To give a practical example, the international classification of disease (WHO 2010) already specifies more than 14,000 codes to classify diseases, each of which represents a hypothesis predicting certain measureable or observable symptoms. Many of these symptoms and clinical signs are ambiguous and of low diagnostic value on their own. Without more abstract causal knowledge, it would virtually be impossible to induce new diseases or even make diagnoses. Abstract causal knowledge about general pathological processes like infections or inflammations, knowledge about biological processes, and general notions about symptoms, causes and disease support the inductive process (see next section for a more in-depth analysis of various forms of abstract causal knowledge).

Equation (1) also illustrates how a single data point may allow us to induce a causal model hypothesis: if the likelihood ratio concerning this data point is very high, i.e. if the observation is way more likely, given a target causal model hypothesis than any other hypothesis, then a single observation may suffice. For example, in the medical domain, the probability of myocardial infarction is not very high, given an observation of chest pain as there are many other likely conditions that may cause this type of pain. By contrast, the presence of antibodies is highly diagnostic of a respective infection.

To sum up, HBMs provide a formal account of causal induction and inference. They assume that induction is guided by abstract theoretical knowledge, which constrains causal model hypotheses, representing the causal structure of a particular system or problem. They also assume that inferences are based on Bayes rule, which allows to infer the posterior probability distributions of causal models (i.e. causal induction), variables within a causal model (e.g. diagnosis and prognosis), and abstract theoretical knowledge (i.e. theory induction) from the likelihoods of the observed data and prior probabilities.

3.Abstract theories in causal induction

Abstract knowledge can come in various forms, and it may form complex hierarchies. The most abstract form of knowledge may be called causal principles, which probably include the assumption that causes precede their effects, that nothing happens without a cause, and that causes generate their effect unless prevented by an inhibitory factor (Audi 1995). A fundamental assumption might also be that a manipulation of a cause changes its effects but not vice versa (Woodward 2003). People seem to automatically consider these assumptions in causal learning (Waldmann 1996). For example, research on the induction of hidden causes has shown that people assume the presence of a hidden cause when they observe an effect that cannot be explained otherwise (Hagmayer and Waldmann 2007; Luhmann and Ahn 2007). Even young children infer that objects having the same observable effect will have the same internal, hidden property causing the effect (Sobel, Yoachim, Gopnik, Meltzoff, and Blumenthal 2007).

Structural principles like trees, causal chains or loops are also highly abstract forms of theoretical knowledge. Research on property induction, for example, has shown that people consider a taxonomic tree structure when judging whether a genetic property of one species can be found in another species. By contrast, people consider causal chains when they make inferences with respect to properties that can be transferred through food chains (e.g. infections, toxins) (Tenenbaum, Kemp, Griffiths, and Goodman 2011). When predicting the effects of interventions in complex systems, people often assume causal chains although causal feedback loops would be more appropriate (Sterman 2000). For example, people expect antibiotics to eliminate bacterial infections, despite the fact that antibiotics increase the bacteria's resistance which may offset the desired effect in the long run.

Causal schemata are assumptions about how multiple causes may interact (Kelley 1973). Two prominent schemata are multiple sufficient causes entailing that various causes may generate an effect on their own and multiple necessary causes, which entail that a certain set of causes has to be present for the effect to occur. However, people may also learn that an effect is only generated when an individual cause is present (see, Lucas and Griffiths 2010). Furthermore, people generally seem to expect that effects of separate causes add up (Beckers, De Houwer, Pineño, and Miller 2005) and that causes act independently (Mayrhofer, Nagel, and Waldmann 2010; see also Novick and Cheng 2004). Waldmann (2007) showed that for extensional properties (e.g. different causal strengths) people assume effects to add up, while for intensional properties (e.g. degrees of liking) people expect effects to average.

A causal framework theory is the assumption that observable causal relations among particular events or objects (tokens) are instantiations of more general causal laws connecting types of events or objects (Kemp, Goodman, and Tenenbaum 2010). Such a framework theory entails that events or objects of the same type (i) generate the same effects with the same likelihood, and (ii) share the same features. (We will describe a respective HBM in the next section of the paper.)

Note that none of these highly abstract theories includes any assumptions about the entities being causally related or the nature of the causal relation. Theoretical knowledge, however, could also be domain-specific. It may include assumptions about the causally relevant entities, their properties and potential relations (Griffiths and Tenenbaum 2009). Research in developmental psychology has shown that infants and young children already have domain-specific expectations about causal entities and their relations (Carey 2009). For example, while children expect temporal and spatial contiguity to be necessary for causation in a mechanical system, they accept causation at a distance when the agents are persons.

Finally, theoretical assumptions may concern the nature of the causal mechanisms. Many studies have shown that people draw different inferences from the same observations depending on whether they know about a potential mechanism underlying the observed relation (Ahn, Kalish, Medin, and Gelman 2000). For example, a moderate statistical relation was seen as good evidence for causation when a plausible mechanism was known, while this was not the case when no mechanism could be envisioned (Koslowski 1996). Developmental research found that children being familiar with causation via electric wiring did not require spatio-temporal contiguity to infer causality while younger children did (Bullock, Gelman, and Baillargeon 1982). Research also shows that people have a hard time to induce causal models, when they have very little abstract knowledge (e.g. Steyvers, Tenenbaum, Wagenmakers, and Blum 2003; see also Lagnado, Waldmann, Hagmayer, and Sloman 2007). In general, performance in causal induction increases substantially, when people can observe temporal relations or can intervene (Lagnado and Sloman 2004). Research on the control of complex systems shows that participants often gain very limited knowledge about the underlying causal structure despite extensive learning experience (Osman 2010). HBMs can explain this finding as the available evidence in these studies was often compatible with numerous causal hypotheses, and participants normally lacked domain specific knowledge (see, Hagmayer, Meder, Osman, Mangold, and Lagnado 2010, for a more detailed discussion).

In sum, there are many forms of abstract theoretical causal knowledge that may guide causal induction. This abstract knowledge can be domain-general or domain-specific. A growing body of evidence shows that such abstract causal knowledge affects causal induction.

4.Induction of causal laws

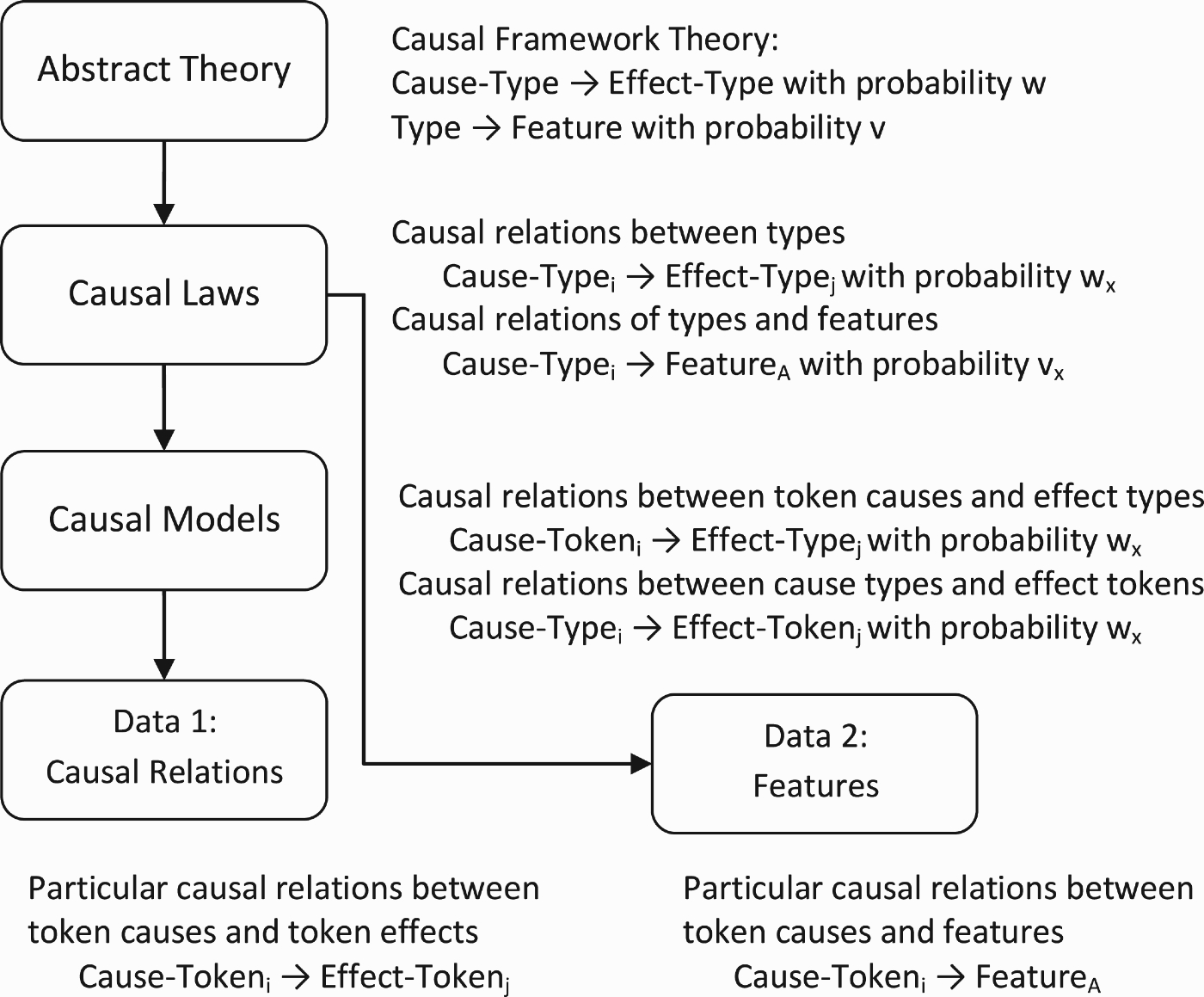
Causal relations may hold between particular objects or event tokens, but also between types of causes and effects. Causal relations on a type level have been called causal laws (Schulz, Goodman, Tenenbaum, and Jenkins 2008). Causal laws specify the structure and strength of the causal relations between types of causes and types of effects. To induce causal laws, both categories of causes and effects as well as the causal relations between them have to be learnt. HBMs allow us to model these inferences (Kemp et al. 2010). Figure 2 provides an illustration. On the most abstract level, there is a framework theory assuming that there are causal relations between types of causes and effects without specifying what these types are. There is also the assumption that tokens of the same type share certain features. On the level of causal laws are causal relations between cause and effect types. Representations of causal relations between types and their features can also be found on this level. Causal models are characterised by causal relations between a type and a token. Data are observations of single causal relations between token causes and token effects and observations of the features of cause and effect tokens.

Figure 2.

Hierarchical Bayesian model of category learning and causal induction.

Some research has been conducted investigating the induction of categories during causal learning. Lien and Cheng (2000) presented participants with objects having different colours and sizes which caused an effect with a certain probability. By manipulating the probabilities, they were able to show that participants induced categories of objects (e.g. warm-coloured versus cold coloured objects) that were optimal for predicting the effect. Crucially, participants used the new categories to predict the effect of objects they had not seen before. Kemp et al. (2010) constructed a HBM which was able to reproduce the findings of a simplified version of the studies by Lien and Cheng (2000).

Waldmann, Hagmayer and colleagues (Waldmann and Hagmayer 2006; Waldmann, Meder, von Sydow, and Hagmayer 2010) extended this research and showed that both causes and effects are spontaneously categorised according to the causal relations they are part of, and that these categories are transferred to later learning episodes even when they do not allow for optimal predictions. This transfer, however, seems to depend on people's abstract causal knowledge (Hagmayer, Meder, von Sydow, and Waldmann 2011). Categories of causes are only used to predict novel effects if these new effects are plausible effects of the type of cause (i.e. if there is a plausible causal mechanism). Abstract structural knowledge also seems to be important. Categories based on one causal relation were transferred to a second causal relation only if the second relation was connected to the first relation forming a continuous causal chain (Hagmayer et al. 2011). Otherwise people preferred to induce separate categories for each causal relation.

Developmental research shows that even pre-schoolers use the causal effects to categorise objects (Gopnik and Sobel 2000) and that these categories may even override perceptual differences between objects (Nazzi and Gopnik 2003). Later studies indicate that pre-schoolers even have the ability to abstract causal laws (Schulz et al. 2008). Children in these studies categorised coloured blocks with respect to their capacity to generate certain sounds when touching other types of blocks. Crucially, children used the observation of one effect to categorise an object and then use the category to make predictions about another effect. HBMs can account for this transfer effect (Schulz et al. 2008).

5.Discussion

The problem of causal induction is a challenge for computational and cognitive theories of causal reasoning. HBMs provide a formal framework which allows us to model causal induction and inferences as well as the induction of causal laws. As the overview provided in the previous sections shows, HBMs have been very successful in describing the inductive behaviour of children and adults (see also Chater and Oaksford, 2008). Importantly, HBMs explain how causal induction based on very limited data is possible when abstract causal knowledge is available to constrain the set of hypotheses. Second, HBMs explain how types of causes and effects can be inferred from the observation of particular objects and events while causal relations on the type level are induced. Other theories have difficulties to account for rapid induction of causal models, causal categories and causal laws (Waldmann and Hagmayer, in press). Data-driven accounts assuming that categories and causal relations are learnt from observations would require huge amounts of learning data and, therefore, fail to explain the findings.

Nevertheless, HBMs have a number of limitations. First, they strongly rely on the existence of previous abstract causal knowledge without providing any explanation about the origin of this knowledge. At least some constraints seem to be necessary to enable causal induction. Hence, some innate knowledge has to be assumed (but see Goodman, Ullman, and Tenenbaum 2011), although this knowledge might be revised based on the given observations (Griffiths and Tenenbaum 2009). The causal principles described above are likely candidates. To gain more insights, not only developmental research is needed, but also cross-cultural comparisons. Recent research has shown that western, educated forms of reasoning may or may not conform to reasoning in other cultural groups (Henrich, Heine, and Norenzayan 2010). Currently, rather little is known about abstract causal beliefs in other cultures (Beller, Bender, and Song 2009). More research is clearly needed in this regard. A second open question is how to account for domain-specific abstract knowledge. Obviously, the causal assumptions underlying intuitive theories of physics, biology and psychology are rather distinct (Carey 2009). It still needs to be shown that HBMs can explain the learning of these differences.

A second point of critique is that there is growing evidence that people's representations of causal models do not conform to causal Bayes nets. A pivotal assumption of causal Bayes nets is the so-called Markov assumption, which informally states that each variable in a causal structure is independent of all variables other than its direct and indirect effects once the state of its direct causes are known. This assumption has a number of implications which can be tested experimentally. For example, consider a model in which a common cause generates two effects. The Markov condition states that the probability of the second effect is the same when the common cause is present regardless of whether the first effect is present or absent. Respective empirical studies did not support the predictions of causal Bayes nets (Rehder and Burnett 2005). The same is true for the prediction of a single effect from a cause (Fernbach, Darlow, and Sloman 2010). Counter to the implications of causal Bayes nets, participants neglected the influence of other causes on the effect in their predictions.

Third, HBMs and causal Bayes nets are formal accounts that do not aim to describe the actual cognitive processes people employ, although some researchers seem to assume that people use some form of Bayesian updating in causal inferences (Gopnik et al. 2004). It has been proposed that people use simpler cognitive heuristics whose performance approaches a Bayesian model (Sloman 2005; Fernbach and Sloman 2009). For example, Mayrhofer and Waldmann (2011) devised a simple heuristic that may underlie causal induction. This heuristic simply counts how often a potential cause fails to bring about an effect. Causal relations that minimise that score are assumed to hold. Simulation studies showed that this heuristic is extremely powerful and is likely to find the causal structure underlying a set of data, given some plausible assumptions. Cue-based models of causal induction have also been devised (Einhorn and Hogarth 1986; Lagnado et al. 2007; Fernbach and Sloman 2009). These models assume that people rely on cues to causality rather than engaging in complex hypothesis testing. For example, Fernbach and Sloman (2009) assume that people rely on local computations and generate hypotheses about causal structure from single observations considering cues like temporal order, co-occurrence, and consequences of interventions. Cue-based models, however, also have to assume that people have intuitive abstract knowledge, which allows them to identify the cues indicating causal relatedness. Cognitive process models of causal induction have limitations, too. They cannot determine optimal inferences under given conditions. Thus, they do not distinguish whether cases of inductive failure are due to insufficient data or heuristic processing.

Taken together, the discussion points out that HBMs and cognitive process models are both needed to understand how causal induction is possible and how people proceed, given a certain set of data and initial knowledge. HBMs show what the optimal inference would be and cognitive process models how these inferences can be realised, given our cognitive limitations. Therefore, we think that that both kinds of models are crucial to explain people's causal reasoning and to create artificial intelligences.