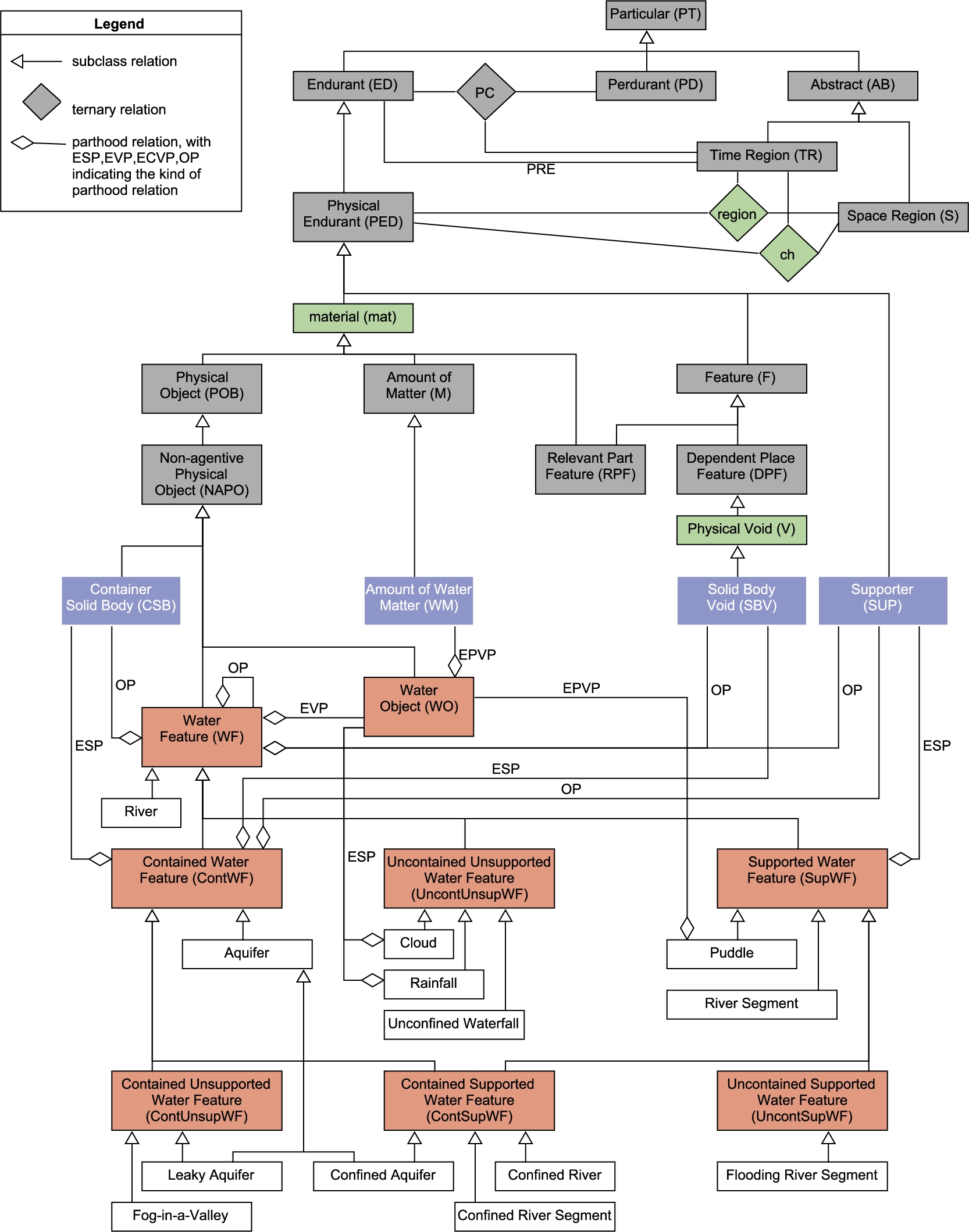
Water features and their parts

Brodaric, Boyan; Hahmann, Torsten; Gruninger, Michael

doi:10.3233/AO-190205

Water features and their parts

Article type: Research Article

Authors: Brodaric, Boyan^{a; *} | Hahmann, Torsten^b | Gruninger, Michael^c

Affiliations: [a] Geological Survey of Canada, Natural Resources Canada, Ottawa, ON, Canada. E-mail: [email protected] | [b] National Center for Geographic Information and Analysis (NCGIA), School of Computing and Information Sciences, University of Maine, Orono, ME, USA. E-mail: [email protected] | [c] Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON, Canada. E-mail: [email protected]

Correspondence: [*] Corresponding author. E-mail: [email protected].

Note: [] Accepted by: Roberta Ferrario

Keywords: Water features, sensors, reference ontology, hydro ontology, physical object parthood

DOI: 10.3233/AO-190205

Journal: Applied Ontology, vol. 14, no. 1, pp. 1-42, 2019

Published: 22 February 2019

Get PDF

Abstract

Water features such as rivers, clouds, and aquifers are primarily understood from sensor measurements. Ontologies for the hydro domain play a key role in describing sensor measurements, particularly to aid water data interoperability, but water features are under-represented in such ontologies. In this paper we build upon existing work in hydro ontologies to enhance the characterization and representation of water features. An enhanced theory of physical object parthood is developed that enables water features to be characterized as wholes with various essential parts, building on Fine’s theory of parts and Hayes’ ontology of liquids. The results are represented as a formal extension of the DOLCE ontology, and advance the HyFO reference ontology for the hydro domain.

1.Introduction

Water features are physical entities located in geographical space and essentially consist of water as well as other things. They are found below, above, and on the planetary surface, with representative examples including rivers, puddles, clouds and aquifers. They are not dependent features in the ontological sense of parasitic entities, such as the edge, bottom or surface of a river (Sanfilippo and Borgo, 2016), but are an associated physical object, i.e. the river, as per custom in the geospatial domain (e.g. Open Geospatial Consortium (OGC), 2009; Varanka and Usery, 2015). Water features are in this sense distinguished from dependent features for the purposes of this paper.

Water features play a key role in many human activities, most notably related to health, climate, agriculture, energy, recreation, and transportation. Information about water features is typically derived from measurements collected by a large number of different sensors, resulting in massive volumes of data, but the things being measured can be subtly different, as can be their units of measure, acquisition protocols, and data structures. With the data being increasingly made available online, interoperability challenges abound and are substantial (Brodaric and Piasecki, 2016). Ontologies are an important tool used to overcome the semantic aspects of such challenges by enabling digital representations of intended meanings to be associated with data and other resources. This allows the data and resources to be used cohesively in tasks such as discovery, retrieval, integration, and orchestration, in support of goals such as scientific analysis for water quantity estimation or complex decision-making for water allotment.

Semantic interoperability in the water domain must especially contend with ontology multiplicity and connectivity. Multiple pertinent ontologies exist for water sensors and their measurements (e.g. Compton et al., 2012; Cox, 2016; Kuhn, 2009), as well as for water features and their inherent qualities (e.g. Buttigieg et al., 2016; Raskin and Pan, 2005; Varanka and Usery, 2015). Critically, these two kinds of ontologies must be connected to adequately describe a particular measurement, for example, to link a sensed water level with the height of some river’s water. Ontological multiplicity can then lead to conflicts if entity representations vary across ontologies, and connectivity is impeded if an ontology is incomplete or vague, e.g. if the river entity or its height quality are omitted or under-represented. Both cases can be found in water ontologies, as water feature descriptions vary widely and the entities measured by predominant types of water sensors are not fully discriminated. Examples of this can be found when comparing international water data standards (Boisvert and Brodaric, 2012; Brodaric et al., 2018; Open Geospatial Consortium (OGC), 2018; INSPIRE Thematic Working Group Geology, 2013; INSPIRE Thematic Working Group Hydrography, 2014), national catalogs of hydrographic features (Duce and Krzysztof, 2010), ontological considerations (Galton and Mizoguchi, 2009; Santos et al., 2005; Sinha et al., 2014; Wellen and Sieber, 2013), and hydro database structures (Maidment and Morehouse, 2002; Strassberg et al., 2011). At the heart of the problem is a disparity about the fundamental nature of a water feature, as different aspects are variously present and diversely represented in distinct ontologies. This gives rise to fundamental questions such as: what is a water feature, what are its key aspects, and how are they organized and represented?

In this paper we undertake an ontological analysis of water features and develop a new characterization and representation that addresses these questions. The characterization is sufficiently foundational to help explicate common ontology conflicts, and is sufficiently complete to enable broad connectivity to sensor ontologies. It is achieved by extending and uniting two significant approaches to physical ontology, namely aspects of Fine’s theory of parts (Fine, 1999) and Hayes’ ontology of liquids (Hayes, 1985). The original contribution includes (1) an extended formal theory of physical object wholes and parts; (2) the identification of a water feature as a specific type of whole with certain essential parts; and (3) a formal characterization of various water features derived from different combinations of essential parts. These results contribute to the ongoing design of the HyFO reference ontology for the hydro domain, which is being developed as a formal logic extension to DOLCE (Hahmann et al., 2016; Hahmann and Stephen, 2018). HyFO aims to help identify semantic heterogeneities, aid interoperability, and inform ongoing representations in the water domain.

This paper is organized as follows: Section 2 describes a motivating scenario, including representative water features and related sensor measurements; Section 3 reviews related work and highlights significant gaps in the understanding and representation of water features; Section 4 informally presents our characterization of water features, including enhanced notions of whole and parts; Section 5 sketches a formal representation; Section 6 outlines some outstanding issues and Section 7 concludes with a brief summary.

2.Motivating scenario

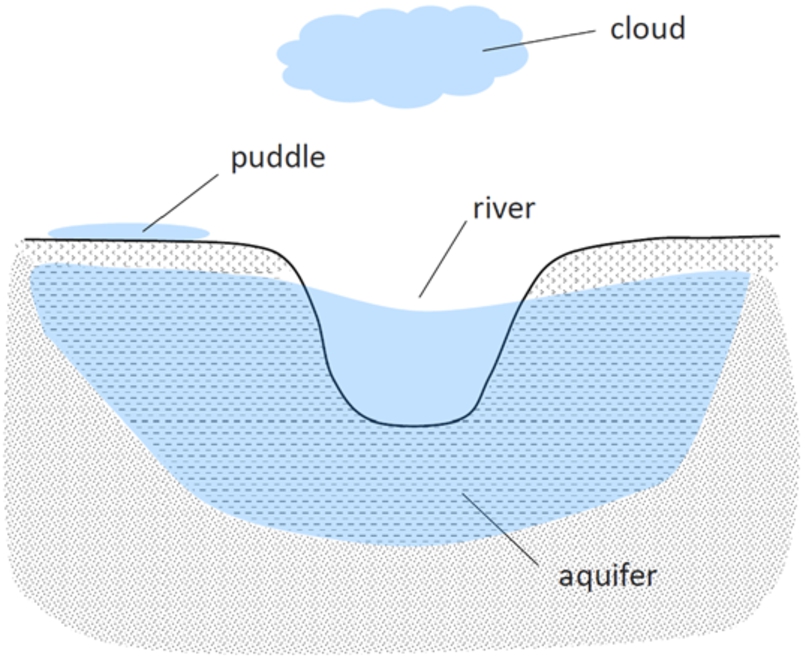
Of primary interest here are the representative water features, their topological and whole-part relations, and the most common sensors associated with these features. As shown in Fig. 1, included are water features that are (1) emplaced in the planetary surface and subsurface, such as rivers and aquifers; (2) spilled on the ground surface, such as puddles and floods, or spilled over a ground surface edge, such as a waterfall; and (3) situated in the atmosphere, such as clouds or fog. The sensors most commonly associated with such features include those that measure water flow and chemistry, surface and subsurface water height, as well as surface overflow. However, it is readily apparent that the water features themselves do not necessarily host many of the the things being measured by the sensors. For example, the chemical elements measured by water quality sensors are constituents of the water, the rate of flow is a quality of the water in relation to a perdurant (a process-like entity), and water height and overflow are qualities of the water in some relation to a container. Indeed, these measurements seem to be often hosted by various aspects of a water feature, rather than by the water feature itself. It appears that water features thus have significant additional structure, that, to the best of our knowledge, is not fully captured by existing hydro ontologies. This highlights a fundamental gap in the understanding and representation of water features.

Fig. 1.

Some representative water features.

3.Related work

The ontological nature of water bodies has been studied in fields as diverse as philosophical ontology, applied ontology, and hydro ontology engineering. Despite the attainment of many important insights, a comprehensive approach remains elusive. Individual efforts focus on specific aspects, such as the nature of changing parts, but without identifying all key parts and often not accounting for the occasional lack of parts, for example, the absent water in dry rivers and lakes.

Philosophical ontology. Fine (1999) uses the water domain as a particularly good exemplar of changing parts: the water in a lake or river retains identity while being composed of different water matter amounts at different times. For instance, the water of the Niagara River remains a single distinct object even as its water matter amounts change over time. According to Fine, such a water object exemplifies a specific kind of whole, called a variable embodiment, that is differentiated from its container and any amounts of water matter: e.g. a river’s water (as a whole object) can have properties distinct from its containing river channel or changing water matter parts, as it can rise without the channel rising and its height remains despite the departure of specific water matter amounts. The key aspects of a river that are thus differentiated by Fine include its water object, container, amounts of water matter and their flow. However, a river is not identified with any of these key aspects and the exact nature of the relationship between a river and each aspect is not explicitly addressed, as river ontology is not the focus of the work.

Applied ontology. The ontology of fluids (Hayes, 1985) recognizes two more key aspects: (1) the void hosted by a container, such as the space in a river channel, and (2) the supporting entity holding up the water, such as a riverbed. Water features are then variously identified with a key aspect, initially with the void and then with the water object. In both cases the identification is problematic, as it implies, for example, contrary persistence conditions in the case of the void, because a river would then exist whenever its channel space exists, and it precludes the existence of dry rivers in the water object case. Whole-part relations are also not used to connect a water feature to its key aspects, such as a river to its container or void, though relations for the support, containment, connectivity, and movement of water matter appear fundamental.

The emphasis on water movement is elevated in a process-oriented approach, in which the processes enacted by an object are essential to its identity and existence, with notable examples including waterfalls and rivers (Galton and Mizoguchi, 2009). However, voids (Casati and Varzi, 1994; Hahmann and Brodaric, 2012) do not play a significant role in the makeup of a water feature in this approach, water features are not clearly differentiated from water objects, and tying water feature identity to enacted processes results in water features that do not exist when the processes stop or pause, e.g. if the water stops running then the hydraulic erosion of the river channel also stops, thus the river does not exist in dry periods.

The potential to differentiate water features from water objects is evident in related work on quantities, such as fluids (Guizzardi, 2010), where a wine vintage is delineated from its wine matter amounts and containers. However, a vintage is only partially similar to a river or its water object, and is not identical to either. It is not like a water object, because the vintage’s constituent fluid matter amounts do not change. It is somewhat like a river as they do share some persistence conditions, i.e. both can persist with the absence of fluid matter, but they differ in that, unlike a vintage, a river will not persist indefinitely without fluid matter. Dependence conditions also differ: a vintage is not dependent on any container as its wine matter could be re-bottled without the vintage losing identity, but a river, or its water object, are both specifically dependent on their container as they cannot be re-located and preserve identity – the Niagara River would not be the same river/water object in a different geographical location, e.g. in the Grand Canyon.

Hydro ontology engineering. Existing hydro ontologies and geospatial feature catalogs focus primarily on inland surface water features, with groundwater features typically a secondary concern (Buttigieg et al., 2016; Feng et al., 2004; Galton and Mizoguchi, 2009; Duce and Krzysztof, 2010; Santos et al., 2005; Varanka and Usery, 2015; Sinha et al., 2014; Wellen and Sieber, 2013; Tripathi and Babaie, 2008; Raskin and Pan, 2005). The key aspects of a water feature are not all distinguished by any one approach, and the complete range of representative water features is not delineated. This also holds true for emerging international standards for hydro data (Boisvert and Brodaric, 2012; Brodaric et al., 2018; INSPIRE Thematic Working Group Geology, 2013; INSPIRE Thematic Working Group Hydrography, 2014; Open Geospatial Consortium (OGC), 2018; Strassberg et al., 2011; Maidment and Morehouse, 2002).

4.Water features, parts, and wholes

Two main insights underlie this work: (1) a water feature is necessarily distinct from its key aspects (see Section 4.1), and (2) this distinction is manifest as a whole to its parts, with the water feature being the whole and its aspects (except flow) being the parts (see Section 4.4). Note that in this paper types are understood to encompass generalizations such as universals, kinds, categories, properties, and classes, and are exemplified by the type River; individuals are particulars that instantiate types, but cannot themselves be instantiated, such as the Niagara River; and an instance is an individual that instantiates a specific type, such as Niagara River instantiating River. Specialization refers loosely to the taxonomic relation, distinct from instantiation, and holds between types as well as between relations: for example, the Aquifer type can be specialized by the ConfinedAquifer subtype (i.e. an aquifer that has its water fully supported), and the physical containment relation can be specialized by the surrounds-mat subrelation (i.e. a material entity fully enclosing another material entity).

4.1.Water feature aspects

The delineation of a water feature from its key aspects arises from comparison of various conditions:

Container:	holds a water object at some time and differs from a water feature in its persistence and dependence conditions. A container, being a solid material body, can exist before and after a water feature, and relatedly, while a contained water feature is dependent on a container for its existence or essence, a container is not dependent on a water feature: a confined (non-flooding) river cannot exist without a specific river channel, but a river channel can exist without a river, i.e. as a landform with a ground depression.
Void:	is a space in a container, and is dependent on the container (which hosts the void, see Casati and Varzi, 1994; Hahmann and Brodaric, 2012). A void can likewise exist before and after a water feature, and voids are immaterial, while a water feature must have at least some material aspects. This also differentiates water features from other possible immaterial parts, such as associated spiritual entities as conceived by various indigenous cultures (Mark et al., 2007; Wellen and Sieber, 2013).
Supporter:	is the supporting entity holding up a water object. It is understood to be a material object – either a solid or liquid, but not a gas – or an associated surface, such as the riverbed hosted by a river channel. Significantly, its persistence conditions differ from that of its water feature, in that a riverbed can exist before and after the river whose water object it supports. Note that while containers and supporters are intimately related, they are in fact distinct as not all supporters are containers, e.g. floods or surface runoff are supported by the ground, but not necessarily contained by it.
Water object:	is constituted by amounts of water matter. It has different persistence conditions and properties from a water feature: the surface of the water object can rise or fall, but if the water feature includes a container or supporter then these do not necessarily rise or fall (Fine, 1999). Moreover, a water object is also differentiated from its water matter amounts, as the amounts can flow, say out of a container, but the water object does not.
Water matter amount:	constitutes a water object. A water feature can exist in the absence of an amount of water matter, and if contained is specifically dependent on its container, unlike the water matter amount which typically flows from one container to the next. An amount of water matter is homeomerous, composed strictly of water matter parts (but see Guizzardi, 2010), though a water feature is not necessarily so, potentially having several different key aspects as parts.
Flow:	is a perdurant (a process-like entity), while a water feature is typically viewed as an endurant (an object-like entity), notwithstanding that some water features are specifically dependent on perdurants, for example, rapids or waterfalls. Moreover, perdurants are typically restricted to temporal parts, whereas water features have physical parts and can in principle exist without flow, such as stagnant lakes or ponds. Unlike the other key aspects, water flow is not a water feature part, being related to a water feature as a perdurant is to its participants rather than as a part to a whole.

4.2.Parts

Understanding water features as wholes, with relevant aspects as parts, requires enhanced notions of wholes and parts. Wholes and parts are often related via ontological dependence, either specifically or generically (Galton, 2014; Guizzardi, 2007; Simons, 1987; Vieu, 2006). In specific parthood a whole is specifically dependent on a distinct part, such as a car on its chassis: a car cannot exist without a specific chassis, and loses its identity with the removal or exchange of the chassis. In generic parthood a whole is generically dependent on some parts of a certain type, such as a car on an engine: a car needs some engine, but not a specific engine, so engines can be exchanged without affecting the car’s identity. In these examples, both categories of parts (e.g. car, engine) are mandatory, in that all instances of the whole must have these parts at least at some of the time, and both categories of parts are also essential, as all instances of the whole require them for their existence or essence. However, not all mandatory parts are essential, and not all parts are mandatory. Thus, here we also identify non-essential mandatory parts, as well as non-mandatory optional parts. Non-essential mandatory parts exhibit a dependence between the whole and part that is not ontological dependence (i.e. not related to existence or essence, hence not specific or generic parthood) such as functional dependence, causal dependence, or legal dependence. For example, a car must have fuel to function, but fuel is not intrinsic to the existence or essence of a car, as a car can exist as it is without fuel. Although non-essential parts cannot have wholes ontologically dependent on them, essential parts can have wholes dependent on them in non-ontological ways: a car is not only ontologically dependent on a chassis and some engine, but is also functionally dependent on them. In contrast, for optional parts it is not necessary for something to be a part, for example, it is not mandatory for a car to have a sunroof though some cars have one.

Parts can also be analysed by their temporal co-existence with the whole (e.g. Guizzardi, 2007). A useful delineation distinguishes persistent parts that co-exist with the whole at all times the whole exists, and temporary parts that co-exist with the whole only at some time the whole exists, with temporary parthood subsuming persistent parthood. Many other temporal categorizations are possible, though it is assumed here that a whole must co-exist at some time with each of its parts. Temporary parthood in this sense enables a whole to have missing parts: it allows a specific part, or type of part, to be absent for some (but not all) time during the life of the whole, and allows a specific part, or type of part, to return to the whole after an absence without change of identity for the part or whole. In this sense, it also allows empty wholes that have all parts temporarily absent at the same time, such as a sports team that has not yet recruited players, or a committee waiting for members to be appointed. Temporary parthood also permits exchangeable parts, that is, numerically distinct parts that can be swapped for other parts, with distinct identities, within the whole. It is important to distinguish exchangeable and modifiable parts here: exchangeable parts are parts that can be replaced within a whole, whereas modifiable parts have some characteristics that can change during the lifespan of the part without changing the identity of the part or whole; though such changes will likely cause the part to cease to exist at some time. Most, if not all, parts are modifiable, but not all are exchangeable. For example, a car cannot exchange its chassis for another and retain identity, but a car’s chassis can change color (due to re-painting) or shape (due to a collision) without affecting the identity of the chassis or car.

Fig. 2.

Taxonomy of parthood relations for physical object wholes.

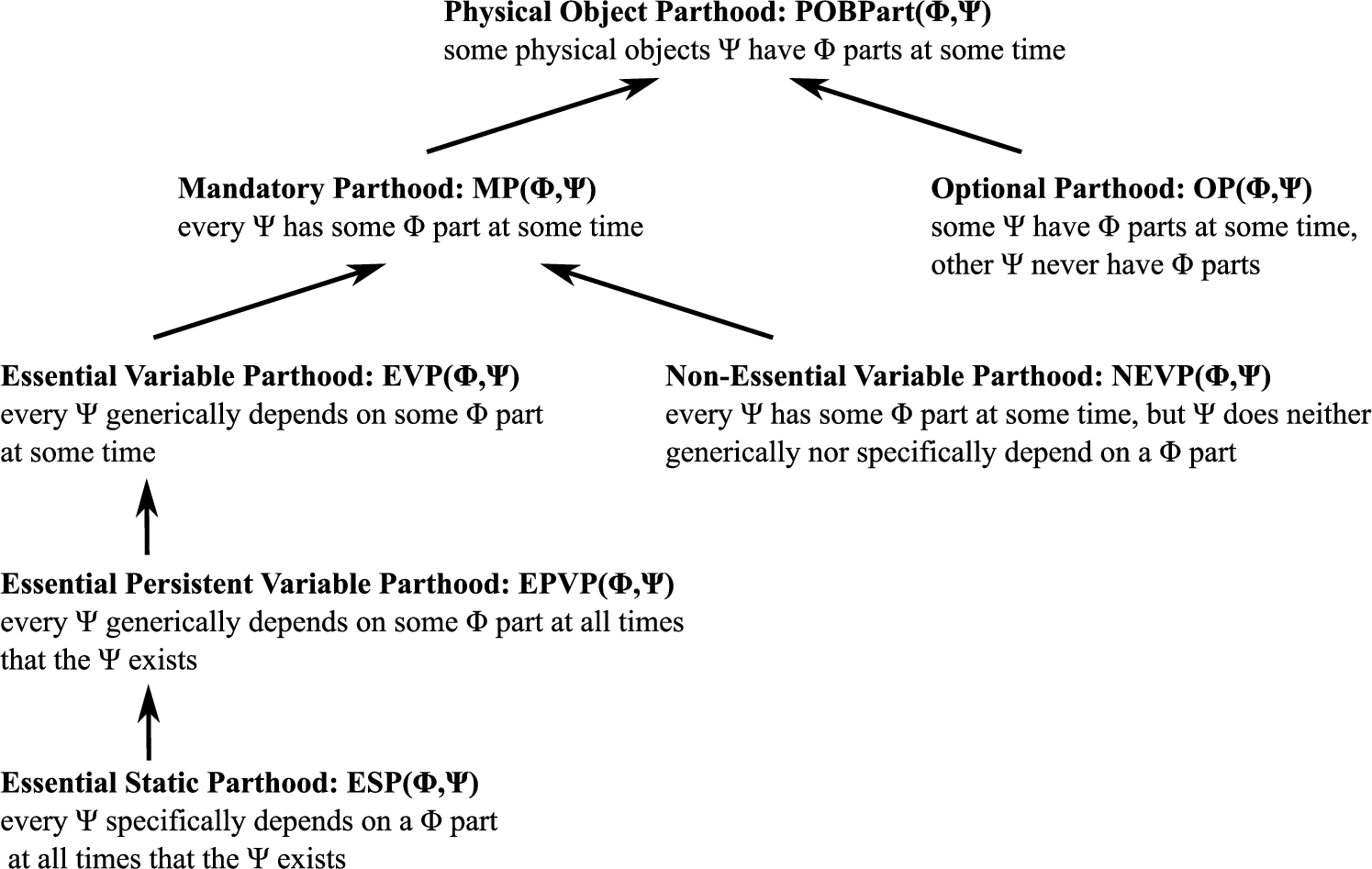
Combining the dependence-based and temporal categorizations of parts leads to the parthood relations shown in Fig. 2 and formalized in Section 5. Wholes are limited in this paper to physical objects for reasons of scope, and are exemplified by rivers, cars, or forests. Parts can be material entities or dependent features: material entities share matter with the whole, e.g. a river and its water matter amounts, and the whole has parts that host the dependent feature, e.g. a river channel and its void. While these choices are obviously limited, they suffice for our water feature needs herein.

All physical parthood relations in this paper hold between types, such that for instances to be in some parthood relation their types must be in a corresponding parthood relation. The most general case of physical object parthood states that some physical objects of a certain type have physical parts of a certain type at some time. This enables missing parts, via temporary parthood, and exchangeable parts, because parts are not restricted to being a specific single instance of a type, but can be manifest as several instances of a type at various times during the lifespan of the whole. All parts are potentially modifiable. Physical parthod is further distinguished as either mandatory or optional physical parthood: in mandatory parthood each whole must have a part of a certain type at some time, but with optional parts not all wholes have such a part. Mandatory parthood can be further refined. Essential mandatory parthood is a specialization that requires ontological dependence of whole instances on part instances, and non-essential mandatory parthood is a specialization that excludes such ontological dependence while requiring other kinds of dependence of the whole on a part. To emphasize that both essential and non-essential mandatory parts can be missing and exchangeable, they are called essential variable parts and non-essential variable parts, respectively.

Essential variable parthood can be further specialized into persistent and static varieties. In essential persistent variable parthood, each whole of a type must have some unspecific part of a type, i.e. be generically dependent on it, at every time during the whole’s existence, hence the part cannot be missing but is exchangeable. In essential static parthood, each whole of a type must have a specific part of a certain type, i.e. be specifically dependent on it, and always be co-temporal with it, hence the part cannot be missing and is not exchangeable. Because generic dependence between types subsumes specific dependence between types, essential persistent variable parthood subsumes essential static parthood.

In a final variety of essential variable parthood, which is not formalized in this paper or illustrated in Fig. 2, each whole of a type can only have a specific instance as part, that is, the part is not exchangeable but can be missing as in, for example, an ephemeral stream with a unique water object that might disappear at times and reappear subsequently while retaining identity.

Several specializations of non-essential variable parthood also arise from its negation of ontological dependence, though these are also not formalized in this paper: they include types of wholes having either zero or some, but not all, instances ontologically dependent on parts. For example, all cars are functionally dependent on some fuel, but no car is ontologically dependent on any fuel, so fuel is a non-essential variable part of a car. In contrast, all stars are both functionally and ontologically (generically) dependent on fuel, so fuel is an essential variable part of a star. Fuel is then a non-essential variable part of FuelBurningThing, as all instances are functionally dependent on fuel, but only some instances (e.g. stars) and not all (e.g. cars) are ontologically dependent on fuel.

To further exemplify the different types of parts, consider again a car: a car has a single unique chassis as an essential static part (essential, cannot be missing, not exchangeable), one or more engines and wheels over time as essential variable parts (essential, can be missing, exchangeable), quantities of fuel as non-essential variable parts (mandatory but not essential, can be missing, exchangeable), and one or more sunroofs as optional parts (not mandatory, can be missing, exchangeable). Essential persistent variable parts are exemplified by amounts of water matter, which must constitute a water object whenever it is present but which can be exchanged (essential, cannot be missing, exchangeable). Note that a complete analysis would also consider the inverse relations, for example, a part ontologically dependent on a whole, such as the exhaust fume parts of a car being specifically dependent on the car; then the car might be considered some sort of mandatory whole for the fumes. A wider analysis could also explore the viability of additional specializations for parthood to represent things such as future (e.g. spare) parts, but these refinements are beyond the scope of this paper.

4.3.Wholes

Simons (1987) distinguishes mereological sums from integral wholes via a unifying condition: such a condition is absent from sums but required for integral wholes. Take for example (1) the sum consisting of a car engine, the number two, and a unicorn, and (2) the car as an integral whole with its parts necessarily organized by a car design. In this paper we focus on integral wholes, in large part due to their relevance to physical ontology and also because sums are viewed as cognitively unintuitive (Pribbenow, 2002). Sticking with integral wholes, then, Fine (1999) uses different unifying conditions to further distinguish rigid embodiments, which we call static wholes, from variable embodiments, which we call variable wholes. A static whole is unified and identified by a relation over its parts at every time of its existence and its parts are fixed, thus the whole loses identity if any of its static parts are exchanged, missing, or related differently. For example, a ham sandwich is unified topologically with the ham between slices of bread, such that exchanging or removing the ham, or changing its relation to the other parts, leads to a sandwich with a different identity. In contrast, a variable whole has exchangeable parts and is unified and identified by a formal principle that picks out its parts over its entire lifetime, thus directly associating each part with the whole and possibly with each other part, at a single time or at different times. For example, a river’s water object and its water matter parts might be unified by a certain environmental process that determines if and when amounts of water matter flow in the river. A change in process would then lead to a change in the identity of the water object, such as a river fed by a flood and then a thunderstorm. However, missing parts and mixed wholes are not explicitly addressed by Fine. Mixed wholes can have some mixture of mandatory or optional parts, such as a car having a chassis and sunroof, respectively, or they can have multiple types of parts within any single parthood category, such as a car having both engines and wheels as essential variable parts.

Fig. 3.

Taxonomy of integral wholes for physical objects.

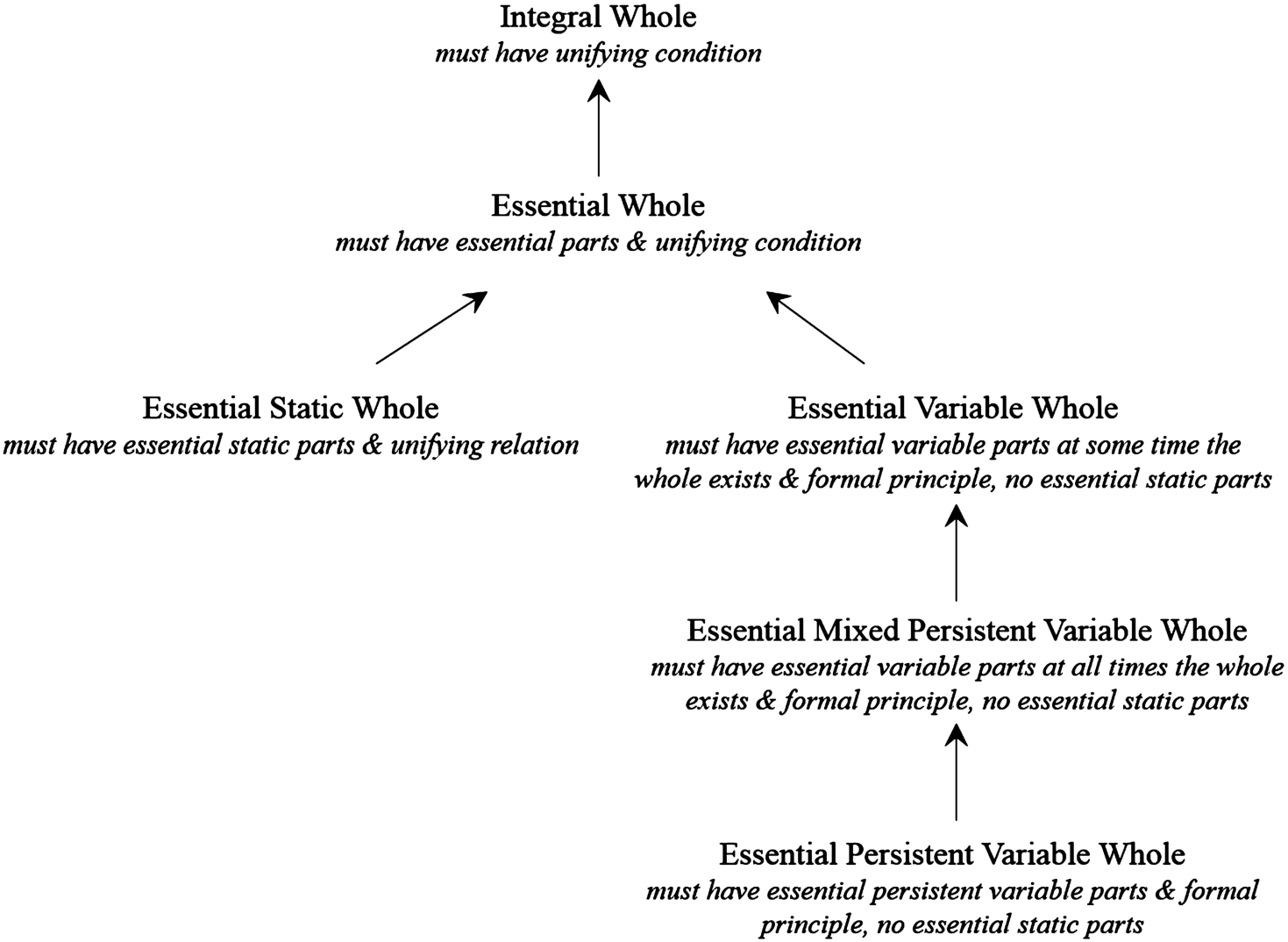
To address missing parts and mixed wholes, we extend static and variable wholes using the typology of parts developed above, as shown in Fig. 3. An essential static whole then must have some essential static parts, it can possibly have essential variable, non-essential or optional parts, and it must have a unifying relation over all parts. A car is therefore an essential static whole, as it must have a unique chassis and follow a car design, and it could have other possible types of parts, as per above. In contrast, all varieties of essential variable wholes must have some essential variable parts (at some time the whole exists), as well as a formal principle to select those parts, and they might also have non-essential and optional parts, but cannot have essential static parts. Essential persistent variable wholes then specialize essential variable wholes as they must have at least one type of essential persistent variable part (that cannot be missing, but is exchangeable). A water object is an example of an essential persistent variable whole as it must always have some (but not necessarily the same) amount of water matter as a part, and might also have some amounts of pollutant as an optional part.

Although not formalized here, essential mixed persistent variable wholes subsume essential persistent variable wholes. Essential mixed persistent variable wholes require some type of essential variable part to co-exist with the whole during its lifespan, but not a specific type of essential variable part, i.e. all types of essential variable parts can be missing at some time during the life of the whole, but not all types can be missing at the same time during its life. For example, assume a ship cannot have missing all its essential variable parts at the same time, such as an engine or hull, and retain identity.

Essential variable wholes are then even more general, and subsume essential mixed persistent variable wholes. They allow all essential variable parts to be missing at the same time during the life of the whole without impacting its identity, such as a professional hockey team that does not have any players under contract at some time. Indeed, a professional hockey team is a good example of an essential variable whole: it must have some hockey players at some time, but not necessarily some players at all times it exists (essential variable parts); it must have some coaches to function (non-essential variable parts) and it can possibly have mascots (optional parts), but no individual is essential (no essential static parts), and it is unified by certain contracts with the team, such that if an individual has such a valid contract at a time then the individual is a part of the team at that time (its formal principle).

Essential wholes further subsume essential static and variable wholes. Essential wholes are integral wholes that must have some essential parts and a unifying condition, as well as possibly non-essential and optional parts. They are introduced to complete the taxonomy of wholes with essential parts, as shown in Fig. 3, and are required to characterize water features. Other types of wholes derived strictly from non-essential or optional parts might also be considered, but are out of scope for this work. Lastly, wholes and parts can be nested (Fine, 1999): something that is a part can also be a whole possessing its own parts. For example, an engine is a variable part of a car, but the engine might also be a variable whole with missing and exchangeable parts, such as pistons and spark plugs.

4.4.Water features and their parts

Thus far the characterization of water features is quite coarse, as it does not specify whether a water feature has a certain key aspect as part and it does not identify the pertinent type of whole or part. To address this deficiency, a taxonomy of water features is derived from Hayes’ (1985) categorization of liquid entities, which is founded on notions of containment, support, movement and connection. Containment and support are the focus here, as these are sufficient to delineate the representative water features. Containment is the physical enclosure of one physical entity by another, and support is the means by which one material entity is held against and buttressed by another. Both containment and support are relations in this sense, and are construed in a maximal sense: a contained entity is fully enclosed and a supported entity has no gaps in support. Their negations, uncontainment and unsupport, then respectively include partial containment and support as well as their complete absence.

To delineate water features, we focus on containment between a solid material container and a water object, and support between a physical entity (liquid or solid) and a water object. As a consequence, all combinations can apply: a contained water object can be fully supported (e.g. by a riverbed) or not (e.g. in a leaky aquifer); a supported water object can be fully contained (e.g. by a riverbed) or not (e.g. in a flood); and a water object can be neither fully contained nor fully supported (e.g. in a cloud). However, these notions of containment and support are insufficient to completely differentiate the representative water features, inasmuch as water objects in rivers and aquifers might be both contained and supported.

Indeed, two refinements of containment (Hahmann and Brodaric, 2013) are required to delineate water features such as rivers and aquifers. Dependent containment implies a physical (material-spatial) dependency between entities that is necessary and essential: if the entities share matter, voids, or a matter-void boundary, they cannot be uncontained without physically changing all of them, unavoidably. For example, an aquifer’s water object is dependently contained by its container because they share matter – the rock matter and water matter spatially overlap at the macroscopic level of granularity of the aquifer (they do not overlap at a microscopic level). In contrast, a river’s water object is detachably contained by the riverbed inasmuch as the two do not share matter. Rivers and aquifers can thus be differentiated by these two kinds of containment.

Note that dependently contained water objects are not necessarily fully physically supported, for example, some aquifers are enclosed by impermeable surfaces that provide full support, i.e. fully confined aquifers, and others are enclosed by surfaces that provide graded support, i.e. leaky aquifers. Also note that support is broadly envisioned here, encompassing, for example, water in bays or oceans supported on some sides by a container and on others by a wall of water, such as where a bay meets the ocean, two oceans meet, or where a river empties into an ocean or another river. These variations require a deeper ontological analysis that is not addressed by this paper and support is simply taken as primitive.

These notions of containment, support, and dependence lead to a three-tier taxonomy of water features in which all representative water features are differentiated, as shown in Fig. 4. The first tier distinguishes between contained, supported and uncontained unsupported water features; the second tier further adds combinations of containment and support; and the third tier adds specializations for detachable containment (det-contains) and dependent containment (dep-contains).

Fig. 4.

Water feature taxonomy using containment, support and dependence as differentiae.

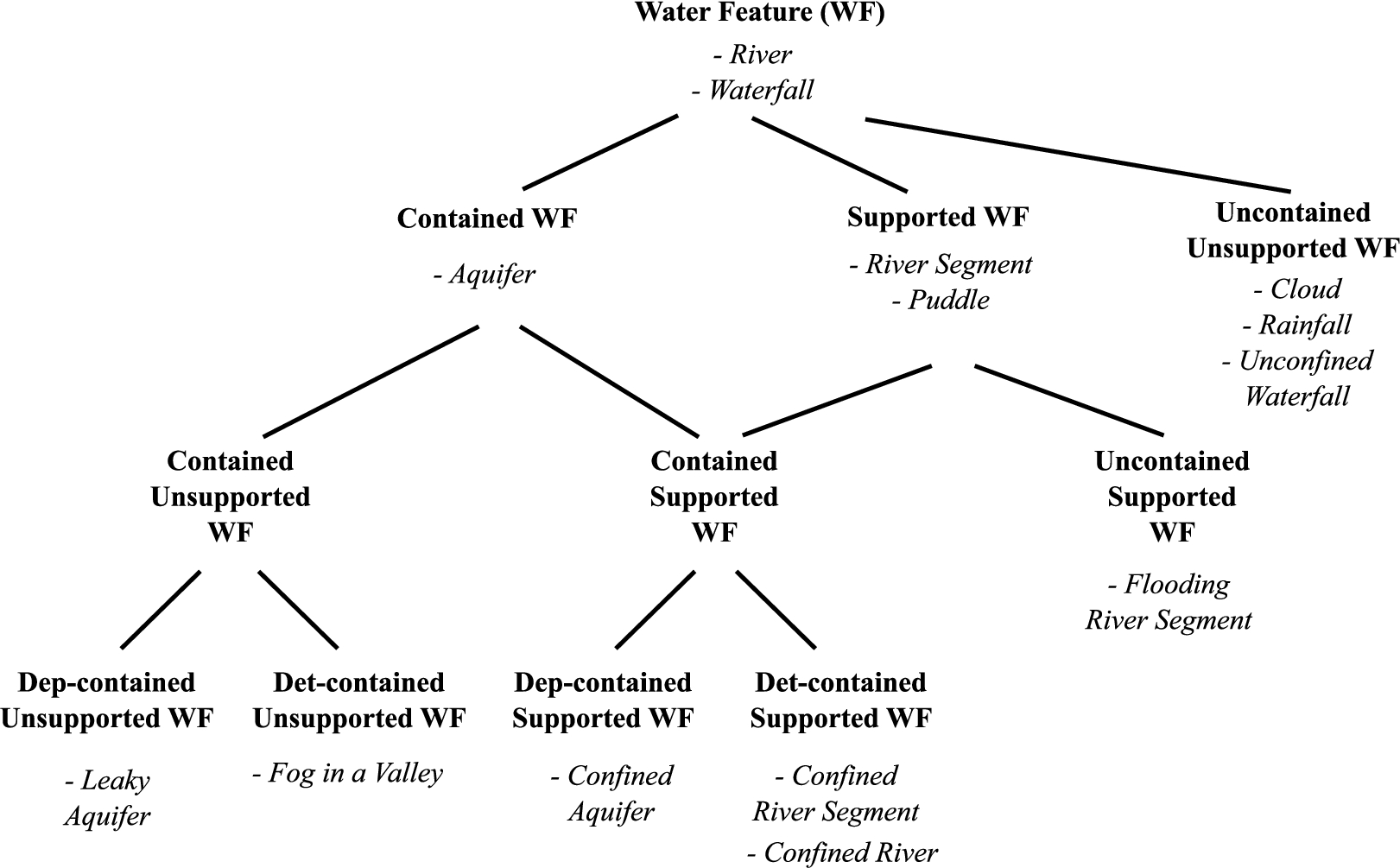
This taxonomy then helps identify the aspects that are essential parts for various water features. Combined with the relevant whole-part distinctions it leads to the following characterizations, which are elaborated formally in Section 5:

Water objects:	are essential persistent variable wholes, with amounts of water matter as essential persistent variable parts. This means water matter amounts can be exchanged, but cannot be missing, and water objects thus exist only when some water matter is present. For example, Lake Ontario’s water object does not exist at a time if there is no water matter amount in its container at that time, even though Lake Ontario might continue to exist in a dry state. As an essential persistent variable whole, the identity of a water object is tied to its formal principle. If the formal principle is a perdurant denoting water supply from a specific source, then the water object will retain identity while that perdurant is active, that is, while water is supplied by the same source. During pauses in water supply the water object will not exist, but once the supply resumes the object will return to existence with the same identity. However, if a new source perdurant supplies water, then the water object will be replaced by a new one with a different identity. Water supply perdurants can be quite intricate, possibly encompassing the range of environmental conditions impacting the water cycle for a geographical region. This perdurant-based formal principle is most straightforward in dry scenarios, in which a prior water object has dried up and new water is added; then the resulting water object is the same as the former if the source is the same, and it is a new water object if the source is different. For example, water objects in ephemeral streams are caused by irregular rainfall events that have unique identity, whereas those in intermittent lakes and streams are caused by repeating seasonal flows, supplemented by other sources such as precipitation, which might be considered in aggregate a single perdurant that stops and starts. Each ephemeral source would then generate a new water object, whereas the intermittent source would generate recurrences of the same water object. However, wet (top-up) scenarios are murkier, in that material is added to an existing water object by possibly multiple new sources, so it is then unclear how much material must be added to change a water object’s identity, and whether all pertinent new sources, possibly co-temporal, then trigger identity change. For example, do successive or simultaneous ephemeral sources change the identity of an existing water object if their individual or joint top-up amount is minimal? The formal principle might then be proportional, with identity change triggered if the amount of added water passes a specific threshold. It is noteworthy that such a formal principle, which binds water object identity to source perdurant identity, aligns generally with notions of objects in which perdurants are key to their identity (Galton and Mizoguchi, 2009).
Water features:	are essential wholes that have a water object as an essential variable part, and optional parts that include water features and other non-perdurant aspects. In essence, in its most general sense, a water feature is a unified whole that minimally must have some water at some time. The inclusion of a water object as an essential part means that each water feature is nested, necessarily having at least one part – the water object – that itself is a whole. Other key aspects that can be wholes and result in such nesting include containers, voids, and supporters. In contrast, a different kind of nesting occurs when parts are also water features, for example, a river possessing a waterfall, which leads to the delineation of complex and simple water features: complex water features must at some time have some parts that are water features, and simple water features do not have water feature parts at any time. This helps characterize a wide variety of water features, such as rivers (having lakes and waterfalls), river networks (having solely other rivers), aquifer systems (having other aquifers), and aquifers (neither having other aquifers nor other water features). The simple versus complex distinction also helps clarify various containment and support scenarios: for example, because rivers can have an open waterfall as a part, they are neither all supported nor all contained, and thus do not all have containers, voids, or supporters as essential parts. In fact, only some rivers have these as essential static parts, and are thus static wholes, such as fully confined rivers in which the water object is located inside the void and enclosed and supported by the container at all times it exists and in every segment. Waterfalls are then analogous to rivers in this sense, inasmuch as they are neither all supported nor all contained, and only some are essential static wholes, e.g. confined waterfalls. Consequently, rivers and waterfalls are essential wholes, because some instances are essential static wholes and others are not. All rivers are, however, inherently complex as each instance has at least one river segment as a mandatory part, while waterfalls do differ from rivers in having both complex or simple instances, e.g. only some have water feature parts such as subsidiary waterfalls. Identity criteria for water features are tied to their unifying criteria. Then a change to the unifying relation (for essential static wholes), the formal principle (for essential variable wholes), or the unifying condition (for essential wholes), will trigger a change to the identity of the water feature. As a result, water feature identity is affected by changes to water object identity only if the water object is an essential static part. As shown in Table 1, many water features do not have water objects as essential static parts, e.g. river segments or aquifers, and their identity is unaffected by water object exchanges or absences. Exceptions are clouds and rainfall, which do have a water object as an essential static part: then a new occurrence of cloud formation or raining will instigate a new cloud or rainfall, respectively. Many water features also have other essential static parts that impact identity, such as containers, supporters, voids or even other water features. Typically these parts are modifiable, evolving over time without triggering identity change in the water feature, e.g. the gradual addition of bends to the container of a river does not make it a different river. Even extreme events that dramatically alter the water feature and its parts, such as earthquakes, landslides or floods, do not necessarily trigger identity change. For example, if a container, supporter and void are essential variable wholes with formal principles tied to containment of a particular water object, then even radical changes to them will not precipitate a change to their identity, and thus to the identity of the contained water feature, if they continue to contain the original water object. If the water object is in turn identified by a distinct source, then the water feature will effectively retain identity as long as the water continues to flow from the same source, e.g. the identity of the Nile is then unaffected by changes to its flow path due to repeated flooding.
Contained water features:	are essential static wholes that have a container and its void as essential static parts, a water object as an essential variable part, and a supporter as an optional part. The supporter is optional because some examples of contained water features are supported and others are not. Because containment is applied strongly, i.e. a water feature is contained if the water object is fully enclosed by the container at all times the water object exists, a wide variety of water features are not contained, such as complex rivers with unenclosed waterfalls or river segments that flood. Dry water features are those in which the container exists but its water is depleted.
Supported water features:	are essential static wholes that have a supporter as an essential static part, a water object as an essential variable part, and a container and its void as optional parts, because not all supported water features are fully contained, such as waterfalls and rivers. Puddles are differentiated from rivers and waterfalls, and other supported water features, by water object parthood: puddles have a water object as an essential persistent variable part, i.e. not missing – there are no dry puddles – while other supported water features have the water object as an essential variable part, i.e. possibly missing, such as in dry waterfalls or dry rivers. In both these cases water objects are exchangeable, for example, when a puddle’s water object changes identity due to a significant top-up of water from a thunderstorm.
Uncontained Unsupported water features:	are essential static wholes that are not contained and not supported (by another liquid or solid endurant). Prototypical examples include clouds, rainfall, and unconfined waterfalls, which are distinguished by water object parthood: clouds and rainfall have water objects as essential static parts, and unconfined waterfalls have them as essential variable parts.

Table 1 summarizes water features as essential wholes with various parts, including all representative water features. This framework now provides sufficient ontological granularity to identify hosts for the qualities being measured by the most common water sensors (from Section 2). These hosts include the three main types of water entities delineated in this analysis, namely, amounts of water matter, water objects, and water features:

Water chemistry	measurements assess qualities such as Arsenic concentration, which are hosted by an amount of water matter. This recognizes that constituents, such as pollutants, can move between water features, which would be impossible if they were hosted by them or their water objects.
Water flow	measurements assess qualities hosted by an amount of water matter necessarily participating in a flow perdurant (Galton, 2007).
Water height	measurements assess a quality hosted by the water object. Height cannot be hosted by a water matter amount, because the height remains when the water matter leaves the water feature, and it cannot be hosted by the water feature, say a river, because not all parts such as the riverbed rise or fall, only the water does (Fine, 1999). Height is also not necessarily tied to a container, e.g. floods can have a height.
Water overflow	measurements, such as the geographical extent or volume of floodwater, are typically estimated from satellite-mounted sensors and assess qualities hosted by a contained water feature, because it is the relevant whole that relates a container and water object. Neither the container nor water object can alone host these measurements: a container is not the thing being spilled, and spillage at best applies to a portion of the water object and only in relation to a container.

Table 1

Summary of water feature wholes and parts with examples in bold. Unifying conditions are not listed

Water feature	Type of integral whole	Essential static part(s)	Essential persistent variable part(s)	Essential variable part(s)	Optional part(s)
Water Feature River, Waterfall	Essential Whole			Water Object	Container Void
Water Feature River, Waterfall					Supporter Water Feature
Contained Water Feature Aquifer	Essential Static Whole	Container Void		Water Object	Supporter
Supported Water Feature River Segment	Essential Static Whole	Supporter		Water Object	Container Void
Supported Water Feature with Water Object as Persistent Variable Part Puddle	Essential Static Whole	Supporter	Water Object		Container Void
Contained Supported Water Feature Confined: Aquifer/River Segment/River	Essential Static Whole	Container Void Supporter		Water Object
Contained Unsupported Water Feature Leaky Aquifer, Fog-in-Valley	Essential Static Whole	Container Void		Water Object
Uncontained Supported Water Feature Flooding River Segment	Essential Static Whole	Supporter		Water Object
Uncontained Unsupported Water Feature Unconfined Waterfall	Essential Whole			Water Object
Uncontained Unsupported Water Feature with Water Object as Static Part Cloud, Rainfall	Essential Static Whole	Water Object
Water object	Essential Persistent Variable Whole		Amount of Water Matter

5.Formalization

A comprehensive formalization for all relevant types of wholes and parts is beyond this paper, though the detailed, yet incomplete, formal sketch presented here is sufficient to characterize water features. Similarly, a formalization for every node in the water feature taxonomy is not possible, for reasons of space, and therefore only some representative water features are formalized, as guidance for application to the rest.

5.1.Background

The formalization extends the DOLCE ontology (Masolo et al., 2003) and builds upon prior work in hydro ontology involving material-spatial interdependence, voids, the physical relations of containment and constitution, as well as broad notions about how these are interrelated in the water domain.

5.1.1.DOLCE foundations

DOLCE provides the basic categories of endurants (ED, entities that exist wholly at individual points in time), perdurants (PD, entities like events or processes that extend in time), and abstract entities such as spatial regions (S) and time regions (TR), which we reuse here as shown in the top part of Fig. 5. Of primary concern here are physical endurants and objects (PED, POB) and, more specifically, non-agentive physical objects (NAPO, e.g. aquifers), that are constituted by amounts of matter (M, e.g. water matter or rock matter amounts) and that host various dependent features (F, e.g. surfaces, boundaries, edges or voids). Material endurants (introduced in Hahmann and Brodaric, 2013) then include physical objects, amounts of matter, as well as relevant part dependent features (RPF, e.g. physical parts of physical objects, such as surfaces). Physical voids (V, e.g. depressions or cavities) are dependent place features (DPF) and important parts of many water features. We assume all the subtype relationships and disjointness among these entities as axioms without explicitly restating them here. The only two categories that are not disjoint are mat and F, their intersection is RPF.

Fig. 5.

The taxonomy of relevant DOLCE entities, including the participation PC and presence PRE relations, the non-DOLCE material entities mat and physical voids V, the region and convex hull functions r() and ch(), and four specializations (in blue) required for hydro ontology (Brodaric and Hahmann, 2014). Also included are examples from the newly developed taxonomy of water features (in red) and their parthood relations. Specific kinds of water features, such as river, aquifer, cloud, or puddle, further specialize these entities. Some relationships, e.g. between river and its specializations, are omitted for reasons of space and readability.

Endurants can participate at different times in perdurants, such as environmental processes, as expressed by the DOLCE participates relation PC(x,y,t), with the last parameter being a time region – either atomic (At; i.e. a time point) or not (i.e. a time interval). The PRE(x,t) relation denotes that the endurant x exists at time t. For brevity, we say that any entity x exists if it is present at some time (Exists-D).

(Exists-D)

Exists(x)≡∃t[PRE(x,t)] (x exists if it is present at some time)

Dependence is a foundational notion in which entities are related in some non-accidental way. Ontological dependence refers to a metaphysical reliance grounded in existence or essence, such that something could not exist, or be the way it is, without the other (Simons, 1987). DOLCE provides two kinds of ontological dependence, generic and specific, in which individuals are co-temporal, that is, constantly co-present in time. Generic constant dependence, GD, relates two types such that any instance of one type requires the constant co-temporal existence of some unspecific instance of the other type, and the types are disjoint, DJ (GD-D). A much stronger variant is specific constant dependence, SD, specified between individuals (SD-D1) and types (SD-D2): then any individual (of one type) requires the co-temporal existence of a specific individual (of the other disjoint type). Generic constant dependence subsumes specific dependence between types (SP-T1). The axioms for GD and SD, as presented here, are slight modifications of DOLCE’s.

(GD-D)	GD(Φ,Ψ)≡DJ(Φ,Ψ)∧∀x[Φ(x)→∃t(PRE(x,t))]∧∀x,t[[Φ(x)∧At(t)∧PRE(x,t)]→∃y[Ψ(y)∧PRE(y,t)]](non-modal version of DOLCE’s generic constant dependence based on Dd71)
(SD-D1)	SD(x,y)≡∃t[PRE(x,t)]∧∀t[PRE(x,t)→PRE(y,t)] (non-modal version of DOLCE’s specific constant dependence between instances based on Dd69)
(SD-D2)	SD(Φ,Ψ)≡DJ(Φ,Ψ)∧∀x[Φ(x)→∃y(Ψ(y)∧SD(x,y))] (non-modal version of DOLCE’s specific constant dependence between types based on Dd70)
(SP-T1)	SD(Φ,Ψ)→GD(Φ,Ψ) (specific constant dependence specializes generic constant dependence; from GD-D, SD-D1, SD-D2)

5.1.2.Spatial regions

The atemporal region function r(x) is introduced in Hahmann (2013) to map the physical space occupied by a physical endurant to a corresponding abstract spatial region (see Hahmann and Brodaric, 2012, 2013, 2014; Hahmann et al., 2014). This enables operating with spatial regions of all dimensions in a purely mathematical-logical formalism – irrespective of whether these regions correspond to meaningful physical endurants. All spatial regions, denoted by the type S, are to be interpreted as finite sets of regular closed regions of some uniform dimension1 1 (Hahmann, 2018). In other words, any spatial region is either (a) a regular closed region homeomorphically embeddable in Rm for some fixed m or (b) composed from a finite set of components – all of which are all homeomorphically embeddable in Rm for the same fixed m and which can only overlap in their boundaries, that is, x∩y⊆(cl(x)∖int(x))∩(cl(y)∖int(y)) must be true for any two components thereof.

Our spatial theory provides intersection (·) and difference (−) operators (Hahmann, 2018), sums as needed, as well as mereotopological predicates, such as spatial containment Cont (S-A5 to S-A9) and connectivity, C. The primitive predicate ⩽dim allows the dimensionality of spatial regions to be defined and compared, and is also used to define various spatial relations, such as spatial (proper) parthood, P and PP (EP-D, EPP-D),2 2 as well as unary predicates, such as MaxDim (MaxDim-D), which denotes a region of maximal dimension (i.e. of codimension zero), and Con (Con-D), which denotes a one-piece spatial region. See Hahmann (2013) for a full treatment of the underlying spatial framework that includes entities of different dimensions (e.g. 3D regions, 2D regions, curves, points).

The region function is extended here by a time parameter to r(x,t) to reflect the spatial region occupied by an endurant x at time t (St-A1). For time points, that is, atomic time regions, r(x,t) either returns the corresponding spatial region or an empty region denoted by rz (St-A2).3 3 For time intervals, that is, non-atomic time regions, r(x,t) only returns a spatial region when the endurant has stayed in the same region during that time. Otherwise, the empty region rz is returned signifying either the endurant did not exist or has moved at some point during that time. All of our spatial relations (e.g. P, PP, C) only apply to nonempty spatial regions as exemplified by (S-A3).4 4

(St-A1)	S(r(x,t)) (the region function returns a spatial region)
(St-A2)	r(x,t)≠rz→TR(t) (the region function only returns a nonempty spatial region if the second parameter is a time region)
(St-A3)	S(x)∧TR(t)→x=r(x,t) (spatial regions are their own region at all times)
(S-A4)	Cont(x,y)→S(x)∧S(y)∧x≠rz∧y≠rz (containment, and thus all defined spatial relations, applies only to nonempty spatial region)
(S-A5)	S(x)∧x≠rz↔Cont(x,x) (Cont reflexive)
(S-A6)	Cont(x,y)∧Cont(y,x)→x=y (Cont antisymmetric)
(S-A7)	Cont(x,y)∧Cont(y,z)→Cont(x,z) (Cont transitive)
(S-A8)	Cont(x,y)→x⩽dimy (inclusion requires lower or equal dimension)
(St-T1)	r(rz,t)=rz (the empty region has always itself as region)5 5
(S-T1)	S(rz) (the empty region is a spatial region; from St-T1 and St-A1)
(S-T2)	x=rz↔S(x)∧∀y[¬Cont(x,y)∧¬Cont(y,x)] (no inclusion for the empty region; from S-T1, S-A4, S-A5)
(EP-D)	P(x,y)≡Cont(x,y)∧x⩽dimy∧y⩽dimx (equi-dimensional parthood)
(EPP-D)	PP(x,y)≡P(x,y)∧¬P(y,x) (equi-dimensional proper parthood)
(MaxDim-D)	MaxDim(x)≡S(x)∧x≠rz∧∀y[S(y)→y⩽dimx] (spatial region of maximal dimension)
(Con-D)	Con(x)↔∀y[PP(y,x)→y·(x−y)≠rz] (self-connected spatial region)

The special spatial function ch(x,t) denotes the convex hull of a entity, which again yields a spatial region (CHt-A1), and is solely defined spatially (CHt-A2) such that a nonempty region is returned only if the convex hull contains the entity’s region at the time t (CHt-A3) (details in Hahmann, 2013).

(CHt-A1)	S(ch(x,t)) (the convex hull function returns a spatial region)
(CHt-A2)	ch(x,t)=ch(r(x,t)) (the convex hull is defined in terms of the occupied region)
(CHt-A3)	ch(x,t)≠rz→TR(t)∧P(r(x,t),ch(x,t)) (a nonempty region is only returned when t is a time region and results in the spatial region being a spatial part of its convex hull)
(CHt-T1)	ch(rz,t)=rz (the empty region is the convex hull of the empty region; from CHt-A3, St-T1, EP-D, S-A4)

Physical endurants are present when occuping a nonempty region (PEDt-A1) of maximal dimension (i.e. a 3D region; PEDt-A2).

(PEDt-A1)	PED(x)→∀t[PRE(x,t)↔r(x,t)≠rz] (a PED is present exactly when it is located in a nonempty region)
(PEDt-A2)	PED(x)∧PRE(x,t)→MaxDim(r(x,t)) (when a PED is present, it is located in a region of maximal dimension)

5.1.3.Containment and constitution

Full physical containment, fully-phys-contains(x,y), is the relation in which one physical endurant y, the containee, is located completely inside another endurant x, the container, such that the containee, at the very least, is located within the convex hull of the container6 6 (FPCont-D). According to this definition, full physical containment applies to cases like the riverbed of a meandering river physically containing the ground partially enclosed by its bends, though the river channel (i.e. the depression where the water is actually located) does not contain the ground enclosed by the bends, because containment by a void additionally requires full spatial overlap of the containee and void.

In previous work (Hahmann and Brodaric, 2013), we have further distinguished different kinds of full physical containment according to (1) whether the container and containee are materially-spatially interdependent (elaborated below in Section 5.2.1), that is, in a mat-dep relation, or not; and (2) the types of container and containee, such as a material endurant containing another material endurant or void, and a void containing a material endurant or another void. Dependent containment, dep-contains(x,y), holds when a container and containee are mat-dep (DepCont-D), otherwise detachable containment, det-contains(x,y) holds (DetCont-D). Amongst the many specializations of fully-phys-contains(x,y), only the following are relevant here: materially-contains(y,x) as the dependent containment between material endurants (MCont-D); submaterial(y,x) as dependent containment between material endurants that share matter (SubMat-D); hosts-v(x,y) as dependent containment between a void and its host (HostsV-D); surrounds-mat(x,y) as detachable containment between material endurants (MSur-D); and mat-inside(y,x) as detachable containment in which a material containee is inside a void (MInside-D).

(FPCont-D)	fully-phys-contains(y,x)↔PED(x)∧PED(y)∧P(r(x),ch(y))∧[¬mat(y)→P(r(x),r(y))] (full physical containment: the containee is completely inside the convex hull of the container)
(DepCont-D)	dep-contains(y,x)↔fully-phys-contains(y,x)∧mat-dep(x,y) (dependent containment: the container and containee are materially-spatially interdependent)
(DetCont-D)	det-contains(y,x)↔fully-phys-contains(y,x)∧¬mat-dep(y,x) (detachable containment: generic containment between materially-spatially independent endurants)
(MCont-D)	materially-contains(y,x)↔dep-contains(y,x)∧mat(x)∧mat(y) (material containment: dependent containment between material endurants)
(SubMat-D)	submaterial(x,y)↔materially-contains(y,x)∧P(r(x),r(y)) (submaterial containment: container and containee share matter)
(HostsV-D)	hosts-v(x,y)↔dep-contains(x,y)∧mat(x)∧V(y) (hosting a void: dependent containment between the void and its host)
(MSur-D)	surrounds-mat(y,x)↔det-contains(y,x)∧mat(x)∧mat(y) (material endurant y surrounds a material endurant x)
(MInside-D)	mat-inside(x,y)↔det-contains(y,x)∧mat(x)∧V(y) (material endurant x is inside the void y)

Constitution relations for material endurants are defined in Hahmann and Brodaric (2014) as specializations of submaterial(y,x) and distinguished by granularity, with intragranular-constituent(y,x) denoting a maximal constituent at the same level of granularity (e.g. between an object and its entire constituting matter; Const-D2). The complementary relation of intergranular constitution relates entities at different levels of granularity (e.g. between an object and a molecule), but is not used here.

(Const-D2)

intragranular-constituent(x,y)↔submaterial(x,y)∧porespaceall(x)=r(x)·porespaceall(y) (intragranular constitution is a submaterial relation where the constituent pore space is equivalent to the pore space of the constituted object7 7)

To express notions of temporal parthood, such as temporarily missing parts or constantly present parts, it is necessary to extend the previous atemporal versions by including a time parameter t for all physical relations. For example, the atemporal definitions from above for containment and its various specializations are replaced by the temporal variants below that carry a t index. These temporal variants denote that physical endurant x is in a particular containment or constitution relation to y at time t, where t is an atomic or non-atomic time region. Even the most general containment relation, fully-phys-contains, requires the involved endurants to be co-present at any time they are in such a relation (FPContt-T1). For the remainder of the formalization and discussion in this paper, only the temporal versions are relevant, essentially superseding the atemporal versions from above.

(FPContt-D)	fully-phys-containst(y,x,t)↔PED(x)∧PED(y)∧TR(t)∧P(r(x,t),ch(y,t))∧[¬mat(y)→P(r(x,t),r(y,t))]
(DepContt-D)	dep-containst(y,x,t)↔fully-phys-containst(y,x,t)∧mat-dept(x,y,t)
(DetContt-D)	det-contains(y,x,t)↔fully-phys-contains(y,x,t)∧¬mat-dep(y,x,t)
(MContt-D)	materially-containst(y,x,t)↔dep-containst(y,x,t)∧mat(x)∧mat(y)
(SubMatt-D)	submaterialt(x,y,t)↔materially-containst(y,x,t)∧P(r(x,t),r(y,t))
(HostsVt-D)	hosts-vt(x,y,t)↔dep-containst(x,y,t)∧mat(x)∧V(y)
(MSurt-D)	surrounds-matt(y,x,t)↔det-containst(y,x,t)∧mat(x)∧mat(y)
(MInsidet-D)	mat-insidet(x,y,t)↔det-containst(y,x,t)∧mat(x)∧V(y)
(Constt-D2)	intragranular-constituentt(x,y,t)↔submaterialt(x,y,t)∧porespaceall(x,t)=r(x,t)·porespaceall(y,t)
(FPContt-T1)	fully-phys-containst(x,y,t)→PRE(x,t)∧PRE(y,t) (full physical containment at time t requires x and y to be co-present at that time; from FPContt-D, EP-D, S-A4, CHt-A3, PEDt-A1)

5.1.4.The hydro ontological square

Previous work (Hahmann and Brodaric, 2012; Brodaric and Hahmann, 2014; Hahmann et al., 2016) outlines a framework of entities central to hydro ontology, called the Hydro Foundational Ontology (HyFO). In its initial form it consists of four key entities: (1) amounts of matter M, with specializations including amounts of fluid matter FM and amounts of water matter WM (FM-A1,A2; derived from Hahmann and Stephen, 2018), which are the material constituents of container solid bodies and water objects, respectively; (2) water bodies WB denoting the water contained by a water feature and that have now been renamed to water objects WO, for improved clarity, and are enhanced below in Section 5.4.1; (3) voids, here called solid body voids SBV, as the voids hosted by solid container bodies (SBV-D) wherein water can be located; and (4) containers, called container solid bodies CSB (CSB-D), as the solid bodies (SB-D) that host voids where water can be located and contained (e.g. river channels or geological formations). These entities, connected by the relations of containment, constitution, and hosting a void, form the original hydro ontological square (HOS) (Brodaric and Hahmann, 2014), an ontology pattern for the water domain. The pattern is further refined in Hahmann et al. (2016); Hahmann and Stephen (2018). Key refinements include the addition of a relation for physical support (Sup-D) and the closely related concept of supporters or supporting boundaries (SUP-A1), which are physical endurants that support material entities. Note supportst(x,y) is currently only a placeholder for the full physical support relation, which requires further analysis and formalization beyond the scope of this paper.

(FM-A1)	FM(x)→M(x) (Fluid Matter is a specialization of Matter)
(FM-A2)	WM(x)→FM(x) (Water Matter is a specialization of Fluid Matter)
(SB-D)	SB(x)≡NAPO(x)∧∃y,t[M(y)∧intragranular-constituentt(y,x,t)]∧∀z,t[intragranular-constituentt(z,x,t)→¬FM(z)](a solid body is a NAPO that is constituted by only non-fluid amounts of matter)
(SBV-D)	SBV(x)≡V(x)∧∃y,z,t[SB(y)∧hosts-vt(y,x,t)] (a solid body void is a void hosted by a solid body submaterial as a generalization of a hydro void HV, from Stephen, 2016)
(CSB-D)	CSB(x)≡SB(x)∧∃y,t[SBV(y)∧hosts-vt(x,y,t)] (a container solid body is a solid body that hosts a solid body void)
(Sup-D)	supportst(x,y,t)→PED(x)∧mat(y)∧TR(t)∧PRE(x,t)∧PRE(y,t) (a physical endurant physically supporting a material entity, both present at time t)
(SUP-A1)	SUP(x)≡∃y,t[supportst(x,y,t)] (a supporter supports some material entity)

5.2.Parthood relations for physical objects

For our immediate purpose of representing water features, parthood relations must include material and immaterial parts such as amounts of matter, voids, and supporters, but wholes can be limited to DOLCE’s physical objects (POB).

5.2.1.Physical object parthood

The most general parthood relation formalized here is physical object parthood (POBPartt-D), henceforth referred to as POB parthood for the relation or POB part for the participating part. This relation between individuals is denoted as POBpartt(x,y,t), meaning that individual x (a material endurant or a dependent feature) is a part of individual y (a physical object) at time t, and that x and y are materially-spatially interdependent – i.e. such wholes and parts must be co-present and share physical space or matter whenever x is part of the whole8 8 (POBPartt-T1, POBPartt-T2, POBPartt-T3).

(POBPartt-D)	POBpartt(x,y,t)≡POB(y)∧[[submaterialt(x,y,t)∧x≠y]∨[DPF(x)∧∃z[mat(z)∧submaterialt(z,y,t)∧hostst(z,x,t)]]](physical object parthood is the relation between a physical object y and a material or feature part that is either a proper submaterial or hosted by a submaterial)9 9
(POBPartt-T1)	POBpartt(x,y,t)→PRE(x,t) (the part must be present at time t; from POBPartt-D, SubMatt-D, HostsVt-D, HostsVt-D, DepContt-D, FPContt-T1)
(POBPartt-T2)	POBpartt(x,y,t)→PRE(y,t) (the whole must be present at time t; from POBPartt-D, SubMatt-D, HostsVt-D, DepContt-D, FPContt-T1)
(POBPartt-T3)	POBpartt(x,y,t)→mat-dept(x,y,t) (the part and whole are materially-spatially interdependent, though not necessarily ontologically dependent; from POBPartt-D, HostsVt-D, SubMatt-D, HostsVt-D, DepContt-D)

POB parthood between types is quite weak, stating that if some instance of type Ψ, a whole, has a physical part that is an instance of type Φ at some time, then Φ is a POB part of Ψ (POBPart-D). We impose that any individual in this parthood relation must exist at some time (POBPart-A1).

(POBPart-D)	POBpart(Φ,Ψ)≡∃x,y,t[Φ(x)∧Ψ(y)∧POBpartt(x,y,t)] (general POB parthood between types: some instance of type Ψ has a part of type Φ at some time t)
(POBPart-A1)	POBpart(Φ,Ψ)∧Ψ(y)→Exists(y) (any instance of a whole in POB parthood must exist)

Remark about Notation 1.

All axioms, definitions, and theorems that use types Φ and Ψ as parameters (e.g. POBpart(Φ,Ψ)) or as indices (e.g. MPΦ,Ψ(x,y,t)) are schemata that must be instantiated for any unary named predicate that specializes PED. A finite number of such types is assumed, and in practice this number is expected to be fairly small. Note that POBPart-D together with POBPartt-T1,T2, imply that all types Φ and Ψ to which POBpart applies must have non-empty extensions.

5.2.2.Mandatory and optional parthood

In Mandatory POB parthood, every instance of Ψ must have an instance of Φ as a part at some time.10 10 Versions of this relation are specified between types (MP-D), typed versions between instances (MPΦ,Ψ-D), and an untyped version between individuals (MPany-D). Mandatory parthood specializes POBparthood (MP-T1) and mandatory parthood is preserved for specializations of Φ (MP-T2).

(MP-D)	MP(Φ,Ψ)≡∀y[Ψ(y)→∃x,t[Φ(x)∧POBpartt(x,y,t)]] (mandatory POB parthood between type Ψ and type Φ)
(MPΦ,Ψ-D)	MPΦ,Ψ(x,y,t)≡MP(Φ,Ψ)∧Φ(x)∧Ψ(y)∧POBpartt(x,y,t) (mandatory POB parthood between instances of type Φ and type Ψ for a time t during which x is a physical object part of y)
(MPany-D)	MPany(x,y,t)≡⋁Φ,Ψ[MPΦ,Ψ(x,y,t)] (mandatory POB parthood between individuals, irrespective of their specific types. This denotes the disjunction over all possible combinations of Φ and Ψ where both are specializations of PED)
(MP-T1)	MP(Φ,Ψ)→POBpart(Φ,Ψ) (mandatory POB parthood specializes POB parthood; from MP-D, POBPart-D)
(MP-T2)	MP(Φ,Ψ)∧∀y[Ψ′(y)→Ψ(y)]→MP(Φ,Ψ′) (mandatory parthood is preserved for specializations of Φ; from MP-D)

Remark about Notation 2.

The notation ⋁Φ,ΨΥ(Φ,Ψ) as used in MPany-D abbreviates the disjunction over the set of all terms Υ(Φ,Ψ) where the term Υ(Φ,Ψ) is true for two named unary predicates Φ and Ψ that are specializations of PED. For example, ⋁Φ,Ψ[MPΦ,Ψ(x,y,t)] denotes the disjunction of all terms MPΦ,Ψ(x,y,t) for any combinations of Φ and Ψ where MP(Φ,Ψ).

In optional POB parthood Φ is an optional POB part of Ψ if not every instance of type Ψ has a POB part instance of Φ at some time; this is expressed for types (OP-D) and instances (OPΦ,Ψ-D).

(OP-D)	OP(Φ,Ψ)≡POBpart(Φ,Ψ)∧¬MP(Φ,Ψ) (optional POB parthood between Φ and Ψ as POB parthood that is not mandatory)
(OPΦ,Ψ-D)	OPΦ,Ψ(x,y,t)≡OP(Φ,Ψ)∧Φ(x)∧Ψ(y)∧POBpartt(x,y,t) (optional POB parthood between instances of Φ and Ψ at a time t)

Also note the following ramifications of using temporal criteria to differentiate mandatory and optional parts, instead of the modal criteria of necessity and possibility: (1) every whole Ψ that accidentally has a part Φ at all times it exists exemplifies mandatory POB parthood instead of possible parthood; and (2) every whole Ψ that accidently does not have a part Φ at all times it exists does not exemplify physical parthood at all. However, these consequences for such marginal cases seem acceptable for practical purposes, and the approach aligns with our prior work, which is non-modal.

5.2.3.Essential and non-essential variable parthood

Mandatory parthood is further delineated into essential variable parthood (EVP) and non-essential variable parthood (NEVP), using ontological dependence as discriminator: essential parts have wholes ontologically dependent on them at some time they exist, though not necessarily at all times they exist, and non-essential parts are mandatory, but do not have wholes ontologically dependent on them. Because of the temporal inconstancy of the ontological dependence in essential variable parthood, generic constant dependence GD is inappropriate and a weaker temporal form is required. This weaker form cannot be expressed non-modally, thus we treat EVP as a primitive notion that specializes MP (EVP-A1). EVP is preserved for specializations of parts (EVP-A2), instance versions are defined in typed (EVPΦ,Ψ-D) and untyped (EVPany-D) forms, such that every instance must have an essential variable part at some time (EVP-T1).

(EVP-A1)	EVP(Φ,Ψ)→MP(Φ,Ψ) (essential variable parthood between types Φ and Ψ specializes mandatory parthood)
(EVP-A2)	EVP(Φ,Ψ)∧∀y[Ψ′(y)→Ψ(y)]→EVP(Φ,Ψ′) (essential variable parthood is preserved for specializations of Ψ)
(EVPΦ,Ψ-D)	EVPΦ,Ψ(x,y,t)≡EVP(Φ,Ψ)∧Φ(x)∧Ψ(y)∧POBpartt(x,y,t) (essential variable parthood between instances at times t when x is actually a POB part of y11 11)
(EVPany-D)	EVPany(x,y,t)≡⋁Φ,Ψ[EVPΦ,Ψ(x,y,t)] (essential variable parthood between individuals irrespective of their specific types)
(EVP-T1)	EVP(Φ,Ψ)∧Ψ(y)→∃x,t[EVPΦ,Ψ(x,y,t)] (essential variable parthood between Φ and Ψ requires that every instance of Ψ has an essential variable part x of type Φ; from EVPΦ,Ψ-D, EVP-A1, MP-D)

Non-essential variable parthood is the relation in which Φ is a mandatory part of Ψ, but Ψ is not ontologically dependent on Φ, rather it is dependent on Φ in some other way, in addition to materially-spatially, such as functionally, causally, or legally. As Φ is not necessarily constantly co-temporal with Ψ, GD is again inappropriate, and non-essential variable parthood is then specified as a mandatory part that is not an essential variable part for types (NEVP-D) and instances (NEVPΦ,Ψ-D). Consequently, if EVP is understood to mean each Ψ is ontologically dependent on some Φ, then its negation in NEVP means that each Ψ might have some, but not all, instances ontologically dependent on some Φ instance, which is a subtle variation on the original intuition behind NEVP due to the formalization.

(NEVP-D)	NEVP(Φ,Ψ)≡MP(Φ,Ψ)∧¬EVP(Ψ,Φ) (non-essential variable parthood between types Φ and Ψ)
(NEVPΦ,Ψ-D)	NEVPΦ,Ψ(x,y,t)≡NEVP(Φ,Ψ)∧Φ(x)∧Ψ(y)∧POBpartt(x,y,t) (non-essential variable parthood between instances of type Φ and Ψ at time t)

5.2.4.Essential persistent variable parthood

Essential parthood, EVP(Φ,Ψ), can be further refined to essential persistent variable parthood, EPVP(Φ,Ψ), where any instance y of Ψ has an instance of Φ (on which y depends) as a part at all times during its lifetime, though that part is exchangeable, that is, different instances of Φ may be a part of Ψ at different times. Because of this exchangeability, we impose the condition that a part exists only on time instants; as for time intervals no single x may exist that is a part throughout the entire interval. There are versions for types (EPVP-D) and instances (EPVPΦ,Ψ-D, EPVPany-D), and it can be shown that generic dependence is implied when types are disjoint (EPVP-T1), and that this parthood can be preserved under specialization of the part Φ (EPVP-T2).

(EPVP-D)	EPVP(Φ,Ψ)≡EVP(Φ,Ψ)∧∀y,t[Ψ(y)∧PRE(y,t)∧At(t)→∃x[Φ(x)∧POBpartt(x,y,t)]] (essential persistent variable parthood between two types Φ and Ψ)
(EPVPΦ,Ψ-D)	EPVPΦ,Ψ(x,y,t)≡EPVP(Φ,Ψ)∧Φ(x)∧Ψ(y)∧POBpartt(x,y,t) (essential persistent variable parthood between two instances of type Φ and Ψ at time t)
(EPVPany-D)	EPVPany(x,y,t)≡⋁Φ,Ψ[EPVPΦ,Ψ(x,y,t)] (essential persistent variable parthood between individuals irrespective of their specific types)
(EPVP-T1)	EPVP(Φ,Ψ)∧DJ(Φ,Ψ)→GD(Ψ,Φ) (essential persistent variable parthood implies generic constant dependence when Φ and Ψ are disjoint types; see proof below)
(EPVP-T2)	EPVP(Φ,Ψ)∧∀y[Ψ′(y)→Ψ(y)]→EPVP(Φ,Ψ′) (essential persistent variable parthood is preserved for specializations of Φ; from EPVP-D)

Proof Sketch for EPVP-T1.

Assume Φ and Ψ are arbitrary types with EPVP(Φ,Ψ) and DJ(Φ,Ψ).

We want to prove GD(Ψ,Φ), that is, DJ(Ψ,Φ)∧∀y[Ψ(y)→∃t(PRE(y,t))]∧∀y,t[[Ψ(y)∧At(t)∧PRE(y,t)]→∃x[Φ(y)∧PRE(x,t)]]. The assumption already entails DJ(Ψ,Φ) because it is a symmetric relation.12 12

To prove ∀y[Ψ(y)→∃t(PRE(y,t))] we assume Ψ(y) for an arbitrary y. By EPVP-D, EVP(Φ,Ψ); by EVP-A1, MP(Φ,Ψ); and by MP-T1, POBPart(Φ,Ψ) all follow. Then by POBPart-A1, Exists(y), and ∃t[PRE(y,t)], the desired goal is reached by Exists-D.

To prove ∀y,t[[Ψ(y)∧At(t)∧PRE(y,t)]→∃x[Φ(x)∧PRE(x,t)]] we assume y to be an entity such that Ψ(y) and At(t) and PRE(y,t). By EPVP-D, ∃x[Φ(x)∧POBpartt(x,y,t)] follows and from POBpartt(x,y,t), PRE(x,t) also immediately follows by POBPartt-T1, resulting in ∃x[Φ(x)∧PRE(x,t)] as desired.

Together, it follows that GD(Ψ,Φ), because both conjuncts in its definition are satisfied. □

5.2.5.Essential static parthood

A further strengthening of essential persistent variable parthood leads to essential static parthood, ESP(Φ,Ψ), where not only some instance x of Φ needs to be part of any y of Ψ at all times of its existence, but it has to be the same instance x throughout y’s entire lifetime (ESP-D). Then, unlike esssential variable parthood, the instance versions of essential static parthood do not require a time parameter t, because it is the same relation at all times when y exists (ESPΦ,Ψ-D, ESPany-D). Essential static parthood specializes specific dependence (ESP-T1), each instance of the whole must have a essential static part at all times (ESP-T2), and this parthood is also preserved for specializations of Φ (ESP-T3).

(ESP-D)	ESP(Φ,Ψ)≡EPVP(Φ,Ψ)∧∀y[Ψ(y)→∃x[Φ(x)∧[∀t[PRE(y,t)→POBpartt(x,y,t)]]]] (essential static parthood between types Φ and Ψ)
(ESPΦ,Ψ-D)	ESPΦ,Ψ(x,y)≡ESP(Φ,Ψ)∧Φ(x)∧Ψ(y)∧∀t[PRE(y,t)→POBpartt(x,y,t)] (essential static parthood between two instances: x is part of y throughout y’s entire lifetime)
(ESPany-D)	ESPany(x,y)≡⋁Φ,Ψ[ESPΦ,Ψ(x,y)] (essential static parthood between individuals irrespective of their types)
(ESP-T1)	ESPΦ,Ψ(x,y)→SD(y,x) (in essential static parthood the whole is specifically dependent on the part; see proof below)
(ESP-T2)	ESP(Φ,Ψ)∧Ψ(y)→∃x[Φ(x)∧ESPΦ,Ψ(x,y)] (for Φ to be an essential static part of Ψ, every instance y of Ψ has an essential static part x, which is an instance of Φ; from ESP-D, ESPΦ,Ψ-D)
(ESP-T3)	ESP(Φ,Ψ)∧∀y[Ψ′(y)→Ψ(y)]→ESP(Φ,Ψ′) (essential static parthood is preserved for specializations of Φ; from ESP-D)

Proof Sketch for ESP-T1.

Assume Φ and Ψ are arbitrary types and ESPΦ,Ψ(x,y) holds for two arbitrary instances x and y.

We want to prove SD(y,x), that is, ∃t[PRE(y,t)]∧∀t[PRE(y,t)→PRE(x,t)] (by SD-D1).

From ESPΦ,Ψ(x,y) follows ∀t[PRE(y,t)→POBpartt(x,y,t)]. Now assume PRE(y,t) for an arbitrary t, then POBpartt(x,y,t) and further PRE(x,t) by POBPartt-T1. Thus, ∀t[PRE(y,t)→PRE(x,t)] holds.

To prove ∃t[PRE(y,t)], observe that ESP(Φ,Ψ)∧Ψ(y) follows from ESPΦ,Ψ(x,y) by ESPΦ,Ψ-D. Further, EPVP(Φ,Ψ) (by ESP-D), EVP(Φ,Ψ) (by EPVP-D), MP(Φ,Ψ) (by EVP-A1), and POBpart(Φ,Ψ) (by MP-T1). By POBPart-A1 Exists(y) follows, which is equivalent to ∃t[PRE(y,t)] by Exists-D.

Together, it follows that SD(y,x). □

5.3.Physical object wholes

5.3.1.Essential static wholes

Intuitively, every essential static whole must have at least one essential static part, and all instances of an essential static whole must satisfy some unifying relation RΨ∗(y) (SW-D1). RΨ∗(y) is introduced only because it, rather than the formula RΨ(y,x→,t), can be later generalized to a unifying condition for all essential wholes (SW-A2) in Section 5.3.3.

Remark about Notation 3.

The vector notation x→ is used to refer to the set of all physical object parts in a whole at a specific time t. The set may include different parts (in number and type) at different times. For SW-D2 (and PVW-D2 in Section 5.3.2) to be fully expandable into a standard first-order logic sentence, it must be assumed that there is some fixed upper limit on the number of parts that a whole of type Ψ can have at any given time. Alternatively, SW-D2 and PVW-D2 are fully first-order expressible if sets (or collections) of parts are included as a special sort of domain entity that is equipped with a primitive membership relation.

SW-D2 expounds what it means to satisfy the unifying relation, namely that there is a relation RΨ that relates the whole to all its parts at any time when the whole exists. SW-A1 is more specific about which parts can participate in the unifying relation, stating that the relation possibly relates all of a whole’s physical object parts – not only its essential static parts – at a time. SW-A2 and SW-A3 ensure that types and subtypes of essential static wholes are interrelated as expected: any subtype is also an essential static whole and any subtype specializes the supertype’s unifying relation. SW-T2 shows that the set of physical object parts related by RΨ is indeed non-empty whenever the essential static whole exists.

As with the types of parthood relations introduced in the previous section, essential state wholes can not only be defined for types (SW-D1), but also for all instances of such types (SW-D3) with the expected interrelation (SW-T1).

(SW-D1)	StaticPOBWhole(Ψ)≡∃Φ[ESP(Φ,Ψ)]∧∀y[Ψ(y)→RΨ∗(y)] (Ψ is a static POB whole iff it has some essential static part and every instance of Ψ satisfies RΨ∗)
(SW-D2)	RΨ∗(y)≡Ψ(y)∧∀t[PRE(y,t)]→∃x→[RΨ(y,x→,t)] (an instance y of type Ψ satisfies RΨ∗ if, and only if, at all times when it is present, there is a set x→ of entities that are related via the unifying relation RΨ(y,x→,t))
(SW-D3)	StaticPOBWhole(y)≡∃Ψ[StaticPOBWhole(Ψ)∧Ψ(y)] (an individual y is a static POB whole iff it is an instance of some type Ψ that is a static POB whole)
(SW-T1)	StaticPOBWhole(y)→∃x[ESPany(x,y)] (a static POB whole y has some essential static part x; from SW-D3, SW-D1, ESPany-D)
(SW-A1)	RΨ(y,x→,t)→Ψ(y)∧PRE(y,t)∧∀x′[x′∈x→↔POBpartt(x′,y,t)] (the unifying relation RΨ(y,x→,t) relates all and only the physical object parts of y at time t)
(SW-A2)	StaticPOBWhole(Ψ)∧∀z[Ψ′(z)→Ψ(z)]→StaticPOBWhole(Ψ′) (any subtype of a type of static whole is also a static whole)
(SW-A3)	StaticPOBWhole(Ψ)∧RΨ′(y,x→,t)∧∀z[Ψ′(z)→Ψ(z)]→RΨ(y,x→,t) (the unifying relation for a subtype Ψ′ of Ψ must also satisfy the unifying relation for Ψ)
(SW-T2)	StaticPOBWhole(Ψ)∧Ψ(y)∧StaticPOBWhole(y)→∀t[PRE(y,t)↔∃x→,x′[RΨ(y,x→,t)∧x′∈x→]] (Explicit existence condition for a static whole: a static POB whole instance y of type Ψ is present whenever it has at least one part participating in its unifying relation, that is, iff there exists a non-empty set x→ of parts of y related by RΨ(y,x→,t); see proof below)

Proof Sketch for SW-T2.

Assume y to be an arbitrary static whole of type Ψ. We separately prove the two directions of the inner biconditional.

→: Assume y to be present at time t, i.e. PRE(y,t). By SW-D3, SW-D1 and SW-D2, a vector x→ exists such that RΨ(y,x→,t). By SW-A1, the vector x→ contains all elements x′ with POBpartt(x′,y,t).

Furthermore, SW-T1 entails that there exists an x′ such that ESPany(x′,y) and ESPany-D then entails ESPΦ,Ψ(x′,y) for that x′ and some Φ. Then via ESPΦ,Ψ-D we entail POBpartt(x′,y,t). Hence, by SW-A1 some x′∈x→ exists.

←: Assume a x→ exists with an x′∈x→ such that RΨ(y,x→,t) holds. Then PRE(y,t) by SW-A1. □

5.3.2.Essential persistent variable wholes

Essential persistent variable wholes do not have an essential static part, but must have some essential persistent variable part. There is a version for types (PVW-D1) possessing a formal principle (PVW-D2) that picks out and relates the physical parts of a persistent variable whole. In contrast to the unifying relation RΨ for a static whole, which relates all the parts of the whole for each temporal snapshot (e.g. how the parts are arranged at that time), the formal principle FPΨ may more freely relate parts at a single time instant or across time instants (e.g. a history of replacements) (PVW-A1).13 13 In the extreme case, each part is only related to the whole but not to other parts; in this case the formal principle simply picks out the parts throughout its lifetime. Note that subtypes of essential persistent variable wholes are either essential persistent variable wholes themselves or – in the case when all instances of a subtype have a static part – are essential static wholes (PVW-A2), with PVW-D3 specifying a version for instances. Formal principles must be preserved under specialization of Ψ (PVW-A3), and each instance must have an essential persistent variable part, but not a essential static part (PVW-T1).

(PVW-D1)	PersistentVariablePOBWhole(Ψ)≡∃Φ[EPVP(Φ,Ψ)]∧¬∃Φ[ESP(Φ,Ψ)]∧∀y[Ψ(y)→FPΨ∗(y)] (Ψ is a persistent variable POB whole iff it has some essential persistent variable part, but no essential static part and every instance of Ψ satisfies FPΨ∗)
(PVW-D2)	FPΨ∗(y)≡Ψ(y)∧∃(x,t)→[FPΨ(y,(x,t)→)] (an instance y of an essential persistent variable whole Ψ has a formal principle FPΨ(y,(x,t)→))
(PVW-A1)	FPΨ(y,(x,t)→)→Ψ(y)∧∀x′,t′[At(t′)→[(x′,t′)∈(x,t)→↔POBpartt(x′,y,t′)]] (the formal principle FPΨ(y,(x,t)→) relates all and only the entities that are physical object parts of y)
(PVW-A2)	[PersistentVariablePOBWhole(Ψ)∧∀z[Ψ′(z)→Ψ(z)]]→[StaticPOBWhole(Ψ′)∨PersistentVariablePOBWhole(Ψ′)](any subtype of an essential persistent variable whole is either an essential static whole or an essential persistent variable whole)
(PVW-A3)	[PersistentVariablePOBWhole(Ψ)∧PersistentVariablePOBWhole(Ψ′)∧FPΨ′(y,(x,t)→)∧∀z[Ψ′(z)→Ψ(z)]]→FPΨ(y,(x,t)→)(the formal principle for a persistent variable whole subtype Ψ′ of Ψ must also satisfy the formal principle for Ψ)
(PVW-D3)	PersistentVariablePOBWhole(y)≡∃Ψ[PersistentVariablePOBWhole(Ψ)∧Ψ(y)] (an individual y is a persistent variable POB whole iff it is an instance of some type Ψ that is a persistent variable POB whole)
(PVW-T1)	PersistentVariablePOBWhole(y)→∃x,t[EPVPany(x,y,t)]∧¬∃x[ESPany(x,y)] (if an individual y is a persistent variable POB whole then it contains at least one essential persistent variable part, but no essential static part; see proof below)
(PVW-T2)	PersistentVariablePOBWhole(Ψ)∧Ψ(y)∧PersistentVariablePOBWhole(y)→∀t′[At(t′)→[PRE(y,t′)↔∃(x,t)→,x′[(x′,t′)∈(x,t)→∧FPΨ(y,(x,t)→)]]](Explicit existence condition for a persistent variable whole: a persistent variable POB whole instance y of type Ψ is present at a time instant t′ iff it has some physical POB part x′ satisfy its formal principle at that time; see proof below)

Proof Sketch for PVW-T1.

Assume y to be an arbitrary persistent variable whole.

Then PVW-D3, PVW-D1, EPVP-D, EVP-T1, EVPΦ,Ψ-D, POBPartt-T1 entail that there exists an x with POBpart(x,y,t) for some time instant t. Then EPVPΦ,Ψ-D and EVPany-D further entail EPVPany(x,y,t) at some time t, which proves the first conjunct in the conclusion of PVW-T1.

From PVW-D3 and PVW-D1 it follows that ¬∃Φ[ESP(Φ,Ψ)]. Then ESPΦ,Ψ-D and ESPany-D entail ¬∃x[ESPany(x,y)], which proves the second conjunct in the conclusion of PVW-T1. □

Proof Sketch for PVW-T2.

Assume y to be an arbitrary persistent variable whole of type Ψ. We separately prove the two directions of the inner biconditional.

→: Assume y to be present at time instant t′, i.e. PRE(y,t′). By PVW-D1, there exists a Φ such that EPVP(Φ,Ψ) and thus, by EPVP-D1, there exists an x′ such that POBpartt(x′,y,t′). By PVW-D1 and PVW-D2, a vector (x,t)→ exists such that FPΨ(y,(x,t)→). Because POBpartt(x,y,t′) holds, (x,t′)∈(x,t)→ follows by PVW-A1, as desired.

←: Assume some (x,t)→ exists such that (x′,t′)∈(x,t)→, and FPΨ(y,(x,t)→) holds. Then POBpartt(x′,y,t′) by PVW-A1 and PRE(y,t′) by POBPartt-T2. □

Remark about Notation 4.

The vector (x,t)→ consists of a set of pairs (x′,t′), each denoting that x′ is a physical object part of the whole at time t′. A part x′ may be involved at multiple different times t′.

5.3.3.Essential wholes

Both essential static wholes and essential persistent variable wholes can be further generalized to, and subsumed by, essential wholes, EssentialPOBWhole. Essential wholes are physical objects that have at least one essential variable part and whose parts are related by some unifying condition UΨ (EVW-D1), which is RΨ for a static whole (SW-A2) and FPΨ for a persistent variable whole (PVW-A4). Essential whole instances (EVW-D2) must have some essential variable part (EVW-T1).

(EVW-D1)	EssentialPOBWhole(Ψ)≡∃Φ[EVP(Φ,Ψ)]∧∀y[Ψ(y)→UΨ∗(y)] (a type Ψ being an essential POB whole)
(SW-A2)	RΨ∗(y)→UΨ∗(y) (any unifying relation RΨ∗ is a unifying condition)
(PVW-A4)	FPΨ∗(y)→UΨ∗(y) (any formal principle FPΨ∗ is a unifying condition)
(EVW-D2)	EssentialPOBWhole(y)≡∃Ψ[EssentialPOBWhole(Ψ)∧Ψ(y)] (an individual is an essential POB whole iff it is an instance of a type that is an essential whole)
(EVW-T1)	EssentialPOBWhole(y)→∃x,t[EVPany(x,y,t)] (an individual y that is an instance of an essential POB whole has some essential variable part; from EVW-D2, EVW-D1, EVPany-D)

Theorems EVW-T2 and EVW-T3 show that both PersistentVariablePOBWhole and StaticPOBWhole are indeed specializations of EssentialPOBWhole for types and thus implicitly, by EVW-D2, also for instances; the instance theorems are omitted here. Furthermore, persistent variable wholes and static wholes are disjoint (EVW-T4). The three formalized notions of wholes and all parthood relations are summarized in Table 2.

(EVW-T2)	PersistentVariablePOBWhole(Ψ)→EssentialPOBWhole(Ψ) (persistent variable POB wholes are essential wholes; from EVW-D1, PVW-D1, PVW-A1)
(EVW-T3)	StaticPOBWhole(Ψ)→EssentialPOBWhole(Ψ) (static POB wholes are essential wholes; from EVW-D1, SW-D1, ESP-D, SW-A1)
(EVW-T4)	¬PersistentVariablePOBWhole(Φ)∨¬StaticPOBWhole(Φ) (a physical object cannot be both a persistent variable and static POB whole; from SW-D1, PVW-D1)

5.4.Describing water features

Various types of water features can now be described as physical object wholes possessing certain parts, with the water object being the only essential part common to all. Please refer to Fig. 4 (water features taxonomy) and Table 1 (summary of water feature wholes and parts) for the complete list of water features to be examined in this section.

Table 2

Signature for parthood relations, wholes, and their informal meanings

Relation	Informal meaning
POBpartt(x,y,t)	Physical object x is a part of physical object y at time t
POBpart(Φ,Ψ)	General POB parthood between types – some instance of type Ψ has a part of type Φ at some time
MP(Φ,Ψ)	Mandatory POB parthood between types Φ and Ψ: every instance of Ψ must have an instance of Φ as a part at some time
MPΦ,Ψ(x,y,t)	Mandatory POB parthood between instance x of type Φ and instance y of type Ψ for a time t, during which x is a physical object part of y
OP(Φ,Ψ)	Optional POB parthood between types Φ and Ψ as specialization of general POB parthood between the types: some instance of type Φ is a POB part of some instance of type Ψ at some time, but not every instance of type Ψ has a POB part instance of type Φ at some time
EVP(Φ,Ψ)	Essential variable parthood between types Φ and Ψ: it is necessary, because of ontological dependence, for each instance of Ψ to have an instance of type Φ as POB part at some time
EVPΦ,Ψ(x,y,t)	Essential variable parthood between instances x and y of types Φ and Ψ (with Φ being in a variable parthood relationship to Ψ) for a time t, during which x is a POB part of y
NEVP(Φ,Ψ)	Non-essential variable parthood between types Φ and Ψ: every instance of Ψ has an instance of type Φ as part at some time, due to some dependence that is not ontological dependence
NEVPΦ,Ψ(x,y,t)	Non-essential variable parthood between instances x of type Φ and y of type Ψ at time t: there is a non-essential variable parthood between the types and x is a POB part of y during the time t
EPVP(Φ,Ψ)	Essential persistent variable parthood between types Φ and Ψ: every instance of type Ψ has, at all times of its existence, an instance of type Φ as part but not necessarily the same instance throughout its existence
EPVPΦ,Ψ(x,y,t)	Essential persistent variable parthood between two instances x and y of types Φ and Ψ at time t, which requires that x is a POB part of y during that time
ESP(Φ,Ψ)	Essential static parthood between types Φ and Ψ: every instance of type Ψ has, throughout its entire existence, one specific instance of Φ as a POB part
ESPΦ,Ψ(x,y)	Essential static parthood between instances of types Φ and Ψ: y of type Ψ has x of type Φ as POB part throughout its existence
StaticPOBWhole(Ψ)	Type Ψ is a static POB whole, i.e. some type is in an essential static parthood relation to Ψ
PersistentVariablePOBWhole(Ψ)	Type Ψ is a persistent variable POB whole, i.e. some type is in an essential persistent variable parthood relation to Ψ and no type is in an essential static parthood relation to Ψ
EssentialPOBWhole(Ψ)	Type Ψ is an essential whole, i.e. some type is in an essential variable parthood relation to Ψ

5.4.1.Water objects as persistent variable POB wholes

A water object is a non-agentive object (WO-A1) that is also a persistent variable whole and must only have water matter amounts as persistent variable parts (WO-A2). This means a water object exists when it contains water matter amounts (WO-T1), and stops to exist as soon as it does not contain any water matter. However, this does not mean that the associated water feature (e.g. a river or aquifer) must also cease to exist, as exemplified by rivers or aquifers that are dry and retain identity. A water object might reappear when the feature is wet again, or a different water object might appear, depending on the water object’s formal principle.

The formal principle for a water object requires any of its water matter amounts to be intragranular constituents supplied from a common water supply process perdurant (FPWO-A1), and this perdurant has the water matter amounts as participants (WO-A3, WO-A4). As discussed in Section 4.4, the perdurant could be a single thunderstorm that temporarily fills a dry river, resulting in a distinct water object after each thunderstorm. It could also be a complex process involving precipitation, runoff and meltwater in a watershed, resulting in a water object that retains identity over intermittent dry periods because the perdurant is the same.

(WO-A1)	WO(o)→NAPO(o) (water objects are non-agentive physical objects)
(WO-A2)	PersistentVariablePOBWhole(WO)∧EPVP(WM,WO)∧∀Φ[EPVP(Φ,WO)→Φ=WM] (water objects are persistent variable POB wholes with water matter amounts as the only persistent variable parts)
(WO-T1)	WO(o)→∃(x,t)→∀t′[At(t′)→[PRE(o,t′)↔∃m[WM(m)∧(m,t′)∈(x,t)→∧FPWO(o,(x,t)→)]]] (water objects as persistent variable POB wholes satisfy the formal principle FPWO for some amount of water matter exactly at those time instants when they are present; see proof below)
(FPWO-A1)	FPWO(o,(x,t)→)→∃p[WaterSupplyPD(p)∧∀m,t′[(m,t′)∈(x,t)→→intragranular-constituentt(m,o,t′)∧SuppliesWaterTPC(m,p,t′)]](the formal principle determines the parts of a water object: only things that are intragranular constituents (i.e. only amounts of water matter) and that participate in a common water supply process p are parts)
(WO-A3)	WaterSupplyPD(p)↔∃m,t[SuppliesWaterTPC(m,p,t)] (a water supply perdurant, i.e. an event or process that supplies water, participates in some water supply participation relation)
(WO-A4)	SuppliesWaterTPC(m,p,t)→PC(m,p,t)∧WM(m)∧PD(p) (supplying water is a specialized version of the participates relation that holds at a time t between the supplied water matter m as endurant and some perdurant p)

WO-A3 and WO-A4 are provided as a placeholder for a more detailed formalization of a water supply perdurant using DOLCE’s participation relation and its refinement to hydrological (flow) processes as in Stephen and Hahmann (2017); note that WO-A4 imposes only minimal type constraints on the concept of “supplying water to some perdurant” without specifying any additional conditions. Likewise, FPWO-A1 is only a partial specification of a water object’s formal principle FPWO(o,(x,t)→), which will be refined in future work, and could contain further constrains such as a quantity threshold that must be exceeded for the object to change identity.

Proof Sketch for WO-T1.

Assume o to be an arbitrary entity such that WO(o).

From WO-A2 PersistentVariablePOBWhole(WO) and EPVP(WM,WO) follow.

Then FPWO∗(o) is entailed by PVW-D1. Then PVW-D2 further entails that there exists some vector (x,t)→ that satisfies FPWO(o,(x,t)→).

We now show that this vector (x,t)→ satisfies the biconditional in WO-T1 for all time instants t′:

PRE(o,t′)↔∃m[WM(m)∧(m,t′)∈(x,t)→∧FPWO(o,(x,t)→)]

→: Assume t′ to be a time instant when PRE(o,t′). Then by EPVP-D, we conclude there exists an m such that WM(m) and POBpartt(m,o,t′). Then by PVW-A1, (m,t′)∈(x,t)→. Then the desired conclusion follows.

←: Assume t′ to be a time instant when ∃m[WM(m)∧(m,t′)∈(x,t)→∧FPWO(o,(x,t)→)] is true. By PVW-A1, POBpartt(m,o,t′) follows, which entails PRE(o,t′) by POBPartt-T2. □

5.4.2.Water features as essential POB wholes

All water features (WF-A1) must have a water object as an essential variable part and can have containers, supporters, voids, and other water features as optional parts (WF-A2). For some, typically contained, water features, such as some rivers or aquifers, the water object could be temporarily absent. For other water features, often uncontained such as clouds, the water feature disappears with the water object.

(WF-A1)	WF(f)→NAPO(f) (water features are non-agentive physical objects)
(WF-A2)	EssentialPOBWhole(WF)∧EVP(WO,WF)∧OP(CSB,SupWF)∧OP(SBV,SupWF)∧OP(SUP,SupWF)∧OP(WF,WF)(water features are POB wholes with a water object as essential variable part and containers, physical voids, supporters and other water features as optional parts)
(WF-A3)	∀Φ[EVP(Φ,WF)→Φ=WO] (water objects are the only essential parts of water features)

We further distinguish between simple and complex water features (SimpleWF-D, ComplexWF-D): simple ones never have other water features as any kinds of parts – not even as optional parts – (SimpleWF-T1) whereas complex ones have such parts at some time (ComplexWF-T1). For example, an aquifer or a puddle is simple, whereas a river may have multiple river segment parts as well as waterfalls or even lakes as parts. Likewise, an aquifer system has multiple aquifers as parts.

(SimpleWF-D)	SimpleWF(f)≡WF(f)∧¬∃x,t[WF(x)∧POBpartt(x,f,t)] (simple water features are water features that have no water feature parts)
(SimpleWF-T1)	¬POBpart(WF,SimpleWF) (simple water features have no water feature parts; from SimpleWF-D, POBPart-D)
(ComplexWF-D)	ComplexWF(f)≡WF(f)∧¬SimpleWF(f) (complex water features are non-simple water features)
(ComplexWF-T1)	MP(WF,ComplexWF) (complex water features have water features as mandatory parts; from ComplexWF-D, SimpleWF-D, MP-D)

In the subsequent discussion, we focus on simple water features, but will use rivers and river segments as examples of how to apply complex water features within our framework.

Note that WF-A2 only states that water features are essential POB wholes, leaving open whether they are static or not. It is also notable, that the kinds of simple water features explored herein and summarized in Table 1 are indeed static POB wholes. All contained or supported simple water features have at least the container or supporter as an essential static part, while unsupported and uncontained simple water features, such as clouds, have the water object as an essential static part. But complex water features, such as rivers, are not always static POB wholes. All of a river’s water feature parts can be exchanged (e.g. segments disappear and new ones get created and thus no single static support object may exist) and the water object may also temporarily disappear.

5.4.3.Contained water features

Contained water features (CWF-A1) have a water object as an essential variable part, a container (Container Solid Body, CSB) and its hosted void (Solid Body Void, SBV) as essential static parts, and a supporter as an optional part (CWF-A2), with no other essential parts (CWF-A3). Its unifying relation RContWF does not need to be explicitly expressed in the description of the whole, because it is entailed: the definition of static POB whole (SW-D1) entails that any type Ψ of static POB whole must have an accompanying unifying relation RΨ. RContWF-A1 elaborates the necessary conditions imposed on contained water features, namely that it must have a container – as CSB part – that hosts some void – an SBV part – such that the void fully contains any of the water feature’s water objects.

(CWF-A1)	ContWF(x)→WF(x) (contained water features specialize water features)
(CWF-A2)	StaticPOBWhole(ContWF)∧ESP(CSB,ContWF)∧ESP(SBV,ContWF)∧EVP(WO,ContWF)∧OP(SUP,ContWF)(contained water features are static POB wholes with container solid bodies and voids as essential static parts, water objects as essential variable parts, and supporters as optional parts)
(CWF-A3)	∀Φ[EVP(Φ,ContWF)→Φ=CSB∨Φ=SBV∨Φ=WO] (containers, voids and water objects are the only essential parts of contained water features)
(RContWF-A1)	RContWF(f,x→,t)→∃c,v∈x→[ESPCSB,ContWF(c,f)∧ESPSBV,ContWF(v,f)∧hosts-vt(c,v,t)∧∀o∈x→[EVPWO,ContWF(o,f,t)→mat-insidet(o,v,t)]](the unifying relation for a contained water feature requires some essential container to host an essential void and any essential water object to be located inside the void when present)

Aquifers are important examples of contained water features (AquiferWF-A1). Aquifers do not differ from contained water features in their essential parts, but the unifying relation is refined (RAquiferWF-T1), such that the water object must be dependently contained in the aquifer, meaning the aquifer’s material includes the water object’s material (RAquiferWF-A1). As with contained water features in general, aquifers are optionally supported.

(AquiferWF-A1)	AquiferWF(f)→SimpleWF(f)∧ContWF(f) (aquifers are simple contained water features)
(RAquiferWF-T1)	RAquiferWF(f,x→,t)→RContWF(f,x→,t) (any aquifer must satisfy the unifying condition for a contained water feature; from AquiferWF-A1, CWF-A2, SW-A2, SW-A3)
(RAquiferWF-A1)	RAquiferWF(f,x→,t)→∃c∈x→[ESPCSB,AquiferWF(c,f,t)∧∀o∈x→[EVPWO,AquiferWF(o,f,t)→submaterialt(o,c,t)]](the unifying relation for an aquifer requires any essential water object, when present, to be a submaterial of some essential container)

5.4.4.Supported water features

Supported water features (SWF-A1), such as river segments or puddles, are not necessarily contained, but have a supporter as an essential static part that cannot be exchanged, though it may change, e.g. be moved or change shape; they also have a water object as an essential variable part, and containers and voids are optional parts (SWF-A2). Supporters and water objects are the only essential parts (SWF-A3). The unifying relation for supported water features states that some supporter must fully support the essential water object part whenever it is present (RSupWF-A1).

(SWF-A1)	SupWF(f)→WF(f) (supported water features are water features)
(SWF-A2)	StaticPOBWhole(SupWF)∧ESP(SUP,SupWF)∧EVP(WO,SupWF)∧OP(CSB,SupWF)∧OP(SBV,SupWF)(supported water features are essential static POB wholes with a supporter as essential static part, a water object as essential variable part, and a container and a void as optional parts)
(SWF-A3)	∀Φ[EVP(Φ,SupWF)→Φ=SUP∨Φ=WO] (supporters and water objects are the only essential parts of supported water features)
(RSupWF-A1)	RSupWF(f,x→,t)→∃s∈x→[ESPSUP,SupWF(s,f)∧∀o∈x→[EVPWO,SupWF(o,f,t)→supportst(s,o,t)]] (the unifying relation for a supported water feature: some essential supporter must support some essential water object)

Some supported water features, such as river segments, may be temporarily dry (e.g. segments in seasonal rivers) and thus impose no further restriction on their water objects. River segments are, however, restricted to having other river segments as their only water feature parts (RiverSegWF-A1). River segments can be simple, i.e. with no water feature parts and thus no river segment parts (SimpleRiverSegWF-D), or complex, i.e. composed of smaller river segments (ComplexRiverSegWF-D).

(RiverSegWF-A1)	RiverSegWF(f)→SupWF(f)∧∀x,t[WF(x)∧POBpartt(x,f,t)→RiverSegWF(x)] (river segments are supported water features that have river segments as only water feature parts)
(SimpleRiverSegWF-D)	SimpleRiverSegWF(f)≡SimpleWF(f)∧RiverSegWF(f) (simple river segments as river segments that are simple water features, i.e. that have no water feature parts and thus no river segment parts)
(SimpleRiverSegWF-T1)	SimpleRiverSegWF(f)→¬∃x,t[RiverSegWF(x)∧POBpartt(x,f,t)] (simple river segments never have a river segment as POB part; from SimpleRiverSegWF-D, RiverSegWF-A1, SimpleWF-D, SWF-A1)
(ComplexRiverSegWF-D)	ComplexRiverSegWF(f)≡ComplexWF(f)∧RiverSegWF(f) (complex river segments are river segments that are complex water features, i.e. that have at some time some water feature part, which must be a river segment itself)
(ComplexRiverSegWF-T1)	ComplexRiverSegWF(f)→∃x,t[RiverSegWF(x)∧POBpartt(x,f,t)] (complex river segments have at some time a river segment as a POB part; from ComplexRiverSegWF-D, RiverSegWF-A1, ComplexWF-D, SimpleWF-D, SWF-A1)

Other supported water features, such as puddles (PuddleWF-A1), must have a water object as essential persistent variable part (PuddleWF-A2), meaning that a specific puddle ceases to exist when no water remains, though a specific puddle may continue to exist when the water object is exchanged (e.g. a new environmental perdurant adds water to the puddle).

(PuddleWF-A1)	PuddleWF(f)→SimpleWF(f)∧SupWF(f) (puddles are simple supported water features)
(PuddleWF-A2)	EPVP(WO,PuddleWF) (a puddle has a water object as an essential persistent variable part: the puddle ceases to exist without water, and the water object may be exchanged if a new environmental perdurant supplies water)

5.4.5.Contained supported water features

Contained supported water features (CSWF-A1), such as lakes, confined aquifers, or confined river segments, are also static wholes (CSWF-T1) and have as essential static parts only a container, void, and supporter, with the water object being the only other essential (variable) part (CSW-T2, CSWF-A2). This contrasts with contained water features, which have the supporter as an optional part. The unifying relations from contained and supported water features apply without modification (RContSupWF-T1).

(CSWF-A1)	ContSupWF(f)→ContWF(f)∧SupWF(f) (contained supported water features are contained and supported water features)
(CSWF-T1)	StaticPOBWhole(ContSupWF) (a contained supported water feature is a static whole; from CSWF-A1, CWF-A2, SW-A2)
(CSWF-T2)	ESP(CSB,ContSupWF)∧ESP(SBV,ContSupWF)∧ESP(SUP,ContSupWF)∧EVP(WO,ContSupWF) (contained supported water features have containers, voids, and supporters as essential static parts, and water objects as essential variable parts;14 14 from CSWF-A1, CWF-A2, SWF-A2, EVP-A2, ESP-T3)
(CSWF-A2)	∀Φ[EVP(Φ,ContSupWF)→Φ=SUP∨Φ=CSB∨Φ=SBV∨Φ=WO] (supporters, containers, voids, and water objects are the only essential parts of supported water features)
(RContSupWF-T2)	RContSupWF(f,x→,t)→RContWF(f,x→,t)∧RSupWF(f,x→,t) (the unifying relation for a contained supported water feature must satisfy the unifying relations for both contained and supported water features; from CSWF-A1, CSWF-T1, SW-A3)

Confined river segments exemplify contained supported water features (ConfRiverSegWF-A1) with the refinement that their water objects – whenever present – are detachably contained by their containers, as captured by the relation surrounds-matt (RConfRiverSegWF-A1), in contrast to aquifers where the water objects are dependently contained by their rock matter containers. Both simple and complex river segments can be confined, but for complex segments all their parts must be confined as well.

(ConfRiverSegWF-A1)	ConfRiverSegWF(f)→ContSupWF(f) (confined river segments are contained supported water features)
(RConfRiverSegWF-A1)	RConfRiverSegWF(f,x→,t)→∃c∈x→[ESPCSB,ConfRiverSegWF(c,f,t)∧∀o∈x→[EVPWO,ConfRiverSegWF(o,f,t)→surrounds-matt(c,o,t)]] (the unifying relation for a confined river segment: the water object, whenever present, must be detachably contained (surrounds-mat) in a container)

5.4.6.Uncontained supported water features

Uncontained supported water features (UncontSupWF-A1) are another specialization of supported water features, and include things such as seasonally flooding river segments or spills on a flat surface, which are not always contained but are still supported at all times.15 15 Like all supported water features, uncontained supported water features have a water object as an essential variable part and a supporter as an essential static part (UncontSupWF-A2). As a consequence, they are static wholes (UncontSupWF-T1) that satisfy the unifying relation of supported water features (RUncontSupWF-T1). While at times, such water features might also be contained by a solid body, this cannot be true throughout their entire existence. Thus, they lack a container as an essential static part and are not contained water features, and do not satisfy the unifying relation of contained water features (RUncontSupWF-T2).

(UncontSupWF-A1)	UncontSupWF(f)→SupWF(f)∧¬ContWF(f) (uncontained supported water features are supported water features that are not fully contained)
(UncontSupWF-A2)	∀Φ[EVP(Φ,UncontSupWF)→Φ=SUP∨Φ=WO] (supporters and water objects are the only essential parts of uncontained supported water features)
(UncontSupWF-T1)	StaticPOBWhole(UncontSupWF) (an uncontained supported water feature is a static whole; from UncontSupWF-A1, SWF-A2, SW-A2)
(RUncontSupWF-T1)	RUncontSupWF(f,x→,t)→RSupWF(f,x→,t) (the unifying relation for an uncontained supported water feature also satisfies that for a supported water feature; from UncontSupWF-A1, UncontSupWF-T1, SW-A3)
(RUncontSupWF-T2)	RUncontSupWF(f,x→,t)→¬RContWF(f,x→,t) (the satisfaction of the unifying relation of uncontained supported water features prevents satisfaction of the unifying relation of contained water features; see proof below)

Proof Sketch ofRUncontSupWF-T2.

Assume that RUncontSupWF(f,x→,t) holds for some f, x→ and t. Then by SW-A1, UncontSupWF(f) and PRE(f,t). Now suppose that RContWF(f,x→,t). Then by RContWF-A1, there exist c and v that make ESPCSB,ContWF(c,f) and ESPSBV,ContWF(v,f) true. But then from ESPΦ,Ψ-D follows ContWF(f), which contradicts UncontSupWF-A1. □

5.4.7.Contained unsupported water features

Contained unsupported water features specialize contained but not supported water features (ContUnsupWF-A1), and have containers, voids, and water objects as their only essential variable parts (ContUnsupWF-A2). As such, they are static wholes (ContUnsupWF-T1) that satisfy the unifying relation of contained water features (RContUnsupWF-T1), but not that of supported water features (RContUnsupWF-T2), because they do not have a supporter as an essential static part. They may still be supported variously at times, but the supporter would not be considered an essential part. As example, a leaky aquifer would not be fully supported – though may be supported in part – and is therefore a contained unsupported water feature (LeakyAquiferWF-D), which satisfies the unifying conditions of both aquifers and contained unsupported water features (RLeakyAquiferWF-T1).

(ContUnsupWF-A1)	ContUnsupWF(f)→ContWF(f)∧¬SupWF(f) (contained unsupported water features are contained and not supported)
(ContUnsupWF-A2)	∀Φ[EVP(Φ,ContUnsupWF)→Φ=CSB∨Φ=SBV∨Φ=WO] (containers, voids and water objects are the only essential parts of contained unsupported water features)
(ContUnsupWF-T1)	StaticPOBWhole(ContUnsupWF) (a contained unsupported water feature is a static whole; from ContUnsupWF-A1, CWF-A2, SW-A2)
(RContUnsupWF-T1)	RContUnsupWF(f,x→,t)→RContWF(f,x→,t) (the unifying relation for a contained unsupported water feature also satisfies that for a contained water feature; from ContUnsupWF-A1, ContUnsupWF-T1, SW-A3)
(RContUnsupWF-T2)	RContUnsupWF(f,x→,t)→¬RSupWF(f,x→,t) (the satisfaction of the unifying relation of contained unsupported water features prevents satisfaction of the unifying relation of supported water features; from SW-A1, RSupWF-A1, ESPΦ,Ψ-D, ContUnsupWF-A1, analogous to the proof of RUncontSupWF-T2)
(LeakyAquiferWF-D)	LeakyAquiferWF(f)↔AquiferWF(f)∧ContUnsupWF(f) (leaky aquifers are aquifers that are contained unsupported water features)
(RLeakyAquiferWF-T1)	RLeakyAquiferWF(f,x→,t)→RContUnsupWF(f,x→,t)∧RAquiferWF(f,x→,t) (the unifying relation for a leaky aquifer satisfies that of a contained unsupported water feature and that of an aquifer; from LeakyAquiferWF-D, SW-A2, SW-A3)

5.4.8.Uncontained unsupported water features

Uncontained and unsupported water features (UncontUnsupWF-A1), such as clouds or unconfined waterfalls, are neither fully contained nor fully supported and, thus, lack both a container and a supporter. All of them have a water object as essential variable part (UncontUnsupWF-T1) and as only essential variable part (UncontUnsupWF-A2). The unifying relation for uncontained unsupported water features requires merely the existence of a water object at some time without constraints on its location (RUncontUnsupWF-T1). It is also provable that no essential container or supporter can fully contain or support the water object at any time (RUncontUnsupWF-T2); here the key is that any container or supporter that contains/supports the water object at some time would not be essential but optional.

(UncontUnsupWF-A1)	UncontUnsupWF(f)→WF(f)∧¬ContWF(f)∧¬SupWF(f) (uncontained unsupported water features are water features that are neither contained nor supported)
(UncontUnsupWF-A2)	∀Φ[EVP(Φ,UncontUnsupWF)→Φ=WO] (water objects are the only essential parts of uncontained unsupported water features)
(UncontUnsupWF-T1)	EssentialPOBWhole(UncontUnsupWF)∧EVP(WO,UncontUnsupWF) (uncontained unsupported water features are essential POB wholes with a water object as an essential variable part; from UncontUnsupWF-A1, WF-A2)
(RUncontUnsupWF-T1)	RUncontUnsupWF(f,x→,t)→∃o,t∈x→[EVPWO,UncontUnsupWF(o,f,t)] (the unifying relation for an uncontained unsupported water feature requires a water object to exist as an essential variable part at some time; from UncontUnsupWF-T1,EVP-T1)
(RUncontUnsupWF-T2)	RUncontUnsupWF(f,x→,t)→¬RContWF(f,x→,t)∧¬RSupWF(f,x→,t) (uncontained unsupported water features cannot satisfy the unifying relation for contained or supported water features; from SW-A1, RContWF-A1, RSupWF-A1, ESPΦ,Ψ-D, UncontUnsupWF-A1, analogous to the proof of RUncontSupWF-T2)

Clouds are special uncontained unsupported water features (CloudWF-A1) with the water object as essential static part (CloudWF-A2). A cloud thus ceases to exist when its water object disappears. Its unifying relation is also a specialization of uncontained unsupported water feature (RCloudWF-A1), with the addition that a cloud is spatially self-connected (i.e. occupies a one-piece region) and spatially limited to its associated water object.

(CloudWF-A1)	CloudWF(f)→UncontUnsupWF(f) (clouds are uncontained unsupported water features16 16)
(CloudWF-A2)	ESP(WO,CloudWF) (clouds have water objects as essential static parts)
(RCloudWF-A1)	RCloudWF(f,x→,t)→∃o∈x→[ESPWO,UncontUnsupWF(o,f)∧CS,t(r(o,t))∧r(o,t)=r(f,t)] (the unifying relation for a cloud requires its water object to be strongly connected, i.e. to occupy a one-piece region, and the cloud to be limited to its water object)

5.4.9.Rivers

Rivers may contain non-confined parts, such as seasonally flooding river segments, and non-supported parts, such as unconfined waterfalls. Consequently, rivers are in general neither contained nor supported water features, but are a specialization of the class of water features. As a specialization of river, confined rivers are (fully) supported and contained water features (ConfRiverWF-D). Unlike river segments, all rivers always have some water feature parts and, more precisely, at least some river segment part (RiverWF-A2). Thus, they are always complex water features (RiverWF-T1).

(RiverWF-A1)	RiverWF(f)→WF(f) (rivers are water features)
(RiverWF-A2)	MP(RiverSegWF,RiverWF) (rivers have river segments as mandatory parts)
(RiverWF-T1)	RiverWF(f)→ComplexWF(f) (rivers are complex water features)
(ConfRiverWF-D)	ConfRiverWF(f)≡RiverWF(f)∧ContSupWF(f) (confined rivers are rivers that are also contained and supported water features)

Proof Sketch of RiverWF-T1.

Assume f to be an arbitrary river. Then it is a WF by RiverWF-A1 and has at some time t a POBPart x of type RiverSegWF (by RiverWF-A2, MP-D). Then by RiverSegWF-A1 and SWF-A1 x is a WF. Then by SimpleWF-D, f is not a SimpleWF. Hence, f must be a ComplexWF by ComplexWF-D. □

The unifying condition for a river water feature requires it to have a unique largest water object o as essential variable part (URiverWF-A1). Here, we must use the general unifying condition U∗ for essential wholes, because some rivers are essential static wholes and others are essential persistent variable wholes. For those rivers that are essential static wholes, it then follows from URiverWF-A1 and SW-A1 that the unifying relation o′,o∈(x)→ holds. Likewise, for rivers that are essential persistent variable wholes, it follows from URiverWF-A1 and PVW-A1 that the formal principle (o′,t′),(o,t′)∈(x,t)→ holds.

(URiverWF-A1)

URiverWF∗(f)→∃o[WO(o)∧∀o′,t′[EVPWO,RiverWF(o′,f,t′)→[submaterialt(o′,o,t′)∧EVPWO,RiverWF(o,f,t′)]]∧∀o″[∀t[EVPWO,RiverWF(o,f,t)→[EVPWO,RiverWF(o″,f,t)∧submaterialt(o,o″,t)]]→o″=o]](Any water object o′ that is part of the river at some time t′ is then a submaterial of o at that time; in addition, no other water object part o″ of f has o as submaterial at all times when o exists, i.e. o is in fact unique.17 17)

5.4.10.Dry water features

Now it is possible to distinguish a dry water feature that can continue to exist even if it does not have a water object as a part at some time (DryWF-D). This distinction applies to all contained or supported water features, because water objects are essential variable parts for them. It excludes some unsupported and uncontained water features such as clouds, which cannot be dry as they immediately cease to exist when their water object disappears (CloudWF-T1).

(DryWF-D)	DryWF(f,t)≡WF(f)∧PRE(f,t)∧¬∃o[EVPWO,WF(o,f,t)] (a water feature is called “dry” at any time it exists, but has no water object as essential variable part)
(CloudWF-T1)	CloudWF(f)→∀t[¬DryWF(f,t)] (clouds can never be dry; follows from DryWF-D, CloudWF-A2, ESP-D, ESPΦ,Ψ-D, EPVP-D, EVPΦ,Ψ-D)

6.Discussion

The characterization of wholes and parts in this paper requires a more thorough exploration of the impact of mixed types of parts on the identity, existence, transitivity, unification and application conditions of integral wholes. Also to be considered are wholes structured around non-essential and optional parts. For example, are optional wholes viable? These might have only optional parts, and no other kinds of mandatory part. Likewise, are non-essential wholes feasible? These wholes might exclude essential parts altogether, but require mandatory non-essential parts and allow optional parts. They might be exemplified by purely functional wholes, such as a franchise corporation that can be incorporated independently and have no essential parts, i.e. the corporation needs franchises to function but not to exist.

Another consideration is the relationship of this whole-part characterization, focused on identity and changing parts, to other categorizations of whole-part relations focused on transitivity and compositional structure (Gerstl and Pribbenow, 1995; Winston et al., 1987), i.e. collection-member (hockey team-player), functional complex-component (car-engine), and quantity-subquantity relations (wine-alcohol; Guizzardi, 2010). While a quantity of matter is often regarded as a static whole, collections and functional complexes could very well be orthogonal to static and variable wholes, as examples of each of the latter can be found for each of the former. These considerations will also likely touch on the issue of physical granularity, that is, parthood relations in which the relata exist within and between granular physical levels (see e.g. Hahmann and Brodaric, 2014; Jansen and Schulz, 2011; Rector et al., 2006). Examples include the parthood relation between a water molecule and its atoms, or between a water molecule and some water matter or water object. A principled account should further explore the relationship to material constitution (Hahmann and Brodaric, 2014), to disambiguate what it means to be a physical part versus a physical constituent.

Further thought is also required on the nature of various unifying conditions, most notably the formal principles for variable wholes, which are particularly difficult to identify and represent. Indeed, what is the formal principle for a mixed persistent variable whole, for example, a ship that can exchange any part, any part can be missing, but not all parts can be missing at the same time? One might imagine this to involve some significant proportion of its essential parts in a persistent relation, with each such part having a replacement history to an original part. The formal principle might then be statistical, historical, and relational, in that if a sufficient amount of such parts exist in a ship relation then the ship retains identity and the relata can be picked out as parts of the same ship.

Additional work is also needed to enable counting constraints to express wholes that rely on a certain minimal or maximal number of parts. For example, a car having exactly one chassis as an essential static part, but having four wheels as essential variable parts. This could be achieved by a notation that resembles the cardinality restrictions from the OWL family of ontology languages.

The notion of support is also under-represented here. For instance, various categories of support are not differentiated, but clearly exist, and their characterization could lead to expansion of the water feature taxonomy. Examples include the water supported by a riverbed, a water drop clinging to the top of a subsurface cavern, a layer of water sitting on another layer of water, a bay or ocean supported on some sides by walls of water, a boat floating on water, a submarine floating in water, sediment floating in water, a plane carrying a sensor flying in the air. It is also likely that things are supported (and contained) in multiple ways, such as a layer of water supported by another layer of water underneath, on some side, and by a rigid container on another side. Moreover, support might be transitive-like for at least some cases: if the top layer of water is directly supported by the water underneath it, which is supported by the riverbed, then the top layer of water might also be seen as indirectly supported by the riverbed. Work on support is also ongoing.

Extension of the water feature taxonomy might also include other key differentiae, such as the movement and connection of water matter as suggested by Hayes (1985). This would help differentiate things such as rapids and rain showers, which are not fully represented in this paper: rain showers are uncontained and unsupported like clouds, and rapids are contained and supported like confined rivers. However, it is an open question whether these additional differentiae and resulting distinctions are sufficiently fundamental to be included in a domain reference ontology like HyFO, or whether they belong in a domain ontology that delineates things such as rivers and streams, or lakes and ponds. Staying within the bounds of a reference ontology, and understanding the boundary between a domain reference ontology and domain ontology (Hahmann and Stephen, 2018, see), for practical ontology engineering, thus also remains an ongoing concern.

7.Summary

Water features, such as rivers and aquifers, are primarily understood through sensor measurements, but related water feature ontologies are incomplete. A new ontological characterization and representation of water features is developed in this paper by extending Fine’s (1999) theory of wholes and parts, as well as Hayes’ (1985) ontology of liquids, and by constructing a taxonomy of water features founded on refined notions of containment and support. Combining the water feature taxonomy with the whole-part theory leads to an enhanced water feature ontology in which water features are differentiated from water objects and their amounts of water matter, but structured such that water features are essential wholes – and often essential static wholes – that have a water object as an essential part. The water object in turn is an essential persistent variable whole that has amounts of water matter as essential persistent variable parts that cannot be missing but are exchangeable. Other parts of water features, variably essential or optional, are containers, voids, and supporters, in addition to other water features. The applicability of this new approach to water features is evident by its possession of distinctions sufficient to host measured water sensor qualities: water flow and chemistry are hosted by water matter amounts, water height is hosted by the water object, and water overflow is hosted by the water feature. The ontology is represented formally as an extension of the DOLCE foundational ontology, and it also forms the core of the HyFO ontology, which is being developed as a reference ontology for the hydro domain. HyFO is currently being tested in various ways, including via formal mappings to other hydro representations (Hahmann et al., 2016; Hahmann and Stephen, 2018).

Notes

1 A regular closed region x satisfies x=cl(x)=cl(int(x)), that is, regions cannot have lower-dimensional artifacts. Mereotopologies typically require all regions to be regular closed (Hahmann and Grüninger, 2012).

2 The relations P and PP in our spatial theory express a notion of “spatial parthood” that is restricted to spatial regions. These relations should not be confused with DOLCEs general mereological relations that are denoted by the same predicates P and PP but that apply not just to spatial regions, but to all kinds of endurants and perdurants – such as physical objects and events – and other kinds of abstract regions – such as time intervals – as described in Masolo et al. (2003). Throughout this article, P and PP refer to our spatial relations; DOLCE’s parthood relations are not used.

3 In prior work, we used the unary predicate ZEX to denote empty regions; rz can be defined as x=rz≡ZEX(x).

4 Our treatment of space differs from DOLCE in various respects. In DOLCE spatial regions (S) are the values of location qualities of endurants at specific times SL(x,s,t). In our approach, spatial regions and entities are not necessarily linked via qualities (though it is not prohibited), but directly by the r(x,t)=s function, which may return a special empty region (or zero region) rz, denoting that the endurant x is not present at time t. An empty spatial region is not allowed and not needed in DOLCE’s formalization.

5 The introduction of St-T1, S-T1, and CHt-T1 and the provability of S-T2 were proposed by Stefano Borgo.

6 Full physical containment includes cases where the container does not support the containee into all directions. For example, a river channel that is open at its ends, i.e. where it meets another channel or a lake, can still full physically contain the water therein, despite the container not delimiting the containee in all directions.

7 porespaceall(x) denotes the space of all voids in x that are of a lower granularity than x, that is, not hosted by x but by its constituent matter. See Hahmann and Brodaric, 2014 for the full development.

8 Note that POBpartt(x,y,t) is irreflexive, i.e. for all physical objects x, POBpartt(x,x,t) is false.

9 The ternary hostst(z,x,t) relation is the time-indexed version of the hosts(z,x) relation introduced in axioms P6–P12 in Hahmann and Brodaric (2012). It intends to capture the relation between a dependent physical endurant entity x and its physical endurant host z. The hosted entity can be either (1) a relevant part feature RPF, which is a material endurant that is a submaterial of the host, or (2) a dependent place feature DPF, which does not overlap the host, such as a void. For the remainder of this work, voids are the only relevant kind of dependent place features, with hosts-vt specializing the general hostst relation.

10 Note that MP(Ψ,Ψ) can be true if each Ψ instance has another Ψ instance as part.

11 The relation EVPΦ,Ψ(x,y,t) is a strong interpretation of essential variable parthood, meaning that during the entire t, x is indeed a physical object part of y, and it is called an essential variable part because of the relationships between x and y’s types; thus EVPΦ,Ψ(x,y,t) specializes MPΦ,Ψ(x,y,t) and POBpartt(x,y,t).

12 Disjointness of Φ and Ψ is only needed in EPVP-T1 because DOLCE includes it as condition for generic dependence, it is not used anywhere else in the proof.

13 Any unifying relation RΨ(y,x→,t) is essentially an abbreviated form of the formal principle FPΨ(y,(x,t)→) in the sense that every x∈x→ from the unifying relation can be expanded into a (possibly infinite) set of tuples (x,ti)∈(x,t)→ for all time instants ti to construct the vector for the formal principle.

14 Note that CSWF-T2 is consistent with CWF-A3 because CWF-A3 only says that a supporter is not essential to a contained water feature, i.e. not every contained water feature necessarily has one. The type ContSupWF then picks out the subset of the contained water features that all have a supporter as an essential part. Analogously, CSWF-T2 is not inconsistent with SWF-A3.

15 Note that “uncontained” is here used as the negation of “fully contained” and thus should be understood as “not fully contained”. Likewise, “unsupported’ should be understood as “not fully supported”.

16 We leave it open whether clouds are always simple or may be complex water features, such as a cloud cover having multiple clouds as parts.

17 This axiom is analogous to how extensionality is often specified in mereology.

Acknowledgements

Stefano Borgo, Barry Smith, and the anonymous reviewers are thanked for their constructive comments and insightful suggestions, which led to significant improvements in the paper. Torsten Hahmann has been in part supported by the National Science Foundation under Grant Number III-1565811, and Boyan Brodaric has been supported by the NRCan Groundwater Geoscience Program.

References

1	Boisvert, E. & Brodaric, B. ((2012) ). GroundWater Markup Language (GWML) – Enabling groundwater data interoperability in spatial data infrastructures. J. Hydroinform., 14: (1), 93–107. doi:10.2166/hydro.2011.172.
2	Brodaric, B., Boisvert, E., Chery, L., Dahlhaus, P., Grellet, S., Kmoch, A., Letourneau, F., Lucido, J., Simons, B. & Wagner, B. ((2018) ). Enabling global exchange of groundwater data: GroundWaterML2 (GWML2). Hydrogeology Journal, 26: (3), 733–741. doi:10.1007/s10040-018-1747-9.
3	Brodaric, B. & Hahmann, T. ((2014) ). Towards a foundational hydro ontology for water data interoperability. In Proc. of the 11th Int. Conference on Hydroinformatics (HIC-2014) (pp. 2911–2915).
4	Brodaric, B. & Piasecki, M. ((2016) ). Water data networks: Foundations, technologies and systems, implementations and uses (editorial). J. of HydroInformatics, 18: , 149–151. doi:10.2166/hydro.2016.000.
5	Buttigieg, P.L., Pafilis, E., Lewis, S.E., Schildhauer, M.P., Walls, R.L. & Mungall, C.J. ((2016) ). The environment ontology in 2016: Bridging domains with increased scope, semantic density, and interoperation. J. of Biomedical Semantics, 7: (1), 57. doi:10.1186/s13326-016-0097-6.
6	Casati, R. & Varzi, A.C. ((1994) ). Holes and Other Superficialities. MIT Press.
7	Compton, M., Barnaghi, P., Bermudez, L., García-Castro, R., Corcho, O., Cox, S., Graybeal, J., Hauswirth, M., Henson, C., Herzog, A., Huang, V., Janowicz, K., Kelsey, W.D., Phuoc, D.L., Lefort, L., Leggieri, M., Neuhaus, H., Nikolov, A., Page, K., Passant, A., Sheth, A. & Taylor, K. ((2012) ). The SSN ontology of the W3C semantic sensor network incubator group. Web Semantics: Science, Services and Agents on the World Wide Web, 17: , 25–32. doi:10.1016/j.websem.2012.05.003.
8	Cox, S. ((2016) ). Ontology for observations and sampling features, with alignments to existing models. Semantic Web, 8: (3), 453–470. doi:10.3233/SW-160214.
9	Duce, S. & Krzysztof, J. ((2010) ). Microtheories for spatial data infrastructures – Accounting for diversity of local conceptualizations at a global level. In S. Fabrikant, T. Reichenbacher, M. van Kreveld and C. Schlieder (Eds.), Intern. Conf. on Geographic Information Science (GIScience 2010). LNCS (Vol. 6992: , pp. 27–41). Springer. doi:10.1007/978-3-642-15300-6_3.
10	Feng, C.-C., Bittner, T. & Flewelling, D.M. ((2004) ). Modeling surface hydrology concepts with endurance and perdurance. In M. Egenhofer, C. Freska and H.J. Miller (Eds.), Int. Conf. on Geographic Information Science (GIScience 2004). LNCS (Vol. 3234: , pp. 67–80). Springer. doi:10.1007/978-3-540-30231-5_5.
11	Fine, K. ((1999) ). Things and their parts. Midwest Studies in Philosophy, 23: (1), 61–74. doi:10.1111/1475-4975.00004.
12	Galton, A. ((2007) ). Experience and history: Processes and their relation to events. Journal of Logic and Computation, 18: (3), 323–340. doi:10.1093/logcom/exm079.
13	Galton, A. ((2014) ). On generically dependent entities. Applied Ontology, 9: , 129–153.
14	Galton, A. & Mizoguchi, R. ((2009) ). The water falls but the waterfall does not fall: New perspectives on objects, processes, and events. Applied Ontology, 4: (2), 71–107.
15	Geospatial Consortium (OGC) ((2018) ). I. Dornblut and R. Atkinson (Eds.): OGC WaterML 2: Part 3 – Surface Hydrology Features (HY_Features) – Conceptual Model. Open Geospatial Consortium (OGC) 14-111r6, v1.0.
16	Gerstl, P. & Pribbenow, S. ((1995) ). Midwinters, end games, and body parts: A classification of part-whole relations. Int. J. Hum.-Comput. St., 43: (5–6), 865–889. doi:10.1006/ijhc.1995.1079.
17	Guizzardi, G. ((2007) ). Modal aspects of object types and part-whole relations and the de re/de dicto distinction. In Intern. Conf. on Advanced Information Systems Engineering (CAISE 2007). LNCS (Vol. 4495: ). Springer.
18	Guizzardi, G. ((2010) ). On the representation of quantities and their parts in conceptual modeling. In Conf. on Formal Ontology in Inf. Systems (FOIS-10) (pp. 317–330). IOS Press.
19	Hahmann, T. ((2013) ). A reconciliation of logical representations of space: From multidimensional mereotopology to geometry. PhD thesis, Univ. of Toronto, Dept. of Comp. Science.
20	Hahmann, T. ((2018) ). On decomposition operations in a theory of multidimensional qualitative space. In S. Borgo, P. Hitzler and O. Kutz (Eds.), Int. Conf. on Formal Ontology in Information Systems (FOIS 2018). Frontiers in Artificial Intelligence and Applications (Vol. 306: , pp. 173–186).
21	Hahmann, T. & Brodaric, B. ((2012) ). The void in hydro ontology. In Conf. on Formal Ontology in Inf. Systems (FOIS-12) (pp. 45–58). IOS Press.
22	Hahmann, T. & Brodaric, B. ((2013) ). Kinds of full physical containment. In Conf. on Spatial Inf. Theory (COSIT-13) (pp. 397–417). Springer. doi:10.1007/978-3-319-01790-7_22.
23	Hahmann, T. & Brodaric, B. ((2014) ). Voids and material constitution across physical granularities. In Conf. on Formal Ontology in Inf. Systems (FOIS-14) (pp. 51–64). IOS Press.
24	Hahmann, T., Brodaric, B. & Grüninger, M. ((2014) ). Interdependence among material objects and voids. In Conf. on Formal Ontology in Inf. Systems (FOIS-14) (pp. 37–500). IOS Press.
25	Hahmann, T. & Grüninger, M. ((2012) ). Region-based theories of space: Mereotopology and beyond. In S.M. Hazarika (Ed.), Qualitative Spatio-Temporal Representation and Reasoning: Trends and Future Directions (pp. 1–62). IGI.
26	Hahmann, T. & Stephen, S. ((2018) ). Using a hydro-reference ontology to provide improved computer-interpretable semantics for the groundwater markup language (gwml2). Int. J. Geogr. Inf. Sci., 32: (6), 1138–1171. doi:10.1080/13658816.2018.1443751.
27	Hahmann, T., Stephen, S. & Brodaric, B. ((2016) ). Semantically refining the groundwater markup language (GWML2) with the help of a reference ontology (short paper). In Short Paper Proceedings of the Intern. Conf. on Geographic Information Science (GIScience 2016), Montreal, Sept. 27–30, 2016.
28	Hayes, P.J. ((1985) ). Naive physics I: Ontology of liquids. In J. Hobbs and R. Moore (Eds.), Formal Theories of the Commonsense World (pp. 71–108). Ablex Publishing.
29	INSPIRE Thematic Working Group Geology ((2013) ). D2.8.II.4_v3.0 INSPIRE data specification on geology – Technical guidelines. Technical report, INSPIRE.
30	INSPIRE Thematic Working Group Hydrography ((2014) ). D2.8.I.8_v3.1 INSPIRE data specification on hydrography – Technical guidelines. Technical report, INSPIRE.
31	Jansen, L. & Schulz, S. ((2011) ). Grains, components and mixtures in biomedical ontologies. J. of Biomedical Semantics, 2: , S2.
32	Kuhn, W. ((2009) ). A functional ontology of observation and measurement. In Intern. Conf. on GeoSpatial Semantics (pp. 26–43). Springer. doi:10.1007/978-3-642-10436-7_3.
33	Maidment, D.R. & Morehouse, S. ((2002) ). Arc Hydro: GIS for water resources. Technical report, ESRI Inc.
34	Mark, D.M., Turk, A.G. & Stea, D. ((2007) ). Progress on yindjibarndi ethnophysiography. In S. Winter, M. Duckham, L. Kulik and B. Kuipers (Eds.), Intern. Conf. on Spatial Information Theory (COSIT 2007). LNCS (Vol. 4736: , pp. 1–19). Springer. doi:10.1007/978-3-540-74788-8_1.
35	Masolo, C., Borgo, S., Gangemi, A., Guarino, N. & Oltramari, A. ((2003) ). Wonderweb deliverable D18 – Ontology library (final report). Technical report, National Research Council – Institute of Cognitive Sci. and Technology, Trento.
36	Open Geospatial Consortium (OGC) ((2009) ). C. Kottmann and C. Reed (Eds.): The OpenGIS abstract specification, topic 5: Features. Open Geospatial Consortium (OGC) 08-126, v5.0.
37	Pribbenow, S. ((2002) ). Meronymic relationships: From classical mereology to complex part-whole relations. In R. Green and C.A. Bean (Eds.), The Semantics of Relationships (pp. 35–50). Kluwer. doi:10.1007/978-94-017-0073-3_3.
38	Raskin, R.G. & Pan, M.J. ((2005) ). Knowledge representation in the semantic web for Earth and environmental terminology (SWEET). Comput. Geosci., 31: (9), 1119–1125. doi:10.1016/j.cageo.2004.12.004.
39	Rector, A., Rogers, J. & Bittner, T. ((2006) ). Granularity, scale and collectivity: When size does and does not matter. J. Biomed. Inform., 39: , 333–349. doi:10.1016/j.jbi.2005.08.010.
40	Sanfilippo, E. & Borgo, S. ((2016) ). What are features? An ontology-based review of the literature. Computer-Aided Design, 80: , 9–18. doi:10.1016/j.cad.2016.07.001.
41	Santos, P., Bennett, B. & Sakellariou, G. ((2005) ). Supervaluation semantics for an inland water feature ontology. In Int. Joint Conf. on Artif. Intell. (IJCAI-05) (pp. 564–569).
42	Simons, P. ((1987) ). Parts – A Study in Ontology. Clarendon Press.
43	Sinha, G., Mark, D., Kolas, D., Varanka, D., Romero, B.E., Feng, C.-C., Usery, L.E., Liebermann, J. & Sorokine, A. ((2014) ). An ontology design pattern for surface water features. In Int. Conf. on Geographic Inf. Sci. (GIScience-14). LNCS (Vol. 8728: , pp. 187–203). Springer.
44	Stephen, S. ((2016) ). Ontological analysis and formal grounding of the groundwater markup language (GWML2) with the hydro foundational ontology. Master’s thesis, University of Maine.
45	Stephen, S. & Hahmann, T. ((2017) ). An ontological framework for characterizing hydrologic flow processes. In E. Clementini, M. Donnelly, M. Yuan, C. Kray, P. Fogliaroni and A. Ballatore (Eds.), Conf. on Spatial Inf. Theory (COSIT-17). Leibniz International Proceedings in Informatics (LIPIcs) (Vol. 86: , pp. 7:1–7:14). Schloss Dagstuhl–Leibniz-Zentrum für Informatik.
46	Strassberg, G., Jones, N.L. & Maidment, D.R. ((2011) ). Arc hydro groundwater: GIS for hydrogeology. Technical report, ESRI Inc.
47	Tripathi, A. & Babaie, H. ((2008) ). Developing a modular hydrogeology ontology by extending the SWEET upper-level ontologies. Comput. Geosci., 34: (9), 1022–1033. doi:10.1016/j.cageo.2007.08.009.
48	Varanka, D. & Usery, E. ((2015) ). An applied ontology for semantics associated with surface water features. In O. Ahlqvist, D. Varanka, S. Fritz and K. Janowicz (Eds.), Land Use and Land Cover Semantics, Principles, Best Practices, and Prospects (pp. 146–168). CRC Press. doi:10.1201/b18746.
49	Vieu, L. ((2006) ). On the transivity of functional parthood. Applied Ontology, 1: , 147–155.
50	Wellen, C. & Sieber, R. ((2013) ). Toward an inclusive semantic interoperability: The case of Cree hydrographic features. Int. J. Geogr. Inf. Sci., 27: (1), 168–191. doi:10.1080/13658816.2012.688975.
51	Winston, M.E., Chaffin, R. & Herrmann, D. ((1987) ). A taxonomy of part-whole relations. Cognitive Sci., 11: (4), 417–444. doi:10.1207/s15516709cog1104_2.