Uncertainty in dynamic constraint satisfaction problems
Abstract
Many real life problems that can be modeled as Constraint Satisfaction Problems (CSPs) come from uncertain and dynamic environments, so the original solution found might become invalid after changes. Here, we study the problem of finding robust solutions for CSPs under the assumptions that domains are significantly ordered and that changes take the form of restrictions or relaxations at the borders of the solution space of the CSPs.
1.Introduction
Real life problems for which the dynamism data (i.e., a list of possible changes, sometimes in the form of an associated probability distribution) is missing or scarce represent difficult situations to deal with. Many approaches from the literature [2] are useless in such problematic situations. The main motivation of this PhD dissertation [1] is to develop approaches that can provide solutions with a certain level of robustness for problems where the only data available is the one required for modeling the CSP. Robust solutions have a high likelihood of remaining valid after further possible changes in the original problem.
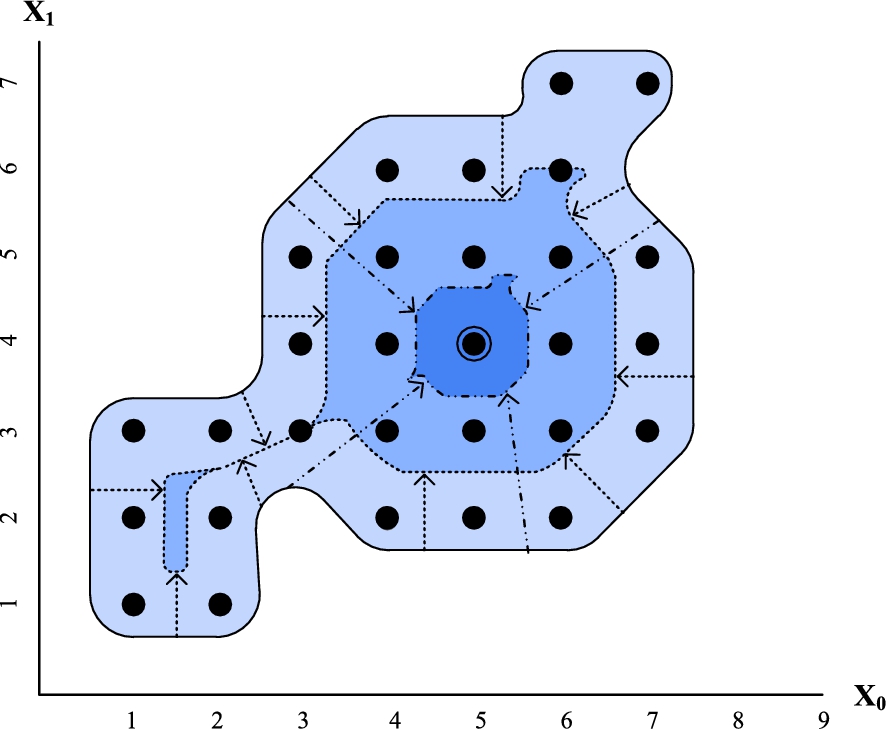
Fig. 1.
Restrictions over the bounds of the solution space. (The colors are visible in the online version of the article; http://dx.doi.org/10.3233/AIC-150657.)
We found it justifiable to make some limited and intuitively reasonable assumptions about the dynamism of problems for which the order over the domain elements is significant (see Section 2). In addition, we present an approach for finding robust solutions in Section 3. Finally, Section 4 concludes this summary.
2.Dynamism in CSPs with ordered domains
Even when the dynamism data associated with a real life problem is partially/completely unknown, the structure of the problems can provide more specific data about their possible dynamism. Here, we make assumptions based on a type of change that problems can undergo, which takes the form of restrictions/relaxations at the borders of a domain or constraint. This is illustrated in the example represented in Fig. 1, which shows a solution space of a CSP (represented with the blue and continuous line). It is composed of two variables
If no specific data is given about the dynamics of the problem, it is not easy to decide which solution should be considered the most robust. In Fig. 1, a smaller solution space coloured with a darker blue hue and discontinuous lines is represented. This reduced space is the result of restrictive modifications over the original constraints and domains of the CSP, which is a type of change that can occur in problems with a significant order over their domains: scheduling, temporal and geometrical reasoning-based problems, design problems, etc. [1]. Given this assumptions we state the following definition.
Definition 2.1.
The most robust solution of a CSP without extra dynamism data is the solution that maximizes the distance from all the dynamic bounds of the solution space.
For the CSP of Fig. 1, the solution (
Fig. 2.
Neighbours of the highlighted solution. (Colors are visible in the online version of the article; http://dx.doi.org/10.3233/AIC-150657.)
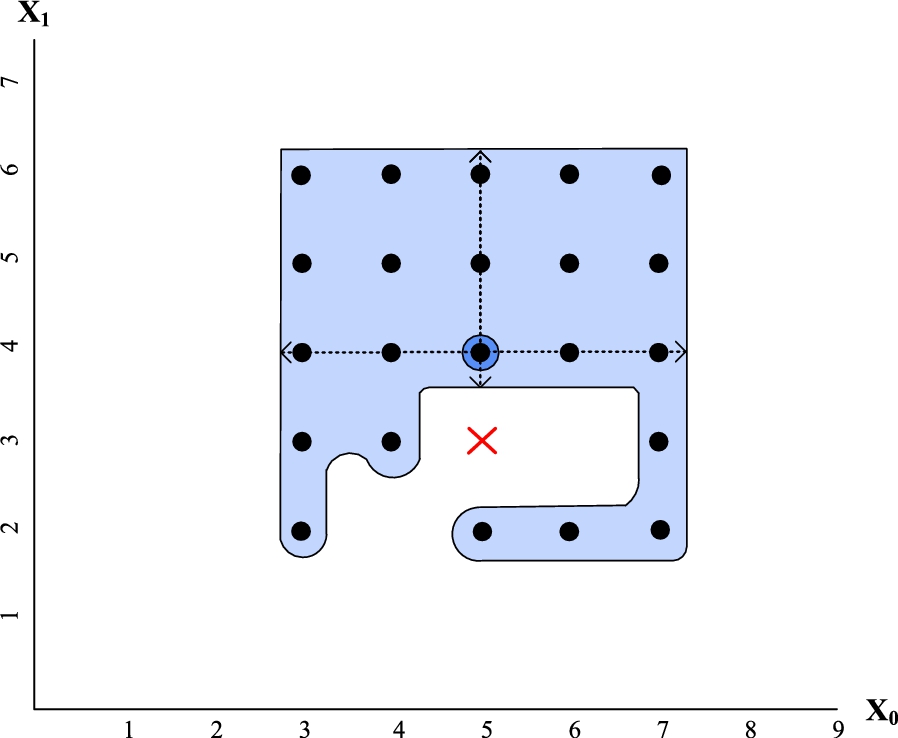
3.Neighbourhood and ‘onion topology’
In this section we explain our approach for finding the most robust solutions of n-dimensional CSPs in the analyzed framework. Figure 2 shows the idea behind our approach, where the highlighted solution has two contiguous neighbours for each of the right, left and upward directions, but none in the downward direction. For this reason, we only can ensure that its minimum distance from the bounds of the solution space is two for the right, left and upward directions. For the downward direction we cannot ensure a minimum distance from the bounds because its closest neighbour in such direction is infeasible (marked with a red cross) and therefore it is not inside the solution space. From this example, we can infer the following lemma.
Lemma 3.1.
It can only be ensured that a solution s is located at a distance d from a bound in a certain direction of the n-dimensional space if all the neighbours at distance lower or equal to d from s in such direction are feasible.
We can characterize the feasibility neighbourhood for CSPs as an ‘onion structure’ and each one of its layers as the convex hull of partial/complete neighbour solutions that surround another one. A solution with more layers is presumed to have a higher probability of remaining valid after changes than one with fewer layers, and therefore, it is more robust. This new framework for dynamic CSPs, as well as an enumeration-based technique for assessing robustness and search algorithms for finding robust solutions are explained in the PhD dissertation [1].
4.Conclusions
In this work we formalize a framework for dynamic CSPs for problems in which ordering of values is significant. We also define robustness for such framework. Furthermore, in this context, we present an approach that allows us to distinguish the robustness of solutions of CSPs models associated with such problems based on their distance from the bounds. This is important when we face restrictive modifications over the bounds of the solution space.
This research is an advance in the state of the art of constraint programming to obtain solutions able to absorb incidences/disruptions in dynamic problems with limited data about changes.
Acknowledgements
This work was supported by the FPU and the project TIN2013-46511-C2-1-P (MINECO, Spain).
References
1 | [[1]] L. Climent, Robustness and stability in dynamic constraint satisfaction problems, PhD thesis, Universitat Politècnica de València, 2013, available at: http://hdl.handle.net/10251/34785. |
2 | [[2]] G. Verfaillie and N. Jussien, Constraint solving in uncertain and dynamic environments: A survey, Constraints 10: (3) ((2005) ), 253–281. |




