Data Science and symbolic AI: Synergies, challenges and opportunities

1.Introduction

The observation of and collection of data about natural processes to obtain practical knowledge about the world has been crucial for our survival as a species. It derives from our curiosity and desire to understand the world in which we live. The detection of regularities such as the daily movement of the sun resulted in the development of calendars, i.e., models of phenomena that allow to undertake more effective actions and also make new discoveries. Astronomy, considered the first science or system of knowledge of natural phenomena, led to the development of mathematics in Mesopotamia, China, and India. In the Middle East, Egypt and Mesopotamia used and expanded mathematics for the description of astronomic phenomena as an intellectual play, and generated large volumes of data about stellar phenomena [10]. Thus, could we consider ancient Babylonians or Egyptians as the first, or early, data scientists?

Recent advancements in science and technology have led to an explosion of our ability to generate and collect data, and led to the era of Big Data. Data is now “big” in volume, in heterogeneity (including different representation formats such as digitized text, audio, video, web logs, transactions, time series, or genome sequences), and complexity (from multiple sources and about different phenomena spanning several levels of granularity, possibly incomplete, unstructured, and of uncertain provenance and quality). Large amounts of complex data are not only generated in empirical science but data collection and generation now penetrates our whole life: mobile phones, Internet of Things, social interactions and communication patterns, bank transactions, personal fitness trackers, and many more. Often, data is collected first and retained to solve specific questions whenever they arise.

Fig. 1.

This figure summarizes our vision of Data Science as the core intersection between disciplines that fosters integration, communication and synergies between them. Data Science studies all steps of the data life cycle to tackle specific and general problems across the whole data landscape.

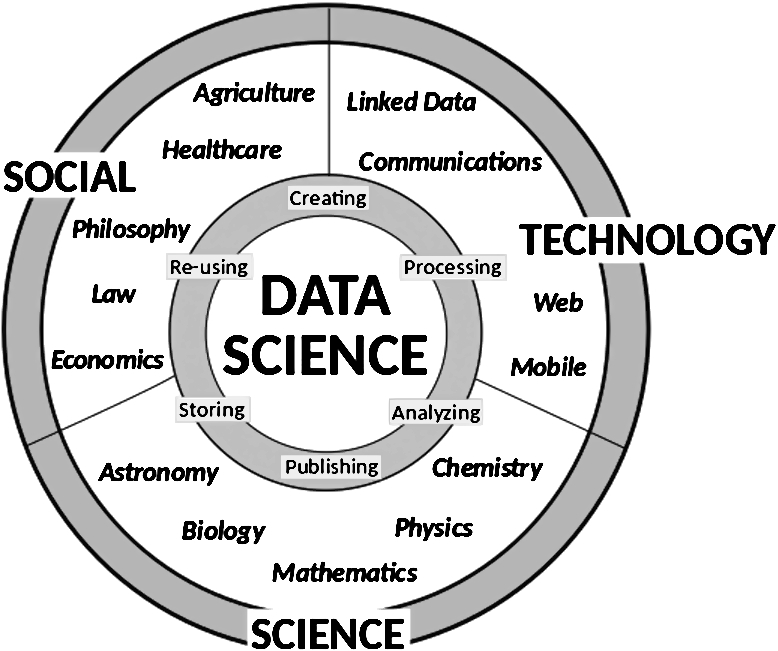
Data Science has as its subject matter the extraction of knowledge from data. While data has been analyzed and knowledge extracted for millennia, the rise of “Big” data has led to the emergence of Data Science as its own discipline that studies how to translate data through analytical algorithms typically taken from statistics, machine learning or data mining, and turn it into knowledge. Data Science also encompasses the study of principles and methods to store, process and communicate with data throughout its life cycle, and starts just after data has been acquired. As illustrated in Fig. 1, the typical data life cycle consists of: 1) creating, 2) processing, 3) analyzing, 4) publishing, 5) storing and 6) re-using the data. These steps require methods for data management, (meta)data description, interpretation, distribution, preservation, and revision. While we do not consider the data acquisition process as a part of Data Science, capture and analysis of (meta)data about the measurement and data generation process falls in the realm of Data Science. In addition to the analysis, Data Science studies how to store data, and methods such as “content-aware” compression algorithms (e.g., for genomic data [57]) also fall in the subject matter of Data Science. We consider Data Science as an emerging discipline at the intersection of fields in science, technology, and humanities, drawing upon methods from social science, statistics, information theory, computer science, and incorporating domain-specific methods (see Fig. 1). As a new and emerging discipline, it becomes important to identify differences and synergies of Data Science with established fields that target similar problems.

To extract knowledge, data scientists have to deal with large and complex datasets and work with data coming from diverse scientific areas. Artificial Intelligence (AI), i.e., the scientific discipline that studies how machines and algorithms can exhibit intelligent behavior, has similar aims and already plays a significant role in Data Science. Intelligent machines can help to collect, store, search, process and reason over both data and knowledge. There are two main approaches to AI, statistical and symbolic [42]. For a long time, a dominant approach to AI was based on symbolic representations and treating “intelligence” or intelligent behavior primarily as symbol manipulation. In a physical symbol system [46], entities called symbols (or tokens) are physical patterns that stand for, or denote, information from the external environment. Symbols can be combined to form complex symbol structures, and symbols can be manipulated by processes. Arguably, human communication occurs through symbols (words and sentences), and human thought – on a cognitive level – also occurs symbolically, so that symbolic AI resembles human cognitive behavior. Symbolic approaches are useful to represent theories or scientific laws in a way that is meaningful to the symbol system and can be meaningful to humans; they are also useful in producing new symbols through symbol manipulation or inference rules. An alternative (or complementary) approach to AI are statistical methods in which intelligence is taken as an emergent property of a system. In statistical approaches to AI, intelligent behavior is commonly formulated as an optimization problem and solutions to the optimization problem leads to behavior that resembles intelligence. Prominently, connectionist systems [42], in particular artificial neural networks [55], have gained influence in the past decade with computational and methodological advances driving new applications [39]. Statistical approaches are useful in learning patterns or regularities from data, and as such have a natural application within Data Science. Advancements in computational power, data storage, and parallelization, in combination to methodological advances in applying machine learning algorithms and solving optimization problems, are contributing to the uptake of statistical approaches in recent years [39], and these approaches have moved areas such as visual processing, object recognition in images, video labeling by sensory systems, and speech recognition significantly forward.

On the other hand, a large number of symbolic representations such as knowledge bases, knowledge graphs and ontologies (i.e., symbolic representations of a conceptualization of a domain [22,23]) have been generated to explicitly capture the knowledge within a domain. Reasoning over these knowledge bases allows consistency checking (i.e., detecting contradictions between facts or statements), classification (i.e., generating taxonomies), and other forms of deductive inference (i.e., revealing new, implicit knowledge given a set of facts). In discovering knowledge from data, the knowledge about the problem domain and additional constraints that a solution will have to satisfy can significantly improve the chances of finding a good solution or determining whether a solution exists at all. Knowledge-based methods can also be used to combine data from different domains, different phenomena, or different modes of representation, and link data together to form a Web of data [8]. In Data Science, methods that exploit the semantics of knowledge graphs and Semantic Web technologies [7] as a way to add background knowledge to machine learning models have already started to emerge.

Here, we discuss current research that combines methods from Data Science and symbolic AI, outline future directions and limitations. In Section 2 we present our vision for how the combination of Data Science and symbolic AI can benefit research illustrated using the Life Sciences domain, in Section 3 we outline methods for using Data Science to learn formalized theories, and in Section 4 we discuss how methods from Data Science can be applied to analyze formalized knowledge. In Section 5, we state our main conclusions and future vision, and we aim to explore a limitation in discovering scientific knowledge in a data-driven way and outline ways to overcome this limitation.

2.Data and knowledge in research – The case of the Life Sciences

The rapid increase of both data and knowledge has led to challenges in theory formation and interpretation of data and knowledge in science. The Life Sciences domain is an illustrative example of these general problems. For instance, in 2016, over 40,000 articles that mention “diabetes” in title or abstract have been published,11 and in addition, many studies have resulted in research data that has been deposited in public archives and repositories; it is no longer possible for an individual researcher to evaluate all these studies and their underlying data completely. Furthermore, not all studies agree in their assumptions, interpretation of background knowledge, research data, and analysis results, and consequently they draw different conclusions and form alternative, competing theories; this situation has led some researchers to conclude that the majority of published research findings are false [31], and has led to a reproducibility crisis in science [44]. There is currently no automated support for identifying competing scientific theories within a domain, determine in which aspects they agree and disagree, and evaluate the research data that supports them. To identify competing scientific theories (e.g., about the mechanisms underlying diabetes), they first have to be made explicit (e.g., through natural language processing techniques that can extract and represent contents of multiple scientific publications); deductive inference can then determine contradictions between theories; and either public research data can be evaluated to identify which theory has stronger experimental support, or new experiments designed to generate such data.

Intelligent machines should support and aid scientists during the whole research life cycle and assist in recognizing inconsistencies, proposing ways to resolve the inconsistencies, and generate new hypotheses. Addressing these challenges requires computational methods that can deal with both scientific data (such as available through scientific databases, or obtained through experiments) and knowledge (such as in publications and formalized theories), can aid in building theories that explain collected data, evaluate existing theories with respect to the underlying data, identify inconsistencies, and suggest experiments to resolve conflicts.

The Life Sciences are a hub domain for big data generation and complex knowledge representation. Life Sciences have long been one of the key drivers behind progress in AI, and the vastly increasing volume and complexity of data in biology is one of the drivers in Data Science as well. Life Sciences are also a prime application area for novel machine learning methods [2,51]. Similarly, Semantic Web technologies such as knowledge graphs and ontologies are widely applied to represent, interpret and integrate data [12,32,61]. There are many reasons for the success of symbolic representations in the Life Sciences. Historically, there has been a strong focus on the use of ontologies such as the Gene Ontology [4], medical terminologies such as GALEN [52], or formalized databases such as EcoCyc [35]. There is also a strong focus on data sharing, data re-use, and data integration [65], which is enabled through the use of symbolic representations [33,61]. Life Sciences, in particular medicine and biomedicine, also place a strong focus on mechanistic and causal explanations, on interpretability of computational models and scientific theories, and justification of decisions and conclusions drawn from a set of assumptions.

Fig. 2.

Data Science as a discipline that transforms data into knowledge. We explicitly mark “knowledge” as an input – i.e., subject matter – of Data Science in addition to “data”; knowledge can be used as background knowledge about the problem domain, to determine whether an interpretation of data is consistent with certain assumptions, or Data Science can treat knowledge as data for its analyses. The two big arrows symbolize the integration, retro-donation, communication needed between Data Science and methods to process knowledge from symbolic AI that enable the flow of information in both directions.

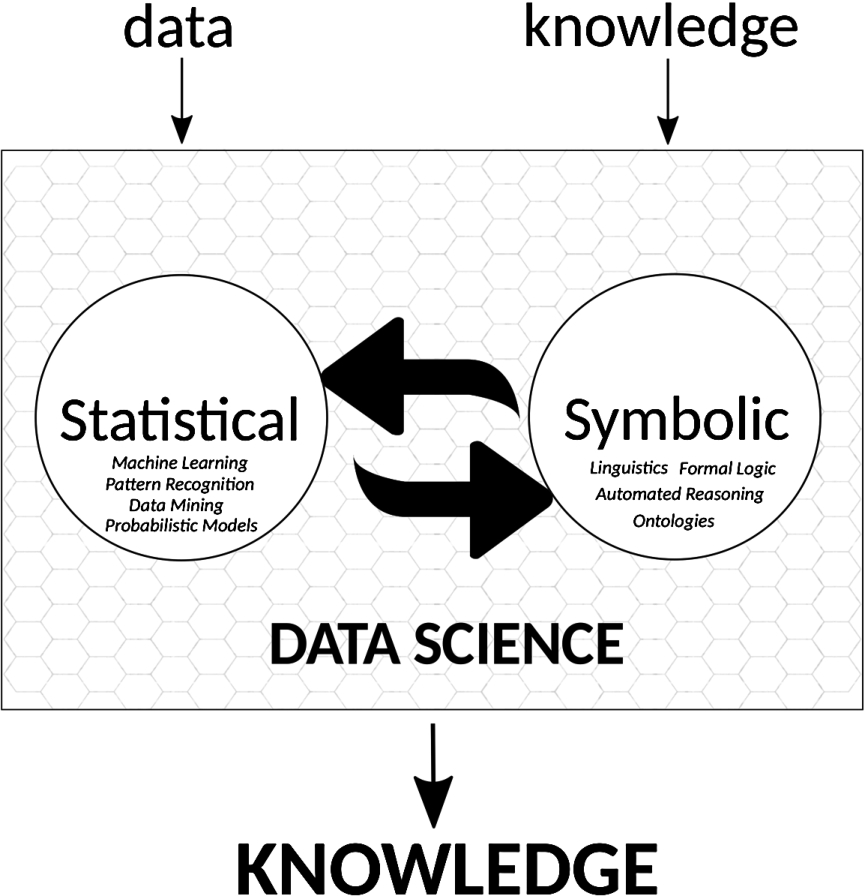
Data Science and symbolic AI are the natural candidates to make such a combination happen. Data Science can connect research data with knowledge expressed in publications or databases, and symbolic AI can detect inconsistencies and generate plans to resolve them (see Fig. 2).

3.Turning data into knowledge

In the ideal case, methods from Data Science can be used to directly generate symbolic representations of knowledge. Traditional approaches to learning formal representations of concepts from a set of facts include inductive logic programming [11] or rule learning methods [1,41] which find axioms that characterize regularities within a dataset. Additionally, a large number of ontology learning methods have been developed that commonly use natural language as a source to generate formal representations of concepts within a domain [40]. In biology and biomedicine, where large volumes of experimental data are available, several methods have also been developed to generate ontologies in a data-driven manner from high-throughput datasets [16,19,38]. These rely on generation of concepts through clustering of information within a network and use ontology mapping techniques [28] to align these clusters to ontology classes. However, while these methods can generate symbolic representations of regularities within a domain, they do not provide mechanisms that allow us to identify instances of the represented concepts in a dataset.

Recently, there has been a great success in pattern recognition and unsupervised feature learning using neural networks [39]. Feature learning (or deep learning) methods can identify patterns and regularities within a domain and thereby learn the “conceptualizations” of a domain, and it is an enticing possibility to use methods from Data Science to automatically learn symbolic representations of these conceptualizations. This problem is closely related to the symbol grounding problem, i.e., the problem of how symbols obtain their meaning [24]. Feature learning methods using neural networks rely on distributed representations [26] which encode regularities within a domain implicitly and can be used to identify instances of a pattern in data. However, distributed representations are not symbolic representations; they are neither directly interpretable nor can they be combined to form more complex representations. One of the main challenges will be in closing this gap between distributed representations and symbolic representations. This gap already exists on the level of the theoretical frameworks in which statistical methods and symbolic methods operate, where statistical methods operate primarily on continuous values and symbolic methods on discrete values (although there are several exceptions in both cases).

Recent approaches towards solving these challenges include representing symbol manipulation as operations performed by neural network [53,64], thereby enabling symbolic inference with distributed representations grounded in domain data. Other methods rely, for example, on recurrent neural networks that can combine distributed representations into novel ways [17,62]. In the future, we expect to see more work on formulating symbol manipulation and generation of symbolic knowledge as optimization problems. Differentiable theorem proving [53,54], neural Turing machines [20], and differentiable neural computers [21] are promising research directions that can provide the general framework for such an integration between solving optimization problems and symbolic representations. If they are to be successful in generating formalized theories, additional meta-theoretical properties will likely have to be incorporated as part of optimization problems; candidates of such properties include the degree of completeness of a theory [63], the degree of inconsistency [25], its parsimony (measured, for example, by the number and complexity of axioms in the theory), and coverage of domain instances.

4.Knowledge as data

Not all data that a data scientist will be faced with consists of raw, unstructured measurements. In many cases, data comes as structured, symbolic representation with (formal) semantics attached, i.e., the knowledge within a domain. In these cases, the aim of Data Science is either to utilize existing knowledge in data analysis or to apply the methods of Data Science to knowledge about a domain itself, i.e., generating knowledge from knowledge. This can be the case when analyzing natural language text or in the analysis of structured data coming from databases and knowledge bases. Sometimes, the challenge that a data scientist faces is the lack of data such as in the rare disease field. In these cases, the combination of methods from Data Science with symbolic representations that provide background information is already successfully being applied [9,27].

In the simplest case, we can analyze a dataset with respect to the background knowledge in a domain. For example, we may wish to solve an optimization problem such as minxf(x) subject to a formal theory T(Σ) over signature Σ. However, as there is no connection between f(x) and T(Σ) that can be utilized to actually constrain the optimization problem with respect to T(Σ), we need to establish a connection between the symbols in f(x) and T(Σ), for example by using an ontological commitment K [23] that assigns an interpretation of the variable and constant symbols in f(x) within T(Σ). Such an integration may make optimization problems easier to solve by eliminating certain possibilities and thereby reducing the search space. One of the greatest obstacles in this form of integration between symbolic knowledge and optimization problems is the question of how to generate or specify the ontological commitment K.

Another application of Data Science is the analysis of knowledge itself, with the aim to identify new knowledge from existing knowledge bases, for example by summarizing existing theories, identifying broad trends in existing knowledge, by generating hypotheses through analogies, or completing missing knowledge. This is already an active research area and several methods have been developed to identify patterns and regularities in structured knowledge bases, notably in knowledge graphs. A knowledge graph consists of entities and concepts represented as nodes, and edges of different types that connect these nodes. To learn from knowledge graphs, several approaches have been developed that generate knowledge graph embeddings, i.e., vector-based representations of nodes, edges, or their combinations [15,36,47,48,50]. Major applications of these approaches are link prediction (i.e., predicting missing edges between the entities in a knowledge graph), clustering, or similarity-based analysis and recommendation.

While qualitative domain data can naturally be represented in the form of a graph, conceptual knowledge is usually expressed through languages with a model-theoretic semantics [6,58] which should be taken into account when analyzing knowledge graphs containing conceptual knowledge. Specifically, theories in Description Logics [5] or first order logic will entail an infinite number of statements (their deductive closure) which should also be considered in data analysis since relevant distinguishing features may not be stated explicitly but rather be implied by axioms within a theory. For example, the fact that two concepts are disjoint can provide crucial information about the relation between two concepts, but this information can be encoded syntactically in many different ways. One option to solve this challenge could be to generate entailments in a systematic way and utilize these for analyzing knowledge graphs; alternatively, a knowledge graph can be queried whether it entails statements following a certain pattern that is deemed relevant, and these entailments can then be utilized in the analysis. For model-theoretic languages, it is also possible to analyze the model structures instead of the statements entailed from a knowledge graph. While there are usually infinitely many models of arbitrary cardinality [60], it is possible to focus on special (canonical) models in some languages such as the Description Logics ALC. These model structures can then be analyzed instead of syntactically formed graphs, and for example used to define similarity measures [13]. The statistical analysis of both entailments and the structure of models combines the strengths of symbolic AI and Data Science, where symbolic AI is used for processing knowledge through generating entailments and construction of models, and Data Science for analyzing large and possibly complex datasets resulting from these entailments.

A different type of knowledge that falls in the domain of Data Science is the knowledge encoded in natural language texts. While natural language processing has made leaps forward in past decade, several challenges still remain in which methods relying on the combination of symbolic AI and Data Science can contribute. For example, reading and understanding natural language texts requires background knowledge [34], and findings that result from analysis of natural language text further need to be evaluated with respect to background knowledge within a domain. Systems such as FRED [18] can connect natural language texts to knowledge graphs by extracting information from natural language texts and linking them to existing knowledge bases, thereby making them amenable to being combined and analyzed with methods for knowledge graph analysis. However, significant challenges still exist in connecting information from text to structured knowledge, and from structured knowledge to unstructured domain data, and, in the opposite direction, identify whether data supports or contradicts a formalized fact, or a statement in natural language.

5.Limits of Data Science

Symbolic AI and Data Science have been largely disconnected disciplines. Data Science generally relies on raw, continuous inputs, uses statistical methods to produce associations that need to be interpreted with respect to assumptions contained in background knowledge of the data analyst. Symbolic AI uses knowledge (axioms or facts) as input, relies on discrete structures, and produces knowledge that can be directly interpreted. These properties make Data Science and symbolic AI complementary disciplines, yet they also present synergies to exploit and opportunities in which both disciplines will converge; we mentioned the opportunities to combine data- and knowledge-based approaches to build and evaluate theories as well as to suggest and design new experiments, the opportunity to turn data into formal knowledge by formulating symbol manipulation as optimization problems in differentiable neural computers, and the opportunity to project background knowledge onto data, e.g., by learning from formal knowledge through knowledge graph embeddings. A key challenge that remains is to establish the formal theoretical frameworks that can span across both disciplines; while symbol manipulation is an exact method, often with formal guarantees of soundness and completeness, statistical methods are approximate and lack similar guarantees (with respect to how they are applied together with symbol manipulation). The intersection of Data Science and symbolic AI will open up exciting new research directions with the aim to build knowledge-based, automated methods for scientific discovery.

It will also be important to identify fundamental limits for any statistical, data-driven approach with regard to the scientific knowledge it can possibly generate. Some important domain concepts simply cannot be learned from data alone. For example, the set of Gödel numbers for halting Turing machines can, arguably, not be “learned” from data or derived statistically, although the set can be characterized symbolically. Furthermore, many empirical laws cannot simply be derived from data because they are idealizations that are never actually observed in nature; examples of such laws include Galileo’s principle of inertia, Boyle’s gas Law, zero-gravity, point mass, friction-less motion, etc. [49]. Although these concepts and laws cannot be observed, they form some of the most valuable and predictive components of scientific knowledge. To derive such laws as general principles from data, a cognitive process seems to be required that abstracts from observations to scientific laws. This step relates to our human cognitive ability of making idealizations, and has early been described as necessary for scientific research by philosophers such as Husserl [29] or Ingarden [30].

One of Galileo’s key contributions was to realize that laws of nature are inherently mathematical and expressed symbolically, and to identify symbols that stand for force, objects, mass, motion, and velocity, ground these symbols in perceptions of phenomena in the world. This task may be achievable through feature learning or ontology learning methods, together with an ontological commitment [23] that assigns an ontological interpretation to mathematical symbols. However, given sufficient data about moving objects on Earth, any statistical, data-driven algorithm will likely come up with Aristotle’s theory of motion [56], not Galileo’s principle of inertia. On a high level, Aristotle’s theory of motion states that all things come to a rest, heavy things on the ground and lighter things on the sky, and force is required to move objects. It was only when a more fundamental understanding of objects outside of Earth became available through the observations of Kepler and Galileo that this theory on motion no longer yielded useful results.

Inspired by progress in Data Science and statistical methods in AI, Kitano [37] proposed a new Grand Challenge for AI “to develop an AI system that can make major scientific discoveries in biomedical sciences and that is worthy of a Nobel Prize”. Before we can solve this challenge, we should be able to design an algorithm that can identify the principle of inertia, given unlimited data about moving objects and their trajectory over time and all the knowledge Galileo had about mathematics and physics in the 17th century. This is a task that Data Science should be able to solve, which relies on the analysis of large (“Big”) datasets, and for which vast amount of data points can be generated. The challenges Galileo faced were to identify that motion processes observed on Earth and the motion observed at stellar objects are essentially instances of the same concept, to identify the inconsistency between the established theory on motion and the data derived from observations of moving stellar objects, and finding a theory that is more comprehensive and predictive of both phenomena as well as supported by experimental evidence (data) in both domains or areas of observation. Identifying the inconsistencies is a symbolic process in which deduction is applied to the observed data and a contradiction identified. Generating a new, more comprehensive, scientific theory, i.e., the principle of inertia, is a creative process, with the additional difficulty that not a single instance of that theory could have been observed (because we know of no objects on which no force acts). Generating such a theory in the absence of a single supporting instance is the real Grand Challenge to Data Science and any data-driven approaches to scientific discovery.

Addressing this challenge may require involvement of humans in the foreseeable future to contribute creativity, the ability to make idealizations, and intentionality [59]. The role of humans in the analysis of datasets and the interpretation of analysis results has also been recognized in other domains such as in biocuration where AI approaches are widely used to assist humans in extracting structured knowledge from text [43]. However, progress on computational creativity [45] and cognitive computing [14], i.e., the simulation of human cognitive processes, aims to reproduce human capabilities and may contribute to further pushing the boundaries of what machines can achieve in generation of scientific theories, interpretation of data, and understanding of natural language. The role that humans will play in the process of scientific discovery will likely remain a controversial topic in the future due to the increasingly disruptive impact Data Science and AI have on our society [3].

If we ever wish to build machines that can “discover” natural laws from data and observations, we will need a revolution similar to the scientific revolution in the 16th and 17th century that resulted in the creation of the scientific method and our modern understanding of natural science. Data Science, due to its interdisciplinary nature and as the scientific discipline that has as its subject matter the question of how to turn data into knowledge will be the best candidate for a field from which such a revolution will originate.